在工程中经常会遇到结构受到冲击产生振动,从而产生结构声辐射[1, 2],但是这种声辐射过程不能被看作稳态过程。冲击激励的时间很短,随之产生的振动也随着时间慢慢衰减,声辐射也慢慢衰减。同时这种冲击激励在工程中一般不可预测,因此由冲击激励造成振动而产生的声辐射也不可预测。很多学者对冲击激励产生的瞬态声辐射进行了不少研究,Hansen等[3]采用球面传感器阵形来扫描任意形状的振源体,并对振源体在时间域内进行声场的重构,获得了较好的效果,用实验验证了用球面传感器阵形扫描任意形状振源体并重构时间域声场可行。
本文对球面瞬态声辐射重构声场的解析解进行推导,并进行数值仿真计算,在计算的过程中分别采用Tikhonov正则化方法和共轭梯度法来处理病态矩阵。结果表明,在一定的误差允许范围内,2种方法都能得到稳定的解。
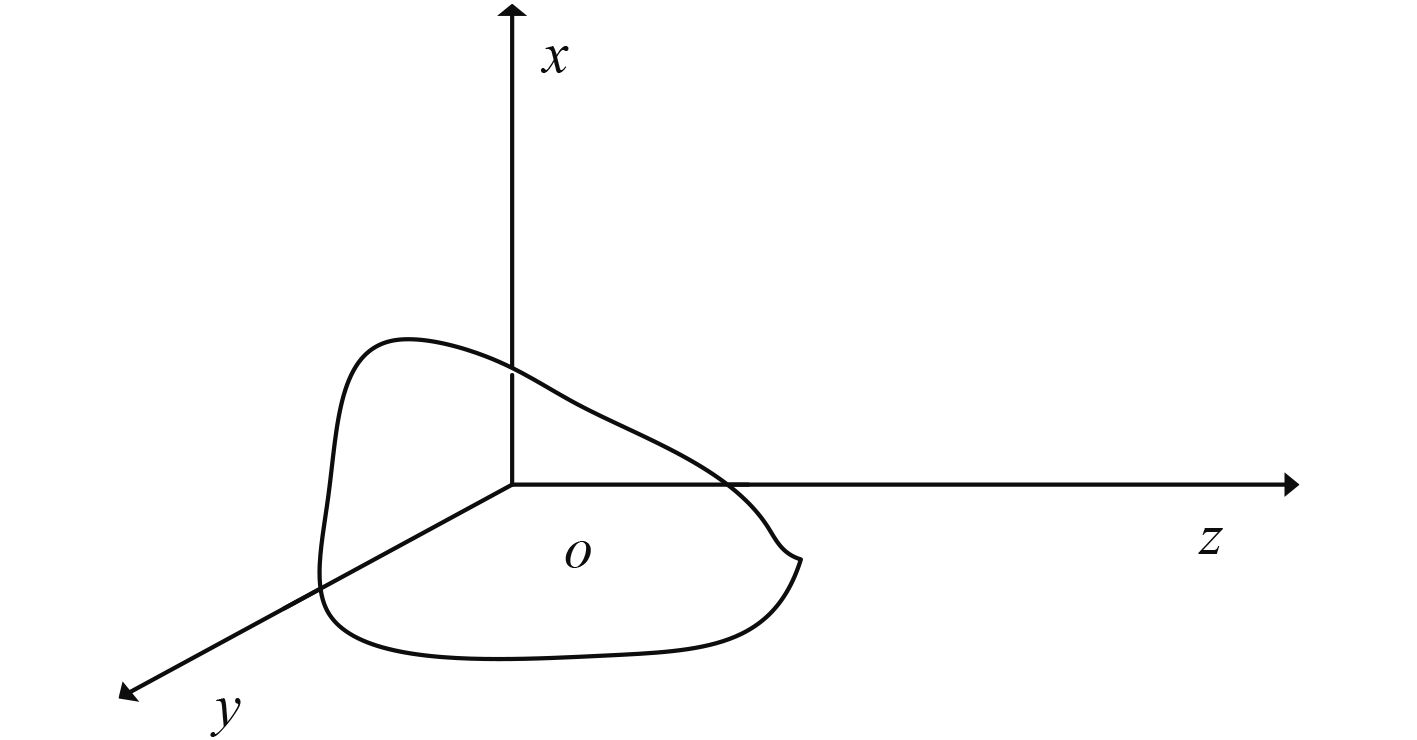
1 解析推导在空间中建立如图1所示球坐标系[4],声源位于球坐标系原点,在t=t0时刻受到激励振动发声,在t<t0前声源体处于静止状态,即
|
图 1 声源体空间分布 Fig. 1 The spatial distribution of sound source |
定义拉普拉斯变换对如下:
| $P(r,\varphi ,\theta ;s) = \int_0^\infty {p(r,\varphi ,\theta ;t){e^{ - st}}{\rm d}t} \text{,}$ | (1) |
| $p(r,\varphi ,\theta ;t) = \frac{1}{{i2π }}\int_{b - i\infty }^{a + i\infty } {P(r,\varphi ,\theta ;s)} {e^{st}}{\rm d}s\text{,}$ | (2) |
对空间中任一点时刻t的声压
| $P(r,\varphi ,\theta ;s) = \int_0^\infty {p(r,\varphi ,\theta ;t){e^{ - st}}{\rm d}t}\text{,} $ |
其中s为拉普拉斯变换的一个复变量,表示一个s平面;a表示一个很大的实数常量。a的取值需要保证变换后
在s域,
| $P(r,\varphi ,\theta ;s) = \sum\limits_{n = 0}^N {\sum\limits_{l = - n}^n {{h_n}(\beta )Y_n^l} } (\varphi ,\theta ){C_{nl}}(s)\text{,}$ | (3) |
其中
| $P({r_{zh}},{\varphi _{zh}},{\theta _{zh}};s) = \psi ({r_{zh}},{\varphi _{zh}},{\theta _{zh}};s)C(s)\text{,}$ | (4) |
其中
对方程(4)求解得到
| $C(s) = {\psi ^ + }({r_{zh}},{\varphi _{zh}},{\theta _{zh}};s)P({r_{zh}},{\varphi _{zh}},{\theta _{zh}};s)\text{,}$ | (5) |
其中
| $\begin{array}{c}{\psi ^ + }({r_{zh}},{\varphi _{zh}},{\theta _{zh}};s) = {({\psi ^H}({r_{zh}},{\varphi _{zh}},{\theta _{zh}};s)\psi ({r_{zh}},{\varphi _{zh}},{\theta _{zh}};s))^{ - 1}}\times \\ {\psi ^H}({r_{zh}},{\varphi _{zh}},{\theta _{zh}};s)\end{array}$ |
其中上标H表示矩阵的共轭转置。
可以建立全息面和声源面的声压和质点振速之间的关系:
| $\begin{split}{p_j}({r_s},{\varphi _s},{\theta _s};t) =& \displaystyle\sum\limits_{m = 1}^M {g_{jm}^p} ({r_s},{\varphi _s},{\theta _s}|{r_{zh}},{\varphi _{zh}},{\theta _{zh}};t)\times \\ &{p_m}({r_{zh}},{\varphi _{zh}},{\theta _{zh}};t)\text{,}\end{split}$ | (6) |
| $\begin{split}{v_j}({r_s},{\varphi _s},{\theta _s};t) =& \displaystyle\sum\limits_{m = 1}^M {g_{jm}^v} ({r_s},{\varphi _s},{\theta _s}|{r_{zh}},{\varphi _{zh}},{\theta _{zh}};t)\times\\& {p_m}({r_{zh}},{\varphi _{zh}},{\theta _{zh}};t)\text{,}\end{split}$ | (7) |
式中:
| $\varPhi ({r_s},{\varphi _s},{\theta _s};s) = - \frac{1}{{{\rho _0}s}}\frac{{\partial \varPsi ({r_s},{\varphi _s},{\theta _s};s)}}{{\partial {r_s}}}\text{,}$ |
式中,
对式(6)和式(7)进行反拉普拉斯变换即可求出声源面上每一点在t时刻的声压和质点振速:
| $\begin{split} {p_j}({r_s},{\varphi _s},{\theta _s};t) =& \sum\limits_{m = 1}^M {g_{jm}^p} ({r_s},{\varphi _s},{\theta _s}|{r_{zh}},{\varphi _{zh}},{\theta _{zh}};t) \\&{p_m}({r_{zh}},{\varphi _{zh}},{\theta _{zh}};t)\text{,}\end{split}$ | (8) |
| $\begin{split}{v_j}({r_s},{\varphi _s},{\theta _s};t) =& \sum\limits_{m = 1}^M {g_{jm}^v} ({r_s},{\varphi _s},{\theta _s}|{r_{zh}},{\varphi _{zh}},{\theta _{zh}};t)\\&{p_m}({r_{zh}},{\varphi _{zh}},{\theta _{zh}};t)\text{。}\end{split}$ | (9) |
其中
| $\begin{aligned}& g_{jm}^p({r_s},{\varphi _s},{\theta _s}|{r_{zh}},{\varphi _{zh}},{\theta _{zh}};t) =\\&\quad \quad\displaystyle\frac{1}{{i2π }}\int_{a - i\infty }^{a + i\infty } {G_{jm}^p} ({r_s},{\varphi _s},{\theta _s}|{r_{zh}},{\varphi _{zh}},{\theta _{zh}};s){e^{st}}{\rm d}s\text{,}\\&g_{jm}^v({r_s},{\varphi _s},{\theta _s}|{r_{zh}},{\varphi _{zh}},{\theta _{zh}};t) =\\&\quad \quad\displaystyle\frac{1}{{i2π }}\int_{a - i\infty }^{a + i\infty } {G_{jm}^v} ({r_s},{\varphi _s},{\theta _s}|{r_{zh}},{\varphi _{zh}},{\theta _{zh}};s){e^{st}}{\rm d}s\text{。}\end{aligned}$ |
对球类声源用共形的全息面测量时,
可以通过下面2式求出来[1]。
| $\begin{split}& g_{jm}^p({r_s},{\varphi _s},{\theta _s}|{r_{zh}},{\varphi _{zh}},{\theta _{zh}};t) =\\&{\left[\displaystyle\sum\limits_{q = 0}^{Q_{jm}^p - 1} \right. {\Pi _{jm}^p (s_{jm}^p} ) _q}{e^{ - {{(s_{jm}^p)}_q}t}} + \\& \quad \quad \displaystyle\sum\limits_{q = 0}^{Q_{jm}^p - 1} {\frac{{\sin \left(\omega _{jm,q}^pt + \gamma _{jm,q}^p \right)}}{{\omega _{jm,q}^p}}} \times \\& \quad \quad \left. \Pi _{jm}^p{(s_{jm}^p)_q}{e^{ - a{{_{jm,}^p}_q}t}}\right]H \left(t - {t_0} - \frac{{{r_{zh}} - {r_s}}}{c} \right)\text{。}\end{split}$ | (10) |
| $\begin{split}& g_{jm}^v({r_s},{\varphi _s},{\theta _s}|{r_{zh}},{\varphi _{zh}},{\theta _{zh}};t) =\\&{ \left[\sum\limits_{q = 0}^{Q_{jm}^v - 1} \right. {\Pi _{jm}^v(s_{jm}^v} )_q}{e^{ - {{(s_{jm}^v)}_q}t}} + \\& \quad \quad \sum\limits_{q = 0}^{Q_{jm}^v - 1} {\frac{{\sin \left(\omega _{jm,q}^vt + \gamma _{jm,q}^v \right)}}{{\omega _{jm,q}^v}}} \times \\& \quad \quad \left. \Pi _{jm}^v{(s_{jm}^v)_q}{e^{ - a{{_{jm}^v}_{,q}}t}} \right] H \left(t - {t_0} - \frac{{{r_{zh}} - {r_s}}}{c} \right)\text{。}\end{split}$ | (11) |
其中
| $\begin{aligned}&\omega _{jm,q}^p = {\mathop{\rm Im}\nolimits} {(s_{jm}^p)_q}\text{,}\\&a_{jm,q}^p = {\mathop{\rm Re}\nolimits} {(s_{jm}^p)_q}\text{,}\\&\gamma _{jm,q}^p = {\tan ^{ - 1}}( - \frac{{{\mathop{\rm Im}\nolimits} {{(s_{jm}^p)}_q}}}{{{\mathop{\rm Re}\nolimits} {{(s_{jm}^p)}_q}}})\text{,}\\&\omega _{jm,q}^v = {\mathop{\rm Im}\nolimits} {(s_{jm}^v)_q}\text{,}\\&a_{jm,q}^v = {\mathop{\rm Re}\nolimits} {(s_{jm}^v)_q}\text{,}\\&\gamma _{jm,q}^v = {\tan ^{ - 1}}( - \frac{{{\mathop{\rm Im}\nolimits} {{(s_{jm}^v)}_q}}}{{{\mathop{\rm Re}\nolimits} {{(s_{jm}^v)}_q}}})\text{。}\end{aligned}$ | (12) |
由于声学重构属于声学反问题,在数值计算的过程中矩阵的条件数比较大,很容易出现病态矩阵以及解的不稳定性,可以使用Tikhonov正则化方法或者共轭梯度法[5]来处理病态矩阵的问题。
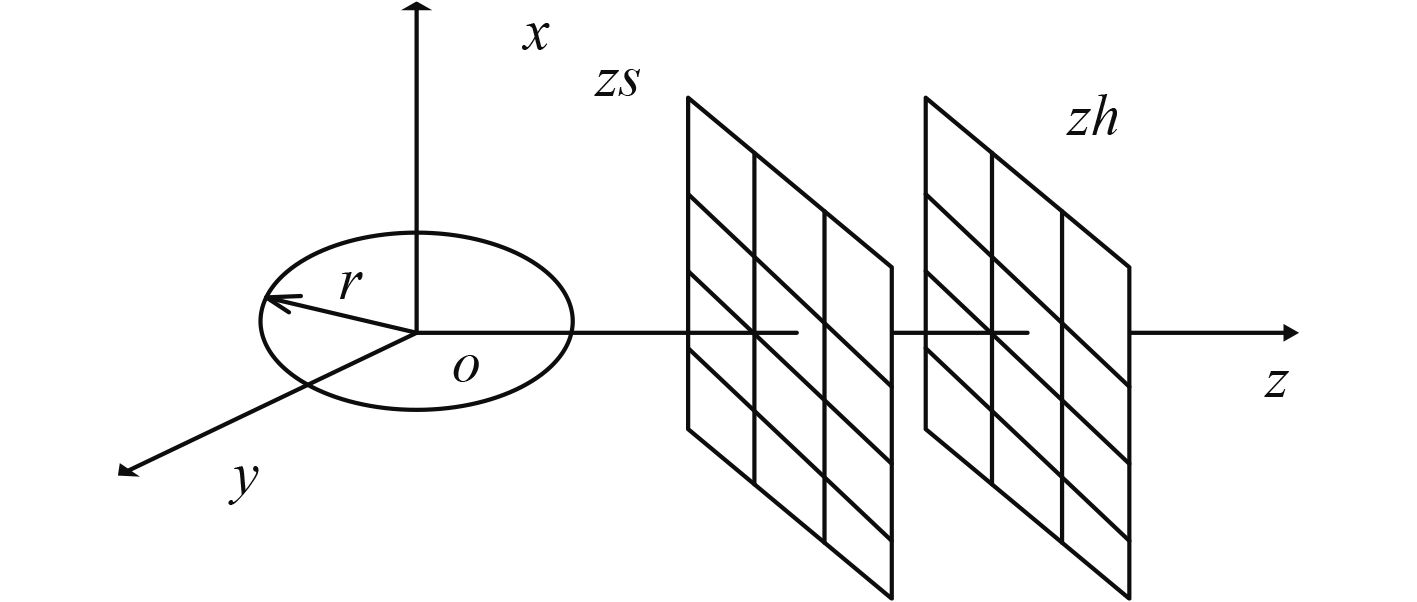
2 数值仿真为了验证算法的可行性,对自由场中球面受到冲击产生的声辐射进行声全息仿真。在声自由场中放置一半径为r的球,球心位于坐标原点建立坐标系,zh处为全息面,zs处为重构面,具体空间位置如图2所示。仿真参数如下:r=0.1 m, zh=0.05 m, zs=0.01 m, 全息面为正方形结构,Lx=Ly=1 m, 全息面上布置的传感器数为M=N=64。现给予球面一个速度冲击v=5 m/s,自由空间中任一点的声压可以用式(13)[7]表示出来:
| $\frac{{p(r,\varphi ,\theta ,t)}}{{\rho cv}} = \frac{{{r_0}{e^{ - (ct - (r - {r_0}))/{r_0}}}}}{r}H(t - \frac{{(r - {r_0})}}{c})\text{,}$ | (13) |
式中
| $H(t) = \left\{ \begin{array}{l}1\text{,}\\1/2\text{,}\\0\text{。}\end{array} \right.\begin{array}{*{20}{c}}{t > 0}\text{,}\\{t = 0}\text{,}\\{t < 0}\text{。}\end{array}$ | (14) |
|
图 2 球面瞬态声全息空间示意图 Fig. 2 Thespatial distribution of transient acoustic holography |
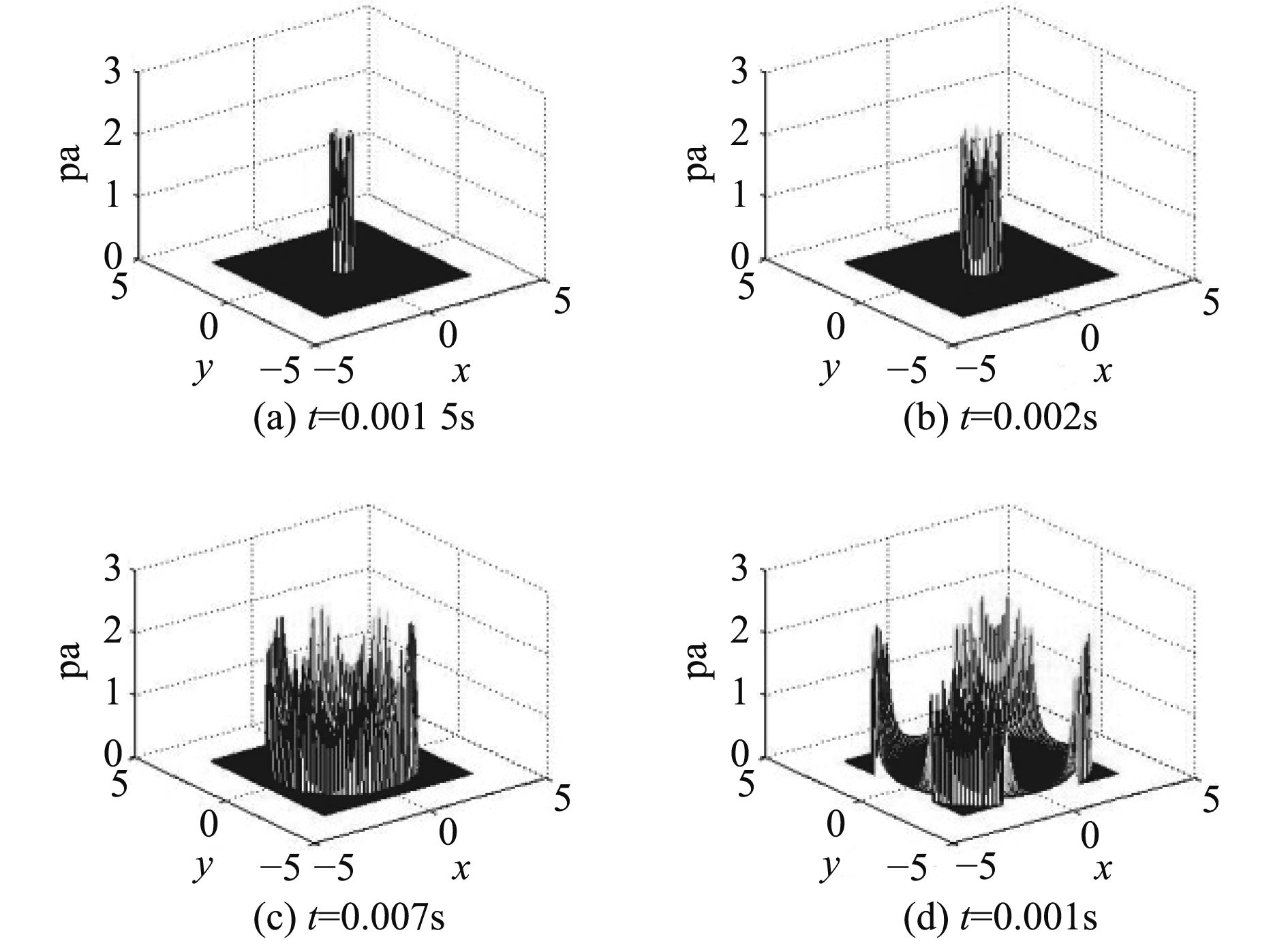
在不同时刻全息面的声压图如图3所示。
|
图 3 不同时刻全息面声压图 Fig. 3 The hologramsound pressure at different time |
从图3中可以看出由于全息面上各点与球心距离不同,球面振动辐射的声波到达全息面上各点的时间也不同,造成了同一时刻全息面上各点声压的不同。但全息面上有许多距球心的距离相等的环形带,环形带上各点在同一时刻的声压相同。随着时间的推移,环形带看起来在向外扩展,直至环形带的半径大于全息面的半径。
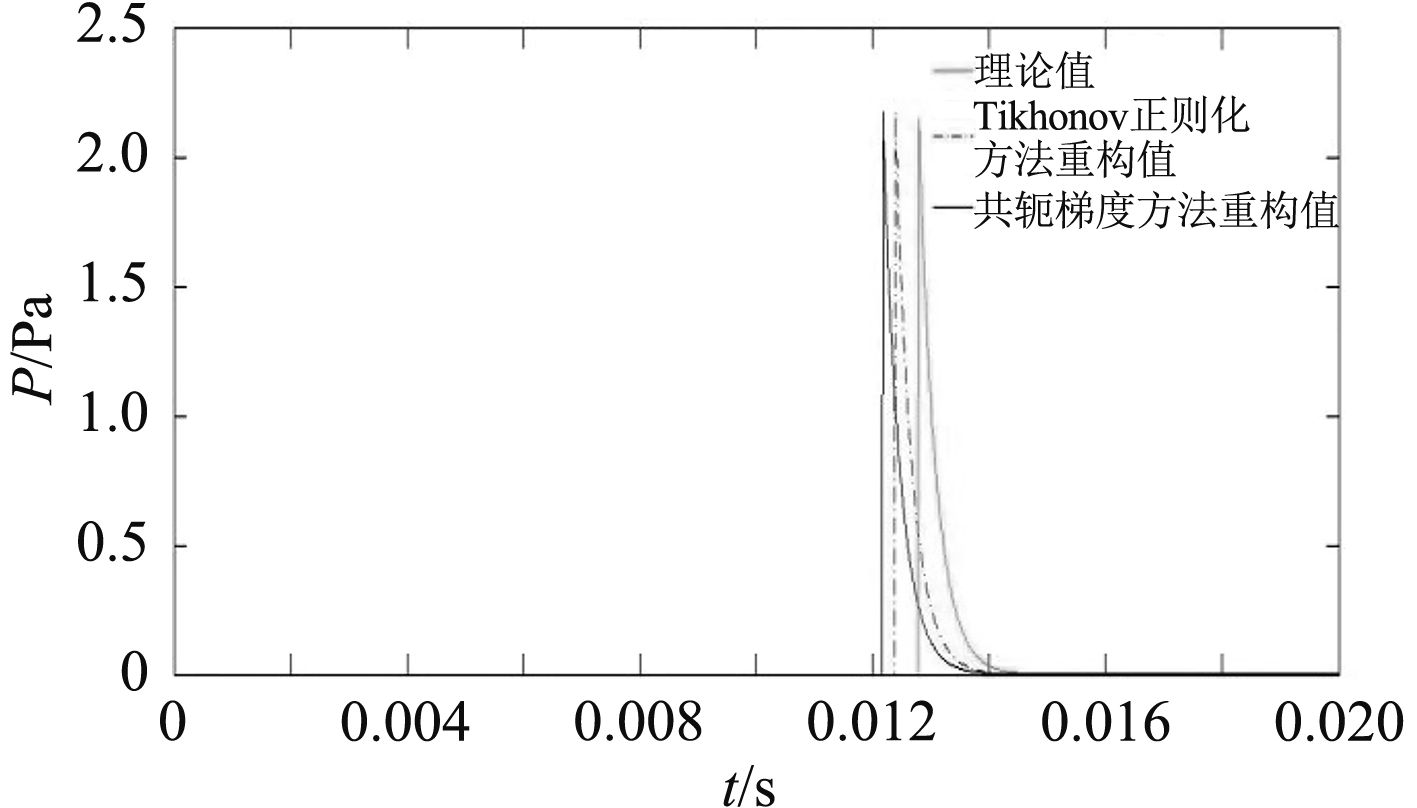
现采用球面瞬态声全息方法在重构面处重构声源,并用Tikhonov正则化方法或者共轭梯度法来稳定得到的解。选取重构面对角和中间各2点的声源随时间变化关系来说明问题。
|
图 4 第(1, 1)个传感器声压随时间变化图 Fig. 4 The pressure changes over time for sensor No.(1. 1) |
|
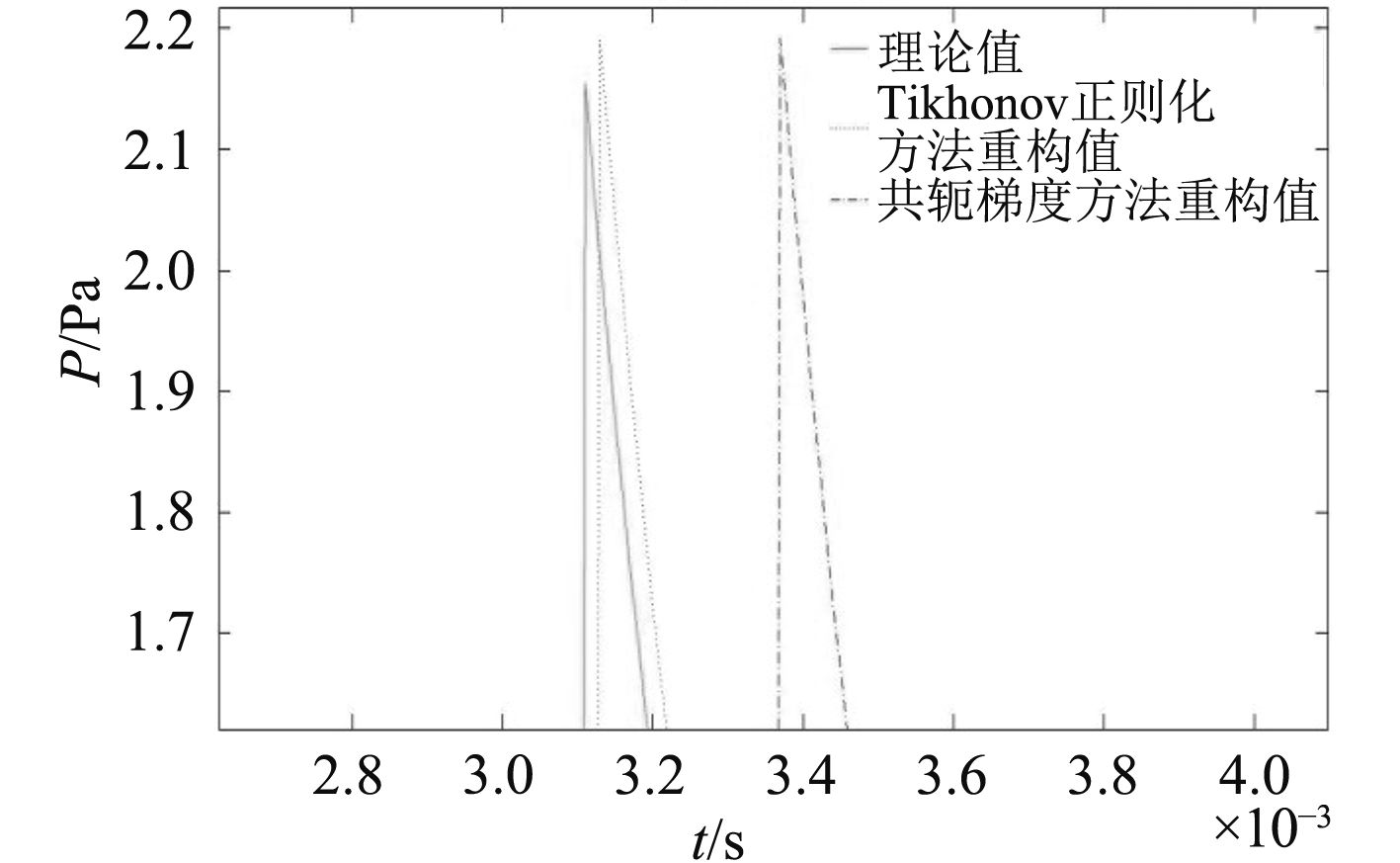
图 5 第(32, 22)个传感器声压随时间变化图 Fig. 5 The pressure changes over time for sensor No.(32.22) |
|
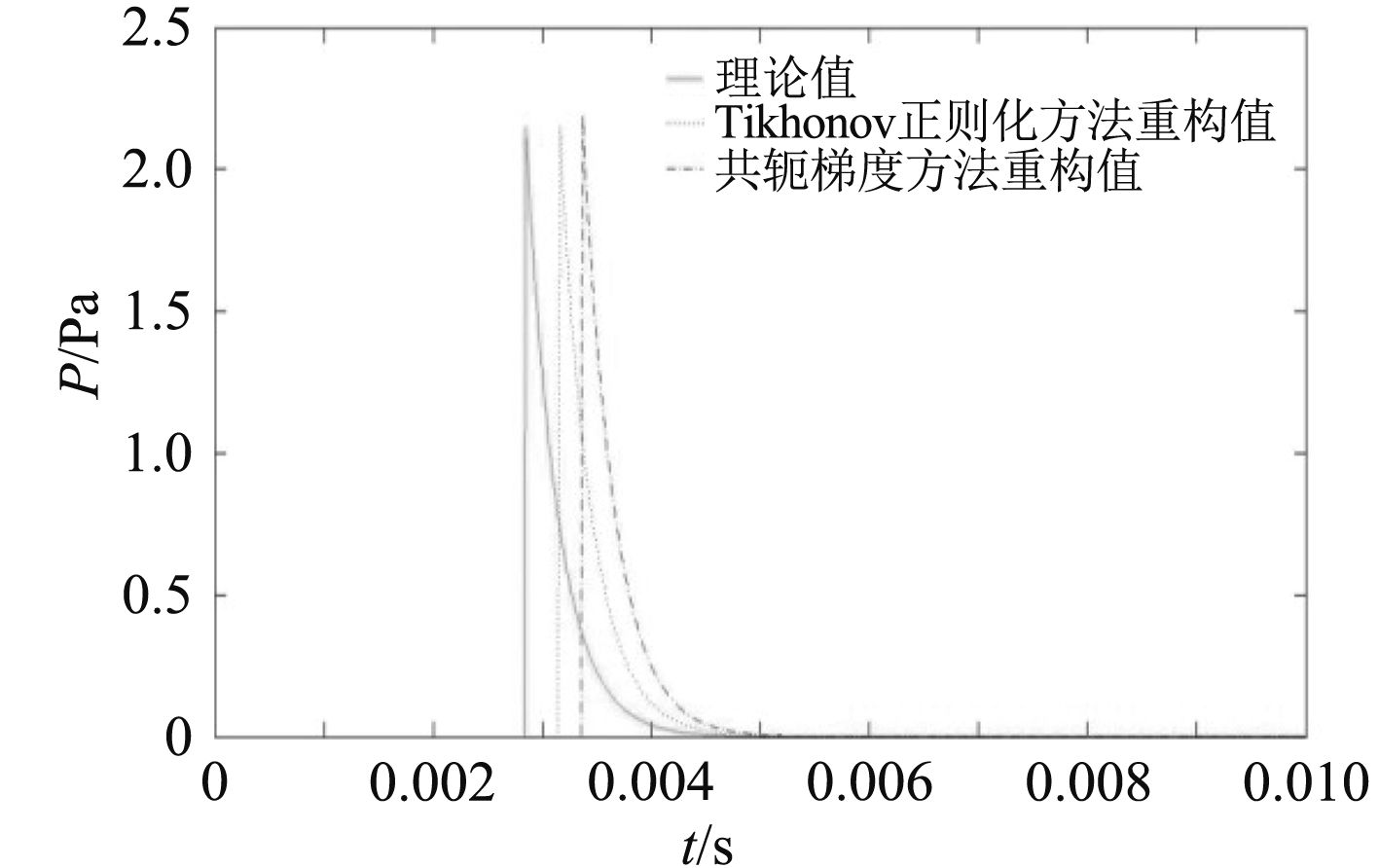
图 6 第(42, 33)个传感器声压随时间变化图 Fig. 6 The pressure changes over time for sensor No.(42.33) |
|
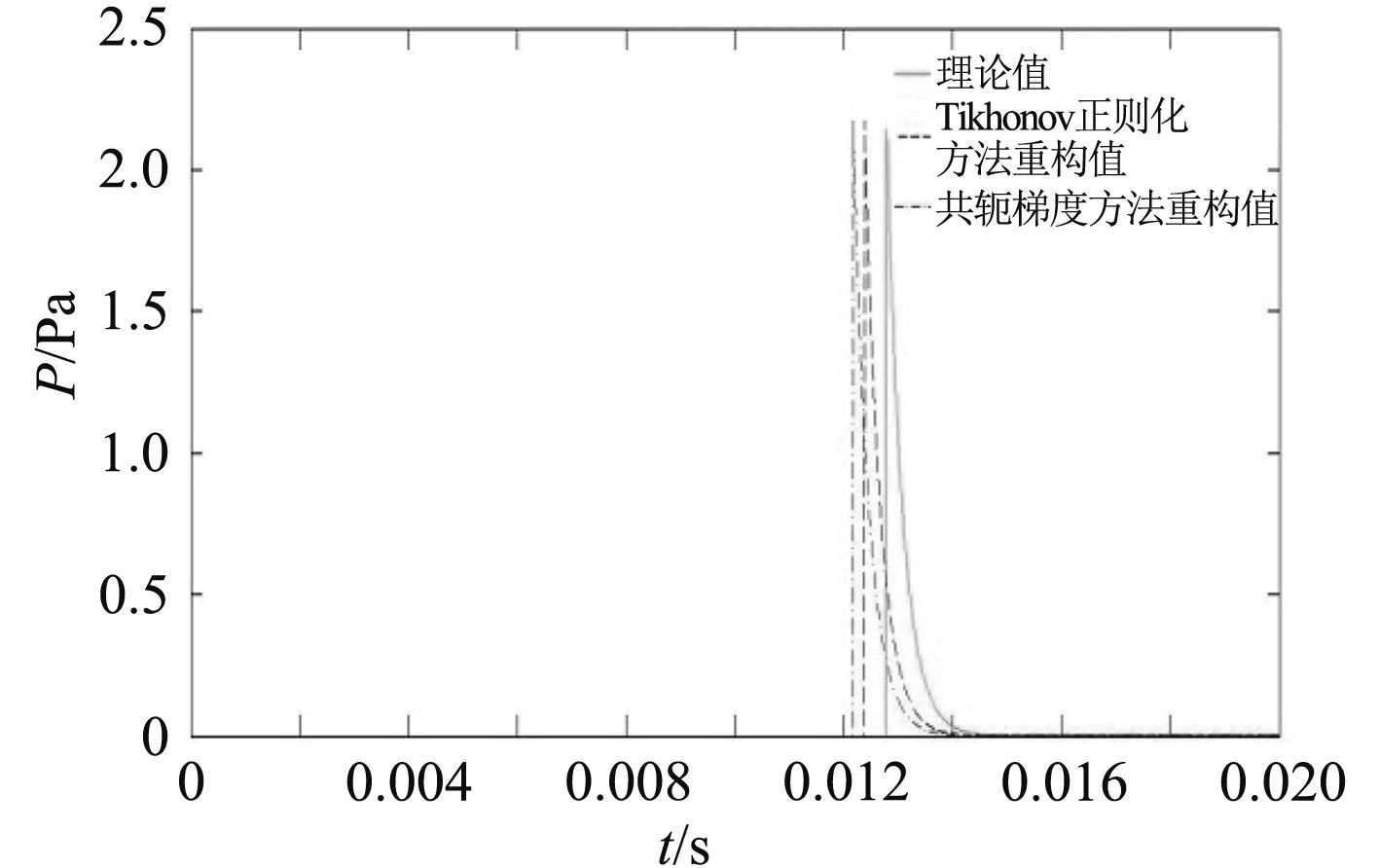
图 7 第(64, 64)个传感器声压随时间变化图 Fig. 7 The pressure changes over time for sensor No.(64.64) |
从图4~图7中可以看出采用Tikhonov正则化方法和共轭梯度法都能较准确地重构出在重构面处各传感器的瞬时声压,从选取点的声压随时间变化曲线看,Tikhonov正则化方法的重构值更加接近于理论值。
3 误差分析由于解析解认为全息面无限大,获取全息面数据的时间无限长,并且全息面上的数据连续,这和实际重建过程相差笔较大[6]。误差主要来源于全息面对数据采样的加窗效应(包括空间加窗和时间加窗)和数据离散化。下面比较通过2种方法进行重构时的误差大小,重构误差可以用下式计算出来:
| $error = \frac{{||{p_{{\text{重构}}}}{\rm{ - }}{p_{{\text{理论}}}}{\rm{||}}}}{{{\rm{||}}{p_{{\text{理论}}}}{\rm{||}}}} \times 100{\rm{\% }}\text{。}$ | (15) |
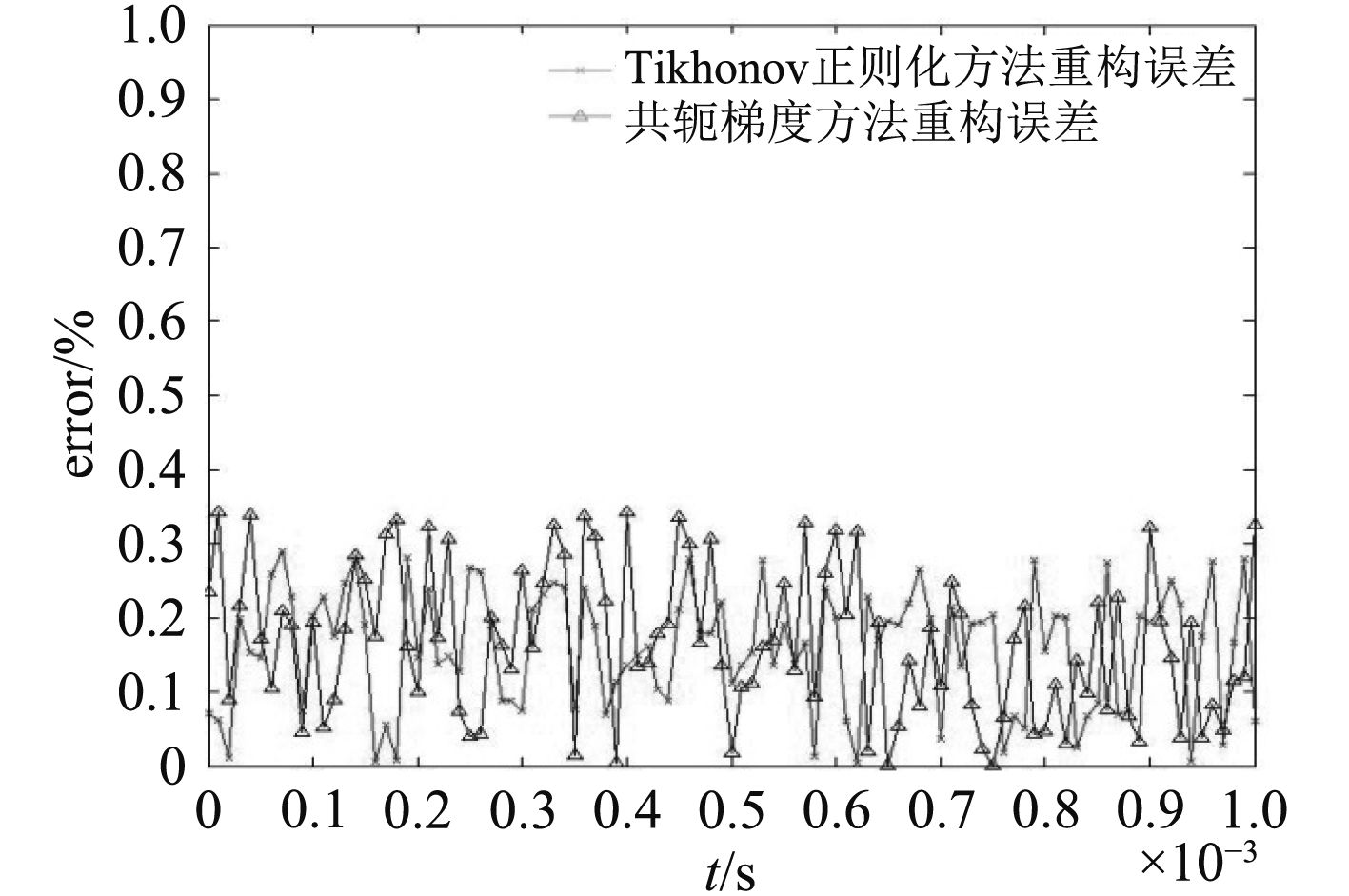
重构误差随时间变化的曲线如图8所示。
|
图 8 两种方法重构误差分布图 Fig. 8 The reconstruction error distribution of two methods |
从图8中可以看出,采用Tikhonov正则化方法和共轭梯度方法都较好地解决病态矩阵的问题,从而获得稳定的解,两者的误差都分布在35%内。在误差允许范围内采用上述任何一种方法都可以获得较精确的解。
4 结 语本文对文献[4]中提出的方法采用Tikhonov正则化方法和共轭梯度方法对球面瞬态的声辐射进行了声全息重构数值仿真计算。数值仿真结果与理论值对比表明,采用Tikhonov正则化方法和共轭梯度方法在进行声辐射的逆运算过程中都能有效应对矩阵病态的问题,得到稳定的解。
| [1] |
毛荣富, 朱海潮, 陈志敏. 基于近场声全息的空压机噪声源识别[J]. 海军工程大学学报, 2011, 23(1): 59–62.
MAO Rong-fu, ZHU Hai-chao, CHEN Zhi-min. Noise source identification and decomposition of air compressor based[J]. The Jonrnal of Naval University of Engineering, 2011, 23(1): 59–62. http://d.wanfangdata.com.cn/Periodical/hjgcdxxb201101012 |
| [2] |
张海滨, 蒋伟康, 万泉. 压缩机噪声的跟踪采样近场声全息实验研究[J]. 振动与冲击, 2010, 29 (11): 51–54.
ZHANG Hai-bin, JIANG Wei-kang, WAN Quan. The experimental study of near-field acoustic holography about the tracking sampling noise compressor[J]. Vibration and Impulse, 2010, 29 (11): 51–54. DOI: 10.3969/j.issn.1000-3835.2010.11.012 |
| [3] | T. Spherical expansions of time-domain acoustic fields: Application to near-field scanning[J]. acoustical society of America, 1995, 98 : 1204–1215. DOI: 10.1121/1.413619 |
| [4] | Seanf, et al. Reconstruction of transient acoustic radiation from a sphere[J]. acoustical society of America, 2005, 117 : 2065–2077. DOI: 10.1121/1.1841771 |
| [5] | Earl G. Regularization methods for near-field Acoustical holography[J]. acoustical society of America, 2001, 110 (4): 1976–1988. DOI: 10.1121/1.1404381 |
| [6] | 张小正, 毕传兴. 瞬态近场声全息理论和实验研究[D]. 合肥: 合肥工业大学, 2012. |
| [7] | MORSE P. M, INGARD K. U. Theoretical acoustics[M]. Princeton University Press, Princeton, NJ, 1986. |
 2017, Vol. 39
2017, Vol. 39
