2. 船舶振动噪声重点实验室,湖北 武汉 430033
2. National Key Laboratory on Ship Vibration and Noise, Wuhan 430033, China
随着舰船声隐身技术和抗冲击要求的提高,橡胶减振器在舰船设备上得到大量应用[1]。橡胶减振器以橡胶材料为弹性体(减振结构),会不可避免的存在减振性能随橡胶材料性能逐渐退化而退化的现象[2–4]。性能大幅退化甚至损坏的橡胶减振器不仅不能起到隔振作用,甚至会因为减振器的蠕变、疲劳等形态变化造成被隔振系统脱离正常工位,进而损坏设备,因此需要开展橡胶减振器在工作载荷下的可靠性研究,而最直接的路径就是通过提取橡胶减振器的动态载荷谱,编制可靠性试验的实验室载荷谱,为进一步开展橡胶减振器的随机振动试验和仿真研究提供数据支撑[5–7]。
施加在振动设备或软件上的载荷谱是橡胶减振器的输入随机激励的功率谱密度,随机信号的功率谱密度分析是获得振动台随机振动试验载荷谱的主要途径之一,随机信号的功率谱密度给出了随机信号能量在频率域的分布,能够直接施加在振动台或仿真分析软件上[8–9]。因此,为了开展橡胶减振器的随机振动试验或随机振动仿真,首先需要进行随机信号的功率谱密度分析。
1 原始信号分析与预处理 1.1 实采随机振动信号本文分析的实采信号为某舰用回转型机械设备隔振系统机角处橡胶减振器上下端的随机振动加速度信号。
|
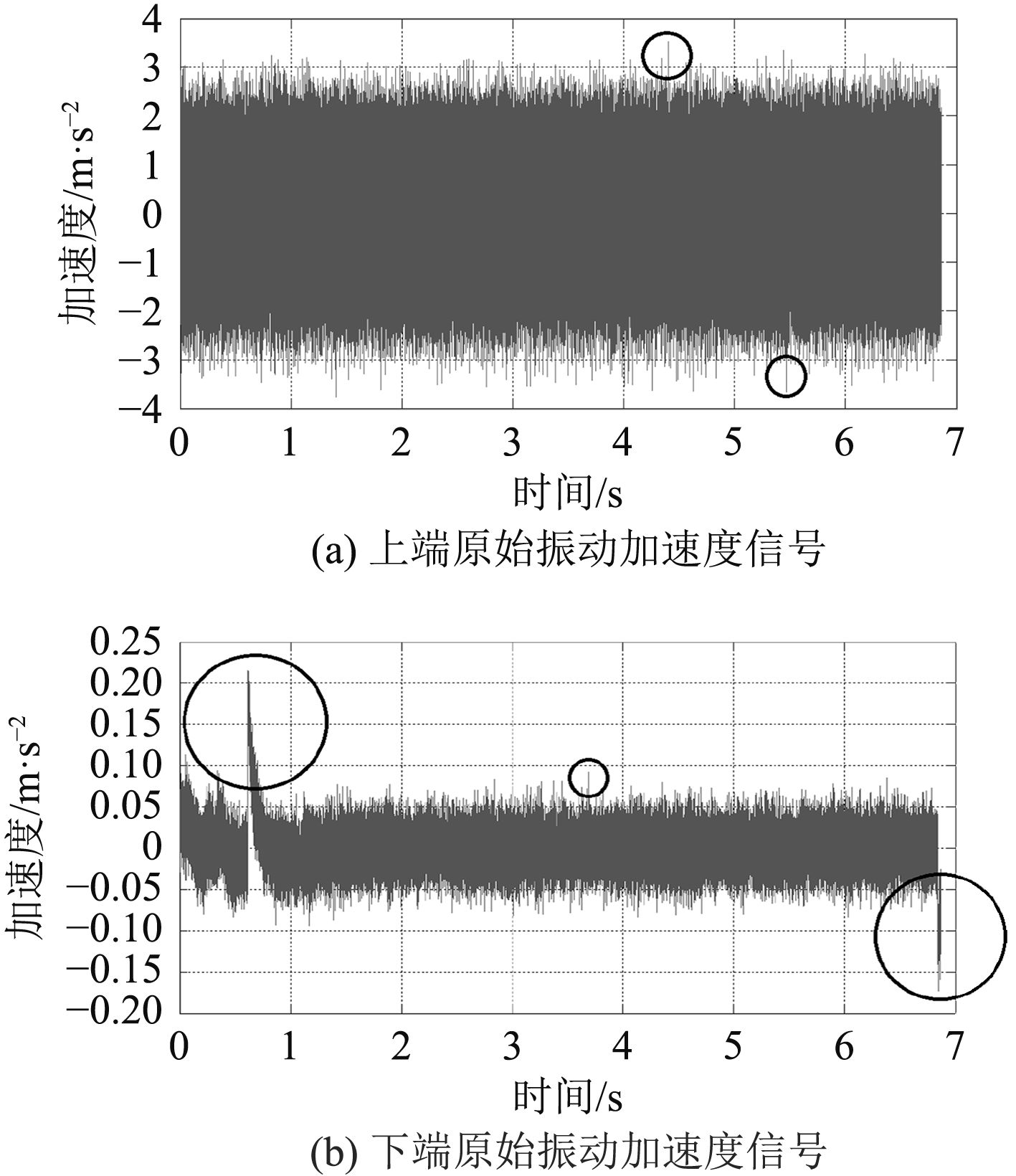
图 1 原始振动加速度信号 Fig. 1 The original vibration acceleration signal |
图1中黑色圆圈内是原始信号的奇异值及毛刺现象,从图中看不出明显的趋势项。由于整个振动信号采集系统线路绕经柴油机、起动机等电、磁、热较为集中的部位, 在测试过程中, 这些因素会对系统采集的信号造成一定干扰。在开展输入激励功率谱密度计算前需对所采信号进行预处理。
1.2 信号预处理根据原始信号特征,对其进行去奇异值、去直流分量、平滑化去毛刺以及去趋势项处理,下面介绍对原始信号进行预处理的各步骤的方法及处理结果。
1.2.1 去奇异值处理载荷谱信号中的奇异点是指信号数据的变化不符合正常变化规律发生的突变现象, 通常奇异点的产生与信号的测量、记录、模数转换及传输过程中的干扰和偶然因素有关。通常可采用拉依达方法去除奇异值。该方法的思想是,如果某测量值与平均值之差大于标准偏差的3倍,则予以剔除,其表达式如下
| $\left| {{x_i} - \bar x} \right| > 3{S_x}\text{,}$ | (1) |
式中:
其Matlab实现的程序段为:
w=3;
yichang=abs(x-mean(x))>w*std(x);
x(yichang)=[];
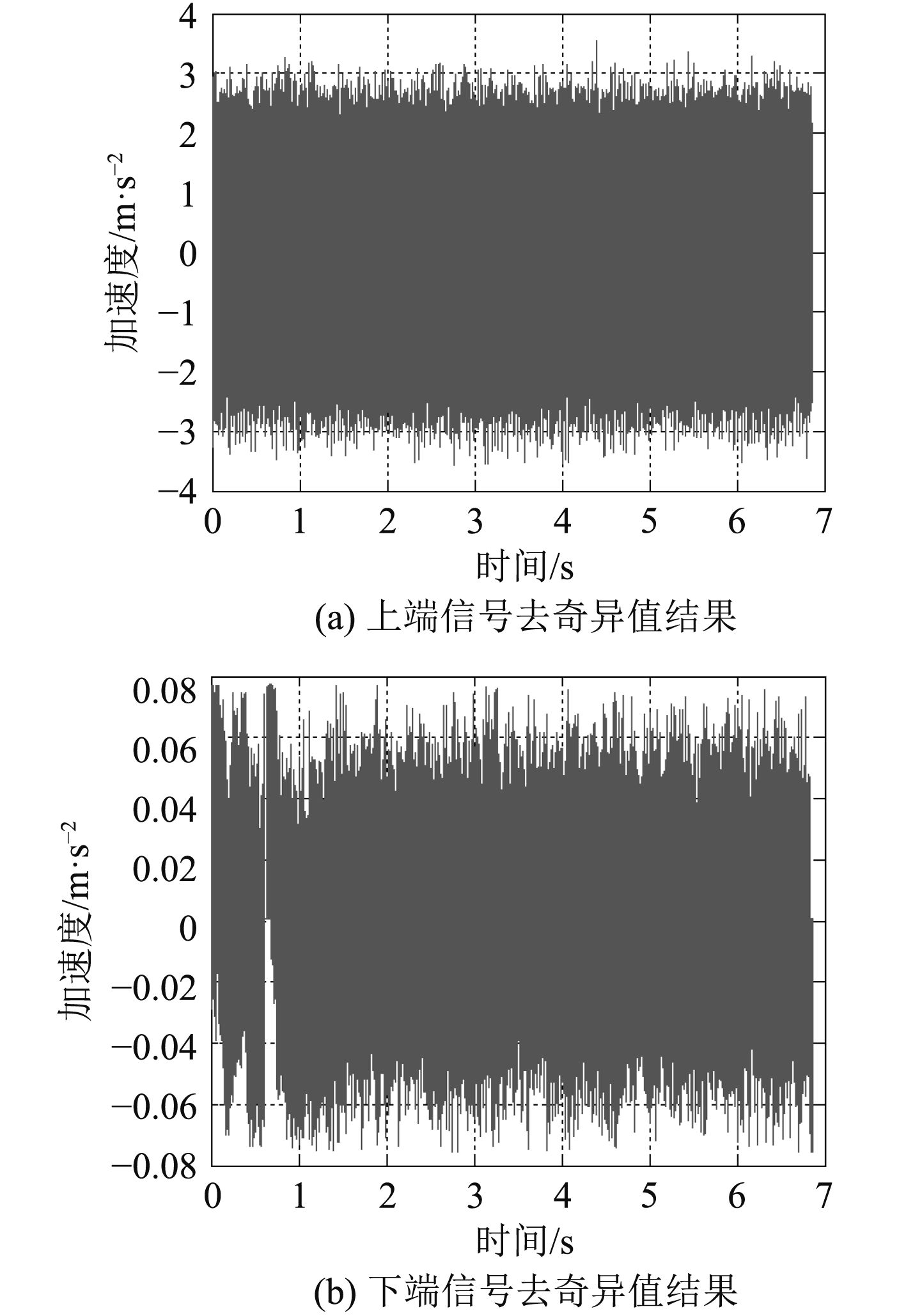
对减振器上端和下端原始信号去奇异值处理后结果如图2所示。
|
图 2 原始振动信号去奇异值结果 Fig. 2 Singular value wiping result of the original signal |
载荷谱信号中的直流成分称作直流分量,去除直流分量的思路是用样本值减去样本均值即可。
本文中减振器上端振动信号的直流分量为1.0613E–004,下端为2.9181E–006, 单位均是m/s2。
1.2.3 平滑化去毛刺在多路信号变化的瞬间,组合逻辑的输出常常产生一些小的尖峰,即毛刺信号。平滑化去毛刺的处理方法通常是对信号进行多次的平滑处理。
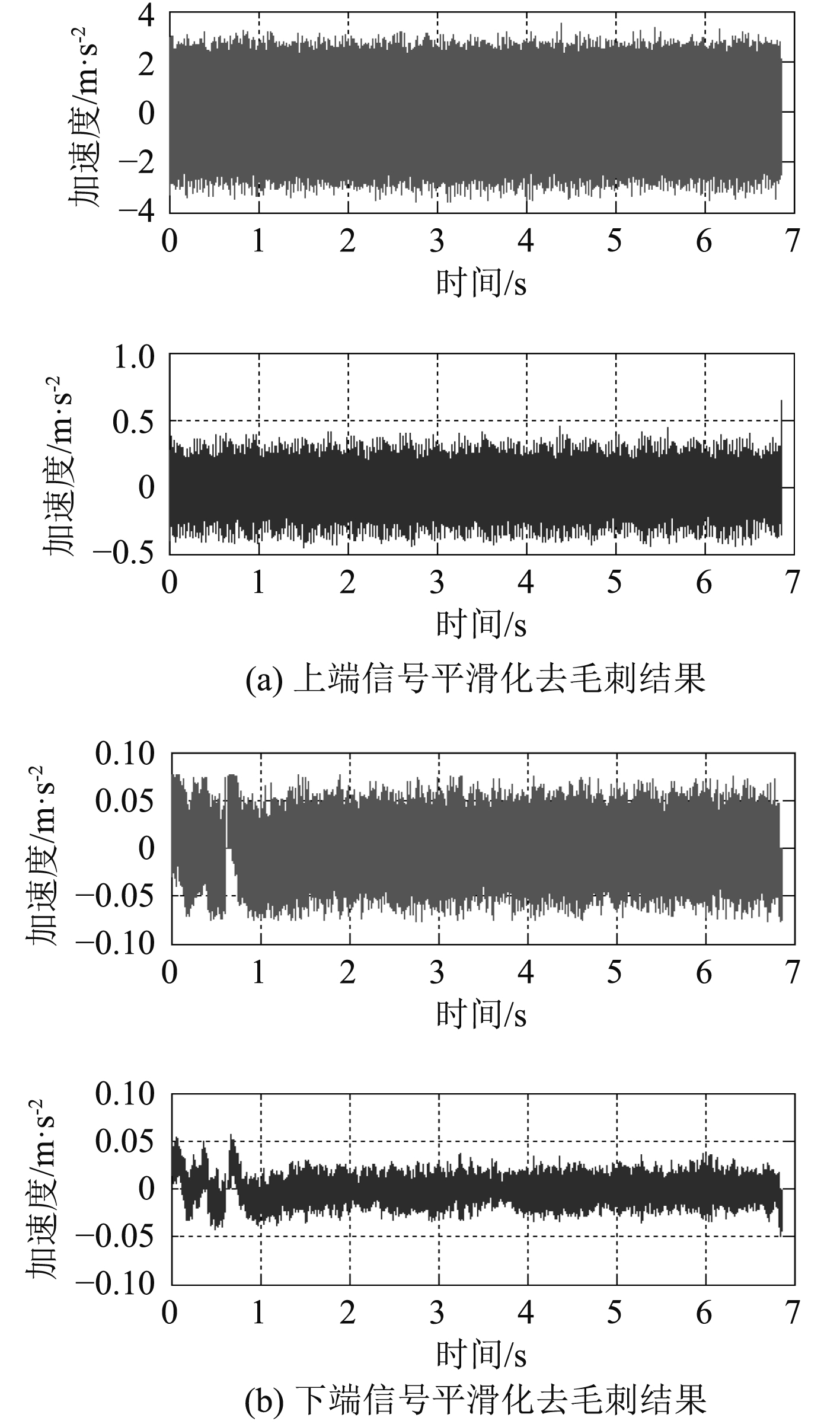
对减振器上端和下端原始信号平滑化去毛刺处理后结果如图3所示。
|
图 3 原始振动信号平滑化去毛刺结果 Fig. 3 Smoothing and burring result of the original signal |
图3中浅色是去奇异值之后的信号,深色是平滑去毛刺后的信号。对比可见,上端信号经过光滑处理后,幅值有大幅下降,这说明光滑处理后信号失真,所以不做光滑处理;下端信号中幅值超过0.05部分的毛刺已经被光滑处理。
1.2.4 去趋势项通常采集的加速度信号中含有长周期趋势项,在对数据进行二次积分时得到的结果可能完全失真,因此需消除长周期趋势项。其Matlab实现方法简单,但是需选取合适的拟合多项式阶数,本文选取的阶数是8阶。
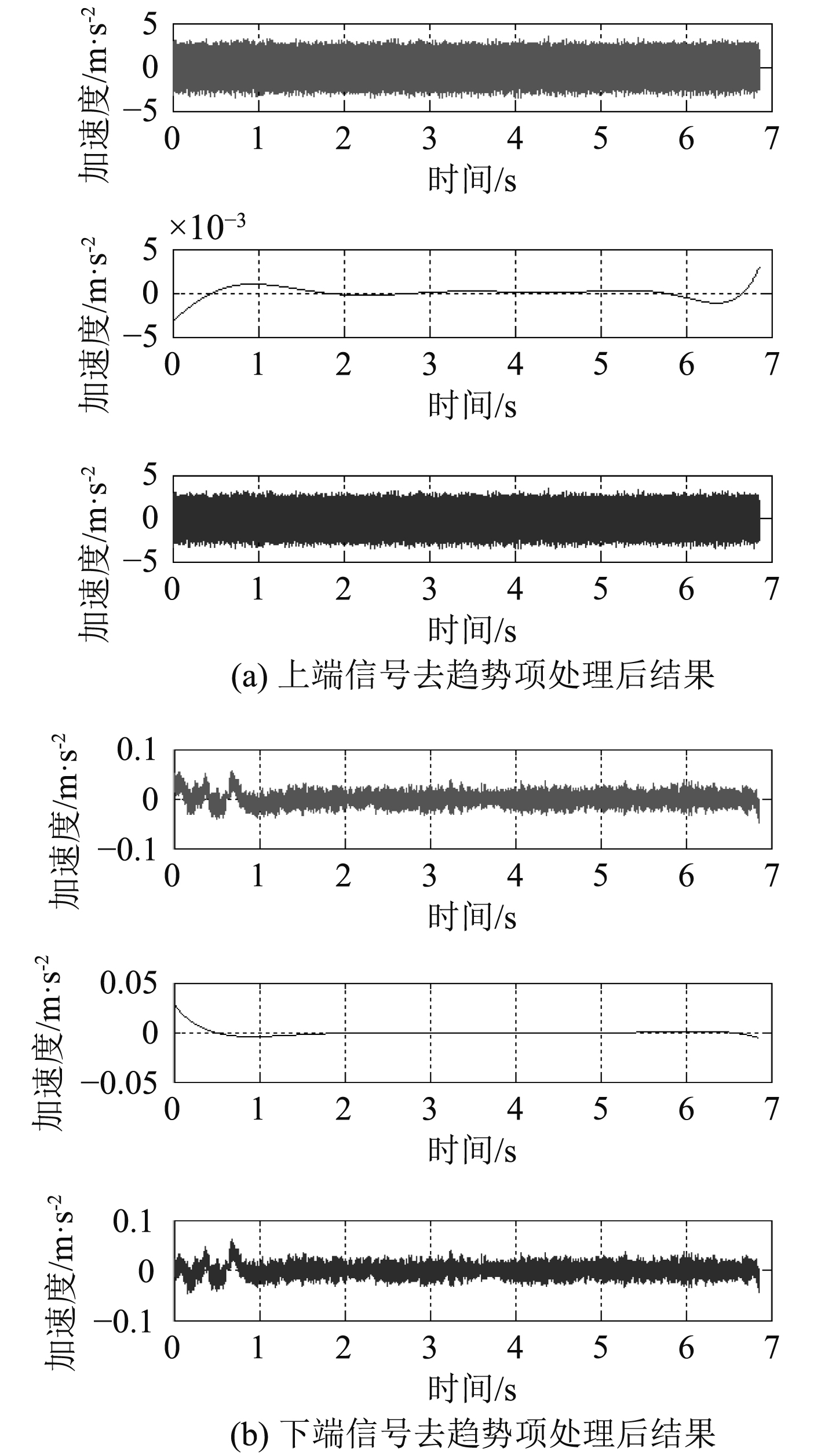
对减振器上端和下端原始信号去趋势项处理后结果如图4所示。
|
图 4 原始振动信号去趋势项处理后结果 Fig. 4 Trend item wiping result of the original signal |
由图4可见,上端振动信号趋势项较小,下端振动信号趋势项较为明显。
2 频谱分析与滤波在振动信号采集时,为全面获取被测点振动信息,通常设置较高的采样频率(如25.6 kHz),但对于实际振动而言,在开展载荷谱提取和编制时需要根据振动工况进行滤波分析,保留主要频段内的振动信号。具体采用何种滤波方式及滤波范围需通过选用低通滤波、带通滤波、高通滤波的方法分别在不同的滤波范围对数据进行滤波处理, 对比滤波前后及不同滤波频带滤波效果进行确定。
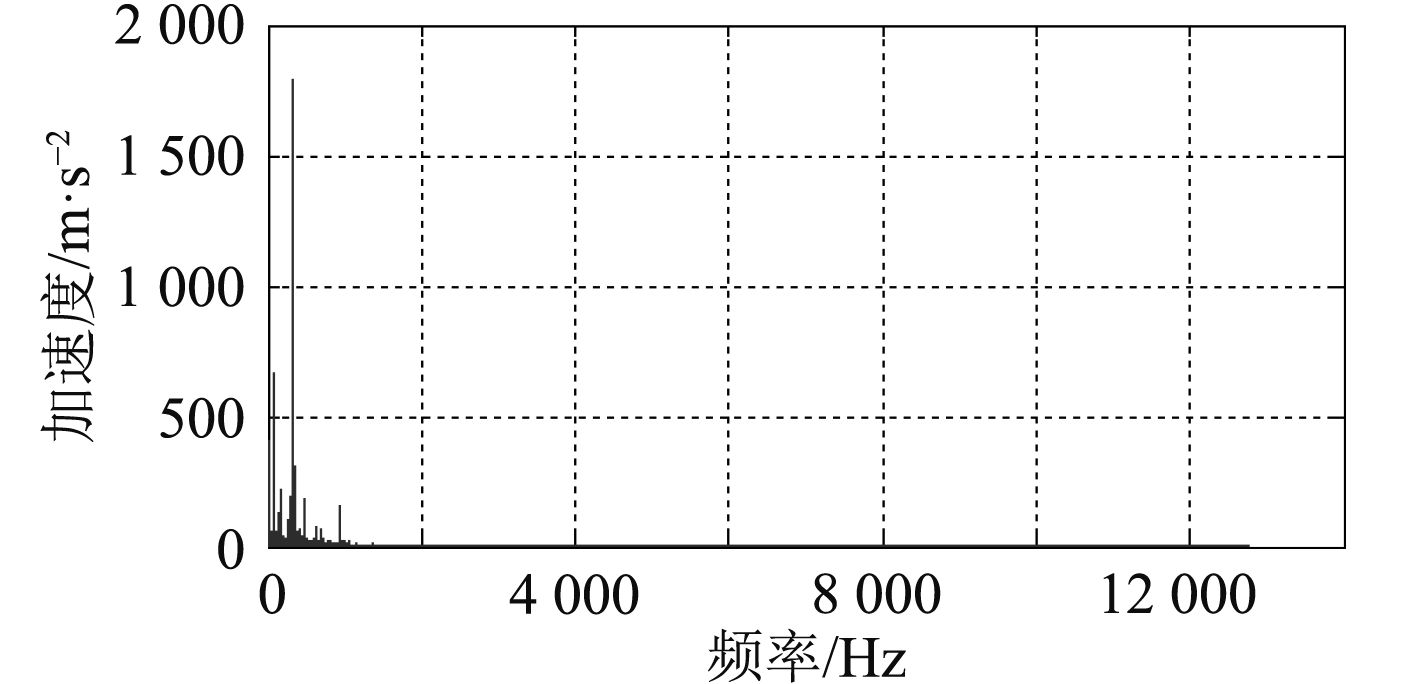
2.1 下端信号频谱分析与滤波首先对下端信号进行频谱分析,频谱分析结果如图5所示。
|
图 5 下端信号频谱分析结果 Fig. 5 Spectral analysis result of the downside signal |
由频谱分析结果可以看出,频谱主要集中在0~1 000 Hz,结合产品使用工况的分析,设备电机转速主耍集中在1 000~3 000 r/min,其的扭振频率主要分布在30~100 Hz范内,对于动载系中其他重要动载荷频率主要分布在10~1 000 Hz范内,高于1000 Hz的信号为干扰信号。因此可对信号进行0~1 000 Hz,1 000~15 000 Hz带通滤波。滤波结果对比如图6所示。

|
图 6 下端信号带通滤波结果 Fig. 6 Band-pass filtering result of the downside signal |
由图可以看出0~1 000 Hz滤波后,幅值没有明显变化,1 000~15 000 Hz带通滤波幅值大幅度减小,因此,首先滤波范围首先选择0~1 000 Hz带通滤波,在消除1 000 Hz以上干扰信号的同时,较完整的保留了原信号的能量。
接着对信号进行0~10 Hz,10~1 000 Hz带通滤波,滤波结果如图7所示。

|
图 7 下端信号低频带通滤波结果 Fig. 7 Low frequency band-pass filtering result of the downside signal |
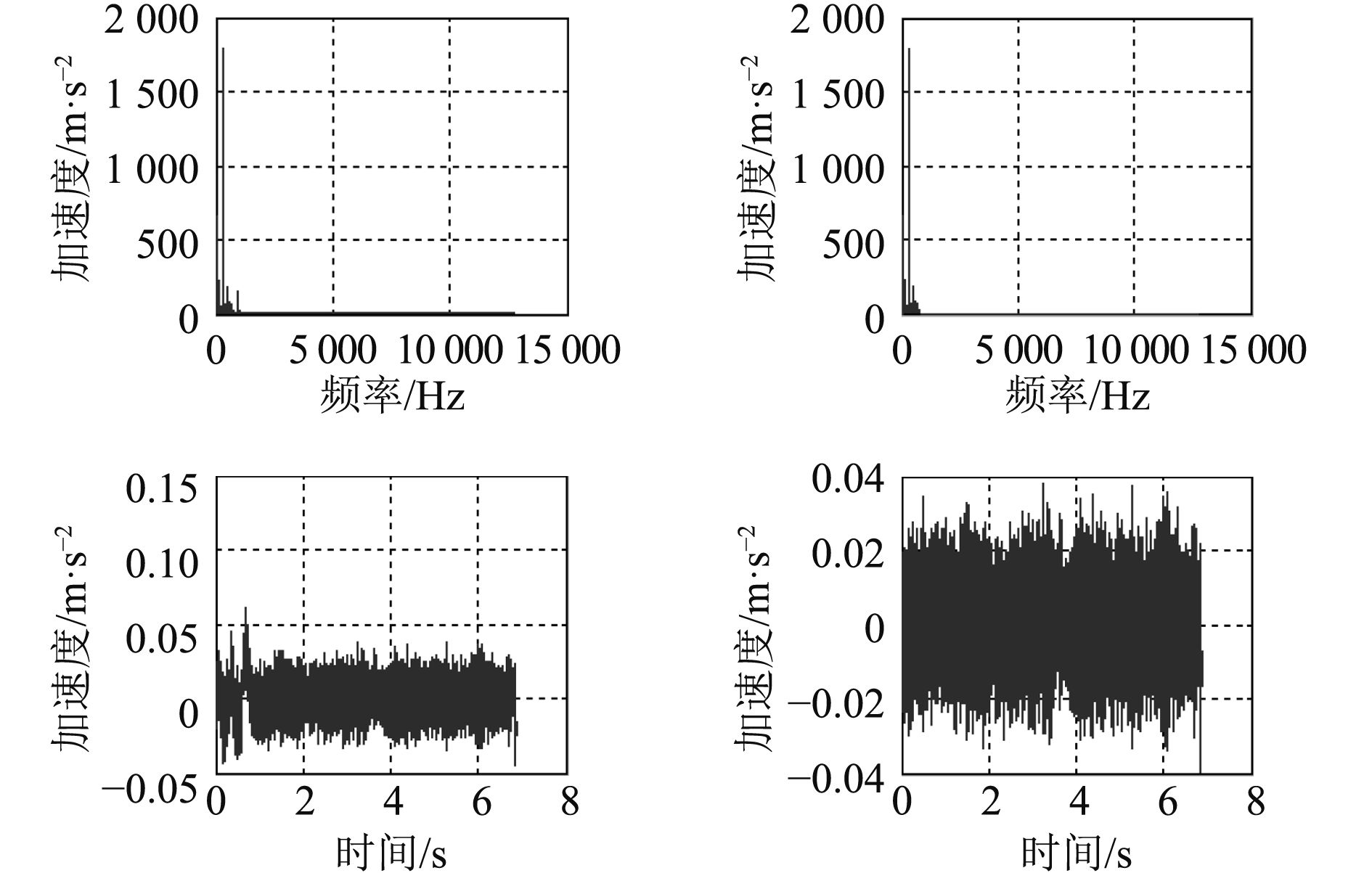
由图7可以看出0~10 Hz带通滤波后,带通滤波幅值大幅度减小,10~1 000 Hz幅值没有明显变化,因此,滤波范围选择10~1 000 Hz带通滤波,在消除10 Hz以下干扰信号的同时,较完整的保留了原信号的能量。如此往复,最终确定滤波范围为10~800 Hz带通滤波。滤波结果如图8所示。
|
图 8 下端信号10~800 Hz带通滤波结果 Fig. 8 10~800 Hz band-pass filtering result of the downside signal |
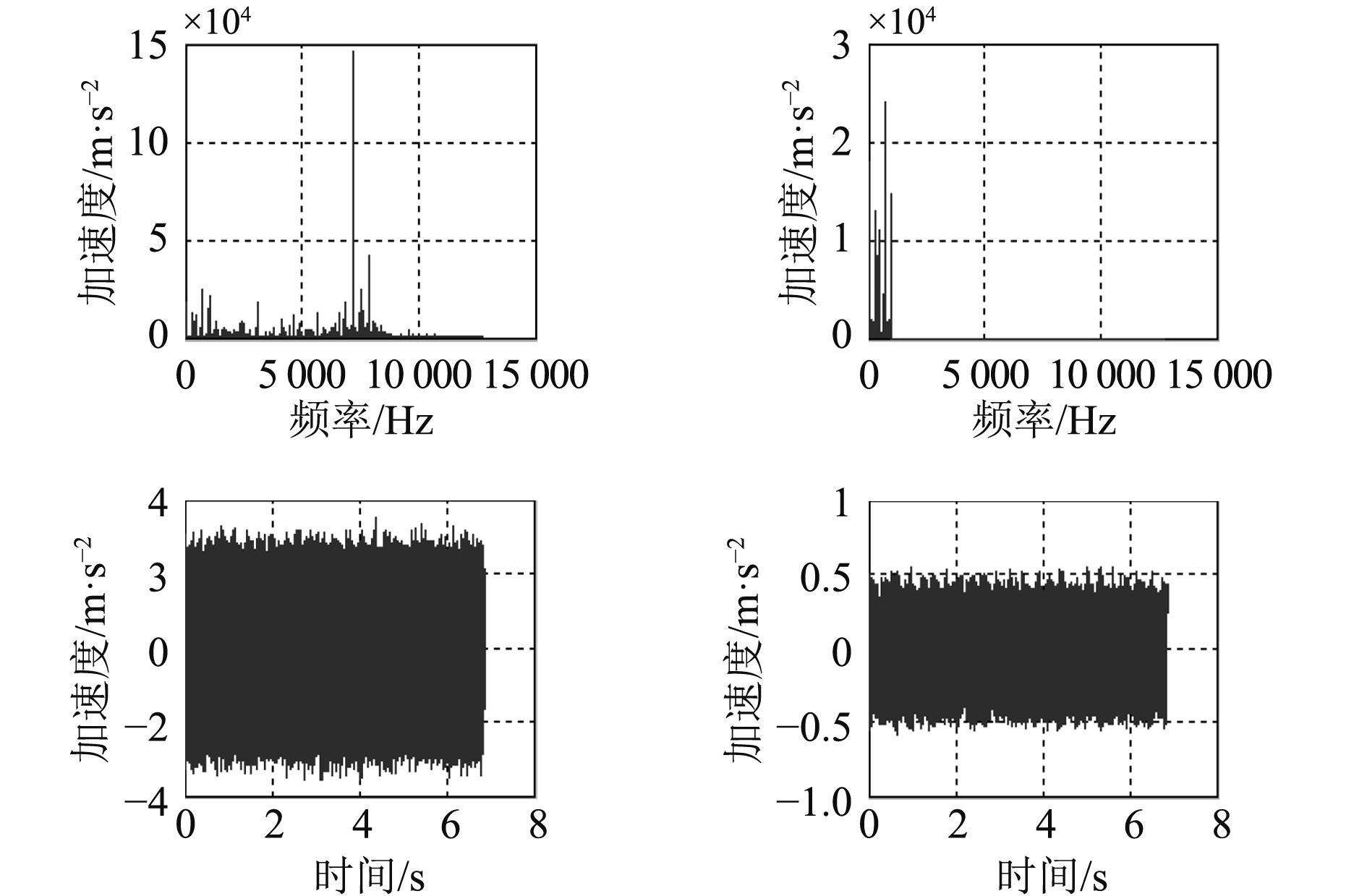
上端信号频谱分析及滤波方式和下端信号类似,首先进行频谱分析,然后对信号进行0~1 000 Hz带通滤波。滤波结果对比如图9所示。
|
图 9 上端信号0~1 000 Hz带通滤波结果 Fig. 9 0~1 000 Hz band-pass filtering result of the upside signal |
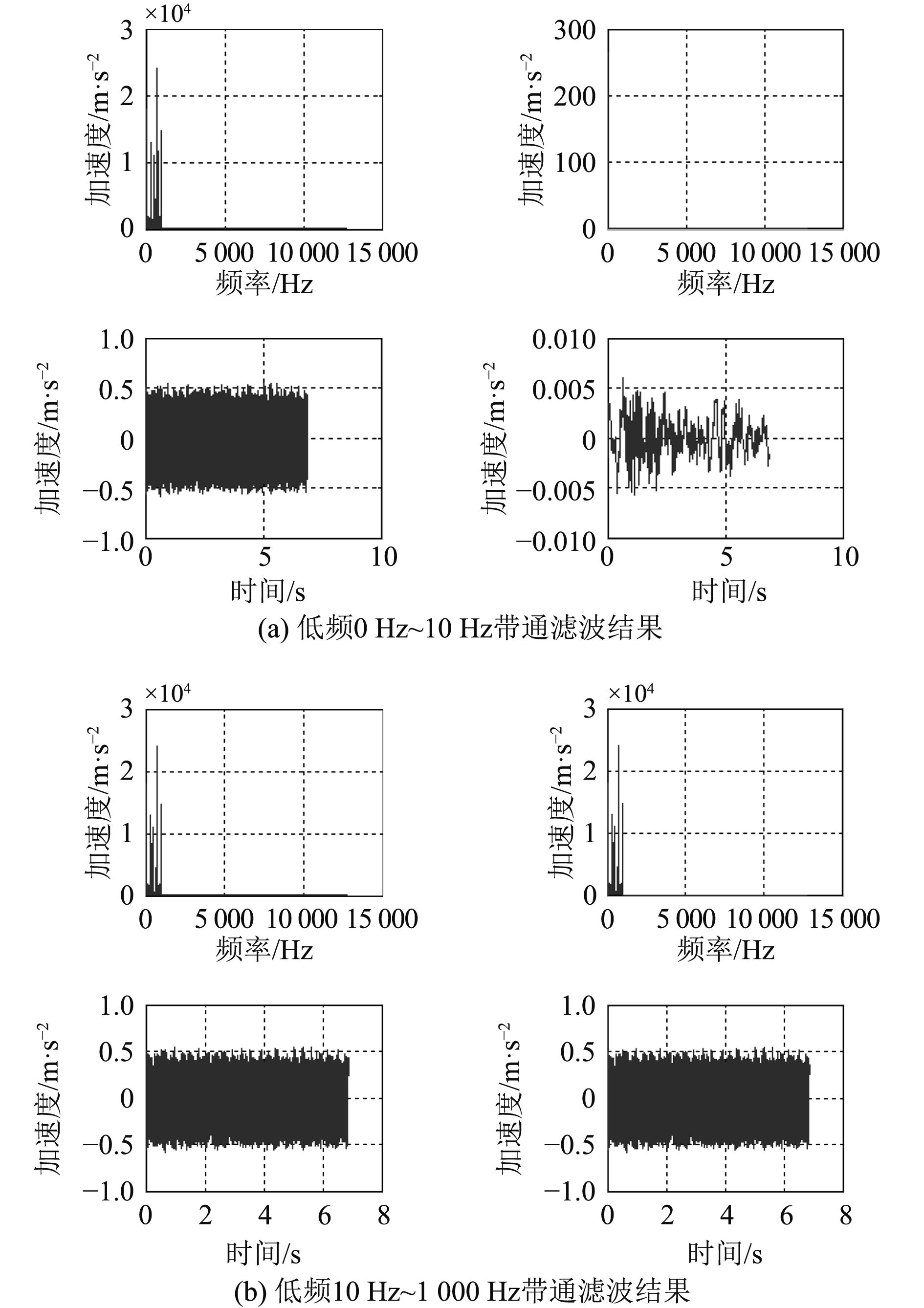
由图可以看出带通滤波后幅值大幅度减小,说明,已经剔除了大于1 000 Hz的高频干扰。接着对信号进行0~10 Hz,10~1 000 Hz带通滤波,滤波结果如图10所示。
|
图 10 上端信号低频带通滤波结果 Fig. 10 Low frequency band-pass filtering result of the upside signal |
由图可以看出0~10 Hz带通滤波后,带通滤波幅值大幅度减小,10~1 000 Hz幅值没有明显变化,因此,滤波范围选择10~1 000 Hz带通滤波,在消除10 Hz以下干扰信号的同时,较完整的保留了原信号的能量。
3 功率谱密度计算分析 3.1 下端信号功率谱密度计算分析调用Matlab中psd函数或pwelch函数,计算带通滤波后的下端振动信号功率谱密度,计算结果如图11所示。

|
图 11 下端信号功率谱密度计算结果 Fig. 11 Power spectral density of the downside signal |
由图可以看出,在70~90 Hz,280~360 Hz之间,存在窄带尖峰,但数值较小,在70~80 Hz,280~320 Hz区间外,信号的功率谱密度近似为一条水平直线,这说明该信号为一窄带随机过程,带宽分别为70~80 Hz,280~320 Hz,但幅值较小,约10–7量级,说明该信号为基体微振动,可等效为固定约束。
3.2 上端信号功率谱密度计算分析上端振动信号功率谱密度计算结果如图12所示。

|
图 12 上端信号功率谱密度计算结果 Fig. 12 Power spectral density of the upside signal |
由图可以看出,在70~90 Hz,280~360 Hz,420~540 Hz,560~720 Hz之间,存在5条窄带尖峰,约10–5量级,在70~90 Hz,280~360 Hz,420~540 Hz,560~720 Hz区间外,信号的功率谱密度近似为一条水平直线,10–9量级,这说明该信号为一窄带随机过程。
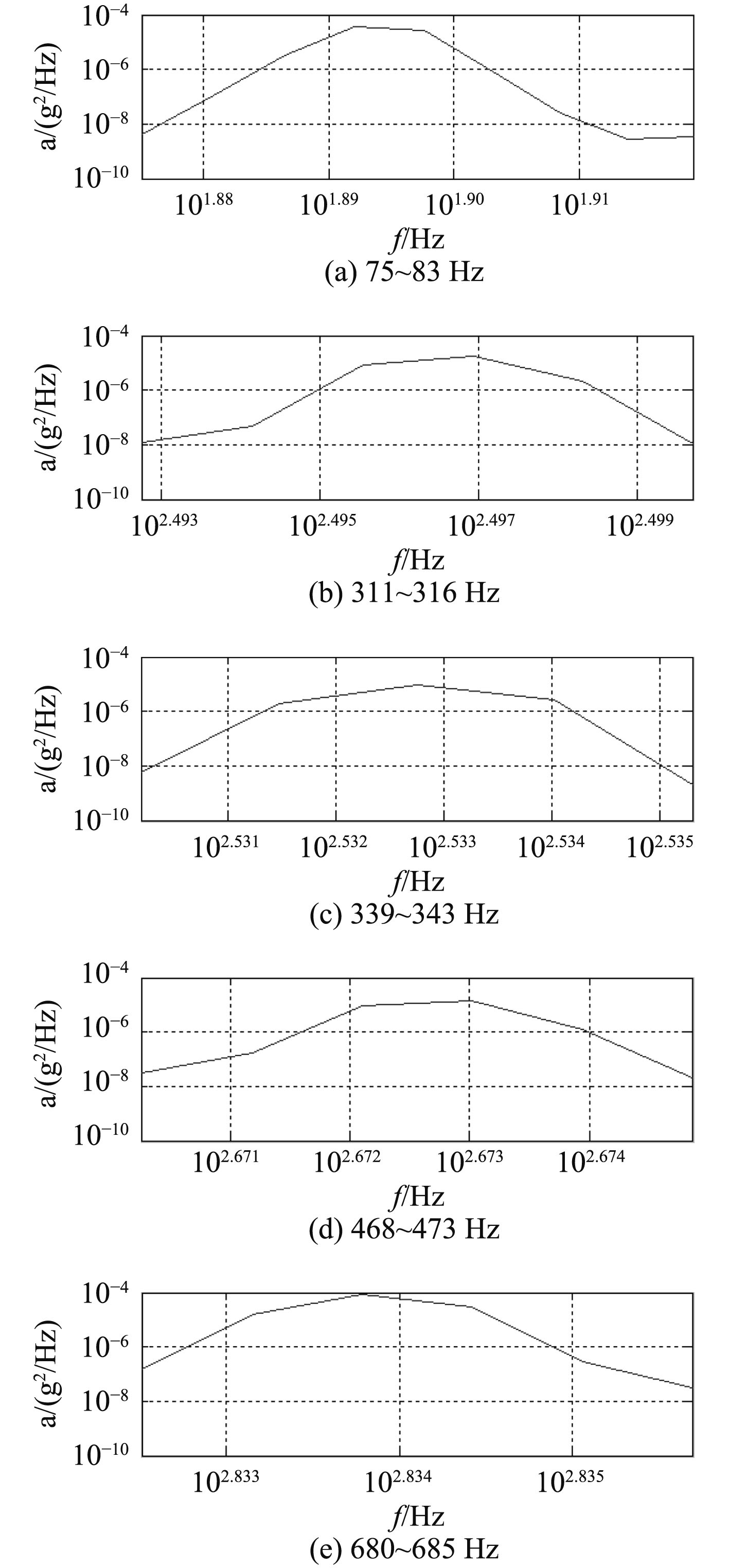
4 实验室载荷谱编制根据功率谱密度计算分析结果,下端信号振幅微弱,可等效为固定约束,上端信号存在5条窄带尖峰。载荷谱编制时,需对上端信号窄带尖峰每个频段内功率谱密度进行计算,功率谱密度计算结果如图13所示。
|
图 13 窄带尖峰功率谱密度计算示意图 Fig. 13 Power spectral density of the narrow-band peak |
由实采随机振动载荷谱编制实验室载荷谱时,重点是计算和保留主要频率上的振动功率谱密度。由上述计算结果可得在测量工况下橡胶减振器的实验室载随机振动载荷谱可编制如表1所示。
|
|
表 1 橡胶减振器的实验室载振动载荷谱 Tab.1 Experimental vibration load spectral of the rubber isolator |
本文以某舰用回转型机械设备隔振系统机角处橡胶减振器上下端的随机振动加速度信号为分析对象,详细介绍了对振动信号进行去奇异值、去直流分量、平滑化去毛刺以及去趋势项等预处理的方法和Matlab实现程序。同时,给出了对预处理后的信号开展频谱分析和滤波处理的方法,使用该方法成功消除了低频和高频段干扰信号,较完整的保留了原信号的能量。最后,介绍了对处理后的振动信号进行了功率谱计算分析的思路,并编制了模拟原始振动工况的实验室随机振动载荷谱。本文的研究成果对舰用橡胶减振器的寿命和可靠性研究及试验开展具有一定的工程应用意义。
| [1] | 朱石坚, 何琳. 船舶减振降噪技术与工程设计[M]. 2002, 北京: 科学出版社. |
| [2] | 邓爱民. 高可靠长寿命产品可靠性技术研究[D]. 长沙: 国防科学技术大学, 2006. |
| [3] |
周鑫, 丁孝均, 魏威. 加速老化试验方法评估典型橡胶密封材料贮存寿命的准确性研究[J]. 航天器环境工程, 2014, 31(3): 287-291.
ZHOU Xin, DING Xiao-jun, WEI Wei. Accuracy on evaluation of natural storage life of rubbery sealing materials by using accelerated life method[J]. Spacecraft Environment Engineering,2014, 31(3): 287-291. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=hthj201403011&dbname=CJFD&dbcode=CJFQ |
| [4] |
丁家松, 张欢, 童宗鹏, 等. 船用橡胶隔振器寿命评估方法研究[J]. 振动与冲击, 2010, 29(12): 230-233.
DING Jia-song, ZHANG Huan, TONG Zong-peng, et al. Lifetime ecaluation of rubber isolator for warship application[J]. Journal of Vibration and Shock, 2010, 29(12): 230-233. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=zdcj201012054&dbname=CJFD&dbcode=CJFQ |
| [5] |
丁智平, 陈吉平, 宋传江, 等. 橡胶弹性减振元件疲劳裂纹扩展寿命分析[J]. 机械工程学报, 2010, 46(22): 58-64.
DING Zhi-ping, CHEN Ji-ping, SONG Chuan-jiang, et al. Analysis of fatigue crack growth life for rubber vibration damper[J]. Journal of Mechanical Engineering, 2010, 46(22): 58-64. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=jxxb201022013&dbname=CJFD&dbcode=CJFQ |
| [6] | TRELOAR LR G. The mechanics of rubber elasticity[J]. Journal of Polymer Science Polymer Symposia, 1976, 48(1): 107-123. https://www.researchgate.net/publication/227595346_The_Mechanics_of_Rubber_Elasticity |
| [7] | KIM B K, YOUN S K. A viscoelastic consititutive model of rubber under small oscillatory load superimposed on large static deformation[J]. Archive of Applied Mechanics, 2001, 75(11): 275-288. https://link.springer.com/article/10.1007/s00419-005-0435-0 |
| [8] |
邹广平, 刘泽, 刘松, 等. 金属橡胶减振器随机振动有限元仿真[J]. 中国机械工程, 2016, 27(14): 1960-1963.
ZOU Guang-ping, LIU Zhe, LIU Song, et al. Finite element simulation of metal rubber damper random vibration[J]. China Mechanical Engineering, 2016, 27(14): 1960-1963. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=zgjx201614020&dbname=CJFD&dbcode=CJFQ |
| [9] |
闫庆华, 程兆刚, 段云龙. AR模型功率谱估计及Matlab实现[J]. 计算机与数字工程, 2010, 38(4): 154-156.
YAN Qing-hua, CHENG Zhao-gang, DUAN Yun-long. Power spectrum density estimation for AR model and the simulation in Matlab[J]. Computer & Digital Engineering, 2010, 38(4): 154-156. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=jssg201004044&dbname=CJFD&dbcode=CJFQ |
 2017, Vol. 39
2017, Vol. 39
