2. 三峡大学 新能源微电网湖北省协同创新中心,湖北 宜昌 443002;
3. 三峡大学 水电机械设备设计与维护湖北省重点实验室,湖北 宜昌 443002
2. New Energy and Micro Grid Collaborative Innovation Center in Hubei Province, China Three Gorges University, Yichang 443002, China;
3. Hubei Key Laboratory of Hydroelectric Machinery Design and Maintenance, China Three Gorges University Yichang 443002, China
在海况复杂多变情况下,进行浮标系泊结构姿态控制时面临起锚角控制问题和水声通讯设备舱与竖直方向的夹角限制问题,不然会造成锚被拖行和水声通讯设备工作效果变差,需选取合适系泊设备,避免上述情况发生。其中确定锚链的型号、长度和重物球的质量成为关键,同时这些参数值可以对设备舱的倾斜角度和浮标吃水深度及游动区域姿态参数进行优化匹配,从而使系泊结构达到最佳控制姿态。
潘生兵等[1]直接通过船舶舾装数计算查表来选取系泊设备。陈宇泉等[2]不仅通过舾装数的计算,还利用环境载荷计算系泊力来选取系泊索,并论证2种不同计算方法的有效性。胡灵斌等[3]通过锚抓持力与外力平衡进行悬链方程求解来确定锚及锚索的尺寸。王丹等[4]推导悬链方程,结合工程船实况运用悬链线方程计算锚链参数, 并确定锚泊设备选型。MEA Yassir等[5]用悬链线方程隐式迭代分析一个多分量悬链线系泊系统。李晓平等[6]应用改进有限段模型对含弹性元件的小型系泊浮标系统进行动力学仿真,得出张力幅值频率响应函数,为系泊系统设计提供指导意义。王磊等[7]基于单点系泊系统非线性动力学模型对浮标系统静态姿态进行计算,方子帆等[8]建立低张力缆索有限元模型为系泊绳的运动分析与设计提供理论依据。但都没有进行系泊结构参数优化匹配计算分析。
以起锚角和设备舱的倾斜角度为约束条件,取锚链型号和重物球质量作为设计变量,建立以锚链垂直高度相对误差最小为目标的参数优化匹配数学模型。结合实例进行浮标吃水深度和游动区域及设备舱的倾斜角度多变量优化计算,得出系泊结构姿态控制的优化结果和调节规律,为系泊结构设计提供理论依据。
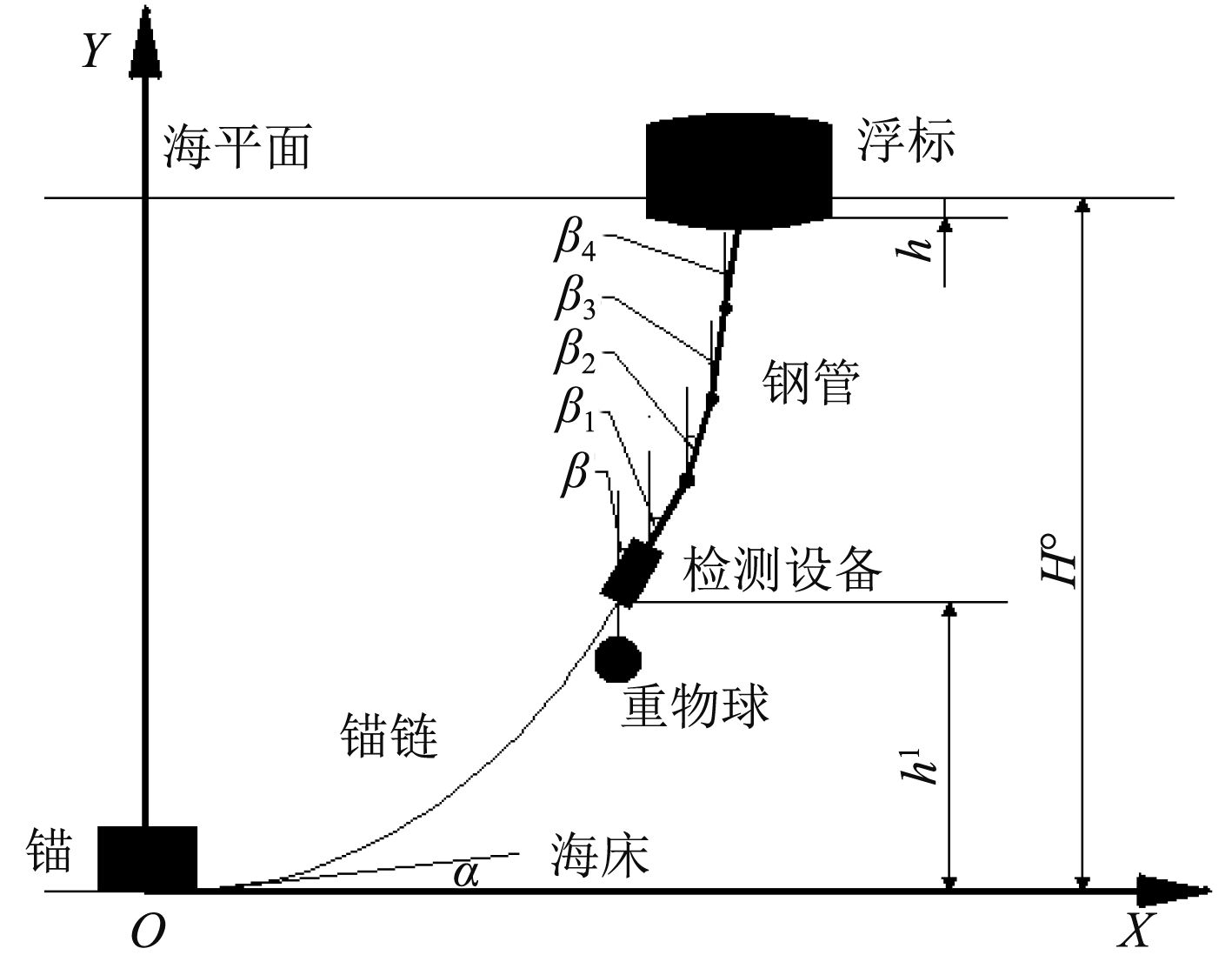
1 浮标系泊系统特性与分析 1.1 浮标系泊系统示意图及其符号约定浮标系泊系统由圆柱体浮标、钢管、检测设备舱、重物球、电焊锚链和特制的抗拖移锚组成,锚链选用无档普通链环,常用型号及其参数见符号列表,钢管共4节。根据实际工况要求起锚角α不能超过16°和装有水声通讯设备的设备舱与竖直方向的夹角β不能超过5°,确定合适锚链的型号、长度和重物球的质量能起到调节的作用。简图如图1所示,符号约定如表1所示。
|
图 1 浮标系泊系统图 Fig. 1 Buoy mooring system diagram |
|
|
表 1 浮标系泊系统符号约定 Tab.1 Sign convention of buoy mooring system |
整个系泊系统在一定风载和水载共同作用下会达到一个平衡状态,故可以简化为静力学分析[9–10]问题,出于力学分析的考虑,需对系泊系统的工作环境及其结构进行简化和假设,模型假设如下:
1)假设海流为平面流,且无垂直方向分量,故简化为二维问题[7];
2)由于静力学分析可不考虑波浪对整个系泊系统的影响;
3)由于锚和锚链的几何形状尺寸未知,故假设在水载作用下阻力为0;
4)水下的锚、锚链、设备舱、钢管的浮力不计。
通过静力学分析,先整体后局部,依次建立X、Y轴力平衡和力矩平衡方程式组。
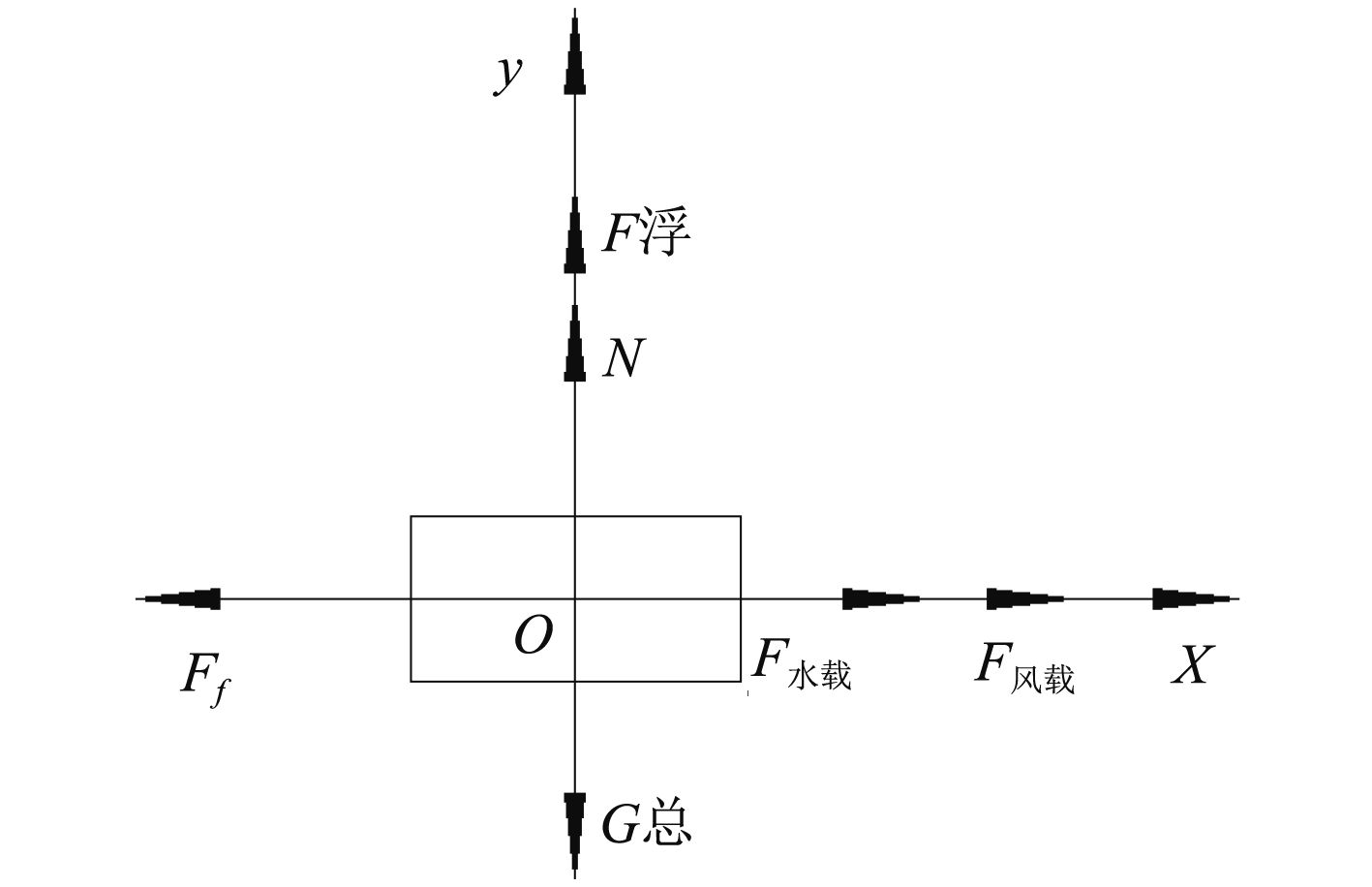
|
图 2 整体受力分析图 Fig. 2 Overall stress analysis |
| $\sum {{F_x} = } N + {F_{{\text{浮}}}} - {G_{{\text{总}}}} = 0\text{,}$ | (1) |
| $\sum {{F_y} = {F_{{\text{风载}}}} + {F_{{\text{水载}}}} - } {F_f} = 0\text{。}$ | (2) |
式中:G总=G浮标+G锚+G0,G0=G锚链+G+G舱+4×G钢管;F风载=0.625×

|
图 3 锚受力分析图 Fig. 3 Analysis of anchorage force |
| $\sum {{F_x} = } T\cos \alpha - {F_f} = 0\text{,}$ | (3) |
| $\sum {{F_y} = } {N_0} + T\sin \alpha - {G_{{\text{锚}}}} = 0\text{。}$ | (4) |
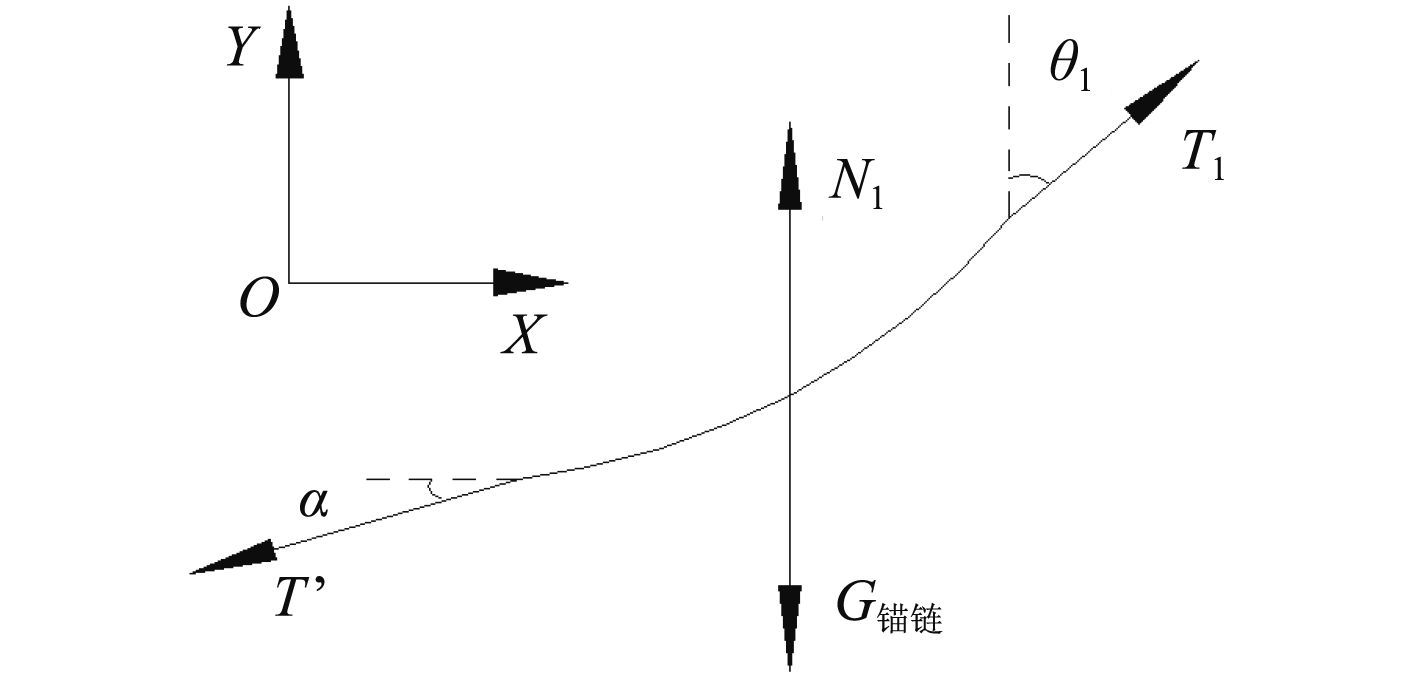
|
图 4 锚链受力分析图 Fig. 4 Analysis of anchor chain force |
| $\sum {{F_x} = } {T_1}\sin {\theta _1} - T'\cos \alpha = 0\text{,}$ | (5) |
| $\sum {{F_y} = } {T_1}\cos {\theta _1} + {N_1} - T'\sin \alpha - {G_{{\text{锚链}}}} = 0\text{,}$ | (6) |
| ${\text{牛顿第二定律}}\;\;\;\;\;\;T = T'\text{。}$ | (7) |
式中:N1为海床对锚链拖地部分的支持力,N;N =N1+N0,锚链若没有着地N1=0。
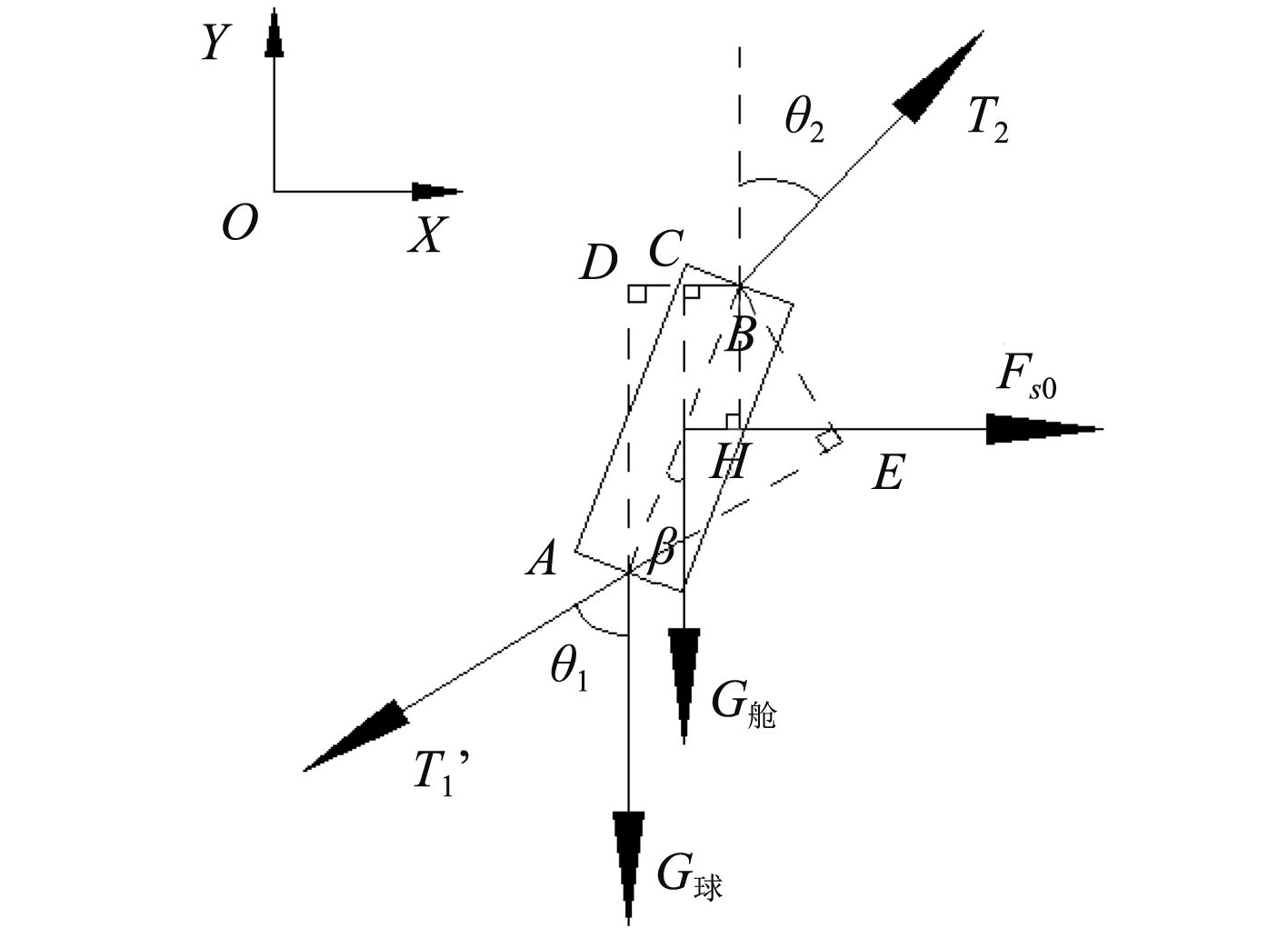
|
图 5 设备舱受力分析图 Fig. 5 Analysis of equipment cabin force |
| $\sum {{F_x} = } {T_2}\sin {\theta _2} + {F_{s0}} - {T_1}'\sin {\theta _1} = 0\text{,}$ | (8) |
| $\sum {{F_y} = } {T_2}\cos {\theta _2} - {T_1}'\cos {\theta _1} - {G_{{\text{舱}}}} - {G_{{\text{球}}}} = 0\text{,}$ | (9) |
| $\begin{split}&\displaystyle\sum {{M_D}} = {G_{{\text{舱}}}}{l_{CB}} + {G_{{\text{球}}}}{l_{DB}} + {F_{s0}}{l_{BH}} - {T_1}{l_{EA}} = 0 \text{,}\\&\displaystyle\sum {{M_D}} = {G_{{\text{舱}}}}\frac{l}{2}\sin \beta + {G_{{\text{球}}}}l\sin \beta + {F_{s0}}\frac{l}{2}\cos \beta - \\&{T_1}l\sin ({\theta _1} - \beta ) = 0\text{。}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\end{split}$ | (10) |
式中:Fs0为设备舱所受水流力,N;T1=T1′。

|
图 6 第 4 根钢管受力分析图 Fig. 6 Fourth steel pipe stress analysis chart |
| $\sum {{F_x} = } {T_3}\sin {\theta _3} + {F_{s1}} - {T_2}'\sin {\theta _2} = 0\text{,}$ | (11) |
| $\sum {{F_y} = } {T_3}\cos {\theta _3} - {T_2}'\cos {\theta _2} - {G_{{\text{钢管}}}} = 0\text{,}$ | (12) |
| $\begin{split}&\displaystyle\sum {{M_D}} = {G_{{\text{钢管}}}}{l_{DE}} + {F_{s1}}{l_{DH}} - {T_2}'{l_{DF}} = 0\text{,}\\&\displaystyle\sum {{M_D}} = {G_{{\text{钢管}}}}\frac{{{l_0}}}{2}\sin {\beta _1} + {F_{s1}}\frac{{{l_0}}}{2}\cos {\beta _1} - \\ &{T_2}'{l_0}\sin ({\theta _2} - {\beta _1}) = 0\text{。}\end{split}$ | (13) |
式中:Fs1为钢管所受水流力,N;T2=T2′。第3、第2、第1根钢管受力分析同上。
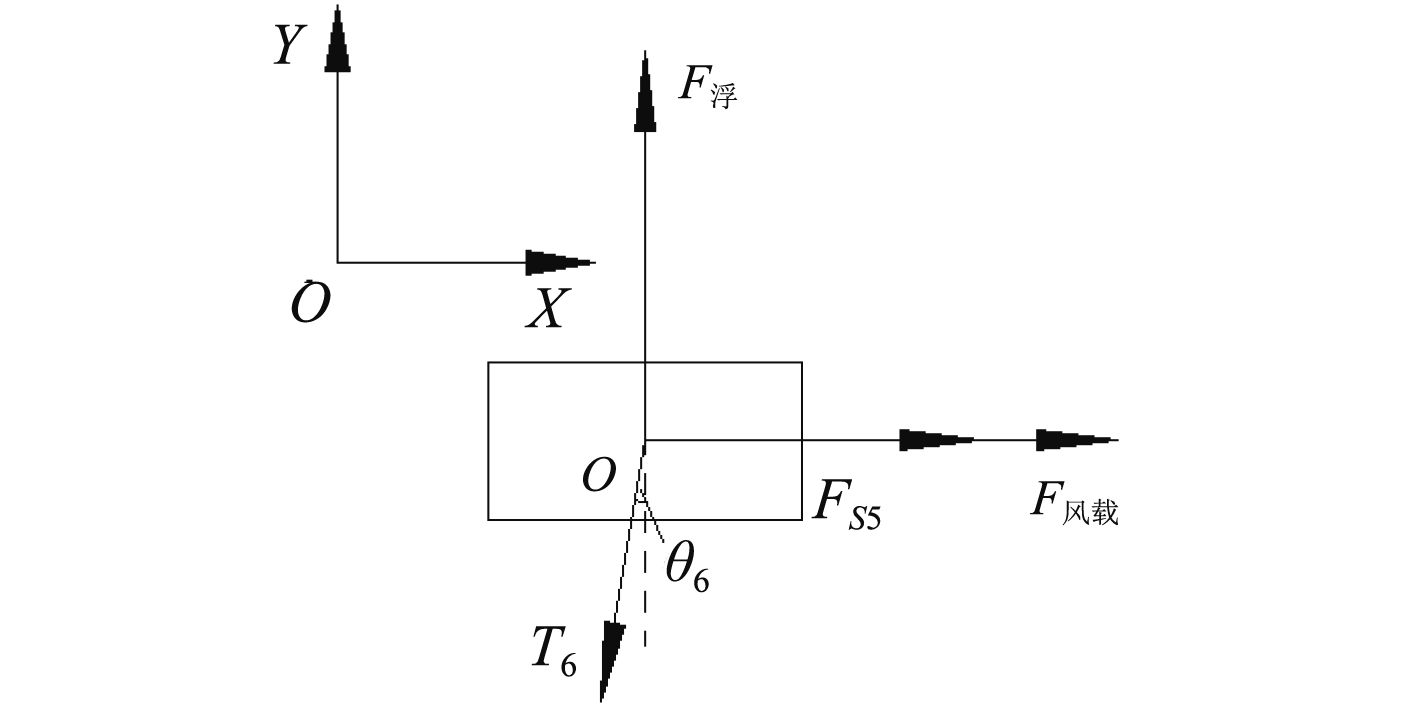
|
图 7 浮标受力分析图 Fig. 7 Buoy stress analysis |
| $\sum {{F_x} = {F_{{\text{风载}}}} + {F_{s5}} - {T_6}\sin {\theta _6} = 0}\text{,} $ | (14) |
| $\sum {{F_y} = {F_{{\text{浮}}}} - {G_{{\text{浮标}}}} - } {T_6}\cos {\theta _6} = 0\text{。}$ | (15) |
式中:Fs5为浮标吃水部分所受水流力,N。
在已知水深H0下,根据确定上述参数值可以求得锚链的实际垂直高度h1。
| $\begin{split}{h_1} =& {H_0} - h - {l_0}\cos {\beta _4} - {l_0}\cos {\beta _3} - {l_0}\cos {\beta _2} - \\& {l_0}\cos {\beta _1} - l\cos \beta \text{。}\end{split}$ | (16) |
根据文献[4]可知一般悬链方程的推导过程,任取悬链线上长度为ΔL的微元,其受力如图8所示。

|
图 8 悬链线微元受力分析图 Fig. 8 Stress analysis of catenary element |
两端为张力T和T+ΔT,其作用线与x轴成θ角,自重为qΔL,张力T+ΔT在x,y轴上的投影为连续函数,用泰勒公式将2个投影分别展开,取1阶微量即可,可得在x轴上的投影为:
| $T\cos \theta + \frac{{{\rm d}(T\cos \theta )}}{{{\rm d}L}} \cdot \Delta L\text{,}$ | (17) |
在y轴的投影:
| $T\sin \theta + \frac{{{\rm d}(T\sin \theta )}}{{{\rm d}L}} \cdot \Delta L\text{,}$ | (18) |
微元受力平衡方程式:
| $\begin{array}{l}\sum {{F_x} = \left[ {T\cos \theta + \displaystyle\frac{{{\rm d}(T\cos \theta )}}{{{\rm d}L}} \cdot \Delta L} \right]} - T\cos \theta = 0\text{,}\end{array}$ | (19) |
| $\begin{split}\sum {F_y} = & \left[ {T\sin \theta + \frac{{{\rm d}(T\sin \theta )}}{{{\rm d}L}} \cdot \Delta L} \right] - T\sin \theta - \\& q \cdot \Delta L = 0\text{。}\end{split}$ | (20) |
由式(19)、式(20)可得微分方程:
| $y'' = \frac{1}{a}\sqrt {1 + y{'^2}} \text{,}$ | (21) |
式中:a=R/q,R为锚链受到的水平分力,N;q为锚链单位长度在水中的重量,N/m。
边界条件:
| $y(0) = 0\text{,}$ | (22) |
| $y'(0) = \tan \theta\text{,} $ | (23) |
可得悬链的一般方程[11]:
| $y = a \cdot {\rm ch}\left[ {\frac{x}{a} + \ln (\tan \alpha + \sec \alpha )} \right] - a \cdot \sec \alpha \text{,}$ | (24) |
对弧长曲线积分
| $L = a \cdot {\rm sh}\left[ {\frac{x}{a} + \ln (\tan \alpha + \sec \alpha )} \right] - a \cdot \tan \alpha \text{。}$ | (25) |
式中:L为锚链的长度;x、y分别为锚链的水平和垂直分量。该悬链方程的垂直高度h2=y,将h2作为拟合值。
2 浮标系泊结构参数优化模型 2.1 设计变量在浮标系泊结构姿态控制过程中,锚链型号和重物球的质量调节至关重要,可以使设备舱的倾斜角度和浮标吃水深度及游动区域参数进一步优化,且锚链型号和重物球一旦确定,整个系泊结构姿态在一定海况下也随之确定,设计变量为锚链型号和重物球的质量。
2.2 约束条件为了使锚链不被拖行,导致系泊系统移动,要求起锚角α不超过16°,则约束条件为:
| ${0^ \circ } \leqslant \alpha \leqslant {16^ \circ }\text{,}$ | (26) |
为了不影响舱内水声通讯设备的工作效果,设备舱的倾斜角度β不超过5°,则约束条件为:
| ${0^ \circ } \leqslant \beta \leqslant {5^ \circ }\text{。}$ | (27) |
悬链方程求解的拟合值h2,与实际锚链垂直高度值h1对比,取相对误差δ=|h1-h2|/h1×100%越小,与实际吻合程度越高。故以相对误差δ最小为目标,即
| $\min \delta = \frac{{\left| {{h_1} - {h_2}} \right|}}{{{h_1}}} \times 100\% \text{。}$ | (28) |
其中,为了使实际情况相符,相对误差控制为δ≤0.1%。
2.4 系泊结构参数优化匹配数学模型综上所述,单目标优化数学模型为
| $\min \delta = \frac{{\left| {{h_1} - {h_2}} \right|}}{{{h_1}}} \times 100\% \text{,}$ | (29) |
| $s.t.\left\{ \begin{array}{l}{0^ \circ } \leqslant \alpha \leqslant {16^ \circ }\text{,}\\{0^ \circ } \leqslant \beta \leqslant{5^ \circ }\text{,}\\\delta \leqslant 0.1\%\text{。} \end{array} \right.$ | (30) |
当相对误差δ为0.1%时,若锚链出现拖地现象(h1<h2且a=0°),应另行求解。
3 模型求解 3.1 求解原理在复杂海况下,风速、水速、水深可变因素较多造成分析困难,利用控制变量法分别加以分析。对于设备舱的倾斜角度和浮标吃水深度及游动区域多参数优化问题,需进行单变量优化计算分析来构成分层多变量优化计算分析方法,再通过最小二乘法fsolve函数逼近求出模型中非线性方程组的解和利用穷举法区间搜索得出最优解。
3.2 求解过程由于海况参数条件多为范围或最值,在满足功能要求下,应考虑极限条件下的系泊结构参数计算,求解流程如图9所示。
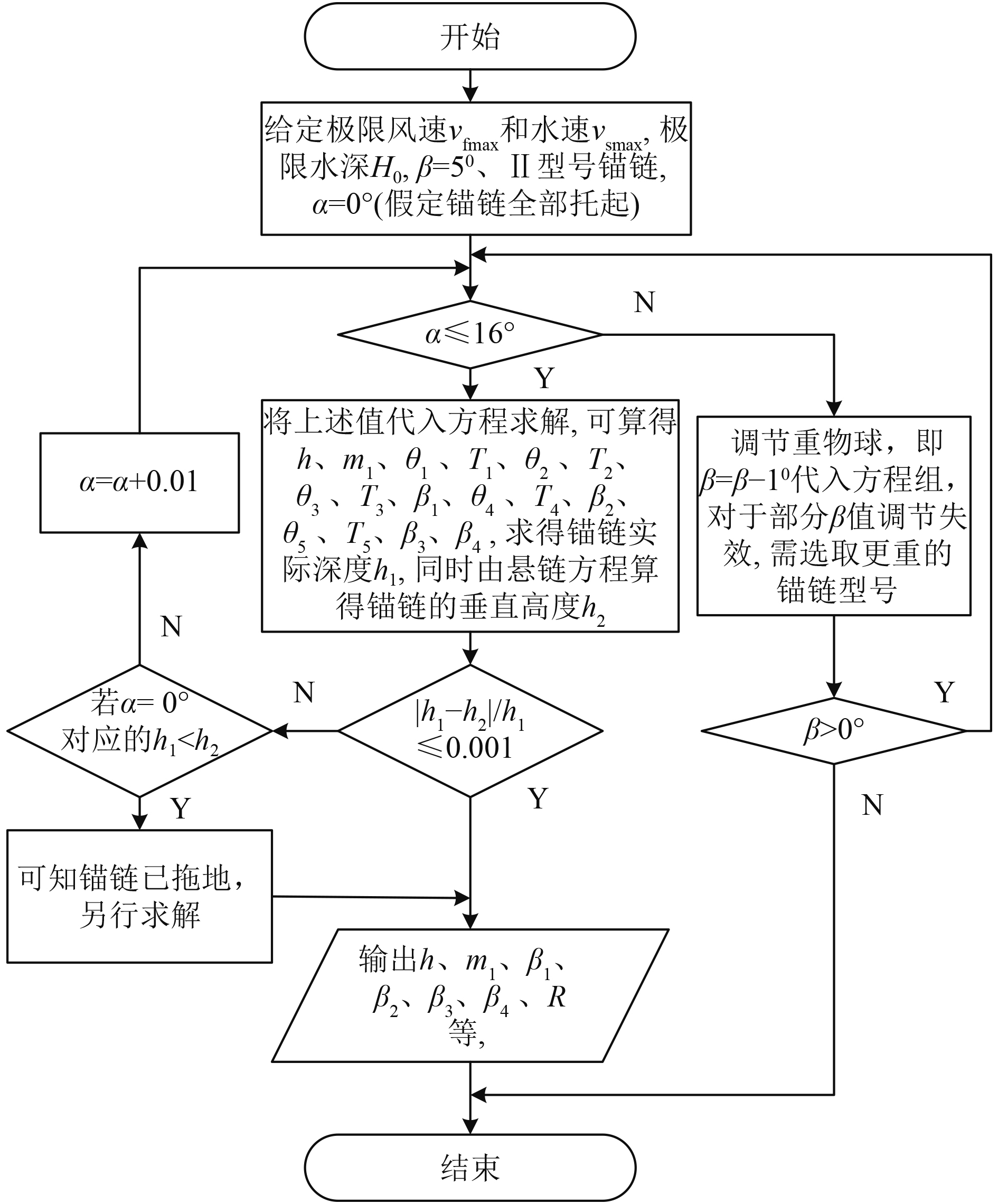
|
图 9 求解流程图 Fig. 9 Solve the flow chart |
由流程图可得,当水深H0一定时,通过调节重物球质量,可求得设备舱的倾斜角度β在0~5°的变化下所对应的系泊系统状态,若起锚角α超过16°,即调节重物球质量失效,需选用重型型号锚链进行调节。另外对于锚链拖地情况即h1<h2,应将锚链实际高度h1作为悬链方程的垂直高度y重新代入原力与力矩平衡方程计算求解系泊结构参数。
4 工程应用 4.1 作业海况与系泊结构由于潮汐因素的影响,布放海域的实测水深介于16~20 m之间。布放点的海水速度最大可达到1.5 m/s、风速最大可达到36 m/s。综合考虑风力、水流力和水深情况下的系泊系统设计,分析不同情况下的设备舱、钢管的倾斜角度、锚链形状、浮标的吃水深度和游动区域。浮标系泊结构参数:圆柱体浮标的底面直径2 m、高2 m,其质量1 000 kg;锚的质量为6 00 kg;钢管每节长1 m、直径50 mm,质量10 kg;装有水声通讯设备的设备舱长1 m、外径30 cm,总质量100 kg。
4.2 重物球质量调节计算结果设定水深H0=16 m、20 m两个极限值,依此可得一个范围解,海水最大速度为vsmax=1.5 m/s,最大风速vfmax=36 m/s,锚链的型号为II,其长度L=22.05 m情况下,系泊系统在设备舱的倾斜角度β变化下的设计情况如表2和图10所示。
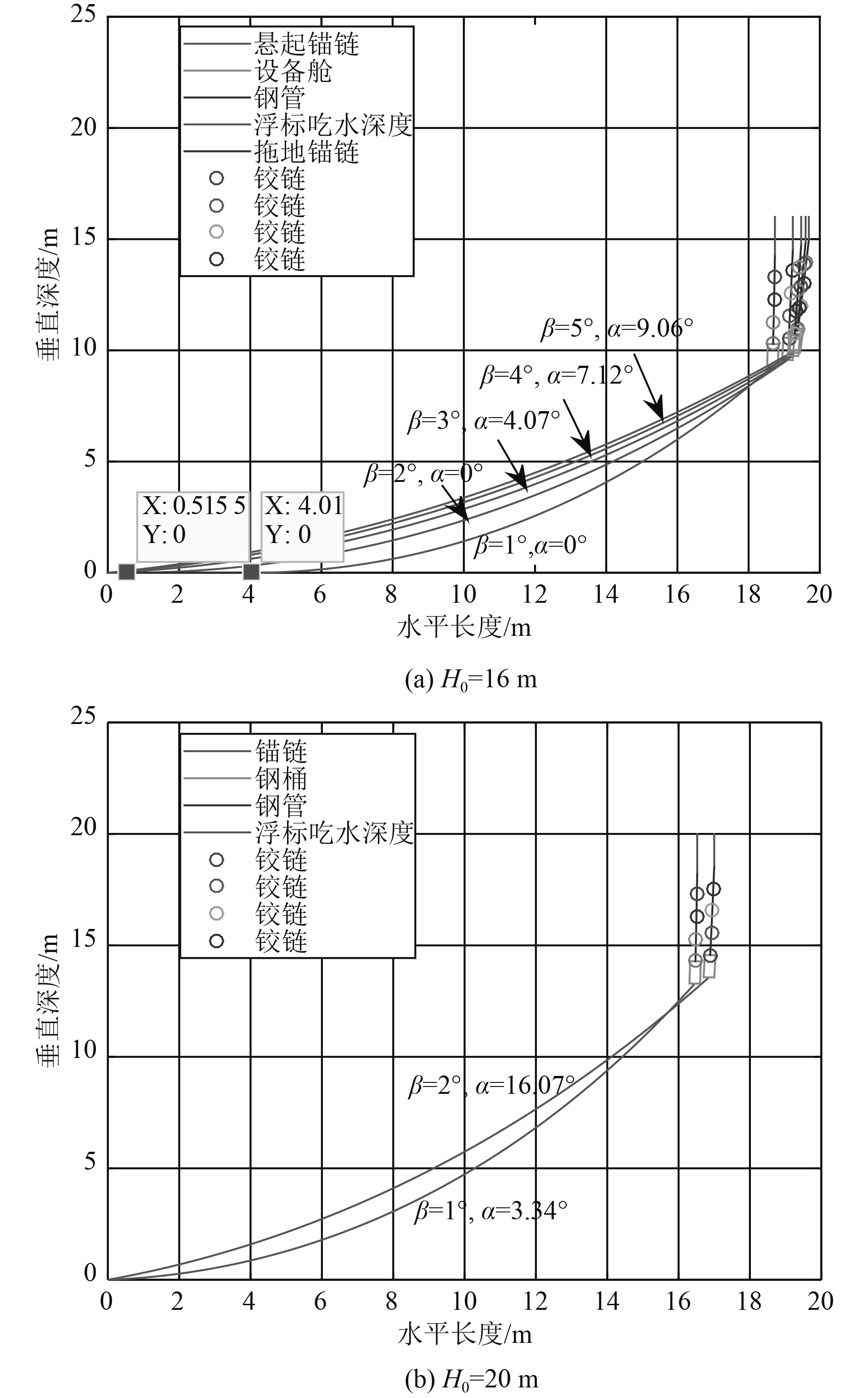
|
图 10 系泊结构姿态图 Fig. 10 Attitude of mooring structures |
|
|
表 2 在H0=16 m下系泊系统状态参数值 Tab.2 Mooring system state parameter values at H0=16 m |
当水深深度H0一定时,设备舱的倾斜角度β越小(设备的工作效果越好),所加载重物球的质量m1越大,导致浮标下降,其吃水深度h增大,但风载减小,故起锚角α和游动区域半径R减小。
4.3 锚链型号优选计算结果在海水深度H0=20 m下,当设备舱的倾斜角度β≥2°时,调节重物球质量已经不能满足α≤16°,应选用重型型号的锚链,优选III型号锚链结果如表3和图11所示。
|
|
表 3 在H0=20 m下系泊系统状态参数值 Tab.3 Mooring system state parameter values at H0=20 m |
当水深H0为20 m时,起锚角α和设备舱的倾斜角度β会超过允许范围,可以通过增大重物球质量或选取重型型号的锚链进行调节,且选取重型型号的锚链能够调节重物球调节β值失效的那一部分,另通过上述H0=20 m,β=1°和2°情况下两者调节系泊系统状态所得α、H、R优化参数值的比较可知选取重型型号的锚链更好,其使浮标的吃水深度H和游动区域R相对更小,起锚角α也更小,从而使系泊系统更趋合理。
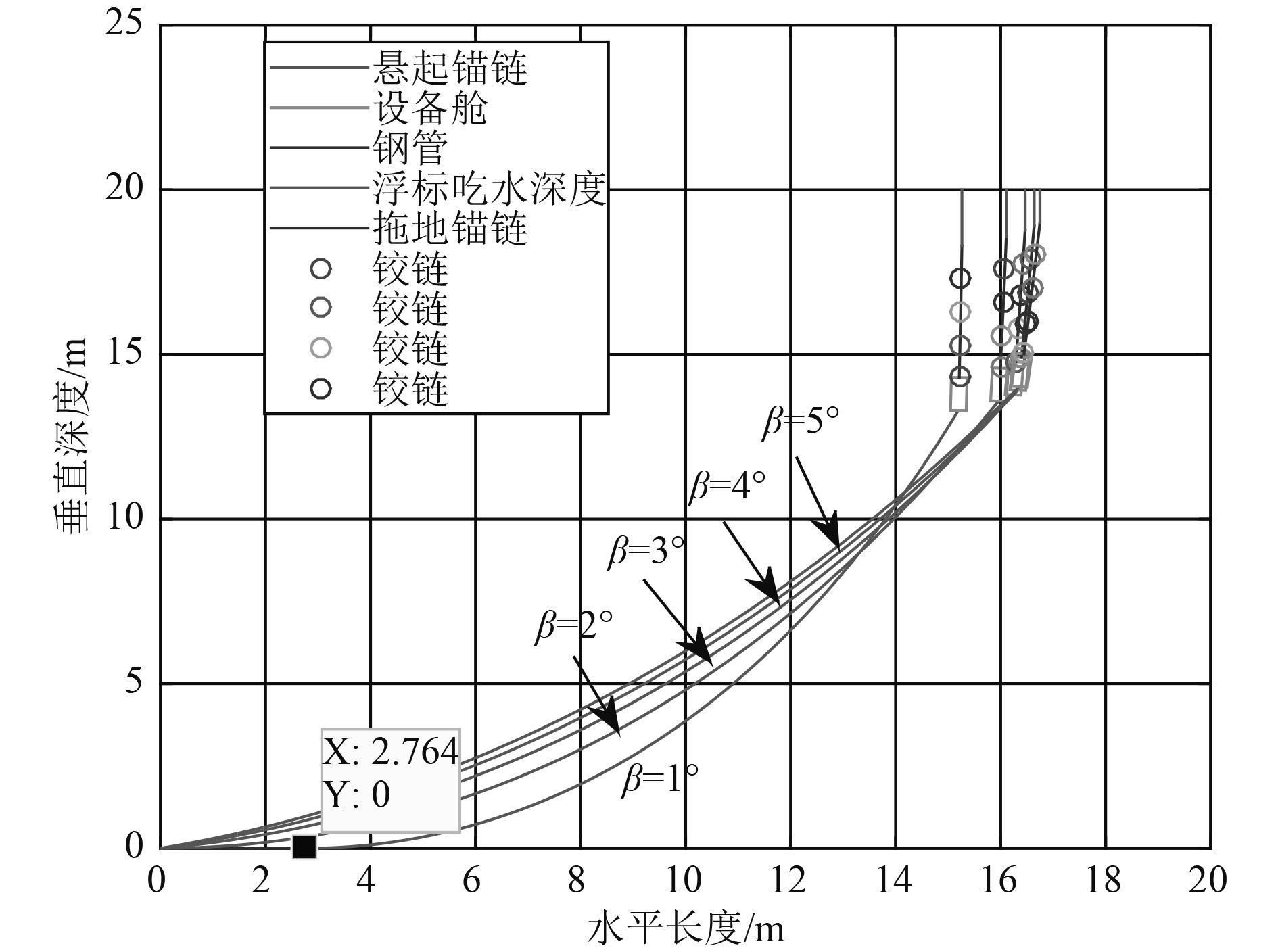
|
图 11 在H0=20 m(III型号锚链)下系泊结构姿态图 Fig. 11 Attitude of mooring structures under H0=20 m (III model anchor chain) |
针对浅海浮标系泊结构参数优化匹配问题,以起锚角和设备舱的倾斜角度为约束条件,取锚链型号和重物球质量作为设计变量,建立锚链垂直高度相对误差最小为目标的参数优化匹配数学模型,在不同水深情况下进行了浮标吃水深度和游动区域及设备舱的倾斜角度多变量优化计算,结论如下:
1)通过分层变量优化计算,当水深和锚链型号一定时,在设备舱不同的倾斜角度β下,可得其与α和R成正比,与m1和h成反比。
2)以系泊结构α,β,h,R为优化参数,通过调节重物球质量和锚链型号进行对比分析,可知选取更重锚链型号比增大重物球更合理,反之若从经济上考虑增大重物球更划算。
3)当系泊结构参数β或α超过允许范围时,可优先通过增大重物球质量调节,若其调节失效,则选取重型型号的锚链来配合调节。
| [1] |
潘生兵, 程慧勇, 李亮, 顾亮亮, 饶勇丰, 胡冰, 等. 船舶舾装数计算及系泊设备参数确定[J]. 船舶标准化工程师, 2014, 3 : 7–11.
PAN Sheng-bing, CHENG Hui-yong, LI Liang, GU Liang-liang, RAO Yong-feng, HU Bing, et al. Calculation of ship outfitting number and parameter determination of mooring equipment[J]. Ship Standardization Engineer, 2014, 3 : 7–11. DOI: 10.3969/j.issn.1005-7560.2014.03.003 |
| [2] | 陈宇泉. 海船系泊系统的设计与安装研究[D]. 哈尔滨: 哈尔滨工程大学, 2013. |
| [3] | 胡灵斌, 唐军. 悬链线方程的求解及其应用[J]. 船舶, 2004, 01 : 17–20. DOI: 10.3969/j.issn.1001-5388.2004.04.007 |
| [4] |
王丹, 刘家新. 一般状态下悬链线方程的应用[J]. 船海工程, 2007, 03 : 26–28.
WANG Dan, LIU Jia-xin. Application of catenary equation in general state[J]. Ship & Ocean Engineering, 2007, 03 : 26–28. DOI: 10.3963/j.issn.1671-7953.2007.03.009 |
| [5] | YASSIR M E A, KURIAN V J, HARAHAP I S H, et al. Parametric study on multi-component catenary mooring lines for offshore floating structures[J]. 2010. |
| [6] | 李晓平. 多体系统动力学建模方法及在水下缆索中的应用研究[D]. 天津: 天津大学, 2004. |
| [7] | 王磊. 单点系泊系统的动力学研究[D]. 青岛: 中国海洋大学, 2012. |
| [8] | 方子帆, 贺青松, 向兵飞, 肖华攀, 何孔德, 杜义贤, 等. 低张力缆索有限元模型及其应用[J]. 工程力学, 2013, 03 : 445–450. |
| [9] | 金德贤. 半潜式钻井平台锚泊系统静力分析[J]. 上海交通大学学报, 1981 (2): 58–68. |
| [10] | SENJANOVIC I, MRAVAK Z. Static analysis of catenary in mooring system[J]. Zbornik Radova Fsb, 1994 . |
| [11] | SUCH M, JIMENEZ-OCTAVIO J R, CARNICERO A, et al. An approach based on the catenary equation to deal with static analysis of three dimensional cable structures[J]. Engineering Structures, 2009, 31 (31): 2162–2170. |
 2017, Vol. 39
2017, Vol. 39
