2. 南京理工大学,江苏 南京 223005
2. Nanjing University of Science and Technology, Nanjing 223005, China
海洋技术研究尤其是深海技术在近二三十年发展迅速,深海载人潜水器技术就是其中一个重要部分,它是目前深海技术发展的前沿。载人潜水器涉及多学科、多领域的复杂系统,包括载体结构、动力与配电、水下推进、压载与纵倾调节、观察导航及控制、声学、液压与作业、应急与潜浮抛载、生命支持等系统[1]。其结构系统作为整个潜水器的骨架和设备安装基座,它的安全可靠性是整个载人潜水器安全可靠的基础,载人球壳和观察窗的可靠是结构系统的重中之重,是保护潜航员的最后一道屏障。潜航器在进行海试的过程中由于长时间受海水循环压力作用会发生疲劳和裂纹扩展,然而,对于潜航器观察窗的疲劳及裂纹扩展的研究相对较少。但是,这种客观存在的安全隐患已不容忽视。
国内外学者对潜航器观察窗进行了一定研究,取得了一定成果:文献[2]研究7 000 m潜水器观察窗的窗座结构优化设计与观察窗的塑性变形分析,利用ABAQUS软件计算窗座围栏与球壳连接过渡处的参数对于观察窗极限强度的影响;文献[3]运用数值计算和软件模拟,对大深度潜水器耐压球壳的结构性能影响研究和极限强度及稳定性分析;文献[4]结合模型试验和数值计算对大深度的球形耐压结构静态力学性能进行研究;文献[5]认为由于观察窗设计是属于有限寿命设计,但通过升降法、对比法等疲劳分析寿命预测方法需要比较多的试件,但是对于该尺寸以及深海高压的实验环境,又不可能提供满足试验方法的条件。
针对大深度载人潜航器的观察窗,通过数值计算方法得出大观察窗和小观察窗的侧向压应力和摩擦剪应力,进而分析观察窗的轴向应力。在传统理论分析方法的基础上,提出适用于锥台形观察窗位移、应力分析的方法,建立相应位移和应力的理论分析模型,对2种边界条件下的位移和应力进行分析;利用有限元分析软件,对比理论计算和有限元分析结果,分析无网格和有网格2种方法的差异与优劣;建立观察窗位移试验台,对主、侧观察窗的轴向位移开展试验研究,并对试验结果进行分析拟合,最后将试验拟合结果与理论计算和有限元分析结果进行对比。对观察窗的Fatigue Life进行分析,分析的疲劳寿命结果代入Miner理论公式中,计算大观察窗和小观察窗的疲劳损伤情况。
1 潜航器观察窗结构及受力分析本文研究观察窗为一个直径为220 mm的主观察窗和2个透光直径为130 mm且对称分布的侧观察窗。主观察窗的厚度为220 mm,采用45°锥体结构,侧观察窗的厚度为130 mm,也采用45°锥体结构。观察窗与窗座是通过固定压环紧密封圈,密封设置在观察窗外侧面的边缘[6]。视窗的锥形面和窗座的锥形面尺寸相同,二者均进行了打磨处理,保持接触边界光滑。观察窗的结构如图1所示。
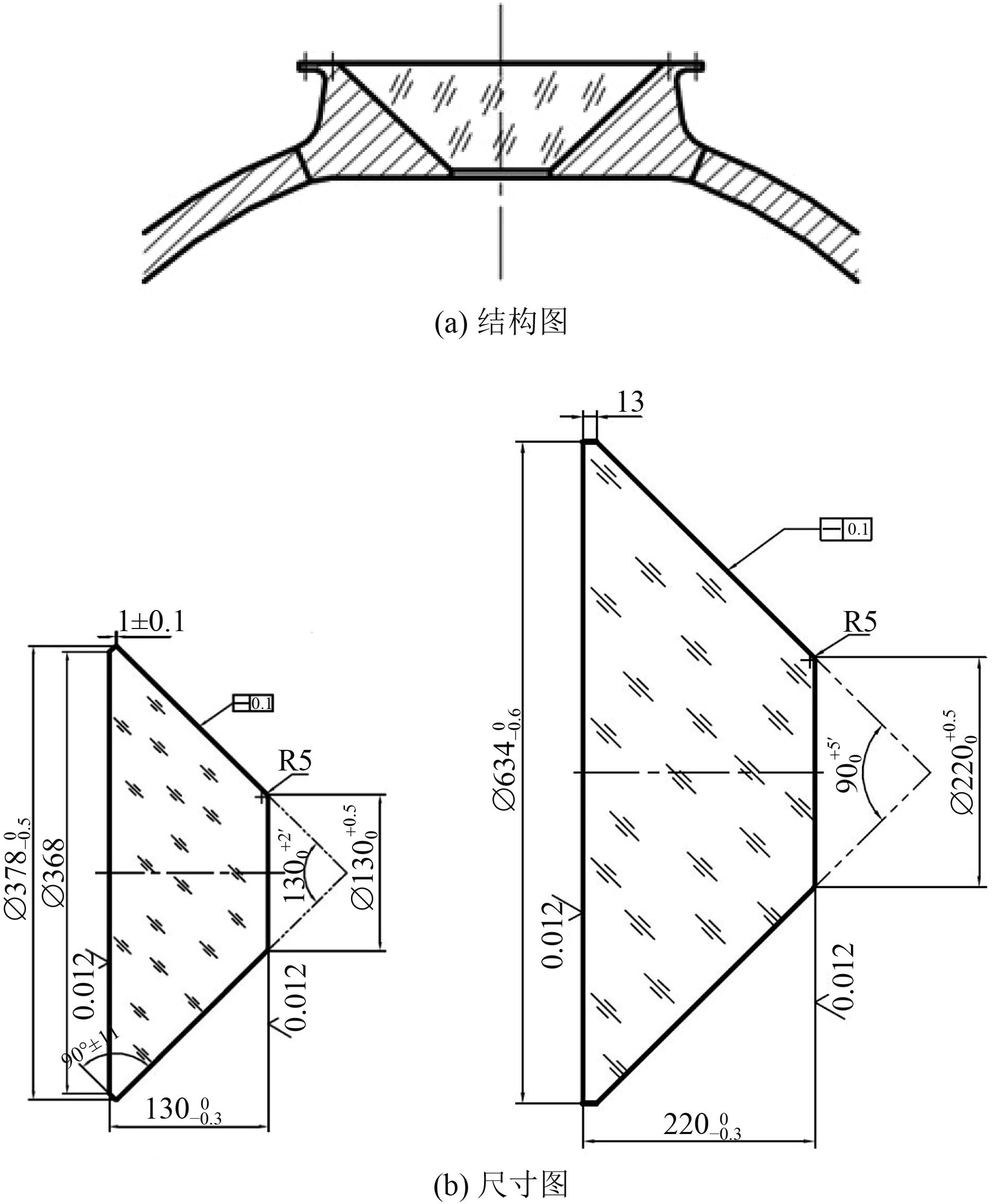
|
图 1 观察窗的结构图 Fig. 1 The structure of the viewport |
大观察窗的结构与小观察窗的结构相同,如图1(b)所示,均为45°锥面的锥台型结构,厚度分别为130 mm与220 mm,大观察窗的大圆面的直径经过测量得到634 mm,小圆面直径为220 mm,小观察窗经过测量,大圆面的直径为378 mm,小圆面的直径为130 mm。材质均为透明度较高的有机玻璃。观察窗与窗座通过固定压环紧密封圈,密封设置在观察窗外侧面的边缘[7]。窗锥形面和窗座的锥形面尺寸相同,二者均进行了打磨处理,接触边界光滑。
1)侧向压应力和摩擦剪应力
深潜器载人球壳的内径为2 100 mm,设有一个直径为220 mm的主观察窗和2个直径为130 mm的辅助观察窗,其中,q、σN、τf分别为潜水器的外压、侧向压力和摩擦剪应力,D1为观察窗的受压面直径,D2为舱内直径,d为观察窗厚度,锥角为45°,模型为轴对称,设观察窗的应力均匀分布[8]。

|
图 2 观察窗受力 Fig. 2 The stress of the viewport |
由锥台的受力平衡得:
| $\left( {{\sigma _N}\sin 45^\circ + {\tau _f}\cos 45^\circ } \right){S_{{\text{扇}}}}{\rm{ = }}q \times \frac{π }{4}D_1^2\text{。}$ | (1) |
取摩擦系数f=0.3,则τf=0.3σN,且
| $1.3{\sigma _N}\left( {D_1^2 - D_2^2} \right) = qD_1^2\text{,}$ | (2) |
则
| $\left\{ \begin{array}{l}\displaystyle{\sigma _N} = \frac{{qD_1^2}}{{1.3\left( {D_1^2 - D_2^2} \right)}}\text{,}\\[8pt]\displaystyle{\tau _f}{\rm{ = }}\frac{{0.3qD_1^2}}{{1.3\left( {D_1^2 - D_2^2} \right)}}\text{。}\end{array} \right.$ | (3) |
2)轴向应力
取d=x的锥台,受力见图2,由受力平衡得到:
| $\frac{{\sqrt 2 }}{2}({\sigma _N} + {\tau _f})\frac{{\sqrt 2 π }}{4}(D_1^2 - D_2^2) = {\rm{q}} \times \frac{π }{4}D_1^2\text{,}$ | (4) |
经过化简得到:
| $\displaystyle{\sigma _x} = \frac{{{{q}}D_1^2 - 1.3{\sigma _N}(\frac{3}{4}D_1^2 + {D_1}x - {x^2})}}{{{{(\displaystyle\frac{{{D_1}}}{2} - x)}^2}}}\text{。}$ | (5) |
3)任意一点应力
上述分析得出,轴向x位置的点的轴向应力的值,下面分析径向位置的一点的侧面应力,由此得到观察窗上任意一点的应力状态[9]。取径距离R,厚度x的任意一点进行应力分析,应力状态图如图3所示。
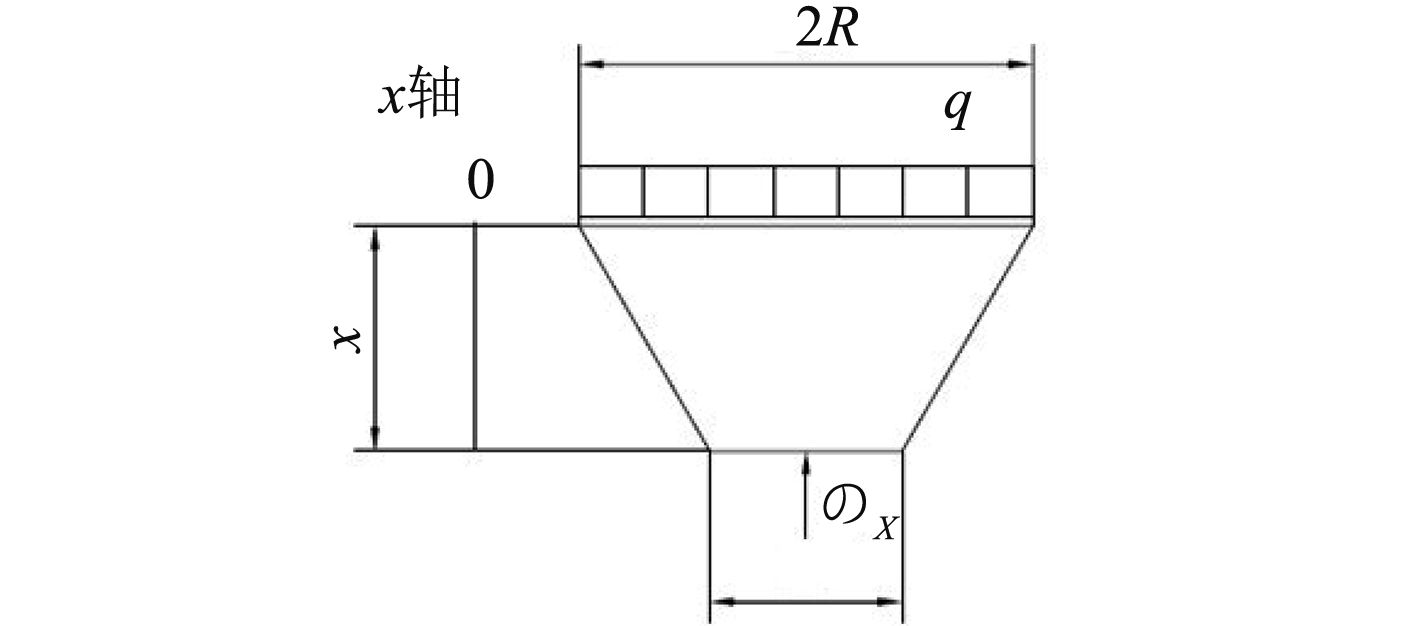
|
图 3 侧面受力示意图 Fig. 3 The stress of side face |
锥台形是轴对称图形,下面探讨从中心轴出发,距离中心轴为R距离位置的受力,取受海水的承压面直径为R,厚度为x,由45°得到下底面直径为
| ${\sigma _x} = \frac{{q{R^2} - 1.3{\sigma _N}\left( {\displaystyle\frac{3}{4}{R^2} + Rx - {x^2}} \right)}}{{{{\left( {\displaystyle\frac{R}{2} - x} \right)}^2}}}\text{,}$ | (6) |
受力平衡得:
侧面受力设为F(力的方向向下为“+”)
| $F + π {R^2}q{\rm{ - }}\frac{{qR^2 - 1.3{\sigma _N}(\displaystyle\frac{3}{4}R^2 + {R}x - {x^2})}}{{{{(\displaystyle\frac{R}{2} - x)}^2}}} = 0\text{,}$ | (7) |
即得到距离R的侧面受力F等于:
| $F = \frac{{qR^2 - 1.3{\sigma _N}(\displaystyle\frac{3}{4}R^2 + {R}x - {x^2})}}{{{{(\displaystyle\frac{R}{2} - x)}^2}}}{\rm{ - }}π {R^2}q\text{。}$ | (8) |
等式中有2个未知量,分别为离中心轴的距离R和距受海水压力的平面距离x。得到(r,x)点处,计算任意一点的侧面力F的大小。
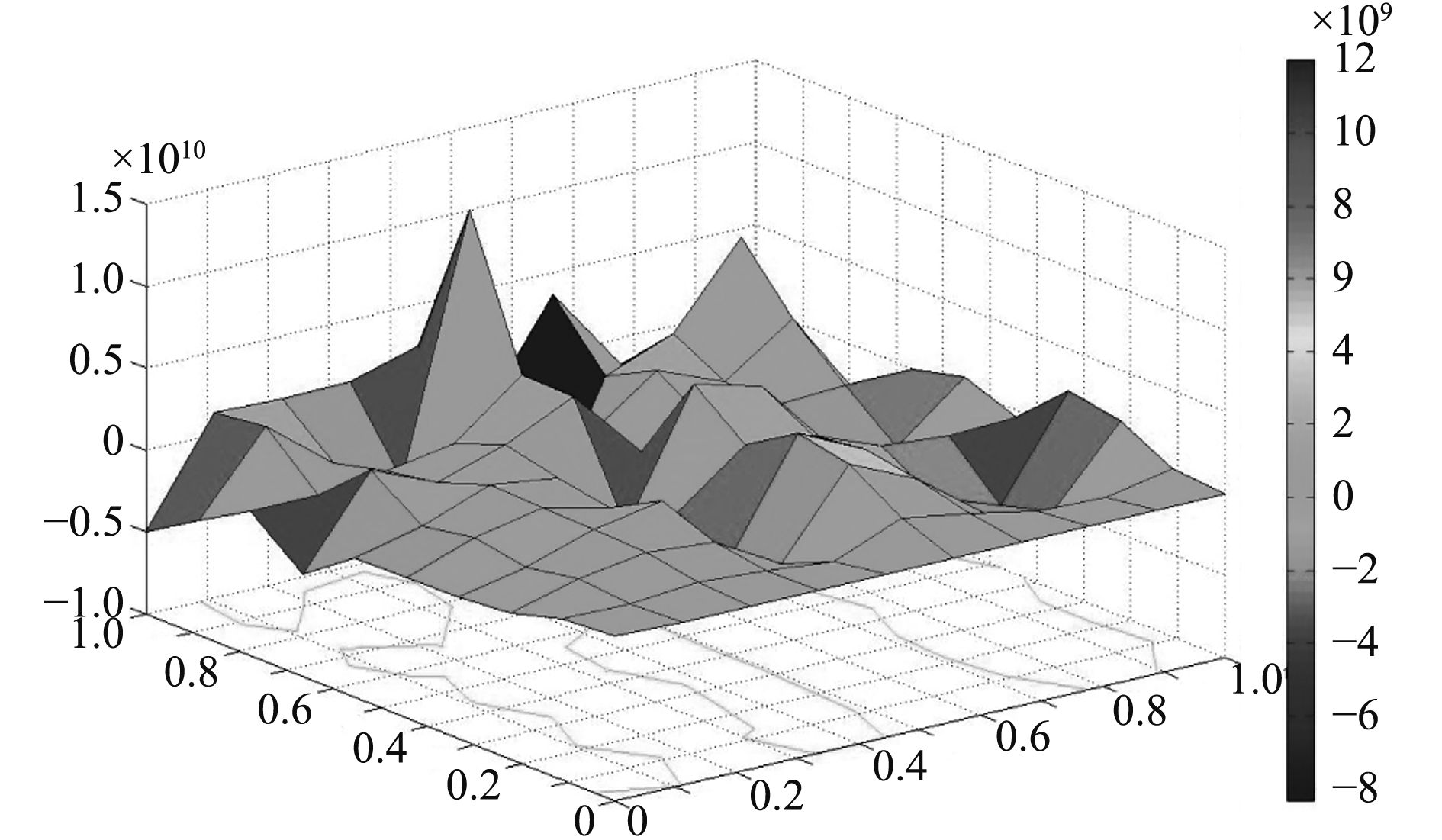
|
图 4 F(r,x)的surf曲面图 Fig. 4 F(r,x)’s surf curved surface |
观察窗的轴向应力为:
| $\sigma z(Z)/q \!=\! - [1 \!-\! \frac{z}{h}(1 - \frac{z}{h}\frac{h}{{{D_1}}}{\rm tg}\alpha )/(1 \!-\! \frac{h}{{{D_1}}}{\rm tg}\alpha )] \cdot {\left( {\frac{{{D_1}}}{D}} \right)^2}\!\!\!\text{,}$ | (9) |
径向应力为:
| ${\alpha _r} = - (1 - f \cdot {\rm tg}\alpha )\left( {f + {\rm tg}\alpha } \right)\left( {1 - \frac{h}{{{D_1}}}{\rm tg}\alpha } \right)\frac{{{D_1}}}{{4h}}q\text{。}$ | (10) |
主观察窗和辅观察窗的结构和受力形式相似,在无量纲z/h中,主观察窗和辅观察窗无量纲应力αz/q完全相同[10],则观察窗上任意一点的应力状态如图5所示。
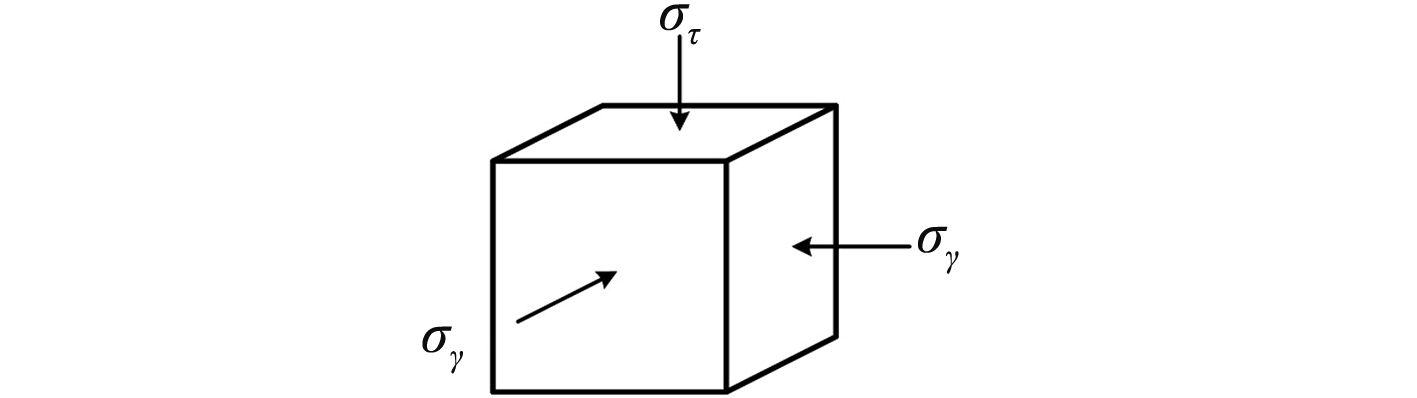
|
图 5 任意一点应力状态 Fig. 5 The stress of any point |
3个主应力为:
| $\left\{ \begin{array}{l}{\alpha _1} = {\alpha _2} = - {\alpha _r}\text{,}\\{\alpha _3} = - {\alpha _z}\text{。}\end{array} \right.$ | (11) |
应力偏量为:
| ${S_z} = {S_3} = {\alpha _3} - {\alpha _m} = \frac{2}{3}\left( {{\alpha _r} - {\alpha _z}} \right)\text{。}$ | (12) |
其中,
| ${\alpha _m} = \frac{1}{3}\left( {{\alpha _1} + {\alpha _2} + {\alpha _3}} \right)\text{,}$ | (13) |
则,等效应力为:
| $\begin{split}{\alpha _i}\! =\! \left( {1/\sqrt 2 } \right)\left[ {{\left( {{\alpha _1} \!-\! {\alpha _2}} \right)}^2} \!+\! {{\left( {{\alpha _2} \!-\! {\alpha _3}} \right)}^2} + \right. \\ \left. {\left( {{\alpha _3} - {\alpha _1}} \right)}^2 \right]^{\frac{1}{2}}= \left| {{\alpha _r} - {\alpha _z}(z)} \right|\text{。}\end{split}$ | (14) |
轴向应变分析和有限元的计算分析都显示体积应变相对较小,因此,由体积应变引起的轴向位移也很小。
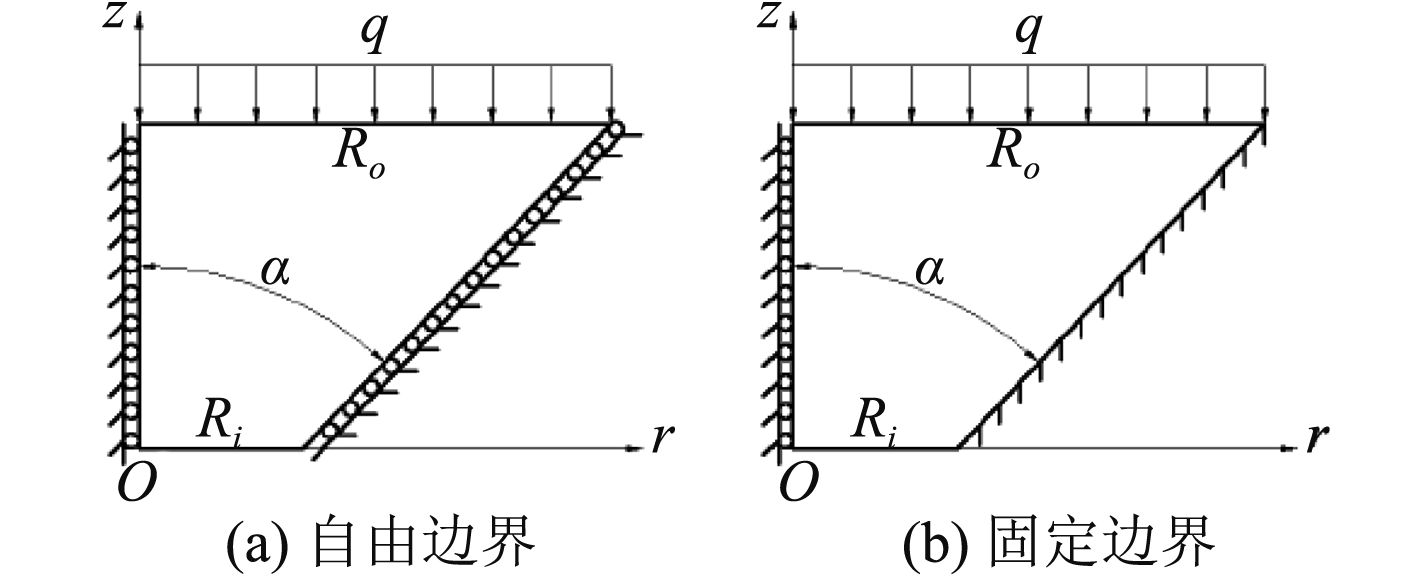
2 观察窗应力和位移分析 2.1 理论计算由于观察窗与窗座之间的安装分为干安装(直接安装)与湿安装(涂油脂安装),故其位移边界条件应该介于自由边界和固定边界之间[11],如图6所示,分别对这2种情况进行分析,边界条件如表1 所示。
|
图 6 锥台形观察窗自由边界和固定边界分析模型 Fig. 6 The analysis model of the taper-shapedviewpoint which free board and fixed border |
|
|
表 1 锥台形观察窗边界条件 Tab.1 The boundary conditions of the taper-shapedviewpoint |
其中,ur为径向位移,mm;Z为轴向体力,N/mm3;z为锥台微元厚度,mm;q为观察窗外表面均布载荷,MPa。
其中k=tanα,假设在锥面边界上的径向位移和轴向位移处处相等,径向位移的值为N,则轴向位移应为N/k。建立锥台形观察窗的位移分量模型:
| $\left\{ \begin{array}{l}{u_r} = \displaystyle\frac{r}{{kz + {R_i}}}N + \left( {1 - \frac{r}{{kz + {R_i}}}} \right)\frac{r}{{{R_i}}}\\ \;\;\;\;\;\;\;\;\left( \begin{array}{l}{A_1} + {A_2}r + {A_3}z + {A_4}{r^2} + {A_5}{z^2} + {A_6}rz\\[3pt] + {A_7}{r^2}z + {A_8}r{z^2} + {A_9}{r^3} + {A_{10}}{z^3}\end{array} \right)\text{,}\\w = \displaystyle\frac{N}{k} + \left( {1 - \frac{r}{{kz + {R_i}}}} \right)\frac{r}{{{R_i}}}\\\;\;\;\;\;\;\;\;\left( \begin{array}{l}{B_1} + {B_2}r + {B_3}z + {B_4}{r^2} + {B_5}{z^2} + {B_6}rz\\[3pt] + {B_7}{r^2}z + {B_8}r{z^2} + {B_9}{r^3} + {B_{10}}{z^3}\end{array} \right)\text{。}\end{array} \right.$ | (15) |
可见,固定边界条件下N=0。假设的位移函数显然可以满足位移边界条件,但无法满足应力边界条件[12]。锥台形观察窗的形变势能为:
| $U = \int\limits_0^{2π } {\int\limits_0^t {\int\limits_0^{kz + {R_i}} {{U_1}r{\rm d}r{\rm d}z{\rm d}\theta } } } \text{。}$ | (16) |
由于Pr=0,且忽略观察窗本身重力的影响(Pz=0),则:
| $\frac{{\partial U}}{{\partial {A_m}}} = \int {{{\bar P}_r}{u_{rm}}} {\rm d}s,\frac{{\partial U}}{{\partial {B_m}}} = \int {{{\bar P}_z}{w_{rm}}} {\rm d}s\text{。}$ | (17) |
在上边界,z=t,
但是由于
最关心的是r=0即对称轴上的应力分布,所以令σz|z=t&r=0=0满足条件,则可得在外侧边界上的位移为:
| $N = \frac{{{R_i}}}{{{R_0}(1 + \mu )}}\left[ { - 2\mu {A_1} + \left( {\mu - 1} \right){R_0}{B_3}} \right]\text{。}$ | (18) |
取式(17)和(18)可解得待定系数表达式:
| $\left\{ \begin{array}{l}{A_m} = {A_m}\left( {{R_i},\alpha ,t,q,E,\mu } \right)\text{,}\\{B_m} = {B_m}\left( {{R_i},\alpha ,t,q,E,\mu } \right)\text{。}\end{array} \right.$ | (19) |
由此可求观察窗的径向位移和轴向位移,并可根据空间轴对称的几何方程和物理方程求出观察窗的应力和应变[13]。代入相关参数,取前15项系数进行计算,观察窗位移和应力分布情况如图7所示。

|
图 7 锥台形观察窗的位移和应力分布 Fig. 7 The displacement and stress distribution of the taper-shapedviewpoint |
利用ABAQUS建立观察窗的分析模型,进行分析,自由边界结果如图8所示,固定边界结果如图9所示。

|
图 8 锥台形观察窗自由边界分析结果 Fig. 8 The result of the taper-shapedviewpoint’s free boardanalyzing |
由图8通过对自由边界条件的锥台形观察窗的有限元分析可以发现:最大径向位移产生在高压面边缘处,最大轴向位移产生在低压面的中心处;在整个观察窗上,径向应力、轴向应力和环向应力均为压应力,且小于有机玻璃的抗压强度,切向应力小于抗剪强度。
|
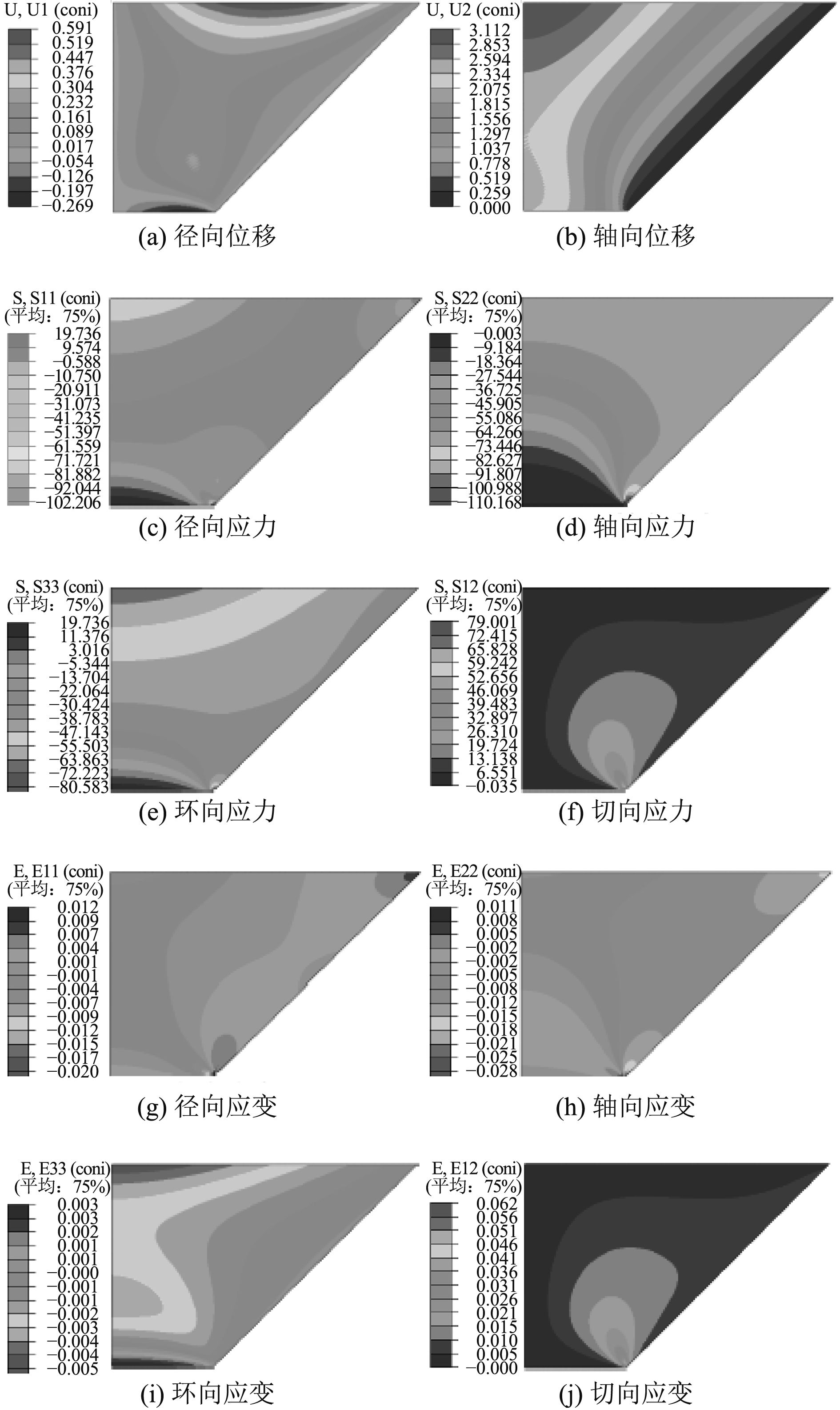
图 9 锥台形观察窗固定边界分析结果 Fig. 9 The result of the taper-shapedviewpoint’s fixed boardanalyzing |
由图9通过对固定边界条件的锥台形观察窗的有限元分析可以发现:最大径向位移产生在高压面二分之一直径的圆周上,最大轴向位移产生在高压面的中心处;在低压面中心,径向应力和环向应力为拉应力,且小于抗拉强度,在低压面边缘处,径向应力、轴向应力和环向应力均为压应力,且小于抗压强度,切向应力小于抗剪强度。
通过对2种边界条件的锥台形观察窗的有限元分析可发现:较之固定边界条件,自由边界条件下的径向位移更小,轴向位移更大,即自由边界条件下的观察窗更容易在窗座上产生滑动,整个观察窗上呈受压状态,受力状态更为良好,观察窗的实际情况介于两者直接,安装前涂抹润滑油,减小摩擦系数,将使观察窗偏向于自由边界条件。
3 观察窗疲劳分析若构件在某恒幅应力水平S作用下,循环至破坏的寿命N,则可定义其在经受n次循环时损伤为:
| $D = n/N\text{。}$ | (20) |
显然在恒幅应力水平S作用下,若n=0,则D=0,构件未受疲劳损伤;若n=N2,则D=1,构件发生疲劳破坏。
构件在应力水平Si作用下,经受Ni次循环的损伤为Di=ni/Ni。若在k个应力水平Si作用下,各经受ni次循环,则可定义其总损伤为:
| $D = \sum\nolimits_1^k {{D_i}} = \sum {{n_i}} /{N_i}\text{。}$ | (21) |
破坏标准为:
| $D = \sum {{n_i}} /{N_i} = 1\text{。}$ | (22) |
其中ni是在Si作用下的循环次数,由载荷谱给出;Ni是在Si作用下循环到破坏的寿命由有限元分析得到。
|
|
表 2 载荷块的数据 Tab.2 The data of block cycle load |
基于Miner线性积累损伤理论对其进行全寿命计算[14],对小观察窗按照载荷谱,进行5次加载,载荷的大小见载荷谱表2,采用有限元的方法计算观察窗的疲劳寿命Fatigue Life,分析得到的小观察窗在相应载荷下的寿命图如图10所示。
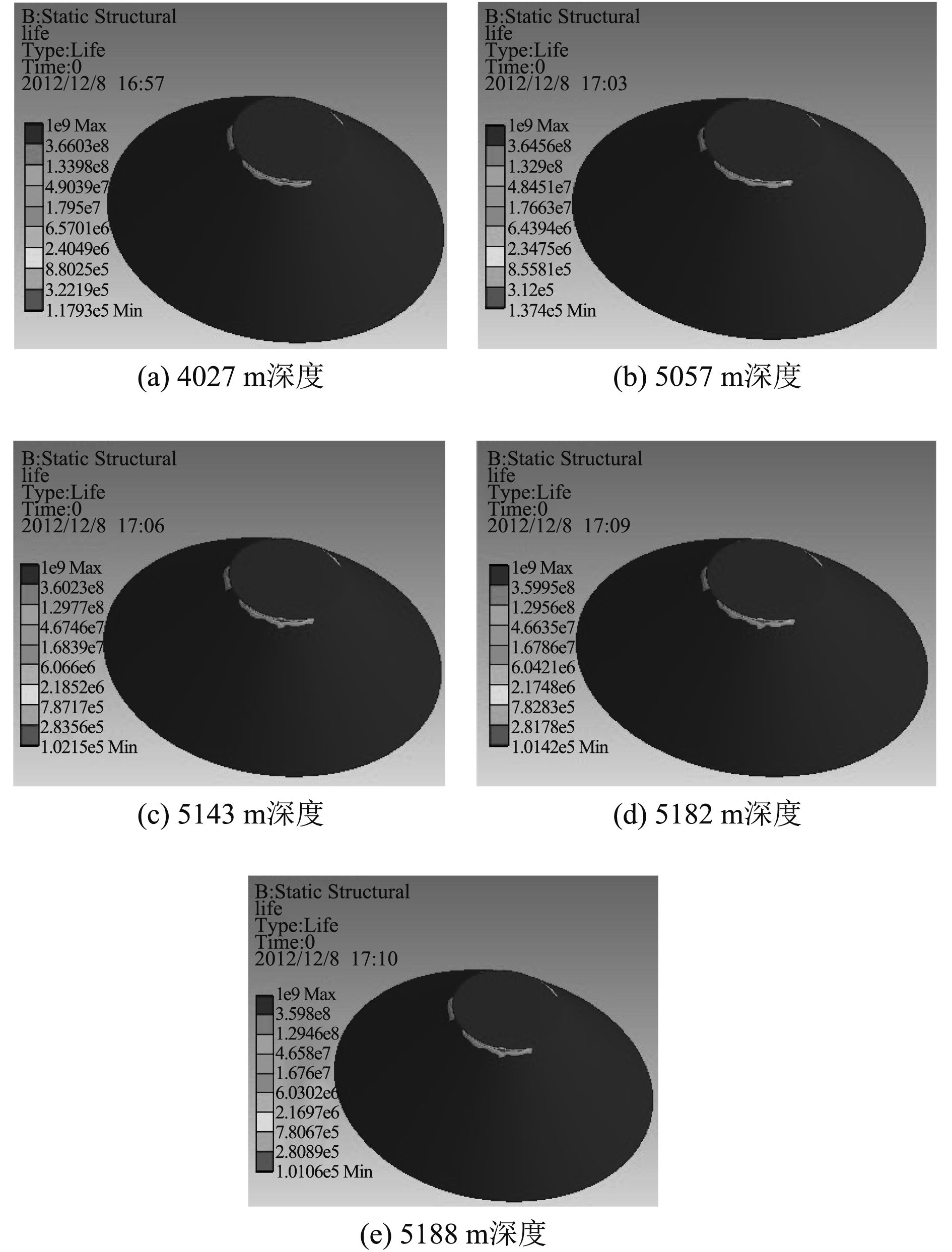
|
图 10 小观察窗疲劳寿命分析 Fig. 10 The analysis of fatigue life based on small viewport |
|
|
表 3 小观察窗载荷(S)-寿命(N)数据表 Tab.3 The data of cycle load(S)- life(N) about small viewport |
计算结果为:
| $D = \sum {{D_i}} = \sum {{n_i}/{N_i}} = 4.68162{e^{ - 5}} < 1\text{。}$ | (23) |
由Miner线性积累损伤理论可以判定小观察窗没有发生疲劳破坏。并且经过计算得到小观察窗的疲劳寿命为:n=1/D=21 359转。即进行相同载荷的5次加载可以使用21 359次。同理,对大观察窗进行相同的有限元计算。计算方法与小观察窗相同。对大观察窗按照载荷谱,进行5次加载,载荷的大小见载荷谱表格2,采用有限元计算观察窗的Fatigue Life,加载方法、材料参数的设置方法以及连接方式相同,得到疲劳寿命云图,有限元计算得到大观察窗在相应载荷下的寿命图。从图11中可以看出观察窗寿命最小值点,即危险点的位置。

|
图 11 大观察窗疲劳寿命分析 Fig. 11 The analysis of fatigue life based on big viewport |
|
|
表 4 大观察窗载荷(S)-寿命(N)数据表 Tab.4 The data of cycle load(S)-life(N) about bigviewport |
计算结果为:
| $D = \sum {{D_i}} = \sum {{n_i}/{N_i}} = 3.7832{e^{ - 5}} < 1\text{。}$ | (24) |
由Miner定理可以判定大观察窗也没有发生疲劳破坏。大观察窗的疲劳寿命:n=1/D=26 432转。
4 试验分析为了能接近实际下潜过程中观察窗的受力情况,本次研究将设计制造高压压力筒,以模拟7 000 m海水的压力作用,便于研究观察窗受海水压力作用时的位移和应力分布情况[15]。根据设计结果,加工制造了压力筒,如图12所示。

|
图 12 压力筒实物图 Fig. 12 The real object of pressure vessel |
试验采用手动液压泵对液压油进行加压。手动液压泵为上海兆帕流体动力有限公司生产的超高压手动泵,型号HHP-1000,其最大压强可加到100 Mpa;轴向位移测量采用千分表[16]。试验过程中,压力由0 MPa加载到70 MPa,取3次加载过程的主、侧观察窗低压面中心点的轴向位移如表5所示。
|
|
表 5 主观察窗的轴向位移 Tab.5 The axle displacement of the bigviewport |
利用Origin分别对主、侧观察窗的轴向位移进行线性拟合,如图13所示,分别得到2条直线:
| $\left\{ \begin{array}{l}y = 0.0553x + 0.0822\text{,}\\y = 0.0307x + 0.0175\text{。}\end{array} \right.$ | (25) |
所得直线的截距分别表示主、侧观察窗装配时与压力筒的微小间隙。
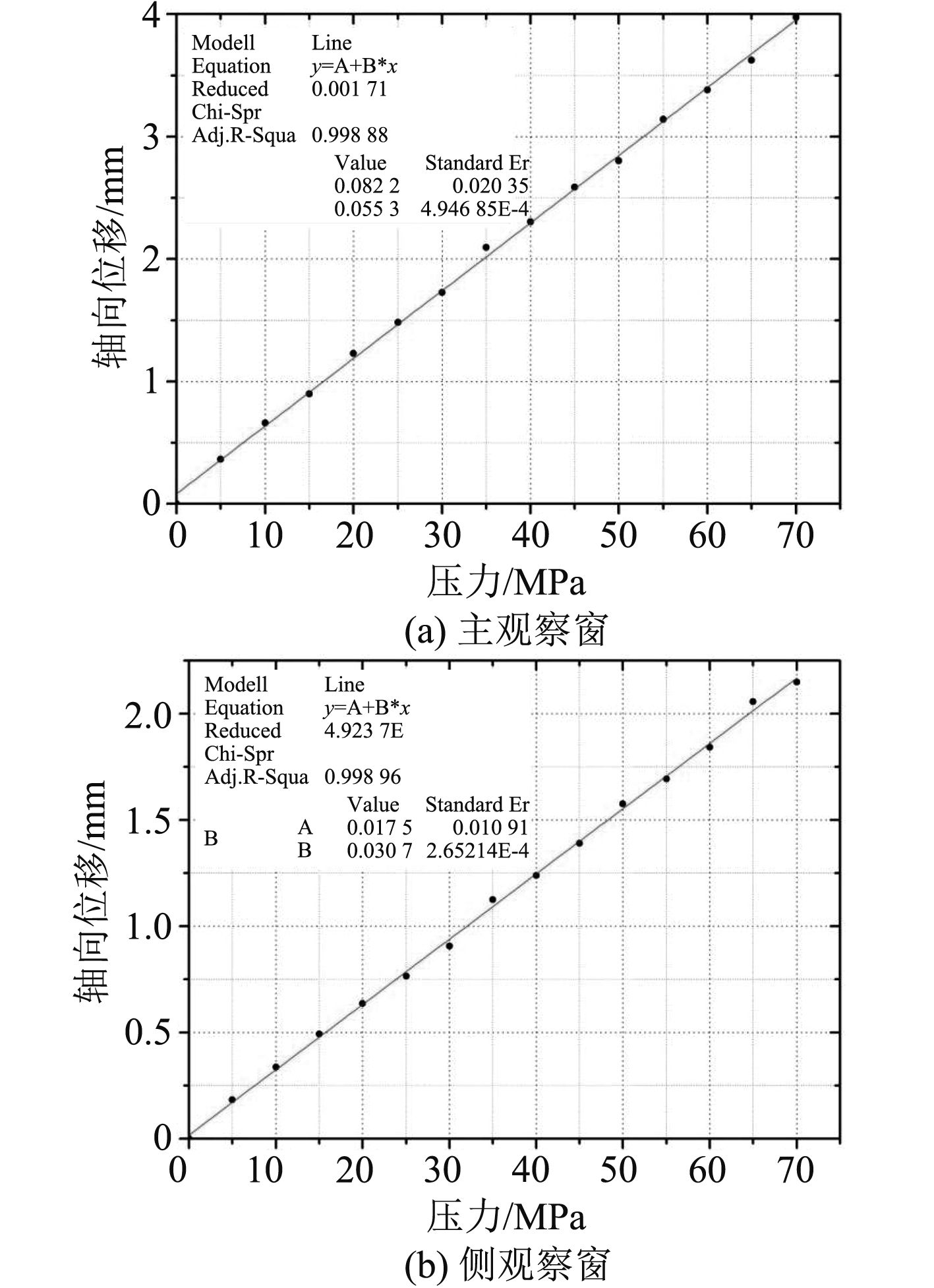
|
图 13 轴向位移拟合 Fig. 13 Curve fitting of the axle displacement |
因此,主观察窗低压面中心的轴向位移的试验拟合值与理论、有限元计算结果的对比如图14和表6所示。

|
图 14 主观察窗的轴向位移对比 Fig. 14 The compare of the axle displacement based on the bigviewport |
|
|
表 6 主观察窗的轴向位移对比 Tab.6 The compare of the axle displacement based on the bigviewport |
在理论分析中,观察窗的实际轴向位移无比接近于自由边界的理论计算值,因此图14只列出了理论计算(自由边界)值。从图中可以看出轴向位移分析结果从大到小依次为:有限元分析(自由边界)、试验拟合、理论计算(自由边界)和有限元分析(固定边界)。由于有机玻璃的粘弹特性,试验加载过程中,不可避免的产生弹性变形以外的蠕变变形,因此试验拟合值略大于理论计算值。另外,有限元分析的结果偏大,即通过有限元分析设计的观察窗趋于保守。
5 结 语针对锥台形观察窗位移、应力建立相应的位移和应力的理论分析模型,对2种边界条件下的位移和应力进行分析;利用有限元分析软件,对比理论计算和有限元分析结果;建立观察窗位移试验台,对主、侧观察窗的轴向位移开展试验研究,并对试验结果进行分析拟合,最后将试验拟合结果与理论计算和有限元分析结果进行对比。对观察窗的Fatigue Life进行分析,分析的疲劳寿命结果代入Miner理论公式中,计算大观察窗和小观察窗的疲劳损伤情况。结果可知:
1)观察窗疲劳损伤情况经过计算,主观察窗的使用寿命为26 432 Circle,侧观察窗的使用寿命为21 359 Circle。
2)对比结果表明:理论计算结果可以较好地反应观察窗上的位移分布,有限元分析结果偏大。理论模型可以较为真实的反映观察窗上的位移和应力分布;但由于有机玻璃的粘弹特性,加载过程不可避免的产生一部分塑性变形,试验结果略大于理论计算结果;另外,有限元分析结果大于试验结果,说明通过有限元设计制造的观察窗将趋于保守。
| [1] |
林景高, 张文明, 冯雅丽, 等. 载人潜水器观察窗研究综述[J]. 船舶工程, 2013 (3): 1–5.
LIN Jingao, ZHANG Wenming, FENG Yali, et al. Review on Viewport Used in Human Occupied Vehicle[J]. Ship Engineering, 2013 (3): 1–5. |
| [2] | KOHNEN W. Human exploration of the deep seas: fifty years and the inspiration continues[J]. Marine Technology Society Journal, 2009, 43 (5): 42–62. DOI: 10.4031/MTSJ.43.5.30 |
| [3] | VEDACHALAM N, RAMADASS G A, ATMANAND M A. Reliability centered modeling for development of deep water Human Occupied Vehicles[J]. Applied Ocean Research, 2014, 46 (11): 131–143. |
| [4] | GALLO N D, CAMERON J, HARDY K, et al. Submersible- and lander-observed community patterns in the Mariana and New Britain trenches: Influence of productivity and depth on epibenthic and scavenging communities[J]. Deep Sea Research Part I Oceanographic Research Papers, 2015, 99 (1): 119–133. |
| [5] | EDWARDS M H, WILKENS R, KELLEY C, et al. Methodologies for Surveying and Assessing Deep-Water Munitions Disposal Sites[J]. Marine Technology Society Journal, 2012, 46 (1): 51–59. DOI: 10.4031/MTSJ.46.1.6 |
| [6] |
施东春, 王帅, 张美荣, 等. 水下运载器球扇形观察窗结构的应力分析[J]. 四川兵工学报, 2014 (7): 139–142.
SHI Dongchun, WANG Shuai, ZHANG Meirong, et al. Stress Analysis on Manned Submersible’s Spherical Sector Viewport Windows[J]. Journal of Sichuan Ordnance, 2014 (7): 139–142. |
| [7] |
宗宇显, 刘道启. 修正的深潜器观察窗应力分析方法[J]. 舰船科学技术, 2014 (1): 38–41.
ZONG Yuxian, LIU Daoqi. A revised stress analysis method of deep-sea submersible viewport[J]. Ship Science and Technology, 2014 (1): 38–41. |
| [8] | LIN J G A, ZHANG W M A, FENG Y L B, et al. Displacement and Stress Analysis of Viewport Used in Human Occupied Vehicle Based on Rayleigh-Ritz[J]. Journal of Ship Mechanics, 2013, 17 (6): 635–644. |
| [9] |
刘道启, 胡勇, 王芳, 等. 载人深潜器观察窗的力学性能[J]. 船舶力学, 2010, 14 (7): 782–788.
LIU Daoqi, HU Yong, WANG Fang, et al. Mechanics analysis on deep-sea Human Occupied Vehicle's view-port windows[J]. Journal of Ship Mechanics, 2010, 14 (7): 782–788. |
| [10] | 岳坤, 田常录. 一种新型深海耐压观察窗的应力分析与优化[J]. 江南大学学报(自然科学版), 2011, 10 (1): 58–62. |
| [11] | GERMAN C R, FORNARI D J, FRYER P, et al. Being there & getting back again: half a century of deep ocean research & discovery with the human occupied vehicle[C]// AGU Fall Meeting Abstracts, 2012. |
| [12] |
宗宇显, 刘道启. 基于弹性半空间理论的深潜器观察窗应力分析[J]. 舰船科学技术, 2013, 35 (2): 60–62.
ZONG Yuxian, LIU Daoqi. Stress analysis of deep-sea vehicle's view-port windows based on elastic half-space theory[J]. Ship Science and Technology, 2013, 35 (2): 60–62. |
| [13] |
刘涛. 大深度潜水器耐压壳体弹塑性稳定性简易计算方法[J]. 中国造船, 2001, 42 (3): 8–14.
LIU Tao. Simplified Method of Inelastic Buckling Analysis of Deep Submersible Pressure Hull[J]. Shipbuilding of China, 2001, 42 (3): 8–14. |
| [14] | 岳坤, 胡勇, 田常录. 深海潜器观察窗的应力分析方法[J]. 固体力学学报, 2011 (s1): 372–375. |
| [15] | 康翌婷, 林景高, 冯雅丽, 等. 潜水器观察窗试验压力容器密封性能分析[J]. 机械设计与制造, 2013 (11): 98–101. DOI: 10.3969/j.issn.1001-3997.2013.11.030 |
| [16] | 罗成利, 姚卫星. 有机玻璃结构疲劳寿命预测的损伤力学方法[J]. 机械强度, 2004, 26 (s1): 87–88. |
| [17] |
岳坤, 田常录. 不同倾角深潜器观察窗应力分析计算方法与比较[J]. 江南大学学报(自然科学版), 2011, 10 (5): 560–563.
YUE Kun, TIAN Changlu. Stress Analysis Method and Comparison of Different Angle of the View-Port Windows of the Deep-Sea Vehicle[J]. Journal of Southern Yangtze University(Natural Science Edition), 2011, 10 (5): 560–563. |
 2017, Vol. 39
2017, Vol. 39
