海洋环境噪声是水声信道中的一种干扰背景场。当利用声呐方程对声呐作用距离进行预报时,要求对海洋环境噪声级进行预估;另外在声呐信号处理方案中,从抗干扰的角度出发,还要求充分掌握噪声场的时空统计特性,找出和利用信号场与噪声场在时空统计特性方面的差异,使声呐系统达到更高的信噪比,以提高声呐设备的抗干扰能力。例如,对无指向性的海洋环境噪声,可以通过设计一个较窄的波束对它进行抑制;而对于有指向性的海洋环境噪声,可以通过设定波束凹槽扫描或零点约束的方法达到抑制噪声的目的。因而,对噪声场的研究与对信号场的研究具有同等的重要性。
近年来,国内外研究者基于不同的模型对海洋环境噪声进行广泛研究,包括环境噪声随深度、频率、地形和舰船密度等环境因素的变化,以及噪声的垂直和水平指向性等。国外Wagstaff [1]和Gaul [2]基于数值计算和实验测量方法研究了北太平洋东部的航船噪声和风关噪声特性,结果表明当接收深度大于临界深度向海底靠近时,航船噪声级明显降低,且在海底附近达到最小值,与临界深度处的噪声级相比,海底附近的噪声级降低了约20 dB。Li[3]对深海低频航船噪声的垂直到达结构进行数值计算。Cavangh [4] 和Carey [5]对低频环境噪声的垂直指向性进行预估。国内中科院声学所将简正波本征函数广义项积分近似应用在了环境噪声场的传播计算上[6–8]。林建恒[9]对风关海洋环境噪声源的静态噪声源和动态噪声源模型进行分析,并对环境噪声源模型的发展方向进行预测,指出破碎浪发声物理模型是当前风关噪声源模型研究的发展方向。
上述海洋环境噪声计算方法大多基于水平海底假设,忽略了地形参数对海洋环境噪声的影响。本文以抛物方程模型为基础,结合声场的互易性,提出一种深海低频航船噪声建模与计算方法,该方法将声源与接收点位置互换,大大降低了声场计算的运行次数和运行时间,而且考虑了海底地形对环境噪声的影响,基于该方法对深海海山附近的航船噪声进行建模计算和特性分析。
1 航船噪声数学模型航船噪声需要分析大范围海域,且远处行船是主要噪声源,这些船离接收水听器几百千米到几千千米甚至更远,因而行船噪声源符合声场传播的远场假设。远场假设决定了航船噪声不仅时间平稳,而且空间平稳。海水中任意一点的噪声是由各个方向传到该点的互不相关的平面波叠加而成。航船噪声的计算示意图如图1所示,首先做以下假设:1)整个海面都是噪声源,接收点
基于以上假设,单位面积内噪声强度可表示为:
| $ns_{jl}^2 = {10^{NS{L_{j,l}}/10}}\text{。}$ | (1) |
将海面所有噪声源加上随机相位后按照划分的面源网格进行叠加得到接收点
| $\begin{split}P(\bar x) = \sum\limits_{l = 1}^L {\exp (i{\psi _l})\sum\limits_{j = 1}^J {\exp (i{\psi _j})n{s_{j,l}}} }\\ \sqrt {are{a_j}} P(\omega ,\bar x,{r_j},{z_s},{\beta _l}) \text{,}\end{split}$ | (2) |
式中:ψl为不同方位的随机相位;ψj为不同距离的随机相位;均在[0, 2π]内均匀分布。
航船噪声源的大面积分布必将导致声场的计算涉及到大面积随地形变化的海域,而抛物方程(Parabolic Equation, PE)模型在计算水平不均匀环境条件下(海底地形随距离变化,声速剖面随距离变化)的声场时相对精确,因而选择PE模型进行声场计算。此外,由于噪声源与接收点的距离往往在几百千米以上,远大于海水深度,因而选择声波按柱面扩展的抛物方程公式。对于一个声源深度为zs,方位角为βl,与接收点距离为rj处的噪声源在接收点
| $P(\omega ,\bar x,{r_j},{z_s},{\beta _l}) = \exp (i{k_0}{r_j})u({r_j},{z_s},{\beta _l})/\sqrt {{r_j}}\text{,} $ | (3) |
式中:k0为参考波数k0=ω/c0,c0=1 500 m/s为海水中的声速。
噪声源范围的选取规则[10]如下:以声基阵位置为圆心,半径从300~3 000 km的环形区域选择为对声基阵处噪声级有贡献的噪声源区域。因为声基阵的近场航船(300 km以内)不属于该处背景噪声的组成部分,应该当成离散干扰源进行单独分析;而对于3 000 km以外的航船,由于声传播衰减很大,对声基阵处航船噪声级的贡献可以忽略不计。如图1(b)所示,深色区域为噪声源区域,首先将圆面划分成L个角度相等的扇形区域,每个扇区的弧度Δβ=2π/L;然后将每个扇区等距离划分成J个扇环,扇环宽度为Δr,每个扇环被视为一个面源,共有L×J个面源,将这些面源在阵元上产生的声压叠加起来,即可得到该处的噪声级。
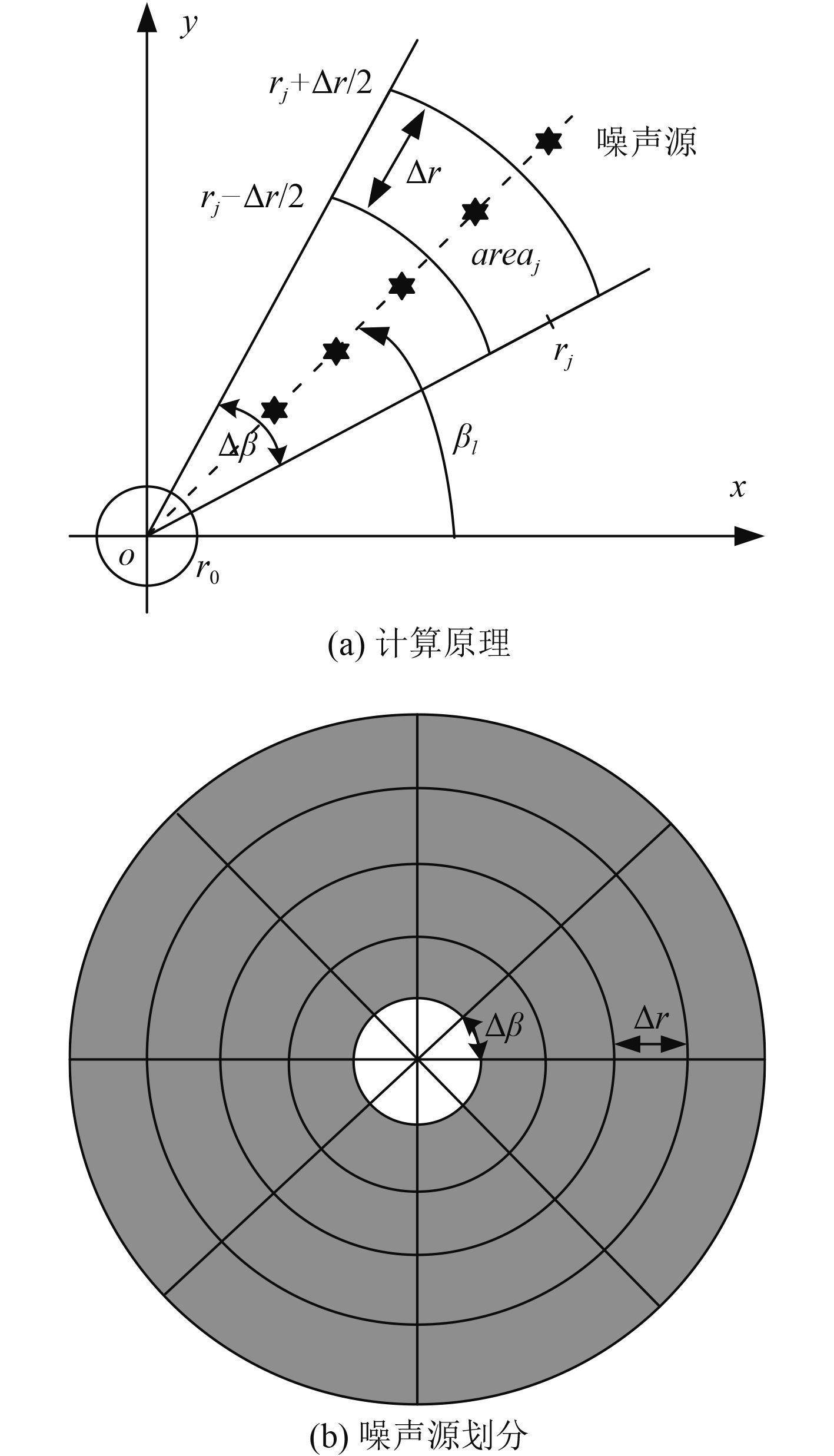
|
图 1 航船噪声计算示意图 Fig. 1 Calculation process of shipping noise |
在真实的海洋波导中,海水深度、声速剖面和海底参数等都随距离变化,特别是海深的变化更为明显。对于求解随距离变化波导中的声学问题,抛物方程模型非常有效。对于随距离变化的波导环境,采用直接方法计算单个扇区的声场示意图如图2(a)所示,H1为声基阵处的海深,H2为较远距离处的海深,对于阵元个数为Np的垂直线列阵,声场每计算一次,只能得到单个声源在Np个接收阵元上的归一化声压。由于各个方向和位置对应的地形和噪声强度有差异,要得到每个阵元的总声压级,每个噪声源都必须单独进行一次声场运算,因而采用直接法共需要进行MD=J×L次声场计算。根据声场的互易性[11],将声源与接收点位置反转,如图2(b)所示,声场每计算一次,可以得到单个声源在J个接收阵元上的归一化声压。要得到每个阵元的总声压级,采用互易方法时声场的计算次数为MR=Np×L次。
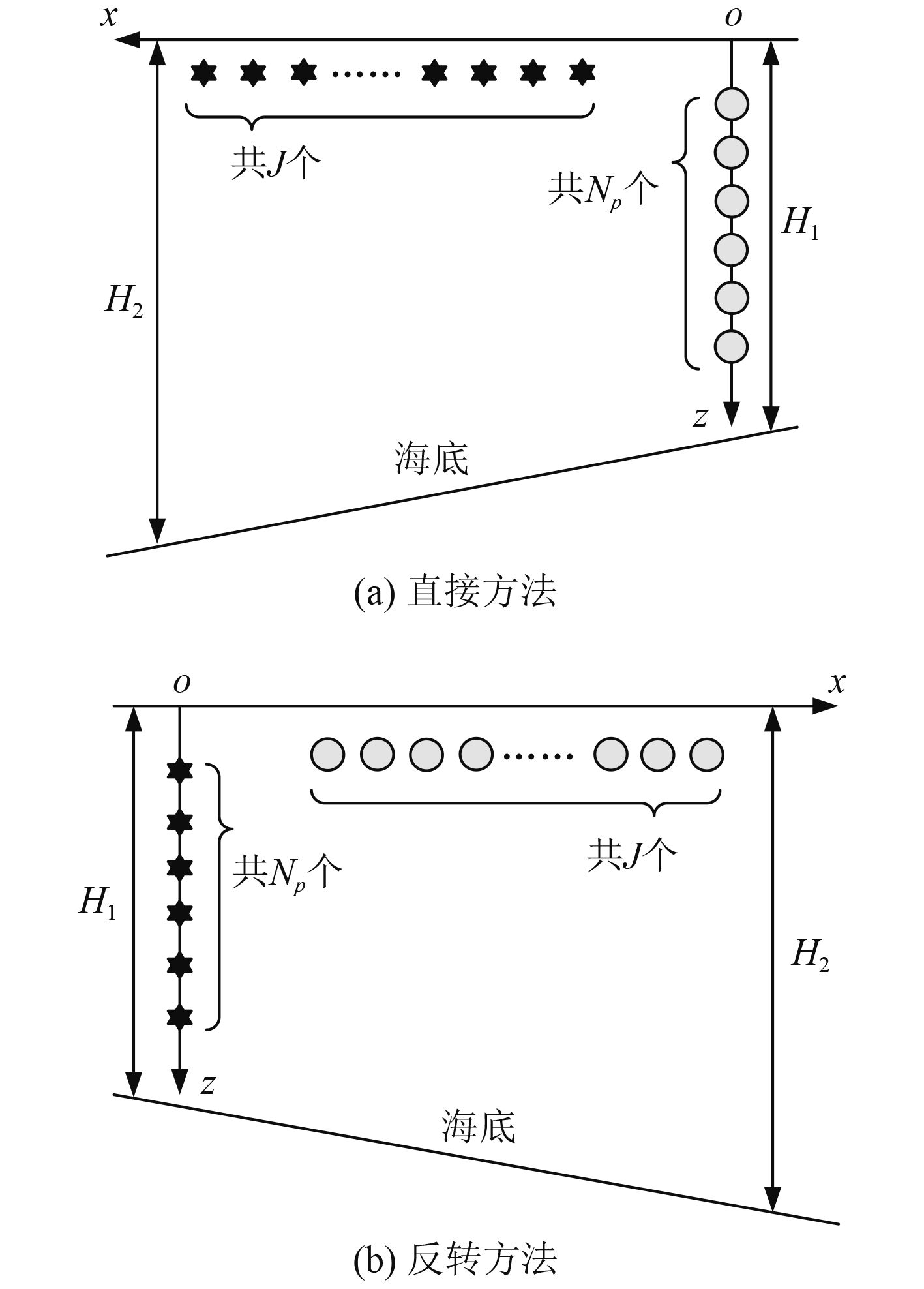
|
图 2 某一扇区方向噪声源与接收阵元的位置关系 Fig. 2 Parabolic equation for the field computations on bearing βl |
当计算距离为R,距离上的步长为Δr,声基阵处的海深为H1,阵元间距为Δd时,分别采用直接法和互易方法时的声场运行次数之比为:
| $\frac{{{M_D}}}{{{M_R}}} = \frac{{R/\Delta r}}{{{H_1}/\Delta d}} \cdot \frac{L}{L} = \frac{{R \cdot \Delta d}}{{{H_1} \cdot \Delta r}}\text{。}$ | (4) |
由于航船噪声计算距离要到几千千米,而接收阵元个数一般只有几十个,使得某一方向上声源个数远远大于接收阵元个数,这样就大大地降低了声场的运行次数。例如:计算距离为R=3 000 km,Δr=1 000 m,声基阵处的海深H1=5 km,Δd=200 m;则MD/MR=120。由此可见,在距离变化的海洋波导中,采用互易方法计算航船噪声可以大大降低声场计算的运行次数。
航船辐射噪声源主要由机械噪声、螺旋桨噪声和水动力噪声构成,而噪声强度往往与航船吨位大小直接相关。广阔的海域中分布着各种类型的航船,不能采用式(1)中单一的形式来表示航船噪声的强度级。按照吨位从大到小将航船分成5类,分别为:超级油轮、大型油轮、商船、普通油轮和渔船。文献[11]中的ANDES模型给出了各种类型航船的声源级综合考虑各种类型航船对单位面积内噪声强度的贡献,引入下式计算单位面积内的航船噪声的声强级[10]:
| $ns_{j,l}^2 = {(1.852)^{ - 2}} \times {10^{ - 9}}\sum\limits_{st = 1}^5 {{d_{j,l}}(st) \cdot {{10}^{SSL(f,st)/10}}} \text{。}$ | (5) |
式中:st为航船类型,st=1, 2, …, 5分别对应5种航船类型;dj, l(st)为每1 000平方海里内其中一种类型航船的个数;SSL(f, st)为其中一种类型航船的噪声声源级。
2 海山周围航船噪声建模与分析 2.1 深海海山周围的声传播损失深海海山主要形成于海底火山的作用,分布于大洋的每个角落,根据外形可分为尖峰海山和平顶海山。由于地理位置的差异,海山的形状、大小各不相同,单个模型难以呈现出所有复杂的海山地貌,但简单模型可以普遍地反映出海山对深海声传播的影响,而这对典型海山地形条件下的环境噪声场建模以及被动声呐探测具有一定的指导意义。假定某深海尖峰海山的几何形状类似于一个圆锥体,如图3(a)所示,海山顶端深度位于海面以下1 000 m处,海山侧面斜坡的坡度θ=14°,海洋深度为5 000 m。图3(b)为海山在不同方向的截面形状,当βl=0°时,海山的截面为三角形,此时海山底端的跨度最大,大约为33 km。
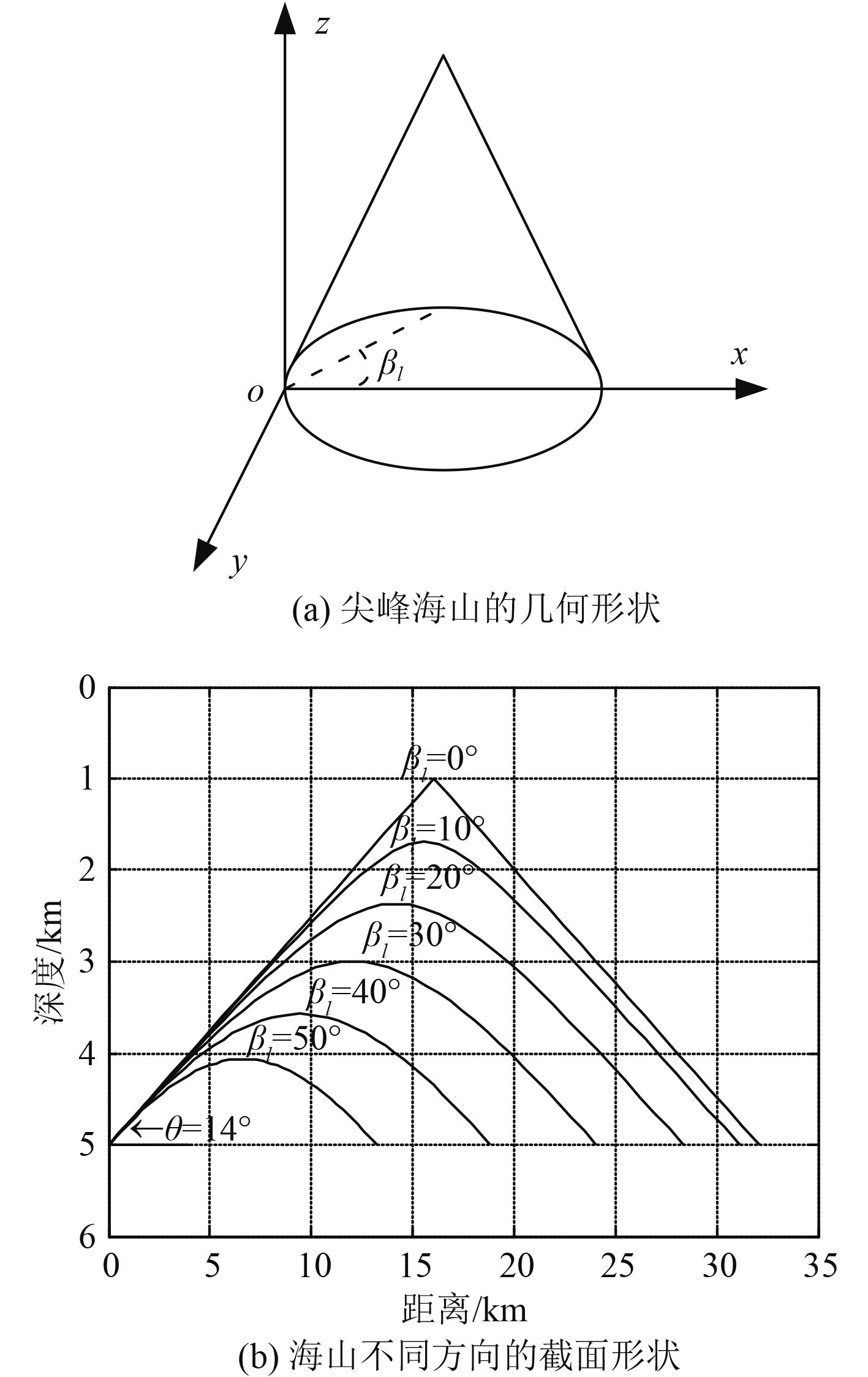
|
图 3 海山几何形状与不同方向的截面形状 Fig. 3 Seamount(a) performs like a cone,(b) the section view of the seamount |
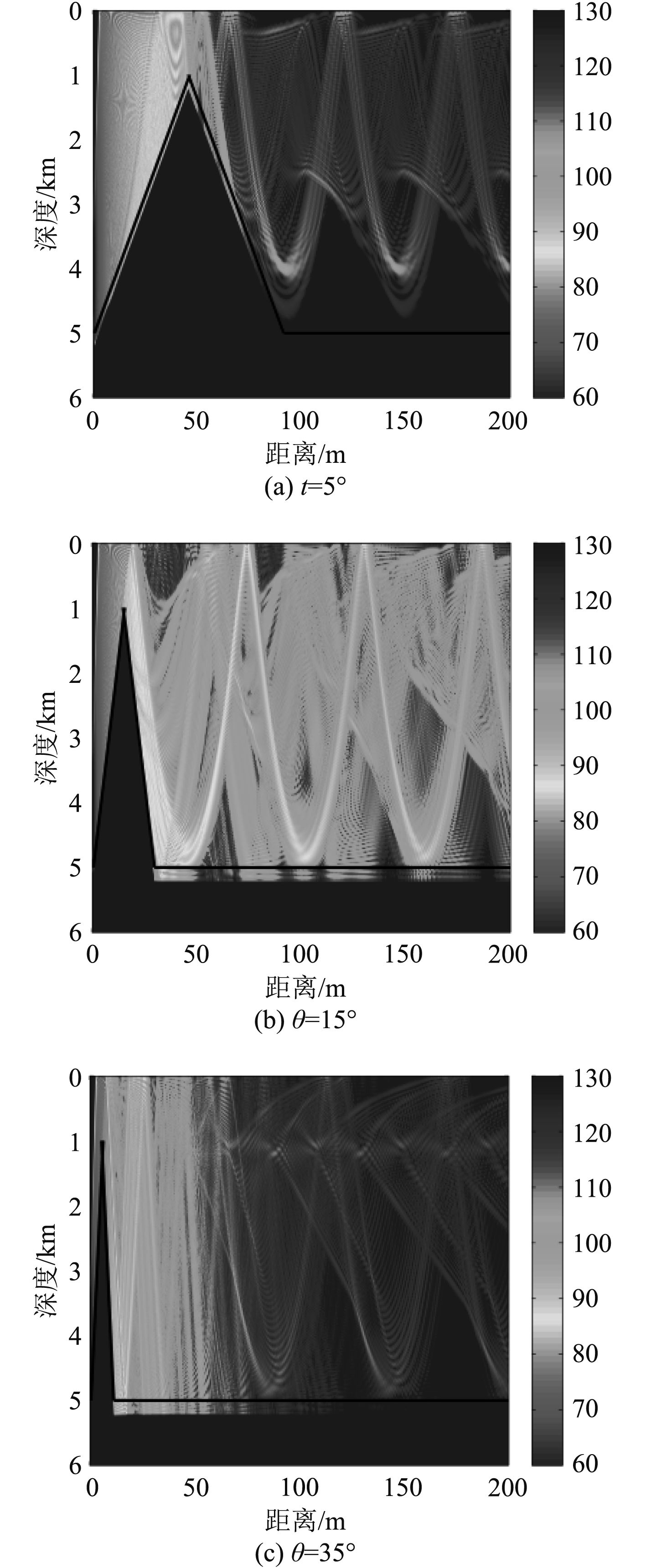
声速剖面采用经典的深海Munk[12]声速剖面,海底参数按深海平原底质选取,设定好环境参数和收发位置后,采用RAMGEO[13]软件对PE声场模型进行求解。计算得到声源与海山不同位置关系时的声传播损失如图4所示,图中色标单位为dB,声源频率为100 Hz。图4(a)和图4(b)分别对应声波从βl=0°和βl=30°方向经过海山时的传播损失,声源位于z轴上,深度均为4 800 m;由图可知声波从βl=0°方向经过海山时的传播损失明显大于从βl=30°方向经过时的传播损失,主要原因是海山在βl=0°方向的截面高度和跨度都比βl=30°方向的大,对声波的遮挡效果更明显。图4(c)和图4(d)中声源深度均为10 m,声源离海山的距离r分别为30 km和110 km,βl=0°;从图中可以看出,当r=30 km时,海山遮挡了声波的绝大部分能量,而当r=110 km时,海山对声波的遮挡效果不明显;因而声源和海山的几何位置关系对声传播损失具有较大影响。

|
图 4 声源与海山不同位置关系时的声传播损失 Fig. 4 Transmission loss for different geometrical relationship between sources and seamount |
本节主要分析海山对航船噪声指向性的影响,忽略航船噪声源空间分布的影响,假定航船噪声源各向均匀分布且强度相等,在50 Hz时的强度级(NSLj, l)为65 dB,参考值为1 μPa2/Hz/m2@1 m。计算得到海山周围航船噪声的水平指向性如图5(a)所示,接收阵元均位于图3(a)中的oz轴上,图中极坐标半径对应的单位为dB,圆周方向与βl一一对应,单位为(°),图中3条曲线对应的接收阵元深度分别为4 000 m、3 000 m和2 500 m。从图中可以看出,在有海山的遮挡的方向,航船噪声级都受到不同程度的遮挡,而且噪声级在βl=0°方向时最小,比βl=180°方向(无海山遮挡)的噪声级小5 dB左右。将一个孔径为300 m的VLA布放于海山顶端正上方50 m~350 m处,阵元间距取半波长,计算得到海山顶端航船噪声的垂直指向性如图5(b)中的虚线所示,从图中可以看出,航船噪声在垂直方向的指向性有4个峰值,分别位于
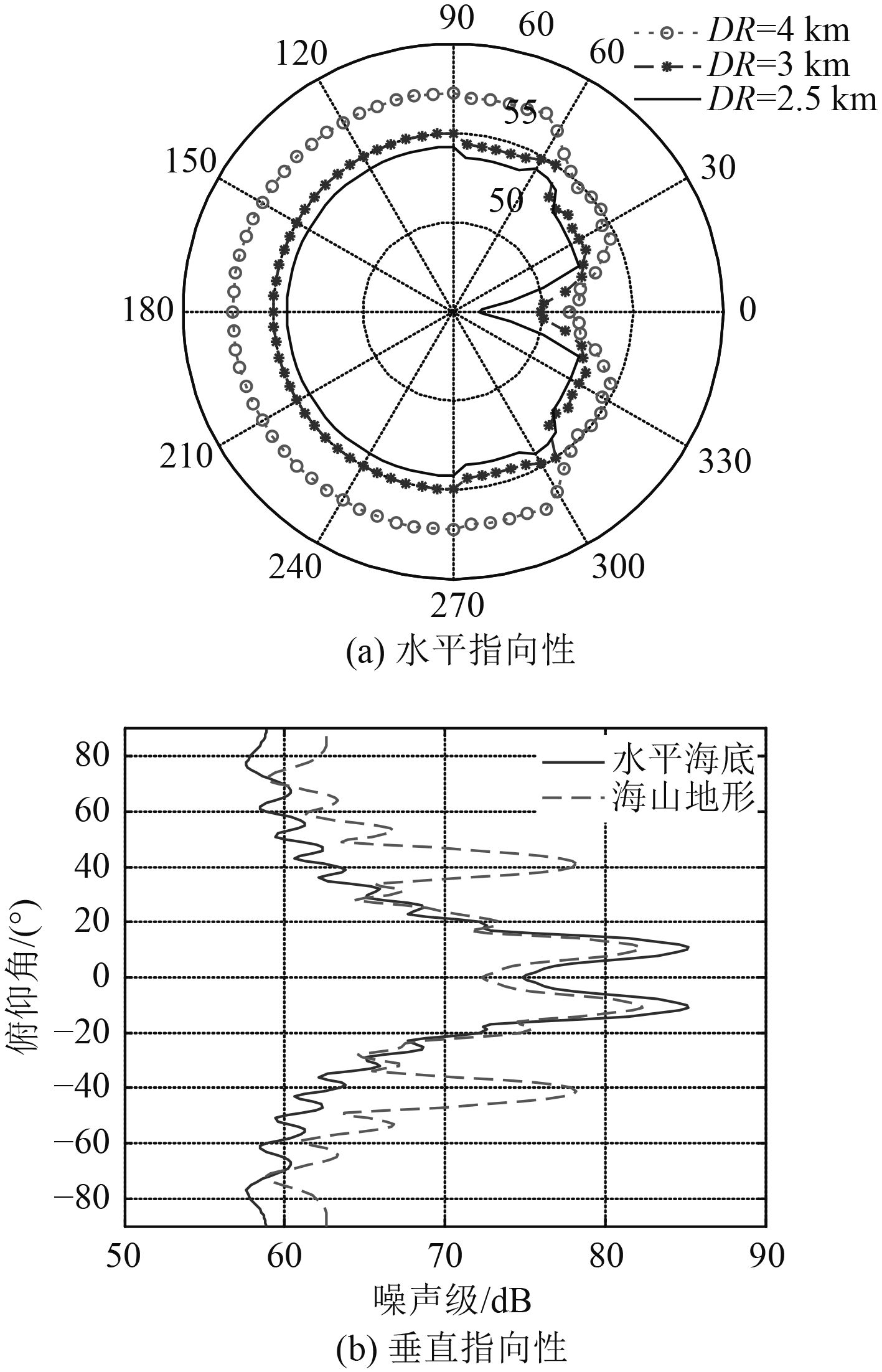
|
图 5 海山附近航船噪声的指向性 Fig. 5 Directivities of shipping noise close to a seamount |
本节主要分析海山地形对其周围航船噪声级的影响,忽略航船噪声源空间分布的影响,假定航船噪声源各向均匀分布且强度相等,在50 Hz时的噪声强度级为65 dB,参考值为1μPa2/Hz/m2@1 m。计算得到海山附近航船噪声场如图6所示,图色标单位为dB。图6(a)为βl=0°方向(Δβ=10°)的噪声源在该方向截面上产生的噪声场,从图中可以看出,有海山遮挡的扇区噪声源在该截面产生的噪声场明显受到海山截面形状的影响。图6(b)为所有航船噪声源(36个扇区)在海山对称截面产生的总噪声场,从图中可以看出,海山对其周围的航船噪声总级具有较小影响,在海山顶端附近的噪声级相比远处下降了2 dB左右,其他位置的噪声级变化不大,主要原因是海山只能遮挡少数方向上的航船噪声,因而海山的遮挡对总噪声级的影响较小。
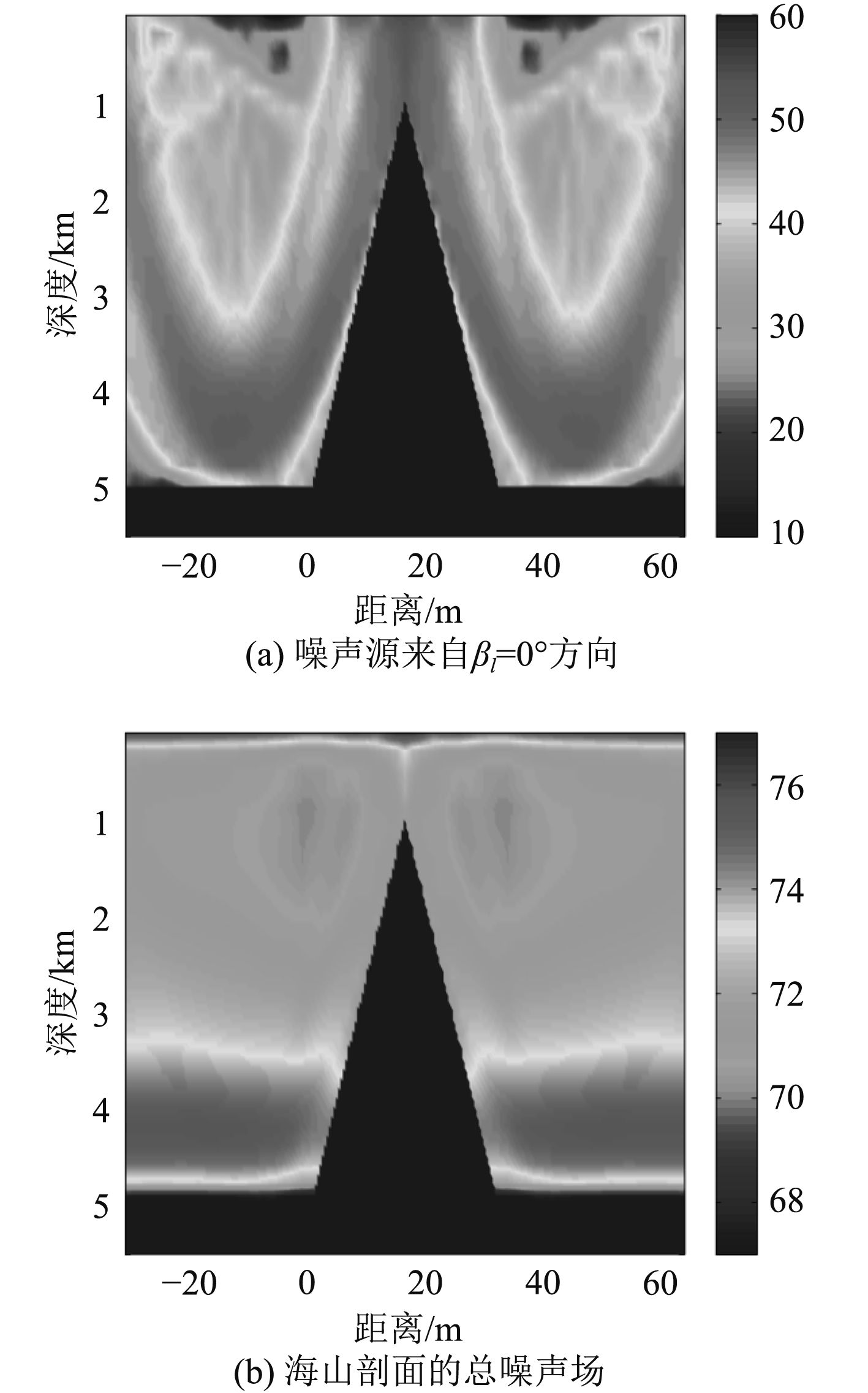
|
图 6 海山剖面的航船噪声场 Fig. 6 Shipping noise field close to the seamount |
航船噪声级随深度的变化关系如图7所示,图中接收阵元位于图3所示的oz轴上。图7(a)为βl=0°,Δβ=10°扇区内的噪声源在接收阵元上产生的噪声级随深度的变化关系,从图中可以看出,有海山遮挡时的噪声级明显低于水平海底时的噪声级。图7(b)为所有噪声源(36个扇区)在接收阵元上产生的总噪声场随深度的变化关系,从图中可以看出,海山对总噪声级的影响不大,与水平海底相比,有海山遮挡时的总噪声级降低了大约2 dB,这种现象也能由图5(a)进行解释。
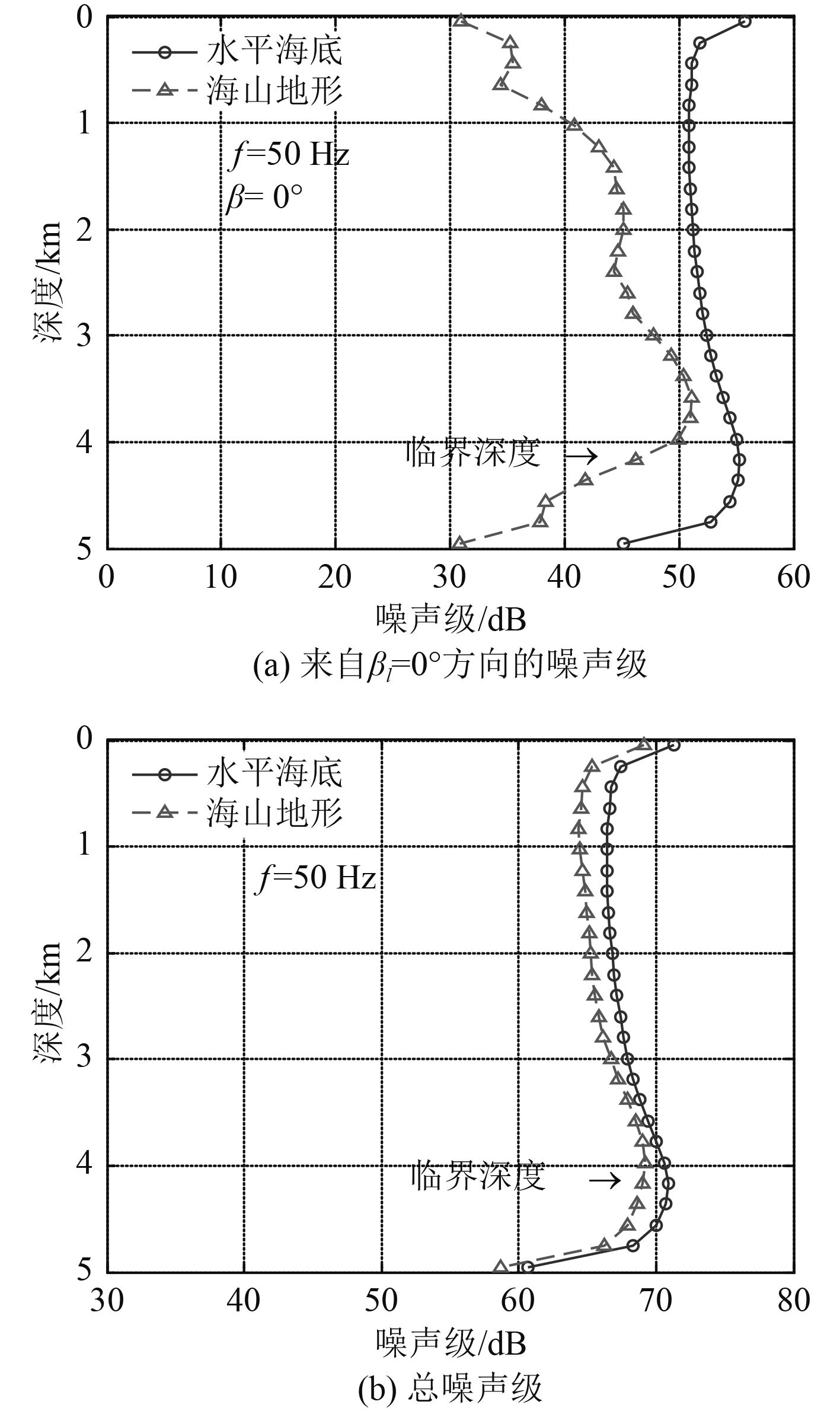
|
图 7 航船噪声级随深度的变化关系 Fig. 7 Shipping noise as a function of depth |
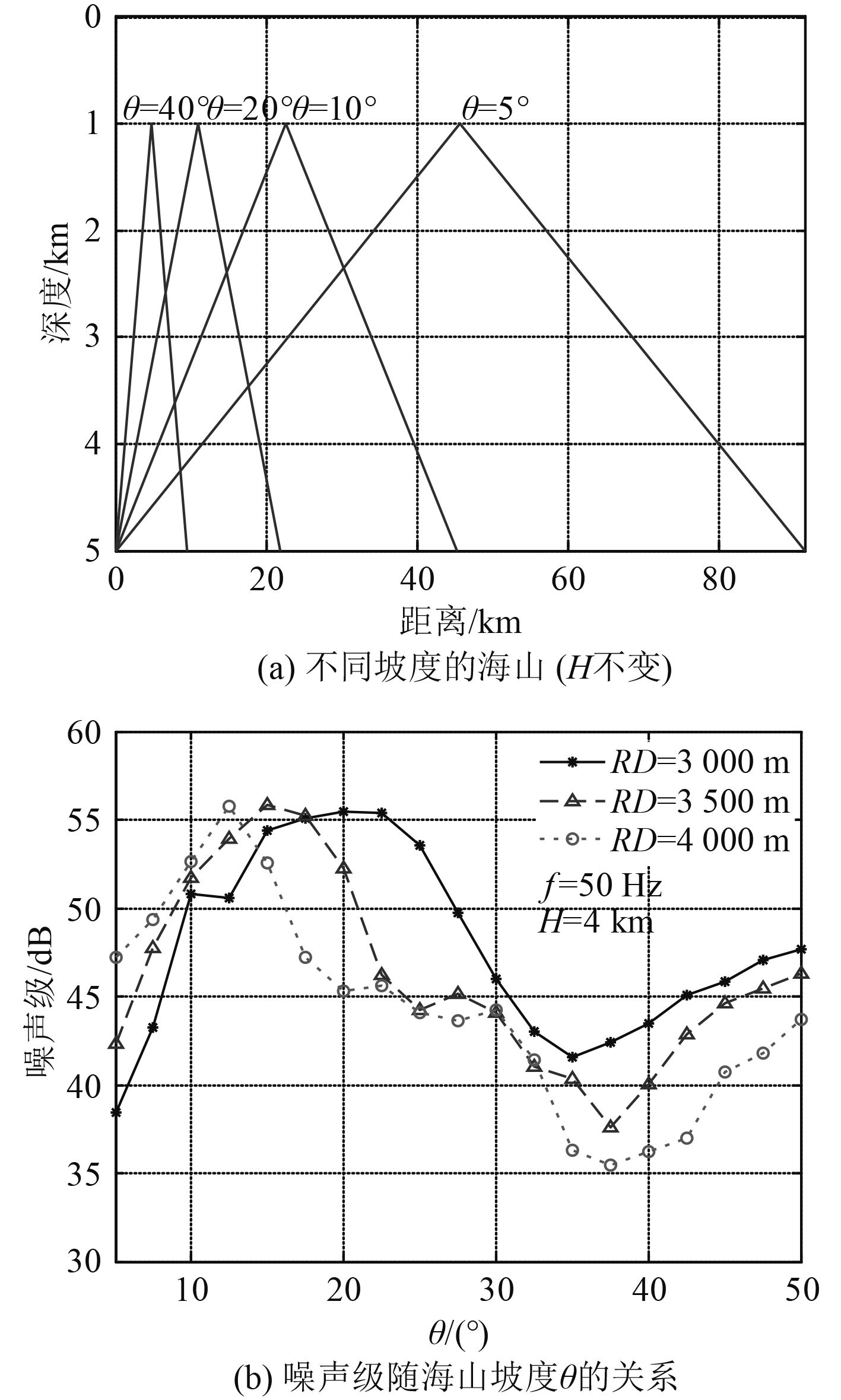
本节主要分析海山高度H和坡度θ对oz轴上阵元接收噪声级的影响,噪声源区域只考虑βl=0°方向的扇区(Δβ=10°);忽略航船空间分布的影响,假定航船噪声源均匀分布且强度相等,在50 Hz时的强度级为65 dB,参考值为1μPa2/Hz/m2@1 m。计算得到βl=0°方向的航船噪声级随海山几何参数的变化关系如图8所示,图中H为海山高度、θ为海山坡度、RD为接收阵元深度。图8(a)中海山跨度保持不变,高度H从1 000 m依次升高至4 000 m,从图8(b)中可以看出,航船噪声级随海山高度H的增大在整体上呈下降趋势。
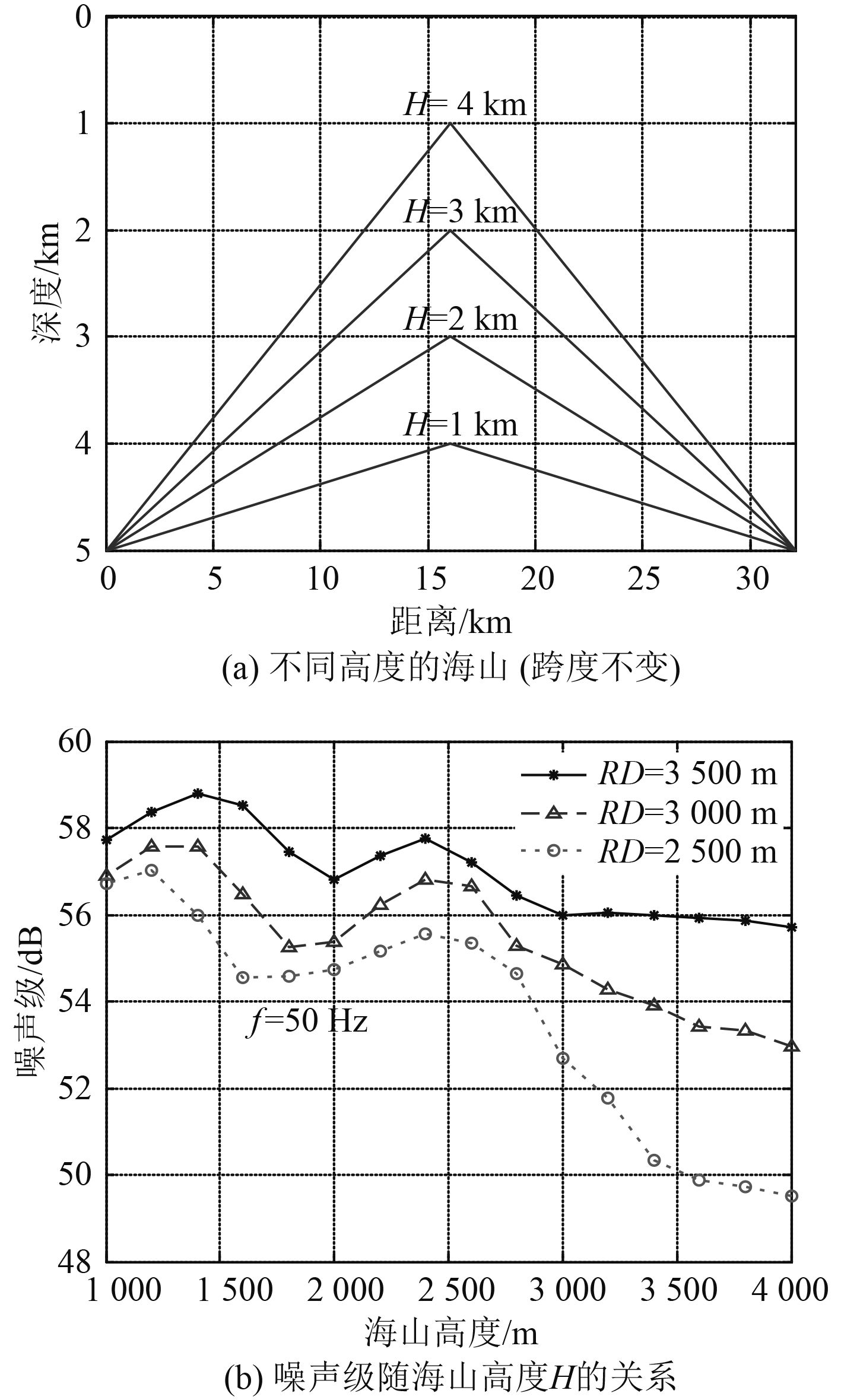
|
图 8 噪声级随海山高度的变化关系(跨度保持不变) Fig. 8 Shipping noise changing by height of the seamount with the same width |
图9(a)中海山坡度θ保持不变,高度H从1 000 m依次升高至4 000 m,从图9(b)中可以看出,航船噪声级随海山高度H的增大在整体上也是呈现出下降趋势。出现上述2种现象的主要原因是海山对声波的遮挡效果随海山高度的增大而更加明显,但由于海山山坡对声波的反射效果有差异,使得它们的变化规律呈现出一定的差异。
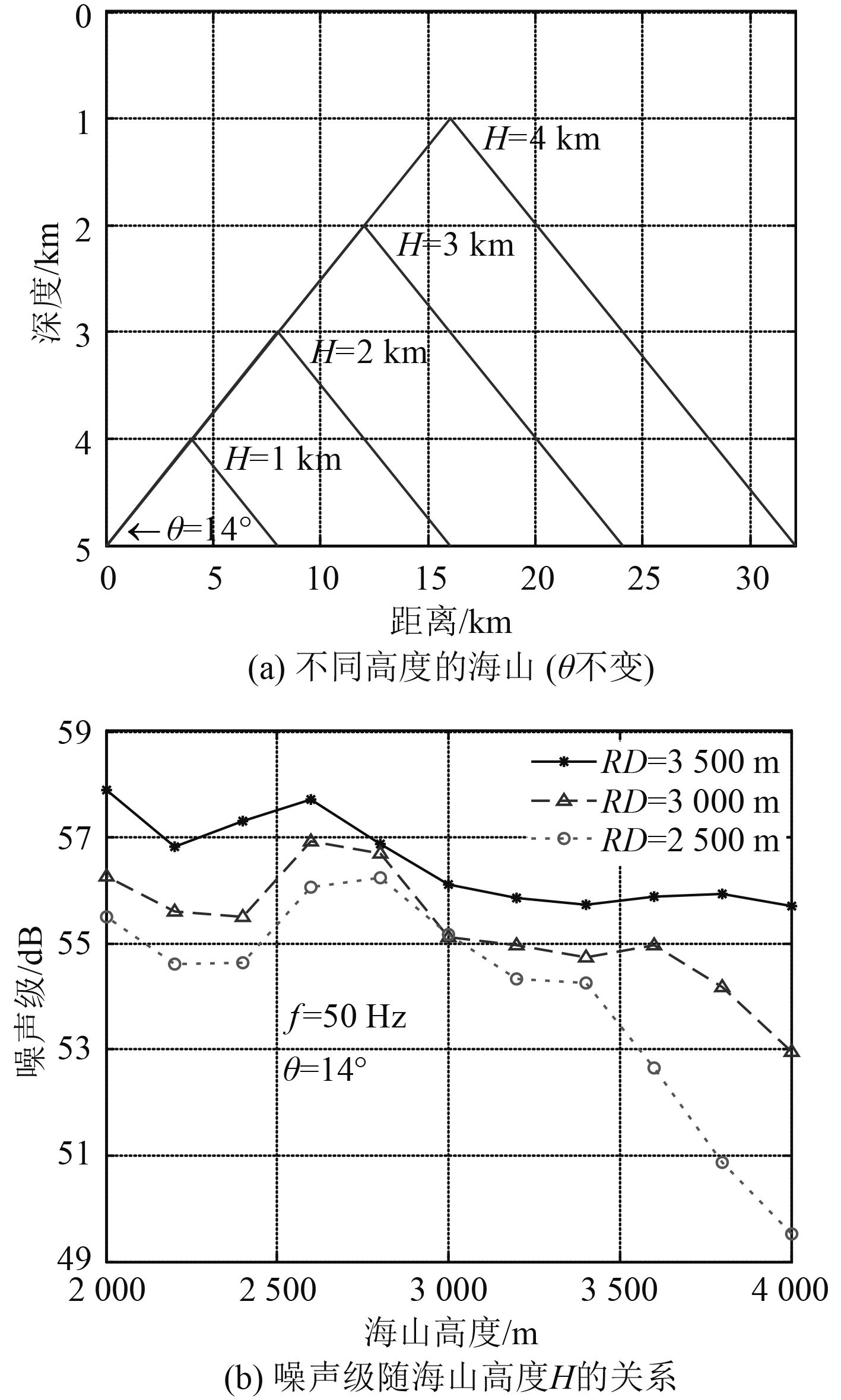
|
图 9 噪声级随海山高度的变化关系(坡度保持不变) Fig. 9 Shipping noise changing by height of the seamount with the same slope |
图10(a)中海山高度H保持不变,坡度θ从5°依次增大至50°,从图10(b)中可以看出,航船噪声级随海山坡度θ的增大呈起伏波动的趋势;这种接收噪声级的波动现象可由图11中的传播损失随海山坡度θ的变化规律进行解释,从图11中可以看出传播损失随海山坡度θ也呈现出类似的起伏规律,根据声场的互易性,接收水听器处的噪声级也呈现出起伏现象。
|
图 10 噪声级随海山坡度的变化关系(高度保持不变) Fig. 10 Shipping noise changing by slope of the seamount with the same height |
|
图 11 传播损失随海山坡度θ的关系 Fig. 11 Transmission loss changing with slope of the seamount |
深海海样环境噪声对声呐作用距离具有重要影响,充分掌握海洋环境噪声的时空统计特性,可以大大提高声呐设备的抗干扰能力。单个模型难以呈现出所有复杂的海洋地貌,但简单模型可以普遍地反映出海山对深海声传播的影响,这对典型海山地形条件下的环境噪声场建模以及被动声呐探测具有重要的指导意义。
本文以抛物方程模型为基础,结合声场的互易性,提出了一种深海低频航船噪声建模与计算方法,该方法将声源与接收点位置互换,大大降低了声场计算的运行次数和运行时间,基于该方法对深海海山附近的航船噪声进行了建模计算和分析。研究结果表明:海山对声传播损失的影响取决于接收阵元与海山的位置关系以及海山的几何参数。海山附近航船噪声的水平指向性具有不均匀性,在有海山遮挡的方向噪声级明显低于无海山遮挡的方向。由于海山的遮挡与反射作用,海山附近航船噪声的垂直指向性会出现多个峰值。此外,海山只对接收阵元某些方向的噪声具有遮挡效果,因而对接收水听器的总噪声级具有较小影响。
| [1] | WAGSTAFF R A. An ambient noise model for the Northeast Pacific Ocean Basin[J]. IEEE J. Ocean. Eng., 2005, 30 : 286–294. DOI: 10.1109/JOE.2004.836993 |
| [2] | GAUL R D, KNOBLES D P, SHOOTER J A, WITTENBORN A F, et al. Ambient noise analysis of deep-ocean measurements in the Northeast Pacific[J]. IEEE J. Ocean. Eng., 2007, 32 (2): 497–512. DOI: 10.1109/JOE.2007.891885 |
| [3] | LI Z Z, ZURK L M, MA B. Vertical arrival structure of shipping noise in Deep Ocean channels[C]// IEEE Conference Publication, OCEANS 2010, 20–23 Sept, 2010: 1–8. |
| [4] | CAVANGH R C, RENNER W W. Vertical directionality and depth dependence of averaged acoustic signal and noise[J]. J. Acoust. Soc. Am., 1980, 68 : 1467–1474. DOI: 10.1121/1.385114 |
| [5] | CAREY W M, EVANS R B, DAVIS J A, BOTSEAS G, et al. Deep-ocean vertical noise directionality[J]. IEEE J. Ocean. Eng., 1990, 15 (4): 324–334. DOI: 10.1109/48.103528 |
| [6] | WANG Q, ZHANG R H. Range and depth-averaged field in Ocean sound channels[J]. J. Acoust. Soc. Am., 1990, 87 : 633–638. DOI: 10.1121/1.398932 |
| [7] | WANG Q, ZHANG R H. Sound spatial correlation in shallow water[J]. J. Acoust. Soc. Am., 1992, 92 (2): 932–938. DOI: 10.1121/1.403963 |
| [8] | 张仁和. 浅海声场的平滑平均理论、数值预报与海底参数反演[J]. 物理学进展, 1996, 16 (3): 489–496. |
| [9] | 林建恒, 衣雪娟, 陈鹏, 等. 风关海洋环境噪声源模型[C]// 声学技术, 全国声学学术会议论文集, 2006, 53–54. |
| [10] | CAREY W M, EVANS R B. Ocean ambient noise measurement and theory[M]. New York: Springer-Verlag New York Press, 2011: 99–125. |
| [11] | RENNER W. Ambient noise directionality estimation system technical description[J]. Science Applications International Corporation, McLean, VA, 1986, 23 : 1645. |
| [12] | MUNK W. Sound channel in an exponentially stratified ocean with applications to SOFAR[J]. J. Acoust. Soc. Am., 1974, 55 : 220–226. DOI: 10.1121/1.1914492 |
| [13] | COLLINS M D. A split-step pade solution for parabolic equation method[J]. J. Acoust. Soc. Am., 1993, 93 : 1736–1742. DOI: 10.1121/1.406739 |
 2017, Vol. 39
2017, Vol. 39
