2. 中国海洋大学 工程学院, 山东 青岛 266100
2. Ocean University of China, College of Engineering, Qingdao 266100, China
结构安全性是放在结构设计的第一位,同样在船舶与海洋工程的设计中,结构的安全性是工程师研究的重点。通常加筋板和船体梁的破坏也先是由板格的屈曲破坏开始[1 – 2] ,因此其极限强度的准确计算对于船舶与海洋工程结构的强度评估具有重要意义。
非线性有限元方法可以较好解决船体板的后屈问题,得到其极限强度的数值解。因此许多学者对该方法进行深入研究。
Imtaz Khan等[3] 采用有限元软件Abaqus分析单轴压力作用下船体板格的极限强度。Paik等[4]采用Ansys,DNV PULS和ALPS/ULSAP等方法研究了板格在受到双轴压缩和侧向压力共同作用下的极限强度。Raviprakash等[5]应用非线性有限元软件,研究在轴向压缩载荷作用下带有初始凹痕的不同厚度的正方形薄板极限强度。Sultana等[6]通过非线性有限元软件,完成在局部点蚀的影响下平板极限强度的计算。张婧等[7]采用非线性有限元法对带有初始变形及受轴向侧向压力同时作用的复杂受力状态下结构的极限承载力进行研究,表明结构的初始缺陷及侧向压力将明显降低其极限承载力。张少雄等[8]运用有限元软件Ansys分析单轴压力作用下的凹痕板的极限强度特性。黄一等[9]通过非线性有限元与模型试验的方法研究点蚀对于单轴压下板的极限强度影响。
本文采用Abaqus软件中的弧长法计算文献[3]中列出9种船体板格模型受轴向压力作用下的极限强度,并将计算结果与其他学者的理论结果进行比对,证明本文计算方法的可信度。然后分别考虑加筋板材料、初始缺陷、模型网格密度、边界条件等敏感因素对该有限元方法计算结果的影响,给出具体的误差结果。
1 弧长法随着计算机仿真技术的快速发展,非线性有限元法已成为计算和评估结构极限承载能力的有效方法,采用非线性有限元方法进行分析,计算结果可视化程度较高,较好地捕捉结构的受力过程,且计算结果具有一定的准确性,是计算结构极限强度的主要方法,其计算流程如图1所示。
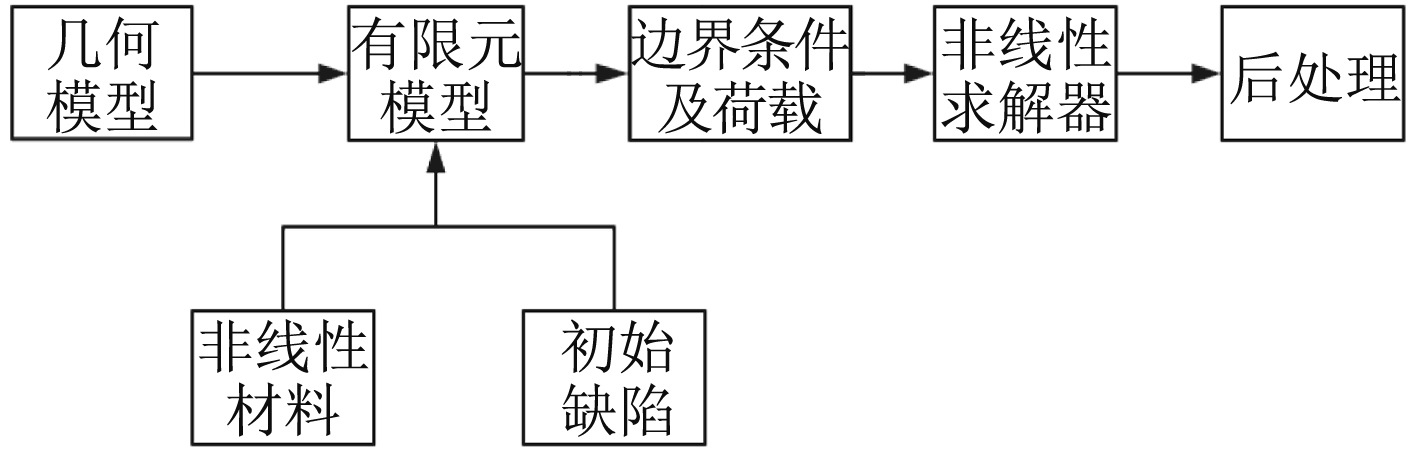
|
图 1 非线性有限元分析流程 Fig. 1 Nonlinear finite element analysis process |
弧长法是一种稳定高效的非线性有限元分析方法。为了求解结构非线性静态平衡方程式(1):
| ${P} - {I} = 0\text{,}$ | (1) |
式中:P为载荷列阵;I为内力列阵。
弧长法通过设置一个弧长参数来控制平衡方程的增量迭代和收敛,可以将式(1)写成式(2)增量形式:
| ${K}_T \Delta u = \Delta P - R \text{,}$ | (2) |
式中:KT为切线刚度矩阵;Δu为位移增量;ΔP为载荷增量;R为残差力。
设第i步迭代的载荷增量为ΔPi,由载荷增量因子Δλi和参考载荷Pref来控制,即
| ${\Delta P} _i = \Delta {\lambda _i}{ {{P_{ref}}} }\text{。}$ | (3) |
将式(3)代入式(2)得到第i步迭代的增量格式:
| $ {{{K}_T}} { {\Delta u} } = \Delta {\lambda _i}{ {{P_{ref}}} } - {{ R }_i}\text{。}$ | (4) |
如图1所示,弧长法在求解中,是把上一步增量计算的平衡点看做圆心,弧长增量Δli为半径,经过牛顿-拉普森迭代找到下一步增量平衡点。每一步的弧长增量Δli、载荷增量因子Δλi以及位移增量{Δu}i均通过下面的约束方程来控制:
| $\left| {\Delta {l_i}} \right| = \sqrt {{{\left| {\left\{ {\Delta {u_i}} \right\}} \right|}^2} + {{\left| {\Delta {\lambda _i}\left\{ {{P_{ref}}} \right\}} \right|}^2}} \text{。}$ |
经过不断的迭代,一直到残差力控制在容差Ri之内。第i步迭代完成时有:
载荷列阵
位移列阵
弧长
在弧长增量Δli中,由于同时有载荷增量ΔPi和位移增量Δui,因此弧长法能跟踪结构在“加载”和“卸载”整个过程中的载荷-位移路径曲线。
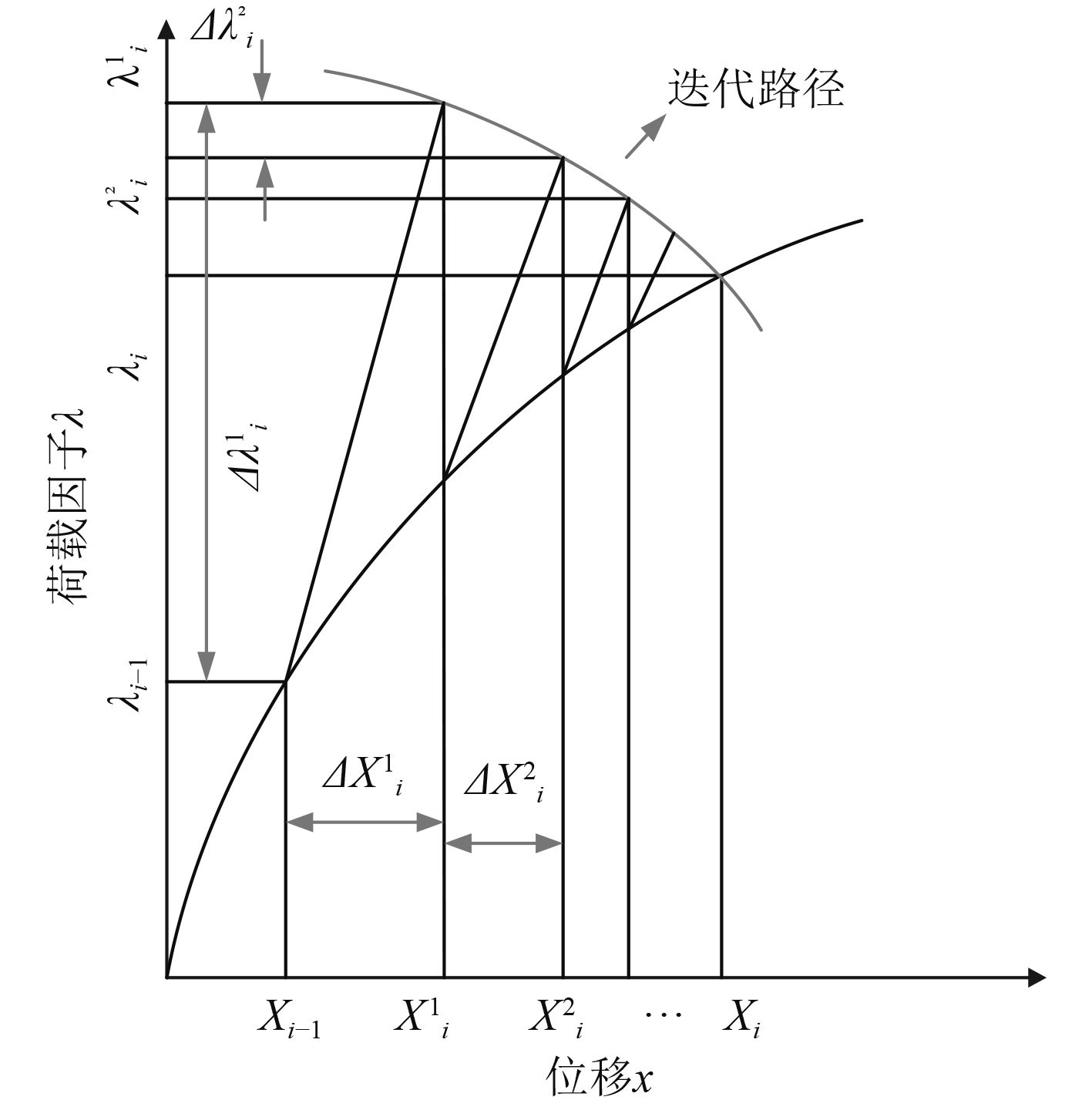
|
图 2 弧长法示意图 Fig. 2 Arc length schematic diagram |
在1883~1975年板格的极限强度计算主要是采用以下几个比较常用的经验公式来进行计算[3]。
BOX(1883):
Von Karman(1924):
Frankland(1940):
Faulkner(1975):
其中板格柔度
目前随着计算机性能不断提高,有限元方法也被普遍采用。本文采用Abaqus软件中弧长法对9种不同柔度的船体板格模型进行极限强度计算,如表1所示。
|
|
表 1 9类柔度板格尺寸,mm Tab.1 Typical sizes of 9 types of plate, mm |
模型材料采用HT32钢材的理想应力应变关系如图3所示。屈服极限为σs=315 MPa。
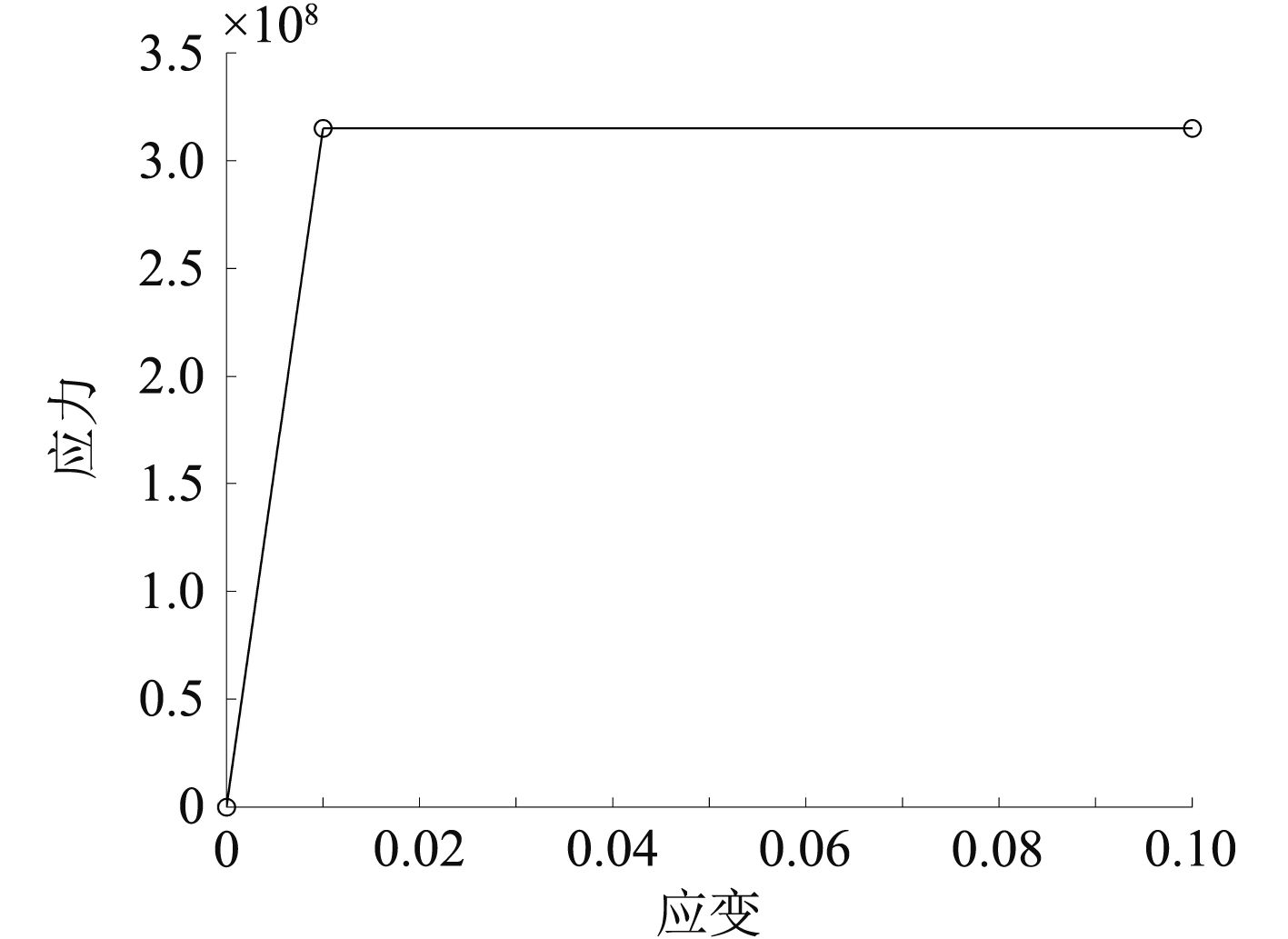
|
图 3 HT32钢材的理想应力应变关系 Fig. 3 The ideal stress-strain relationship of HT32 steel |
单元类型均为四节点的四边形单元,边长约为40 mm,约束AB边及CD边绕y轴及z轴的转动自由度;AD及BC边在z向固定,同时约束绕y轴及z轴的转动自由度;在AD边及BC边设置参考点,使AD边及BC边沿x轴方向具有相同的位移,如图4所示。
模型采用右手笛卡尔坐标系,坐标x和y在板格平面内,x轴与板格的AB边方向平行,y轴与板格AD边方向平行,z轴垂直于xy平面。

|
图 4 B类板格的数值模型 Fig. 4 The numerical model of the class B grid |
采用有限元法首先板格模型进行特征值屈曲分析,然后将分析结果作为初始缺陷引入到后屈曲分析中,由于低阶模态相比高阶模态具有更小的应变能,结构更有可能按照低阶模态的形状变形,一般选择低阶模态作为初始缺陷,如图5所示。比例因子一般按公式ω2[10]计算选取。
| ${\omega _2} = 0.005b\text{。}$ |

|
图 5 一阶屈曲变形 Fig. 5 First-order buckling deformation |
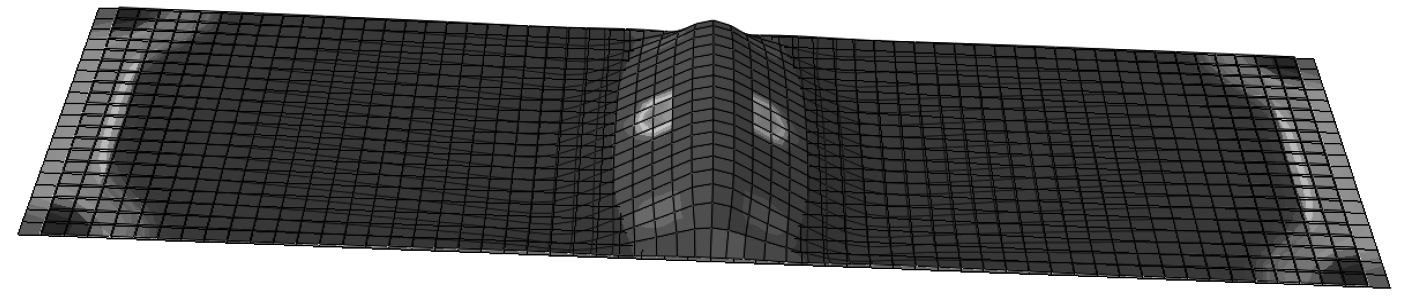
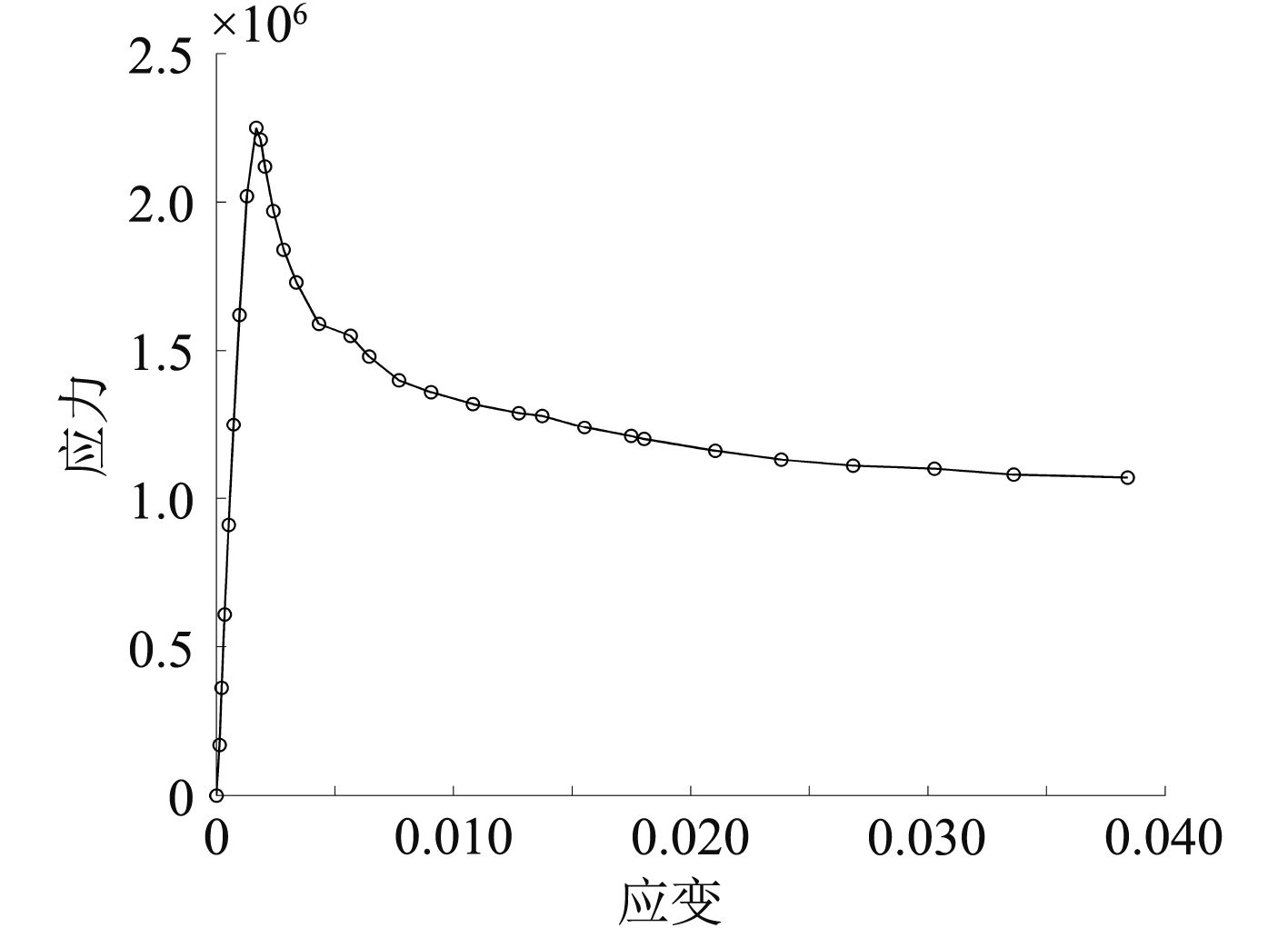
使用有限元软件提供的修正的弧长法(STATIC,RIKS)计算得到板格受沿纵向轴压力作用下的板格极限强度如表2所示,σu1表示本文计算结果,σu表示使用Faulkner公式计算结果,σu2表示文献[3]中计算结果。图6为有限元计算结果与文献[3]中的结果和Faulkner公式计算结果之间的比较。图7和图8分别为第B类板格受纵向轴压的变形结果与板格沿纵向所受的平均压力和相应的位移关系曲线。
|
|
表 2 有限元计算结果和其他公式计算结果比较,MPa Tab.2 Comparison of ultimate strength of plate of finite element calculation and other formulas, MPa |
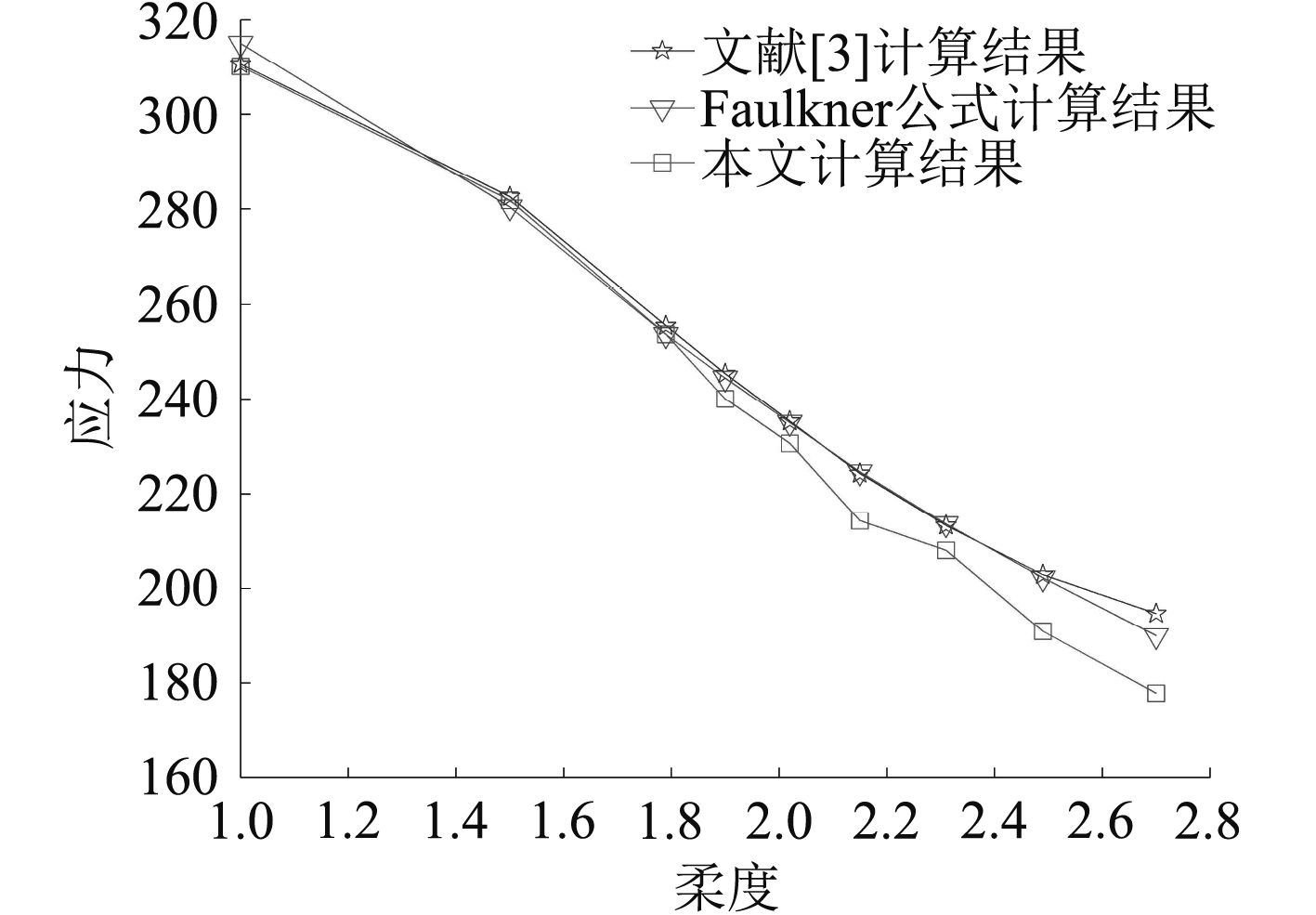
|
图 6 有限元计算结果与其他公式计算结果比较 Fig. 6 Compar finite element calculation results with others |
|
图 7 B类板格受纵向轴压的变形结果 Fig. 7 The deformation results of the longitudinal axial compression of the class B panel |
|
图 8 B类板格平均力-位移曲线图 Fig. 8 Average force-displacement graph of the class B grid |
由表2和图6可以看出本文计算结果与Faulkner经验公式最大误差在6%左右,结果符合较好。该结论与文献[3]得出的结果误差最大在8%。其余误差均在5%之内。说明本文计算方法的可信度较高。
3 有限元敏感因素分析在实际的船舶施工过程之中包括实验模型在内,都将会产生初始缺陷。比如几何初始缺陷、初始损伤、残余应力等。初始缺陷将很大程度上降低结构的屈曲强度。本文将分别考虑板的材料属性、网格密度、边界条件、屈曲模态、初始缺陷因子等因素对模拟结果的影响,通过与实验结果的比较,给出误差分析。
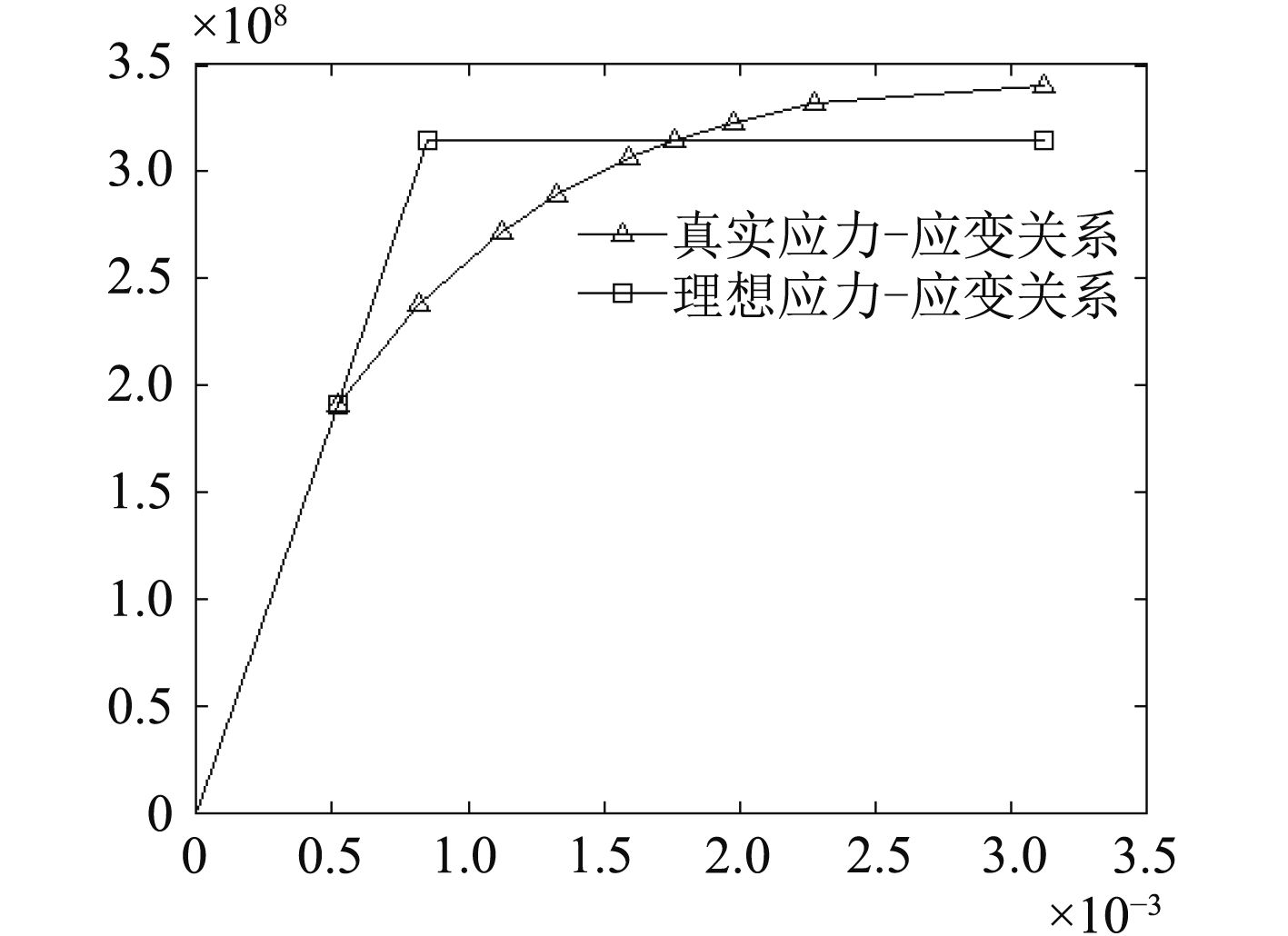
3.1 材料属性理想的应力应变关系是将材料的应力-应变非线性阶段做线性延伸,因此会给计算带来很大误差,特别是比例极限远小于屈服极限的非线性程度较大的材料[11]。取材料的真实应力应变关系与理想应力应变关系分别作为材料的塑性变形,研究二者对有限元模拟结果的影响。理想应力应变关系与真实应力应变关系如图9所示。材料参数为:弹性模量为E=205 800 N/mm2,泊松比ν=0.3,比例极限σu=190.512 MPa,屈服极限为σs=340.2 MPa(据文献[11]该高强度钢材的屈服极限名义值为315 MPa,平均值为340.2 MPa)。
分别采用上述2种应力应变关系得到的结果见表3,其中σu1表示采用真实应力应变关系的计算结果,σu2表示采用理想应力应变关系的计算结果。
|
图 9 真实应力-应变关系与理想应力-应变关系曲线 Fig. 9 The real stress-strain curve and the ideal stress-strain curve |
|
|
表 3 不同应力应变关系计算值,MPa Tab.3 Values of different stress-strain relations, MPa |
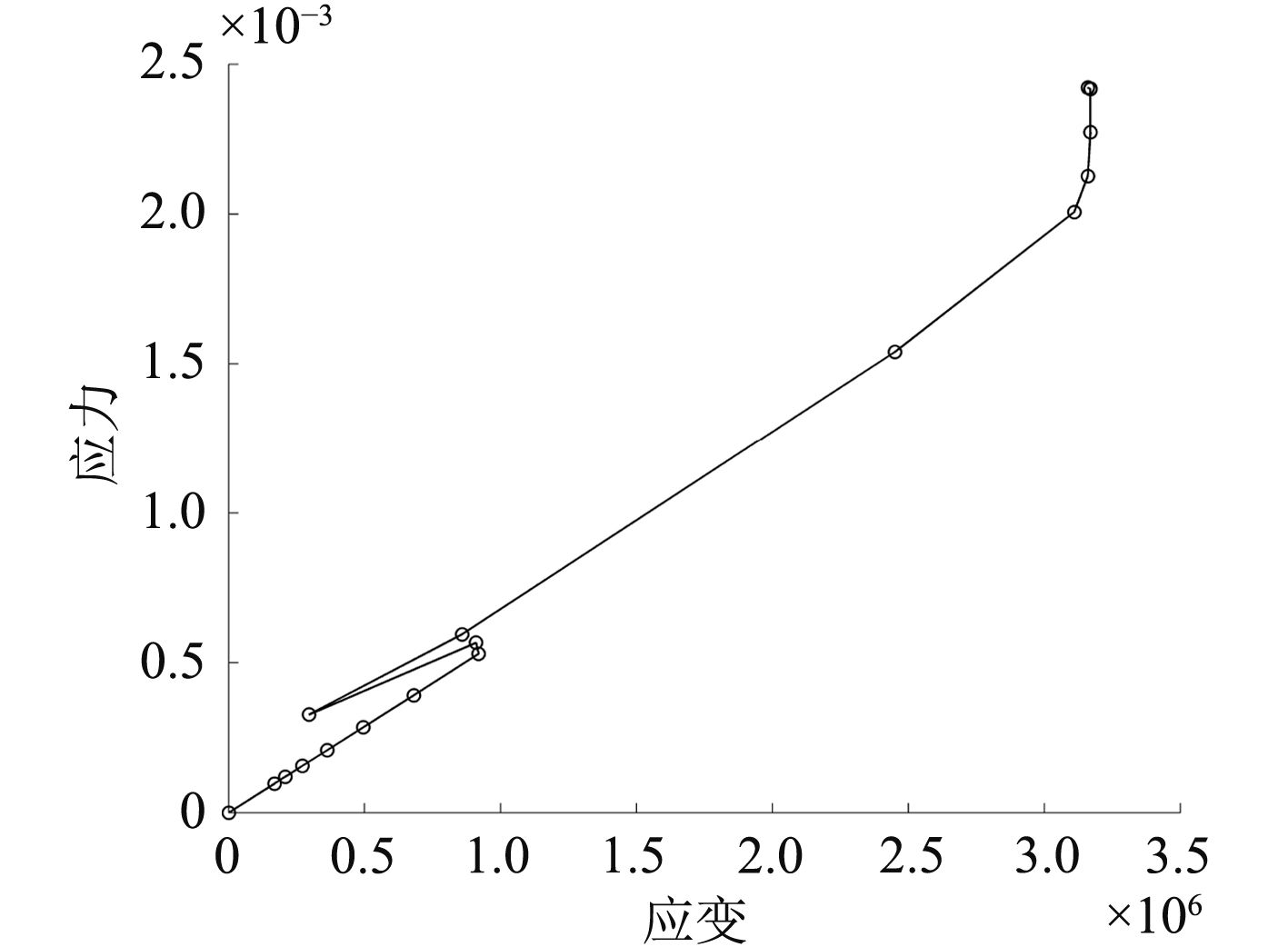
由表3可以看出理想的应力应变关系所得到的结果普遍比用真实应力应变关系的结果大,最大差距在8.57%。因此用理想应力应变关系会使得所得结果偏于危险。但是在采用真实应力应变关系时会存在不收敛现象见图10。
|
图 10 不收敛应力应变曲线 Fig. 10 The no convergence stress strain curve |
在第1步用屈曲模拟初始缺陷时,均设置了10阶屈曲模态,选择第C类板格将10阶屈曲模态分别当做初始缺陷引入到后屈曲分析当中,分析不同屈曲模态对结果的影响,比例因子均取0.005 b,计算结果如表4所示。
|
|
表 4 不同屈曲模态计算结果,MPa Tab.4 values of different stress-strain relations, MPa |
与1阶屈曲模态得到的结果比较来看,最大误差在20.6%。因此屈曲模态对计算结果具有较大的影响。但是从表格中可以看出前3阶误差在1%以内,前4阶误差在2%左右。因此在计算时引入单阶模态计算结果以低阶模态结果为主。
3.3 缺陷因子在考虑初始缺陷对板格极限强度的影响时,通常需要将特征值屈曲分析的结果引入到后屈曲分析当中,在引入时,需要添加比例因子,比例因子通常取板长的1/1 000,文献[10]给出了3个计算初始缺陷的公式:
| $\begin{aligned}&{\omega _1} = 0.025t{\beta ^2}\text{,}\\&{\omega _2} = 0.005b\text{,}\\&{\omega _3} = 0.3t{\beta ^2}\text{。}\end{aligned}$ |
为研究比例因子对数值模拟结果的影响本文将取9类板格作为研究对象,将1阶的特征值屈值引入到后屈曲分析过程中,采用理想应力应变关系,网格密度保持统一。将取1/1 000 b作为比例因子计算结果用σu1表示,公式ω1的计算值作为比例因子计算结果用σu2表示,公式ω2的计算值作为比例因子计算结果用σu3表示,公式ω1与公式ω3的平均值作为比例因子计算结果用σu4表示。探究比例因子对数值模拟结果的影响。计算结果如表5所示。
|
|
表 5 4种不同比例因子的计算结果 Tab.5 The results of four different scale factors |
从表格中可以看出板格极限强度随比例因子的减小而增大。不同的比例因子对结果影响较大,且由于柔度的不同,影响程度也不一样。其中由比例因子1/1 000 b最大误差在17.1%,比例因子ω1最大误差在12%,比例因子(ω1+ω3)/2最大误差在14%。因此比例因子是有限元分析中敏感因素。并且将比例因子取得过小时,会出现不收敛现象。
3.4 网格密度分析为研究网格密度对有限元结果的影响,设计不同的网格密度计算结果见表6。
|
|
表 6 不同密度下板格数值计算结果 Tab.6 Results of plate with different grid densities |
由结果可以看出不同的网格形状网格密度之间最大误差在3.7%。且不是网格设置越密计算结果越准确。并且网格设置过于稀疏时会出现结果不收敛情况。因此网格设置要合理,网格大小设置在40×40左右的正方形比较合适。
3.5 边界条件为了研究横向加强构件对于板格的影响,选取3种模型,模型1:1/2+1+1/2。模型2:两横向加强构件之间板格。模型3:1/2+1/2。计算结果见表7。
|
|
表 7 三种不同边界条件计算结果 Tab.7 Results of three different boundary conditions |
由计算结果可以看出,模型1与模型2之间多数误差在5%以内,最大误差为5.9%,模型3与模型2之间多数误差在5%之内,最大误差为7.2%。但是采用模型3时得到结果普遍偏大,因此取模型3时得到的结果偏于危险。考虑到建造模型的方便,选择模型2即可。
4 结 语本文探究了运用数值模拟船体板格极限强度所涉及到的比例因子、材料属性、网格密度、屈曲模态边界条件等敏感因素对数值模拟的影响。具体得到以下结论:
1)材料属性设置是有限元分析的敏感因素,最大误差会在8.6%左右。但是在采用真实应力应变关系时会存在结果不收敛现象。且用理想应力应变所得结果普遍比真实应力应变关系所得结果偏大,因此偏于危险。
2)屈曲模态对于数值模拟影响较大,最大误差在20%左右。前3阶模态误差在1%以内,选用低阶模态结果较为准确。
3)比例因子是敏感因素,误差达到17.1%,并且比例因子选择太小时会出现结果不收敛现象。选用公式ω2=0.005 b作为比例因子较合适。
4)对于网格形状和网格密度,选择正方形的网格形状。网格密度的选择对于结果的影响不大,误差在3.7%左右。网格大小选择40×40的正方形网格。
5)边界条件对结果影响不大,不同模型计算结果之间多数误差在5%以内最大误差在7.2%左右。但是选择模型3时会使得结果偏于危险。考虑到建模方便选择两横向加强构件之间的板格即可。
| [1] |
冯亮, 等. 加筋板极限强度简化计算及其可靠性分析[J]. 华中科技大学学报(自然科学版), 2016, 44 (9): 73–76.
FENG Liang, et al. The simplified calculation and reliability analysis of stiffened plate ultimate strength[J]. Journal of huazhong university of science and technology (Natural science edition), 2016, 44 (9): 73–76. |
| [2] |
冯亮, 等. 箱型梁极限弯矩简化计算方法[J]. 哈尔滨工程大学学报, 2017, 38 (3): 1–5.
FENG Liang, et al. The calculation method of the box girder limit bending moment simplifies[J]. Journal of Harbin engineering university, 2017, 38 (3): 1–5. |
| [3] | Shengming ZHANG. Imtaz Khan Buckling and ultimate capability of plates and stiffened panels in axial compression[J]. Marine Structures, 2009 (22): 791–808. |
| [4] | PAIK J K, KIM B J, SEO J K. Methods for ultimate limit state assessment of ships and ship-shaped offshore structures: Part I—Unstiffened plates[J]. Ocean Engineering, 2008, 35 (2): 261–270. DOI: 10.1016/j.oceaneng.2007.08.004 |
| [5] | RAVIPRAKASH A V, PRABU B, ALAGUMURTHI N. Residual ultimate compressive strength of dented square plates[J]. Thin-Walled Structures, 2012, 58 : 32–39. DOI: 10.1016/j.tws.2012.04.009 |
| [6] | S, et al. Influence of corrosion on the ultimate compressive strength of steel plates and stiffened panels[J]. Thin-Walled Structures, 2016 (96): 95–104. |
| [7] |
张婧, 施兴华, 顾学康. 具有初始缺陷的船体加筋板结构在复杂受力状态下的极限强度研究[J]. 中国造船, 2013 (1): 60–70.
ZHANG Jing, SHI Xing Hua, GU Xue Kang. The study of stiffened plate ultimate strength with the initial defect in the complex force[J]. Chinashipbuilding, 2013 (1): 60–70. |
| [8] |
张少雄, 余友谊. 有凹痕的板在轴向压力作用下的极限强度[J]. 武汉理工大学学报(交通科学与工程版), 2004, 38 (3): 315–317.
ZHANG Shaoxiong, YU Youyi. Ultimate Strength of Dented Panel Under Axial Compression[J]. Journal of Wuhan University of Technology (Transportation Science & Engineering), 2004, 38 (3): 315–317. |
| [9] | HUANG Y, ZHANG Y, LIU G, et al. Ultimate strength assessment of hull structural plate with pitting corrosion danification under biaxial compression[J]. Ocean Engineering, 2010, 37 (17): 1503–1512. |
| [10] | ESTEFEN T P, ESTEFEN S F. Buckling propagation failure in semi-submersible platform columns[J]. Marine Structures, 2012, 28 (1): 2–24. DOI: 10.1016/j.marstruc.2012.05.003 |
| [11] |
雒高龙, 张淑茳, 任慧龙. 船用钢应力—应变关系的数学表达及其在计算加筋板屈曲应力中的应用[J]. 造船技术, 2006 (3): 13–18.
LUO Gao Long, ZHANG Shu Jiang, REN Hui Long. The mathematical expression of the ship's steel stress-strain relationship and its application in the calculation of buckling stress of reinforcement plate[J]. Shipbuilding technology, 2006 (3): 13–18. |
 2017, Vol. 39
2017, Vol. 39
