物理波浪水池是船舶流体力学研究的重要试验设施,为船舶水动力性能研究提供高效而又可靠的实验数据,但是物理波浪水池花费时间和费用多,实验周期长,在非规则波的模拟以及消波上还存在许多问题[1]。随着计算机技术的飞速发展,用数值模拟波浪及波浪与船舶的相互作用变成了可能。数值波浪水池在造波和消波方面具有物理波浪水池不具有的优势。采用基于波浪理论的方法进行造波和消波,可以获得详细的流场信息。
本文基于Fluent软件建立了二维数值波浪水池,分别采用仿物理造波法和直接输入造波法模拟了无限水深(
对于规则波,采用仿物理造波法时,模拟真实水池中推板式造波机,往复推板在水池中作正弦运动,运动轨迹及速度方程[2]如下:
| $s(t) = \frac{{{X_o}}}{2}\sin \omega t\text{,}$ | (1) |
| $u(t) = \frac{{{X_o}}}{2}\omega \cos \omega t\text{。}$ | (2) |
由线性造波理论可知:生成波浪的波面方程和速度势为:
| $\varsigma = \frac{{2{X_0}\cosh kd \cdot \sinh kd}}{{kg(\sinh 2kd + 2kd)}}\cos (kx - \omega t)\text{,}$ | (3) |
| $\phi = \frac{{2{X_0}\sinh kd\cosh k(y + d)}}{{k(\sin 2kd + 2kd)}}\cos (kx - wt)\text{。}$ | (4) |
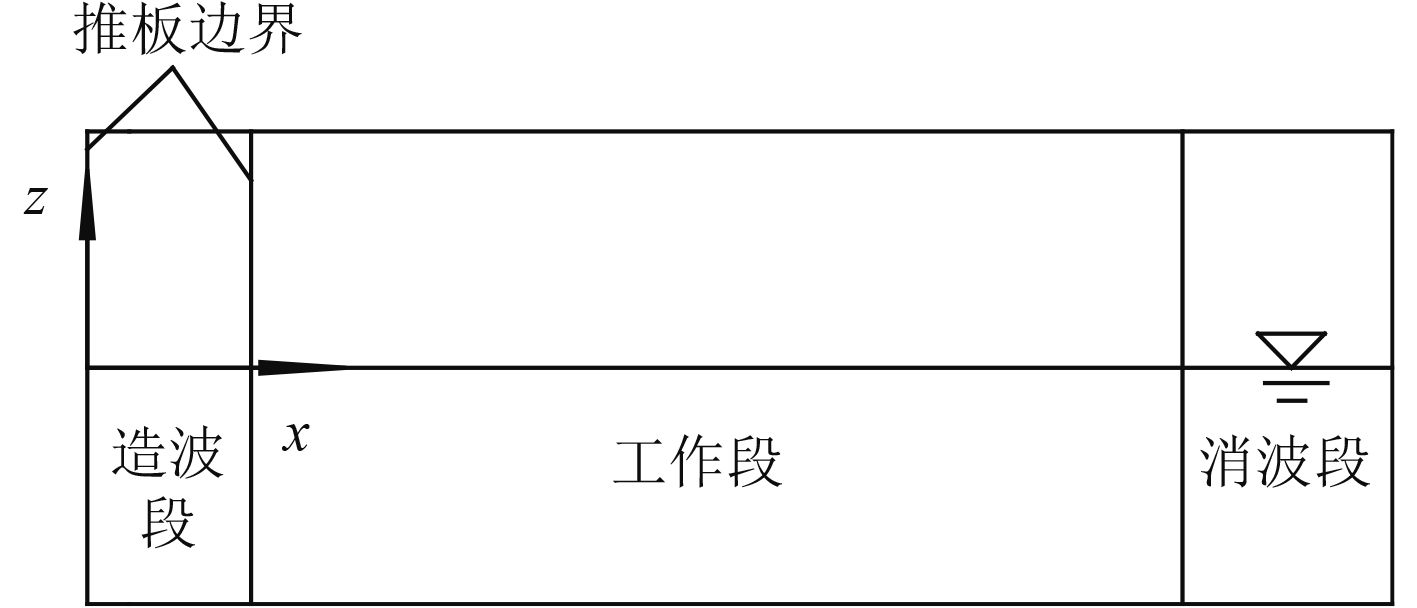
图1为仿物理造波法的数值波浪水池。水池左边界为模拟推板的动边界,式(2)表示为运动边界的速度方程。采用Fluent自带UDF编程,造波板按式(1)表示的轨迹运动,速度按式(2)。一旦造波板的运动频率和行程确定以后,即可以获得相应频率和波高的规则波。图1中右边界为消波区,波浪进入该区域以后将逐渐衰减,最终趋于平静[3]。
|
图 1 仿物理造波法数值水池示意图 Fig. 1 Diagram of numerical pool for physics simulation of the wave-making method |
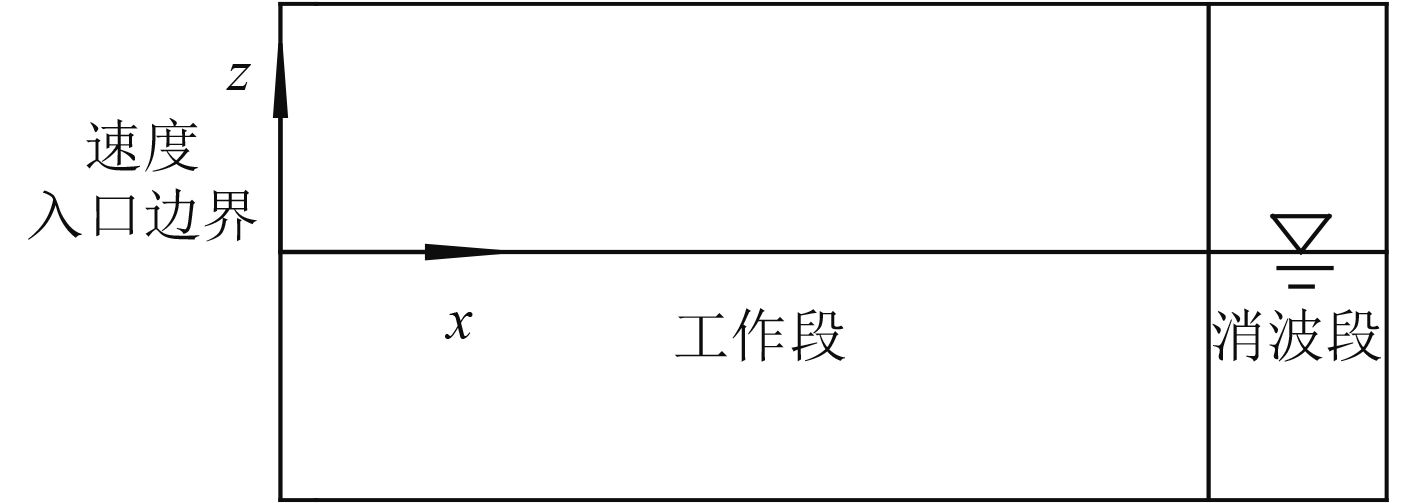
采用直接输入法造波需要在入口边界上给定流体的速度或压力,模拟波浪的速度场或压力场,该方法原理简单,消耗机时较少,数值波浪水池如图2所示。
|
图 2 直接输入法数值波浪水池示意图 Fig. 2 Diagram of numerical pool for direct wave-making method |
对于规则波的模拟,根据波浪理论,可得到相应波浪的速度场,由线性假设,无限水深条件下,规则波的波面方程可表示为:
| $\varsigma = a\cos (kx - \omega t)\text{,}$ | (5) |
速度势:
| $\varphi = \frac{{ag}}{\omega }{e^{kz}}\sin (kx - \omega t)\text{,}$ | (6) |
色散关系:
| ${\omega ^2} = \frac{{2π g}}{\lambda }\text{,}$ | (7) |
规则波的速度场:
| $\left\{ \begin{array}{l}u = \displaystyle\frac{{\partial \varphi }}{{\partial x}} = a\omega {e^{kz}}\cos (kx - \omega t)\text{,}\\[8pt]v = \displaystyle\frac{{\partial \varphi }}{{\partial y}} = 0\text{,}\\[8pt]w = \displaystyle\frac{{\partial \varphi }}{{\partial z}} = a\omega {e^{kz}}\sin (kx - \omega t)\text{,}\end{array} \right.$ | (8) |
压力场:
| $p = {p_0} + \rho g[a{e^{kz}}\cos (kx - \omega t) - z]\text{。}$ | (9) |
式中:k为波数,ω为波浪圆频率,a为波幅,x轴为波浪传播方向,z轴为波动方向,p0为大气压强,z轴自由液面以下取负值。
将规则波质点的速度表达式(8)作为数值水池入口边界条件,用UDF编程定义入口边界水平和垂向的波浪速度函数。
为了防止波浪反射对计算域的影响,在下游设置消波区。数值波浪水池中常采用的消波技术-阻尼消波区。
阻尼消波区是在特定的自由边界加入人工粘性项,对流体质点的垂向速度做强制衰减,通过对消波区网格沿波浪传播方向逐渐变稀,增加阻尼,达到快速消波的目的[4]。为了保证计算域内流动的连续性,在水平方向的速度不做衰减[5]。
人工阻尼系数如式(10)所示:
| $\mu (x,z) = \alpha \cdot {\left(\frac{{x - {x_s}}}{{{x_e} - {x_s}}}\right)^2}\left(\frac{{{z_b} - z}}{{{z_b} - {z_{fs}}}}\right)\text{,}$ | (10) |
则消波区波动方向的速度为:
| ${w_r} = \mu (x,z)w\text{。}$ | (11) |
式中:α为阻尼控制参数;下标s为消波区的起点,e为消波区的终点;b为底部;fs为自由面;w为流体质点在波动方向的速度。
在消波段的动量方程中加入阻尼项,如下式:
| $\begin{split}\frac{{\partial (\rho u)}}{{\partial t}}\! +\! u\frac{{\partial (\rho u)}}{{\partial x}} \! +\! w\frac{{\partial (\rho u)}}{{\partial y}} = \! -\! \frac{{\partial p}}{{\partial x}} + \\ \mu \left[\frac{{{\partial ^2}u}}{{\partial {x^2}}}\! +\! \frac{{{\partial ^2}u}}{{\partial {y^2}}}\right]\! +\! \gamma u\text{,}\end{split}$ | (12) |
| $\begin{split}\frac{{\partial (\rho v)}}{{\partial t}} + u\frac{{\partial (\rho v)}}{{\partial x}} + w\frac{{\partial (\rho v)}}{{\partial y}} = - \frac{{\partial p}}{{\partial x}} +\\ \mu \left[\frac{{{\partial ^2}v}}{{\partial {x^2}}} + \frac{{{\partial ^2}v}}{{\partial {y^2}}}\right] - \rho g + \gamma u\text{。}\end{split}$ | (13) |
式中:γ为消波系数;μ为动力粘性系数。
对γ的确定,要考虑使消波区内流体的运动满足连续性方程。Laesen和Dancy给出了消波系数[6]:
| $\gamma (x) \!\!=\!\! \left\{ \begin{array}{l}\exp [({2^{ - x/\Delta x}} - {2^{ - {x_s}/\Delta x}})\ln \alpha ],\;\;\;0 \leqslant x \leqslant {x_s}\text{,}\\1,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{x_s} \leqslant x\text{。}\end{array} \right.$ | (14) |
式中:xs为消波区的长度;Δx为消波区的网格尺寸;α为常数。
2 数值模拟方法 2.1 计算域和网格划分首先采用仿物理造波法模拟规则波,数值波浪水池模型尺寸为30×8 m,其中水深5 m,消波区长10 m。数值水池网格划分如图3所示;在自由液面附近加密网格,利于捕捉自由液面,距出口边界10 m处将计算域分为2个分区,后部分区中网格沿波浪传播方向,网格逐渐变稀,稀疏的网格增加了额外的阻尼,利于消波。

|
图 3 数值波浪水池网格 Fig. 3 Numerical wave tank grid |
采用气液两相流模型,非定常分离隐式求解器求解离散方程组。选择RNG
自由液面用VOF方法捕捉,压力速度耦合方程用PISO算法。定义左侧边界为造波推板其运动速度随时间变化如式(2),网格的更新采用动网格重构法。
2.3 边界条件仿物理造波法,在计算域的边界上采用下列边界条件:左端、下端和上端边界设为无滑移壁面,右端为静压力出口;水池采用壁面边界条件。由于流动非定常,设定初始速度为0。直接输入法边界条件除左端为速度入口边界外其余和仿物理造波法相同。
2.4 计算结果和分析图4为t=14.3s时数值波浪水池的波形图。为测量数值水池中波浪随时间的变化,在4 m的位置设置浪高仪。图5为4 m处波幅的时历曲线与理论波形的比较。

|
图 4 数值波浪水池的波形图 Fig. 4 Waveform of numerical wave tank |
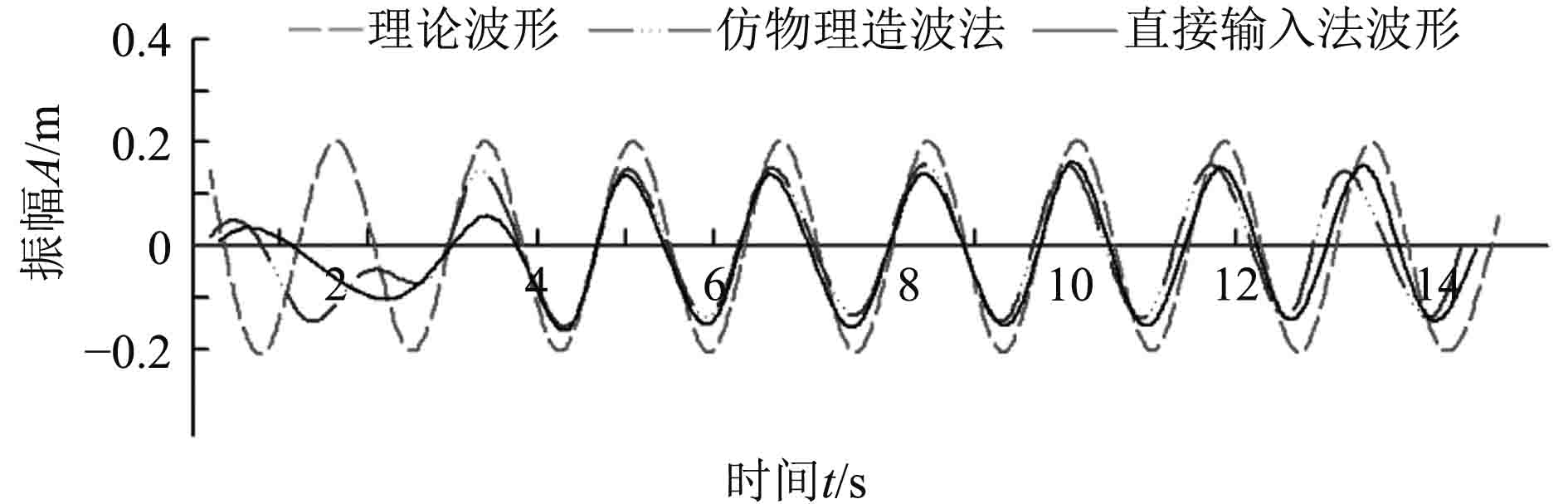
从图5中可看出仿物理造波法波形与理论波形总体上吻合,但存在30°左右的相位差,而且波幅低于理论波形,这主要是由造波推板以及流体的粘性的影响造成的。采用直接输入法得到的波浪,波形与理论波形两者之间存在大约15°左右的相位差,且波高小于理论值,这主要是由于流体的粘性使得波浪在传播过程中逐渐衰减造成的,与实际情况相符。表1和表2给出了与理论波形相比数值波形的波幅及周期的相对误差。
|
图 5 不同造波方法的波形对比 Fig. 5 Waveform comparison of different wave-making methods |
|
|
表 1 二维数值波形与理论值的误差对照表(仿物理造波法) Tab.1 Error comparison between two dimensional numerical waveform and theoretical value (physics simulation of the wave-making method) |
对比2种方法得到的波形,直接输入法的波形与理论波形吻合度更好,同时考虑到仿物理造波法存在动网格重构、计算时间长等因素及推板对流场的影响。而直接输入法,只要设定波动速度入口,对流场不会产生影响。故采用直接输入法预报波浪中的船舶水动力性能更有优势。
|
|
表 2 二维数值波形与理论值的误差对照表(直接输入法) Tab.2 Error comparison between two dimensional numerical waveform and theoretical value (direct Wave-making method) |
将二维数值波浪水池中的直接输入造波法和消波技术应用到三维数值波浪水池中。三维数值波浪水池的计算域、边界条件及控制参数和二维数值波浪水池相近。波形图如图6所示。

|
图 6 三维波浪水池波形图 Fig. 6 Waveform of three dimensional wave pool |
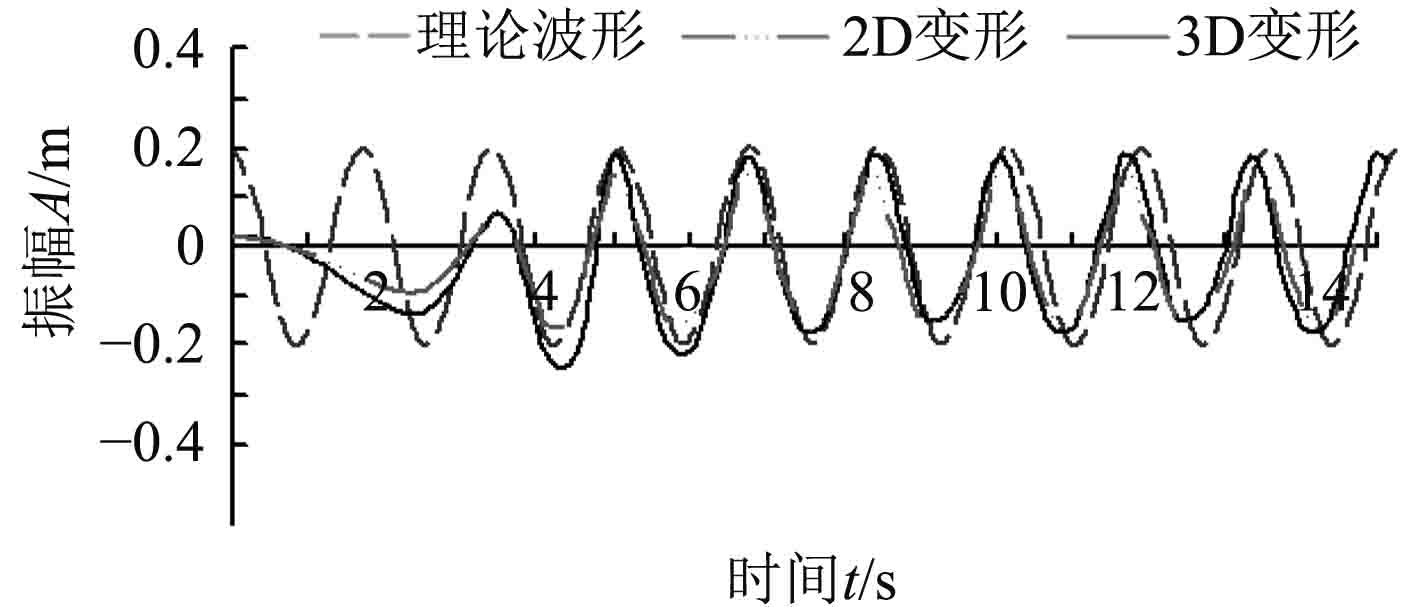
图7为4 m处三维数值波浪水池和二维数值波浪水池中的波形与理论波形的比较。通过比较可知三维波形与理论波形吻合度最好。但是三维波形达到稳定需要的时间更长,二维波形在6 s时基本稳定,而三维波形则要到8.1 s以后才稳定。三维波形波高的衰减要比二维数值波浪水池小很多,由表3可知,4 m处三维数值波浪水池中波幅与理论波幅相比最大误差为–5.5%,远低于二维数值水池,且三维波形的周期更接近理论周期,与理论波形吻合的程度要优于二维数值波浪水池。
|
图 7 数值波形与理论波形的比较(x=4 m) Fig. 7 Comparison between numerical and theoretical (x=4 m) |
|
|
表 3 三维数值波形与理论值的误差对照表 Tab.3 Error comparison between three dimensional numerical waveform and theoretical value |
1)通过对2种造波方法所得到的数值波形进行对比,直接输入法简单易懂,误差较小,且没有造波板对流场的干扰,可更快得到稳定的规则波,节省计算机时间。
2)在数值波浪水池下游加入消波区,采用人工阻尼法消波,消波区水面逐渐趋于平静,在水池出口处已基本不存在波动,说明人工阻尼法用于规则波的消波可行。
3)由RNG
4)通过计算直接输入法造波的二维与三维数值波浪水池可知,直接输入法用于三维数值波浪水池造波所得到的波形与理论波形相比误差要小于二维数值波浪水池。
| [1] | 张亚群. 造波机的控制及其实现[D]. 武汉: 武汉理工大学. 2007. |
| [2] | 邹志利. 水波理论及其应用[M]. 北京: 科学出版社, 2005. |
| [3] | JOUMEE J M J. Experiments and calculations on 4 Wighy hull forms in head waves[R]. Report of Delft University of Technology, Ship Hydromechanics Laboratory, The Netherlands, 1992. |
| [4] | 吴乘胜, 周德才, 兰波, 等. 高速三体船波浪中运动与增阻CFD计算研究[J]. 船舶力学, 2010, 51 (4): 1–10. |
| [5] | 方昭昭, 朱仁传, 缪国平. 数值波浪水池中航行船舶辐射问题的数值模拟[J]. 水动力学研究与进展, 2011, 26 (1): 66–72. |
| [6] | 郭海强. 船舶性能数值水池的研究及其若干应用[D]. 上海: 上海交通大学, 2009. |
 2017, Vol. 39
2017, Vol. 39
