导管螺旋桨是一种常用的操纵水下潜器主动控制装置,水面控制人员通常通过脐带缆将控制信号发送到导管螺旋桨来实施对水下潜器的轨迹与姿态操纵[1–4]。准确地模拟导管螺旋桨周围的流场分布有助于提高对导管螺旋桨性能和流场分布特征的了解与认识,从而为设计出水动力性能优良的导管螺旋桨提供理论指导[5]。
文献[6]中描述到导管螺旋桨叶梢区域会产生漩涡,梢涡的产生会使得导管螺旋桨及其所属水下潜器系统产生许多不利因素,如产生较大噪声、增加了不稳定性,干扰水下潜器的正常工作,不利于设计节能高效的水下潜器。另一方面,梢涡的产生破坏了桨叶上荷载的合理分布,导致桨叶容易在漩涡区发生剥蚀和变形现象,损伤桨叶结构,降低螺旋桨的使用寿命。本文采用滑移网格技术对导管螺旋桨的叶梢漩涡、螺旋桨周围流场和推力特性进行数值计算,并且通过组合不同类型的导管对比分析了梢涡的改善方法和推力性能的优化方案,从而设计出了梢涡和尾涡范围较小、推进效率更高、运行更稳定的导管螺旋桨。
1 控制方程、几何模型 1.1 控制方程本文分析中设定流体为不可压缩流体,则导管螺旋桨周围流场的控制方程为[7]:
1)连续性方程
| $\frac{{\partial {u_i}}}{{\partial {x_i}}} = 0\text{,}$ | (1) |
2)动量方程
| $\begin{split}\rho \left[ {\frac{{\partial {u_i}}}{{\partial t}} + \frac{{\partial \left( {{u_i}{u_j}} \right)}}{{\partial {x_j}}}} \right] = - \frac{{\partial P}}{{\partial {x_i}}} + \rho {g_i} + \\ \rho \frac{\partial }{{\partial {x_j}}}\left[ {\mu \left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right) - \overline {u_i'u_j'} } \right]\text{。}\end{split}$ | (2) |
式中:xi,xj均为坐标分量(i,j=1,2,3);ui,uj均为速度分量时均值(i,j=1,2,3);ρ为流体密度;t为时间;P为压力时均值;gi为重力加速度分量;
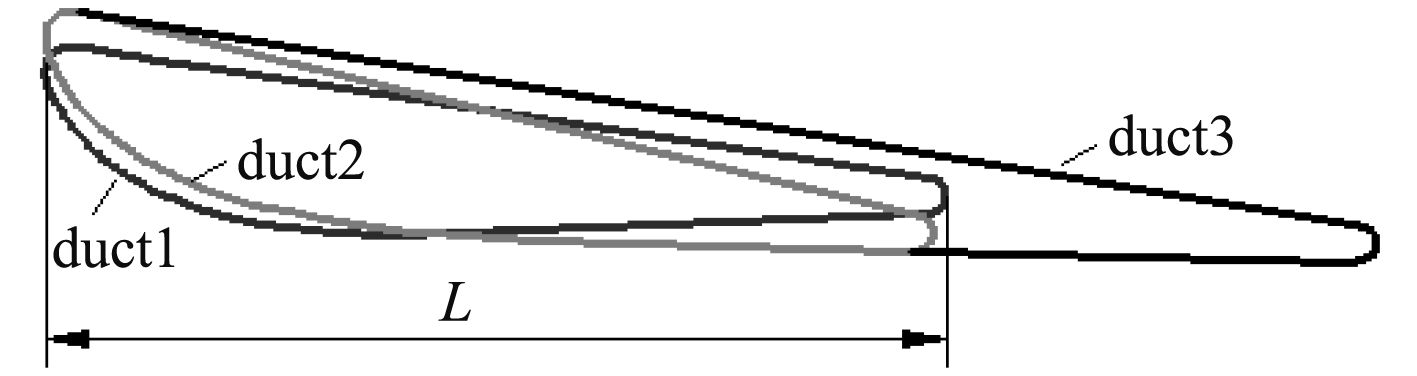
本文采用的基础模型是ka 4-70/19A导管螺旋桨(见图1),该桨采用的是No.19A导管。本文旨在研究以ka 4-70螺旋桨装配不同类型导管的组合结构的匹配性和性能优劣。图2为不同导管剖面示意图,其中,duct1为No.19A导管,duct2是duct1导管迎角增加5°,duct3是将duct2导管延长0.5 L。表1和表2分别为螺旋桨和3种导管的主要参数。

|
图 1 导管螺旋桨几何模型 Fig. 1 Geometrical model of ducted propeller |
|
图 2 不同导管剖面示意图 Fig. 2 Sections of different ducts |
|
|
表 1 螺旋桨主要参数 Tab.1 Primary parameters of the propeller |
|
|
表 2 导管主要参数 Tab.2 Primary parameters of the ducts |
本节通过改变导管类型的设计旨在改善导管螺旋桨叶梢区域的漩涡,改进螺旋桨周围流场的分布,以及优化导管螺旋桨的性能。将导管螺旋桨转速设为20 r/s,通过改变进速的方法计算不同进速系数J的工况。
2.1 导管螺旋桨漩涡分布
|
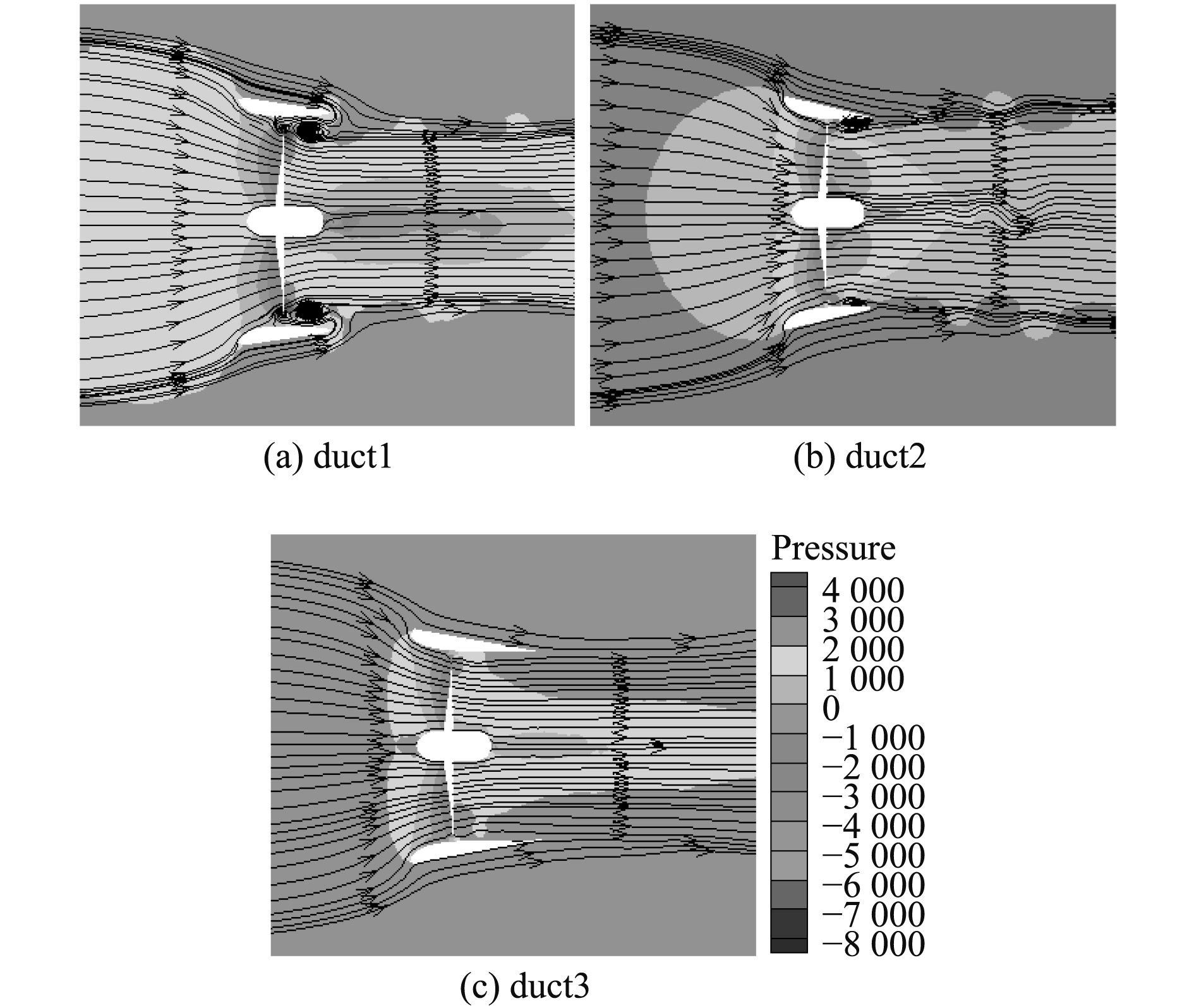
图 3 不同导管螺旋桨y=0切面流线图 Fig. 3 Streamline distribution of different ducted propellers in the section y=0 |
图3为J=0.2时,duct1,duct2,duct3导管螺旋桨在y=0切面的流线图,从图中可发现以下特点:
1)duct1,duct2,duct3导管螺旋桨叶面叶梢位置均存在高压区,叶根和桨毂后均存在低压区。
2)duct1导管螺旋桨由于水流经过桨盘面后有收缩作用,使得叶梢离开叶面后一定距离的位置出现低压,进而导致导管外的流体沿着导管内表面回流至该位置形成漩涡,另有部分流体翻越叶梢继续回流至叶背处形成漩涡。
3)duct2导管螺旋桨增大导管迎角后避免了导管外流体的回流,消除了叶背处的漩涡,改善了叶面后叶梢区域的漩涡,使得涡核后移,降低了漩涡对螺旋桨的干扰;duct2导管螺旋桨相较于duct1导管螺旋桨,改善了梢涡的产生,但也使得桨毂后面出现了涡街现象。
4)duct3导管螺旋桨是在duct2导管螺旋桨的基础上对导管进行加长处理,改进后在延续duct2导管螺旋桨的优点之后还进一步消除了桨毂后的涡街现象;同时,从宏观上观察叶背叶面的荷载分布也比前二者更均匀。
|
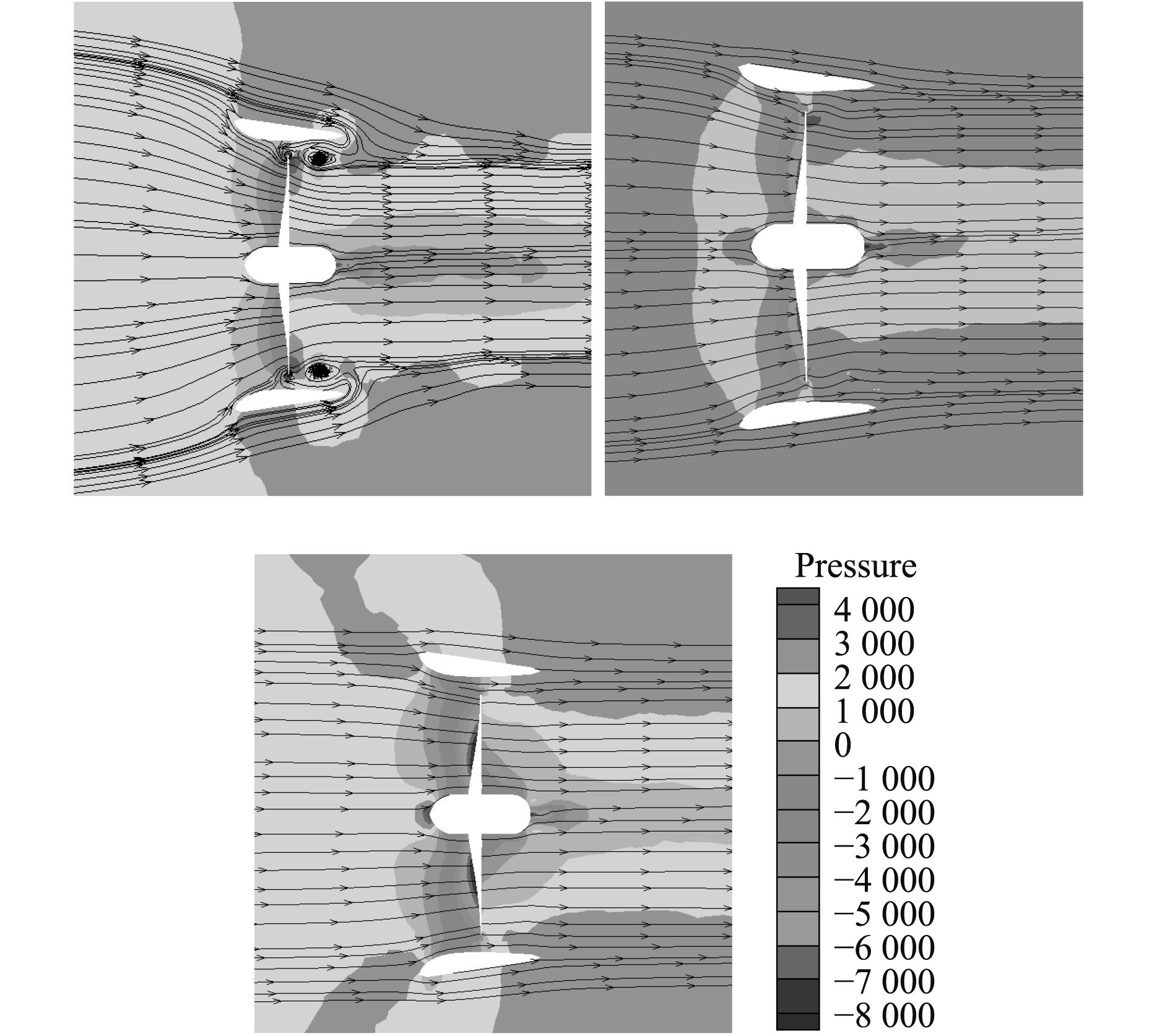
图 4 No19A导管螺旋桨在不同进速系数(J=0.2, 0.4, 0.6)时流线图 Fig. 4 Streamline distribution of No19A ducted propeller under different J |
图4是No19A导管螺旋桨在不同进速系数(J=0.2, 0.4, 0.6)时流线图,从图中可看出:
1)导管螺旋桨在低进速系数下叶梢区域会产生较大漩涡,随着进速系数的增大,漩涡逐渐消失,而进速系数与螺旋桨的进速和转速有关,所以合理设计螺旋桨的前进速度和转速十分重要。
2)从微观上分析,不同的进速和转速直接影响着来流与桨叶叶元体的攻角α,随着J的增加,攻角α随之减小,叶梢区域的漩涡也随之减小,因此可认为螺旋桨叶梢区域的漩涡与来流的攻角α呈正相关性。
3)不同进速系数J,流体与导管切面的攻角也不同,进而影响导管周围的流场,影响导管外的流体回流。
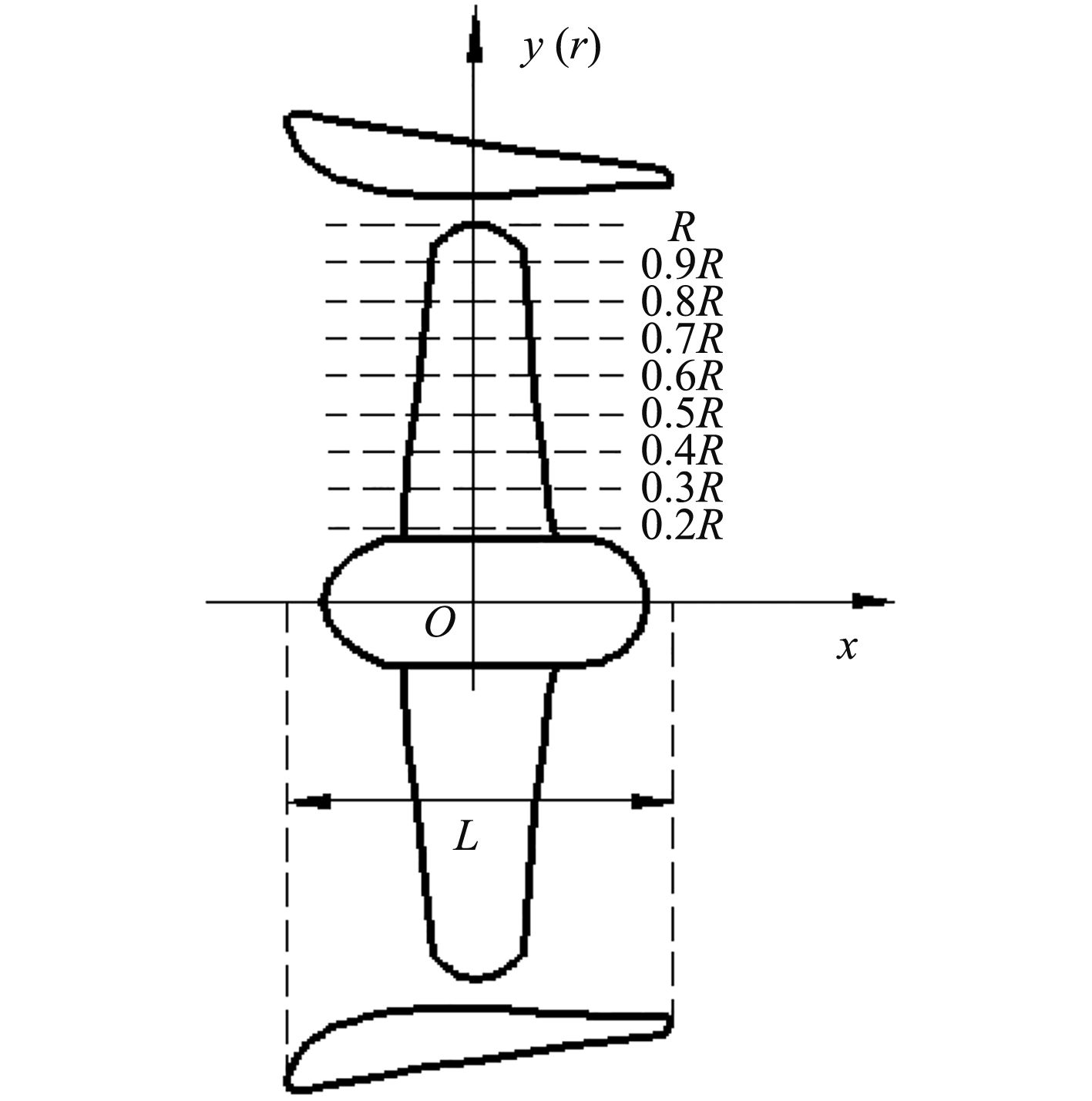
2.2 螺旋桨周围流场的分布图5是导管螺旋桨中纵剖面(z=0)坐标示意图,坐标原点位于桨毂中心。桨叶相对半径Rr的定义为:
| ${R_r} = r/R\text{。}$ | (3) |
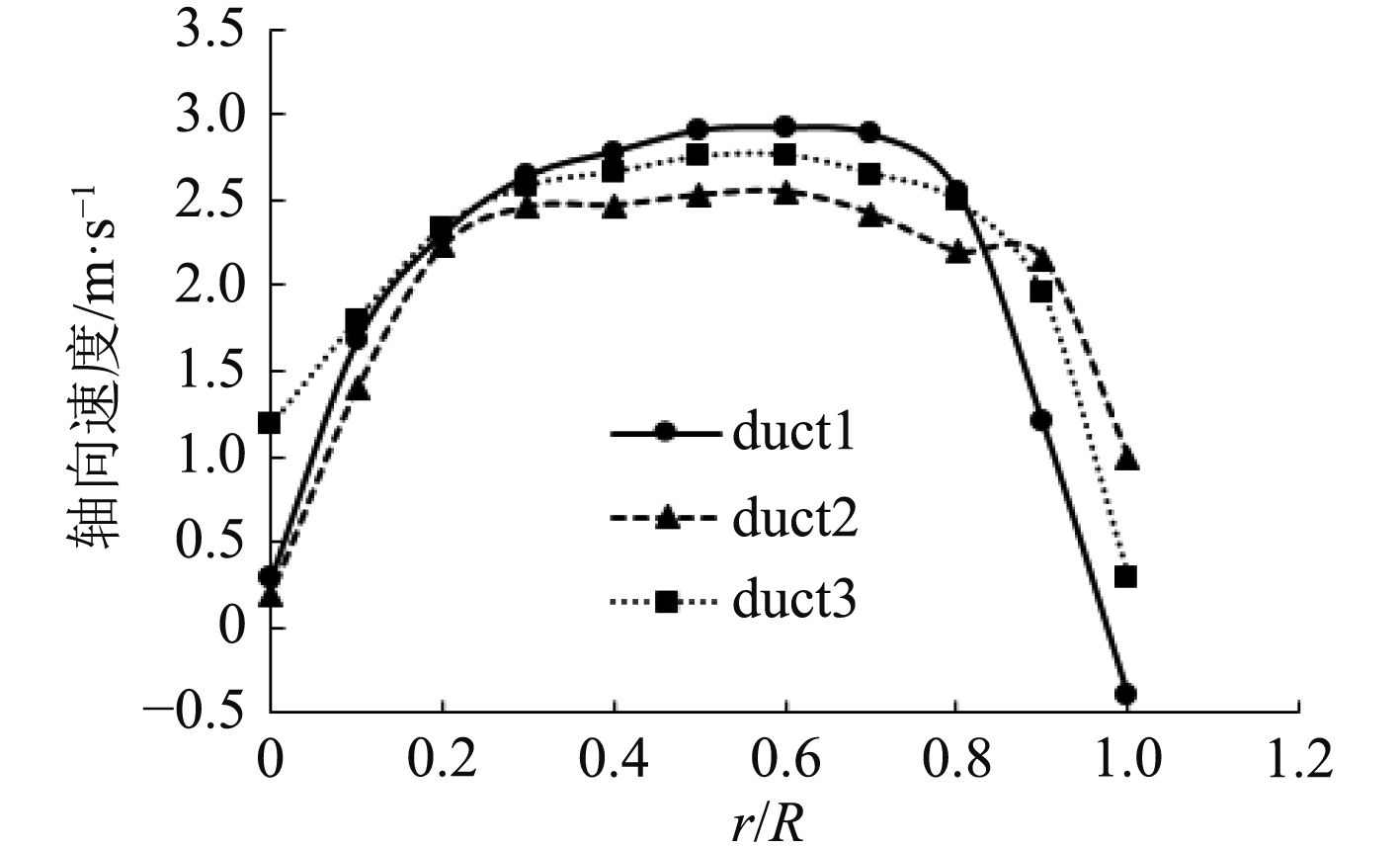
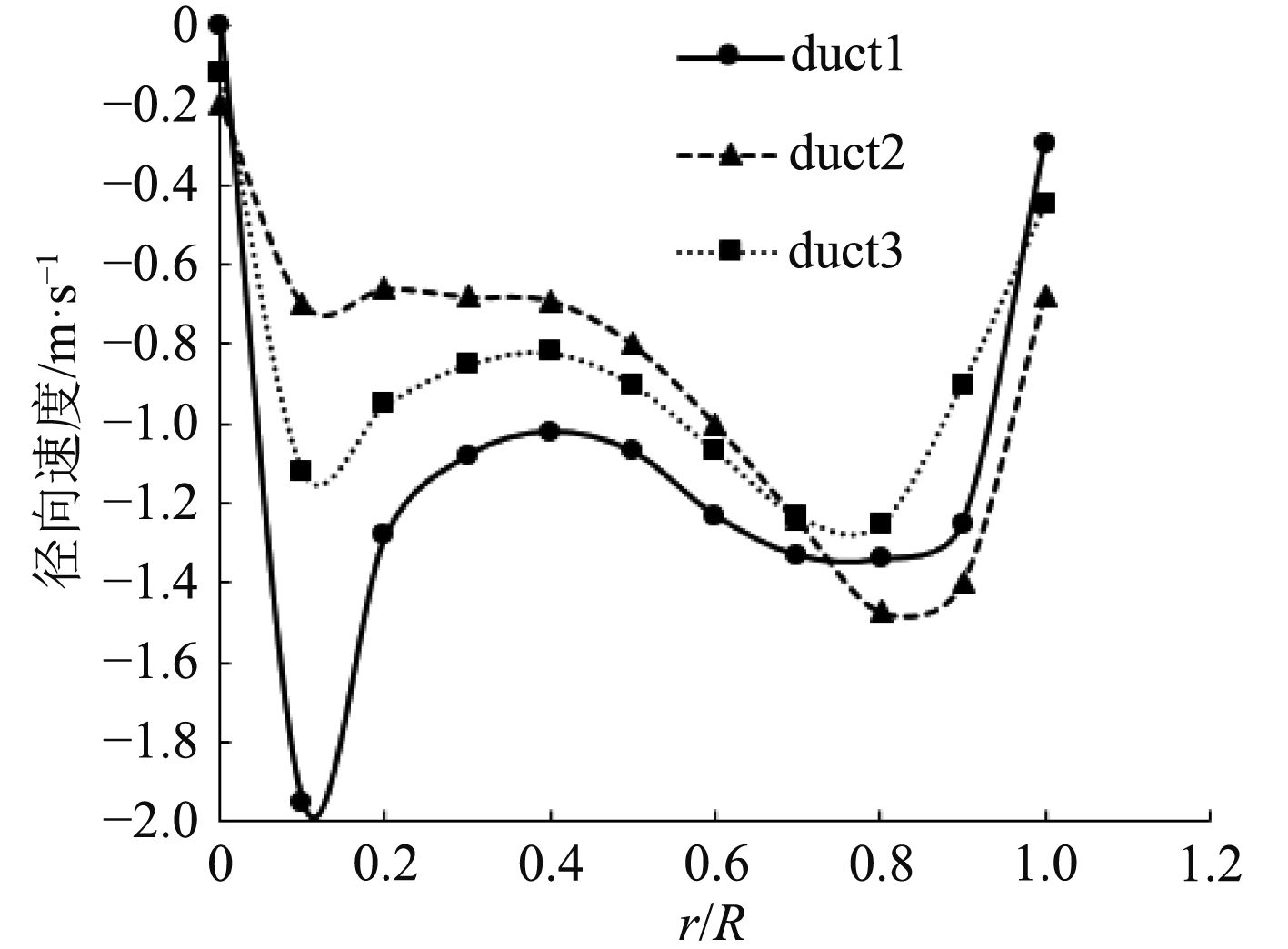
图6~图7为不同导管螺旋桨在J=0.2时,x/L=0.5切面处的轴向速度和径向速度沿桨叶半径方向的分布。轴向速度以从导管进口指向导管出口(x轴正方向)为正,径向速度以从轴心向外指向为正。从图6和图7可以观察到:
1)当Rr<0.2时,duct1和duct2导管螺旋桨的轴向速度明显低于duct3导管螺旋桨的轴向速度,这说明桨后尾流受桨毂的影响程度为duct2最大,duct1次之,duct3最小;当0.2≤Rr≤0.8时,3种导管螺旋桨轴向速度沿径向的分布较为均匀,三者的轴向速度也相差不大;各导管螺旋桨桨叶大相对半径(0.8<Rr)处,轴向速度迅速减小,这是因为经过盘面后从导管流出的尾流有一种明显沿径向向轴心收缩的倾向;另外,duct1导管螺旋桨叶尖(Rr=1)处轴向速度为负值,因为该处漩涡形成了低压区,导致导管外的流体沿着导管内壁回流。
2)duct3导管螺旋桨径向速度沿桨叶半径方向的分布相较于duct1和duct2导管螺旋桨更平稳,波动更小,这表明duct3导管螺旋桨工作时更加的稳定,有助于提升其所属水下潜器的稳定性和可控性。
|
图 5 螺旋桨坐标示意图 Fig. 5 Coordinate of propeller |
|
图 6 轴向速度沿桨叶径向分布 Fig. 6 Axial velocity distribution along the radial direction |
|
图 7 径向速度沿桨叶径向分布 Fig. 7 Radial velocity distribution along the radial direction |
螺旋桨桨叶产生推力的机理是叶面、叶背之间存在压力差,压力差的大小直接反映了推力的大小。同时,叶面、叶背压力的分布也直观地反映了荷载的分布情况,桨叶上荷载较为均匀的分布有利于增加桨叶的使用寿命和提高螺旋桨的稳定性。
式(4)为压力系数CP的计算公式,式(5)为推力T的无因次化,式(6)为导管螺旋桨产生的推力总和[8]:
| ${C_P} = \frac{{{P_b} - {P_0}}}{{\displaystyle\frac{1}{2}\rho V_A^2}}\text{,}$ | (4) |
| ${C_T} = \frac{T}{{\displaystyle\frac{1}{2}\rho V_{_A}^2{A_{rot}}}}\text{,}$ | (5) |
| $T = {T_{rot}} + {T_{duct}}\text{。}$ | (6) |
式中:Pb为叶切面计算点处的压力;P0为大气压力;ρ为水的密度;VA为导管进口处的平均进速;Trot,Tduct分别为桨叶推力和导管推力;Arot为桨盘面面积。
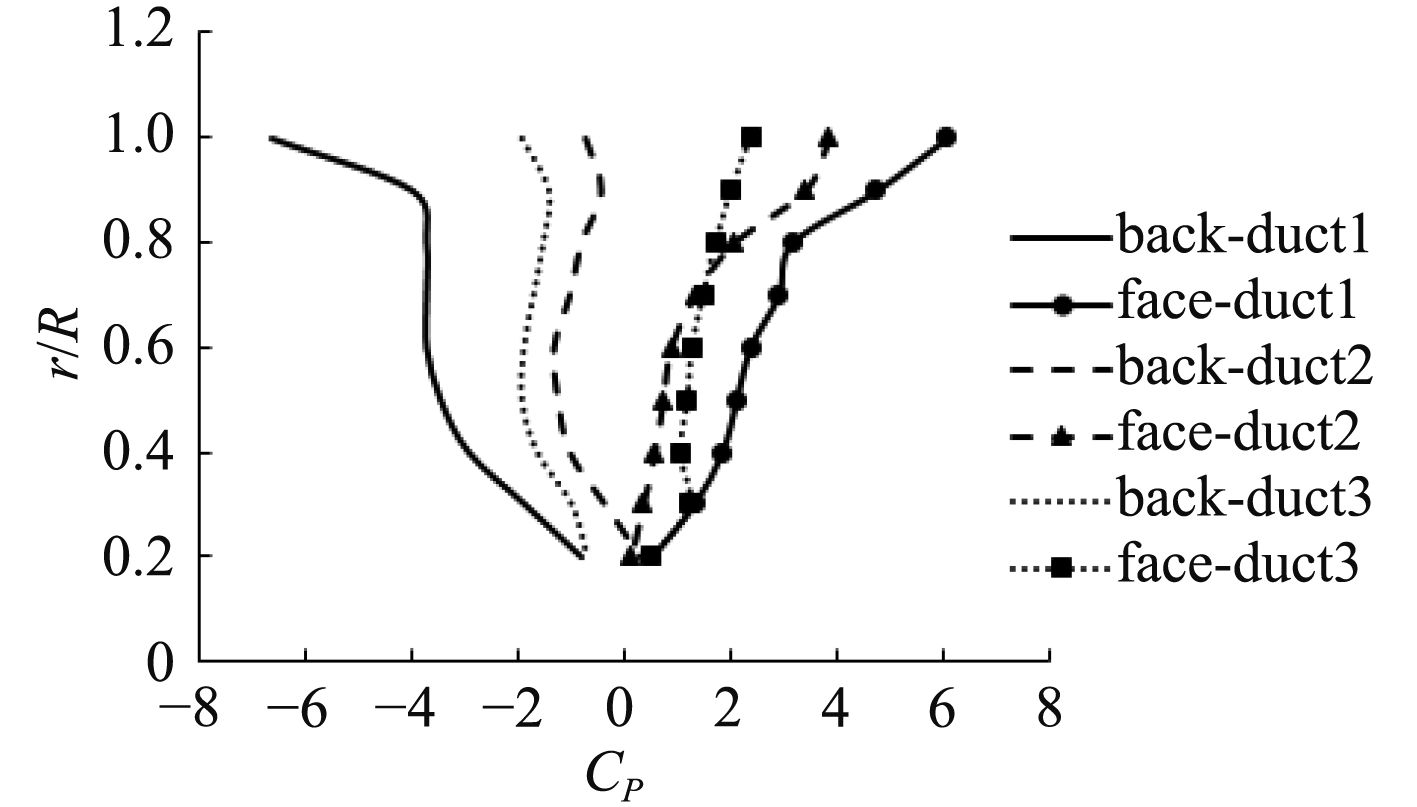
图8为J=0.2时,不同导管螺旋桨叶背和叶面压力系数沿桨叶径向的分布,从图中有以下观察和结论:
1)duct1,duct2和duct3三种导管螺旋桨压力沿桨叶径向分布的规律大致相似,叶根区域压力最小,叶面压力随着相对半径Rr的增大而增长,并在叶梢部分达到峰值;叶背正好相反,在叶根处压力最大,随着相对半径Rr的增大,压力减小,在叶梢部分降到最低。
2)duct3导管螺旋桨叶面压力分布较前两者更为均匀;duct1导管螺旋桨叶背压力沿桨叶半径方向波动较大,而duct2和duct3分布特点十分相似,且沿桨叶半径方向变化不大,说明后两者叶背荷载分布较为均匀。
3)duct1导管螺旋桨叶面压力在叶梢区域迅速增长,这是因为该区域产生了漩涡,并且叶面处在涡核外围高压区域。
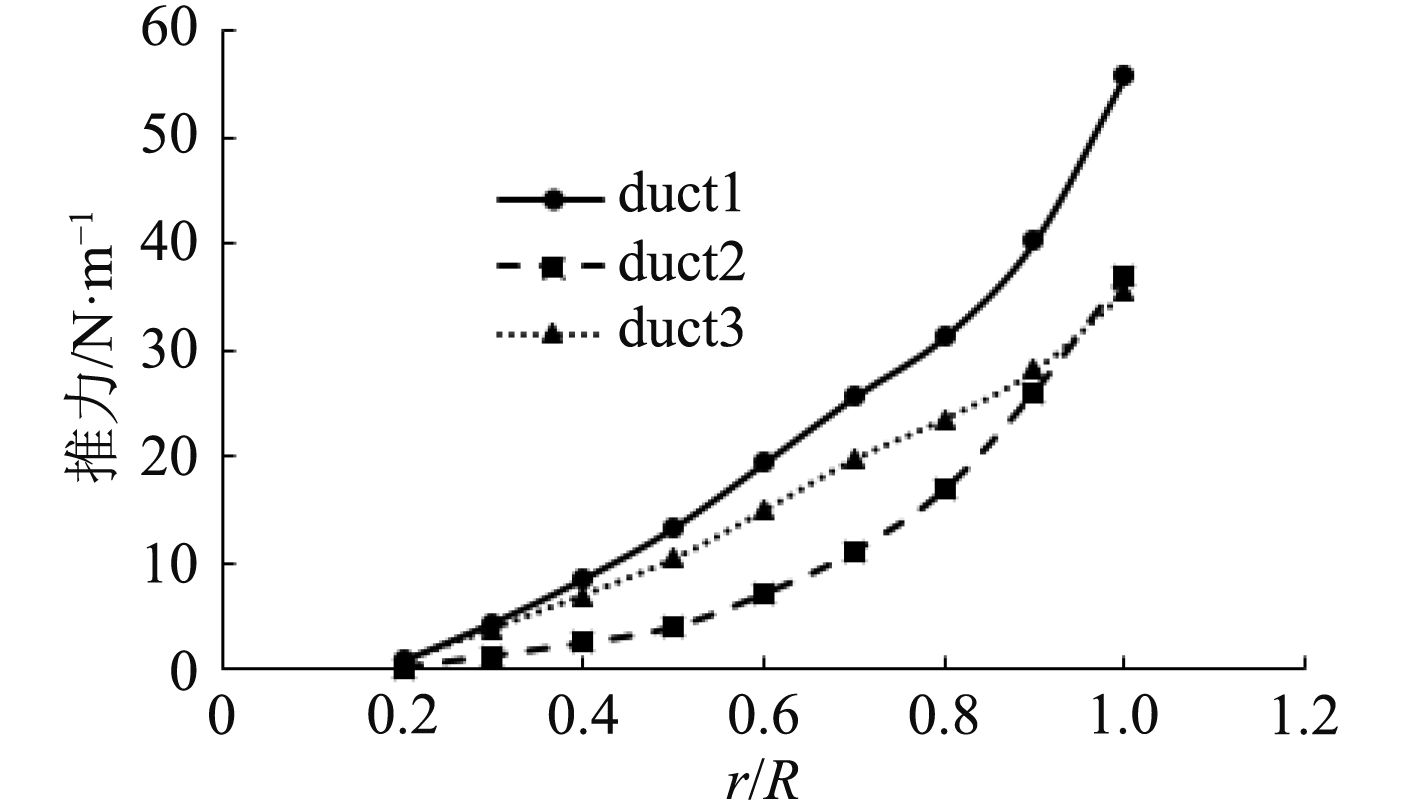
从图8的结论中可知叶梢贡献了螺旋桨推力的绝大部分,表3和图9分别为不同导管螺旋桨叶梢推力份额和单个桨叶推力沿桨叶半径方向的分布,综合表3和图9可以观察到以下特点:
1)duct1导管螺旋桨桨叶所发出的推力最大,duct3导管螺旋桨次之,duct2导管螺旋桨桨叶发出的推力最小。
2)螺旋桨所发出的推力主要分布在叶梢部分,越接近叶根,推力分量所占的份额越少;而在相对半径Rr=1时,单位长度上推力达到最大值。
3)3种导管螺旋桨叶梢(0.8≤Rr≤1)部分产生的推力占桨叶所产生的总推力的绝大部分,其中duct2导管螺旋桨所占的份额最大,duct1导管螺旋桨次之,duct3导管螺旋桨最小;duct3导管螺旋桨推力沿桨叶半径方向的变化梯度小于duct1和duct2,使桨叶受力更均匀,提高了螺旋桨的稳定性。
|
图 8 叶面叶背压力系数径向分布 Fig. 8 Pressure distributions between the face andback of propeller blade along the radial direction |
|
图 9 单个桨叶推力沿半径方向分布 Fig. 9 Thrust distribution along the radial direction of one blade |
|
|
表 3 不同导管螺旋桨叶梢推力份额 Tab.3 Proportion of the blade tips in different ducted propellers |
|
|
表 4 不同J下导管螺旋桨计算数据 Tab.4 Datas of the ducted propellers under different J |
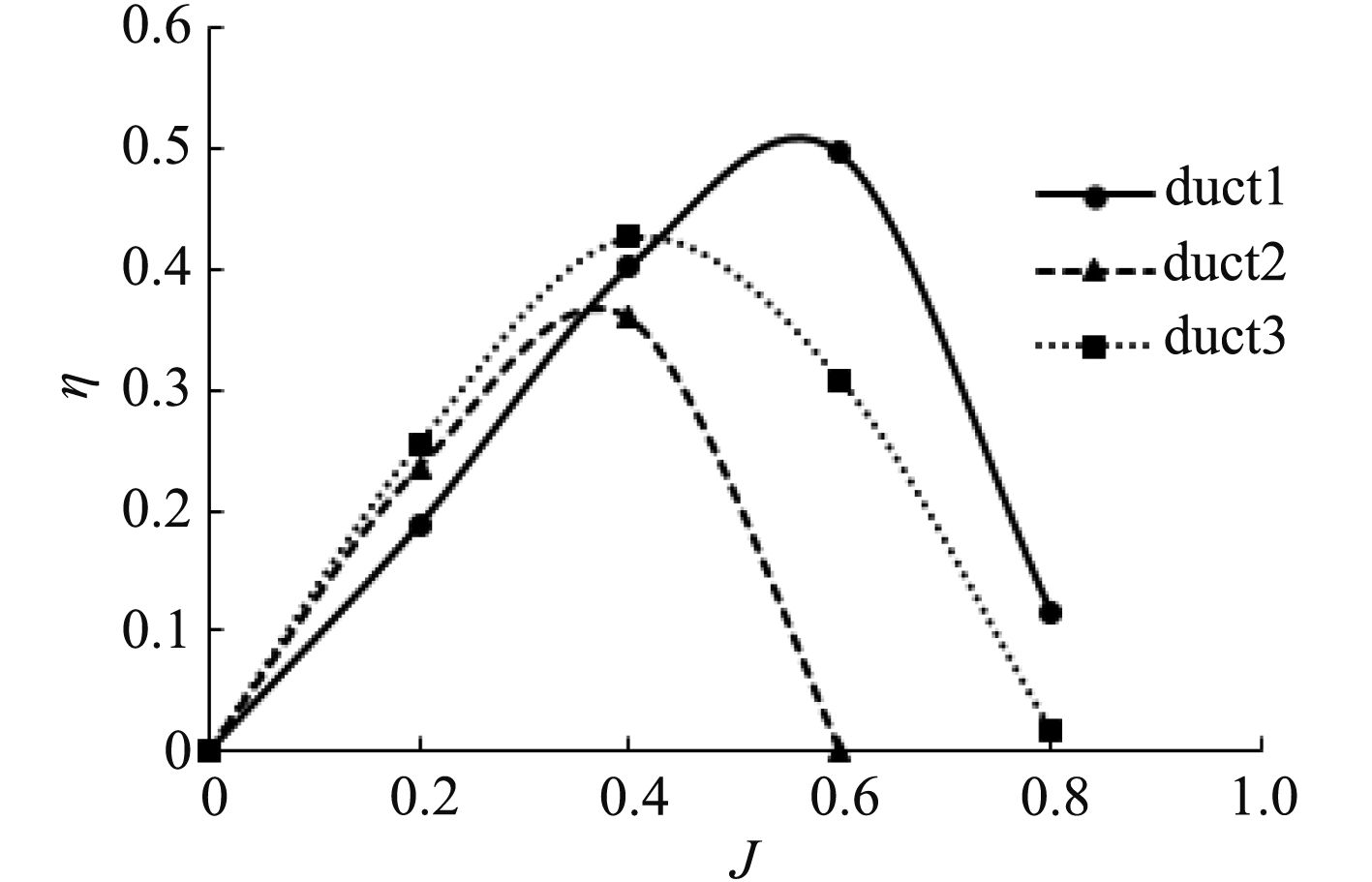
图10~图11分别为不同进速系数J时,无因次推力系数CT和效率η的计算数据,如表4所示。结合图10、图11和表4不难得到以下结论:
1)由于低进速系数J接近0时,进速VA接近于0,此时CT趋于无穷大,所以只计入J≥0.2时的情况;3种导管螺旋桨的无因次推力系数CT具有相同的变化趋势,即随着进速系数J的增大而减小,该特征在J≤0.4时显著;duct1和duct3导管螺旋桨的CT比较接近,duct2导管螺旋桨的CT比前二者略小。
2)在较低的J时,3种导管螺旋桨的效率η随着J的增大而增大,达到峰值点后,η随着J的增大而减小,并且三者进速系数J的临界值大小关系是duct2<duct3<duct1;进速系数J达到临界值前,三者的效率关系是duct3>duct2>duct1,但临界值后,三者的效率关系变为duct1>duct3>duct2。
3)综合对比duct1,duct2和duct3三种导管螺旋桨的无因次推力系数CT和效率η后,当J≤0.4时,可选择推力大,效率高的duct3导管螺旋桨,而当J > 0.4时,可考虑采用更高效的duct1导管螺旋桨。
4)duct2导管螺旋桨在J≥0.6时,以及duct3 J≥0.8时产生的推力总和为负值,可从表5中观察到此时桨叶或导管产生的推力是负值导致二者的合推力是负方向的。造成该现象的原因是此时流体以某一个负的几何攻角和叶元体或导管切面相遇,导致作用于叶元体或导管切面上的升力和阻力在螺旋桨轴向上的合力方向与螺旋桨的前进方向相反,即产生负推力。避免该现象的做法是减小进速系数J,可采用增大转速的方法予以消除。

|
图 10 无因次推力系数CT随J的变化 Fig. 10 CT at different J |
|
图 11 效率η随J的变化 Fig. 11 η at different J |
表5为桨叶和导管在不同进速系数J时所发出的推力的计算结果,其中导管推力份额的计算公式如下:
| $\zeta = \frac{{\left| {{T_{duct}}} \right|}}{{\left| {{T_{rot}}} \right| + \left| {{T_{duct}}} \right|}} \times 100\%\text{,} $ | (7) |
式中:Trot和Tduct分别为导管产生的推力和桨叶所产生的推力。
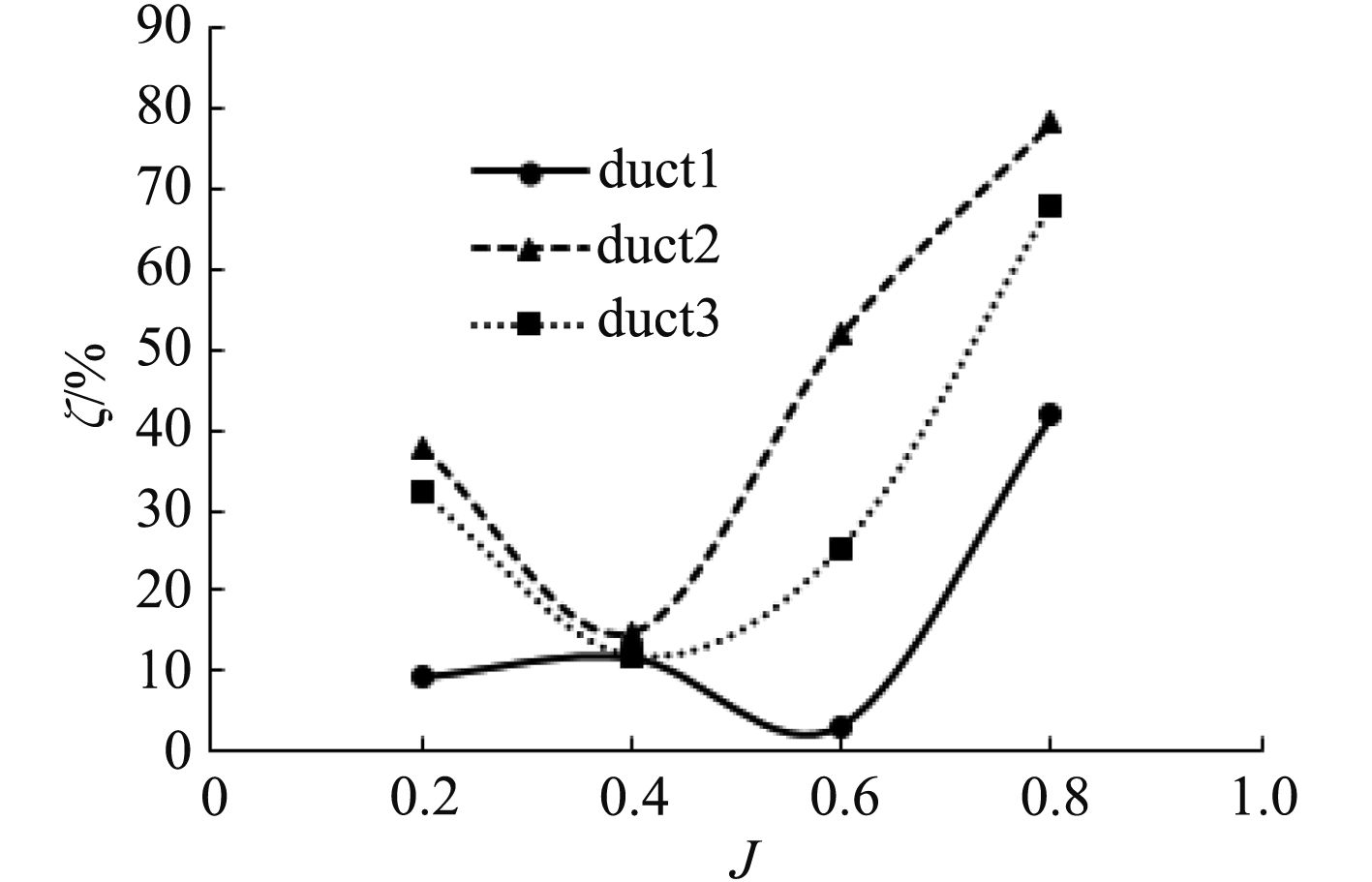
图12为导管推力所占份额ζ随进速系数J的变化曲线,可观察到:1)导管推力份额ζ随进速系数J的变化趋势基本是先减小后增大,其中duct1导管螺旋桨比duct2和duct3导管螺旋桨的变化相对更平缓;2)duct1,duct2,duct3三者的ζ在J=0.4时比较接近,且duct2和duct3处于最低点;3)导管螺旋桨中导管主要作用是起整流并提供较小份额的附加推力,考虑到导管结构作用和材料强度小的属性,应尽量避免导管所产生的推力占螺旋桨总推力较大份额,所以导管螺旋桨应设计在J=0.4附近正常工作较为合理。
|
图 12 导管推力份额ζ随J的变化 Fig. 12 The proportion of ducted propeller with different J |
|
|
表 5 桨叶和导管的推力计算结果 Tab.5 Thrusts from the ducts and propellers |
1)调整导管螺旋桨中的导管迎角,并延长导管有助于改善导管螺旋桨叶梢漩涡的产生和改善桨毂后的尾流,有利于提高导管螺旋桨的稳定性,提高推进效率;增大导管迎角并延长导管能够使得桨叶上荷载和推力分布更加均匀。
2)因为水下潜器航速较低,进速系数J也处在相对较小的范围,综合考虑叶梢漩涡范围,桨后尾流特点,以及推力大小和效率,应当选择duct3导管螺旋桨更合适。
3)导管螺旋桨中导管主要作用是起整流并提供较小份额的附加推力,考虑到导管结构作用和材料强度小的属性,应尽量避免导管所产生的推力占螺旋桨总推力较大份额,所以导管螺旋桨应设计在J=0.4附近正常工作较为合理。
4)导管在低进速系数时能够产生正的附加推力,但在高进速系数时产生负的推力,即变成附加阻力。
| [1] | AVILA J P J, ADAMOWSKI J C. Experimental evaluation of the hydrodynamic coefficients of a ROV through Morison’s Equation[J]. Ocean Engineering, 2011, 38 : 2162–2170. DOI: 10.1016/j.oceaneng.2011.09.032 |
| [2] | JAULIN L. Robust set-membership state estimation; application to underwater robotics[J]. Automatica, 2009, 45 : 202–206. DOI: 10.1016/j.automatica.2008.06.013 |
| [3] | LI J H, JUN B H, LEE P M, et al. A hierarchical real-time control architecture for a semi-autonomous underwater vehicle[J]. Ocean Engineering, 2005, 32 : 1631–1641. DOI: 10.1016/j.oceaneng.2004.12.003 |
| [4] |
陈健, 吴家鸣, 徐灜, 等. 立式翼型主体拖曳式水下潜器的设计及操纵性能[J]. 海洋技术学报, 2015, 34 (4): 1–6.
CHEN Jian, WU Jia-ming, XU Ying, et al. Study on design and control performance of the underwater towed vehicle with verticle airfoil main body[J]. Journal of Ocean Technology, 2015, 34 (4): 1–6. |
| [5] |
吴家鸣, 邓威, 赖华威. 回转状态下导管螺旋桨水动力特性的数值模拟[J]. 华南理工大学学报: 自然科学版, 2010, 38 (7): 90–96.
WU Jia-ming, DENG Wei, LAI Hua-wei. Numerical simulation of hydrodynamic characteristics of ducted propeller in turning motion[J]. Journal of South China University of Technology (Natural Science Edition), 2010, 38 (7): 90–96. |
| [6] |
吴家鸣, 赖宇锋, 李江伟, 等. 导管螺旋桨的推力、进速与诱导速度沿盘面的分布特征[J]. 船舶工程, 2016, 38 (12): 1–5.
WU Jia-ming, LAI Yu-feng, LI Jiang-wei, et al. Distribution Characteristics of Thrust, Advanced and Induced Velocity on Ducted Propeller Disk[J]. Ship Engineering, 2016, 38 (12): 1–5. |
| [7] | VERSTEEG, MALALASEKERA. An introduction to computational fluid dynamics: the finite volume method[M]. Wiley, New York, 1995. |
| [8] | BONTEMPO R, CARDONE M, MANNA M, et al. Ducted Propeller Flow Analysis by Means of a Generalized Actuator Disk Model[J]. Energy Procedia, 2014, 45C : 1107–1115. |
 2017, Vol. 39
2017, Vol. 39
