端部球面舱壁是水下航行器耐压壳体的重要组成部分,需要有足够的结构强度以抵御外部深水压力。与平面舱壁相比,球面舱壁具有空间利用高、重量轻等优点,广泛应用于大潜深航行器结构中。球面舱壁结构一般可由球壳、过渡环壳和耐压柱(锥)体组合而成[1]。
由于结构形式的对称性,弹性基础梁法和传递矩阵法等(半)理论方法常用于球面舱壁应力强度的计算分析,可考虑过渡环连接处厚薄板中曲面不一致[2]、斜率不连续[3]、变厚度等影响,为球面舱壁规范设计[4]提供理论依据。采用有限元可直观分析球面舱壁主要参数对其静强度的影响规律[5]。研究表明,采用圆弧光顺过渡能明显缓和过渡环区域应力强度问题。因此本文将圆弧光顺过渡形式的球-环-柱组合壳作为研究对象,进一步研究圆弧过渡环球面舱壁的应力强度特征。在耐压球壳结构极限承载这一方面,在理论计算中,主要是将球壳局部缺陷看作受球壳其余部分弹性约束的独立扁球壳[6, 7],运用壳体理论进行解析求解,此外不少学者借助有限元研究了局部缺陷、特征屈曲模态缺陷及球壳整体圆度偏差[8-10]对承载能力的影响,得出部分影响规律,但针对球-环-柱型式的球面舱壁结构承载能力及影响分析尚未有详细研究。
本文针对球-环-柱组合壳型式球面舱壁结构,首先分析球面舱壁结构应力特征,初步提出球面舱壁“扁平度”的概念,能表征其几何形状和力学特性,在此基础上分析了扁平度对结构静强度的影响,并综合初始挠度作用,研究扁平度对球面舱壁结构极限承载能力的影响规律及破坏机理。
1 球面舱壁扁平度及其对静强度影响 1.1 球面舱壁应力分布特征球面舱壁模型结构形式如图1所示。模型中球壳半径R=1 340 mm,过渡环半径r=340 mm,柱壳半径R0=1 100 mm,过渡环长度H1=221 mm,球壳球冠高H2=469 mm(为满足过渡环两端光顺连接,H1和H2随R和r变化),球面舱壁长度H(即H1和H2之和),舱壁厚度t=16 mm。A,B两点分别为柱-环和球-环的连接点。计算中弹性模型E=1.96×105 MPa,泊松比μ=0.3,均布外压P=3 MPa。在环肋柱壳末端采用刚性固支边界,模型中设置有4档肋位的柱壳是为了消除边界效应对舱壁结构的影响。

|
图 1 球-环-柱球面舱壁结构形式示意图 Fig. 1 The sketch of sphere-toroid-cylinder spherical bulkhead |
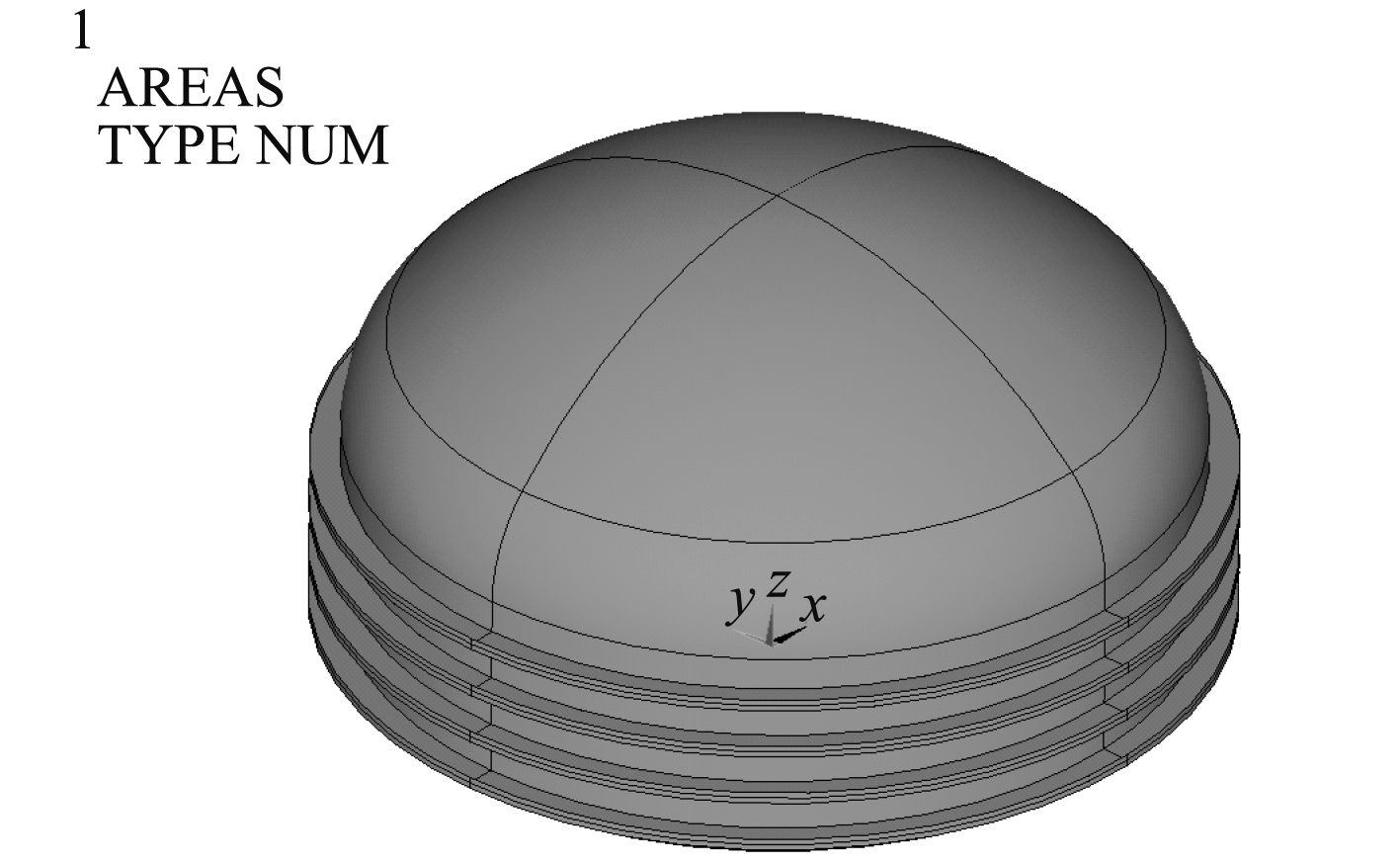
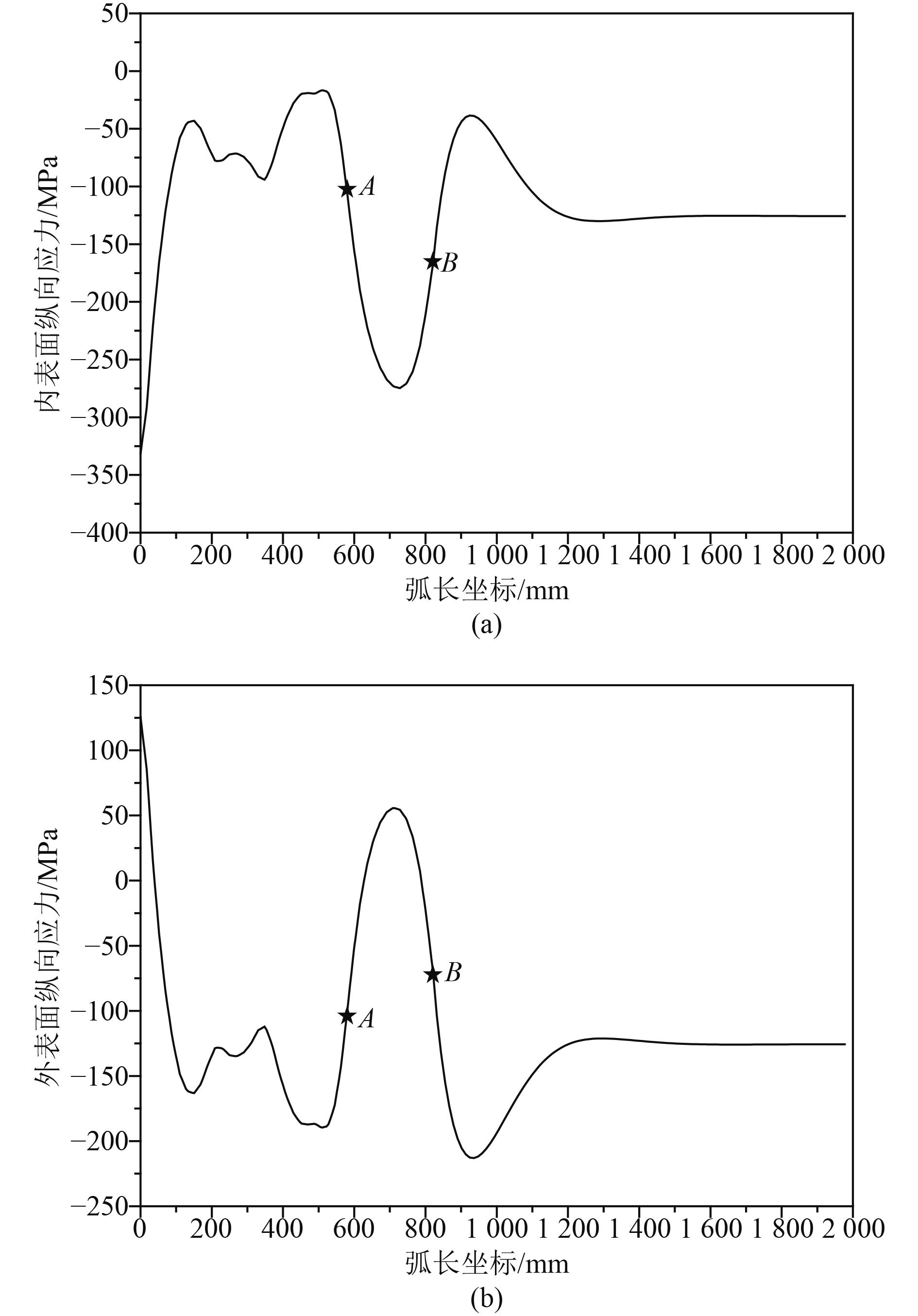
球面舱壁几何模型如图2所示,利用有限元软件进行静力计算,并绘制应力分量沿母线弧长(起始于柱壳端部,终于球壳顶点)方向的分布图,如图3所示。有如下应力特征:在远离球-环过渡的球壳部分基本处于薄膜应力状态;过渡环中间区域内表面存在高水平的纵向压应力(见图3(a)),过渡环连接处附近球壳外表面纵向压应力较高(见图3(b)),这两点的纵向应力值是球面舱壁结构应该考察的重点。
|
图 2 球面舱壁几何模型 Fig. 2 The geometric model of spherical bulkhead |
|
图 3 表面纵向应力分布 Fig. 3 Longitudinal stress distribution on surface |
研究表明[11],当R尽量取小、r取大,即舱壁长度H较大时(最大时等于R0,此时球壳和过渡环变成半球壳结构)应力状态更理想。在工程应用中,由于舱室总体布置、空间利用等因素使得H受到一定的约束。在限定H内,如何协调过渡环和球壳的尺寸使得整体应力水平更低,是一个值得探讨的问题。针对球-环-柱型式的球面舱壁结构,本文用过渡环长度与球面舱壁长度之比,即H1/H,来反映过渡环和球壳的组合关系,提出扁平度的概念,用F表示,即
| $F = \frac{{{H_1}}}{H}\text{。}$ | (1) |
扁平度F能直观地描述球面舱壁结构的几何形状特征。F越大,环壳长度相对较长,球壳半径和过渡环半径越大,整个球面舱壁结构显得越扁平丰盈,如图4所示。此外当F和H确定时,R和r也随之确定,即整个球面舱壁的几何形状确定。

|
图 4 不同扁平度F时球面舱壁形状图 Fig. 4 The shape of spherical bulkhead varying flatness F |
F还能表征球面舱壁的力学特征。F较小时,球壳部分较大,球面舱壁薄膜应力状态区域较大,球面舱壁应力分布更近似于完整球壳的应力状态(仅在较短的过渡环区域,由于过渡急锐,存在应力变化剧烈的现象)。F越大,球冠高H2越小,球-环连接处附近区域的弯矩及其波及范围也越大,球壳部分薄膜应力状态区域越小,弯曲应力为主要应力成分;当F趋于1时,球壳趋于平面,球壳区域的应力分布类似平面舱壁(无水平大梁等加强材)应力分布。
1.3 扁平度对球面舱壁应力强度的影响为研究扁平度对球面舱壁结构应力强度的影响,本文先取H=650 mm,F取0.1,0.2,0.3,0.4,0.5,0.6,0.7分别计算,如图5所示。

|
图 5 扁平度变化时表面纵向应力分布 Fig. 5 Longitudinal stress distribution on surface varying flatness |
由图5可知:当F较小时,由于过渡环中间纵向弯矩较大,该区域内表面纵向压应力较大,外表面可能出现拉应力较高的情形;F增大时,纵向弯矩和内表面纵向应力均显著减小。当扁平度过大时,纵向弯矩和内表面纵向应力反而有所增加,此外球壳长度也会过小,球壳无矩状态的区域会很小,不利于结构布置(如开口等)。
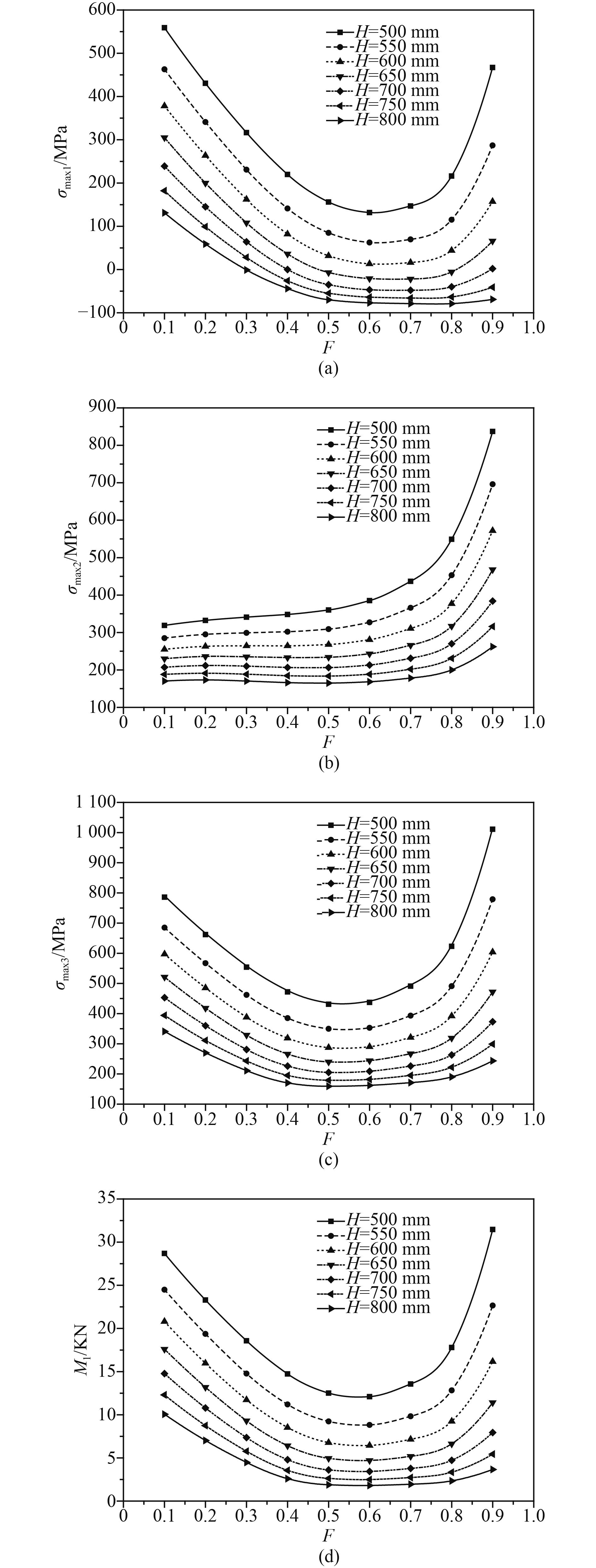
为验证扁平度的普遍影响作用,本文选取4个幅值较大的应(内)力分量作为参考:过渡环内表面纵向压应力最大值
|
图 6 不同H下4个参考量随F的变化 Fig. 6 4 conference items change with flatness varying H |
不同H下,扁平度对应力状态的影响作用基本一致:扁平度过小时,由于M1较大,
此外,H越小时,扁平度F的对应力幅值的影响灵敏度越高;在相同扁平度下,H越大,弯矩峰值和应力水平就越低,即在总体布置条件许可下,尽量取较大H。
2 扁平度对极限承载能力的影响 2.1 计算模型球面舱壁模型如图2所示,进行结构极限承载能力计算时考虑双重非线性。整个结构采用理想弹塑性模型材料,材料屈服准则采用Von Mises准则;考虑结构的几何非线性,并在模型中引入初始挠度,使用弧长法,采用商用软件Ansys进行非线性计算。
目前研究的初挠度形式主要包括:局部缺陷形式、特征屈曲模态缺陷形式、实物或模型真实挠度形式。真实挠度形式受工艺制造的影响具有较大的随机性,此外有研究表明整体特征值屈曲模态缺陷形式对结构最为不利[10],因此本文采用整体特征值屈曲模态作为初挠度形式。考虑到工程中有建造偏差的限制,本文研究的初挠度幅值f不超过0.6 t(t为板厚)。
2.2 不同扁平度F对含初挠度球面舱壁结构极限承载能力的影响为研究扁平度F对球面舱壁结构极限承载能力的影响,F取0.1~0.8,计算在各幅值初挠度f下的球面舱壁极限承载能力,结果如表1所示。
|
|
表 1 各幅值初挠度下的球面舱壁极限承载能力 Tab.1 Ultimate bearing capacity with different F and amplitude of initial imperfection f |
将表1结果绘制成不同扁平度下极限破坏压力随初挠度幅值的变化曲线组,如图7所示。

|
图 7 不同扁平度和初挠度幅值下球面舱壁的极限承载能力 Fig. 7 Ultimate bearing capacity with different F and f |
由图7可知,结构破坏压力随初挠度幅值增大而减小;当扁平度较小时,破坏压力随初挠度幅值的变化较为平缓,尤其在初挠度幅值约小于0.2时;当扁平度较大时,破坏压力随初挠度幅值的变化较明显,即破坏压力对初挠度幅值的敏感度较大;此外,当初挠度幅值较小(约小于0.20)时,随扁平度的增大,结构破坏压力先增大后减小,当初挠度较大(约大于0.45)时,破坏压力均随扁平度增大而减小。
为更直观清晰不同初挠度幅值下扁平度对破坏压力的影响作用,做出云图如图8(a)~图8(c)所示。由图显见,当F取0.35~0.55且初挠度幅值较小时,破坏压力取得较大值;当F较大时,云图变化梯度较大,即破坏压力随初挠度幅值变化较为明显。当H取600 mm和800 mm时,其云图分布形式与H=700 mm相似,即F对含初挠度的球面舱壁结构极限承载能力的影响具有一般的规律。当F约取0.35~0.55时,球面舱壁结构在较小初挠度幅值范围内(小于约0.3)有较高的极限承载能力。此外,由图8(d)可知,当H取600 mm,700 mm,800 mm时,破坏压力响应曲面依次向上分布,即H越大,结构承载能力越强。

|
图 8 不同H时极限压力云图 Fig. 8 Contours of ultimate bearing pressure with different H |
为了研究不同扁平度球面舱壁结构的破坏形式及机理,本文选取几个典型的扁平度进行分析。
当扁平度为0.1时,过渡环过渡比较急锐,内表面应力水平较高,内表面率先进入塑性阶段;随着载荷的增大,塑性变形逐渐向过渡环外表面扩展,直至整个过渡环区域塑性不可限制,达到了极限破坏压力;在卸压阶段,由于过短环已经完全处于塑性状态,产生较大形变,塑性变形迅速流动至球-环连接处及相邻球壳区域,最终在过渡环及相邻球壳区域发生局部凹陷。

|
图 9 塑性扩展及破坏形式 Fig. 9 Plastic extension and failure mode |
当扁平度为0.4时,过渡环内表面也先产生塑性变形,但未得到充分发展;当载荷继续增大时,在球壳缺陷区域出现塑性变形,并迅速流动发展,最终在初挠度区域产生凹陷破坏。
当扁平度为0.7时,球面舱壁过渡段相对较长,过渡环区域弯曲应力较小,然而在球壳区域较大范围内存在弯曲应力,球壳初挠度区域外表面首先出现塑性变形;塑性变形逐渐向球壳内表面及周边区域扩展。在卸压过程中,球壳凹陷区域变形进一步增大,致使相邻凹陷区域中间部分内表面受挤压形成塑性铰线,产生大幅塑性应变直至压溃,并产生撕裂破坏。
综上所述,当球面舱壁扁平度较小时,容易在过渡环产生塑性并迅速发展,破坏压力较小;当扁平度过大时,球壳区域存在弯曲应力,结构的破坏压力受初挠度影响较为明显。当扁平度适中时,能兼顾过渡环和球壳部分,整个结构不会迅速产生塑性破坏,使得承载能力较高。
3 结 语本文对球-环-柱型式球面舱壁的结构强度进行了分析。初步提出了扁平度的概念,并研究了扁平度对球面舱壁结构应力强度和极限承载能力的影响规律,得到以下结论:
1)初步提出了扁平度的概念,能表征球面舱壁结构几何形式和力学特征;当扁平度较小时,球面舱壁显得比较深长,过渡环内表面纵向应力较大;当扁平度过大时,舱壁形状显得丰盈扁平,球壳部分存在弯曲应力,降低了利用膜应力抵御外界压力的能力。
2)扁平度对球面舱壁结构极限承载能力有着一定的影响:当扁平度较小时,破坏压力随初挠度幅值变化较小,塑性应变出现在过渡环,并在过渡环段流动扩展直至结构失效;当扁平度过大时,球壳部分本身存在一定的弯曲应力,加上初挠度的扰动影响,使得弯曲应力更为突出,在初挠度区域产生塑性应变并迅速扩展。
3)综合扁平度对球面舱壁结构应力强度及极限承载能力的影响,建议扁平度取值范围为0.35~0.55。
| [1] | 许辑平. 潜艇强度[M]. 北京: 国防工业出版社, 1980. |
| [2] |
朱邦俊, 王丹, 万正权. 端部球面舱壁应力近似解[J]. 船舶力学, 2011, 15 (11): 1255–1263.
ZHU Bang-jun, WANG Dan, WAN Zheng-quan. An analytical solution for stresses of the end spherical bulkhead[J]. Journal of Ship Mechanics, 2011, 15 (11): 1255–1263. DOI: 10.3969/j.issn.1007-7294.2011.11.009 |
| [3] |
黄旎, 夏飞, 杨宇华, 万鹏, 等. 环-锥处折角对球-环-锥组合壳的影响[J]. 舰船科学技术, 2011, 33 (10): 25–28.
HUANG Ni, XIA Fei, YANG YU-hua, WAN Peng, et al. A effect study on the curved angle in toroid-cone of the sphere-toroid-cone combined shells[J]. SHIP SCIENCE AND TECHNOLOGY, 2011, 33 (10): 25–28. DOI: 10.3404/j.issn.1672-7649.2011.10.006 |
| [4] |
GJB/Z 21A-2001. 潜艇结构设计计算方法[S]. 北京: 国防科技工业委员会, 2001.
GJB/Z21A-2001. Method for design and calculation of submarine structure [S]. Beijing: COSTIND, 2001. |
| [5] |
范名琦, 王永军, 刘鑫. 潜艇端部舱壁结构分析[J]. 船舶力学, 2007, 11 (4): 94–599.
FAN Ming-qi, WANG Yong-jun, LIU Xin. Analysis of dome for submarine structure[J]. Journal of Ship Mechanics, 2007, 11 (4): 94–599. |
| [6] |
郑衍双, 陆正福, 张定武. 均匀外压下有几何缺陷球壳的破坏压力[J]. 中国造船, 1986 (1): 48–58.
ZHENG Yanshuang, LU Zhengfuand, ZHANG Dingwu. Collapse Pressure of Spherical Shells with Initial Imperfections under Uniform Pressure[J]. SHIPBUILDING OF CHINA, 1986 (1): 48–58. |
| [7] |
李天匀, 郑衍双. 均匀外压下非完善球壳的非线性稳定性分析[J]. 华中理工大学学报, 1997, 25 (11): 90–92.
LI Tianyun, ZHENG Yanshuang. Nonlinear Stability Analysis of Spherical Shell with Imperfection under Uniform External Pressure[J]. J. Huazhong Univ. of Sci. & Tech, 1997, 25 (11): 90–92. |
| [8] |
王自力, 王仁华, 俞铭华, 李碧良, 等. 初始缺陷对不同深度载人潜水器耐压球壳极限承载力的影响[J]. 中国造船, 2007, 48 (2): 45–50.
WANG Zi-li, WANG Ren-hua, YU Ming-hua, LI Liang-bi, et al. The Influence of the Initial Imperfections on the Ultimate Strength of Manned Deep-sea Submersible Pressure Sphere Hull[J]. SHIPBUILDING OF CHINA, 2007, 48 (2): 45–50. |
| [9] |
陆蓓, 刘涛, 崔维成. 深海载人潜水器耐压球壳极限强度研究[J]. 船舶力学, 2004, 8 (1): 51–58.
LU Bei, LIU Tao, CUI Wei-cheng. Ultimate strength of pressure spherical hull in deep-sea manned submersibles[J]. Journal of Ship Mechanics, 2004, 8 (1): 51–58. |
| [10] |
王仁华, 俞铭华, 李良碧, 等. 初始缺陷对深海载人潜水器耐压球壳弹塑性稳定性影响[J]. 海洋工程, 2006, 23 (4): 111–115.
WANG Ren-hua, YU Ming-hua, LI Liang-bi, et al. Influence of initial deflection on plastic stability of manned deep-sea submersible’s pressure sphere hull[J]. THE OCEAN ENGINEERING, 2006, 23 (4): 111–115. |
| [11] |
黄旎. 球-环-锥旋转组合壳强度和稳定性研究[D]. 武汉: 中国舰船研究设计中心, 2012.
HUANG Ni. Strength and stability analyses for sphere-toroid-cone rotational shells[D]. Wuhan: China Ship Development & Design Center, 2012. |
 2017, Vol. 39
2017, Vol. 39
