2. 北京理工大学,北京 100081
2. Beijing Institute of Technology, Beijing 100081, China
潜射装置抗冲击性能主要由筒体结构间的减震环节决定。为提高抗冲隔震性能,国外导弹通常采用层筒结构,并在外筒与内筒之间,内筒与弹体之间布置减震垫、适配器以及气密环等结构作为减震环节。
为明确这类减震结构的性能,国内外学者对双层减震系统进行研究。例如Gurgoze[1]利用格林函数法和假设模态法对中间离散安装弹簧质量的双层悬臂梁结构进行理论分析,研究系统固有频率和模态。Simsek等[2]研究了双层梁在不同边界条件下的移动简谐载荷响应。Zhang等[3 – 4]针对具有不连续特性的复杂结构梁提出一种分析方法。Ariaei等[5]根据铁木辛柯梁理论对离散弹性连接的多层梁结构在移动载荷下的响应进行理论分析,并通过实例分析弹性连接的刚度、移动载荷的移动速度对结构响应的影响。这些研究主要集中在双自由度双级减震模型或单层梁结构减震模型中,对具有双级减震特点,又具有弹性梁变形的模型研究不多。
本文结合双层筒潜射装置结构特点,将减震系统等效为具有双层梁结构的梁柱模型,并利用多体动力学方法,对这类双级减震结构的冲击响应特性进行深入的研究和分析。
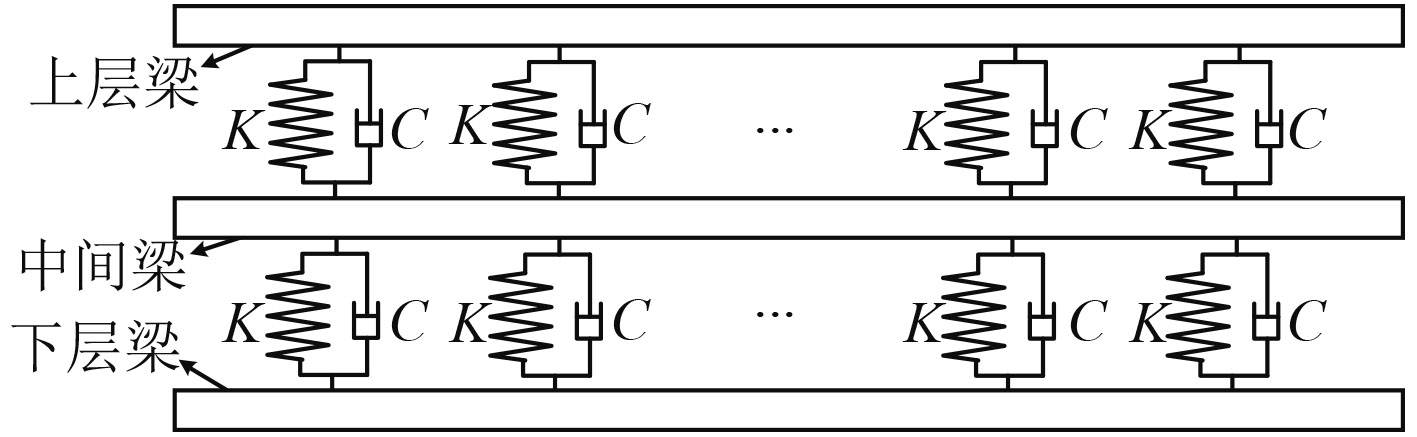
1 计算模型 1.1 模型设置结合双层筒潜射装置结构特点,将其简化为如图1所示的3层梁模型。其中上层梁用于表示发射系统中的弹体结构及响应变形,中层梁和下层梁分别表示发射装置的内筒、外筒的结构和变形。各层梁之间的弹簧-阻尼结构用于表示内外筒之间或弹筒之间的减震环节[6-7]。模型中的梁均为可变形柔性体,以表征实际结构的弯曲变形。假设梁上各个位置具有相同的力学性能,弹簧具有相同的刚度且等间隔布置。
|
图 1 梁-弹簧模型示意图 Fig. 1 Sketch map of the beam-spring model |
为分析双层梁-弹簧结构在冲击载荷作用下的响应特性,这里采用半正弦加速度作为基础的激励载荷[8-9],其加速度峰值为50 g、冲击时间为6 ms。为便于计算分析,这里采用位移法,将加速度冲击经2次积分转换为位移载荷进行计算处理,冲击激励的表达式为:
| $x = \left\{ {\begin{aligned}& { - \displaystyle\frac{{50g}}{{{\omega ^2}}}\sin (\omega t) + \displaystyle\frac{{50g}}{\omega }t} \text{,} &{t \leqslant {t_0}}\text{,}\\& {\displaystyle\frac{{100g}}{\omega }t - \displaystyle\frac{{50g}}{\omega }{t_0}} \text{,}& {t > {t_0}}\text{。}\end{aligned}} \right.$ | (1) |
式中g=9.8 m/s2,t0=6 ms,ω=π/t0。
在实际结构中,筒体中部往往是挠度变形最大区域,因此在考察梁-弹簧模型的抗冲击响应时,同样取梁中间位置的挠度作为主要分析对象。这里分别取上层梁中间位置的绝对加速度时域最大值Abmax、中间梁与上层梁中间位置的相对位移时域最大值Ybmax、以及中间梁与下层梁中间位置的相对位移时域最大值Zbmax作为梁-弹簧模型的抗冲击评价指标。涉及的模型参数如下:
| $\left\{\begin{array}{l}{A_1}{\rm{ = }}{b_1}{h_1}\;\;\text{,}\;\;{A_2} = {b_2}{h_2}\;\;\text{,}\;\;{A_3} = {b_3}{h_3}\text{,}\\{k_{tup}} = n{k_{up}}\text{,}\;\;\;\;{k_{tdown}} = n{k_{down}} = {k_{tup}}/Fb \text{,}\\P{b_1} = \sqrt {{k_{tup}}/{m_{up}}} \text{,}\;\;\;{\xi _{up}} = {c_{up}}/\left( {2\sqrt {{k_{tup}}{m_{up}}} } \right) \text{,}\\Fb = {k_{tup}}/{k_{tdown}}\text{,}\;\;\;Lb = {m_{up}}/{m_{mid}}\text{,}\\{\xi _{down}} = {c_{down}}/\left( {2\sqrt {{k_{tdown}}{m_{down}}} } \right)\text{。}\end{array}\right.$ | (2) |
式中:A1,A2和A3分别各层梁的截面积;b1,b2和b3为梁截面宽度;h1,h2和h3为梁截面高度;kup,kdown为上,下层单个弹簧的刚度;n为上下层弹簧数量;ktup,ktdown分别为上,下层弹簧的刚度之和;Pb1为上层频率;梁-弹簧模型中上层频率为上层弹簧刚度之和与上层梁质量比值的平方根值;mup,mmid和mdown分别为各层梁的质量。
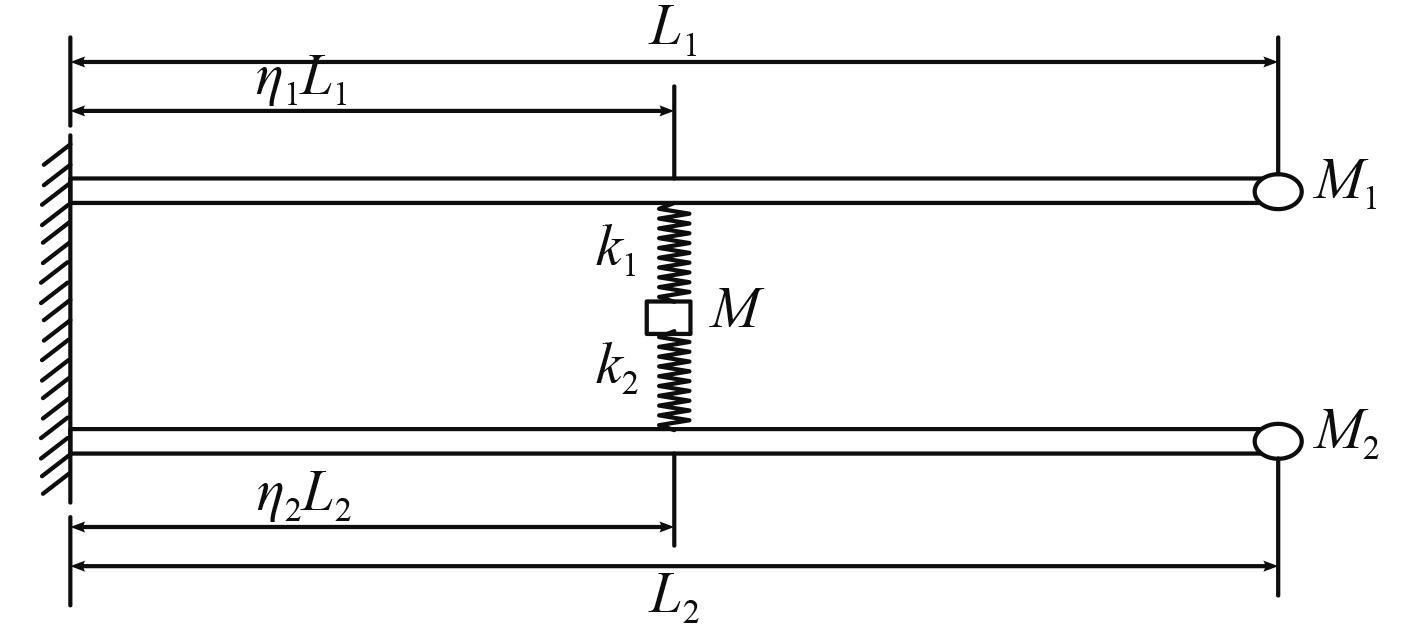
1.2 模型校验这里结合参考文献[1]给定的模型和结果数据,对梁-弹簧结构的计算模型进行校验。在校验模型中,采用双层梁结构,如图2所示。其主结构为自由端各有一集中质量点的2条悬臂梁,中间通过弹簧质量系统连接。
|
图 2 近似验证模型 Fig. 2 Approximate verification model |
校验模型中悬臂梁的长度为L1=L2=10 m,弹簧质量系统的无量纲化安装位置为0.5,梁材料选择为刚材料,其截面宽度和高度均为0.1 m,2层梁端点结构的质量是中间部分质量的2倍。
为分析梁结构分段数量对结构的影响,分别建立8,16,32,64段双层梁模型进行模态分析,计算得到双层梁模型的固有频率并对其无量纲化,获得系统前10阶固有频率的无量纲化数据对比结果如表1所示。从表中可以看出,当柔性梁分段数量大于16时,采用柔性梁方式计算得到的系统固有有频率与理论计算值均比较接近,误差在5%以内。为保证计算精度和计算效率,后文采用分段数量为32的柔性梁模型。
|
|
表 1 不同分段数固有频率 Tab.1 Natural frequencies of different segment |
为分析基于梁-弹簧模型的双级减震系统冲击响应特性,首先采用梁长度为10 m、截面为0.1 m正方形、上层频率为10 rad/s、梁质量为780.1 kg、弹簧数量为7、弹簧刚度比为1.2、梁质量比为2.7的模型,对响应状态进行计算分析。
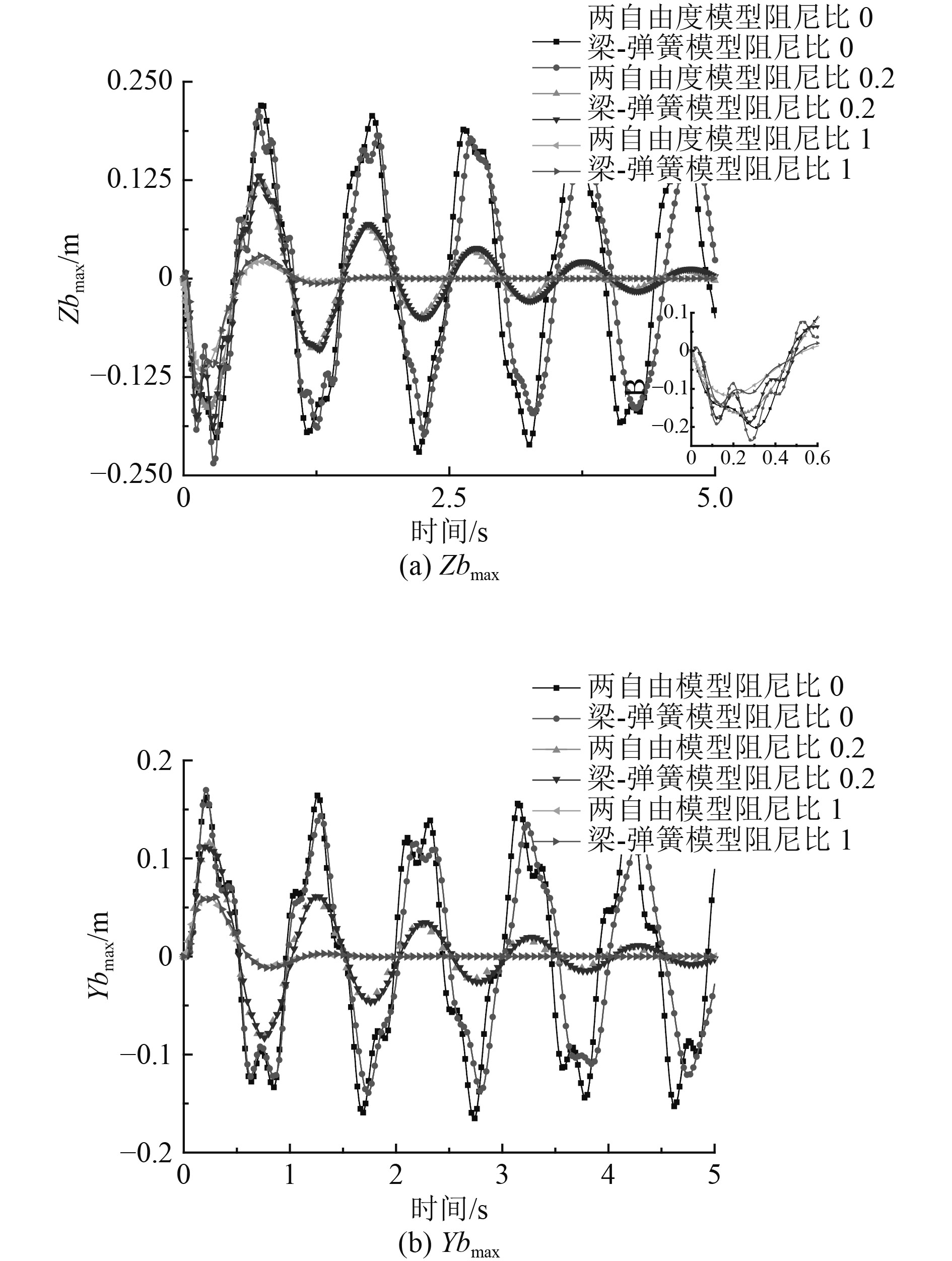
计算获得梁-弹簧模型相对最大位移Zb、Yb随时间的变化规律与简化两自由度模型的对比如图3所示。从图中可以看出,在冲击的初始阶段,中间和下层梁间距离缩小,而中间和上层梁间间距增大。在经过约0.6 s后,各层梁间的相对位置呈振荡变化规律,并在阻尼作用下震荡幅值逐渐减小。此外,梁-弹簧模型和两自由度模型相对位移随时间的变形规律基本一致,幅值相差不大。在初始冲击的0~0.6 s,受柔性梁变形产生的挠度影响,梁-弹簧模型的波形曲线上有较高频率的微小波动。
|
图 3 相对位移随时间的变化规律 Fig. 3 Change rule of relative displacement with time |
图4给出了梁-弹簧模型中上层梁(模拟弹体)中部加速度变化与两自由度模型结果的对比曲线。从图中可以看出,受双级减震结构作用,传递到上层梁上的加速度峰值小于1.8 g,有效降低了外部载荷对上层梁的冲击作用。与相对位移的响应类似,在经过约0.6 s后,上层梁加速度呈振荡变化趋势,并在阻尼作用下逐渐衰减。同样,受梁的变形影响,在初始冲击阶段,梁-弹簧模型与两自由度模型结果存在一定差异,由此可以看出,在初始冲击阶段,梁结构的刚强度,对双级减震系统存在一定的影响。

|
图 4 上层梁加速度随时间变化规律 Fig. 4 Acceleration law of the upper beam with time |
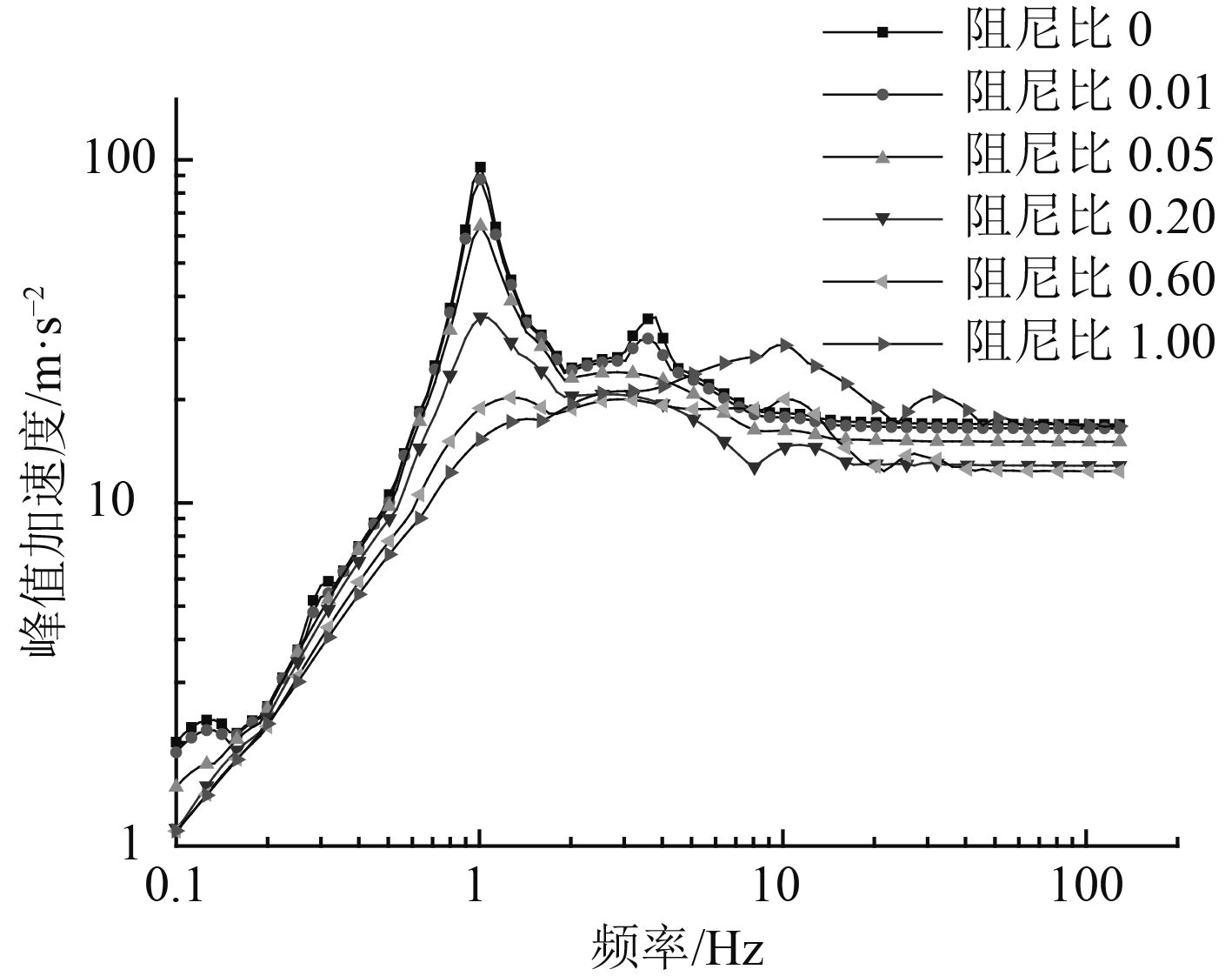
为分析冲击载荷作用下的冲击响应谱,利用Smallwood方法[10]对时域结果进行计算处理。图5给出了从上层梁中部位置加速度时域响应中获得的冲击响应谱状态。从图中可以看出,对于阻尼较小的系统,冲击响应谱具有2个明显的峰值,2个波峰对应的频率分别为1 Hz和3.5 Hz。当模型中的阻尼比超过0.6时,其上层梁中部加速度时域响应随时间迅速衰减,从而使得其冲击响应谱结果在频率大于1 Hz时随频率的增加变化更加平稳,不具有明显的波峰。
|
图 5 梁-弹簧模型冲击响应谱结果 Fig. 5 Shock response spectrum results of beam spring model |
从结构时域和频域响应结果可以看出,在冲击载荷作用下,系统的初始响应受阻尼影响不大;而在振荡变化阶段,系统阻尼有着重要影响。因此这里先将阻尼设置为0,对刚度比、质量比对响应特性的影响进行分析;进而增加系统阻尼,研究阻尼对响应特性的影响。
为研究刚度比和质量比的影响,这里选取上层梁-弹簧系统频率Pb1为10,上层梁和下层梁质量为780.1 kg,层间弹簧数量为7的模型进行考察和分析。通过调整中层梁质量和下层梁-弹簧系统频率,分别对质量比在0.1~9.8、刚度比在0.2~9.7间的多个状态进行计算处理。
3.2 最大响应特性分析图6分别给不同质量比和刚度比条件下梁间最大相对位置Zbmax和Ybmax的变化规律。从图中可以看出,在相同刚度比条件下,中间梁与下层梁在中间位置的相对位移Zbmax随着质量比的增加逐渐减小;当质量比大于2.8后,Zbmax随质量比的变化趋于平缓,表明在这种条件下,质量比对系统响应的影响显著减小。在相同质量比条件下,Zbmax随刚度比的增加而增加。当刚度比为0.2时,位移Ybmax随着质量比的增加而减小,当刚度比大于0.7时,Ybmax随着质量比的先增加后减小,并趋于稳定。大多数情况下,Ybmax随着刚度比的增加而减小。

|
图 6 层间最大相对位置变化规律 Fig. 6 Maximum relative position variation between layers |
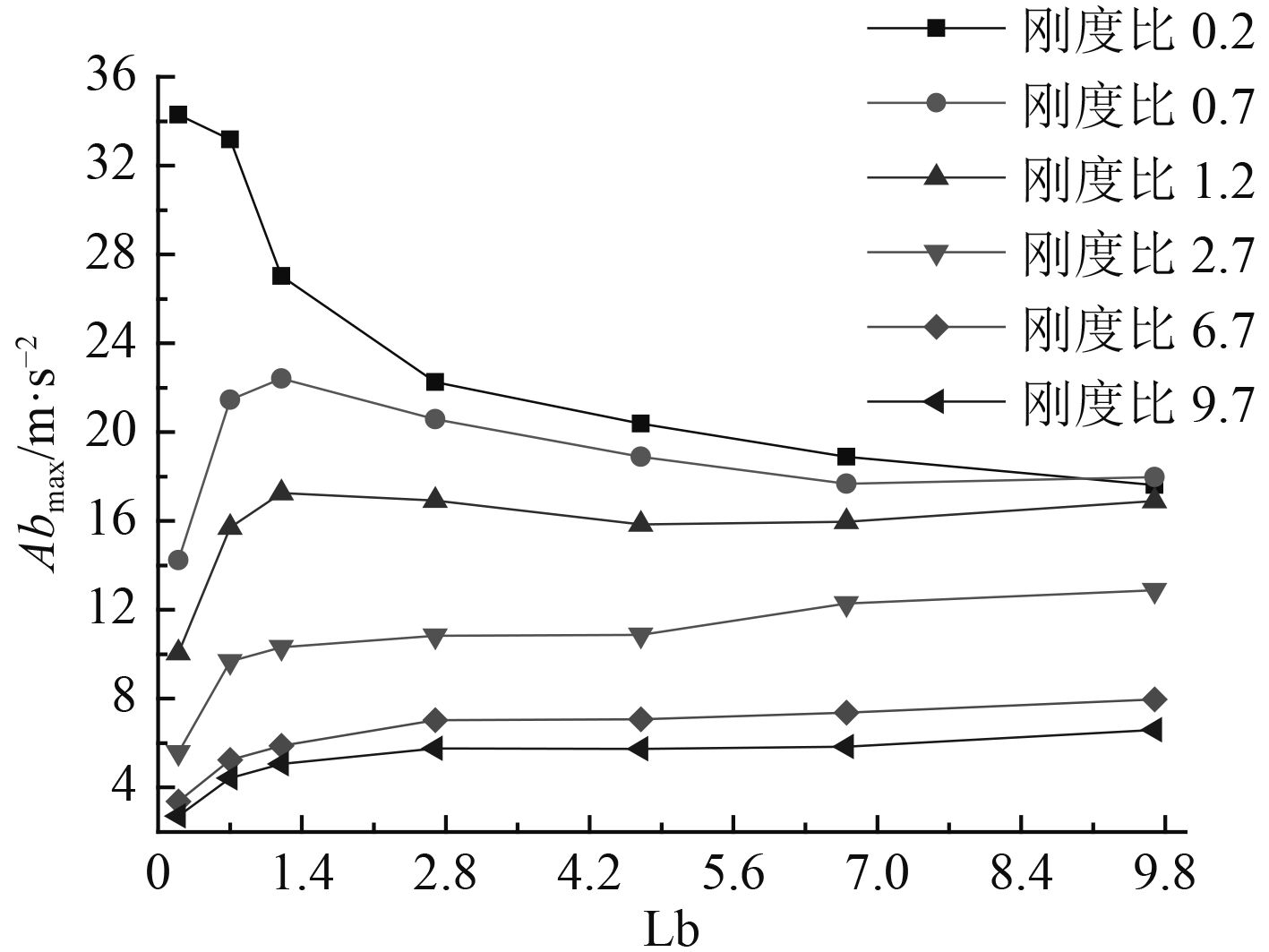
图7给出了不同质量比和刚度比条件下上层梁中部最大加速度Abmax变化规律。可以看出其变化规律与Ybmax基本一致。
|
图 7 上层梁中部最大加速度变化规律 Fig. 7 The maximum acceleration variation in the middle of the upper beam |
结合潜射装置双级减震系统的结构特点,建立含3层梁-弹簧的仿真模型,对双级减震系统在冲击载荷作用下的响应特性以及结构质量比、减震环节刚度比等对响应状态的影响进行计算和分析,获得如下结论:
1)针对作用在基础上的冲击载荷,双级减震系统能够起到有效的抗冲击作用,使上层梁冲击过载显著降低。
2)随着下层减震环节与上层减震环节刚度比的增加,模拟弹体的上层梁冲击过载响应减小,而上下层间的相对位移增加。
3)中间层质量较小情况下,系统冲击响应受该层质量影响较大,随着该质量的增加,对系统响应的影响减小。
| [1] | GÜRGÖZE M. Bending vibrations of beams coupled by a double spring–mass system[J]. Journal of Sound and Vibration, 2001, 243 (2): 361–369. DOI: 10.1006/jsvi.2000.3442 |
| [2] | SIMSEK M, CANSIZ S. Dynamics of elastically connected double-functionally graded beam systems with different boundary conditions under action of a moving harmonic load[J]. Composite Structures, 2012, 94 (9): 2861–2878. DOI: 10.1016/j.compstruct.2012.03.016 |
| [3] | ZHANG Z, CHEN F, ZHANG Z, et al. Vibration analysis of non-uniform Timoshenko beams coupled with flexible attachments and multiple discontinuities[J]. International Journal of Mechanical Sciences, 2014, 80 : 131–143. DOI: 10.1016/j.ijmecsci.2014.01.008 |
| [4] | ZHANG Z, HUANG X, ZHANG Z, et al. On the transverse vibration of Timoshenko double-beam systems coupled with various discontinuities[J]. International Journal of Mechanical Sciences, 2014, 89 : 222–241. DOI: 10.1016/j.ijmecsci.2014.09.004 |
| [5] | ARIAEI A, ZIAEI-RAD S, GHAYOUR M. Transverse vibration of a multiple-Timoshenko beam system with intermediate elastic connections due to a moving load[J]. Archive of Applied Mechanics, 2011, 81 (3): 263–281. DOI: 10.1007/s00419-010-0410-2 |
| [6] | 何佳磊, 周川, 周宁波. 基于动态设计分析方法的舰载鱼雷发射装置抗冲击特性研究[J]. 鱼雷技术, 2015, 23 (2): 139–144. |
| [7] | HUANG X, CHEN Y, HUA H, et al. Shock isolation performance of a nonlinear isolator using Euler buckled beam as negative stiffness corrector: Theoretical and experimental study[J]. Journal of Sound and Vibration, 2015, 345 : 178–196. DOI: 10.1016/j.jsv.2015.02.001 |
| [8] | 张春辉, 赵建华, 汪玉. 平方阻尼在冲击隔离中的特性与作用研究[J]. 船舶力学, 2014 (7): 834–840. |
| [9] | LOU J, SUN J, TANG S, et al. Study on the optimization of the shock isolation system based on the limiting performance analysis[J]. International Journal of Dynamics and Control, 2014, 2 (3): 415–424. DOI: 10.1007/s40435-013-0045-6 |
| [10] | Irvine T. An introduction to the shock response spectrum[J]. Rev P, Vibrationdata, 2002 . |
 2017, Vol. 39
2017, Vol. 39
