冰岛北极理事会于2004年发布的《北极人类发展报告》称:未来数十年北极必将成为人类进行油气勘探与开发以及海上运输的主要场所之一[1]。北极航道的成功开辟将减少我国对常规航道的依赖、降低航运风险同时降低航运成本。但漂浮在航道内的浮冰与流动的冰山,对航行于该海域的运输船舶构成了极大威胁,使得船冰碰撞概率大大增加。船-冰碰撞的全过程可分为船-冰远场、船-冰近场逼近、船-冰接触碰撞、速度为0或船-冰分离4个阶段,第3阶段的接触碰撞过程中产生的瞬间强冲击力,固然是研究船-冰碰撞最为值得关注的载荷,事实上,在船冰接触之前的第2阶段,船冰之间的水由于受到船冰的挤压而预先产生一个高压力场也是不可忽略的重要因素,该压力场一方面使船冰之间产生一个降低速度的“水垫效应”,同时在船-冰结构上产生一个瞬间高压力载荷。因此,正确模拟碰撞过程中船-水-冰三者的相互作用,是准确获得船-冰碰撞载荷的前提。
随着CFD学科的飞速发展,利用软件进行数值模拟研究越来越受到关注,例如英国格拉斯哥大学的船舶与海洋工程系[2]分别利用CFD方法和船模试验方法对水面快艇在静水中的受力问题进行研究对比。因此,逐渐采用CFD方法模拟复杂的船舶运动流场为船舶水动力性能研究另辟途径 [3 – 4]。在众多的CFD模型中,目前求解RANS方程的方法[5 – 8]在船舶阻力数值预报领域应用最广。由于该方法可以涉及到非线性自由表面兴波和流体粘性影响,因此其计算结果更为可靠。
船-冰碰撞过程中,不同的碰撞速度对船体的结构响应以及冰体的破损程度具有很大影响,基于船体与冰体采取迎面撞击的模式。本文将开展基于数值模拟的动网格技术研究,建立可以有效模拟船冰大位移运动的动态网格更新技术,由于船首表面具有曲线变化,因此如何实现网格的更新是本论文的一个技术难点;然后通过基于RANS方程和改进的双相流流体体积函数(VOF)模型,实时预报船冰靠拢全过程船体、冰体表面的压力变化。从而构建出船体表面压力P与相对速度V的函数关系,即P(V)函数。从而将水介质对船冰碰撞载荷的影响简化为对船体、冰体碰撞面预加载荷来实现,达到解耦目的。
1 数值计算 1.1 三维曲面模型的创建本文将以1艘无限航区的成品油船为研究对象,该船的主尺度见表1。考虑到水介质中船冰发生碰撞的部位主要是船首和船体的肩部,在此只对船体的首部湿表面进行缩尺建模,建模范围为Fr150-Fr180号肋位,船首与实际模型的缩尺比λ=1∶25,通过三维建模软件Catia创建,并将建好的曲面生成实体进行后期计算。生成后的缩尺模型如图1所示;冰体为边长10 m的正方体,缩尺比与船舶模型保持一致,取为λ=1∶25。
|
|
表 1 成品油船主尺度 Tab.1 Oil ship owners scale |
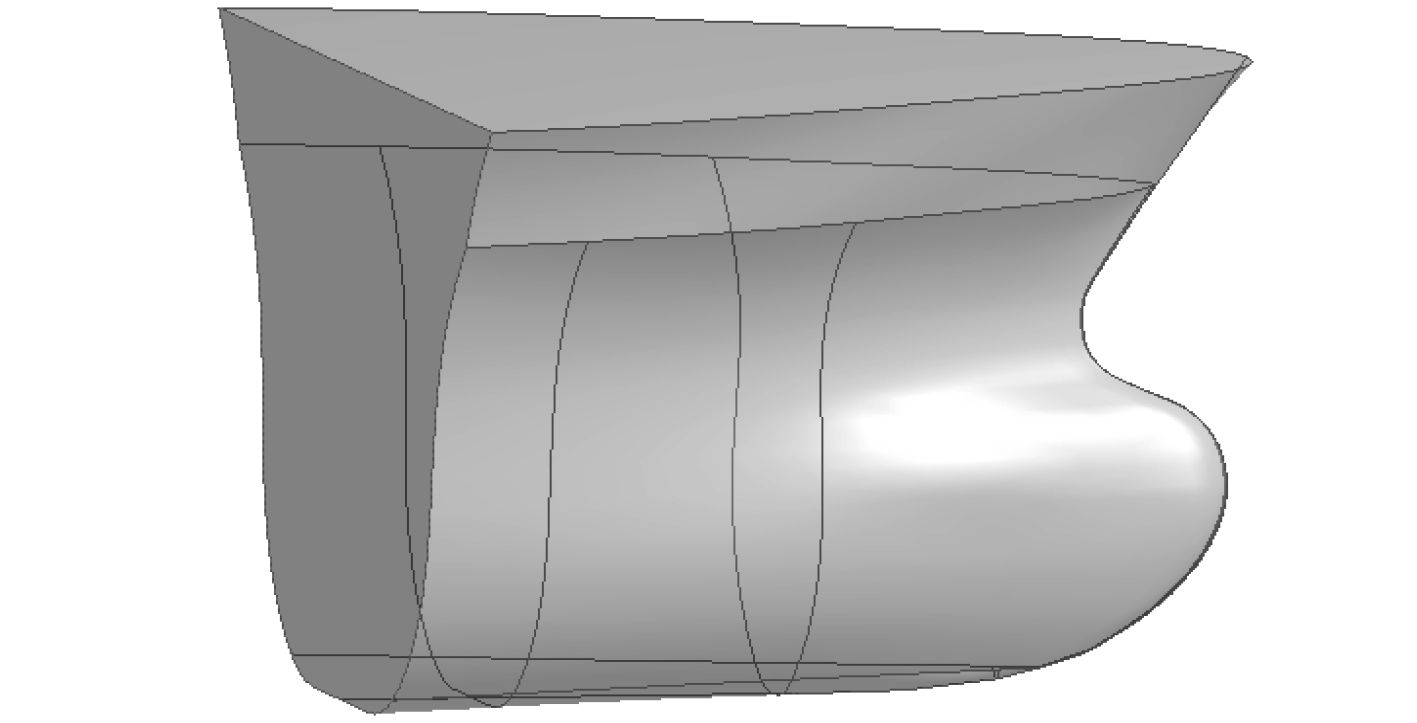
|
图 1 船首湿表面模型 Fig. 1 The ship bow wet surface model |

|
图 2 船、冰、流场位置关系 Fig. 2 Relationship ship, ice and flow field |
船体与冰体的初始距离L=80 cm,正方形冰体的90%位于水线面以下。整体计算域划分为内域与外域,内域采用非结构网格,外域采用结构网格,因本文模拟的为二相流,故划分了空气流域与水流域,并对自由液面进行了网格细化。图2给出了计算控制域内船、冰、流场位置关系以及网格划分情况。
1.2.2 计算原理控制方程为非定常连续性方程和RANS方程,湍流模型上选择RNG κ-ε模型,流体体积函数法(VOF)用于捕捉自由液面,压力与速度的耦合采用PISO方式。入口条件设置为速度入口,出口条件设置为压强出口,使用Fluent中的UDF功能,且通过编写UDF程序实现船冰的相对运动,编写UDF程序后期加载到Fluent中去。
1.2.3 检测点设置本文的研究主要为后期水介质中船-冰碰撞进行解耦,求得船-冰碰撞前的高压力,为更准确的将压力施加到后期船冰有限元模型中,在此将船首划分为几个区域,检测每个区域内代表性点的压力值。冰体在设置监测点时,采用投影的方式,将船首表面的监测点P1,P2,P3,P12,P13投影到冰体上。其船首、冰体监测点设置如图3所示。
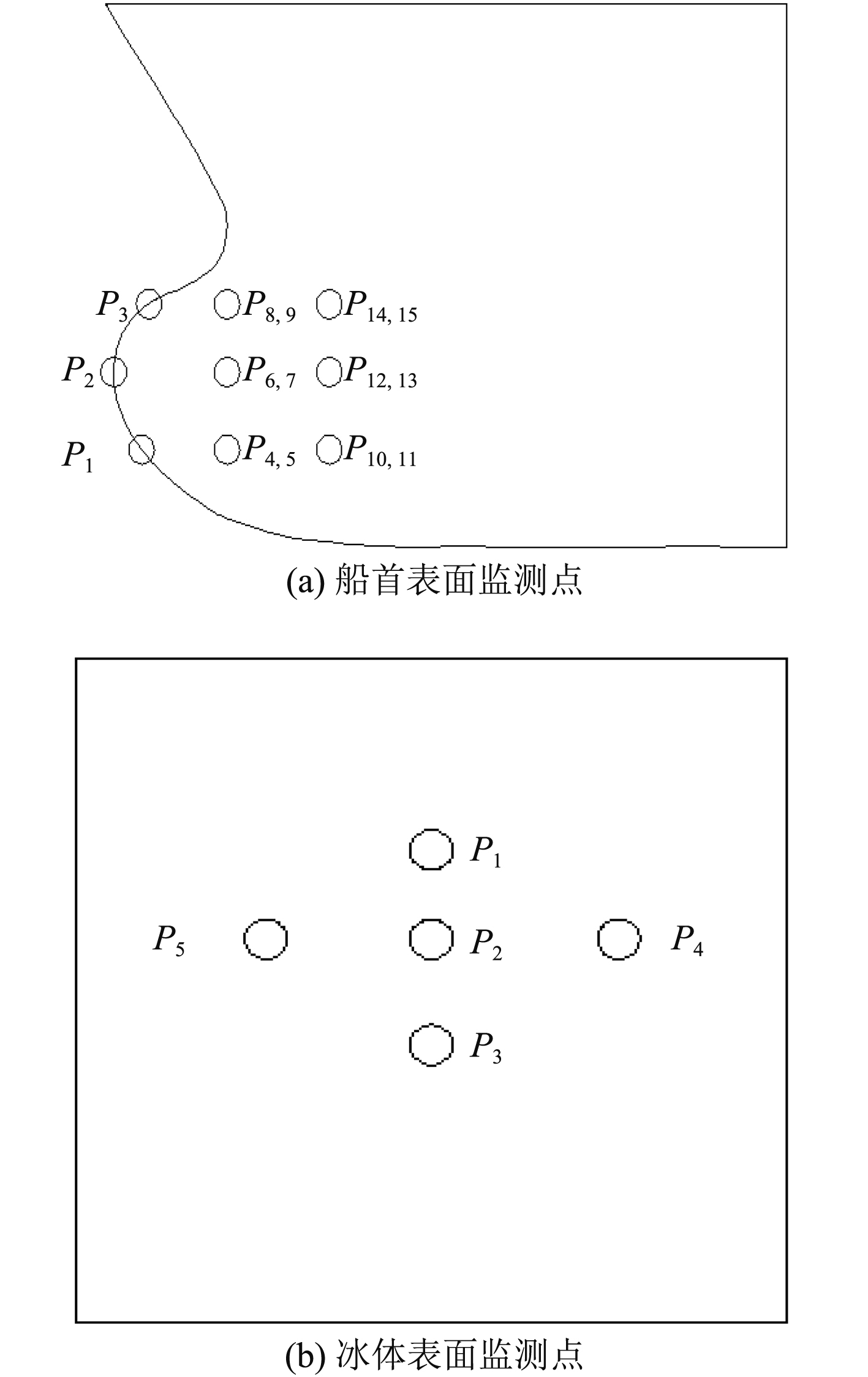
|
图 3 监测点设置 Fig. 3 Monitoring point Settings |
船冰碰撞过程中,相对碰撞速度V会对碰撞效果产生巨大影响,在此针对不同的速度V进行数值模拟,从而为后期基于水介质的船-冰碰撞进行解耦。根据傅汝德数Fr相似以及实船实际航行速度,在此将相对速度设置为0.9 ~2 m/s,具体计算工况如表2所示。
|
|
表 2 相对运动速度表 Tab.2 Relative to the speed table |
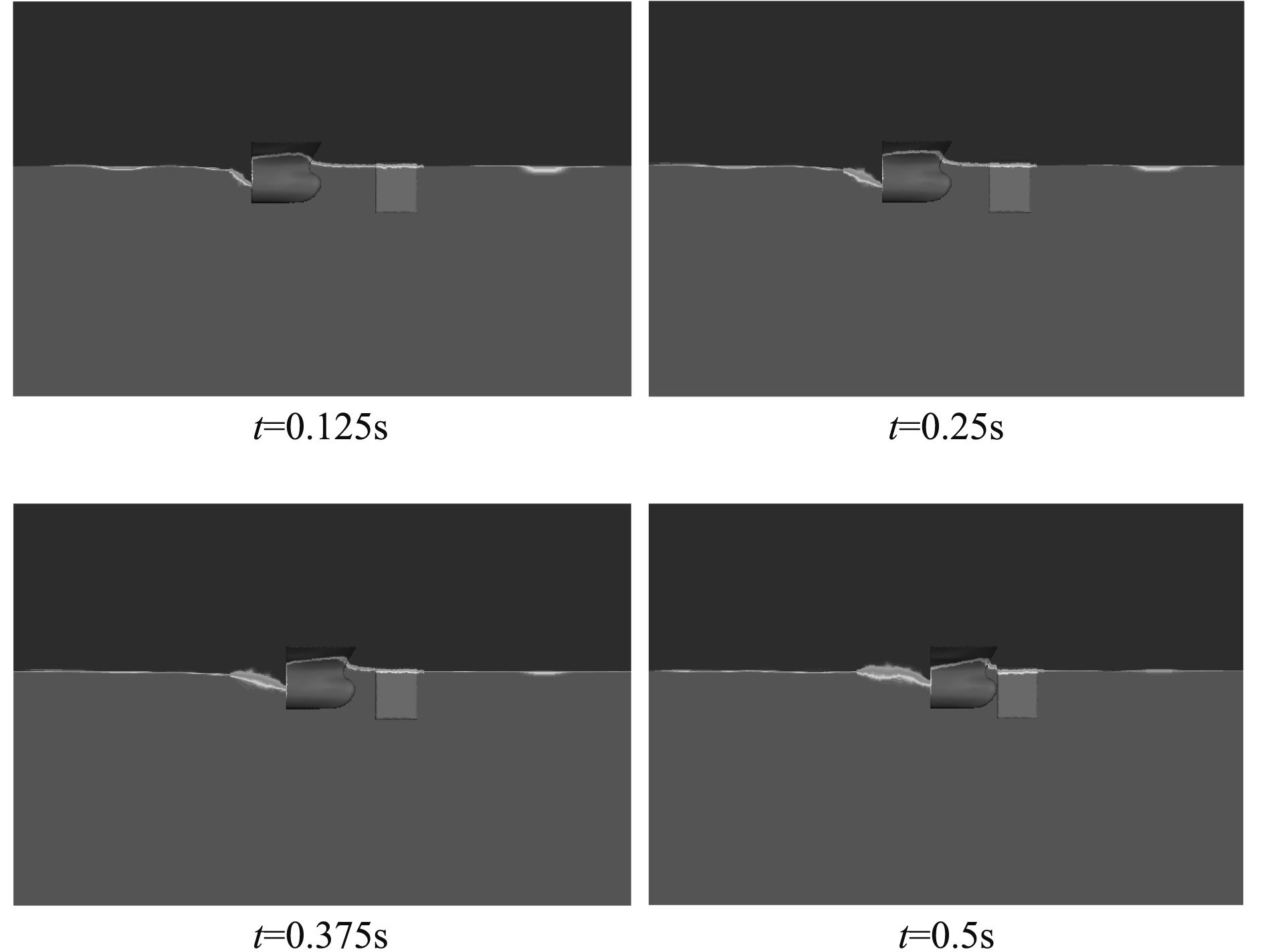
|
图 4 不同时刻下水汽两相图 Fig. 4 Water vapor phase diagram at different moments |
图4给出了在特征速度V=1.6 m/s时,不同时刻下的水汽两相云图,船体在趋近冰体的过程中,带动周围流场一起运动,运动过程中船体碰撞面自由液面升高,背离碰撞面的自由液面形成一个漏斗的形状下陷,称之为“吸气”现象。随着船体不断的趋近冰体,冰体碰撞面受到来流作用的影响越来越大,冰体碰撞面前的驻点流体速度为0,此时由于正压力的增大,使得自由液面逐渐升高。
1.2.6 各测点压力峰值变化曲线 1.2.6.1 同一速度下不同测点压力峰值变化曲线以速度V为变量,将速度从0.9~2 m/s进行计算,从而对船体、冰体表面各监测点的压力峰值进行分析,根据前文设计的船体迎面撞击冰体,此时的碰撞角度为0°,所以船体左右两舷的压力相等,在此分别对船体监测点P1,P2,P3,P4,P6,P8,P10,P12,P14,冰体监测点P1,P2,P3,P4进行分析。

|
图 5 V=1.6 m/s时各监测点压力峰值变化曲线 Fig. 5 The pressure peak curve of the monitoring points at V=1.6 m/s |
图5分别给出了当速度V=1.6 m/s时船体、冰体表面各监测点压力峰值变化曲线,从图5(a)可以看出,压力峰值在船、冰接触点P2处急剧增大,在点P3~P14处压力峰值变化相对平缓;从图5(b)可看出,压力峰值在船、冰接触点P2处急剧增大,其余对应测点压力峰值变化相对稳定,从而说明在船-冰碰撞过程中,接触碰撞区在发生碰撞之前会预先形成一个高压力。
1.2.6.2 不同速度下各测点压力峰值变化曲线

|
图 6 不同速度下船、冰表面各测点压力峰值变化曲线 Fig. 6 Pressure peak curve of the ship and ice surface points at different speeds |
图6给出了不同速度下船、冰表面各测点压力峰值变化曲线,图6(a),图6(b),图6(c)中的船体表面各测点入水深度大小相等,到冰体的距离不相等,从中可看出随着远离碰撞区域其压力峰值逐渐减小。而随着相对速度的增大,其压力峰值逐渐增大,尤其是监测点P2压力峰值变化量最大。图6(d)为冰体上各测点压力峰值变化曲线,从图可以看出船-冰正撞点P2的压力峰值远大于其余测点,伴随着来流速度的增大,各测点压力峰值呈现增大趋势。
1.3 压力载荷预报在基于大量的数值仿真数据之上,将计算得到的数值仿真结果进行数据统计分析,应用Matlab软件拟合出数值仿真结果曲线,然后进行经验公式的回归,得到一般性规律,为后期船冰碰撞提供必要的载荷输入。
表3和表4分别以船体、冰体上的监测点P1为例,给出了船体、冰体在不同相对运动速度(0.9~2.0 m/s)时的压力峰值。将相对运动速度设置为X轴,压力峰值设置为Y轴,画出曲线。应用Matlab对曲线进行拟合,从而得到图7所示的图形,图中深色曲线代表了计算压力峰值随速度变化,浅色曲线代表了拟合压力峰值随速度变化曲线。
|
|
表 3 船体表面P1处在不同相对速度时压力峰值 Tab.3 The monitor P1 of the pressure peak on the ship surface at different velocity |
|
|
表 4 冰体表面P1处在不同相对速度时压力峰值 Tab.4 The monitor P1 of the pressure peak on the ice surface at different velocity |

|
图 7 压力峰值随相对速度变化曲线及拟合曲线 Fig. 7 The peak pressure with the of the change of velocity curve and fitting curve |
根据计算获得压力峰值与相对速度拟合曲线,从而得到船体上测点P1的拟合公式:P1:y=0.51x2+0.33x+1.99,拟合度达98.82%;冰体上测点P1的拟合公式:P1:y=0.55x2+0.15x+2.46,拟合度达96.86%。
依次对船体、冰体其余测点压力峰值曲线进行拟合,可得到拟合公式,如表5和表6所示。
|
|
表 5 船体其余监测点拟合公式 Tab.5 The fitting formula of the rest of the hull monitoring points |
|
|
表 6 冰体其余监测点拟合公式 Tab.6 The fitting formula of the rest of the ice monitoring points |
本文利用CFD对船冰碰撞之前所形成的预压力进行了数值模拟,通过对不同的船冰相对速度进行模拟计算,获得了船冰在趋近过程中所形成的压力峰值,对不同速度下的压力峰值进行分析可获得如下结论:
1)在相同计算速度下,船体、冰体表面各监测点的压力峰值大小不等,其中正撞点P2处压力峰值最大,随着远离碰撞点压力峰值逐渐减小。
2)随着相对速度的增大,船体、冰体表面的压力峰值分别呈现递增趋势,其中正撞点P2处压力峰值递增幅度最大,远离碰撞点的递增幅度逐渐减小。
3)通过对不同监测点的压力峰值进行载荷预报,后期可对水介质中船冰碰撞进行解耦,将水对船冰碰撞之前所形成的预压力施加在有限元模型中,为研究水介质中船冰碰撞开辟了一种全新的方法。
| [1] | ORAN R, YOUNG, NIELS E. The arctic human development report [R]. Iceland: Arctic Council, 2004. |
| [2] | TVEITNES T, VARYANI K S, FAIRLIE-CLARKE A C. Department of naval architecture and ocean engineering, university of glasgow. CFD analysis and experience work on water impact forces on transverse sections of planing craft[J]. MARNET-CFD First Workshop-Barcelona 1999. |
| [3] | 刘应中, 张怀新, 李谊乐, 等. 21世纪的船舶性能计算和RANS方程[J]. 船舶力学, 2001, 5 (5): 66–84. |
| [4] | STERN F, YANG J, WANG Z, SADAT-HOSSEINI H, MOUSAVIRAAD M, BHUSHAN S, XING T, et al. Computational ship hydrodynamics: Nowadays and way forward[J]. International Shipbuilding Progress, 2013, 60 (1-4): 3–105. |
| [5] | LARSSON L, STERN F, BERTRAM V. Benchmarking of computational fluid dynamics for ship flows: the Gothenburg 2000 workshop[J]. Journal of Ship Research, 2003, 47 (1): 63–81. |
| [6] | CARRICA P M, WILSON R V, STERN F. An unsteady single-phase level set method for viscous free surface flows[J]. International Journal for Numerical Methods in Fluids, 2007, 53 (2): 229–256. DOI: 10.1002/(ISSN)1097-0363 |
| [7] | 倪崇本. 基于CFD的船舶阻力性能综合研究[D]. 上海: 上海交通大学, 2011. |
| [8] | GAO Q. The effect of free surface on classical ship hydrodynamics using RANSE - resistance, manoeuvring, propulsion, seakeeping and stability[D]. Universities of Strathclyde and Glasgow, 2012. |
 2017, Vol. 39
2017, Vol. 39
