0 引　言

国际海事组织（IMO）的“国际散装运输液化气体船舶构造与设备规则”（IGC CODE）定义的独立液舱系指自身支持的液舱，不构成船体结构的一部分，对船体强度不是必需的^[1]。独立液舱分为A型、B型和C型三类：A型独立液舱主要由平面结构组成，应用传统的船舶结构分析程序的公认标准（“公认标准”系指由主管机关承认的船级社制定和保持的标准）进行设计；B型独立液舱有平面结构型式和球罐型式2种，设计应采用模型试验、精确的分析手段和分析方法确定其应力水平、疲劳寿命和裂纹扩展特性；C型独立液舱一般为球型、单耳型或双耳型，应满足压力容器的设计要求^[2]。

2016年1月1号生效的新版IGC明确要求应采用三维加速度椭球法计算独立液舱的内部压力，相对于传统的二维计算法，该方法能够更加准确地确定液舱各位置的内部压力，但是计算也更加复杂，尤其对于几何形状不规则的液舱。本文以采用蝶形封头的C型双耳液舱为例，研究了三维加速度的计算方法，并分别采用解析法和离散法计算最大液柱高度，进而求得液舱内部压力，具有重要的实际应用意义。

1 内部压力计算公式

根据IGC规则，内部压力P_eq由设计蒸汽压力P₀和内部液体压力P_gd组成，按下式计算^[2]：

${P_{eq}} = {P_0} + {\left( {{P_{gd}}} \right)_{\max }}\;\;\;\;{\rm{MPa}}\text{。}$

(1)

内部液体压力P_gd由重力和动力加速度的联合作用引起，按下式计算：

${P_{gd}} = {a_{{\beta _r},{\beta _p}}} \cdot {Z_{{\beta _r},{\beta _p}}} \cdot \left( {\frac{\rho }{{1.02 \times {{10}^5}}}} \right)\;\;\;{\rm{MPa}}\text{，}$

(2)

式中： ${\beta _r},{\beta _p}$ 为船舶任意横倾角与纵倾角组合所确定的空间方向； ${a_{{\beta _r},{\beta _p}}}$ 为在任意的（ ${\beta _r},{\beta _p}$ ）方向上由重力和动载荷引起的无因次加速度； ${Z_{{\beta _r},{\beta _p}}}$ 为从压力计算点沿（ ${\beta _r},{\beta _p}$ ）方向向上量至液舱壳板的最大液柱高度，m。

2 ${{\mathit{\boldsymbol{a}}}_{{{\bf{\beta }}_{\bf{r}}},{{\bf{\beta }}_{\bf{p}}}}}$ 计算公式

根据新IGC规则，船舶在北大西洋中以相当于概率水平为10^–8的运动而产生的加速度分量按照下式计算^[2]：

${a_x} = \pm {a_0}\sqrt {0.06 + {A^2} - 0.25A} \text{，}$

(3)

${a_y} = \pm {a_0}\sqrt {0.6 + 2.5{{\left( {\frac{X}{{{L_0}}} + 0.05} \right)}^2} + K{{\left( {1 + 0.6K\frac{Z}{B}} \right)}^2}} \text{，}$

(4)

${a_z}\! =\! \pm {a_0}\! \sqrt {1 \! +\! {{\left( {5.3 \! -\! \frac{{45}}{{{L_0}}}} \right)}^2}\! {{\left( {\frac{X}{{{L_0}}} \! +\! 0.05} \right)}^2}{{\left( {\frac{{0.6}}{{{C_B}}}} \right)}^{1.5}}\! +\! {{\left( {\frac{{0.6Y{K^{1.5}}}}{B}} \right)}^2}} \text{，}$

(5)

${a_0} = 0.2\frac{V}{{\sqrt {{L_0}} }} + \frac{{34 - \left( {\displaystyle\frac{{600}}{{{L_0}}}} \right)}}{{{L_0}}}\text{，}$

(6)

$A = \left( {0.7 - \frac{{{L_0}}}{{1200}} + 5\frac{Z}{{{L_0}}}} \right)\left( {\frac{{0.6}}{{{C_B}}}} \right)\text{。}$

(7)

式中：V为营运速度；K为13 GM/B或1，取大者；GM为静稳心高度；L₀为规范船长；C_b为方形系数；B为型宽；X为液舱重心到船中的纵向距离（重心位于船中前，X为正值，船中后，X为负值）；Y为液舱重心到船中纵剖面的横向距离；Z为液舱重心到船舶实际水线的垂向距离（重心位于水线以上，Z为正值，水线以下，Z为负值）。

如图1所示，以椭球中心为原点建立空间坐标系，x轴沿船长方向（指向船首为正），y轴沿船宽方向（指向左舷为正），z轴沿型深方向（指向上为正），则加速度椭球方程为：

$\frac{{{x^2}}}{{a_x^2}} + \frac{{{y^2}}}{{a_y^2}} + \frac{{{z^2}}}{{a_z^2}} = 1\text{。}$

(8)

过空间点（0，0，1）建立一条空间直线，并假设该直线与xoz平面的夹角为横倾角β_r，与yoz平面的夹角为β_p，则该直线的方向向量为 $\left( {{\rm{tan}}{\beta _p},{\rm{tan}}{\beta _r},1} \right)$ ，则该空间直线的方程为：

$\frac{x}{{{\rm{tg}}{\beta _p}}} = \frac{y}{{{\rm{tg}}{\beta _r}}} = \frac{{z - 1}}{1}\text{。}$

(9)

联立加速度椭球和空间直线方程即可求得交点 $\left( {{x_0},{y_0},{z_0}} \right)$ ，进而可得：

${a_{{\beta _r},{\beta _p}}} = \sqrt {x_0^2 + y_0^2 + {{\left( {{z_0} - 1} \right)}^2}} \text{。}$

(10)

省略计算过程，可得^[3]：

$\begin{split}{a_{{\beta _r},{\beta _p}}} =& \left[ {\frac{{1 + {a_z}\sqrt {1 + \left( {a_z^2 - 1} \right)\left( {\displaystyle\frac{{{\rm{t}}{{\rm{g}}^2}{\beta _p}}}{{a_x^2}} + \displaystyle\frac{{{\rm{t}}{{\rm{g}}^2}{\beta _r}}}{{a_y^2}}} \right)} }}{{1 + a_z^2\left( {\displaystyle\frac{{{\rm{t}}{{\rm{g}}^2}{\beta _p}}}{{a_x^2}} + \displaystyle\frac{{{\rm{t}}{{\rm{g}}^2}{\beta _r}}}{{a_y^2}}} \right)}}} \right] \times\\& \sqrt {1 + {\rm{t}}{{\rm{g}}^2}{\beta _r} + {\rm{t}}{{\rm{g}}^2}{\beta _p}} \text{。}\end{split}$

(11)

且横倾角β_r和纵倾角β_p应满足以下范围^[3]：

$\frac{{{\rm{t}}{{\rm{g}}^2}{\beta _p}}}{{a_x^2}} + \frac{{{\rm{t}}{{\rm{g}}^2}{\beta _r}}}{{a_y^2}} \leqslant \frac{1}{{1 - a_z^2}}\text{。}$

(12)

3 ${Z_{{\beta _r},{\beta _p}}}$ 计算方法

由于A型、B型、C型独立液舱形状各异，且因型线布置等原因，每种液舱在基本形状的基础上又有所变化，因此如何准确、快速地求得 ${Z_{{\beta _r},{\beta _p}}}$ 是液舱内部压力计算的关键。

3.1 解析法

采用蝶形封头的C型双耳液舱广泛应用于中小型LPG和LNG船，其边界比主要由平面构成的A型或B型液舱复杂很多，因此本文以此为例展开研究。

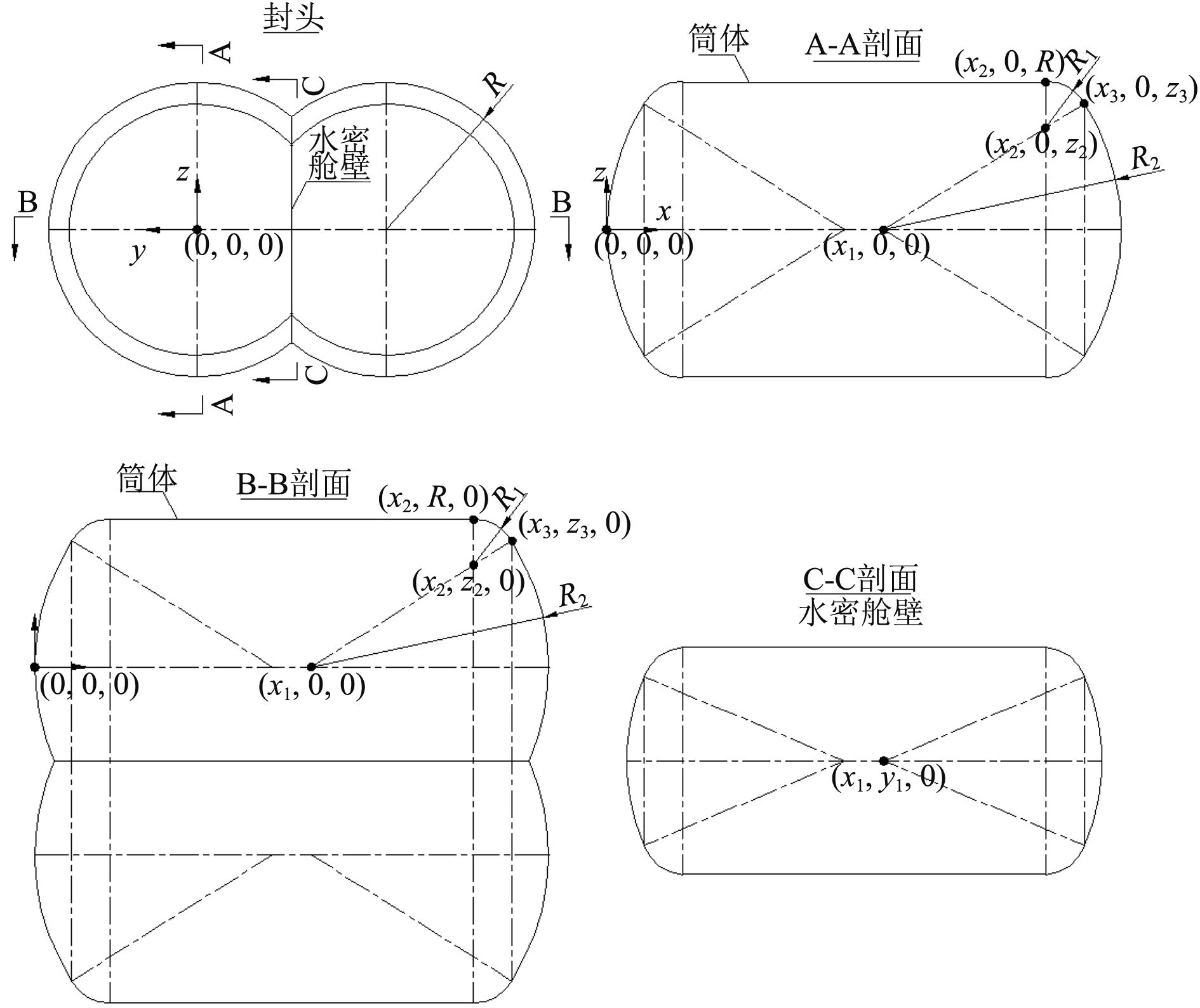
如图2所示，以封头与回转轴的交点为原点建立空间坐标系，x轴沿船长方向（指向船首为正），y轴沿船宽方向（指向左舷为正），z轴沿型深方向（指向上为正）。x₁，x₂，x₃，y₁，z₂，z₃，R，R₁与R₂均为已知。

简单分析易知，考虑到液舱的对称性，仅需计算y≥0部分的后半舱；且对位于上述区域的任意计算点，产生最大液柱高度的液舱边界点总是位于前半舱的封头上，因此只需用数学表达式对组成封头的2个曲面进行数值描述即可。

对于任意（ ${\beta _r},{\beta _p}$ ），三维加速度的方向向量为 $\left( {{\rm{tg}}{\beta _p},{\rm{tg}}{\beta _r},1} \right)$ ，假设计算点坐标为（x_c，y_c，z_c），则过计算点且与加速度方向垂直的空间平面方程为：

$\left( {x - {x_c}} \right){\rm{tg}}{\beta _p} + \left( {y - {y_c}} \right){\rm{tg}}{\beta _r} + \left( {z - {z_c}} \right) = 0\text{。}$

(13)

该型液舱封头由圆弧回转面和球面2部分组成，分析可知，圆弧回转面的数学表达式为：

${y^2} \!+\! {z^2} = {\left( {R\! -\! {R_1}\! +\! \sqrt {R_1^2\! - \!{{\left( {x\! -\! {x_2}} \right)}^2}} } \right)^2}\text{且}\left\{ {\begin{array}{*{20}{c}}{\!\!{x_2} \leqslant x \leqslant {x_3}}\text{，}\\{\!\!{y_1} \leqslant y \leqslant R}\text{，}\\{ \!\!- R \leqslant z \leqslant R}\text{。}\end{array}} \right.\!\!\!\!\!$

(14)

球面的数学表达式为：

${\left( {x - {x_1}} \right)^2} + {y^2} + {z^2} = R_2^2\;\;\;\text{且}\left\{ {\begin{array}{*{20}{c}}{{x_3} \leqslant x \leqslant \left( {{x_1} + R} \right)}\text{，}\\\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!{{y_1} \leqslant y \leqslant {z_3}}\text{，}\\\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!{ - {z_3} \leqslant z \leqslant {z_3}}\text{。}\end{array}} \right.$

(15)

上述两曲面上任一点（x_i，y_i，z_i）到上述平面的距离即为对应该点的液柱高度：

${({Z_{{\beta _r},{\beta _p}}})_i} = \frac{{\left| {\left( {{x_i} - {x_c}} \right){\rm{tg}}{\beta _p} + \left( {{y_i} - {y_c}} \right){\rm{tg}}{\beta _r} + \left( {{z_i} - {z_c}} \right)} \right|}}{{\sqrt {1 + {\rm{t}}{{\rm{an}}^2}{\beta _r} + {\rm{t}}{{\rm{an}}^2}{\beta _p}} }}\text{。}$

(16)

分别将式（14）与式（15）代入式（16），求得各自极值点分别为：

$\left\{ {\begin{split}& {x = {x_2} + {R_1}{\rm{ \cdot sin}}{\beta _p}}\text{，}\\& {y = \left[ {R - {R_1}(1 - \cos {\beta _p})} \right] \cdot \sin {\beta _r}}\text{，}\\& {z = \left[ {R - {R_1}(1 - \cos {\beta _p})} \right] \cdot \cos {\beta _r}}\text{。}\end{split}} \right.$

(17)

$\left\{ {\begin{split}& {x = {x_1} + {R_2}{\rm{ \cdot sin}}{\beta _p}}\text{，}\\& {y = {R_2} \cdot \cos {\beta _p} \cdot \sin {\beta _r}}\text{，}\\& {z = {R_2} \cdot \cos {\beta _p} \cdot \cos {\beta _r}}\text{。}\end{split}} \right.$

(18)

将满足曲面方程取值范围的极值点坐标代入式（16）即可求得最大液柱高度 ${Z_{{\beta _r},{\beta _p}}}$ 。

对于主要由平面结构构成的菱形液舱（A型、B型），仅需将所有顶点坐标代入式（16）即可求得对应的最大液柱高度 ${Z_{{\beta _r},{\beta _p}}}$ ^[4]。

3.2 离散法

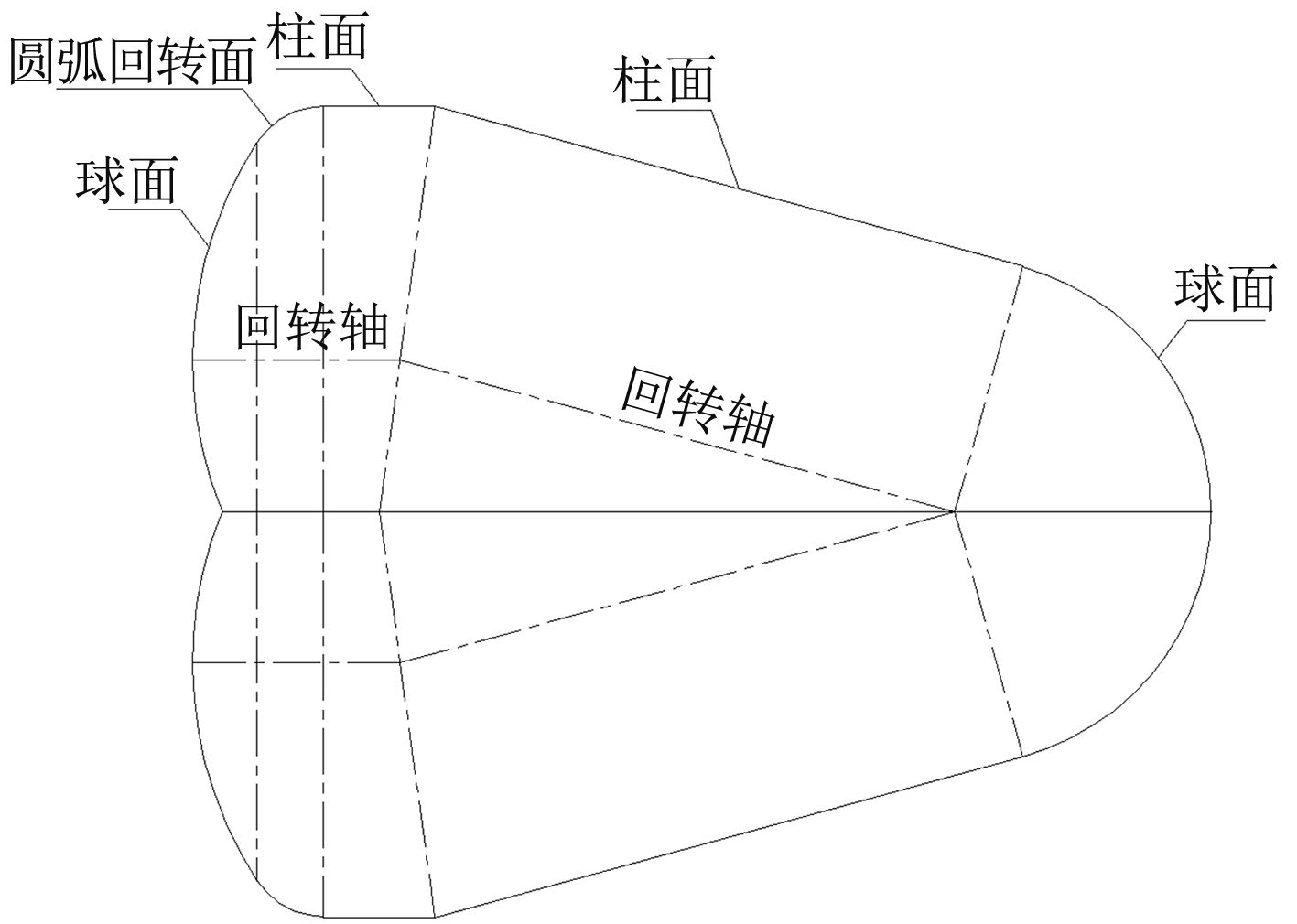
当液舱边界几何形状相对复杂时，如图3所示（后半舱采用蝶形封头，前半舱采用球形封头，中间通过两部分柱面连接过渡），很难用数学表达式描述全部曲面及各自取值范围，此时便可使用离散法^[5]。

离散法的核心思想是将液舱边界曲面通过有限元建模软件（MSC.Patran，HyperMesh等）离散为一定密度的节点^[6]，假设任一节点坐标为（x_i，y_i，z_i），则其至计算点（x_c，y_c，z_c）沿三维加速度方向的高度 ${({Z_{{\beta _r},{\beta _p}}})_i}$ 便可使用式（16）计算^[7]。

历遍全部节点得到最大的 ${({Z_{{\beta _r},{\beta _p}}})_i}$ 即为最大液柱高度 ${Z_{{\beta _r},{\beta _p}}}$ 。

4 内部压力编程计算

对于任意类型的独立液舱，内部压力的计算流程如下：

步骤 1 选定任一（ ${\beta _r},{\beta _p}$ ）组合；

步骤 2 按第2节中式（11）求得相应的三维加速度 ${a_{{\beta _r},{\beta _p}}}$ ；

步骤 3 按第3节中解析法或离散法求得相应的最大液柱高度 ${Z_{{\beta _r},{\beta _p}}}$ ；

步骤 4 按第1节中式（2）求得相应的内部液体压力 ${P_{gd}}$ ；

步骤 5 历遍全部（ ${\beta _r},{\beta _p}$ ）组合求得 ${\left( {{P_{gd}}} \right)_{{\rm{max}}}}$ ，

步骤 6 按第1节中式（1）求得内部压力 ${P_{eq}}$ 。

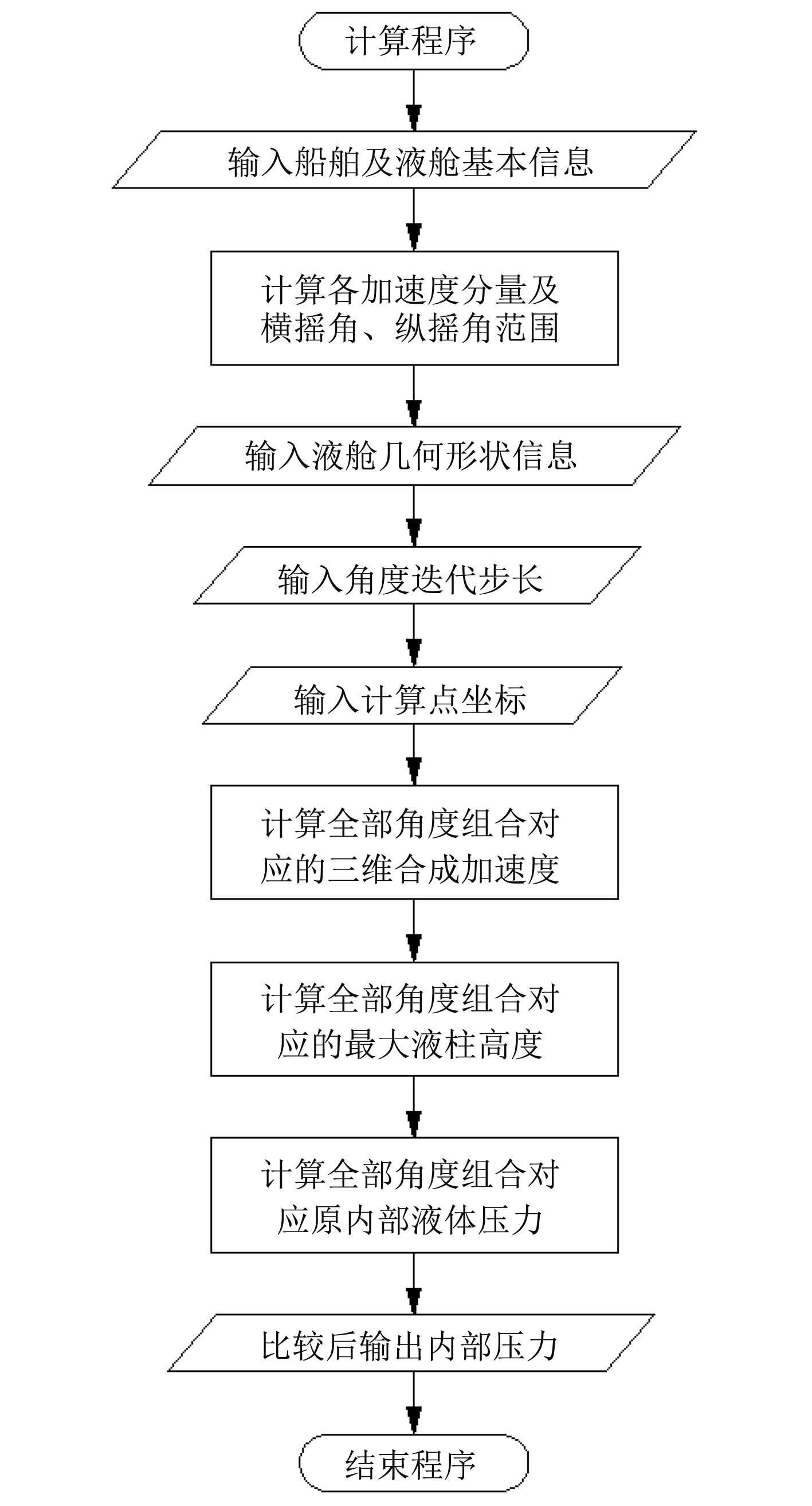
由于内部压力计算涉及大量数据迭代，无法手动完成，因此本文编制了专门的计算程序，流程如图4所示。

5 实船应用

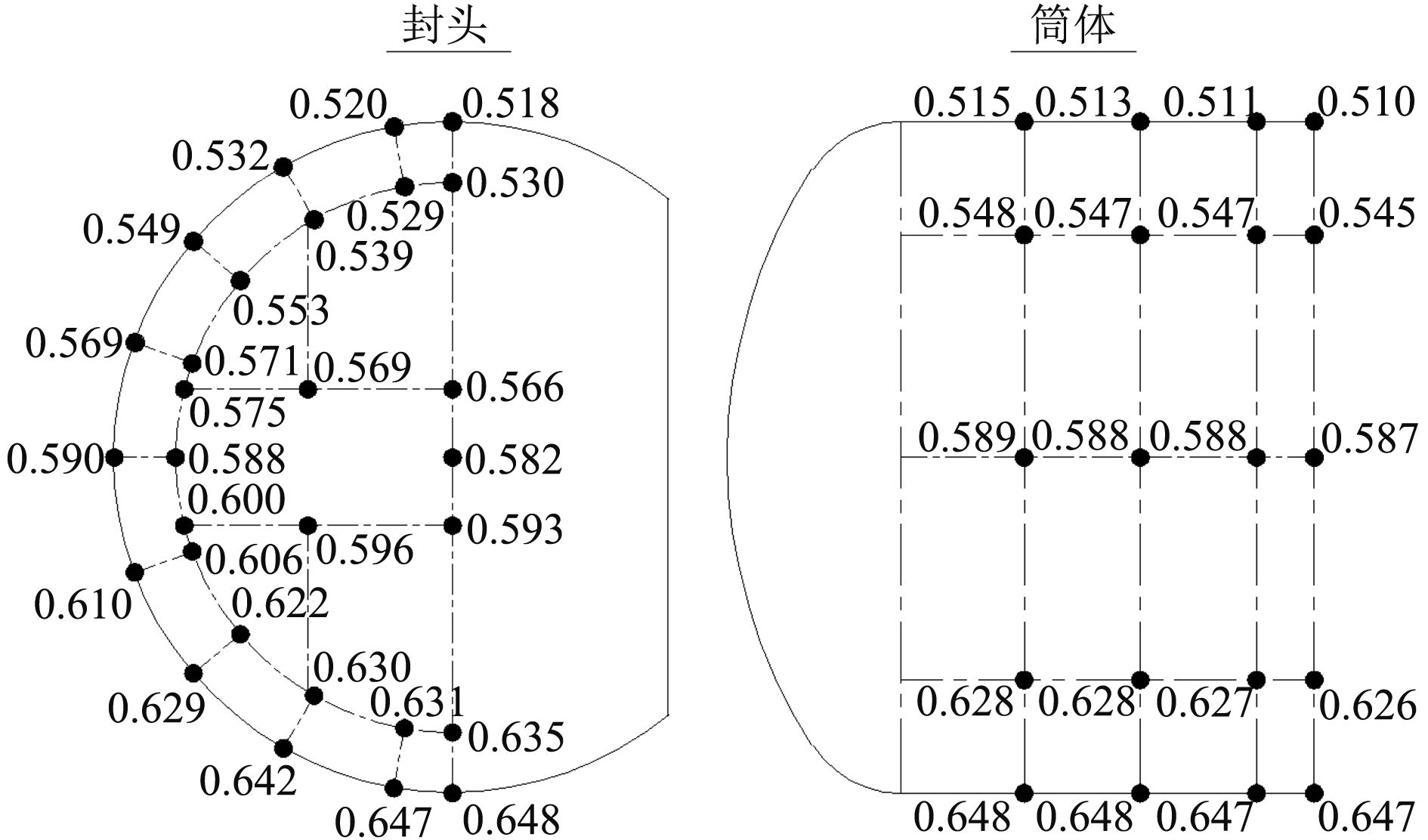
以某型22 000 m³LPG实船3#液舱为例，采用上述计算程序计算得到的内部压力如图5所示。

6 结　语

相对于传统的二维计算法，三维计算法更加复杂^[8]。本文详细研究了内部压力的计算方法，给出了三维加速度及最大液柱高度的计算公式，编制了专用计算程序，并将其应用于某型实船液舱内部压力计算。本文还得出以下结论：

1）采用解析法计算最大液柱高度的关键和难点在于如何用数学表达式描述液舱边界曲面；

2）相对于离散法，解析法具有计算量小、精度高等优点，对于形状规则的独立液舱，应首选该方法；

3）离散法的能够适用于各型边界形状复杂的液舱，缺点是计算量大、耗时长；

4）角度迭代步长及节点密度直接影响到离散法的计算时间，应选取合适的值以在保证计算精度的前提下尽量缩短计算时间。