在高速旋转机械中,容易发生半速涡动和油膜振荡,为了提高系统稳定性,经常采用可倾瓦轴承,可倾瓦轴承瓦块常取3~5块,瓦块的底面是弧面或球面,瓦块可在轴承孔中自由摆动,可倾瓦轴承的结构复杂多样,对于齿轮箱轴承,同一轴承在不同工况下,承载力方向不同,相当于轴承的布置方向不同,不同布置方向对性能的影响规律对设计至关重要。
随着可倾瓦轴承的广泛应用,对其性能影响因素研究的较多,王永亮等[1]研究了可倾瓦轴承瓦块摆动特性;谭召生[2]研究了可倾瓦轴承的加工与装配;Simmons,J.[3]对直径为200 mm偏心支承的可倾瓦轴承进行性能试验研究;Nicholas,J.C. [4]研究了可倾瓦轴承设计。本文主要探讨了同一尺寸可倾瓦轴承不同布置方向对轴承油膜温度、承载力、功耗及动态系数等性能的影响,在轴承试验台上,对轴承3种布置方向下轴瓦温度进行测量,为今后滑动轴承的设计提供参考。
1 基本方程计算应用基本方程[5]:雷诺方程、能量方程及温粘关系方程,计算时由于布置方向不同,承载区域及相关边界条件都会相应变化。
1.1 雷诺方程静态载荷时,可倾瓦轴承的雷诺方程的无量纲形式为:
|
$\begin{split}& \frac{\partial }{\partial \varPhi }\left( \frac{{{{\bar{h}}}_{i}}^{3}}{{{{\bar{\mu }}}_{i}}{{R}_{x}}}\frac{\partial {{{\bar{p}}}_{i}}}{\partial \varPhi } \right)+{{(\frac{R}{L})}^{2}}\frac{\partial }{\partial \lambda }\left( \frac{{{{\bar{h}}}_{i}}^{3}}{{{{\bar{\mu }}}_{i}}{{R}_{z}}}\frac{\partial {{{\bar{p}}}_{i}}}{\partial \lambda } \right)= \\ & -6{{\varepsilon }_{im}}\sin (\varPhi -\theta (z)) \text{。}\\ \end{split}$
|
其中:p为油膜压力;R为轴颈半径;L为轴承宽度;εim为偏心率;hi为油膜厚度;Rx,Rz为紊流因子;
能量方程无量纲形式:
|
$\begin{split}& ({\overline h _i} - \displaystyle\frac{{{{\overline h }_i}^3}}{{6{{\overline \mu }_i}{R_x}}}\frac{{\partial {{\overline p }_i}}}{{\partial \varPhi }})\frac{{\partial {{\overline T }_i}}}{{\partial \varPhi }} - {(\frac{D}{L})^2}\frac{{{{\overline h }_i}^3}}{{6{{\overline \mu }_i}{R_Z}}}\frac{{\partial {{\overline p }_i}}}{{\partial \lambda }}\frac{{\partial {{\overline T }_i}}}{{\partial \lambda }} = \\&K\displaystyle\frac{{{{\overline \mu }_i}}}{{{{\overline h }_i}}}(1 + \frac{{{{\overline h }_i}^4}}{{12{{\overline \mu }_i}^2}}({(\frac{{\partial {{\overline p }_i}}}{{\partial \varPhi }})^2} + {(\frac{D}{L})^2}{(\frac{{\partial {{\overline p }_i}}}{{\partial \lambda }})^2}))\text{。}\end{split}$
|
其中:
用指数函数的形式列出温粘方程来近似地替代温粘关系。温粘方程无量纲形式:
|
${\overline \mu _i} = A{e^{ - B{{\overline T }_i}}}\text{。}$
|
其中:A,B 为温粘方程的待定系数,用最小二乘法计算。
2 计算实例结果分析轴承参数:轴承直径D=100 m,宽度L=90 mm,间隙比ψ=0.001 5,载荷10 000 N,中心支撑。
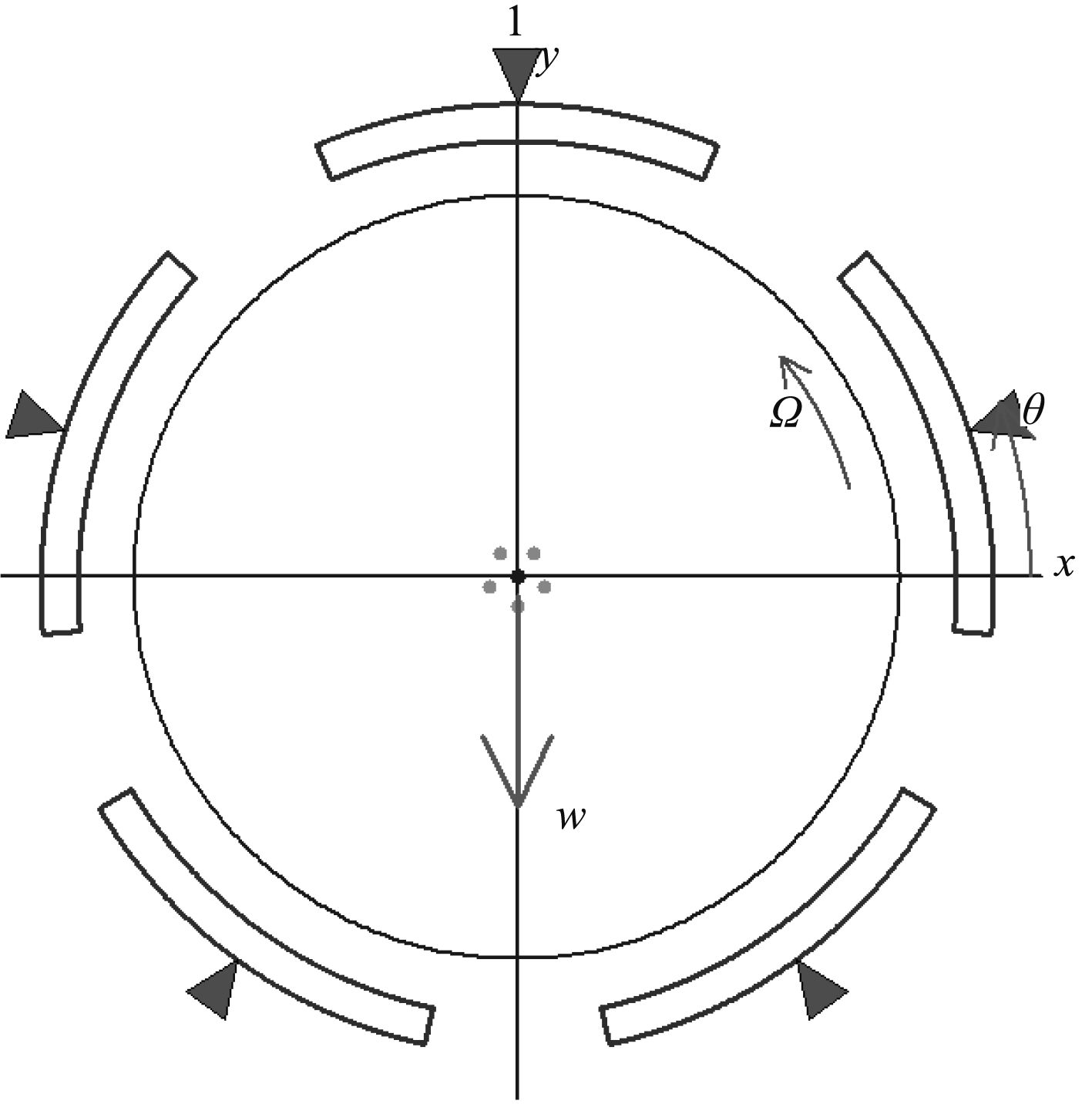
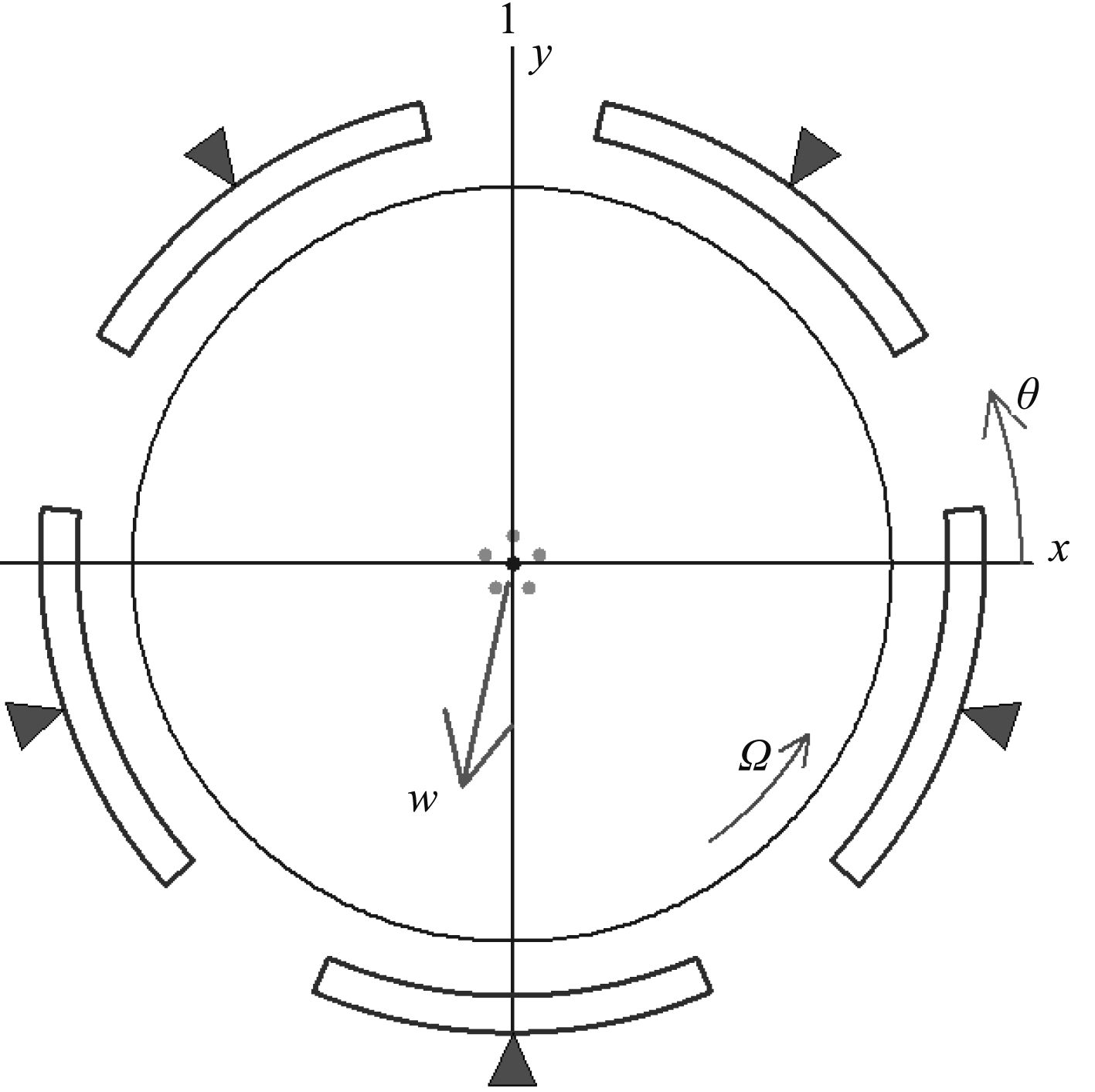
轴承瓦块包角为50°,预负荷m=0.35,轴承布置如图1~图3所示。
|
图 1 布置方向(1)载荷在瓦块 Fig. 1 Load between two pads arrangement direction (1) |

|
图 2 布置方向(2)载荷在瓦块上 Fig. 2 Load on the pad arrangement direction (2) |
|
图 3 布置方向(3)载荷在瓦块前部 Fig. 3 Load on front pad arrangement direction (3) |
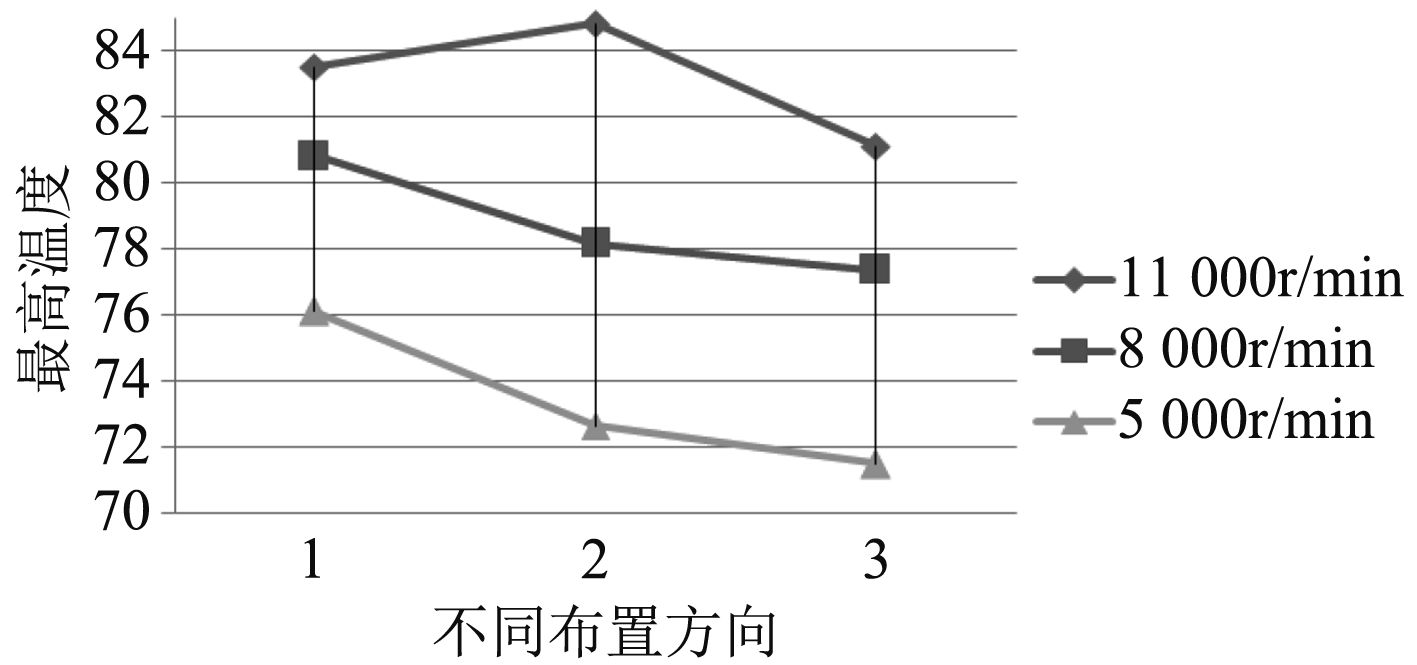
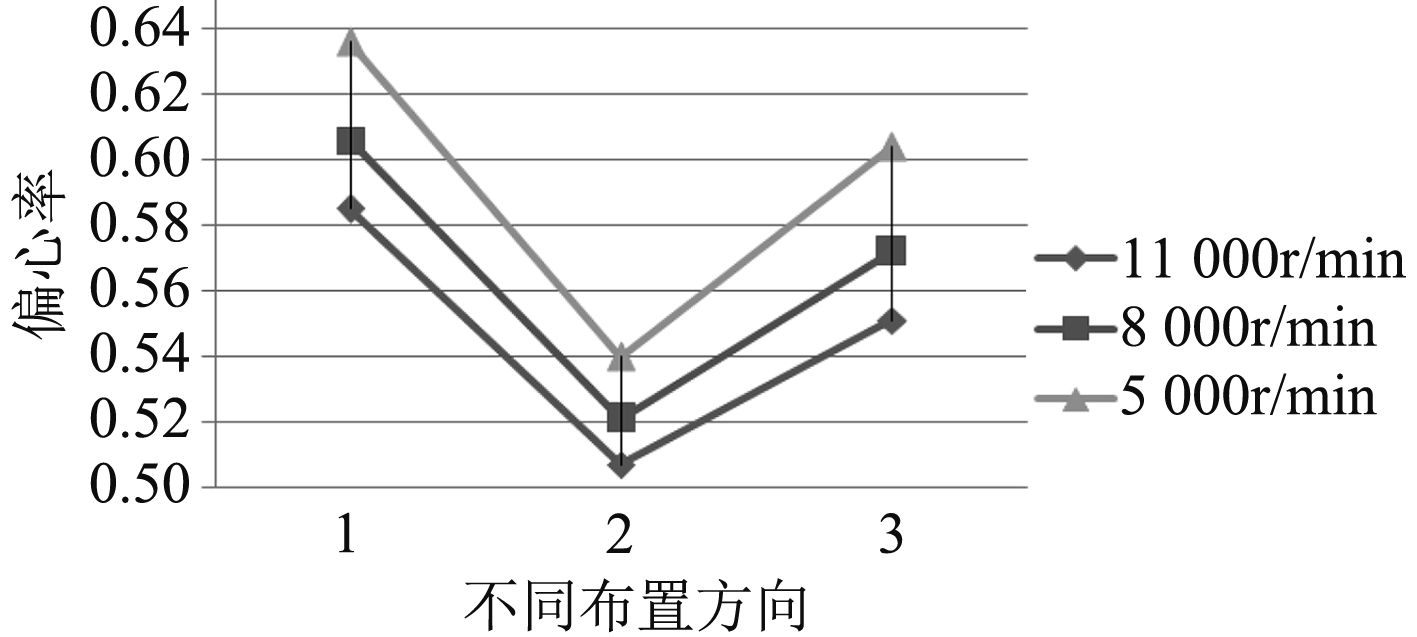
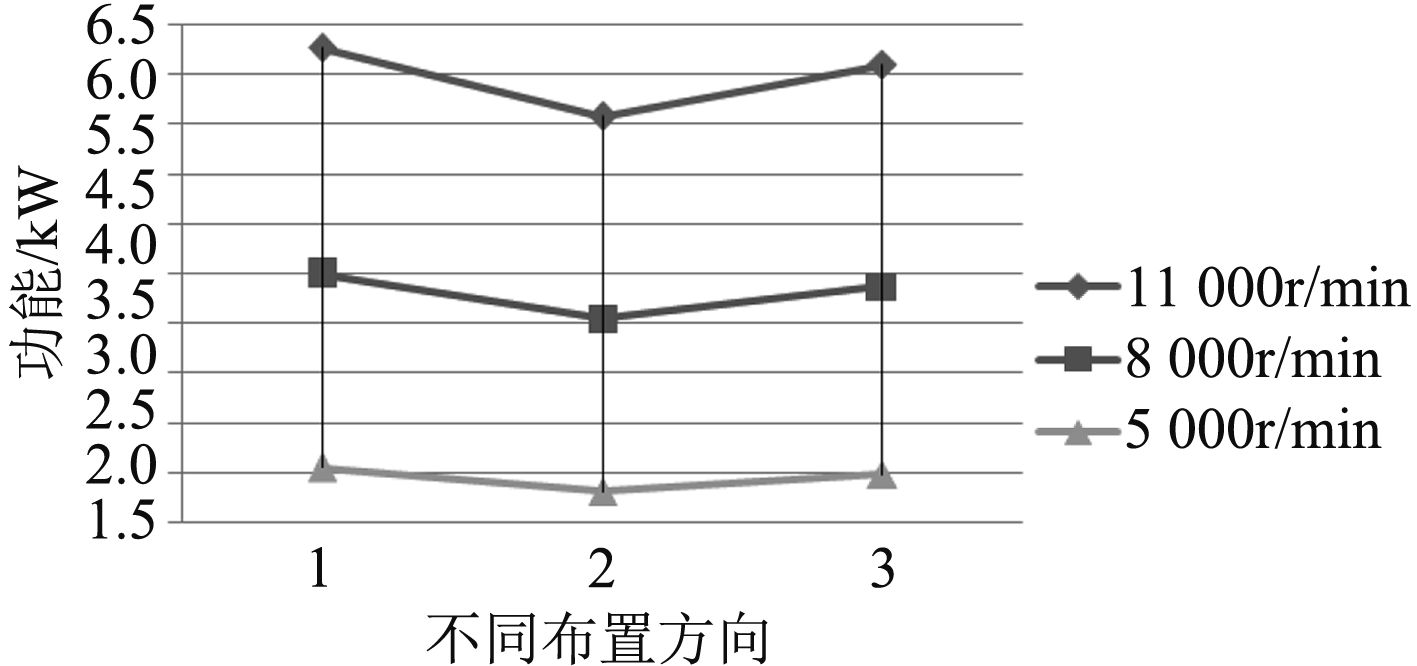
分别计算了轴承瓦块3种布置方向,不同转速下轴承静态性能。图4~图7分别为不同布置方向对轴承油膜温度、承载能力、功耗和流量的影响趋势。其中,承载能力用同一载荷下偏心率大小表示。
|
图 4 对最高油膜温度的影响 Fig. 4 Effect on maximum temperature of oil film |
|
图 5 对承载能力的影响 Fig. 5 Effect on loading capacity |
|
图 6 对功耗的影响 Fig. 6 Effect on power loss |
从图中可以看出,不同布置方向对轴承性能有一定的影响,规律不尽相同。在轴转速为5 000 r/min和8 000 r/min时第1种到第3种布置方向,油膜最高温度逐渐减小,而当转速11 000 r/min时,载荷在瓦块上时油膜最高温度最高。载荷在瓦块上时,承载能力最大,功耗较小,但需要的供油量大。其中对承载能力的影响较明显。

|
图 7 对供油量的影响 Fig. 7 Effect on oil feed |
分别计算了图1~图3中3种布置方向,不同转速下轴承的八大动态系数,即轴承刚度和轴承阻尼。计算结果列于表1和表2中,其中x轴、y轴选取布置图所示。
|
|
表 1 轴承刚度 Tab.1 Bearing stiffness |
|
|
表 2 轴承阻尼 Tab.2 Bearing damping |
1)不同布置方向对x向和y向的主刚度的影响规律不同,载荷作用在瓦上比载荷作用在瓦间的y方向主刚度Kyy大,x方向主刚度Kxx规律正好相反,并且变化量较大,相差一个数量级,而作用在瓦块前部时的主刚度值介于两者之间;
2)交叉刚度Kxy和Kyx在第1种情况作用在瓦块间和第2种作用在瓦块上时为0,而作用在瓦块前部时交叉刚度不再是0;
3)轴承阻尼值的变化规律与刚度的变化规律相一致。
3 轴承静态性能的试验验证为验证理论计算,对不同布置方向对轴承油膜温度影响进行了试验验证,试验件及试验装置如图8和图9所示。
3.1 试验装置[6]试验台由电机驱动,通过增速箱、膜片联轴器与试验轴相联,试验采用倒置式结构,即试验轴有2个支持轴承支承,试验轴承及轴承座悬浮在试验轴上,实现自由加载。加载装置应用液压加载,液压缸顶起,通过5:1的杠杆,使得载荷增加到油压载荷的5倍,加载部位在轴承座处,通过拉力传感器与轴承座相连,实现加载和载荷测量。
3.2 试验方法为实现不同布置位置转换,需要调节周向定位销的位置,实现了不同布置方向的模拟。其他试验参数均与计算保持一致。

|
图 8 试验台 Fig. 8 Test bed |

|
图 9 试验件 Fig. 9 Test piece |
|
|
表 3 试验数据与理论数据对比 |
|
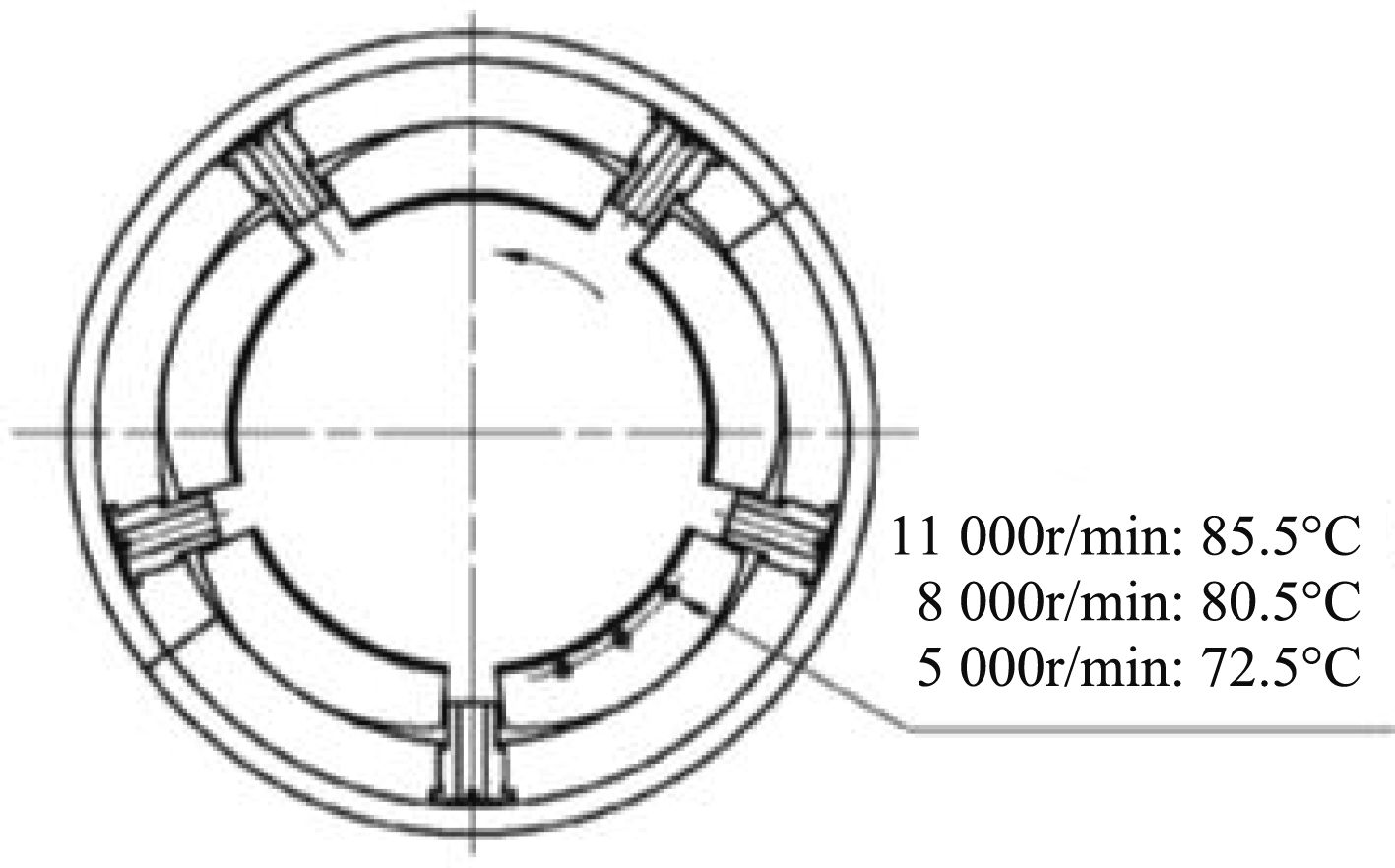
图 10 载荷在瓦块间测点温度 Fig. 10 Measuring point temperature of load between two pads |
|
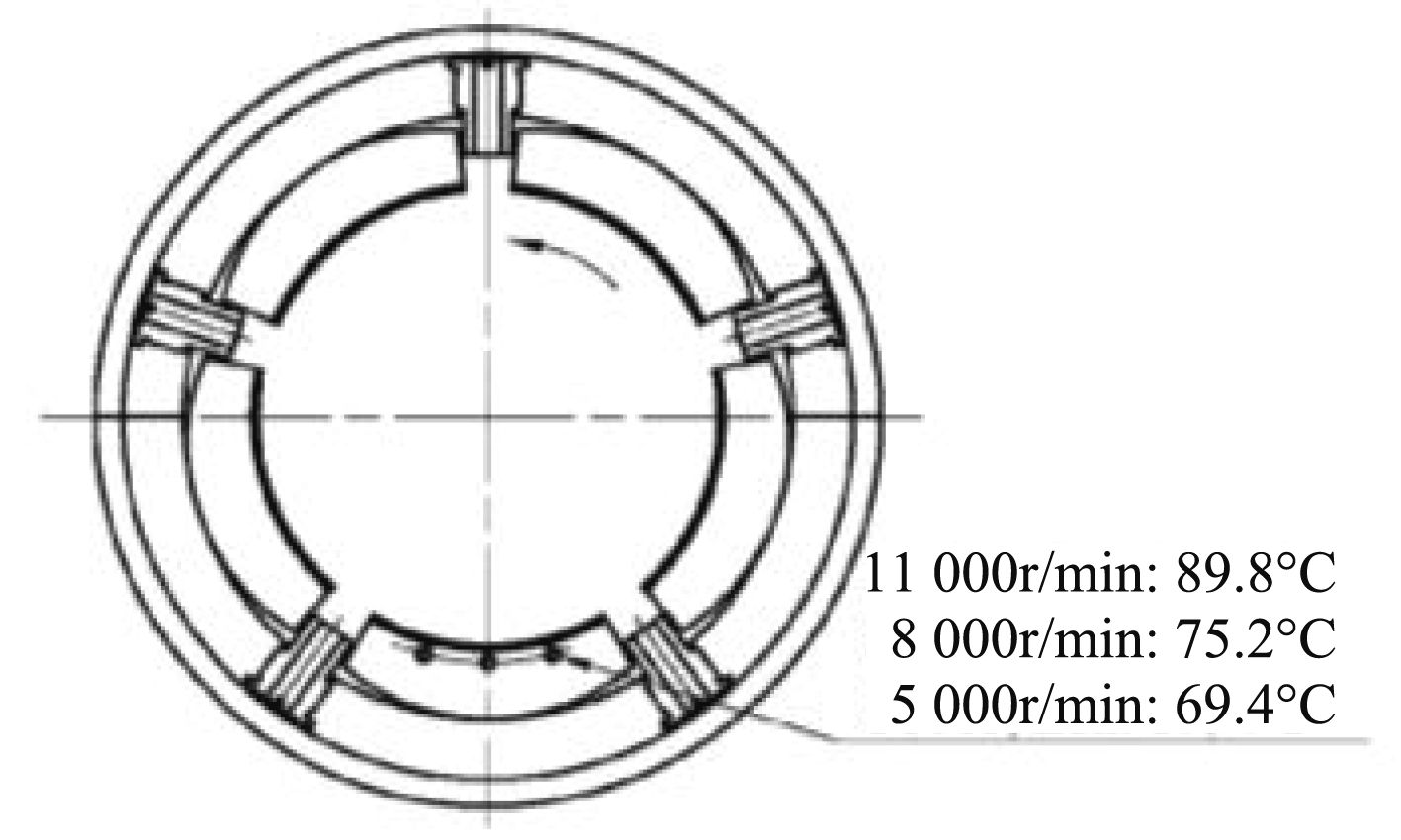
图 11 载荷在瓦块上测点温度 Fig. 11 Measuring point temperature of load on the pad |

|
图 12 载荷在瓦块前部测点温度 Fig. 12 Measuring point temperature of load on front pad |
图10~图12中给出的试验温度值是3个测点中的高值。由表3和图5可知:试验数据与理论计算有所不同,高速时试验温度高于计算温度,较低速度时试验温度低于计算温度。变化趋势与理论计算相似,在转速为5 000 r/min和8 000 r/min时,第1种布置方式(载荷在轴瓦间)时轴承温度高,当转速为11 000 r/min时,第2种布置方式(载荷在轴瓦上)轴承温度更高。最高温度差最大达到8.8 ℃。试验测得的不同布置方向下轴承测点油膜温度差值大于理论计算差值。
4 结 语可倾瓦轴承随着转速的增加,轴承温度、承载能力、功耗及流量均会有所增加;可倾瓦轴承瓦块布置方向不同,对轴承性能有一定的影响,其中,对油膜温度和承载能力影响较大,但在不同转速下,影响规律不同。理论计算与试验结果趋势一致;从理论计算看:可倾瓦轴承瓦块布置方向不同,对轴承动态性能影响比较明显。设计时,建议根据应用工况范围合理选择布置方式。
| [1] |
王永亮, 刘占生, 谭召生. 可倾瓦轴承瓦块摆动特性[J]. 哈尔滨工业大学学报, 2011, 43(9): 62–66.
WANG Yong-liang, LIU Zhan-sheng, TAN Zhao-sheng. Asway performance of tilting-pad bearing[J]. Journal of Harbin Institute of Technology, 2011, 43(9): 62–66. |
| [2] |
谭召生. 可倾瓦轴承的加工与装配[J]. 汽轮机技术. 2004, 46(3): 232–232.
TAN Zhao-sheng. Manufacture and assembled of tilting-pad bearing[J]. Turbine technology. 2004, 46(3): 232–232. |
| [3] | SIMMONS J, LAWRENCE C. Performance experiments with a 200mm, offset pivot journal pad bearing, STLE Tribology Transactions, 1996, 39, 969–973. |
| [4] | NICHOLAS J C. Tilting pad bearing design[C]// Proceedings of the 23rd Turbomachinery Symposium, Texas A& M University,1994, 179–194. |
| [5] |
张直明, 等. 滑动轴承的流体动力润滑理论[M]. 北京: 高等教育出版社. 1986.
ZHANG Zhi-ming, et al. Hydrodynamic lubrication theory of sliding bearing[M]. Beijing: Higher Education Press, 1986. |
| [6] |
胡朝阳, 常山. 大型径向和推力滑动轴承试验台结构设计与应用[J]. 齐齐哈尔大学学报, 2005, 21(1): 79–82.
HU Chao-yang, CHANG Shan. Design and application of large radial and trust bearing test-bed[J]. Journal of Qiqihar University, 2005, 21(1): 79–82. |
 2017, Vol. 39
2017, Vol. 39
