2. 中国船舶重工集团公司第七二三研究所,江苏 扬州 225001
2. The 723 Research Institute of CSIC, Yangzhou 225001, China
目前雷达辐射源信号分选技术大多是基于到达时间(TOA)为主分选,同时利用脉冲宽度(PW)、脉冲幅度(PA)、载频(RF)、到达角(DOA)等参数[1]。基于PRI分选的方法是目前应用最为普遍,针对不同信号环境也衍生出了不同的改进算法。基本方法主要包括累积差值直方图法、序列差值直方图法,PRI变换及其改进算法[2 – 5]。但是随着雷达技术的不断提高,信号环境也越来越复杂,发射信号的PRI值分布范围变广,传统算法所估计的PRI值会淹没在脉冲的抖动中,PRI值难以准确估计,使传统算法的分选能力大打折扣。
针对以上问题,在传统改进的PRI变换算法基础上,进一步改进,加入一个非常重要的参数脉内特征,新方法首先根据脉内特征将脉冲划分为多个脉冲子流,再对各个脉冲子流进行PRI估计,降低了脉冲信号的复杂度,可以有效降低PRI谱图中噪声的影响,能够很好地解决PRI分布范围广的问题,能够适应当前的高密集度信号环境,通过仿真实验验证了该算法的有效性。
1 PRI算法原理及脉内特征分析 1.1 传统改进PRI算法原理设脉冲到达时间采用脉冲的前沿时间来表示。令tn(n=0,1,…,N-1)为脉冲的到达时间,其中N为采样脉冲数。由于只使用TOA这一个参数,采样脉冲就可以模型化为单位冲激函数的和:
|
$g(t) = \sum\limits_{n = 0}^{N - 1} {\delta (t - {t_n})}\text{,} $
|
(1) |
式中:
|
$D(\tau ) =\int_{ - \infty }^\infty g(t)g(t + \tau \exp (2\pi jt/\tau ){\rm d}t \text{,}$
|
(2) |
式中:
将式(1)代入式(2)得:
|
$\begin{split}D(\tau ) =\sum\limits_{n = 0}^{N - 1} {\sum\limits_{m = 0}^{n - 1} {\delta (\tau - {t_n} + {t_m})} }\cdot \exp [2\pi j{t_n}/({t_n} - {t_m})]\text{。}\end{split}$
|
(3) |
PRI变换与自相关函数的区别在于加入了相位因子
由于经典的PRI算法在估计存在抖动脉冲时,真正的PRI会被淹没在噪声中,究其原因主要有:
1)随着TOA远离时间起点,PRI变换中的相位因子的相位误差增大。
2)本应该集中在同一个PRI箱中的脉冲对由于PRI的抖动而将分布在平均PRI值附近的几个箱中。
所以现在广泛应用的PRI算法是对传统算法改进后的算法,具体原理如下。
令
|
$\begin{array}{l}{\tau _k} = (k - \displaystyle\frac{1}{2})[({\tau _{\max }} - {\tau _{\min }})/K] + {\tau _{\min }}\text{,}\\k = 1,2, \cdots K\text{。}\end{array}$
|
(4) |
传统的改进算法利用交叠PRI箱
为了便于分析,采用PRI变换的离散形式为:
|
$\begin{array}{l}{D_{_k}} = \int {_{{\tau _k} - {b_k}/2}^{{\tau _k} + {b_k}/2}} D(\tau ){\rm d}\tau = \\[5pt]\sum\limits_{{\tau _k} - {b_k}/2 < \atop{t_n} - {t_m} < {\tau _k} + {b_k}/2} \!\!\!\!\!\!\!\!\!\!\!\!\!\!{\exp [2\pi j{t_n}} /({t_n} - {t_m})]\text{。} \end{array}$
|
(5) |
传统改进算法中采用了观察时间原则、消除谐波原则以及消除噪声原则[5]来设定变换后的检测门限,目的是为了能检测出真正的PRI谱值。
1)观察时间原则:
|
$\left| {{D_k}} \right| \geqslant \alpha \frac{T}{{{\tau _k}}} \text{,} $
|
(6) |
2)消除谐波原则
|
$\left| {{D_k}} \right| \geqslant \beta {C_k} \text{,}$
|
(7) |
3)消除噪声原则
|
$\left| {{D_k}} \right| \geqslant \gamma \sqrt {T{\rho ^2}{b_k}}\text{。} $
|
(8) |
式中:T为观察时间;Ck为自相关函数;
|
${A_k} = \max \left\{ {\alpha \frac{T}{{{\tau _k}}},\beta {C_k},\gamma \sqrt {T{\rho ^2}{b_k}} } \right\}\text{。}$
|
(9) |
式中:α,β,γ为可调因子。
1.2 雷达脉内特征分析雷达脉内特征被称为是雷达信号的指纹特征[6],主要是人为的脉内调制,包括相位调制、频率调制、幅度调制和3种调制组合的混合调制。针对各种不同的雷达信号包括简单脉冲信号、重频滑变信号、重频抖动信号、重频参差信号和频率捷变信号以及脉冲压缩信号(LFM(线性调频)信号和PSK(相移键控信号))等不同的信号形式,可利用信号的这些特征结合已有算法进行综合信号分选。
雷达信号的脉内参数主要是雷达的载频和脉内调制方式,其信号形式如下:
单频常规信号(CW):
|
$s(n) = A\exp \{ j[\frac{{2\pi {f_0}n}}{{{f_c}}} + \varphi ]\}\text{,} $
|
(10) |
线性调频信号(LFM):
|
$s(n) = A\exp \{ j2\pi [\frac{{{f_0}n}}{{{f_c}}} + \frac{{\mu {n^2}}}{{2f_c^2}}]\} \text{,}$
|
(11) |
相位编码信号(PSK):
|
$s(n) = A\exp \{ j[\frac{{2\pi {f_0}n}}{{{f_c}}} + \varphi (n)]\}\text{,} $
|
(12) |
频率编码信号(FSK):
|
$s(n) = A\exp \{ j[\frac{{2\pi {f_k}n}}{{{f_c}}} + \varphi ]\}\text{。} $
|
(13) |
式中:A为振幅;fc为采样频率;f0为载频;
单频常规信号没有脉内频率和相位调制,根据式(10)可求得其差分自相关函数
|
$\begin{array}{l}R(k) = {A^2}E\\[3pt] \left\{ \begin{array}{l}2\exp [j2\pi {f_0}k/{f_c}] - \exp [j2\pi {f_0}(k - 1)/{f_c}]\text{,}\\[3pt] - \exp [j2\pi {f_0}(k + 1)/{f_c}]\text{。}\end{array} \right.\end{array}$
|
(14) |
式中:f0为信号载频,fc为采样频率,具体推导过程见文献[7]。
对于简单的常规脉冲信号,当k一定时,
线性调频信号[8]是脉冲压缩雷达中最常见的信号形式,这种体制的雷达具有发射脉冲宽、平均功率大的特点,能够提高雷达的作用距离,在接收时采用匹配滤波器压缩脉冲从而获得窄脉冲,提高距离分辨率,所以这种体制的雷达可以很好地解决距离和距离分辨率的矛盾。
LFM信号的数学表达式为:
|
$s(t) = Arect(\frac{t}{T})\exp [j2\pi ({f_c}t + \frac{K}{2}{t^2})]\text{,}$
|
(15) |
式中:fc为载波频率;
|
$f = {f_c} + Kt,\,\left( - \frac{T}{2} \leqslant t \leqslant \frac{T}{2}\right)\text{,}$
|
(16) |
典型信号如图1所示:
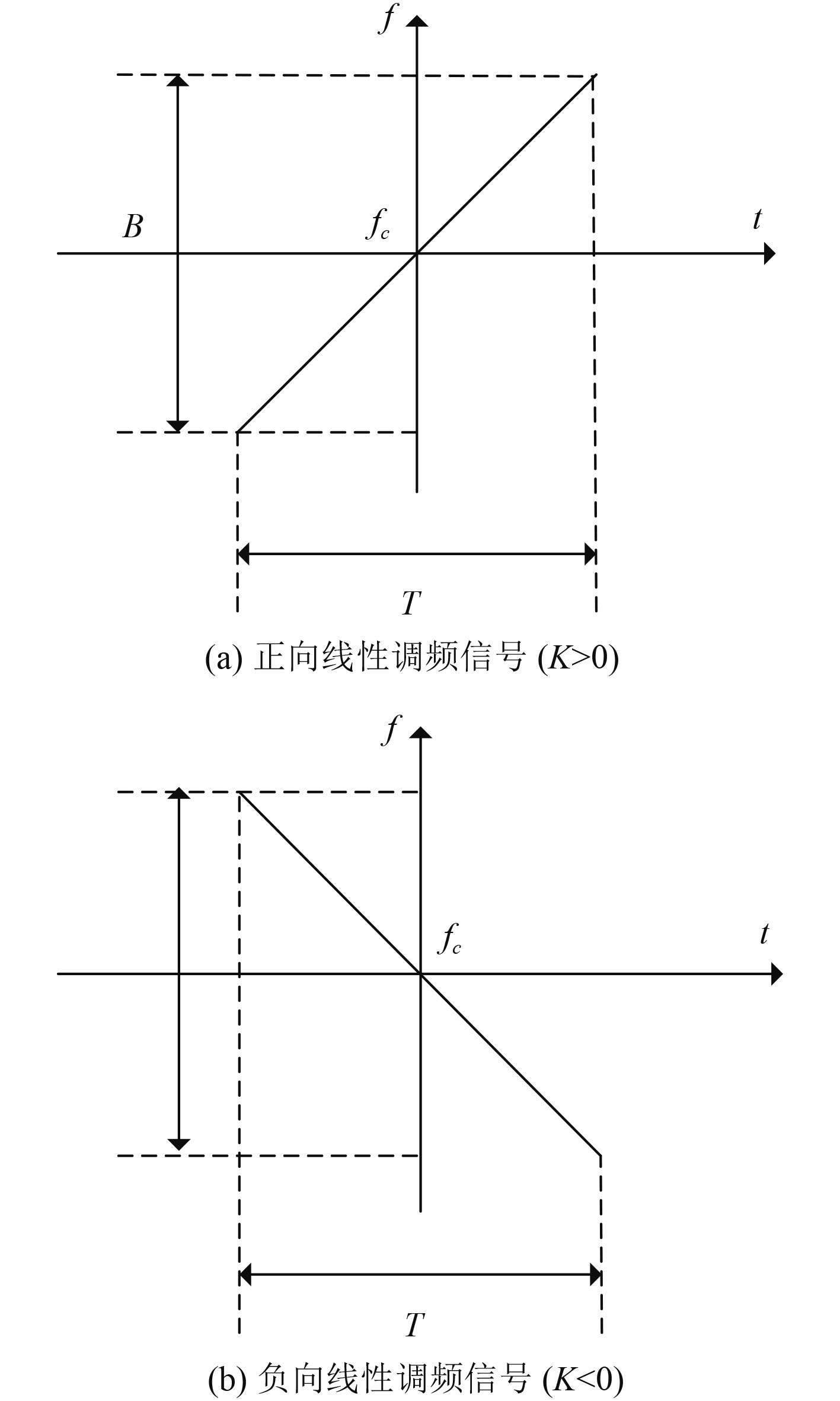
|
图 1 典型线性调频信号 Fig. 1 Typical signal of LFM |
根据文献[8]的推导,可得它的幅度表达式:
|
$|S(f)| = \frac{A}{{\sqrt {2k} }}{\{ {[c({k_1}) + c({k_2})]^2} + {[s({k_1}) + s({k_2})]^2}\} ^{1/2}}\text{,}$
|
(17) |
相位表达式:
|
$\begin{split}\theta (f) = - \displaystyle\frac{\pi }{k}{(f - {f_c})^2}+ \arctan \left[\displaystyle\frac{{s({k_1}) + s({k_2})}}{{c({k_1}) + c({k_2})}}\right]\text{。}\end{split}$
|
(18) |
式中:运用Fresnel积分公式,
在满足大时宽带宽积的条件下,根据上式可知LFM信号有如下特性:1)信号的振幅谱接近于矩形函数,频谱宽度近似等于信号的调频变化范围B,与时宽T无关;2)信号的相位谱具有平方律特性。
根据LFM信号的特点,可以在信号的接受端设计匹配滤波器,进行脉冲压缩处理,对其进行信号的识别。
1.2.3 相位编码信号(PSK)和频率编码信号(FSK)PSK和FSK信号形式见式(12)和式(13),雷达信号采用PSK调制后,信号实际上是一种脉冲压缩扩谱信号,信号频谱展宽,功率谱密度降低,接收机可以利用匹配接收得到信号增益,还可以利用数字接收技术对编码序列进行改变。对于FSK信号,脉内各子码频率不同,在子码范围内,瞬时自相关码元无跳变时即为CW信号。
2 基于脉内特征的PRI变换算法为了解决在复杂电磁环境下,脉冲PRI值分布范围广、抖动严重的问题,由第1节的分析提出一种基于脉内特征的PRI变换算法,在信号的接收端,利用信号的脉内特征信息,先将不同调制方式的信号提取分离,再对稀释后的脉冲进行PRI变换,得到雷达脉冲信号的PRI值。
算法实现过程如下:
1)接收端接收包含脉内特征和到达时间的脉冲流,假设信号的脉内特征已经正确识别,首先根据脉冲的不同调制方式将脉冲流进行划分,形成脉冲子流并编号,此时脉冲流得到了稀释。
2)对各个脉冲子流进行PRI变换实现不同脉冲的信号分选,不同体制的雷达脉冲对应不同的PRI谱图。
3)对估计出的PRI进行分析与识别,以便后续处理。
具体流程框图如图2所示。
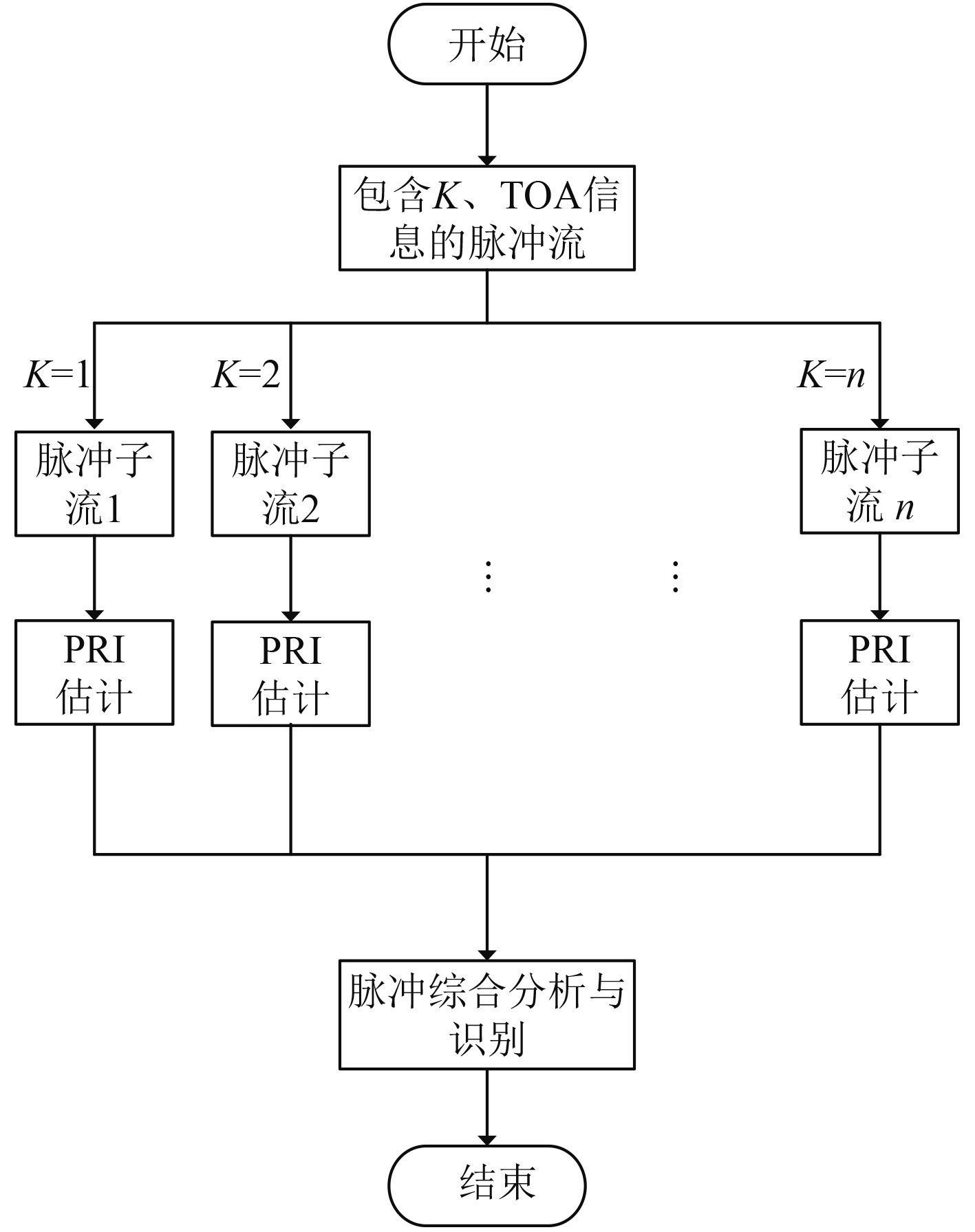
|
图 2 算法实现流程 Fig. 2 Algorithm implementation process |
流程图中的K表示不同调制方式的雷达信号,TOA为脉冲到达时间,先利用脉冲的不同调制信息将脉冲流划分为多个脉冲子流,再对多个脉冲子流进行PRI估计,PRI估计运用改进的PRI变换算法,分析见1.1节,具体工作流程如下:
步骤 1 初始化,设
步骤 2 设
步骤 3 寻找
步骤 4 取
步骤 5 当
步骤 6 初始化时间起点,如果第k个PRI箱第1次使用,设
步骤 7 计算初始相位,
步骤 8 转换时间起点,当满足条件:v=1,
步骤 9 计算相位
步骤 10
步骤 11
为了验证本算法的有效性,计算机仿真采用不同脉冲序列进行实验,尽可能模拟出实际的序列特征,结合仿真结果图,将新算法与传统算法进行对比,分析并给出结论。仿真环境为:windows 10,intel core i7,编程平台为:Matlab R2015b。
仿真实验脉冲序列由六部雷达脉冲组成,抖动统一设置为10%,其中三部为常规雷达脉冲,两部为线性调频雷达脉冲,一部为相位编码脉冲,各脉冲设置如表1所示。
|
|
表 1 仿真脉冲序列设置 Tab.1 Settings of simulation sequence |
|
|
表 2 PRI变换的参数设置 Tab.2 Settings of transform parameters |
为了便于叙述,仿真时设置脉内特征为K,当K=1时为CW信号,K=2时为LFM信号,K=3时为FSK或PSK信号。
如图3所示,图3(a)和图3(b)分别为传统改进PRI变换算法和新算法的PRI值检测结果。
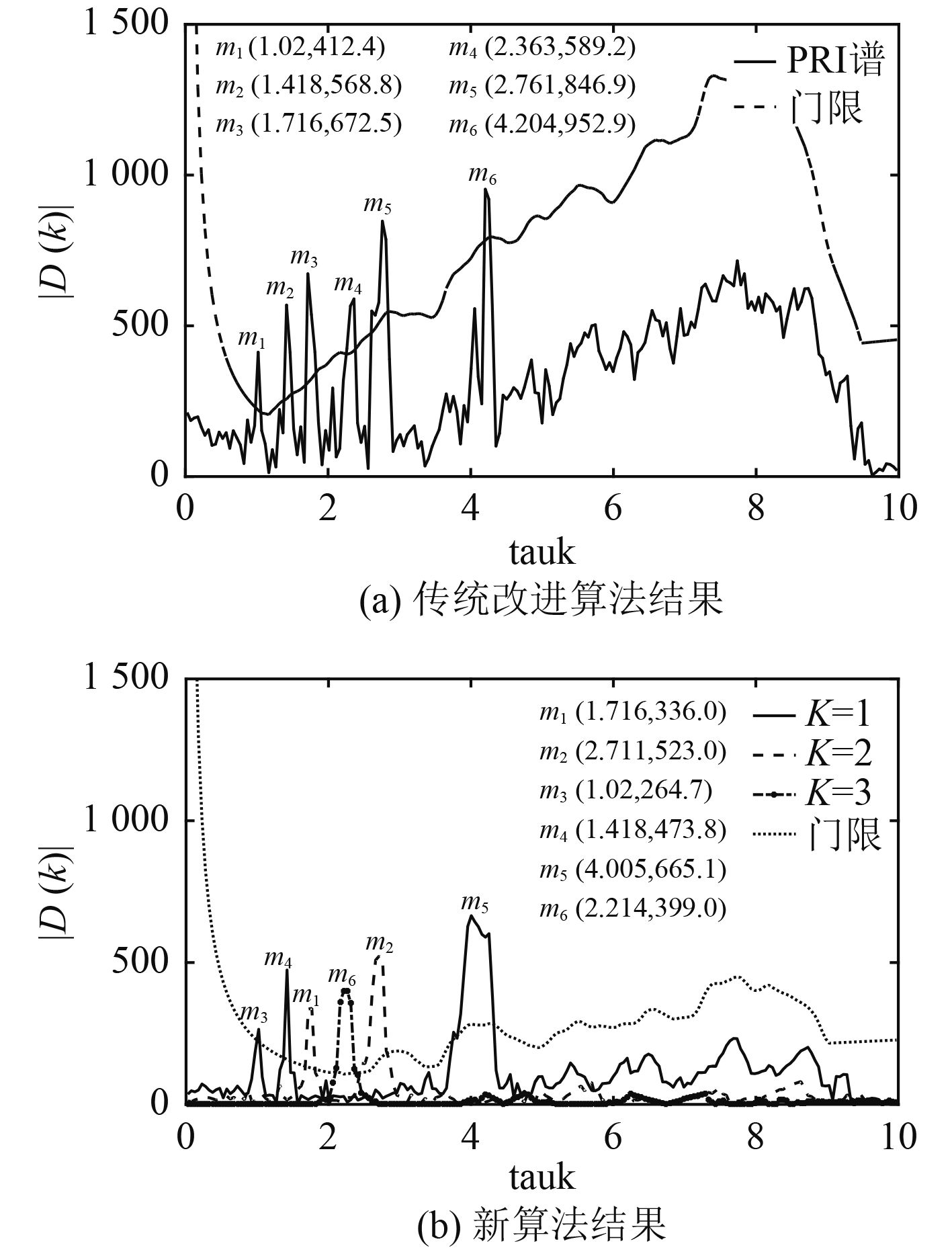
|
图 3 PRI值估计结果 Fig. 3 Estimated results of PRI value |
仿真结果如图3所示,图3(a)为传统改进算法的结果图,检测出6个PRI谱值,分别为m1,m2,m3,m4,m5和m6。图3(b)为新方法的仿真结果,K表示不同脉内特征所对应的PRI谱图,检测出K=1时有2个PRI值,分别为m1和m2,K=2时有3个PRI值分别为m3,m4,m5,K=3时有1个PRI值为m6。
不同方法估计的PRI值如表3。
|
|
表 3 检测结果统计表 Tab.3 Statistical table of detection results |
由仿真结果可以看出,传统改进算法和本文算法均能检测出正确结果,但是采用新方法与传统改进算法相比有3个明显的优势:
1)传统算法的检测结果误差为0.071 7,新算法误差仅为0.005 4,检测结果更接近真实的PRI值,而且峰值非常明显,所受抖动的影响明显小于传统改进算法;
2)由于加入了脉内特征作为分选参数,将脉冲以脉内特征为依据划分为不同的脉冲子流,再对每个脉冲子流进行处理,很大程度地稀释了脉冲,降低了数据的复杂度;
3)本文算法的结果除了包含检测出的PRI值,还有其对应的脉内特征,利于进一步分析与处理。
4 结 语本文在传统改进的PRI变换算法的基础上,加入脉内特征作为划分脉冲流的依据,提出一种新的改进方法,通过仿真实验加以验证,从结果上可以看出新方法除了保留原有算法正确性的同时,能够更好地检测出接近真实的PRI,可以降低复杂电磁环境下脉冲抖动的影响,PRI分选准确率较高,可以满足当前高密集度信号环境的要求,具有一定的工程应用价值。
| [1] |
何明浩. 雷达对抗信息处理[M]. 北京: 清华大学出版社, 2010.
HE Ming-hao. Radar countermeasure information processing [M]. Beijing Tsing Hua University Press, 2010. |
| [2] |
乔宏乐, 王超, 王鹏. 基于PRI变换法的脉冲信号分选算法[J]. 火控雷达技术, 2012 (2): 34–38.
QIAO Hongle, WANG Chao, WANG Peng. Pulse Signals De-interleaving Algorithm Based on PRI Transform[J]. Fire Control Radar Technology, 2012 (2): 34–38. |
| [3] | MARDIA H K. New techniques for the deinterleaving of repetitive sequences[J]. Radar & Signal Processing Iee Proceedings F, 1989, 136 (4): 149–154. |
| [4] | MILOJEVIĆ D J, POPOVIĆ B M. Improved algorithm for the deinterleaving of radar pulses[J]. Radar & Signal Processing Iee Proceedings F, 1992, 139 (1): 98–104. |
| [5] | MAHDAVI A, PEZESHK A M. A fast enhanced algorithm of PRI transform[C]// International Symposium on Parallel Computing in Electrical Engineering. 2011: 179–184. |
| [6] |
魏东升, 巫胜洪. 雷达信号脉内细微特征的研究[J]. 舰船科学技术, 1994 (3): 23–30.
WEI Dongsheng, WU Shenghong. Study on the subtle characteristics of radar signal[J]. Ship Science and Technology, 1994 (3): 23–30. |
| [7] |
陈韬伟. 基于脉内特征的雷达辐射源信号分选技术研究[D]. 成都: 西南交通大学, 2010.
CHEN Tao-wei. Deinterleaving technology for radar emitter signals based on the intra-pulse features [D]. Chengdou: Southwest Jiaotong University, 2010. |
| [8] |
贾立印, 张洪顺. LFM脉冲压缩雷达信号的时频分析及其应用[C]// 全国无线电应用与管理学术会议. 2008.
JIA Li-yin, ZHANG Hong-shun. Time-frequency analysis of LFM pulse compression radar signal and appliance [C]// National Conference on Radio Application and Management, 2008. |
 2017, Vol. 39
2017, Vol. 39
