0 引 言

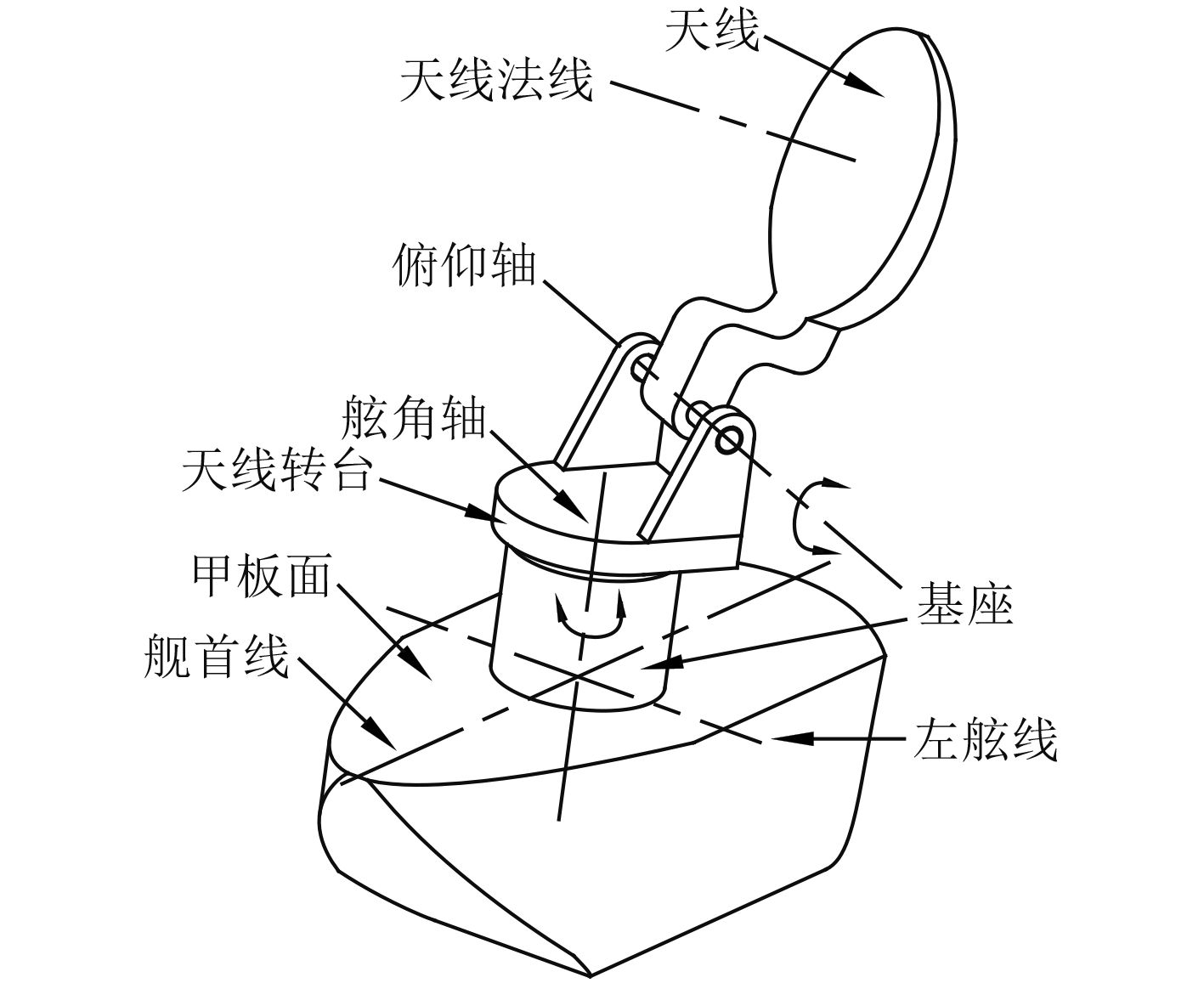
舰船在水面航行时船体会产生纵摇、横摇运动和航向的改变，这些会对舰载雷达的波束指向产生重大影响。舰载雷达两轴转台系统（见图1）机械结构简单，可对雷达天线法线的姿态角（方位角和俯仰角，相对大地）进行控制以保证雷达波束指向，但舰船发生摇摆时，雷达波束绕天线法线发生旋转，所以两轴转台系统通常适用于单束锥形波雷达。

1 坐标系及姿态角定义

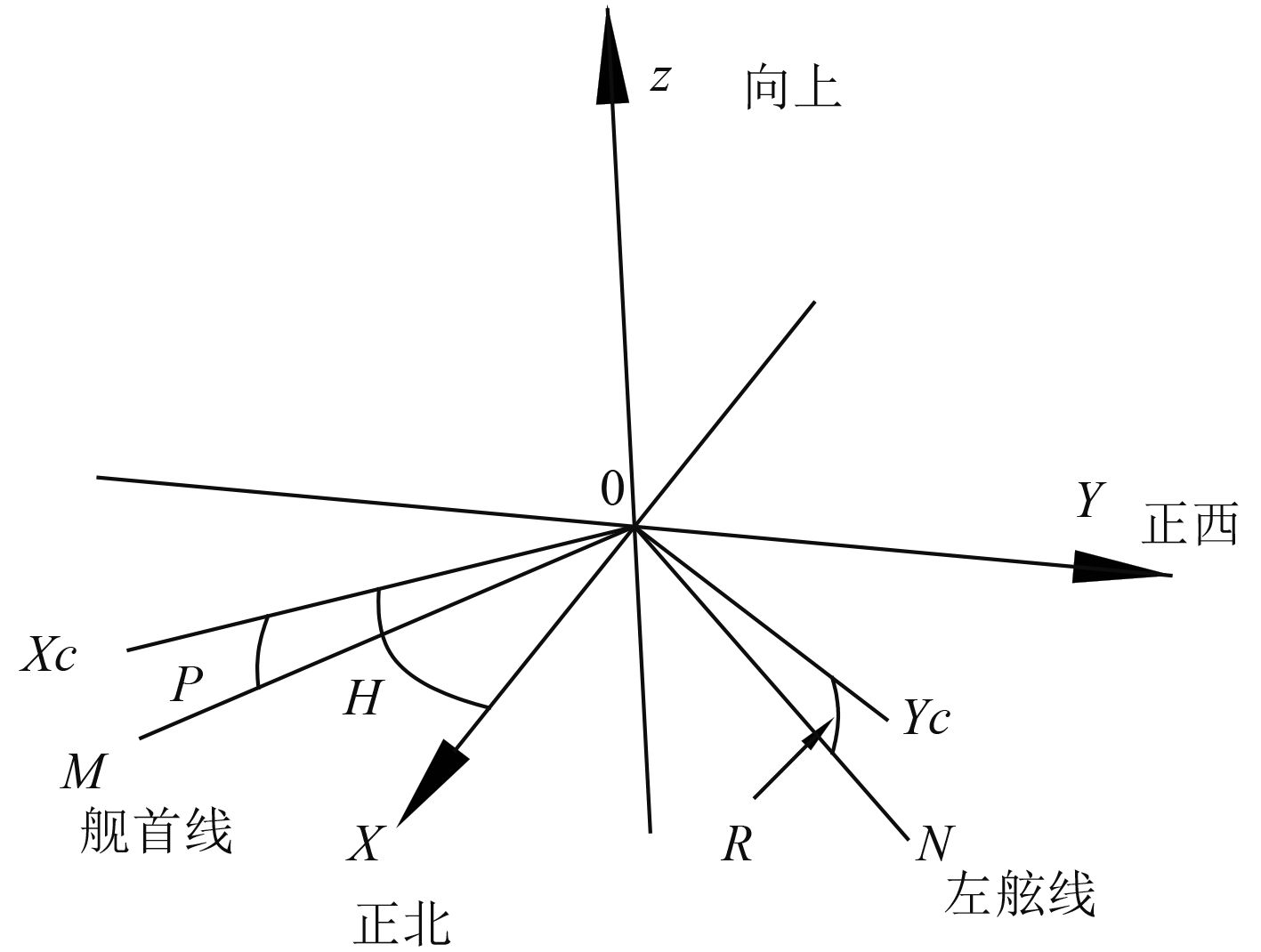
平台罗经提供舰船在大地直角坐标系O-XYZ中的纵摇角、横摇角和航向角。原点O位于舰船甲板中心，X轴平行于水平面，正北为正；Y轴平行于水平面，正西为正；Z轴垂直于水平面XOY，铅垂向上为正（见图2，图中H=40°，P=–10°，R=–15°）。

舰船航向角、纵摇角和横摇角定义如下：

H为航向角，正北线OX顺时针到线OXc （舰首线OM在水平面投影线）的角度，水平面内测量。

P为纵摇角，舰首线OM与水平面的夹角，在过舰首线OM的铅垂面内测量，舰首线在水平面上方（舰首抬高）为正。

R为横摇角，甲板面（面MON）绕舰首线OM旋转的角度，即舰船左舷线ON和线OYc（过左舷线的舰船横剖面与水平面交线）的夹角；其测量平面（横摇面）垂直于甲板面且垂直于舰首线（即OM⊥横摇面NOYc），左舷线在水平面上方（左舷抬高）为正。

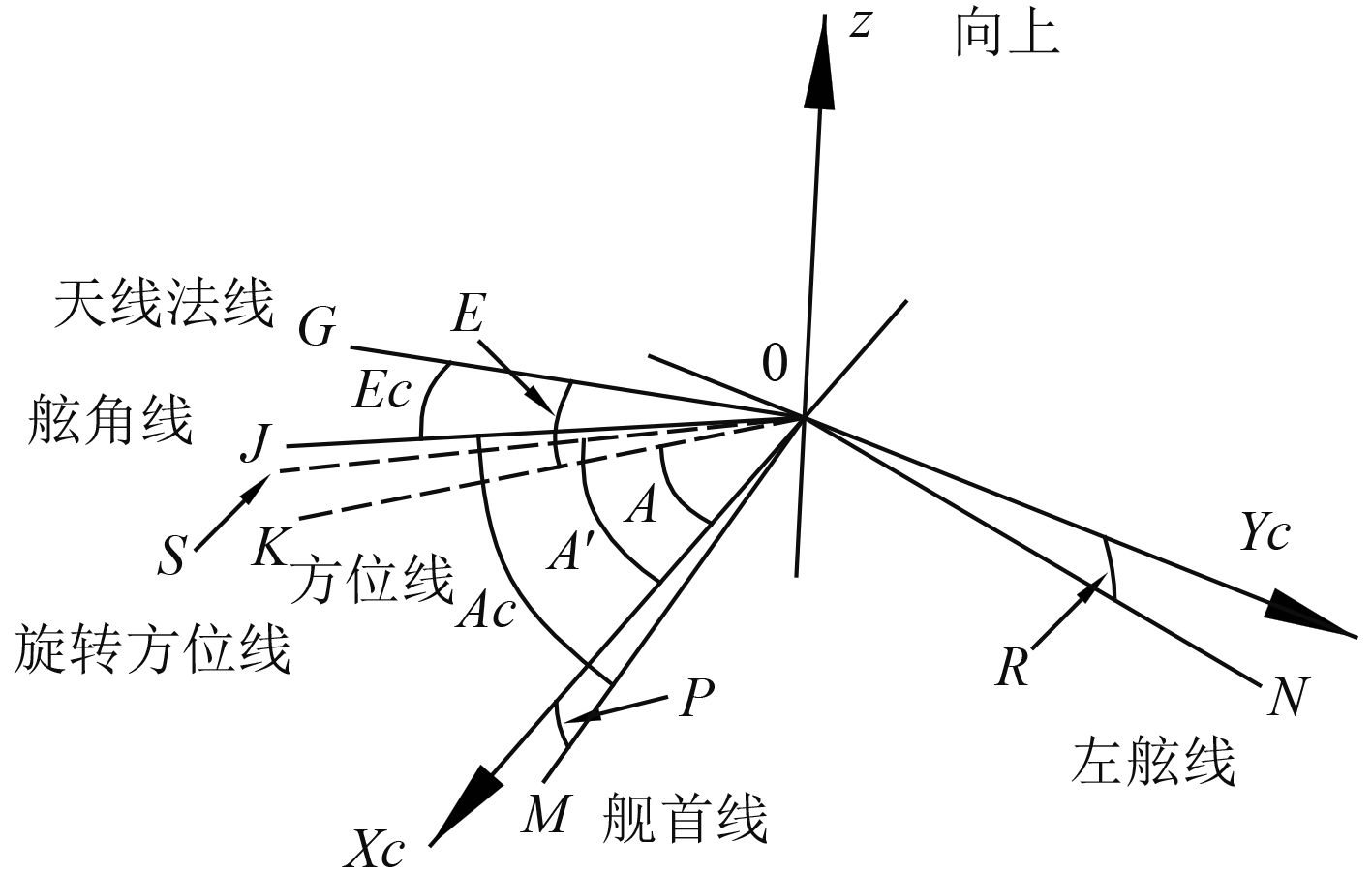
Z轴在过舰首线OM的铅垂面内，OM⊥OYc，OZ⊥OYc，可知OYc⊥铅垂面MOZ，OYc⊥OXc，O-XcYcZ为直角坐标系，即舰船直角坐标系（见图3）。

大地直角坐标系绕Z轴顺时针旋转航向角H得舰船直角坐标系，本文公式在舰船直角坐标系（不考虑航向值）中推导。在不影响推导结果前提下，各姿态角的顶点设在O。

舰载雷达转台系统有2根轴：舷角轴和俯仰轴，舷角轴为天线转台（安装在基座上，基座与甲板面一体）中心轴，舷角轴垂直于甲板面；俯仰轴安装在天线转台上方，俯仰轴垂直于舷角轴。舰载雷达绕舷角轴和俯仰轴运动。

Ac 为天线甲板面舷角，天线转台绕舷角轴顺时针运动的角度，即舰首线OM顺时针到舷角线OJ（天线法线OG在甲板面MON内投影线）的角度，甲板面内测量。

Ec 为天线甲板面俯仰角，天线绕俯仰轴运动的角度，即天线法线OG与舷角线OJ的夹角，在平面GOJ（过天线法线且垂直于甲板面的平面）内测量，夹角在甲板面上方为正（因雷达机械结构限制，该角度一般不超过±30°）。

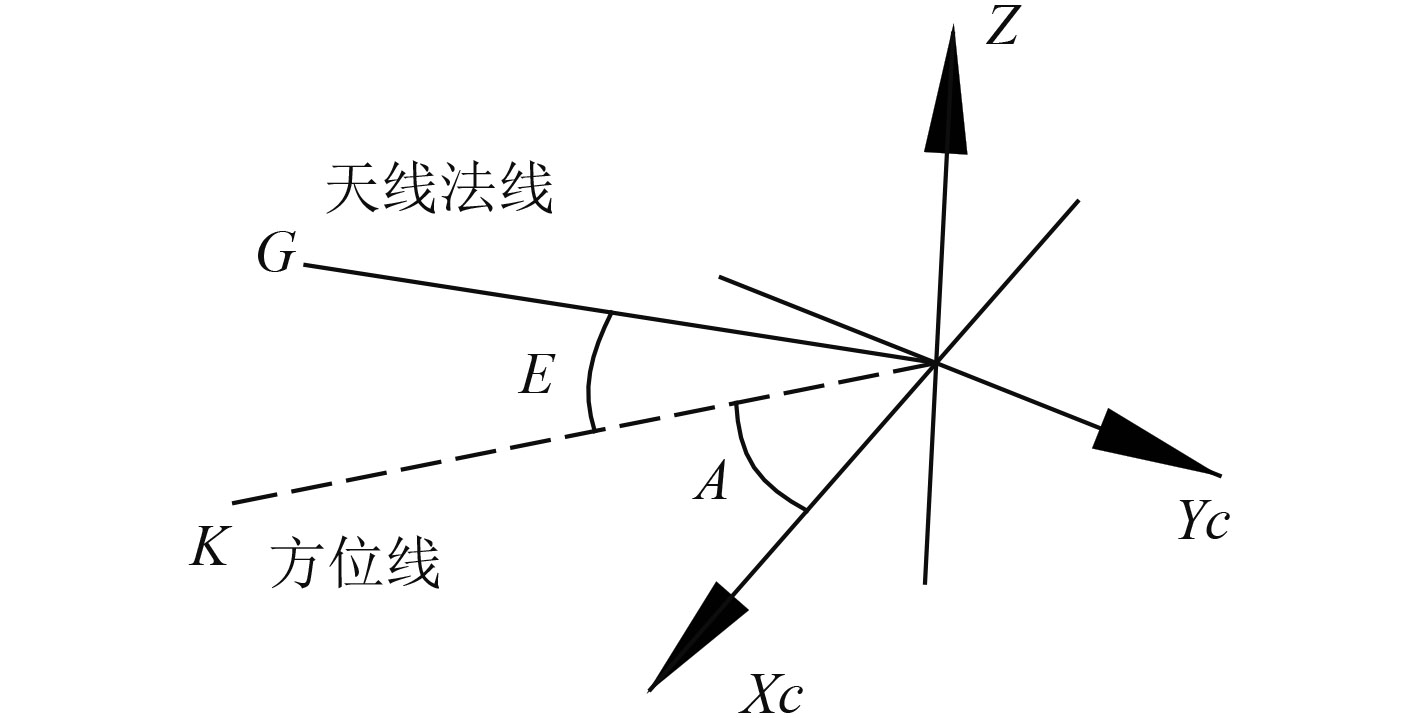
A为天线方位角，线OXc顺时针到方位线OK（天线法线OG在水平面投影线）的角度，水平面内测量。

E 为天线俯仰角，天线法线OG与方位线OK的夹角，在平面GOK（过天线法线的铅垂面）内测量，夹角在水平面上方为正。

φ 为波束旋转角，平面GOK与平面GOJ的夹角（锐角）。沿天线法线方向看（点O到G），面GOK绕天线法线OG逆时针到面GOJ的角度φ为正，顺时针为负。

A 为波束旋转方位角，线OXc顺时针到旋转方位线OS（平面GOJ与水平面的交线，取该交线与天线法线OG夹角为锐角的部分）的角度，水平面内测量；At 为雷达目标真方位角，由大地直角坐标系和舰船直角坐标系的关系可知，雷达目标真方位值即为航向角H与天线方位角A值之和。

2 稳定方程推导

工程项目中，往往是已知舰船平台罗经信号（P，R）和天线姿态角（A，E），求解稳定方程（即执行环节角度（Ec，Ac））和波束旋转角φ。取线OM、线ON、线OG、线OJ、线OK、线OS等为单位长度（见图3，图中P=–10°，R=–15°，Ac=50°，Ec=+20°，A=41.55°，E=+23.82°，A=49.44°，φ=+18.94°）。

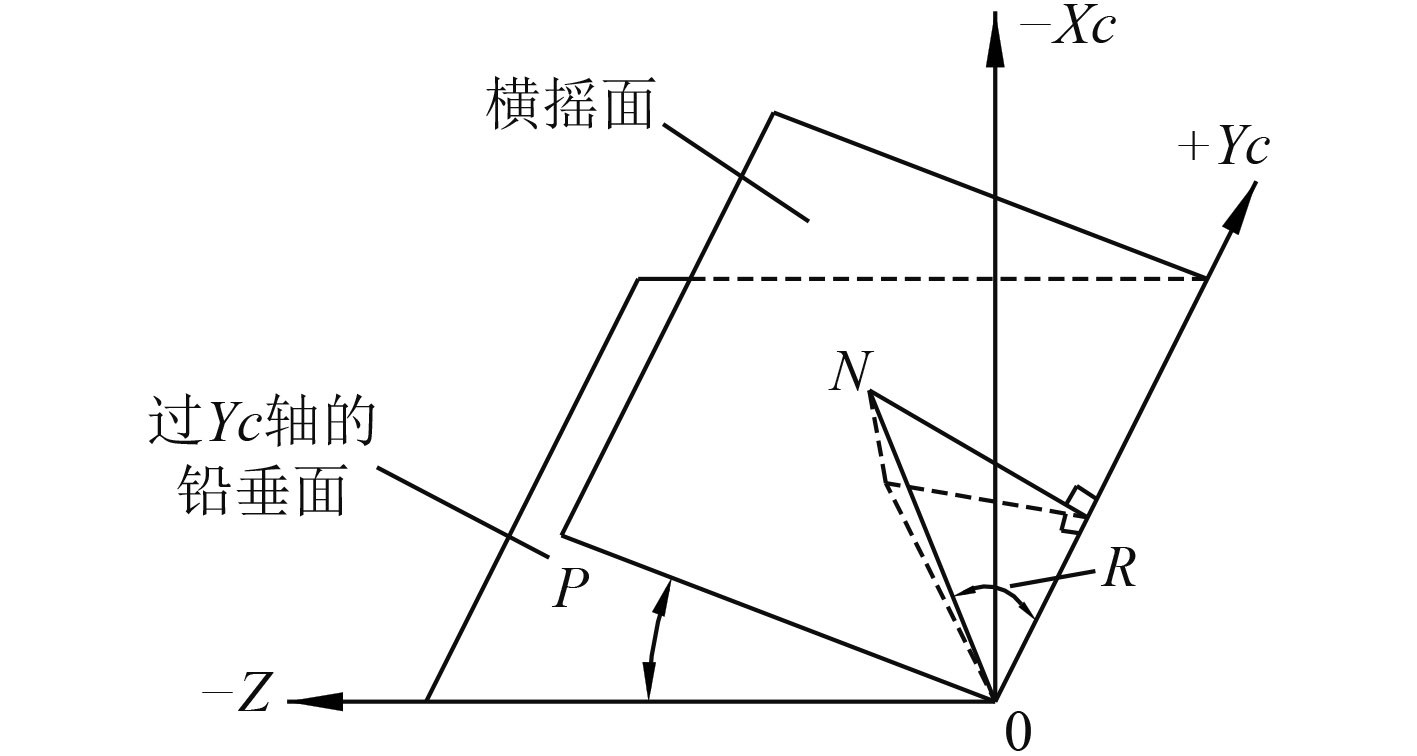
2.1 甲板面方程

由空间解析几何法，舰首线上M点（见图3）空间坐标为(cosP, 0, sinP)，左舷线上N点（见图4）空间坐标为(–sinR sinP, cosR, sinR cosP)，甲板面过O，M，N三点，得其方程为：

${\rm{sin}}P{{x}} + {\rm{tan}}R{{y}} - {\rm{cos}}P{{z}} = 0 \text{。}$

(1)

2.2 过天线法线垂直于甲板面的平面方程

天线法线上G点（见图5）空间坐标为(cosAcosE, –sinAcosE, sinE)，由方程（1）可知甲板面法线（设为OF）方向向量为(sinP, tanR, –cosP)，过O，G，F三点的平面即为过天线法线垂直于甲板面的平面，得其方程为：

${{{m}}_1}{{x}} + {{{n}}_1}{{y}} + {{{k}}_1}{{z}} = 0\text{，}$

(2)

其中，

$\left\{ {\begin{array}{*{20}{l}}\!\!\!\! {{{{m}}_1} = \left( {\displaystyle\frac{{\cos {{P}}}}{{\sin {{P}}}} - \displaystyle\frac{{\tan {{R}}}}{{\sin {{P}}}}\displaystyle\frac{{\cos {{A}}\cos {{E}}\cos {{P}} + \sin {{E}}\sin {{P}}}}{{\cos {{A}}\cos {{E}}\tan {{R}} + \sin {{A}}\cos {{E}}\sin {{P}}}}} \right){{{k}}_1}}\text{，}\\\!\!\!\! {{{{n}}_1} = \left( {\displaystyle\frac{{\cos {{A}}\cos {{E}}\cos {{P}} + \sin {{E}}\sin {{P}}}}{{\cos {{A}}\cos {{E}}\tan {{R}} + \sin {{A}}\cos {{E}}\sin {{P}}}}} \right){{{k}}_1}}\text{，}\\\!\!\!\! {{{{k}}_1} = 1}\text{。}\end{array}} \right.$

2.3 舷角线向量

设甲板面MON与过天线法线垂直于甲板面的平面GOJ的交线（过原点O）方向向量为 $\left( {{{{m}}_2},{{{n}}_2},{{{k}}_2}} \right)$ ，由方程（1）和方程（2）得该交线一般方程：

$\left\{ {\begin{aligned}& {\sin {{P}}{{{m}}_2} + \tan {{R}}{{{n}}_2} - \cos {{P}}{{{k}}_2} = 0}\text{，}\\& {{{{m}}_1}{{{m}}_2} + {{{n}}_1}{{{n}}_2} + {{{k}}_1}{{{k}}_2} = 0}\text{。}\end{aligned}} \right.$

由上方程组得：

$\left\{ {\begin{aligned}& {{{{m}}_2} = \left( { - \displaystyle\frac{{{{{k}}_1}}}{{{{{m}}_1}}} - \displaystyle\frac{{{{{n}}_1}}}{{{{{m}}_1}}}\displaystyle\frac{{\cos {{P}} + \displaystyle\frac{{{{{k}}_1}}}{{{{{m}}_1}}}\sin {{P}}}}{{\tan {{R}} - \displaystyle\frac{{{{{n}}_1}}}{{{{{m}}_1}}}\sin {{P}}}}} \right){{{k}}_2}}\text{，}\\& {{{{n}}_2} = \displaystyle\frac{{\cos {{P}} + \displaystyle\frac{{{{{k}}_1}}}{{{{{m}}_1}}}\sin {{P}}}}{{\tan {{R}} - \displaystyle\frac{{{{{n}}_1}}}{{{{{m}}_1}}}\sin {{P}}}}{{{k}}_2}}\text{。}\end{aligned}} \right.$

该交线（方向向量 $\left( {{{{m}}_2},{{{n}}_2},{{{k}}_2}} \right)$ ）与天线法线（方向向量 $\left( {\cos {{A}}\cos {{E}}, - \sin {{A}}\cos {{E}},\sin {{E}}} \right)$ ）的夹角为α（可设k₂=1）：

$\cos {{\alpha }} = \frac{{{{{m}}_2}\cos {{A}}\cos {{E}} - {{{n}}_2}\sin {{A}}\cos {{E}} + {{{k}}_2}\sin {{E}}}}{{\sqrt {{{m}}_2^2 + {{n}}_2^2 + {{k}}_2^2} }}\text{。}$

设中间向量 $\left( {{{{m}}_3},{{{n}}_3},{{{k}}_3}} \right)$ ，当 $\cos {{\alpha }} \geqslant 0$ 时， ${{{m}}_3} = {{{m}}_2}$ ， ${{{n}}_3} = {{{n}}_2},{{{k}}_3} = {{{k}}_2} = 1$ ，当 $\cos {{\alpha }} < 0$ 时， ${{{m}}_3} = - {{{m}}_2},\;{{{n}}_3} = - {{{n}}_2},$ ${{{k}}_3} = - {{{k}}_2} = - 1$ 。

将向量 $\left( {{{{m}}_3},{{{n}}_3},{{{k}}_3}} \right)$ 单位化，得舷角线方向向量 $\left( {{{{m}}_4},{{{n}}_4},{{{k}}_4}} \right)$ 。

2.4 天线甲板面舷角Ac和俯仰角Ec

设舷角线（单位向量 $\left( {{{{m}}_4},{{{n}}_4},{{{k}}_4}} \right)$ ）与舰首线OM（单位向量 $\left( {{{\rm cos}}P,0,\sin {{P}}} \right)$ ）的夹角为β，得

$\cos {{\beta }} = {{{m}}_4}\cos {{P}} + {{{k}}_4}\sin {{P}}\text{，}$

(3)

天线甲板面舷角Ac为：

当n₄ $\leqslant$ 0时， ${{Ac}} = {{\beta }} = {\cos ^{ - 1}}\left( {{{{m}}_4}\cos {{P}} + {{{k}}_4}\sin {{P}}} \right)$ ，当n₄>0时， ${{Ac}} = 2{{π }} - {{\beta }} = 2{{π }} - {\cos ^{ - 1}}\left( {{{{m}}_4}\cos {{P}} + {{{k}}_4}\sin {{P}}} \right)$ 。

设舷角线OJ（单位向量 $\left( {{{{m}}_4},{{{n}}_4},{{{k}}_4}} \right)$ ）与天线法线的夹角为γ：得

$\cos {{\gamma }} = {{{m}}_4}\cos {{A}}\cos {{E}} - {{{n}}_4}\sin {{A}}\cos {{E}} + {{{k}}_4}\sin {{E}}\text{。}$

(4)

雷达波束甲板面俯仰角Ec为：

当k₄ $\leqslant$ sinE时， ${{Ec}} = \gamma = {\cos ^{ - 1}}({{{m}}_4}\cos {{A}}\cos {{E}} - $ ${{{n}}_4}\sin {{A}}\cos {{E}} + {{{k}}_4}\sin {{E}})$ ，当k₄>sinE时， ${{Ec}} = {{\gamma }} = $ $- {\cos ^{ - 1}}\left( {{{{m}}_4}\cos {{A}}\cos {{E}} - {{{n}}_4}\sin {{A}}\cos {{E}} + {{{k}}_4}\sin {{E}}} \right)$ 。

2.5 波束旋转方位角A′

由方程（2），水平面（方程为z=0）与过天线法线垂直于甲板面的平面GOJ的交线（过原点O）的一般方程为：

$\left\{ {\begin{array}{*{20}{l}}\!\!\! {z = 0}\text{，}\\\!\!\! {{{{m}}_1}x + {{{n}}_1}y + {{{k}}_1}z = 0}\text{。}\end{array}} \right.$

该交线点向式方程为：

$\left\{ {\begin{array}{*{20}{l}}\!\!\! {\displaystyle\frac{{{x}}}{{{{{n}}_1}}} = \displaystyle\frac{{{y}}}{{ - {{{m}}_1}}}}\text{，}\\\!\!\! {z = 0}\text{。}\end{array}} \right.$

该交线（方向向量为 $\left( {{{{n}}_1}, - {{{m}}_1},0} \right)$ ）与天线法线夹角为 ω：

$\cos {{\omega }} = \frac{{{{{n}}_1}\cos {{A}}\cos {{E}} + {{{m}}_1}\sin {{A}}\cos {{E}}}}{{\sqrt {{{n}}_1^2 + {{m}}_1^2} }}\text{。}$

设中间向量 $\left( {{{{m}}_5},{{{n}}_5},{{{k}}_5}} \right)$ ，当cosω $\geqslant$ 0时， ${{{m}}_5} = {{{n}}_1}$ ， ${{{n}}_5} = - {{{m}}_1},{{{k}}_5} = 0$ ，当cosω<0时， ${{{m}}_5} = - {{{n}}_1},{{{n}}_5} = {{{m}}_1},$ ${{{k}}_5} = 0$ 。

将 $\left( {{{{m}}_5}{\rm{,}}{{{n}}_5}{\rm{,}}0} \right)$ 单位化后得旋转方位线OS方向向量，记为 $\left( {{{{m}}_6},{{{n}}_6},0} \right)$ 。

设旋转方位线OS（方位向量 $\left( {{{{m}}_6},{{{n}}_6},0} \right)$ ）与正北线OX（方向向量（1，0，0））夹角为α：

$\cos {{\alpha }} = \frac{{{{{m}}_6}}}{{\sqrt {{{m}}_6^2 + {{n}}_6^2} }}\text{。}$

波束旋转方位角A′为：

当m₆ $\leqslant$ 0时， ${{{A}}'} = {{\alpha }} = {\cos ^{ - 1}}\left( {\displaystyle\frac{{{{{m}}_6}}}{{\sqrt {{{m}}_6^2 + {{n}}_6^2} }}} \right)$ ，当m₆>0时， ${{{A}}^{\rm{'}}} = 2{{π }} - {{\alpha }} = 2{{π }} - {\cos ^{ - 1}}\left( {\displaystyle\frac{{{{{m}}_6}}}{{\sqrt {{{m}}_6^2 + {{n}}_6^2} }}} \right)$ 。

2.6 波束旋转角φ

过天线法线（方向向量 $\left( {\cos {{A}}\cos {{E}}, - \sin {{A}}\cos {{E}},\sin {{E}}} \right)$ ）的铅垂面方程为：

$\sin {{A}}\cos {{Ex}} + \cos {{A}}\cos {{Ey}} = 0$ （过z轴）。

由2.2节可知，过天线法线垂直于甲板面的平面方程为：

${{{m}}_1}{{x}} + {{{n}}_1}{{y}} + {{{k}}_1}{{z}} = 0\text{，}$

可得：

$\cos {{\varphi }} = \frac{{\left| {{{{m}}_1}\sin {{A}}\cos {{E}} + {{{n}}_1}\cos {{A}}\cos {{E}}} \right|}}{{\sqrt {{{\left( {\sin {{A}}\cos {{E}}} \right)}^2} + {{\left( {\cos {{A}}\cos {{E}}} \right)}^2}} \sqrt {{{m}}_1^2 + {{n}}_1^2 + {{k}}_1^2} }}\text{。}$

当雷达天线法线（方向向量 $(\cos {{A}}\cos {{E}}, - \sin {{A}}\cos {{E}},$ $\sin {{E}})$ ）在水平面上方时：

$\sin {{E}} > 0,\left| {{{A'}} - {{A}}} \right|\left\langle {180,{{A'}}} \right\rangle A$ 时：

${{\varphi }} \!=\! {\cos ^{ - 1}}\left( {\displaystyle\frac{{\left| {{{{m}}_1}\sin {{A}}\cos {{E}} + {{{n}}_1}\cos {{A}}\cos {{E}}} \right|}}{{\sqrt {{{\left( {\sin {{A}}\cos {{E}}} \right)}^2} + {{\left( {\cos {{A}}\cos {{E}}} \right)}^2}} \sqrt {{{m}}_1^2 + {{n}}_1^2 + {{k}}_1^2} }}} \right)\text{，}$

$\sin {{E}} > 0,\left| {{{A'}} - {{A}}} \right| < 180,{{A'}} < A$ 时：

${{\varphi }} \!=\!- {\cos ^{ - 1}}\left( {\displaystyle\frac{{\left| {{{{m}}_1}\sin {{A}}\cos {{E}} + {{{n}}_1}\cos {{A}}\cos {{E}}} \right|}}{{\sqrt {{{\left( {\sin {{A}}\cos {{E}}} \right)}^2} + {{\left( {\cos {{A}}\cos {{E}}} \right)}^2}} \sqrt {{{m}}_1^2 + {{n}}_1^2 + {{k}}_1^2} }}} \right)\text{，}$

$\sin {{E}} > 0,\left| {{{A'}} - {{A}}} \right| > 180,{{A'}} > A$ 时：

${{\varphi }} = - {\cos ^{ - 1}}\left( {\displaystyle\frac{{\left| {{{{m}}_1}\sin {{A}}\cos {{E}} + {{{n}}_1}\cos {{A}}\cos {{E}}} \right|}}{{\sqrt {{{\left( {\sin {{A}}\cos {{E}}} \right)}^2} + {{\left( {\cos {{A}}\cos {{E}}} \right)}^2}} \sqrt {{{m}}_1^2 + {{n}}_1^2 + {{k}}_1^2} }}} \right)\text{，}$

$\sin {{E}} > 0,\left| {{{A'}} - {{A}}} \right| > 180,{{A'}} < A$ 时：

${{\varphi }} = {\cos ^{ - 1}}\left( {\displaystyle\frac{{\left| {{{{m}}_1}\sin {{A}}\cos {{E}} + {{{n}}_1}\cos {{A}}\cos {{E}}} \right|}}{{\sqrt {{{\left( {\sin {{A}}\cos {{E}}} \right)}^2} + {{\left( {\cos {{A}}\cos {{E}}} \right)}^2}} \sqrt {{{m}}_1^2 + {{n}}_1^2 + {{k}}_1^2} }}} \right);$

当雷达天线法线（方向向量 $( \cos {{A}}\cos {{E}}, - \sin {{A}}\cos {{E}}, $ $\sin {{E}})$ ）在水平面下方时：

$\sin {{E}} < 0,\left| {{{A'}} - {{A}}} \right|\left\langle {180,{{A'}}} \right\rangle A$ 时：

${{\varphi }} = - {\cos ^{ - 1}}\left( {\displaystyle\frac{{\left| {{{{m}}_1}\sin {{A}}\cos {{E}} + {{{n}}_1}\cos {{A}}\cos {{E}}} \right|}}{{\sqrt {{{\left( {\sin {{A}}\cos {{E}}} \right)}^2} + {{\left( {\cos {{A}}\cos {{E}}} \right)}^2}} \sqrt {{{m}}_1^2 + {{n}}_1^2 + {{k}}_1^2} }}} \right)\text{，}$

$\sin {{E}} < 0,\left| {{{A'}} - {{A}}} \right| < 180,{{A'}} < A$ 时：

${{\varphi }} = {\cos ^{ - 1}}\left( {\displaystyle\frac{{\left| {{{{m}}_1}\sin {{A}}\cos {{E}} + {{{n}}_1}\cos {{A}}\cos {{E}}} \right|}}{{\sqrt {{{\left( {\sin {{A}}\cos {{E}}} \right)}^2} + {{\left( {\cos {{A}}\cos {{E}}} \right)}^2}} \sqrt {{{m}}_1^2 + {{n}}_1^2 + {{k}}_1^2} }}} \right)\text{，}$

$\sin {{E}}\left\langle {0,\left| {{{A'}} - {{A}}} \right|} \right\rangle 180,{{A'}} > A$ 时：

${{\varphi }} = {\cos ^{ - 1}}\left( {\displaystyle\frac{{\left| {{{{m}}_1}\sin {{A}}\cos {{E}} + {{{n}}_1}\cos {{A}}\cos {{E}}} \right|}}{{\sqrt {{{\left( {\sin {{A}}\cos {{E}}} \right)}^2} + {{\left( {\cos {{A}}\cos {{E}}} \right)}^2}} \sqrt {{{m}}_1^2 + {{n}}_1^2 + {{k}}_1^2} }}} \right)\text{，}$

$\sin {{E}}\left\langle {0,\left| {{{A'}} - {{A}}} \right|} \right\rangle 180,{{A'}} < A$ 时：

${{\varphi }} = - {\cos ^{ - 1}}\left( {\displaystyle\frac{{\left| {{{{m}}_1}\sin {{A}}\cos {{E}} + {{{n}}_1}\cos {{A}}\cos {{E}}} \right|}}{{\sqrt {{{\left( {\sin {{A}}\cos {{E}}} \right)}^2} + {{\left( {\cos {{A}}\cos {{E}}} \right)}^2}} \sqrt {{{m}}_1^2 + {{n}}_1^2 + {{k}}_1^2} }}} \right);$

当 ${{A'}} = A$ 时， ${{\varphi }} = 0$ 。

3 数据验证

验证推导公式，当P，R，E，A分别过奇点时，可用其近似值代替；如0用0.001代替，这样既可避免推导过程中出现无穷大值（公式分母为0），又不会影响验证结果。

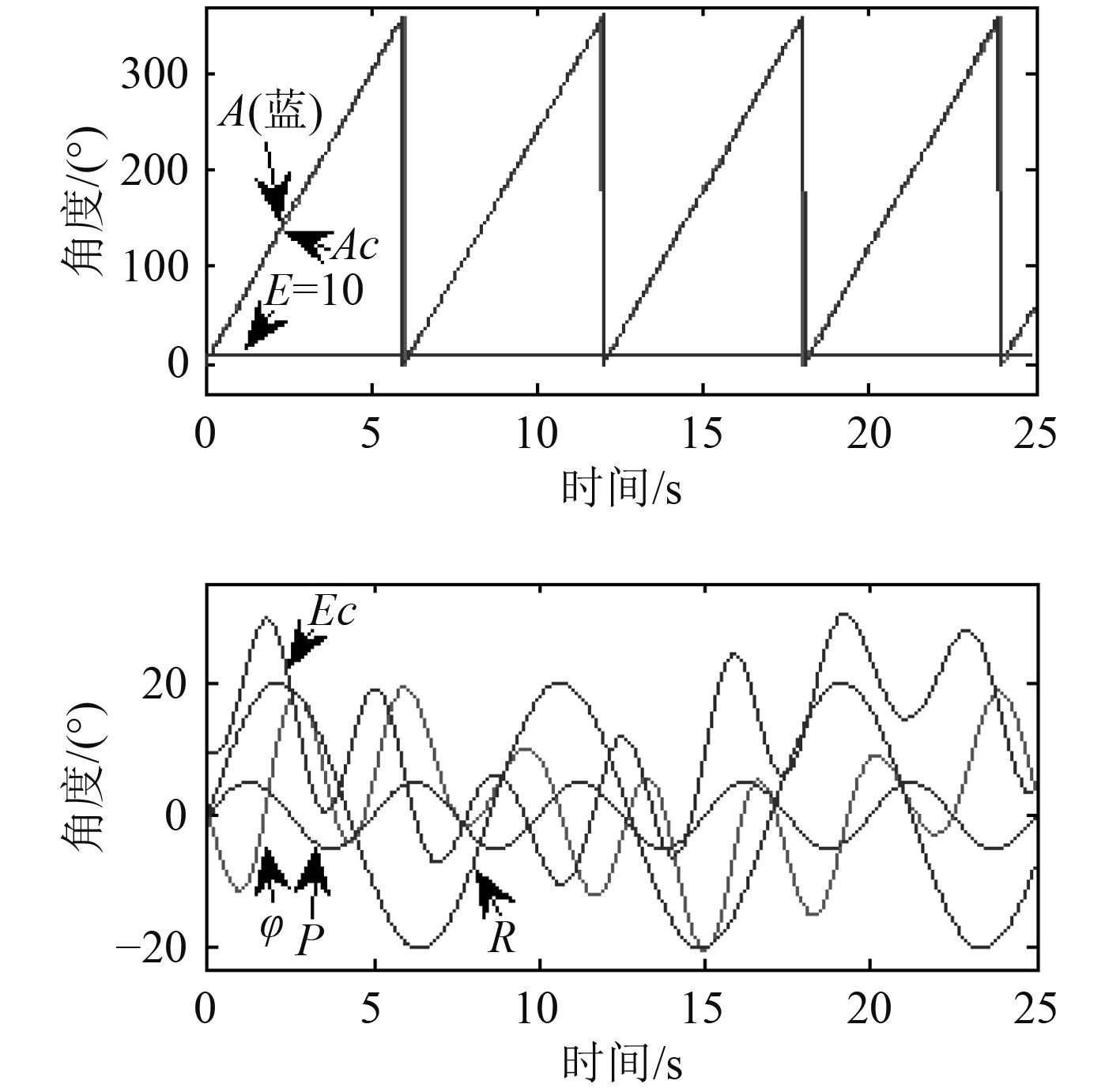
设纵摇是幅值5°，周期5 s的正弦信号，横摇是幅值20°，周期8.5 s正弦信号，方位增量为60°/s，俯仰值E=+10°，雷达转台系统数据见图6，数据与工程实践相符。

4 结 语

本文推导出已知平台罗经数据（P，R）和雷达天线法线姿态角（A，E）时两轴转台系统稳定方程和波束旋转角 φ 的方程，为舰载雷达两轴转台系统伺服控制和雷达波束相关补偿提供理论依据。