2. 哈尔滨工程大学 水声技术重点实验室,黑龙江 哈尔滨 150001
2. Acoustic Science and Technology Laboratory, Harbin Engineering University, Harbin 150001, China
声呐对目标检测是通过接收的信号与检测门限比较做出决断,在复杂海洋环境下,主动声呐接收的目标回波信号往往淹没在噪声或混响中。
在实际工作中,即使目标的运动状态比较理想,声呐工作正常,也不能保证接收到的测量数据不存在野点,造成野点的原因有很多,由于野点的存在,使有价值的信号处于野点的淹没中,为了使声呐能探测远距离被野点湮没的目标,检测门限就需要降低,但与此同时又增加了从野点中拣选出有价值信号的难度。对于传统的水声目标检测与跟踪的整个过程而言,需要对目标回波进行匹配滤波,但海洋环境复杂,由鱼群、气泡,舰船等反射的回波经匹配滤波处理后形成较高的虚警,严重干扰了人工对目标真实轨迹的判决。如何实现声呐设备自动剔除野点,对有价值信息的目标轨迹进行数据关联,已成为当今水下目标跟踪领域研究的热点问题之一。
比较常用的数据关联算法有“最近邻”算法(NN),概率数据关联法(PDA)和Reid提出多假设跟踪(MHT)算法[1, 2],其中MHT是数据关联最优算法[3]。多假设跟踪算法根据传感器接收的量测数据推测信息源,并通过产生合并各个信息源达到轨迹延续的目的。
传统的MHT算法由于假设数目将随着时间指数增长,计算复杂度和存储数据所需空间也随之指数增长,这在工程应用上不易实现。为此要通过假设删除,固定滑窗等技术进行优化。本文首先介绍了传统的MHT算法,而后研究针对传统多假设跟踪改进算法m-MHT,并以Murty算法作为其假设管理的核心,在不必计算所有观测值与假设值对应关系的情况下,得到m个最优的假设关系,抑制假设数目随时间指数增长的关系,降低MHT的计算量。通过数据仿真结果表明该算法计算简单,工程应用前景广阔。
1 多假设跟踪原理多假设跟踪的思想基于检测前跟踪思想而来。对每个新接收到的测量,先不通过检测门限进行筛选,而是通过一个延迟判决,建立多个候选假设,通过假设的产生、假设概率计算最后形成假设判决剪枝来实现数据关联。在这个过程中,MHT算法中提出“聚簇”的概念。聚族可以看成目标与量测之间的一种隶属关系。声呐探测目标时,可将探测范围内的目标和量测分割成若干独立的“簇”,这样就把大规模跟踪问题化解为若干小规模跟踪问题来处理。
m-MHT算法是Ingema等在Reid的MHT算法基础上,结合寻找分配问题m个最优解的方法,提出的一种次优MHT算法[4],用以改善MHT算法运算速度,使其达到工程应用的标准。其中心思想在于通过采用一定的约简方法,在一个时间滑窗范围内剔除概率低的假设,只存留m个最优假设,来达到抑制假设数随时间指数增长的目的。给定k–1时刻的
m-最优MHT算法主要包括7个关键步骤:
1)初始化先验目标。包括对先验各个目标状态的初始化和初始假设的生成。
2)接收量测数据集。包括目标量测数据及干扰数据。
3)目标时刻更新。
4)聚族的形成(CLUSTR)。“聚族”是彼此相交跟踪门的最大集合,其内在目标和量测存在一定的关联关系[5]。MHT方法主要研究对象是基于聚而形成的假设和目标,聚中包含了可能的航迹及这些航迹相关联的量测。如果k时刻的某一量测分别与k–1时刻任意2个聚相关,则这2个聚可看成是一个“超聚”。定义聚矩阵M(k)为:
|
$\begin{array}{l}{ M}\left( k \right) = \left[ {{v_{jt}}} \right],j = 1,2, \ldots \ldots {m_k};\\t = 0,1 \ldots \ldots T,T + 1, \ldots \ldots ,T + {m_k}\text{。}\end{array}$
|
(1) |
式中:T为k时刻已知的目标数目,mk为k时刻的所有量测总数。
5)假设生成(HYPGEN)。假设生成的过程即形成新的关联假设,并对假设概率进行计算,更新各个假设的量测关联。需要注意假设是若“聚簇”内一组量测和目标互相关联,同一个聚簇内可存在若干个假设,同时每个假设还可存在若干个相容的聚族。故假设生成必须遵循以下2个原则,首先在聚矩阵的每一行,选出且仅选出一个作为可行假设矩阵在该行唯一的非零元素,保证每个量测有唯一的源。其次,在得到的可行假设矩阵中,除第一列外,每列最多只能有一个非零元素,保证每个目标最多只有一个量测以其为源[5]。
假设Ωk表示直到k时刻的关联假设集,
|
${\varTheta ^{k,l}} = \{ {\varTheta ^{k - 1,s}},{\theta _k}\}\text{,} $
|
(2) |
利用贝叶斯公式,假设
|
$\begin{split}& p({\varTheta ^{k,l}}/{Z^k}) = p({Z^k}/{\theta _k},{\varTheta ^{k - 1,s}},{Z^{k - 1}}) = \displaystyle\frac{1}{c}p \\& ({Z^k}/{\theta _k}\! ,{\varTheta ^{k \! - \! 1,s}}\! ,{Z^{k \! - \! 1}})p({\theta _{^k}}/{\varTheta ^{k \! - \! 1,s}}\! ,{Z^{k \! - \! 1}})p({\varTheta ^{k \! - \! 1,s}}/{Z^{k \! - \! 1}})\text{,}\!\!\!\!\!\end{split}$
|
(3) |
其中
当量测
|
$p({Z^k}/{\theta _k},{\Theta ^{k - 1,s}},{Z^{k - 1}}) = {V^{ - (\psi + v)}}\mathop \Pi \limits_{i = 1}^{{m_k}} {({\Lambda _{k,i}})^{{\tau _i}}}\text{,} $
|
(4) |
其中
|
$\begin{array}{l}p({\theta _k}/{\varTheta ^{k - 1,s}},{Z^{k - 1}}) = \\p({\theta _k}/\delta ({\theta _k}),\psi ({\theta _k}),v({\theta _k}))p(\delta ({\theta _k}),\psi ({\theta _k}),v({\theta _k}))\text{。}\end{array}$
|
(5) |
式中:
|
$\begin{split}& p({\Theta ^{k,l}}/{Z^k}) = \displaystyle\frac{1}{c}\frac{{\varPhi !\upsilon !}}{{{m_k}!}}{\mu _n}(\upsilon ({\theta _k})){\mu _f}(\Phi ({\theta _k})) \times \\& \prod {{{(p_D^t)}^{{\delta _t}({\theta _k})}}{{(1 - p_D^t)}^{1 - {\delta _t}({\theta _k})}} \times } \prod\limits_{i = 1}^{{m_k}} {{{({ \wedge _{k,i}})}^{{\tau _i}}}} p({\Theta ^{k,l}}/{Z^k})\text{。} \end{split}$
|
(6) |
其中
6)假设管理
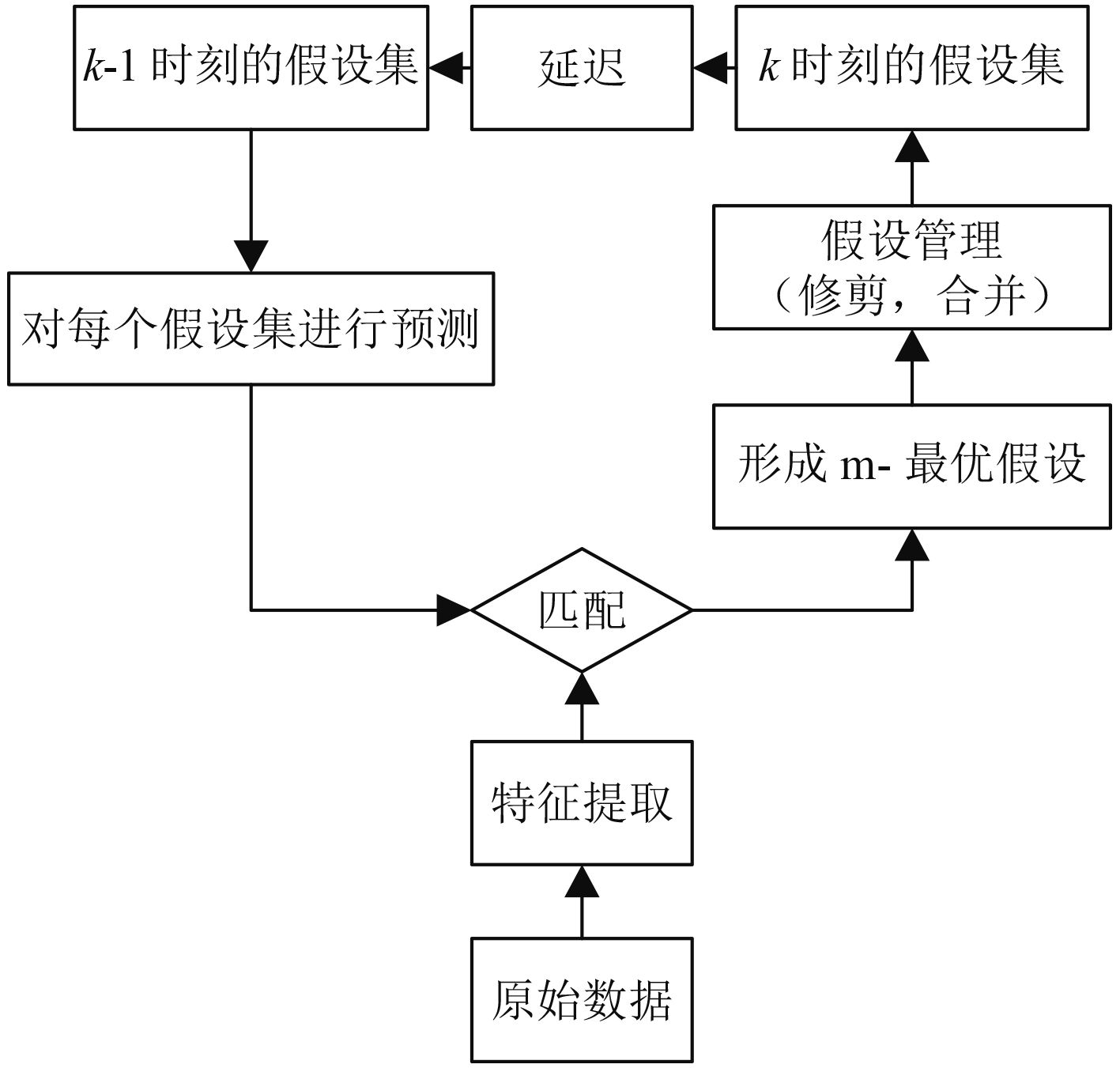
为缩减MHT算法运算时间以实现工程应用,需要对由假设生成的假设树进行约简即为假设管理。通过假设管理,可对接收到的部分时强时弱干扰杂波进行过滤,对不稳定回波进行筛选,只保留假设概率最高的若干假设[7]。基于MHT算法有多种假设管理方法,可对生成的假设进行剪枝,以筛选出概率最大的目标轨迹。本文选用的Mutry算法可较快速的找到最优的假设分配关联却不用计算所有假设分配概率进行逐一比较[8]。具体的m-最优假设形成如图1所示。
|
图 1 MHT假设管理 Fig. 1 MHT hypothesis management |
Murty[9]算法是在不用计算所有假设的概率情况下,筛选m个概率最大假设的方法。m的大小由系统资源决定,系统的存贮空间和计算能力大时,可以取大的m值。m越大则搜索速度越慢,但会搜索更加精确。
具体实现步骤如下:
1)找出第k时刻目标的量测值,建立权值矩阵。
2)利用匈牙利算法[9],找出m个概率最大的目标与量测值的关联。
3)计算出各个量测点与目标所属概率。
1.3 跟踪轨迹剪枝本文参考Blackman S S的剪枝法[10],通过限制对假设树的指数增长,提高算法效率。
1)轨迹树深度N表示只记录最近N个扫描周期的假设。
2)节点数M即前文Murty算法的m个概率最大关联。
|
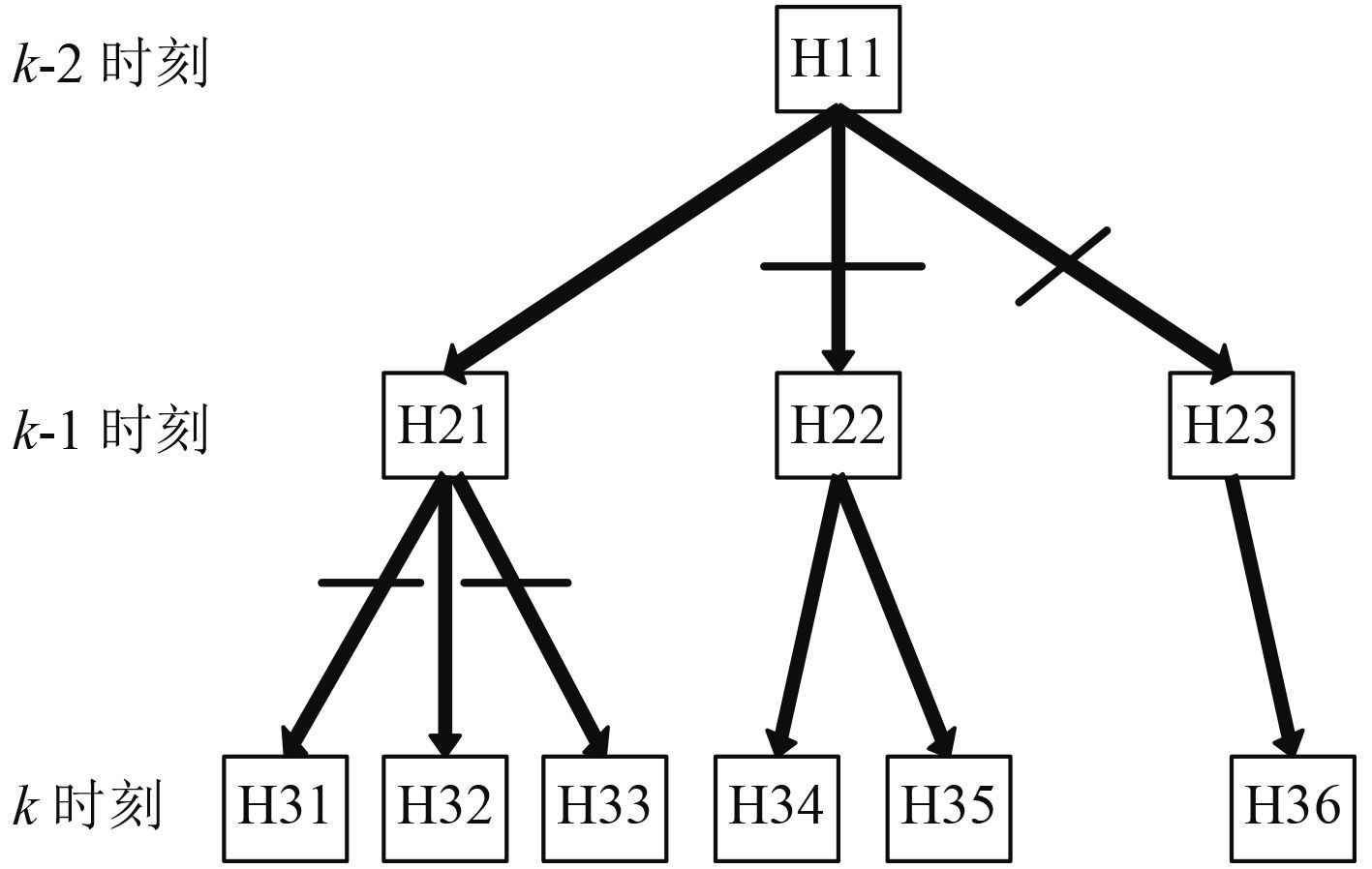
图 2 假设树剪枝 Fig. 2 MHT hypothesis trees |
图2中,假设树的深度N取2,在k时刻假设树执行剪枝,经过计算,枝叶节点H32所在路径的假设概率最高,则存留假设树的H11和H21及H32这一脉络的枝叶,删除k–2时刻根节点H22,H23节点及子节点,随时间进程以此类推,但要始终保持假设树的深度为N。
2 仿真验证与比较 2.1 精度评价指标[11]本文取多次运行的蒙特卡罗仿真的均方根误差(Root Mean Square Error,RMSE)作为衡量算法效果好坏的量化指标。单次运行的均方根误差通过下式计算:
|
$RMSE = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {{{\left( {{x_k} - \overline {{x_k}} } \right)}^2}} }\text{,} $
|
(7) |
式中:xk为目标状态真实值;
J次蒙特卡罗试验的RMSE均值:
|
$\mu = \frac{1}{J}\sum\limits_{i = 1}^J {RMS{E_i}} \text{。}$
|
(8) |
J次蒙特卡罗试验的RMSE均方差:
|
$\varsigma = \sqrt {\frac{1}{J}\sum\limits_{i = 1}^J {{{\left( {RMS{E_i} - \mu } \right)}^2}} } \text{。}$
|
(9) |
虚警环境下定位到的目标位置和接收到的杂波干扰统一用“*”表示。目标的状态矢量表示为
|
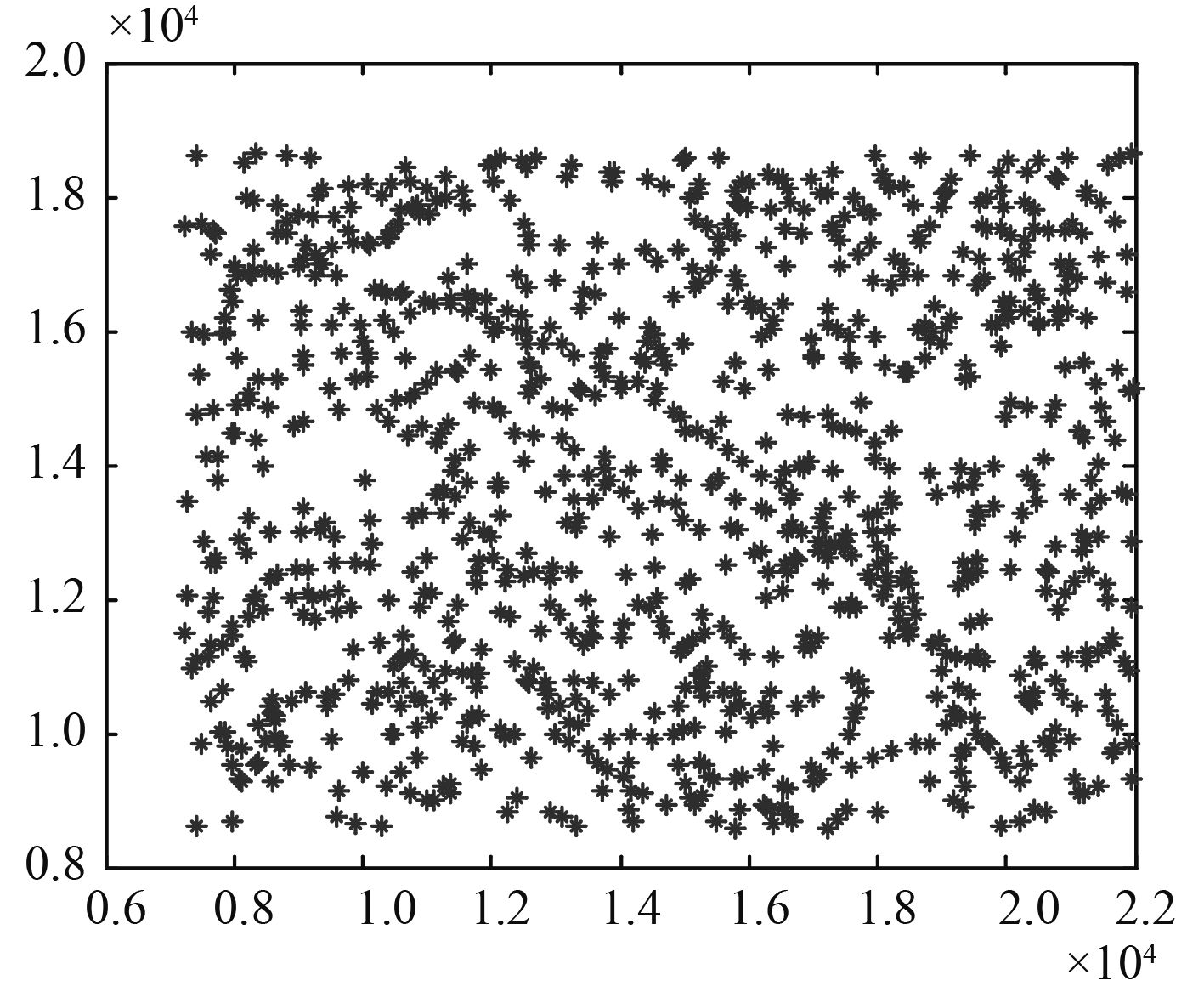
图 3 负对数数值为2E–7跟踪原始数据 Fig. 3 The negative logarithm is 2E–7 for tracking result of original data |
|
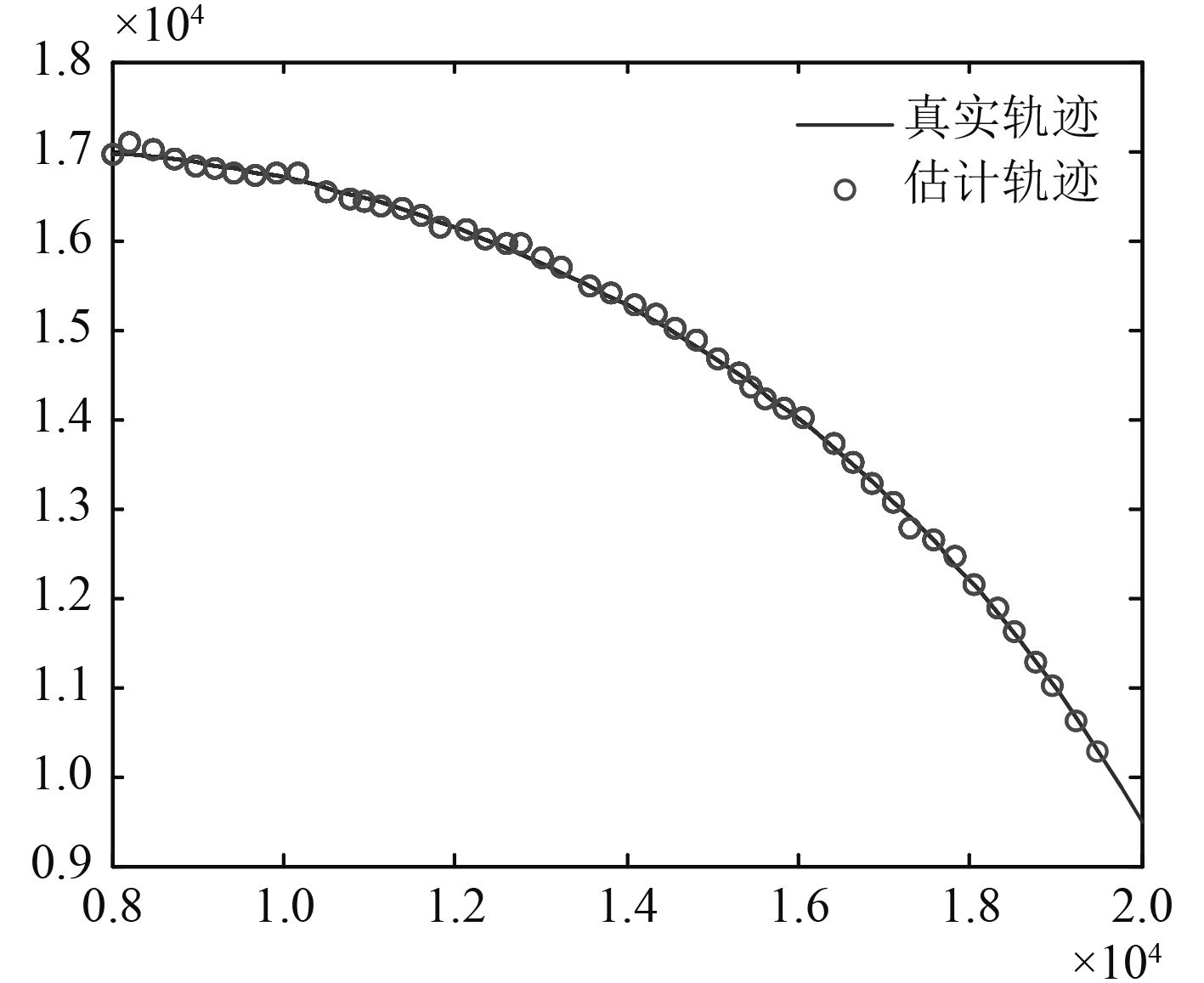
图 4 负对数数值为2E–7的基于m-MHT跟踪处理结果 Fig. 4 The negative logarithm is 2E–7 for tracking result of m-MHT |

|
图 5 负对数数值为5E–7跟踪原始数据 Fig. 5 The negative logarithm is 5E–7 for tracking result of original data |
|
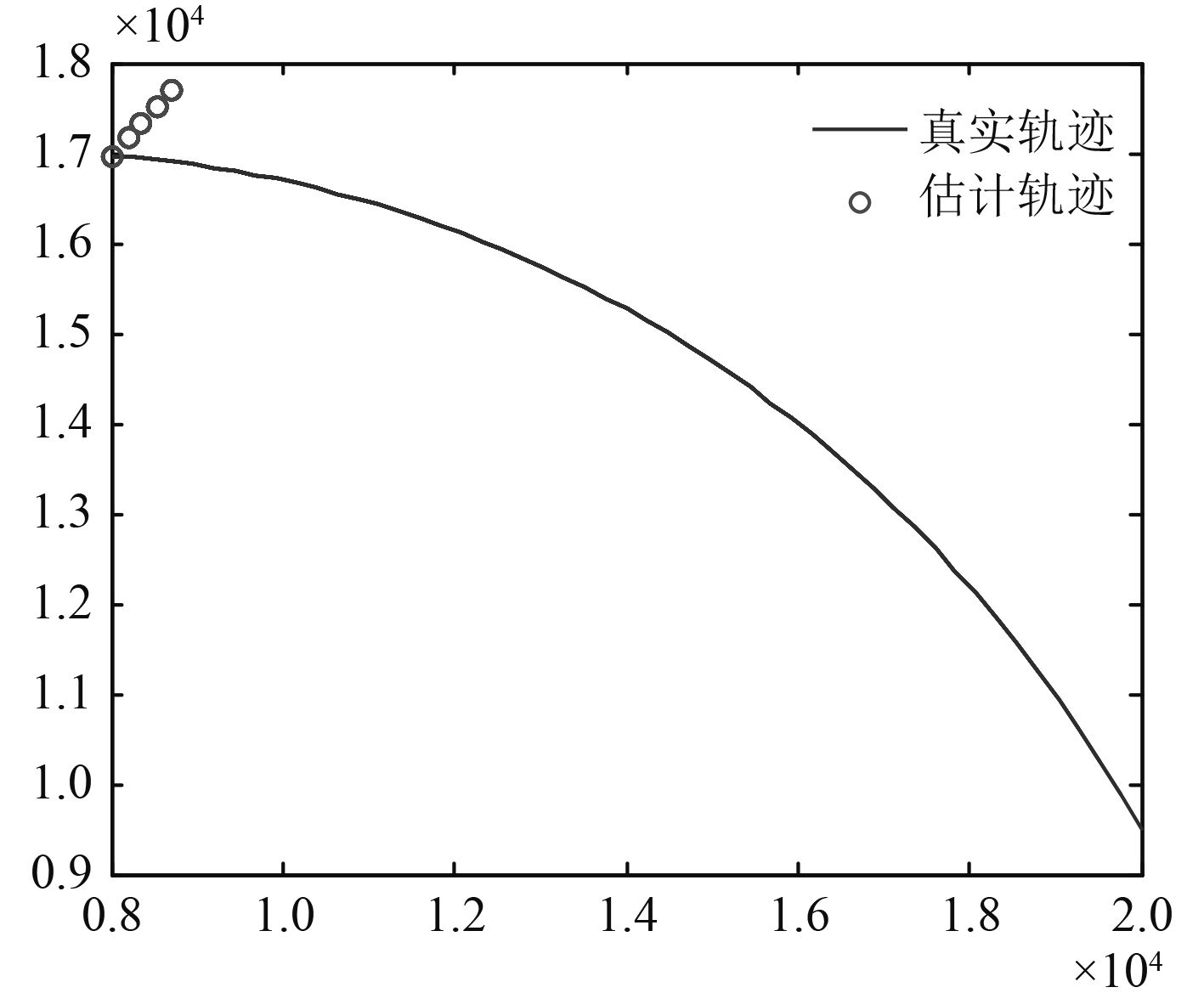
图 6 跟踪目标丢失 Fig. 6 Tracking failure |
图3中目标位置数据坐标点附近都有杂波,较多的杂波严重干扰了人工对目标进行跟踪,由于没有对接收的原始数据进行处理,目标轨迹湮没在杂波中,无法完成目标跟踪。图4为通过m-MHT算法处理后的跟踪效果图,对比图3和图4可见接收的回波具有时空连续性,m-MHT算法就是将这些具有时空连续性的回波提取出来,而无规则的杂波则被排除,采用m-MHT方法可以实现目标跟踪,同时也表明该算法可以较好的适应密集杂波环境的目标跟踪问题,图5为增大虚警情况下的原始数据,算法对目标跟踪丢失时的结果如图6所示,对于目标跟丢次数与杂波密度关系,由表1给出。
表1和表2均为不同轨迹树深度的500次蒙特卡罗仿真,态势环境参数与前文一致。表1实验只改变了杂波分布概率,随着杂波密度增加,失跟率增大,同时估计目标位置的误差RMSE也增大。表2的杂波概率负对数为2E–7的对比实验在原情景下只改变轨迹树深度N值。
|
|
表 1 不同杂波密度500次蒙特卡罗仿真对比 Tab.1 Different clutter density after 500 times monte carlo simulation |
|
|
表 2 不同轨迹树深度500次蒙特卡罗仿真对比 Tab.2 Different height of the hypothesis trees after 500 times monte carlo simulation |
通过对比表1和表2可以发现,同样的杂波分布下,增大轨迹树N的深度,可以提高跟踪成功率,但运行时间会急剧增大,同时也进一步印证了m-MHT算法对于传统的MHT算法改进的意义,即MHT要判断量测信息的来源是虚警、已有目标、新目标,还要考虑聚的生成,聚矩阵的行列维度较高,轨迹树深度N越大,算法执行时间越长,因此需要通过轨迹树深度参数来调节算法运行时间,在运行结果精度与运行时间上做取舍。
对比以上两表结果可以看出,杂波密度对算法运行效果影响比较明显,随着杂波减少,跟踪成功率和RMSE均值均有改善。
3 结 语本文m-MHT算法核心思想是基于多假设跟踪理论,通过假设约简及Murty算法寻找m个最大假设概率,进而缩减MHT运算时间。通过仿真试验数据分析,证明该算法能保证在一定跟踪成功率前提下,降低运算量,改善杂波区目标跟踪效果,使通过该算法实现声呐在杂波环境下对目标进行跟踪成为可能。
| [1] | JOHNSTON L A, KRISHNAMURTHY V. Performance analysis of a dynamic programming track before detect algorithm[J]. IEEE Transactions on Aerospace & Electronic Systems, 2002, 38 (1): 228–242. |
| [2] | REID D B. An Algorithm for Tracking Multiple Targets[J]. IEEE Transactions on Automatic Control, 2013, 24 (6): 843–854. |
| [3] | STONE L D, CORWIN T L, BARLOW C A. Bayesian multiple target tracking[M]. Artech House, Inc. 1999. |
| [4] | COX I J, MILLER M L. On Finding Ranked Assignments With Application to Multi-Target Tracking and motion Correspondence[J]. Aerospace & Electronic Systems IEEE Transactions on, 1996, 31 (1): 486–489. |
| [5] |
彭冬亮. 多传感器多源信息融合理论及应用[M]. 北京: 科学出版社. 2010. 166–169.
PENG Dong-liang. Multi-sensor multi-source information fusion theory and application [M]. Bei-jing: Science Press, 2010: 166–169. |
| [6] |
潘泉. 多源信息融合理论及应用[M]. 北京: 清华大学出版社. 2013. 420–425.
PAN Quan. Multi-source information fusion theory and its application [M]. Beijing: Tsinghua University Press, 2013: 166–169. |
| [7] |
翟海涛. 多假设跟踪算法研究及其应用[J]. 信息化研究, 2010, 36 (8): 25–27.
ZHAI Hai-tao. Reseach on Multiple Hypothesis Tracking Algorithm and Its Application[J]. Informatization Research, 2010, 36 (8): 25–27. |
| [8] |
文云峰, 石章松, 王芳. 基于多假设的航迹关联方法研究[J]. 舰船科学技术, 2011, 32 (2): 116–120.
WEN Yun-feng, SHI Zhang-song, WANG Fang. Research on track association algorithm based on multi-hypothesis thought[J]. Ship Science and Technology, 2011, 32 (2): 116–120. |
| [9] | MURTY K G. An Algorithm for Ranking all Assignments in Order of Increasing Cost[J]. Operations Research, 1968, 16 (3): 682–687. DOI: 10.1287/opre.16.3.682 |
| [10] | BLACKMAN S S, DEMPSTER R J, ROSZKOWSKI S H. IMM/MHT applications to radar and IR multitarget tracking[J]. Proceedings of SPIE - The International Society for Optical Engineering, 1997, 3163 : 429–439. |
| [11] |
孙春艳. 被动声呐目标探测与多基地跟踪方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2013.
SUN Chun-yan. Research methods of passive sonar detection and multi-sonar tracking [D]. Harbin: Harbin Engineering University, 2013. |
 2017, Vol. 39
2017, Vol. 39
