被动声呐探测利用各种信号处理技术对接收到的舰船辐射噪声进行处理,以达到从复杂的背景噪声中检测目标的存在,并对其各种参数进行估计的目的。
随着减振降噪技术的发展,舰船辐射噪声越来越微弱。21世纪各类舰船辐射噪声的声源级由于新型隔音材料和消声瓦等的使用而不断降低。潜艇的辐射噪声级由原来的160 dB左右降到110 dB左右。美国90年代建造的SN21(海狼级)核潜艇噪声仅为95 dB,已经低于海洋环境噪声。再加之远距离传播的损失以及复杂的背景噪声的干扰,到达接收机的信号往往具有很低的信噪比。要想探测到目标并获取它的方位信息,就要尽量消除噪声的干扰。因此,要想从复杂的背景噪声中检测到目标的存在并获取相应的参数信息,同时还要尽量的远和准,就必须想办法提高信噪比。笔者在研究含噪信号的压缩感知方法时发现,压缩感知本身可以降低噪声,提高信噪比,这无疑是有利于舰船辐射信号的检测和跟踪。而要将压缩感知理论应用到舰船辐射信号的处理上,则需要后者满足压缩感知理论的基本条件。
1 压缩感知的基本理论压缩感知理论包括3个基本要素:信号的稀疏表示,观测矩阵的选择以及信号重构算法。数学表达式如下:
1)原始信号X在基底
|
$X = \mathop \sum \limits_{i = 1}^N {\theta _i}{\psi _i}\;{\rm{or}}\;X = \varPsi \varTheta \text{,}$
|
(1) |
2)利用观测矩阵
|
$Y = { \varPhi} X = \varPhi \varPsi \varTheta = {A^{CS}}\varTheta \text{,}$
|
(2) |
3)已知
|
$\hat X = {{ \varPhi} ^{ - 1}}Y\text{,}\left\{ {\text{满足}Y = {A^{CS}}\varTheta \text{的最稀疏解}} \right\}\text{。}$
|
(3) |
Candès和Tao在文献[1]中指出,信号如果在某领域的变换系数满足具有幂次速度衰减,就可以用压缩感知理论得到恢复,同时指出,光滑信号的Fourier系数、小波系数、离散余弦系数等都具有足够的稀疏性,可以通过压缩感知理论恢复信号。如果变换系数的非零个数(或绝对值较大的系数个数)为K,则称信号为K-稀疏信号,K为信号的稀疏度。
观测矩阵
信号重构就是在已知
|
${\rm min}{\varPsi ^{\rm T}}{X_p}\;\;s.t.\;\;\;Y = {\Phi} \varPsi \varTheta \text{,}$
|
(4) |
其中,
如果要将压缩感知理论应用到舰船辐射噪声,则后者需满足压缩感知理论的基本条件,即信号的稀疏性。以某类舰船噪声为例,图1是该噪声时域波形的一段,共4 800个采样点。在时域内,舰船辐射噪声显然不是稀疏信号。现分析并验证其傅里叶变换(FFT)系数以及离散余弦变换(DCT)系数的稀疏性。

|
图 1 某舰船辐射噪声信号时域波形 Fig. 1 Time-domain waveform of ship-radiated noise |
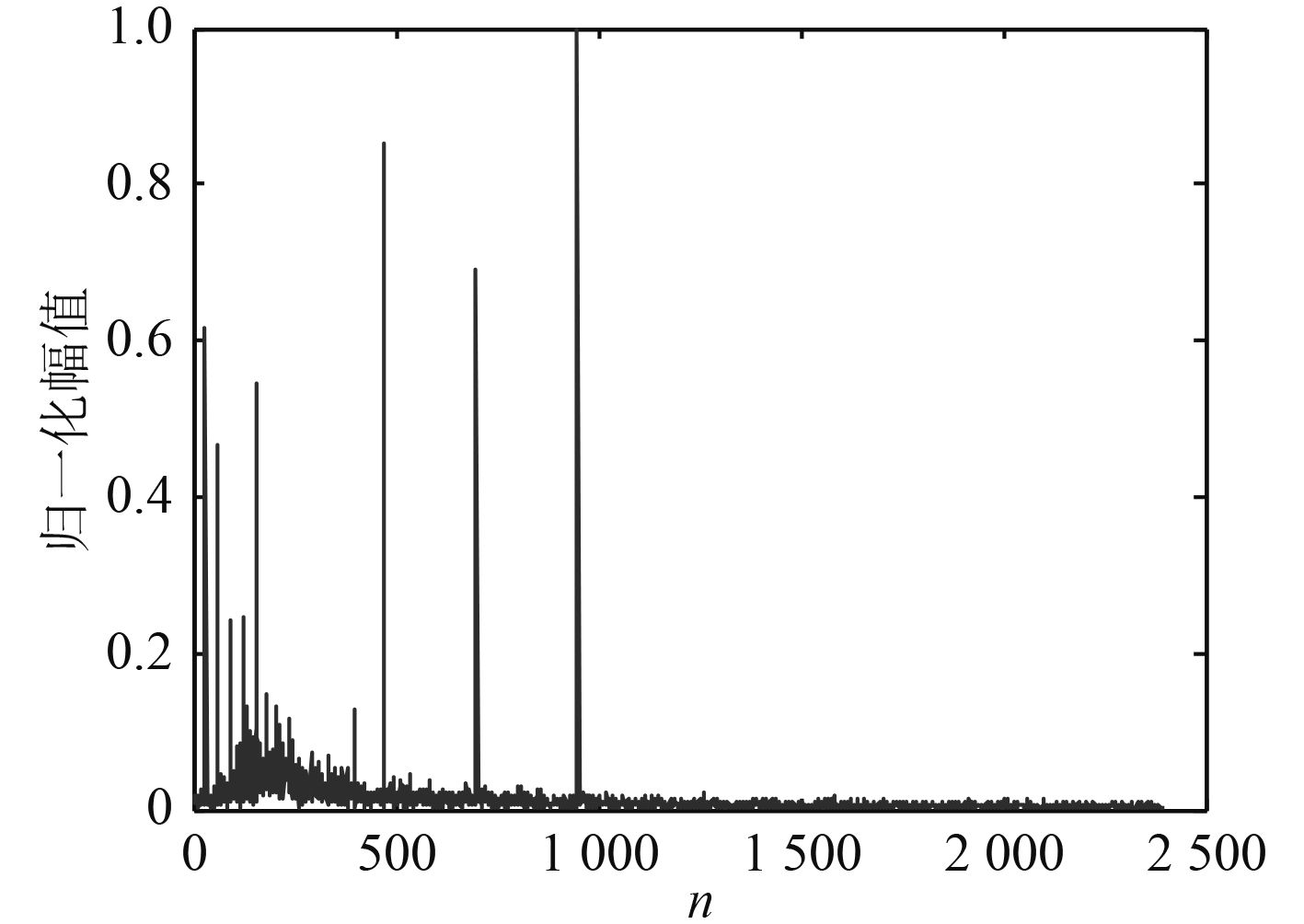
对该信号进行傅里叶变换,频域波形如图2所示。从图中可见舰船辐射噪声的频谱包括线谱和连续谱2种,且线谱幅值高于连续谱幅值。根据压缩感知理论,对于存在少量大系数和大量接近零值的小系数组成的信号也可以视为稀疏信号。利用文献[1]给出的稀疏性的定义进行验证。
|
图 2 舰船辐射噪声的频域波形 Fig. 2 Frequency-domain waveform of ship-radiated noise |
将舰船辐射噪声的傅里叶变换系数按从大到小的顺序排列,得到

|
图 3 舰船辐射噪声FFT系数衰减曲线 Fig. 3 FFT attenuation of ship-radiated noise |
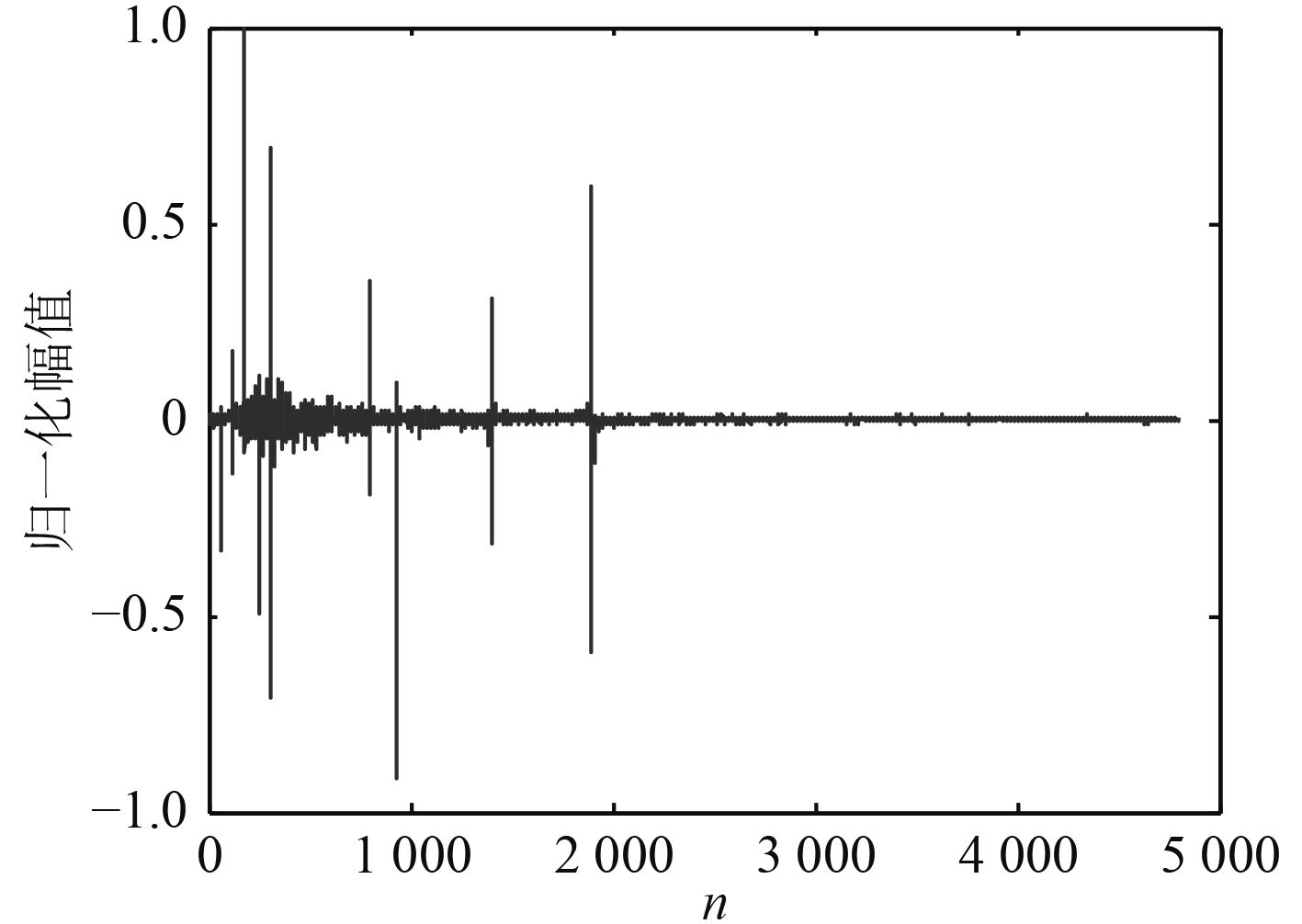
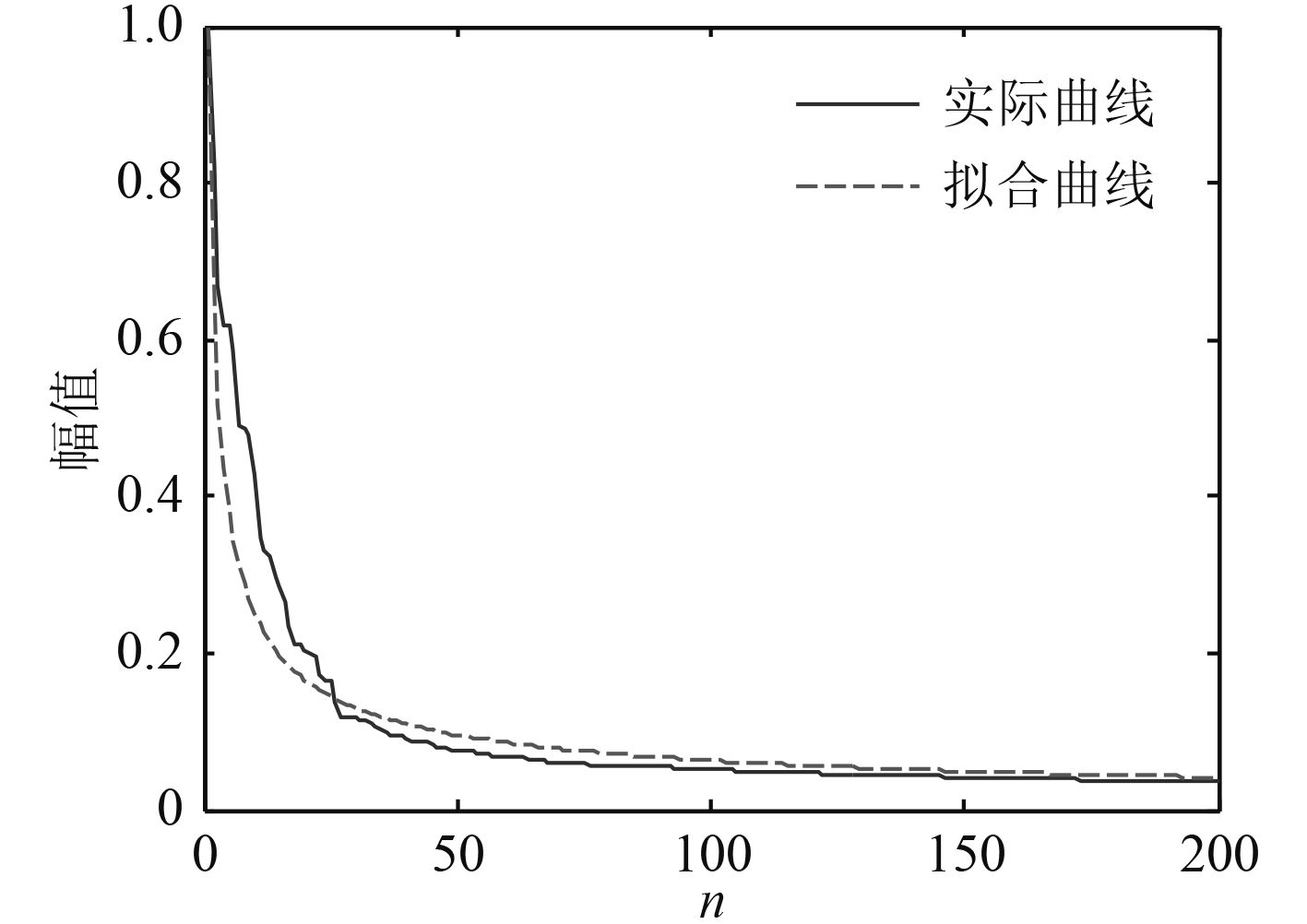
对舰船辐射噪声进行离散余弦变换,其变换系数波形如图4所示,用相同的办法验证。将该系数按从大到小排列,并对其进行指数形式的拟合,得到拟合曲线仍为
|
图 4 舰船辐射噪声的DCT波形 Fig. 4 DCT waveform of ship=radiated noise |
|
图 5 舰船辐射噪声DCT系数衰减曲线 Fig. 5 DCT attenuation of ship-radiated noise |
明显地,舰船辐射噪声在傅里叶变换下和离散余弦变换下都稀疏,可以利用压缩感知理论。
3 压缩感知的降噪性能研究笔者在将压缩感知理论应用到含有背景噪声的舰船辐射信号时发现,如果信号的变换域(稀疏空间)已知,压缩感知过程本身具有抑制噪声的功能。下面对压缩感知的降噪性能进行深入的分析与研究,并结合实际数据计算在不同信噪比下,重构效果随观测值个数的变化情况。
一般情况下,信号含有服从高斯分布的加性噪声,可建立如下数学模型:
|
$S = X + {N_0}\text{,}$
|
(5) |
其中:X为不含噪声的原始信号;
|
$\begin{array}{l}S = X + {N_0} = \mathop \sum \limits_{{\rm{i}} = 0}^N \left( {{\theta _i}{\varphi _i} + {\theta _{0i}}{\varphi _i}} \right)\text{,}\\\;\;\text{或者}S = X + {N_0} = \varPsi \left( {\Theta + {\Theta _0}} \right)\text{。}\end{array}$
|
(6) |
式中,
对于高斯噪声,
噪声的存在也使观测值发生了变化,含噪情况下观测值Y变为
|
$\hat Y = { \varPhi} X + {N_0} = {A^{CS}}\varTheta + {A^{CS}}{\varTheta _0}\text{,}$
|
(7) |
式(7)与式(2)相比,增加了一项
根据压缩感知原理,对于稀疏信号,当观测矩阵
根据以上分析,观测值
在一定重构误差要求下,不同的观测矩阵、不同的重构算法所需的观测值数目也不相同。以高斯随机观测矩阵和OMP重构算法为例,根据经验公式
仿真实例采用舰船辐射噪声信号,观测矩阵采用高斯随机矩阵,重构算法采用正交匹配追踪法。取舰船辐射噪声其中的256个采样点。
1)一定信噪比、一定观测值数目下的信号重构情况仿真
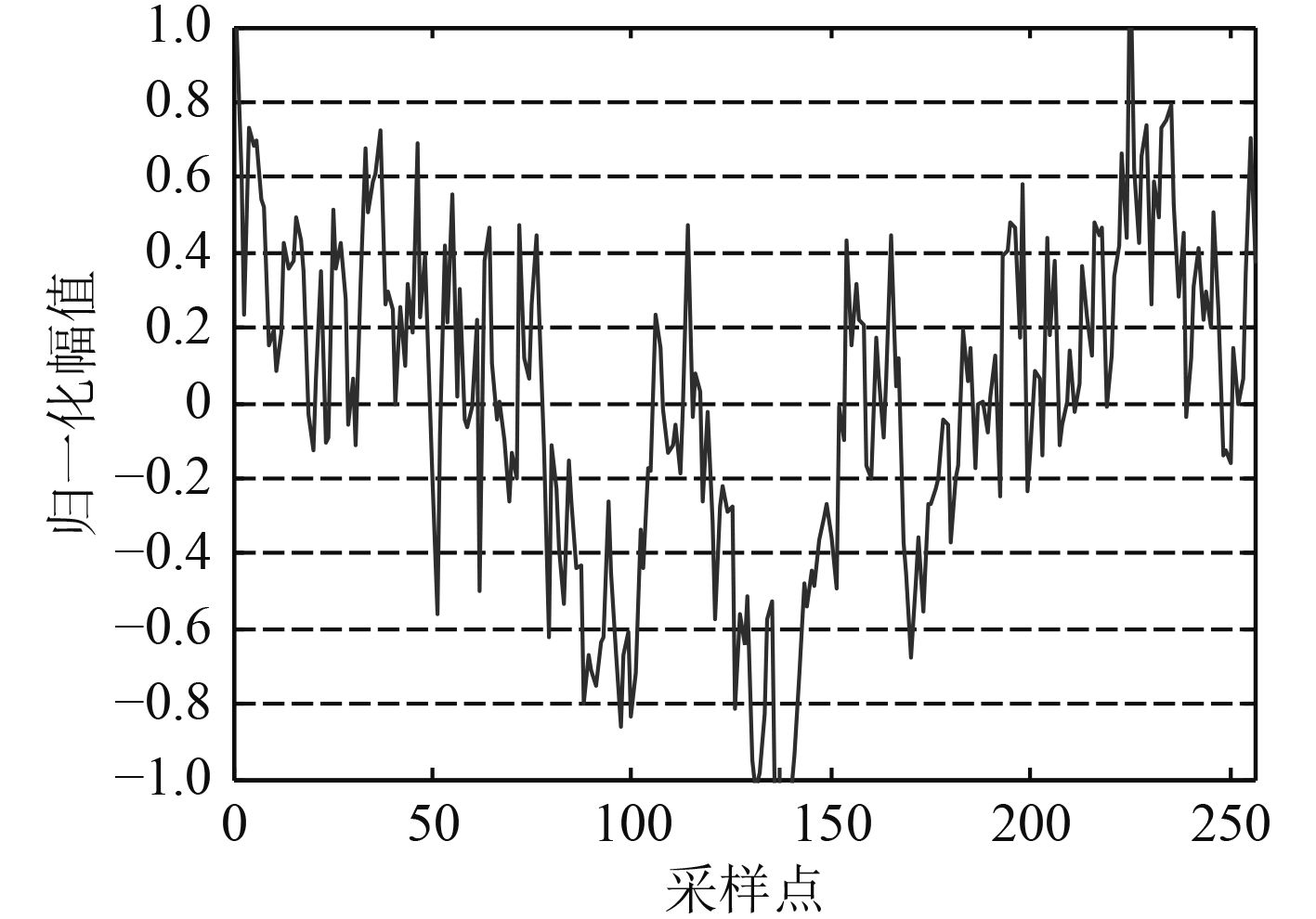
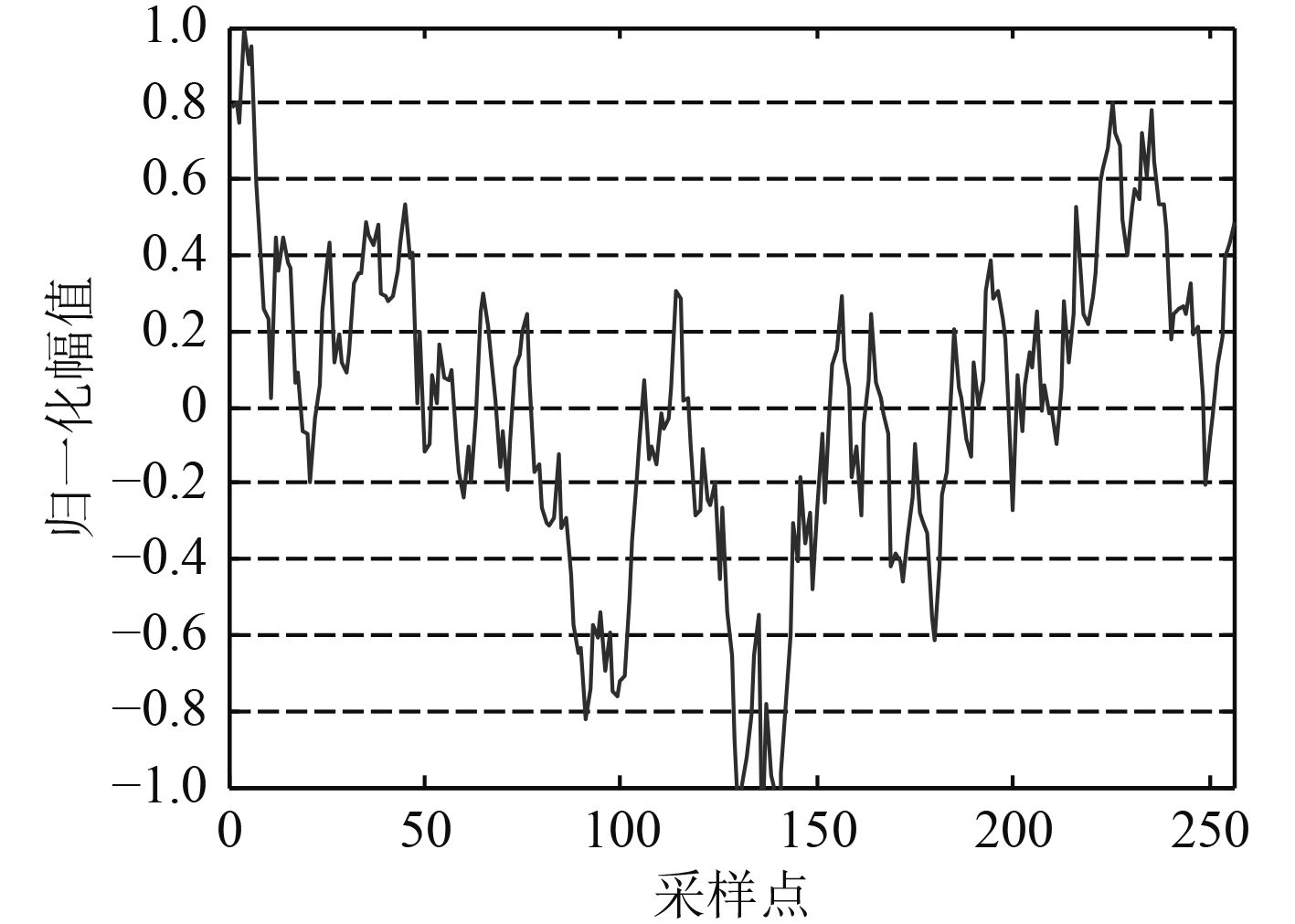
将舰船辐射噪声信号加入一定信噪比的背景噪声,取信噪比SNR=5 dB和SNR=10 dB,时域波形分别如图6和图7所示。
|
图 6 SNR=5 dB的舰船辐射信号 Fig. 6 The ship-radiated noise when SNR=5 dB |
|
图 7 SNR=10 dB的舰船辐射信号 Fig. 7 The ship-radiated noise when SNR=10 dB |
根据舰船辐射噪声的线谱组成,取稀疏度K=6,由经验公式
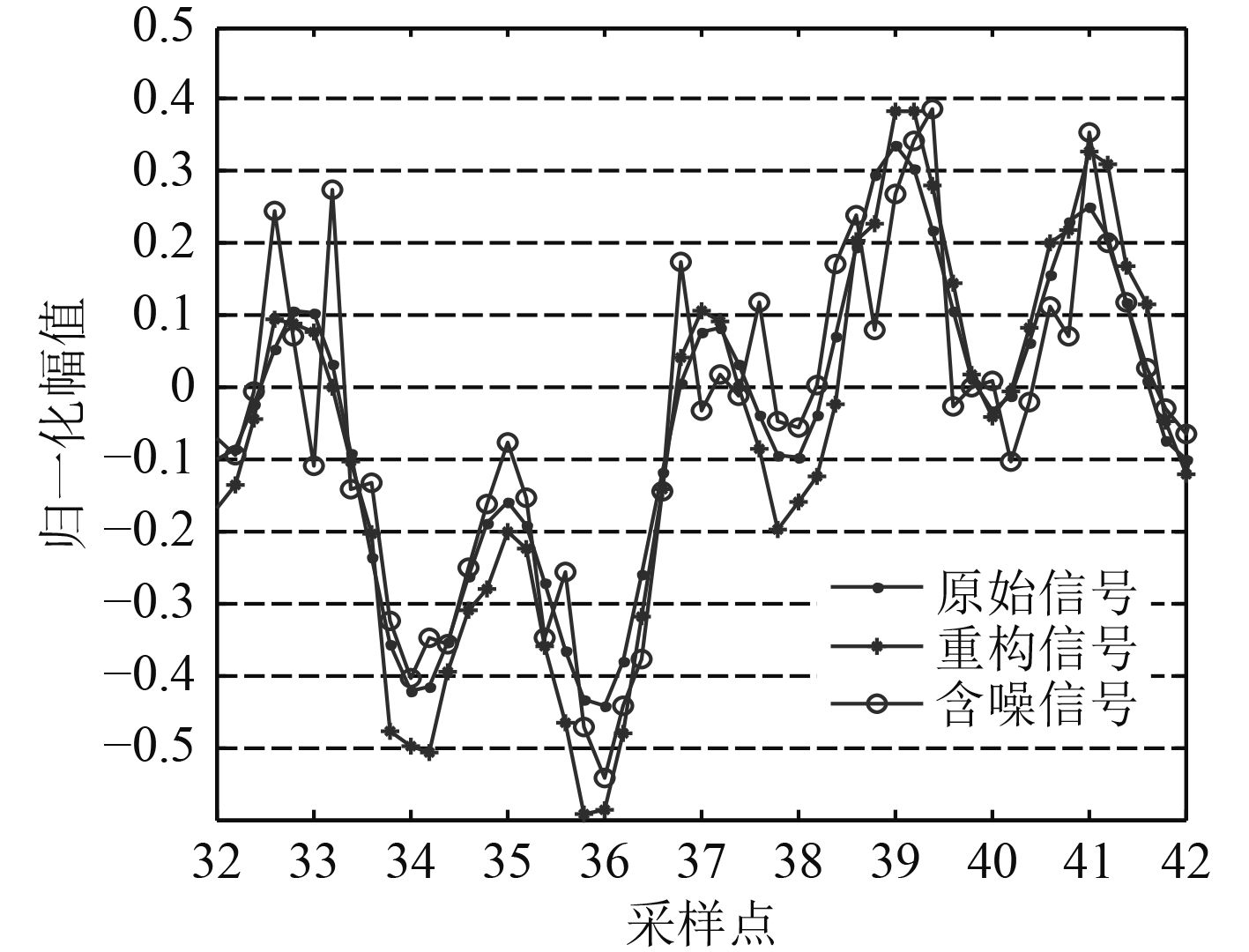
|
图 8 SNR=5 dB M=58时的重构性能 Fig. 8 The reconstruction effect when SNR=5 dB and M=58 |
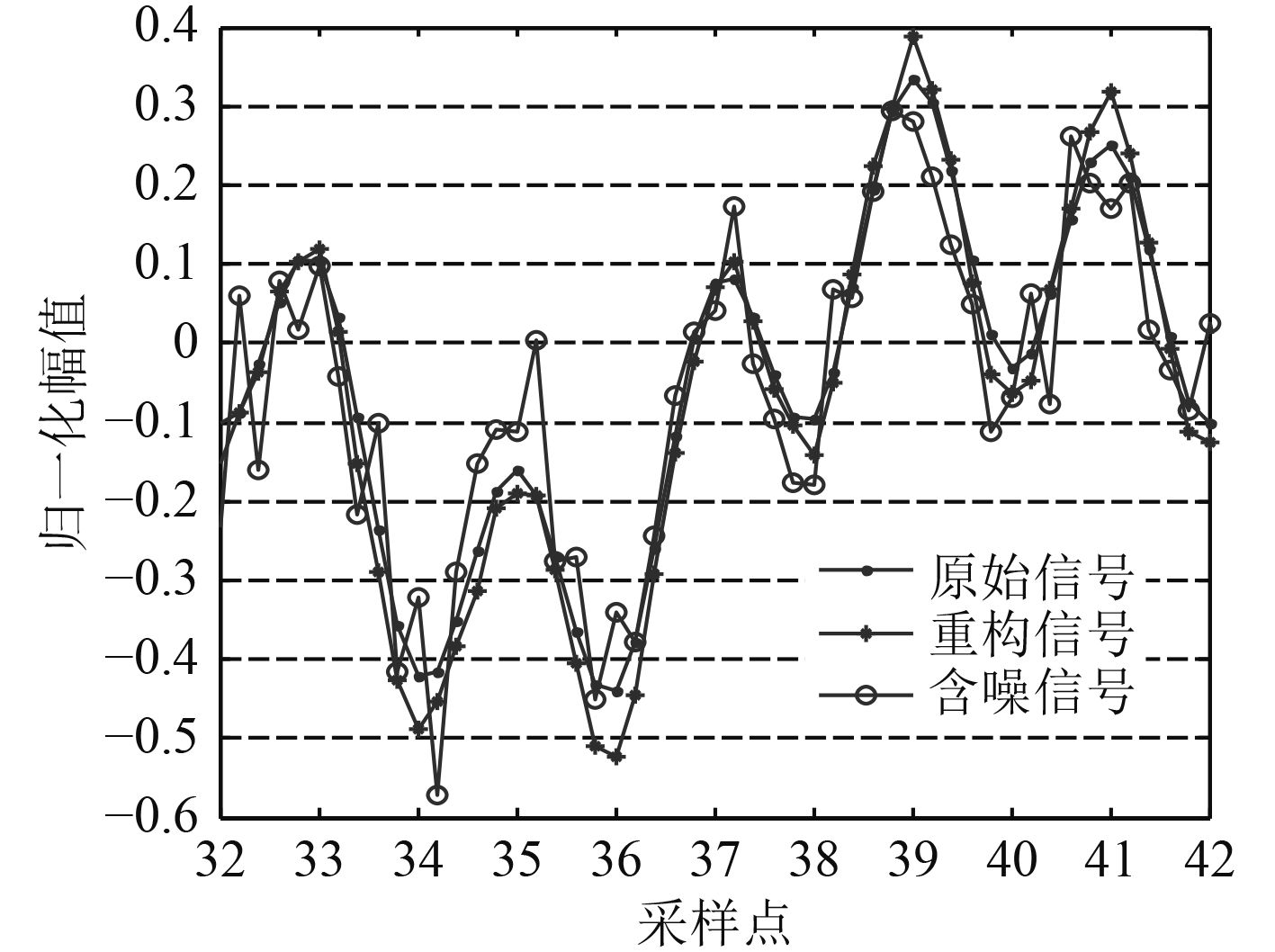
|
图 9 SNR=10 dB M=62时的重构性能 Fig. 9 The reconstruction effect when SNR=10 dB and M=62 |
图8中,SNR=5 dB,观测值数目为M=58,重构信号
图9中,SNR=10 dB,观测值数目为M=62,重构信号
2种情况下,观测值数目均小于M0,重构信号的均方误差也都小于含有背景噪声的信号误差,即重构信号比含噪信号本身更接近原始信号,压缩感知过程间接起到了提高信噪比的作用。这显然有利于舰船辐射噪声的检测与跟踪。
2)不同信噪比下,重构效果随观测值数目变化趋势的仿真
在不同信噪比条件下,需要的最佳观测值个数也不相同。为得出一定信噪比下存在的最佳压缩比,现对不同信噪比条件下重构效果随观测数目的变化情况进行仿真。重构效果的衡量采用文献[6]给出的匹配度,定义如下:
设X为原始信号,
|
${Mat}_{rate} = 1 - \frac{{{{{{\hat X}}}^{\rm{'}}} - {{{X}}^{\rm{'}}}_2}}{{{{{{\hat X}}}^{\rm{'}}} + {{{X}}^{\rm{'}}}_2}}\text{,}$
|
(8) |
从定义式可以看出,匹配度的取值一定为正,且介于0~1之间,重构信号和原始信号之间的误差越小,匹配度越大,其值越接近1,说明匹配性越好,重构效果也就越好。
分别取信噪比SNR为0 dB,5 dB,10 dB,20 dB,得到匹配度随观测值数目的变化曲线如图10~图13所示。
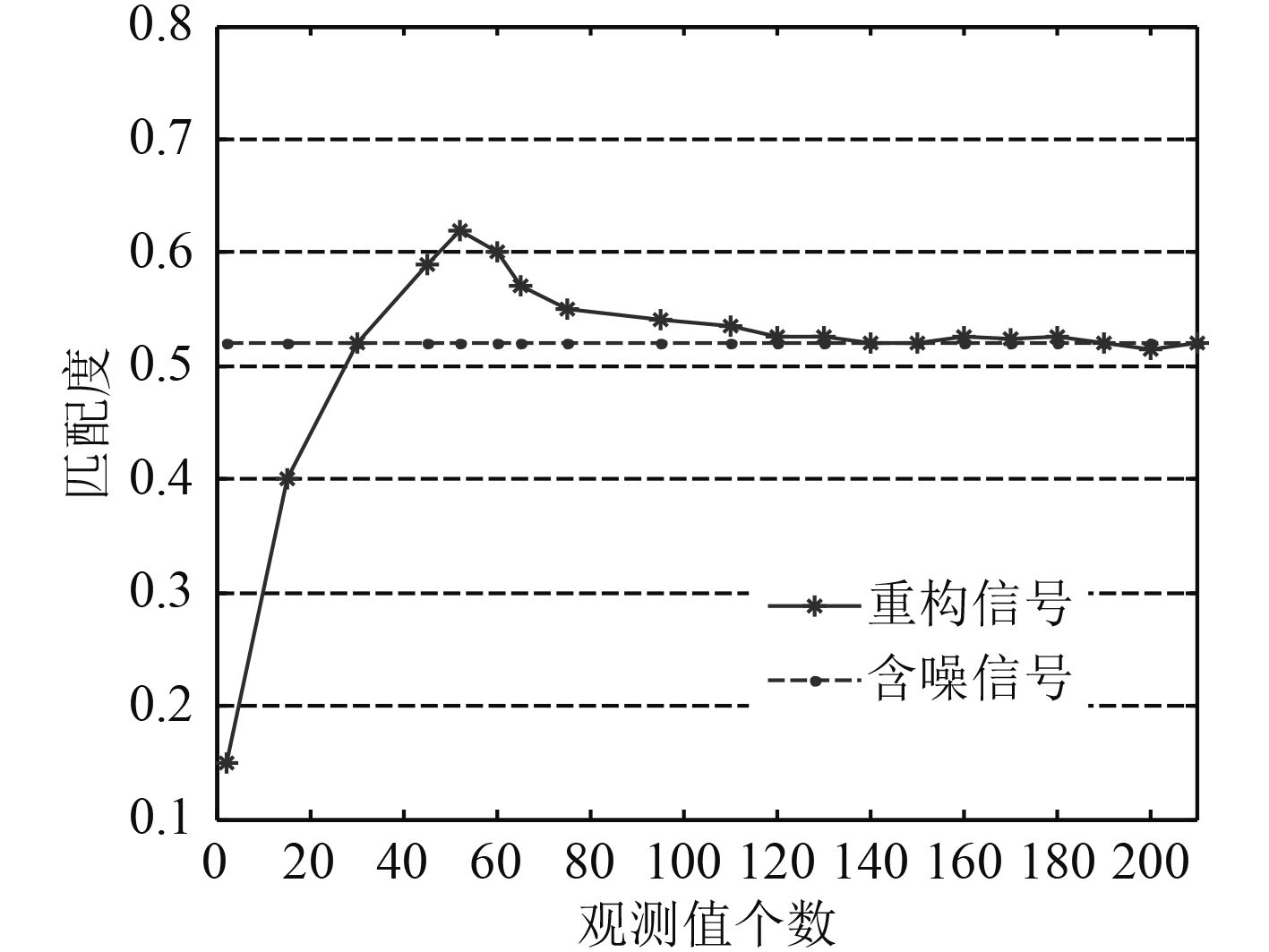
|
图 10 SNR=0 dB时匹配度随观测值变化曲线 Fig. 10 MR cure along with the number of measurements when SNR=0 dB |
|
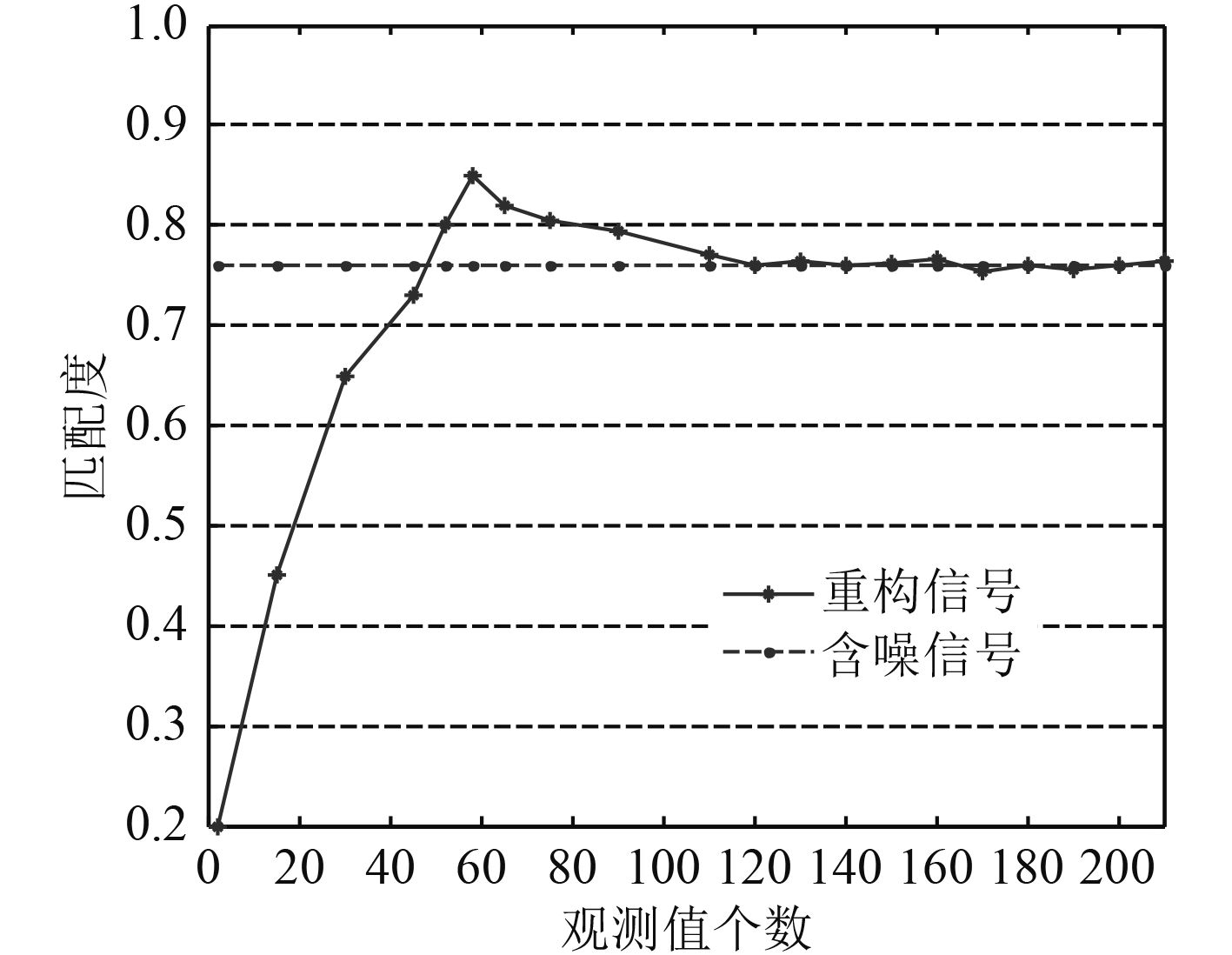
图 11 SNR=5 dB时匹配度随观测值变换曲线 Fig. 11 MR cure along with the number of measurements when SNR=5 dB |

|
图 12 SNR=10 dB时匹配度随观测值变化曲线 Fig. 12 MR cure along with the number of measurements when SNR=10 dB |
|
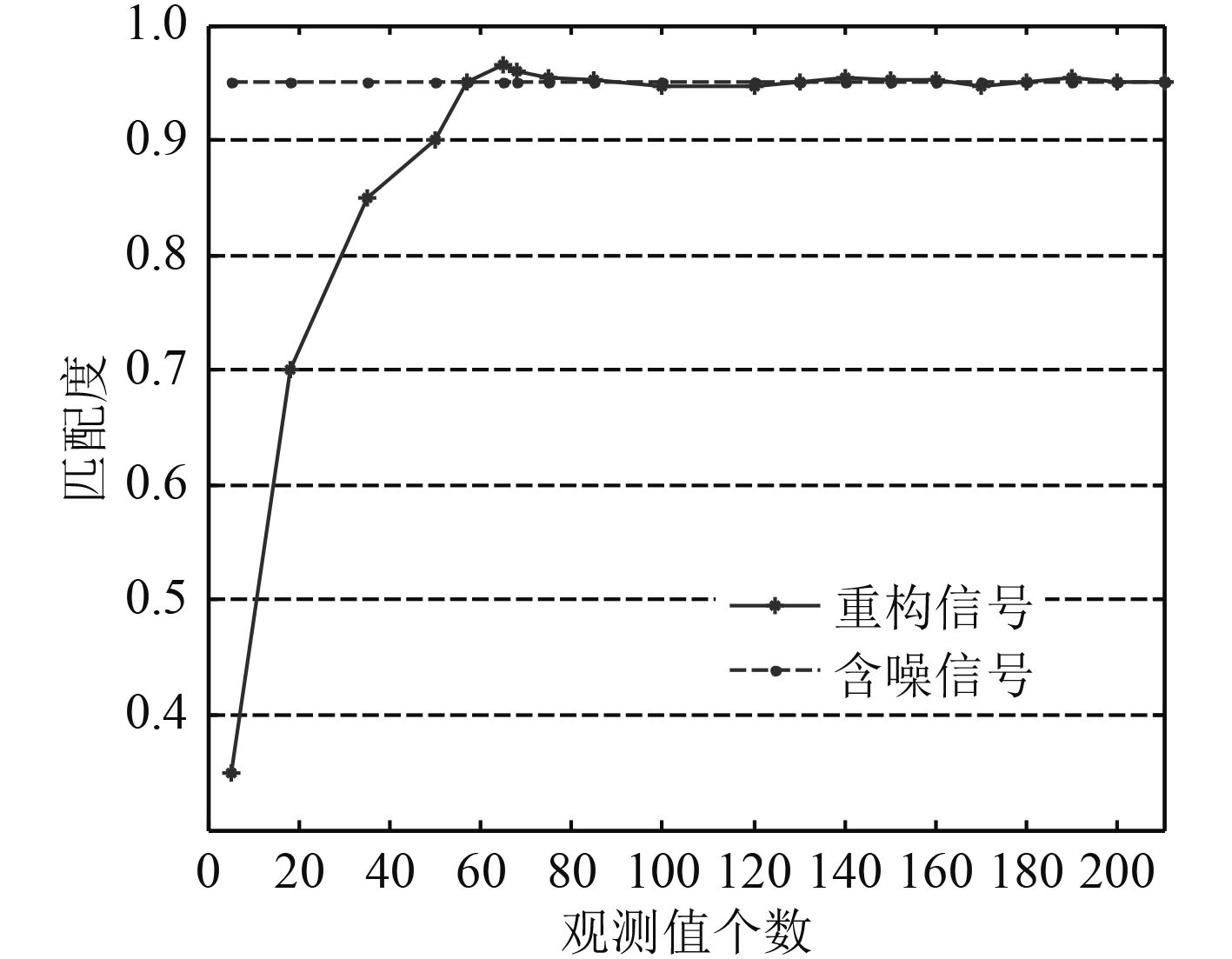
图 13 SNR=20 dB时匹配度随观测值变换曲线 Fig. 13 MR cure along with the number of measurements when SNR=20 dB |
分析图10~图13,当信噪比取0 dB,5 dB,10 dB时,重构信号的匹配度随观测值个数的变化曲线均出现一个峰值,且该峰值大于相应信噪比下含噪信号的匹配度。峰值左边,重构信号的匹配度随着观测值数目的增加而增大;峰值右边,观测值数目增加,匹配度逐渐下降,并趋于相应信噪比下含噪信号的匹配度。3种信噪比下峰值对应的观测值个数分别为52,58,62,均小于67。因此可以得出在固定信噪比下,总存在最佳观测值使得重构信号比含噪信号本身更接近原始信号。
另外,从图中还可以看出,峰的尖锐程度随着信噪比的增大而减小,表明信噪比越高,压缩感知的降噪性能越不明显。当信噪比为20 dB时,重构信号的匹配度就基本不存在峰值,而是随着观测值数目的增加单调上升。这是因为,信噪比较高时,噪声对信号的影响几乎消失,重构信号的误差只和重构算法本身有关。
5 结 语压缩感知具有降噪功能,主要是因为信号在稀疏空间内被完整地保留,而具有非稀疏特性的噪声却没有,从而在信号重构时,原始信号得以完全重构,而噪声不能完全重构,间接起到提高信噪比的作用,这在舰船辐射噪声的探测和跟踪方面帮助很大,而对于含有非高斯背景噪声的舰船辐射信号,则需要做进一步的研究工作。
| [1] | BARANIUK R. A lecture on compressive sensing[J]. IEEE Signal Processing Magazine, 2007, 24 (4): 118–121. DOI: 10.1109/MSP.2007.4286571 |
| [2] | E CANDÈS, J ROMBERG. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information[J]. IEEE Trans on Information Theory, 2006, 52 (2): 489–509. DOI: 10.1109/TIT.2005.862083 |
| [3] | D L DONOHO. Compressed sensing[J]. IEEE Trans on Information Theory, 2006, 52 (4): 1289–1306. DOI: 10.1109/TIT.2006.871582 |
| [4] | D NEEDELL, J A TROPP. CoSaMP: Iterative signal recovery from incomplete and inaccurate samples[J]. Appl Comp Harmonic Anal, 2009, 26 (3): 301–321. DOI: 10.1016/j.acha.2008.07.002 |
| [5] | LI Xiao-bo. The research of measurement matrix based on compressed sensing[D], Beijing: Beijing Jiaotong University, 2010. |
| [6] | 周灿梅. 基于压缩感知的信号重建算法研究[D]. 北京: 北京交通大学, 2010. |
 2017, Vol. 39
2017, Vol. 39
