0 引　言

被动声呐系统最重要的功能是估计目标相对于水听器基阵的方位（DOA）^[1]。常规波束形成的方位分辨力受限于“瑞利极限”，而以MVDR和MUSIC为代表的两类高分辨方位估计算法^{[2 – 5]}的方位分辨能力明显优于常规波束形成方法，成为研究的热点之一。相对来说，MUSIC算法比MVDR算法有更尖锐谱峰，同时旁瓣更低，可以实现目标超分辨力方位估计^{[5 – 8]}。

但是在被动声呐中，基阵接收的信号都是宽带信号，而目前大部分高分辨方位估计算法基于窄带信号假设进行处理，所以处理宽带信号时通常的做法是通过短时傅里叶变换将宽带信号分段成为互不重叠的多个子带，再对每个子带采取相应的处理算法^{[9 – 11]}。TAMVDR^{[12 – 13]}通过希尔伯特变换对宽带信号构造时域解析信号引入了复数形式的权向量，增加了权向量自由度，因此只需对一次快拍进行处理，不对多个快拍进行频域子带分解即可求得最优解，大大减少了运算量，并获得良好的波束形成处理效果。

本文提出将宽带时域解析信号与MUSIC算法相结合，宽带时域解析信号^[14]构建复数形式的协方差矩阵，并采取MUSIC算法对复数协方差矩阵进行特征分解，利用构造的广义噪声子空间的正交性获取与方向信息相关的尖峰状谱峰，从而实现波束形成处理。仿真数据和海试数据处理的结果表明：新算法可以获得更尖锐的谱峰，提高目标的角度分辨力。

1 时域解析信号MUSIC算法原理 1.1 常规算法

假设由M个水听器组成阵列，在其远场有D个宽带声源（D＜M）以平面波的形式传播，其波达方向分别为 $\varTheta = [{\theta _1},\cdots,{\theta _d},\cdots,{\theta _D}]$ 。则第m个水听器所接收到的时域宽带信号为：

${x_m}(t) = \sum\limits_{d = 1}^D {{s_d}(t - {\xi _m}({\theta _d}))} + {v_m}(t)\text{，}$

(1)

其中： ${s_d}(t)$ 为第d个声源信号； ${\xi _m}({\theta _d})$ 为第d个声源相对于第m个水听器的传播延迟； ${v_m}(t)$ 为叠加在第m个水听器上的高斯白噪声。

传统波束形成和空间谱估计方法中，需要用到阵列协方差矩阵，可以用一段子带数据快拍来估计。其实现方法为：首先将观察时间T₀分为K个子段，每段时间为T_d，记T_d内的时域数据点数为一次快拍。假设T₀时间段内满足短时平稳假设，对快拍数据进行离散傅里叶变换，假设得到J个子带，则阵列协方差矩阵的估计可以表示为：

${\hat{ R}_f}({f_j}) = \frac{1}{K}\sum\limits_{k = 1}^K {{{X}_k}(j){X}_k^H} (j),\;\;(j = 1, \cdots J)\text{，}$

(2)

式中：下标f为频域处理；下标k为快拍序号； $ {{X}_k}(j) = $ $ [{X_1}(j), \cdots{X_M}(j)]_k^{\rm T}$ 为通过DFT处理得到的第j个子带数据向量的第k个快拍；K为快拍次数。需要K次快拍阵列协方差矩阵才能收敛。

1.2 时域解析信号协方差矩阵

为加快协方差矩阵收敛速度，可构建时域解析信号搭建复数阵列协方差矩阵，引入复权向量，在权向量自由度上是常规实数权向量的2倍，并可获得更好处理效果。

构造时域解析信号为：

${Y} = {{Y}_s} + {{Y}_v} = {X} + j \cdot \bar{ X}\text{，}$

(3)

式中：Y_s和Y_v分别为解析期望信号和解析噪声，j为虚数单位。

对M个阵元的阵列接收信号经A/D采样、数字时延 $\Delta {\tau _i}(1 \leqslant i \leqslant M)$ 以及分数时延滤波之后的期望信号构造时域复数信号为：

$Y = X + jH(X)\text{，}$

(4)

其中 $H( \cdot )$ 为希尔伯特变换，它的作用是将实数数据变换成复数数据，即时域解析信号，在一次快拍的前提下增加了信号处理的信息量，可以获得更大的权向量自由度。

基阵输出的协方差矩阵由一次快拍时间内的数据估计得到，即

$\hat R = \frac{1}{N}\sum\limits_{i = 0}^{N - 1} {Y{Y^H}}\text{，}$

(5)

自适应阵列输出可表示为：

$C = {{W}^H}{Y} = {{W}^H}{{Y}_s} + {{W}^H}{{Y}_v}\text{，}$

(6)

上标H为转置共轭， ${W} = {[{w_1}{\rm{ }}{w_2}{\rm{ }} \cdots {\rm{ }}{w_M}]^{\rm T}}$ 。

在期望信号、干扰与阵元间噪声互不相关的条件下，注意到解析信号实部与虚部正交，可得阵列输出功率为：

$P = E\{ C{C^*}\} = {{W}^H}{RW}{\text{。}}$

(7)

1.3 基于时域解析信号的广义MUSIC算法

不同自适应波束形成算法的权向量计算规则不同，导致出现不同的性能。本文根据新时域解析信号特点，提出了适应信源目标个数不确定的广义MUSIC算法。

由于噪声的存在，且各阵元噪声互不相关，其功率为 $\sigma _m^2 > 0$ ，因此协方差矩阵 $\hat R$ 为满秩矩阵，对应有M个特征值，按降序排列，记为 $ {\lambda _1} \geqslant {\lambda _2} \geqslant {\lambda _3} \geqslant \cdots \geqslant $ $ {\lambda _M}$ ，其所对应的特征向量为 ${\nu _1},{\nu _2},\cdots,{\nu _M}$ ，各特征向量互相正交。噪声子空间由M–D个较小特征值对应的特征向量构成，记为 $U = \left[ {{\nu _{D + 1}},{\nu _{D + 2}},\cdots,{\nu _M}} \right]$ 。则空间功率谱为：

$P(\theta ) = \frac{1}{{{B^H}U{U^H}B}}\text{，}$

(8)

式中：B为来波方向的导向矢量，由于宽带信号已由数字延迟线以及分数时延滤波器补偿了角度θ带来的影响，所以有

$B = {\left[ {1,1,\cdots,1} \right]^{\rm T}}\text{，}$

(9)

文献[15]的研究发现当信噪比发生改变时会影响MUSIC的性能。为了使算法适应信噪比的变化，可以对其进一步改进，定义新的噪声子空间为：

$G = \left[ \displaystyle{\frac{{{\nu _{D + 1}}}}{{\lambda _{D + 1}^p}},\frac{{{\nu _{D + 2}}}}{{\lambda _{D + 2}^p}},\cdots,\frac{{{\nu _M}}}{{\lambda _M^p}}} \right]\text{。}$

(10)

新的噪声子空间中在原特征向量信息构造的基础上增加了特征值信息，这是一种广义噪声子空间，p为调节指数。当p=0时有G=U，广义噪声子空间退化为基本的噪声子空间。广义噪声子空间输出功率谱为：

${P_G}(\theta ) = \frac{1}{{{B^H}G{G^H}B}}{\text{。}}$

(11)

由于调节指数p可根据实际需要调整，因此适用范围更广，上述算法即为基于时域解析信号的广义MUSIC算法，即TAMUSIC算法（Time-domain Analytical MUSIC Algorithm）。

2 仿真数据分析

仿真实验中的数据包含模拟舰船辐射噪声和模拟环境噪声。特定方向上的目标来波在圆阵声吶各路通道上对应着不同的时延，将单路舰船辐射噪声经精确时延处理模拟多路阵元接收的目标信号，在此基础上叠加上各路互不相关的高斯白噪声，从而构造出多路圆阵声呐阵元域接收信号。将360°空间方向分为512个波束，波束形成时选取来波方向附近若干路阵元信号处理，波束形成一次快拍长度为2 048点。

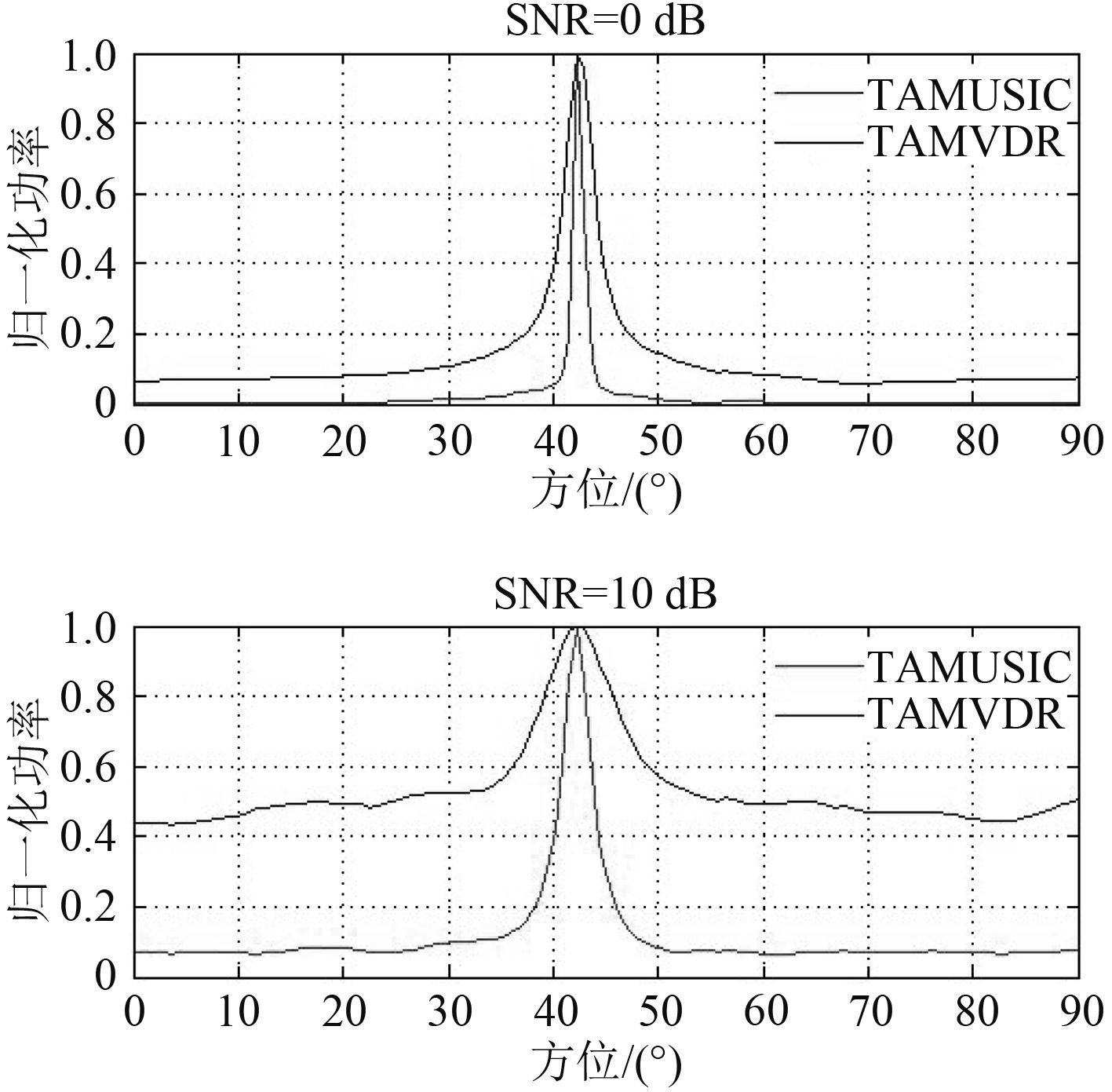
2.1 仿真1单目标仿真

仿真中固定单目标信号位于43°方位，改变模拟环境噪声的大小，当信噪比分别为SNR=0 dB和SNR=–10 dB时，TAMVDR和TAMUSIC算法处理后的归一化功率输出如图1所示。

从图中发现，TAMUSIC具有比TAMVDR更低的旁瓣，且随着信噪比的降低，TAMUSIC旁瓣抬高较小，而TAMVDR波束旁瓣抬高明显；随着信噪比降低，2种算法的波束宽度均有所展宽，但TAMUSIC比TAMVDR具有更窄的波束宽度。这意味着TAMUSIC具有比TAMVDR更强的信噪比适应能力和更高的波束分辨力。

2.2 两目标仿真

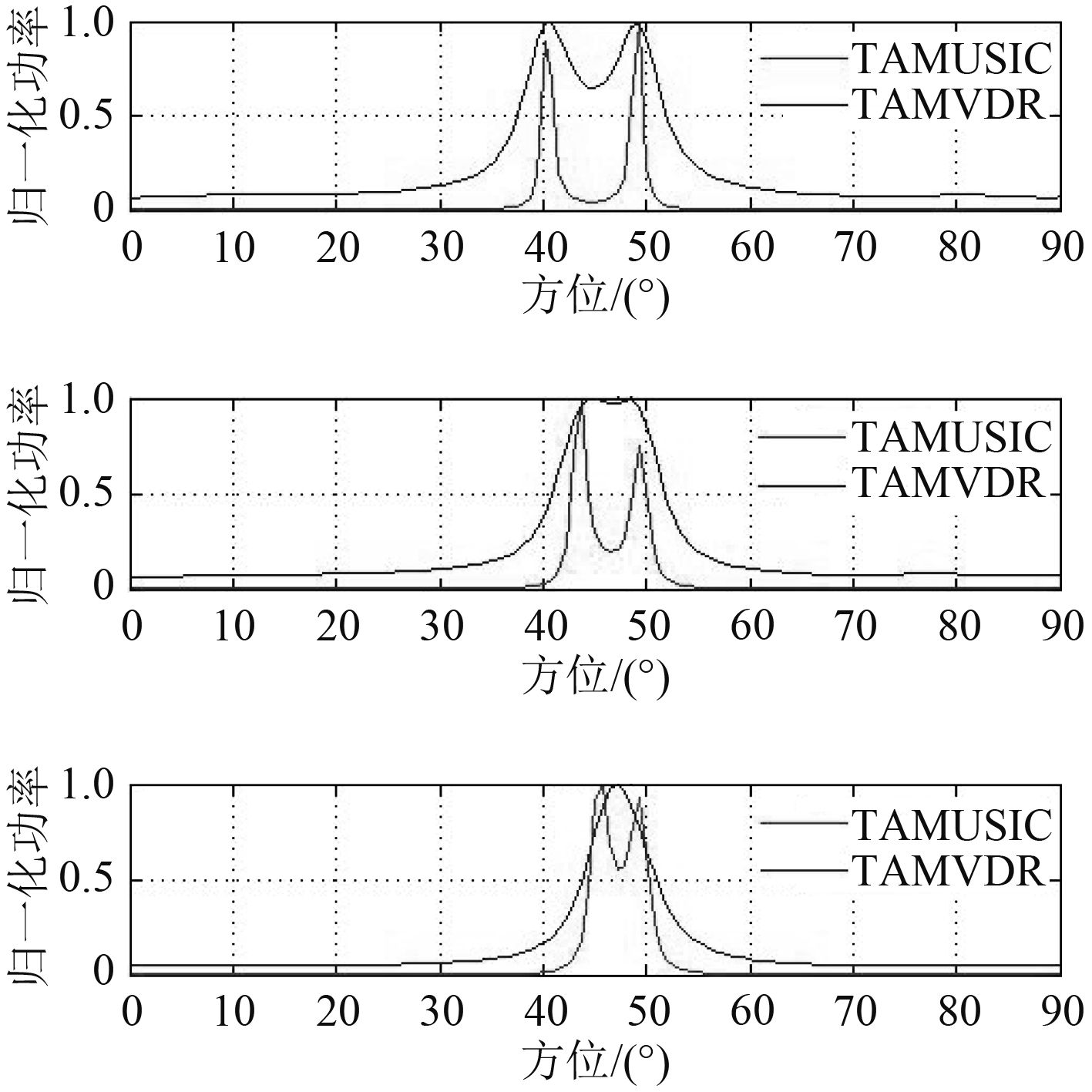
仿真2个等信噪比为SNR=0 dB的目标，其中静止目标位于方位50°处，运动目标在方位上逐渐向静止目标靠近，当两目标方位分别间隔10°，间隔7°及间隔5°情况时，TAMVDR和TAMUSIC算法的归一化功率输出如图2所示。

从图中发现，两目标间隔较大时，当两目标间隔7°时，TAMVDR已经不具备分辨两目标方位的能力，而此时TAMUSIC依然有很清晰的两目标波束输出；在当前仿真前提下，TAMUSIC的极限分辨率大约为4°～5°。

3 海试数据分析

为进一步验证TAMUSIC算法性能，利用32通道圆阵水听器基阵在海上录取阵元宽带数据处理，分别采用常规波束形成（CBF）、时域解析信号MVDR算法（TAMVDR）和本文新算法（TAMUSIC）进行处理。由于被动声呐信号处理中信源数目无法准确估计，因此无法采用MUSIC算法进行处理。TAMUSIC算法中，一次快拍长度为2 048点，设置调节指数p=0.75。

1）单快拍数据对比

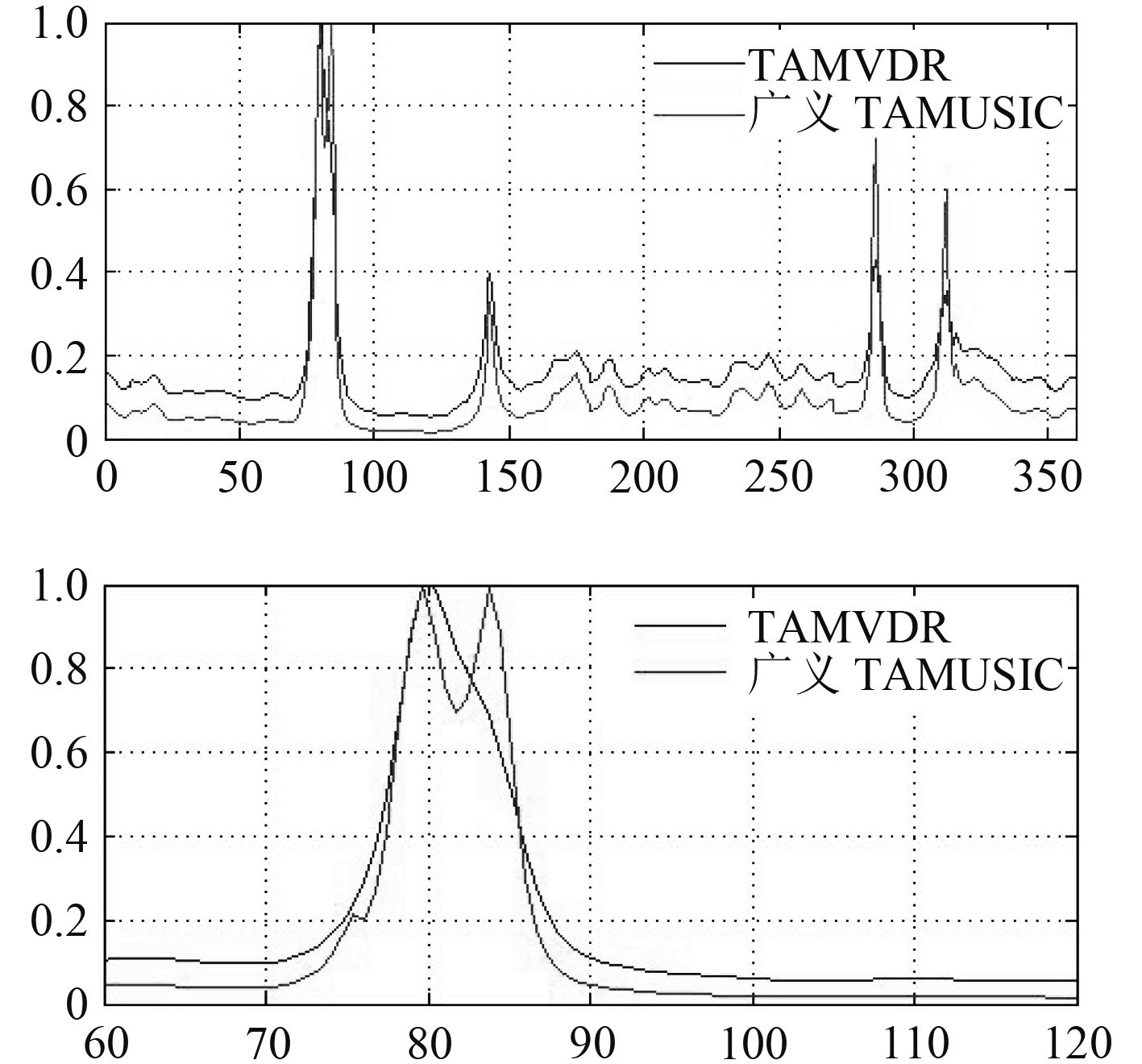
图3展示的是第1 380次快拍时刻TAMVDR和TAMUSIC算法输出，从图中可以发现TAMUSIC具有比TAMVDR更强的角度分辨力。

针对第1 300～1 900次快拍时刻在方位80°附近采用三波束比值法判别两目标，数学统计表明：TAMVDR可明确判别两目标的次数为131次；而TAMUSIC可明确判别两目标的次数为338次，是TAMVDR算法的2.5倍。可见，TAMUSIC算法通过改变调节指数的权重能改变弱目标相对强度，有利于小目标的探测。

2）历程数据对比

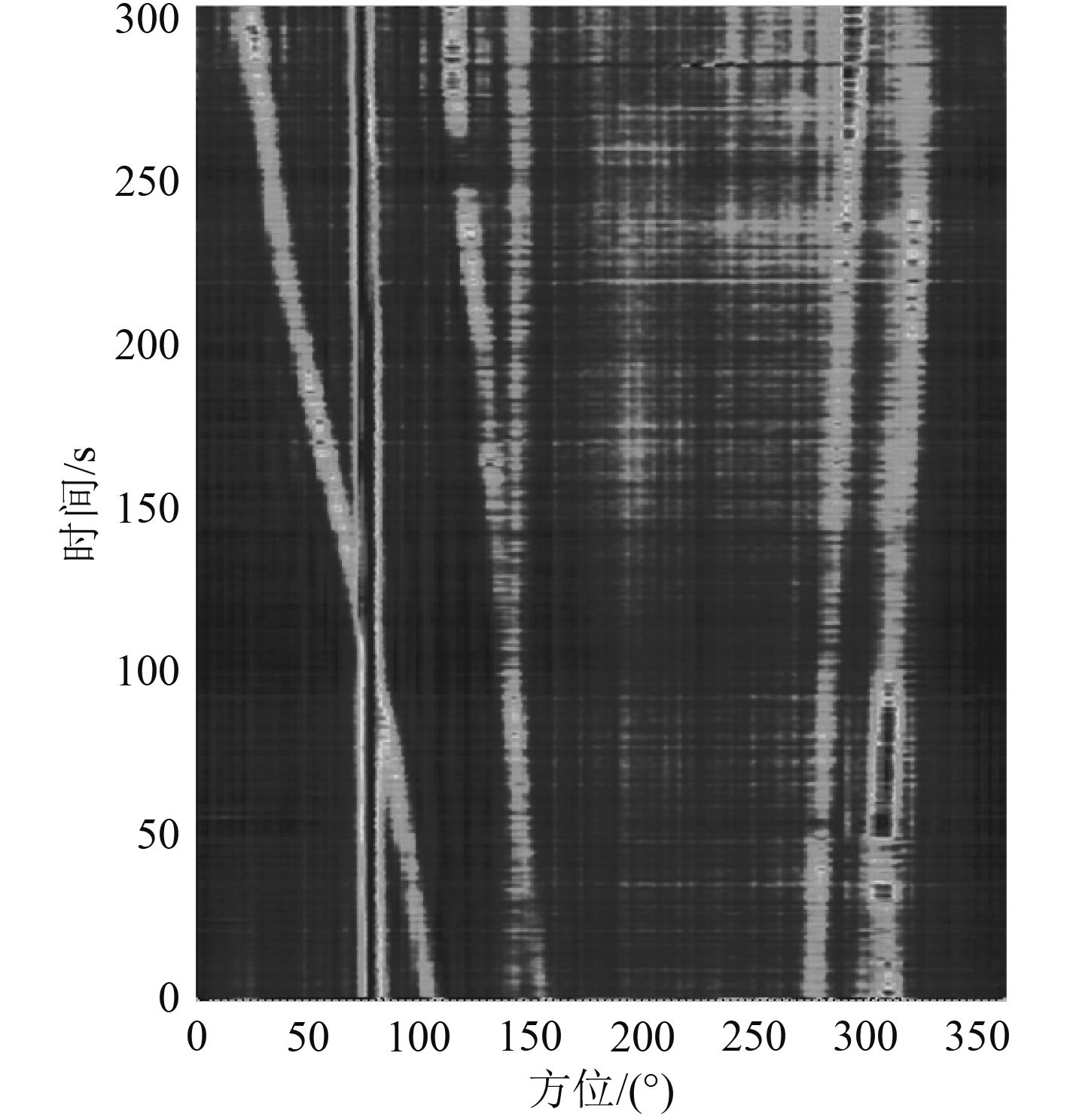
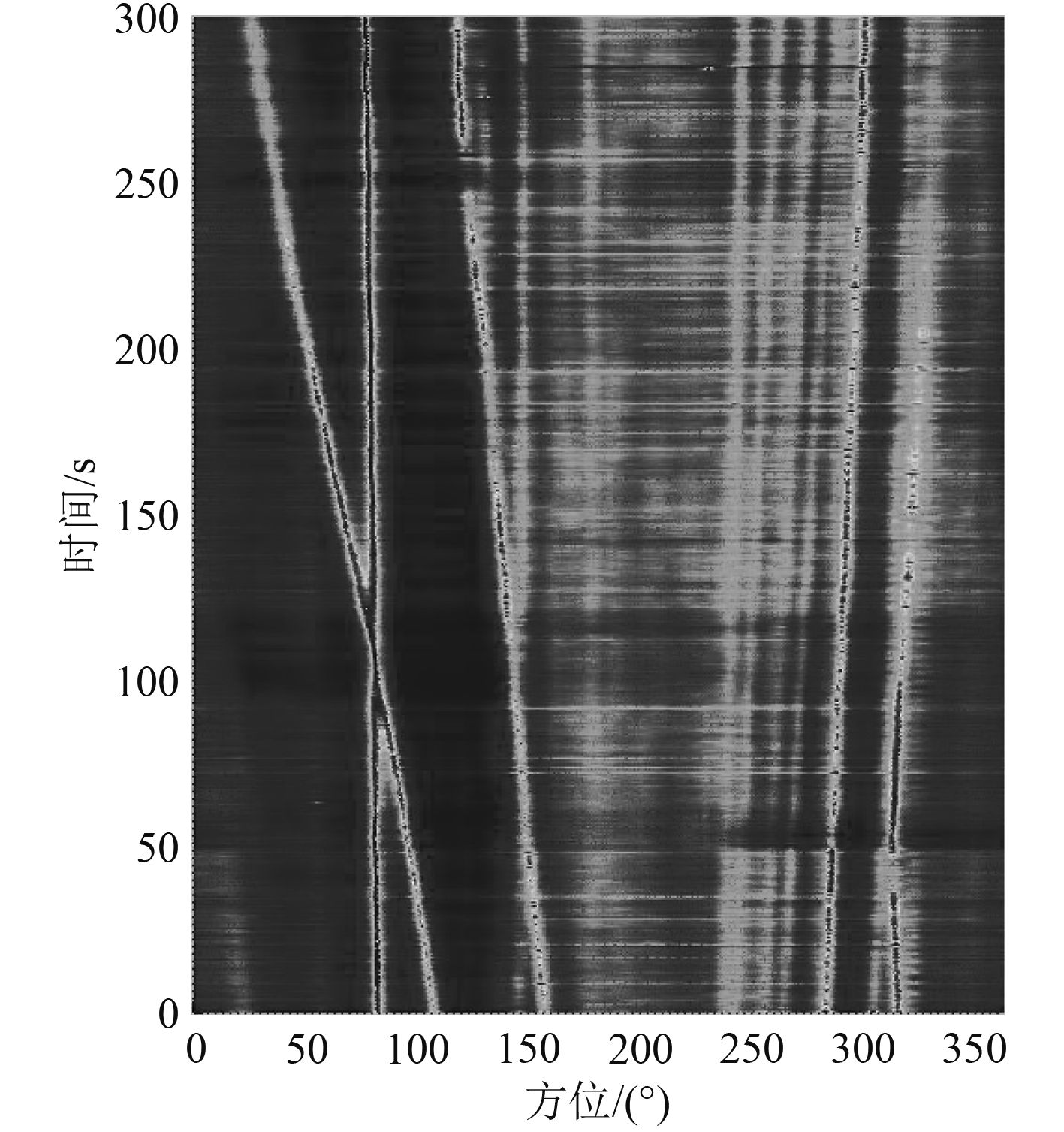
图4、图5和图6分别为CBF，TAMVDR和TAMUSIC算法处理的时间-历程图结果。

对比发现，图5和图6比图4具有明显的改进，主要体现在100时刻两目标的分辨时间以及250°方位多个目标的检测能力。可见TAMVDR和TAMUSIC两自适应波束形成算法在波束宽度和多目标分辨能力的提升。

通过图6可以看出，通过调节指数引入，TAMUSIC算法能够在未知信源准确数目的前提下进行多目标的检测。图5和图6对比可知，图6在方位250°附近的弱小目标被TAMUSIC算法容易从背景中分辨，TAMUSIC算法清晰地反映弱小目标的航路历程。可见，本文提出的TAMUSIC算法比TAMVDR算法具有更好的波束分辨能力。

4 结　语

本文提出的基于时域解析信号TAMUSIC算法，将宽带时域解析信号与MUSIC算法相结合，充分发挥了各自优点，同时采取措施避免各自的不足。

1）TAMUSIC算法继承了TAMVDR算法时域解析信号的复数加权优势，增加了权向量自由度；获得良好的波束形成处理效果。

2）TAMUSIC算法无需对多个快拍进行频域子带分解，只需对一次快拍进行处理即可求得最优解，大大减少了运算量。

3）TAMUSIC算法继承了传统MUSIC算法分辨率高的优点，实现了优于TAMVDR的目标分辨和检测能力。

4）TAMUSIC算法通过构建新的广义噪声子空间，克服了信源数目估计不准确对结果的影响，提升了在信源数目未确知条件下的目标探测能力，并改变调节指数的权重能改变弱目标相对强度，提高对小目标的发现能力。

海上实录数据验证了TAMUSIC算法处理性能的优越性，该算法有望在声呐装备基阵波束形成信号处理中得到应用。