2. 船舶振动噪声重点实验室,湖北 武汉 430033
2. National Key Laboratory on Ship Vibration and Noise, Wuhan 430033, China
管路系统是舰船辅助系统组成部分之一,实践证明其产生的振动噪声严重影响舰船的声隐身性能。在管路与船体结构之间安装弹性支撑是控制振动传递的重要途径,国内外相关专家学者对管路系统振动进行研究,其中尹志勇[1]对管路系统振动、声传播及其控制技术的理论研究、实验研究的现状进行总结;Lig[2]对流经管路系统振动功率流,充液弯管振动传输、橡胶接头功率流进行系统研究;蔡华标[3]提出了新型弹性支撑减振降噪的设计方案,实验证明该设计方案有良好的减振性能;柯兵[4]在管路系统详细设计阶段采用有限元方法进行振动噪声计算,并对控制元件参数对管路振动噪声传递影响进行初步研究,得到了一些有益的结论;He Tao[5]通过有限元计算将充液管路等效为梁结构得出管路系统振动噪声数值算法,并通过实验得到了有效的管路低噪声配置方法;王艳林[6]介绍了舰船管路系统振动噪声主被动控制的研究进展,探讨了未来舰船管路系统振动噪声控制发展趋势,并提出合理的建议;李伟刚[7]分析了舰船液压管路系统振动噪声产生的原因,并在流体动力噪声控制中提出了采用弹性安装以减小管路振动向船体的传递;周艳丽[8]针对导管不同构型下支撑与卡箍,采用不同的简化方式建立了有限元模型,通过实验找到了有效的支撑简化方法;闫辉[9]基于有限元理论建立了隔振器有限元模型并进行仿真计算,通过与实验结果对比验证了其仿真结果的准确性,为弹性支撑隔振器的有限元计算分析奠定了基础。
对于复杂管路系统,国内缺乏对弹性支撑相关参数下管路振动传递特性研究。本文采用有限元理论,在合理简化管路系统弹性支撑的基础上,对管路进行有限元仿真,分析弹性支撑在不同间距、不同刚度、不同位置的情况下管路的振动传递特性,为舰船管路系统弹性支撑的低噪声安装与设计提供理论依据。
1 管路系统弹性支撑数学模型舰船管路系统很多,有为全船提供海、淡水的供水管路系统,燃油和滑油输送管路系统,消防管路系统,舱底水排除管路系统等。管路系统的构成和功能多种多样,但都是由设备、管段、法兰、挠性接管、弹性支承件等基本部件组成。
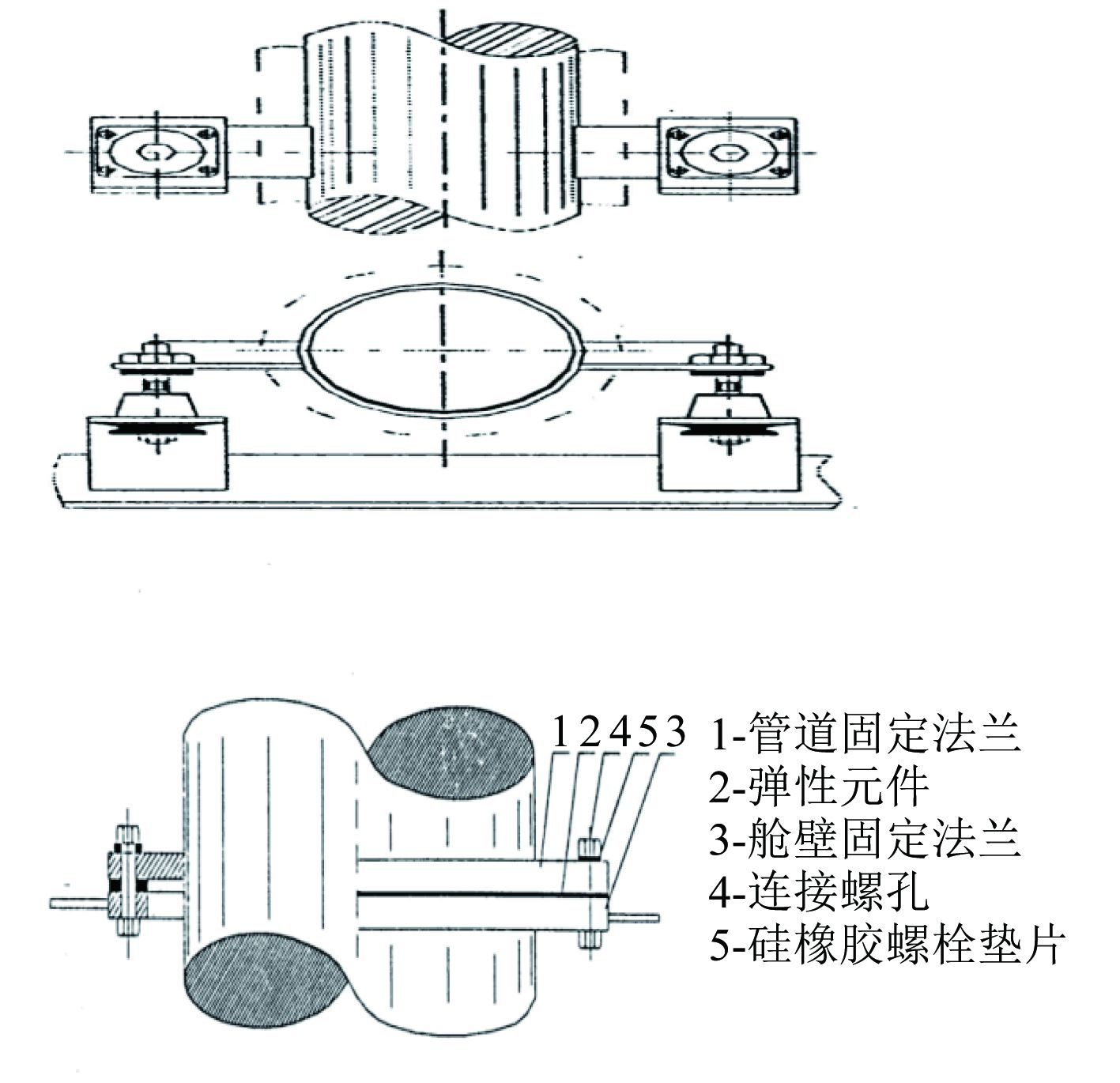
|
图 1 管路系统典型弹性支撑结构示意图 Fig. 1 Pipeline system typical elastic support structure diagram |
引起管路振动原因有3种:共振;流体压力脉动;动力平衡性差或基础设计不当。共振分2种:一是管路系统机械共振,由于管路系统本身也相当于一个弹性系统当激励频率与某阶固有频率接近时即发生管路共振;二是气柱共振,管路系统中的气体也是振动系统,当激励频率与某阶固有频率接近也会产生共振。流体压力脉动:管路系统中处于压力脉动状态的管流遇到弯头、控制阀件等产生随时间变化的激励力使管路系统产生振动。动力机械如泵、压缩机等安装不平衡以及基础设计不当同样会使管路系统产生振动。
典型的弹性支撑主要由弹性元件、支撑结构等组成,支撑与基座之间插入隔振器等隔振单元,构成组合式弹性支撑。其振动系统简化模型如图2所示。
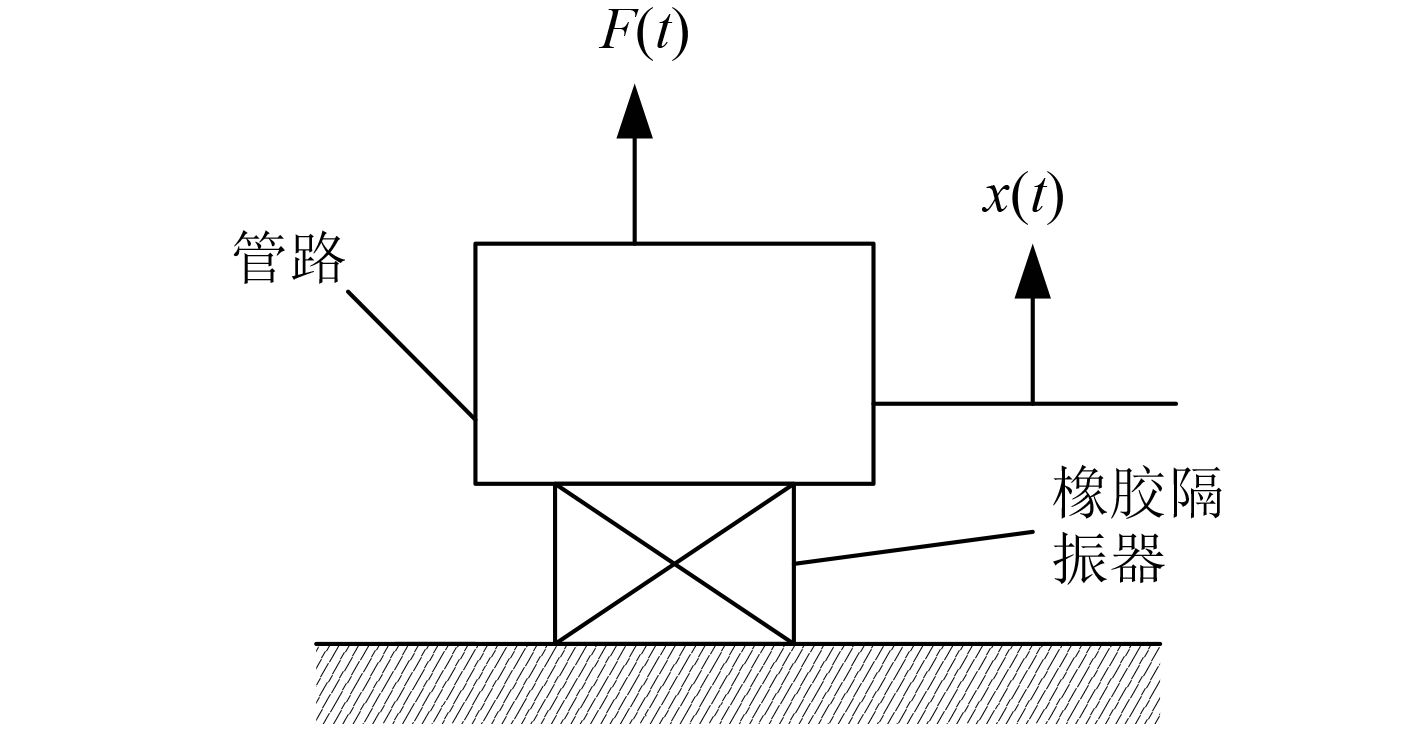
|
图 2 弹性支撑振动系统模型 Fig. 2 Elastic support vibration system model |
|
$m\ddot x + (k' + jk'')x = {F_0}{e^{j\omega t}}\text{。}$
|
(1) |
设方程的稳态解为
|
$- m{\omega ^2}X + (jk'' + k')X{e^{j\omega t}} = {F_0}{e^{j\omega t}},$
|
(2) |
|
$X = \frac{{{F_0}}}{{k' - m{\omega ^2} + jk''}}\text{。}$
|
(3) |
则基座所受到的力为:
|
${F_T}(t) = \frac{{{F_0}(k' + jk'')}}{{k' - m{\omega ^2} + jk'}}{e^{j\omega t}}\text{。}$
|
(4) |
式中:
|
${T_A} = \frac{{\left| {{F_{T0}}} \right|}}{{{F_0}}} = \sqrt {\frac{{1 + {\eta ^2}}}{{{{\left( {1 - \frac{{{\omega ^2}}}{{{\omega _n}^2}}} \right)}^2} + {\eta ^2}}}} ,$
|
(5) |
式中:
DN80管路参数如表1所示,管路弹性支撑有限元模型的材料属性如表2所示。
|
|
表 1 DN80管路参数 Tab.1 Parameter of DN80 pipeline |
|
|
表 2 模型材料属性 Tab.2 Model material data |
Abaqus有10个功能模块依次完成有限元建模、属性赋予、网格划分、分析计算、后处理等。在有限元中建立管路弹性支撑有限元模型,模型建立:在Part模块创建所需分析的模型,文中把管路简化为梁结构,考虑到弹性支撑对称性可以把其简化为弹簧结构。在Property模块定义模型的材料属性和截面,选择适当的本构关系,并确立管路以及弹性支撑部件的相关参数。管路的截面属性以Pipe属性定义,弹性支撑简化为弹簧结构之后的等效刚度为8×106 N/m,弹簧属性是在模型建好之后在Assembly模块中建立的。进行有限元计算时,必须处理结构的边界条件。边界条件:Load模块中定义边界条件和载荷。本文除铺板设为固支之外,其他边界条件均设为自由。载荷处理及振源描述:在管路的左端管口设置沿Z轴向上的单位激励力。管路、弹性支撑和铺板的Abaqus模型如图3所示。

|
图 3 管路、弹性支撑和铺板的Abaqus模型 Fig. 3 Piping, elastic support and plank Abaqus model |
管路支撑间的振动传递特性与支撑间距有关,取DN80管为研究对象,不考虑其他因素,仅考虑管路支撑间距影响,在单位激励力作用下,研究管路支撑的振动传递特性。整个简化模型由3部分组成:管路、弹性支撑和铺板。选取具有等间隔支撑的直管支撑于铺板上,计算当一端受到单位激励力作用时,在不同的支撑间距时的各支撑点的响应。
图4~图6分别是支撑间距为0.5 m,1 m,1.5 m的Abaqus仿真计算的结果。
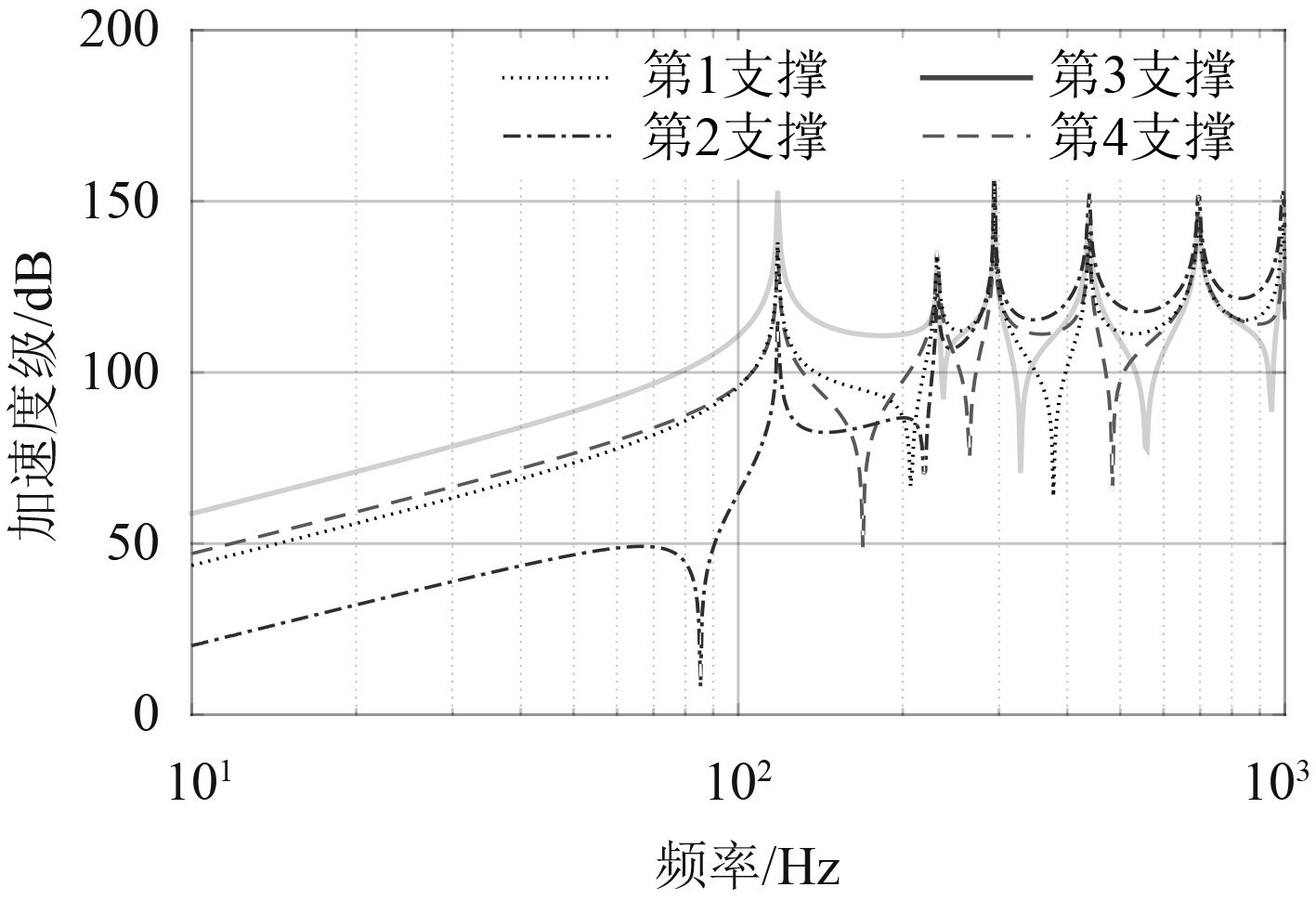
|
图 4 支撑间距为0.5 m管路支撑点响应 Fig. 4 0.5 m support spacing line support response |
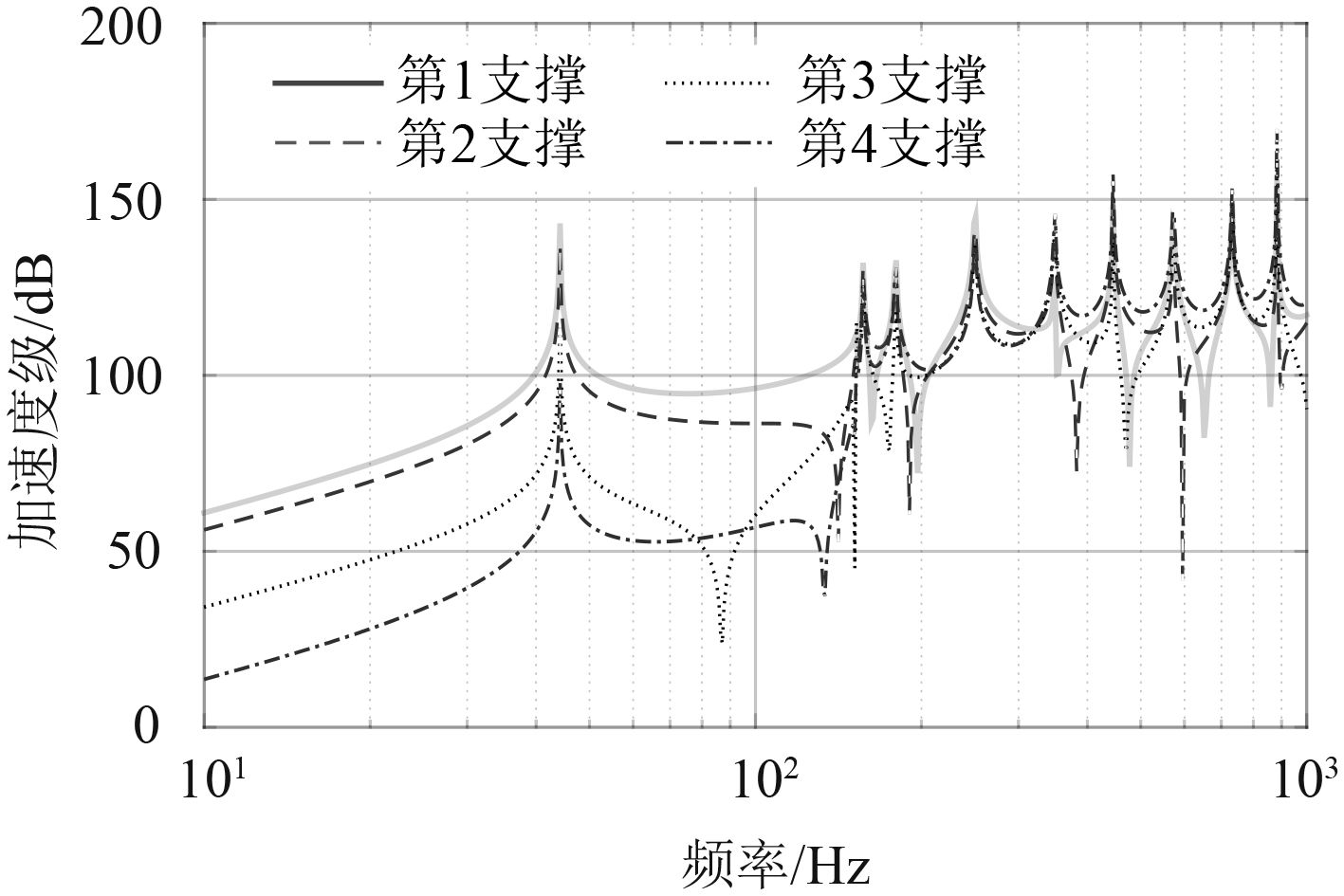
|
图 5 支撑间距为1 m管路支撑点响应 Fig. 5 1 m support spacing line support response |
|
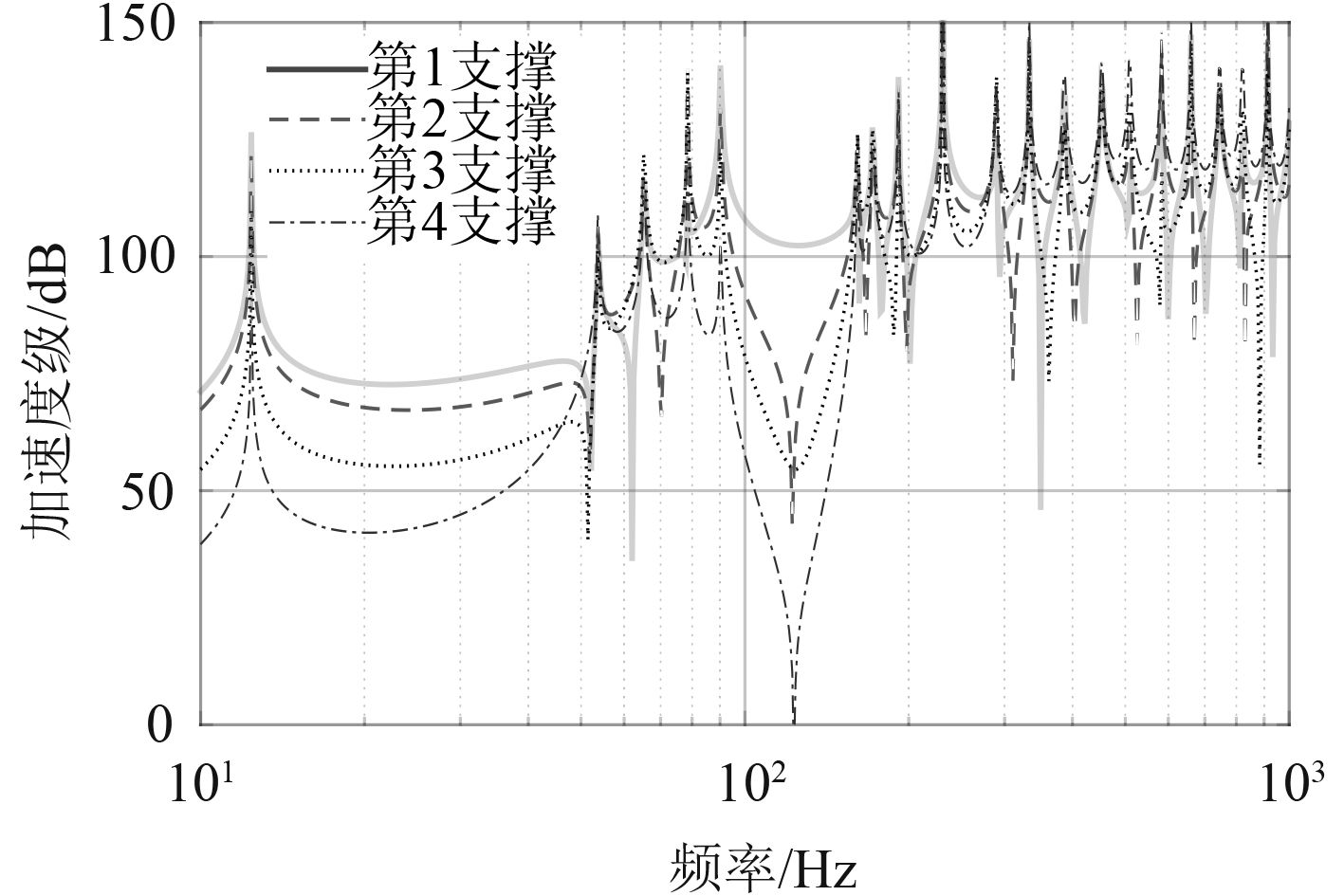
图 6 支撑间距为1.5 m管路支撑点响应 Fig. 6 1.5 m support spacing line support response |
图4~图6表明低频段各管路支撑之间的振动衰减比高频大,而且在低频段的衰减有较宽的频率范围,并且由低频段的高传递损失到高频段的低传递损失有比较明显的频率分界点。当管跨距离较小,一阶固有频率较高时,低频段的振动衰减频段较宽,反之高频段的振动衰减较窄。相同支撑间距的管路在低频段传递到基座的力随着支撑点离激励点距离的增加明显减小,高频段传递率基本不变。在不同支撑间距下管路在低频段传递损失相应减小。激励力传递到各支撑点的力随着支撑间距的增加有所减小。
管路的振动传递特性与管跨的固有特性关系密切,同时管跨的固有振动特性与支撑间距、管道直径、弹性支撑与船体的阻抗都有关系。所以,对同一规格的管道,使用不同的支撑或安装在船体不同的位置,根据振动衰减的需要,应该对弹性支撑间距提出不同的要求。判断支撑布置合理性的主要依据是支撑间的振动衰减特性,振动衰减越大、频段越宽就认为布置越合理。
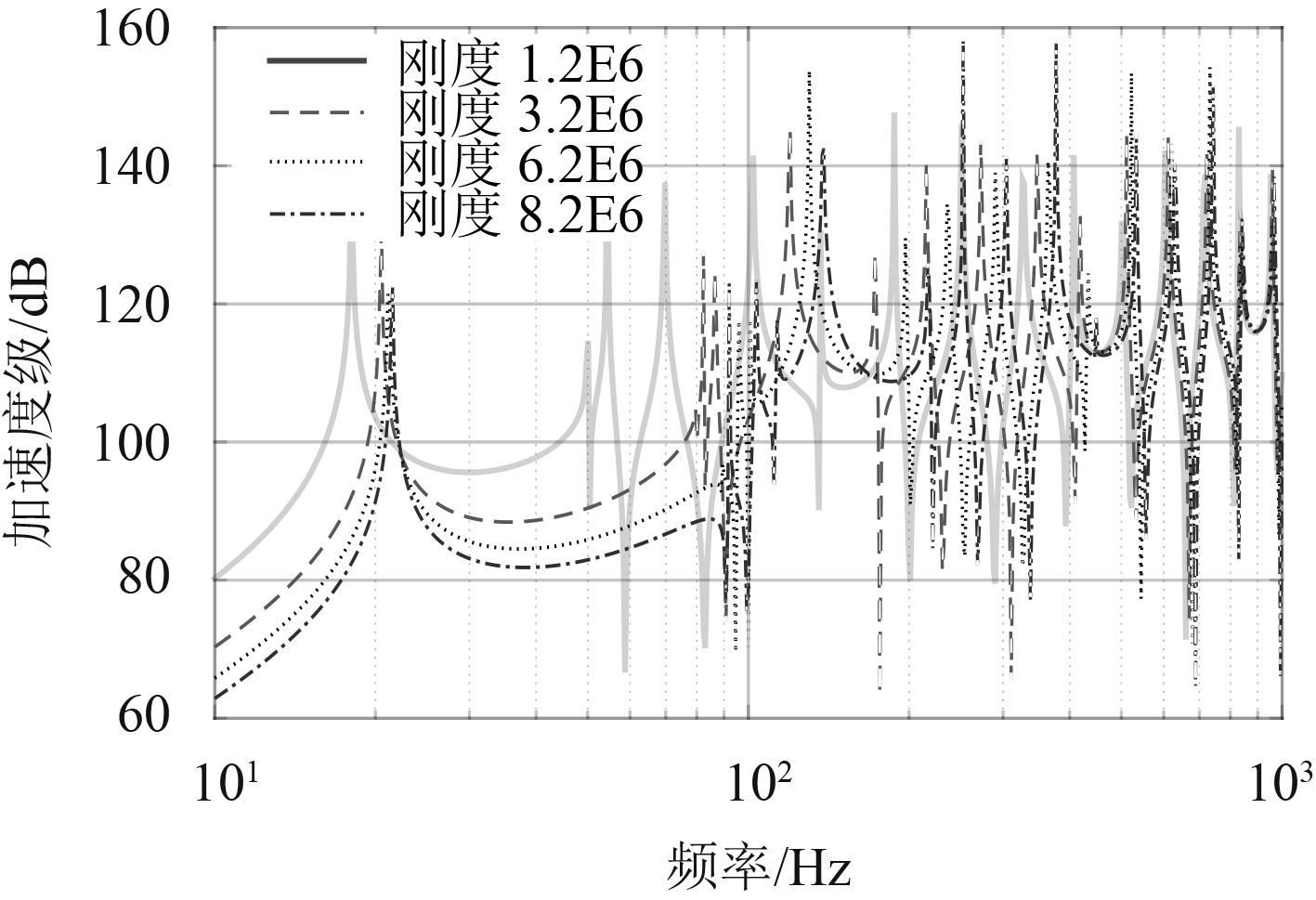
3.2 弹性支撑刚度影响由于弹性支撑的结构形式不同,管路与弹性支撑之间所选用的弹性元件的结构和材料也不同。一般认为在为管路设计弹性支撑时,选用的弹性元件的刚度要适中,基础刚度要尽量的大,才能达到良好的管路低噪声安装效果。为了研究管路弹性支撑的刚度参数对管路系统振动的影响,如图所示等支撑间距下弹性支撑刚度分别为1.2×106 N/m,3.6×106 N/m,6.0×106 N/m,8.4×106 N/m弹性支撑点的响应。
|
图 7 不同支撑刚度下支撑点的响应 Fig. 7 The response of the support point under different support stiffness |
支撑刚度变化对100 Hz以上船体振动的高频区域影响不大,但是对100 Hz以下低频区的振动影响比较明显。现取100 Hz以下的船体振动为研究对象,分析支撑刚度变化对船体振动的影响,如图8所示为100 Hz以下船体总振级随支撑刚度变化的曲线。
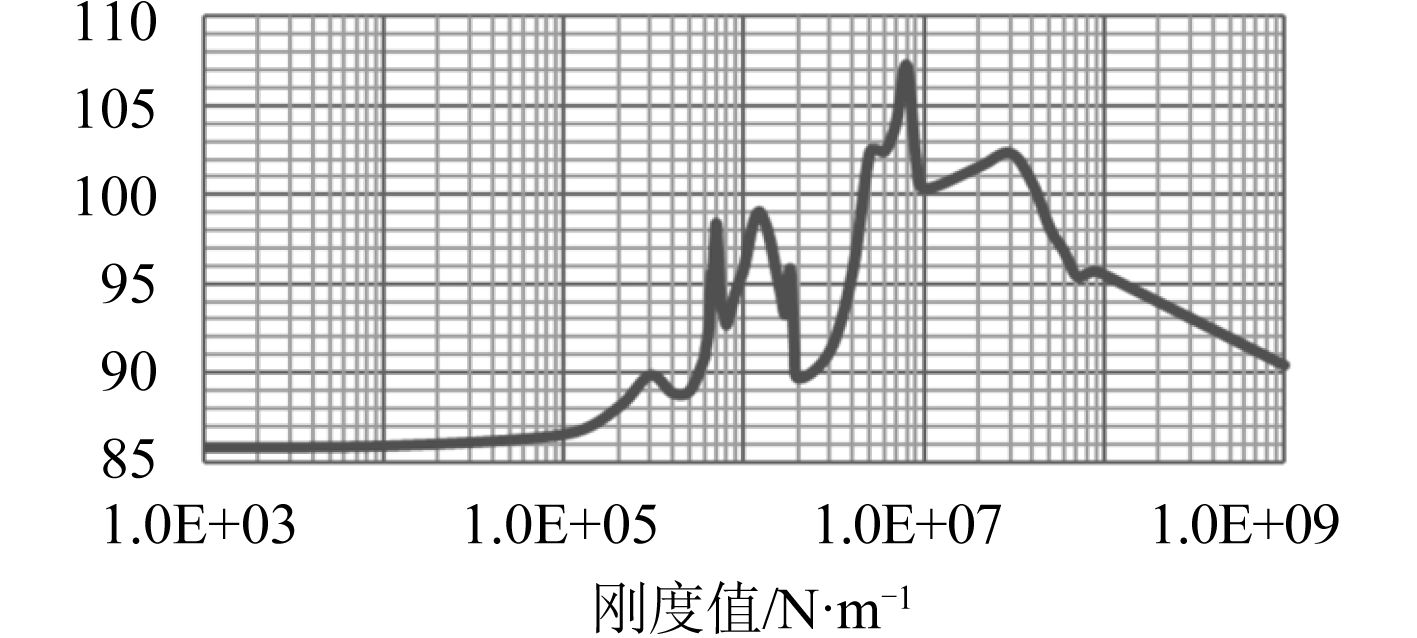
|
图 8 100 Hz以下船体振动总级随弹性支撑刚度变化曲线 Fig. 8 Hull vibration level below 100 Hz change with elastic support stiffness curve |
由图8可知在刚度低于1.0×105 N/m时,船体振动几乎不随管路支撑刚度变化,表示船体和管路系统的耦合振动较弱。在管路支撑刚度为7×105,1.2×106和8×106 N/m附近,此时100 Hz以下船体振动加速度总级达到峰值,表示船体和管路系统的耦合振动最强;管路支撑刚度大于1.0×107 N/m时,船体振动呈现随支撑刚度增大而线性下降的趋势,甚至支撑的阻抗大于船体阻抗,但是此情形在现实工况中很少出现。
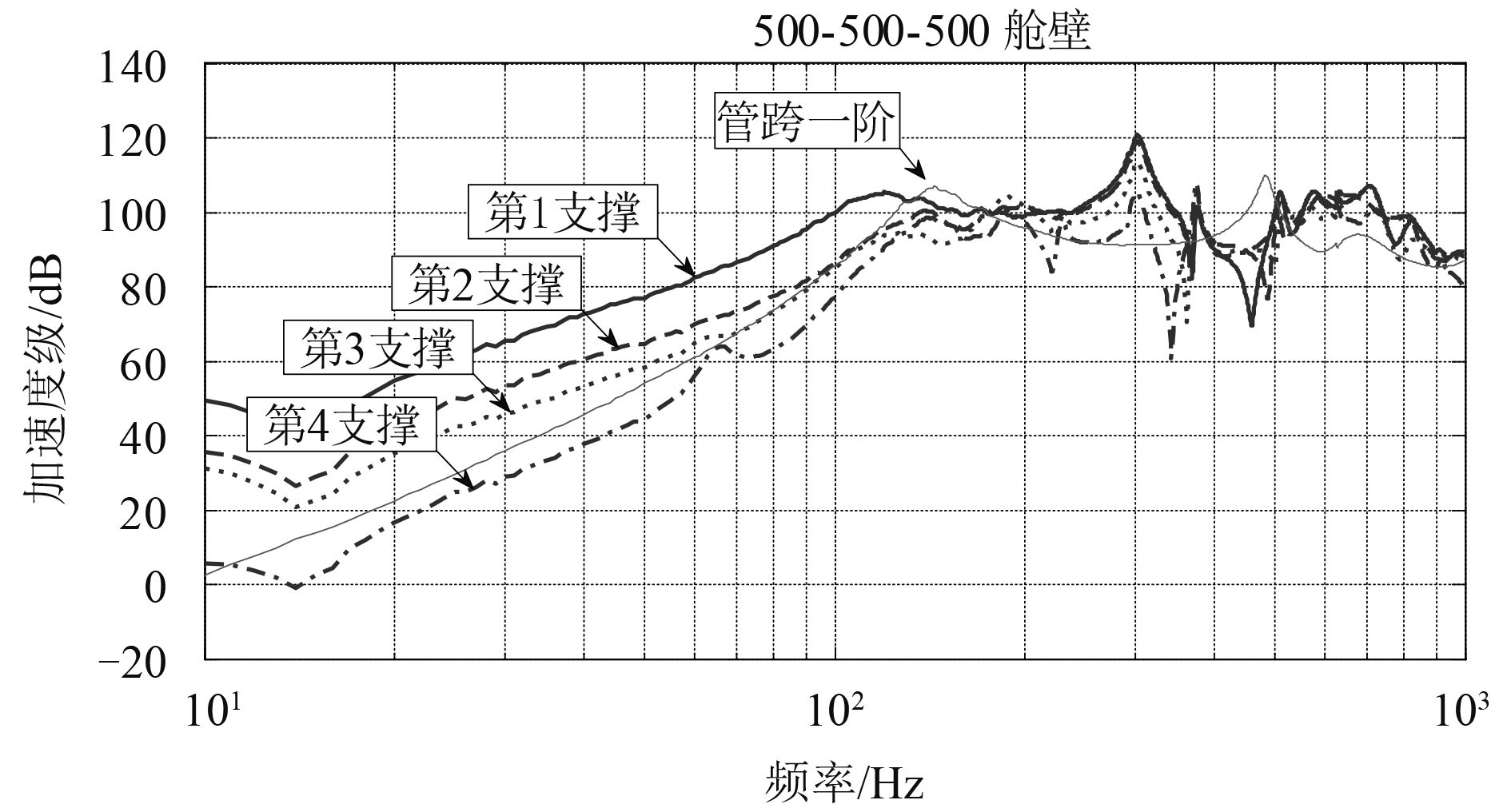
3.3 弹性支撑位置影响弹性支撑布置在机舱的不同位置会影响管路系统振动传递特性。现在将管路分别置于耐压壳、舱壁以及普通薄铺板上,图9~图11为管路分别在铺板、耐压壳和舱壁上的计算结果。
|
图 9 支撑安装在舱壁上的频谱图 Fig. 9 Support installed in the tank wall spectrum |
|
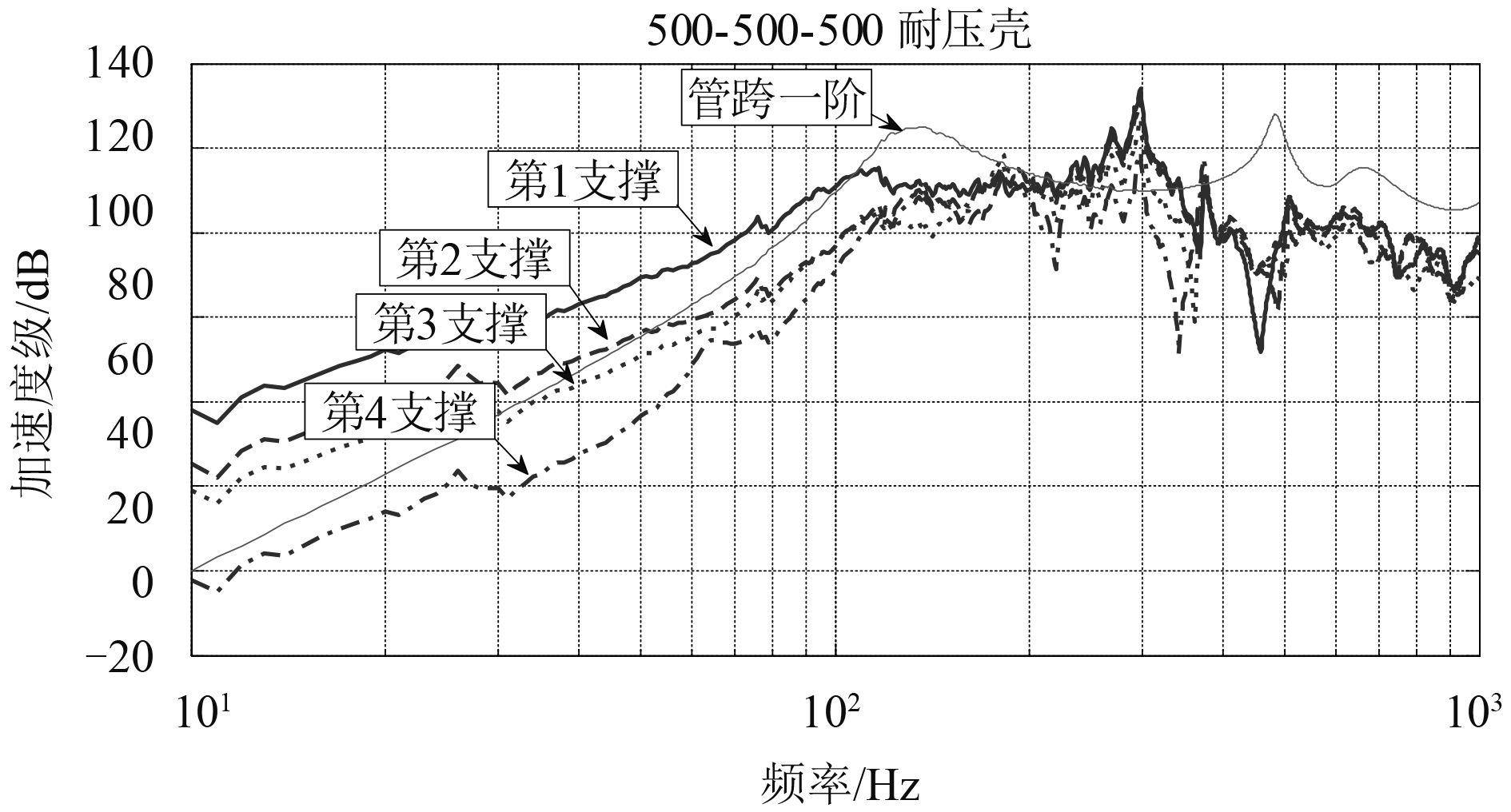
图 10 支撑安装在耐压壳体上的频谱图 Fig. 10 Support installed in the pressure shell spectrum |
|
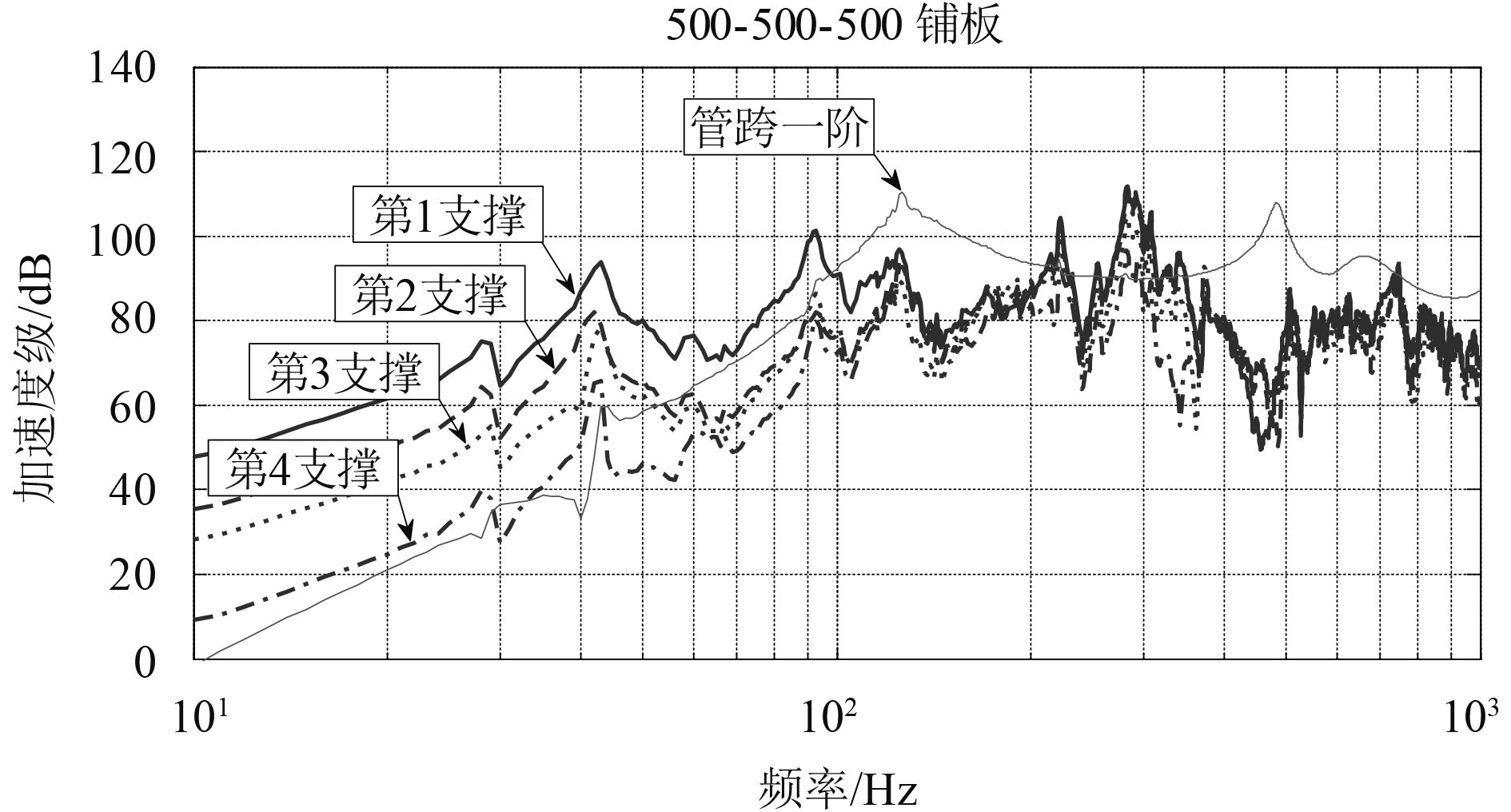
图 11 支撑安装在铺板上的频谱图 Fig. 11 Support installed in the planking spectrum |
图中“管跨一阶”是指两端用弹性马脚支撑的管道在一端受单位力激励的管跨的一阶固有频率,它反映的是组成整个直管管路的单一管跨的振动传递特性。由上图可以看出管路弹性支撑安装在耐压壳有较低的加速度级,相比安装在耐压壳和舱壁安装在铺板上时有更多低频共振峰。在对比船体输入阻抗的数据图谱之后,发现这些共振峰与铺板阻抗曲线的反共振峰相对应,这说明铺板上管路振动传递受铺板共振的影响比较明显。故可认为管路安装在较强的结构上时,对实现支撑与船体结构的阻抗失配是比较有利的,更有利于管路的隔振。进一步可以得出结论为实现管路的低噪声安装弹性支撑最好布置在结构较强的舱壁或者耐压壳体上。
4 结 语通过弹性支撑安装间距、刚度、位置安装工艺影响因素的研究可以得出以下结论:
1)合理选择管路弹性支撑间距对管路低噪声安装有重要意义。对同一规格的管道,使用不同的支撑或安装在船体不同的位置,根据振动衰减的需要,应对其弹性支撑提出不同的要求,支撑布置合理性的主要依据是支撑间的振动衰减特性,振动衰减越大、频段越宽就认为布置越合理。为了获得较好的隔振效果,对不同通径的管路,通过数值计算获得了支撑布置间距对于上述DN80管最佳支撑间距为800~1 200 mm。
2)合理选择管路弹性支撑的刚度参数有利于加强弹性支撑管路系统的隔振效果。管路设计弹性支撑时,选用的弹性元件的刚度要适中,支撑元件刚度要尽量的大,才能达到良好的管路低噪声安装效果。仿真计算表明管路刚度为8.4×106 N/m时管路系统和船体耦合振动较弱,隔振效果良好。
3)管路安装在较强的结构上时,对实现支撑与船体结构的阻抗失配比较有利,更有利于管路的隔振。进一步可以得出结论为实现管路的低噪声安装弹性支撑最好布置在结构比较强的舱壁或者耐压壳体上。
| [1] |
尹志勇, 钟荣, 刘钟族. 管路系统振动噪声控制技术研究现状与展望[J]. 舰船科学技术, 2006, 2 : 23–28.
Zhi-yong YIN, ZHONG Rong, LIU Zhong-zu. Piping system vibration and noise control technology research status and prospect[J]. Journal of Marine Science and Technology, 2006, 2 : 23–28. |
| [2] | LIG X, PAIDOUSSIS M P. Stability, double degeneracy and chaos in cantilevered pipes conveying fluid[J]. International Journal of Non-linear Mechanics, 1994, 29 (1): 83–107. DOI: 10.1016/0020-7462(94)90054-X |
| [3] |
蔡标华, 俞健, 白亚鹤. 舰船管路系统弹性减振设计与实验[J]. 舰船科学技术, 2011, 11 : 61–64.
Biao-hua CAI, Jian YU, Ya-he BAI. Ship piping system elastic vibration reduction design and experiment[J]. Journal of Ship Science and Technology, 2011, 11 : 61–64. DOI: 10.3404/j.issn.1672-7649.2011.06.015 |
| [4] |
柯兵, 周进华. 低噪声管路系统设计研究[J]. 舰船科学技术, 2006, 2 : 117–120.
Bing KE, Jin-hua ZHOU. Low noise pipe system design and research[J]. Journal of Ship science and technology, 2006, 2 : 117–120. |
| [5] | HE Tao, SUN Yu-dong, WU Wen-wei, et al. Low noise collocation on fluid pipeline system[J]. Journal of Ship Science and Technology, 2015, 9 : 1149–1158. |
| [6] |
王艳林, 王自东, 宋卓斐, 王强松. 潜艇管路系统振动噪声控制技术的现状与发展[J]. 舰船科学技术, 2008, 12 : 34–38.
Yan-lin WANG, Zi-dong WANG, Zhuo-fei SONG, Qiang-song WANG. The vibration and noise control technology of present situation and the development of submarine pipeline system[J]. Journal of Ship Science and Technology, 2008, 12 : 34–38. DOI: 10.3404/j.issn.1672-7649,2008.01.004 |
| [7] |
李伟刚, 王春健, 李兵尚. 潜艇液压系统管路振动与噪声的分析控制[J]. 机床与液压, 2011, 7 : 70–73.
Wei-gang LI, Chun-jian WANG, Bing-shang LI. the vibration analysis and noise control of submarine hydraulic pipeline system[J]. Journal of Hydraulic and Machine Tools, 2011, 7 : 70–73. DOI: 10.3969/j.issn.1001-3881.2011.04.022 |
| [8] |
周艳丽, 陆波. 飞机液压管路支撑的有限元建模方式对应力分析的影响[J]. 民用飞机设计与研究, 2014, 113 : 84–87.
Yan-li ZHOU, Bo LIU. The influence of finite element modeling of plane hydraulic line support on stress analysis[J]. Journal of Civil Aircraft Design and Research, 2014, 113 : 84–87. DOI: 10.3969/j.issn.1674-9804.2014.02.023 |
| [9] |
闫辉, 姜洪源, 李瑰贤, 崔虎. 航空发动机管路支撑用钢丝隔振器仿真研究[J]. 航空学报, 2006, 11 : 1080–1084.
Hui YAN, Hong-yuan JIANG, Gui-xian LI, Hu CUI. Aeroengine pipe support wire vibration isolator simulation[J]. Journal of Aviation, 2006, 11 : 1080–1084. DOI: 10.3321/j.issn:1000-6893.2006.06.017 |
| [10] |
施引, 朱石坚, 何琳. 舰船动力机械噪声及其控制[M]. 北京. 国防工业出版社, 1990.
SHI Yi, ZHU Shi-jian, HE Lin. Ships machinery noise and its control[M]. Beijing. National defense industry press, 1990. |
 2017, Vol. 39
2017, Vol. 39
