0 引　言

船舶电力推进相比传统推进方式具有很多优点，近年来在发达国家船舶中广泛应用。电力推进所用的永磁同步电机功率密度高、效率高、恒功率运行范围宽，可以很好地适用于船舶海上航行。但是，由于呈现出高度磁饱和和非线性化特性，永磁同步电机的控制更加复杂^[1]。直接转矩控制具有结构简单、转矩响应速度快和鲁棒性强等优点。直接转矩控制存在着显著的缺点，比如磁链及转矩脉动大、逆变器开关频率不恒定等问题。这与工业生产中对电机性能不断提高的需求不符。目前已经有许多关于对直接转矩控制改进的论文发表。文献[2]增加零电压矢量，采用有效电压矢量和零电压矢量共同作用于逆变器，改进了电压矢量开关表，但降低转矩脉动效果不明显。文献[3]提出采用恒定开关频率的直接转矩控制，但电机参数变化容易影响控制效果。文献[4]采用空间电压矢量调制技术，减小转矩脉动，同样该改进方法对系统参数变化敏感，鲁棒性不是很好。

滑模变结构控制在控制领域应用得越来越多。它具有许多优点，如鲁棒性强、对外界扰动有抑制作用、动态响应快等^{[5 – 9]}。针对传统直接转矩控制中转矩和磁链脉动过大的问题，将滑模变结构控制应用到其中，并结合空间电压矢量调制。使系统对参数变化和外界干扰的鲁棒性增强，且具有快速动态响应效果。

1 永磁同步电机数学模型

假设转子永磁磁场在气隙空间分布为正弦波；忽略定子铁心饱和；不计铁心涡流与磁滞损耗；转子上无阻尼绕组。在以上假设下，建立在d-q 坐标系下的永磁同步电机数学模型，其电压方程为：

$\left[ \begin{array}{l}{u_d}\\{u_q}\end{array} \right] = \left[ \begin{array}{l}R + p{L_{d\;}}\;\;\;\;\;\; - {\omega _r}{L_q}\;\\\;\;{\omega _r}{L_d}\;\;\;\;\;\;\;R + p{L_d}\end{array} \right]\left[ \begin{array}{l}{i_d}\\{i_q}\end{array} \right] + \left[ \begin{array}{l}\;\;\;0\\{\omega _r}{\psi _f}\end{array} \right],$

(1)

其中u_d和u_q是d-q轴定子电压；i_d和i_q是d-q轴定子电流；R是定子电阻；L_d和L_q是d-q轴电感；p是微分算子；ω_r是转子电角速度；ψ_f是永磁铁励磁产生的磁链。

式（1）通过坐标变换可以得到α-β坐标系下电压方程：

$\begin{split}\left[ \begin{array}{l}{u_\alpha }\\{u_\beta }\end{array} \right] = & \left[ \begin{array}{l}R + p{L_d}\;\;\;\;\;\;\;\;\;\;{\omega _r}({L_d} - {L_q})\\ - {\omega _r}({L_d} - {L_q})\;\;\;\;R + p{L_d}\end{array} \right]\left[ \begin{array}{l}{i_\alpha }\\{i_\beta }\end{array} \right] +\\ &\left[ {({L_d} - {L_q})({\omega _r}{i_d} - {{\dot i}_q}) + {\omega _r}{\psi _f}} \right]\;\left[ \begin{array}{l} - \sin {\theta _r}\\\;\cos {\theta _r}\end{array} \right]{\text{。}}\end{split}$

(2)

其中θ_r为d轴与α轴的夹角。

令式（2）后半部分为扩展反电动势：

$\left[ \begin{array}{l}{e_\alpha }\\{e_\beta }\end{array} \right] = \left[ {({L_d} - {L_q})({\omega _r}{i_d} - {{\dot i}_q}) + {\omega _r}{\psi _f}} \right]\;\left[ \begin{array}{l} - \sin {\theta _r}\\\;\cos {\theta _r}\end{array} \right]{\text{。}}$

(3)

式（2）用状态方程表示为：

$\begin{split}\left[ \begin{array}{l}{{\dot i}_\alpha }\\{{\dot i}_\beta }\end{array} \right] = & \left[ \begin{array}{l} - R/{L_d}\;\;\;\;\;\;\;\;\;\;\;\; - {\omega _r}({L_d} - {L_q})/{L_d}\\{\omega _r}({L_d} - {L_q})/{L_d}\;\;\;\;\; - R/{L_d}\end{array} \right]\left[ \begin{array}{l}{i_\alpha }\\{i_\beta }\end{array} \right] - \\ &\left[ \begin{array}{l}1/{L_d}\;\;\;0\\0\;\;\;\;\;\;\;1/{L_d}\end{array} \right]\;\left[ \begin{array}{l}{e_\alpha }\\{e_\beta }\end{array} \right] + \frac{1}{{{L_d}}}\left[ \begin{array}{l}{u_\alpha }\\{u_\beta }\end{array} \right]{\text{。}}\end{split}$

(4)

α-β坐标系下定子磁链方程为：

$\left\{ \begin{array}{l}{{\dot \psi }_\alpha } = {u_\alpha } - R{i_\alpha },\\{{\dot \psi }_\beta } = {u_\beta } - R{i_\beta }{\text{。}}\end{array} \right.$

(5)

其转矩方程为：

$T = \frac{{3{p_n}}}{2}({\psi _\alpha }{i_\beta } - {\psi _\beta }{i_\alpha }),$

(6)

其中p_n为极对数。

磁链幅值的平方为：

$\psi = \psi _\alpha ^2 + \psi _\beta ^2{\text{。}}$

(7)

2 滑模控制器设计 2.1 确定切换函数

将转矩偏差和定子磁链偏差作为输入状态变量，设计合适的参数，状态变量渐渐稳定于参考值。状态变量进入到滑模面后，系统控制性能不受电机参数变化影响，只与滑模参数有关，体现出鲁棒性强的优点。

选取转矩和磁链的切换函数为：

${S} = {\left[ {{S_T}\;{S_\psi }} \right]^{\rm T}},$

(8)

$\left\{ \begin{array}{l}{S_T} = {k_{p{\rm{1}}}}{e_T} + {k_{i{\rm{1}}}}\int_0^t {{e_T}{\rm d}t}, \\[5pt]{S_\psi } = {k_{p{\rm{2}}}}{e_\psi } + {k_{i{\rm{2}}}}\int_0^t {{e_\psi }{\rm d}t}{\text{。}} \end{array} \right.$

(9)

式中： ${e_T} = {T^ * } - T$ ， ${e_\psi } = {\psi ^ * } - \psi $ 。其中e_T为转矩偏差量，e_ψ为磁链偏差量，T^*和ψ^*分别为转矩参考值和磁链参考值的平方。T和ψ分别为实时计算出的转矩值和磁链幅值平方，k_p和k_i是正值。

2.2 滑动模态控制率

系统滑模面的微分可以表示为

$\dot{ S} = {\left[ {{{\dot S}_T}\;{{\dot S}_\psi }} \right]^{\rm T}} = {F} + {DU},$

(10)

式中：F，D为系数矩阵，U为控制律矩阵。

根据式（9）求导得：

$\left\{ \begin{array}{l}{{\dot S}_T} = {k_{p1}}{{\dot e}_T} + {k_{i1}}{e_T},\\{{\dot S}_\psi } = {k_{p{\rm{2}}}}{{\dot e}_\psi } + {k_{i{\rm{2}}}}{e_\psi }{\text{。}}\end{array} \right.$

(11)

${F} = {\left[ {{F_1}\;{F_2}} \right]^{\rm T}}$

(12)

$\left\{ \begin{split}\!\!\!\!& {F_1} = - \displaystyle\frac{3}{2}{k_{p1}}{p_n}{\rm{\{ }}[{\omega _r}({L_d} - {L_q}){\psi _\alpha }{i_\alpha } - R{\psi _\alpha }{i_\beta } - \\[3pt]& \quad\quad{\psi _\alpha }{e_\beta }]/{L_d} + [{\omega _r}({L_d} \!-\! {L_q}){\psi _\beta }{i_\beta } \!+\! R{\psi _\beta }{i_\alpha } \!+\\[3pt] & \quad\quad{\psi _\beta }{e_\alpha }]/{L_d}{\rm{\} }} \!+{k_{p1}}{\rm{(}}{T^ * } \!-\! T{\rm{)}},\\\!\!\!\!& {F_2} = 2{k_{p2}}(R{\psi _\alpha }{i_\alpha } + R{\psi _\beta }{i_\beta }) + {k_{i2}}({\psi ^ * } - \psi ){\text{。}}\end{split} \right.$

(13)

${U} = {\left[ {{u_\alpha }\;{u_\beta }} \right]^{\rm T}},$

(14)

${D} = - \left[ \begin{array}{l}\displaystyle\frac{3}{2}{p_n}({i_\beta } - {\psi _\beta }/{L_d})\;\;\;\displaystyle\frac{3}{2}{p_n}({\psi _\alpha }/{L_d} - {i_\alpha })\\\;\;\;\;\;\;\;\;\;\;\;{\rm{2}}{\psi _\alpha }\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{2}}{\psi _\beta }\end{array} \right]{\text{。}}$

(15)

2.3 系统稳定性

选取李雅普诺夫函数

$V = \frac{1}{2}{{S}^{\rm T}}{S},$

(16)

并对其求导得：

$\dot V = {{S}^{\rm T}}\dot{ S} = {{S}^{\rm T}}({F} + {DU}),$

(17)

控制系统稳定需要满足 $\dot V < 0$ ，同时要求滑模控制系统在正常运动阶段具有良好的动态品质，选取指数趋近律来设计滑模控制器，即可取控制律

${U} = - {{D}^{ - 1}}\left[ \begin{array}{l}{F_1} + \;{K_1}{S_T} + \;{K_2}sign({S_T})\\{F_2} + {K_3}{S_\psi } + {K_4}sign({S_\psi })\end{array} \right],$

(18)

其中K₁，K₂，K₃，K₄是指数趋近律参数。

将式（8）、式（12）、式（15）、式（18）代入到式（17）可得：

$\begin{split}\dot V = & - {S_T}\left[ {{K_1}{S_T} + {K_2}sign({S_T})} \right] - \\ &{S_\psi }\left[ {{K_3}{S_\psi } + {K_4}sign({S_\psi })} \right]{\text{。}}\end{split}$

(19)

由于S_T与 ${K_1}{S_T} + {K_2}sign({S_T})$ 符号相同，S_ψ与 ${K_3}{S_\psi } + {K_4}sign({S_\psi })$ 符号相同，所以 ${S_T}\left[ {{K_1}{S_T} +} \right. > 0$ $\left. {{K_2}sign({S_T})} \right] > 0$ ， ${S_\psi }\left[ {{K_3}{S_\psi } + {K_4}sign({S_\psi })} \right] > 0$ ，即 $\dot V < 0$ 。证明系统可以运动到滑模面上，系统在李雅普诺夫意义下稳定。

根据式（25）计算出u_α，u_β参考值，送入SVPWM模块作为输入，输出控制逆变器开关通断的电压矢量信号，驱动电机正常运行。

2.4 系统鲁棒性

系统在稳定运行时，切换函数会受到外界扰动和系统内部器件参数变化的干扰的影响。假设系统稳定运行时受到的干扰为H， ${H} = {\left[ {{H_1}\;{H_2}} \right]^{\rm T}}$ 为扰动总和，则

$\dot{ S} = {F} + {DU} + {H},$

(20)

将式（20）代入式（17）得：

$\begin{split}\dot V = & - {S_T}\left[ {{K_1}{S_T} + {K_2}sign({S_T}) - {H_1}} \right] - \\ &{S_\psi }\left[ {{K_3}{S_\psi } + {K_4}sign({S_\psi }) - {H_2}} \right]{\text{。}}\end{split}$

(21)

根据此式，只要满足 ${K_2} > \left| {{H_1}} \right|$ ， ${K_4} > \left| {{H_2}} \right|$ ，也能证明 $\dot V < 0$ 。由此可推知，只要设计合理的滑模控制器参数，系统参数变化或外干扰作用下，控制系统仍然具有很强鲁棒性。

3 滑模变结构控制系统仿真与分析

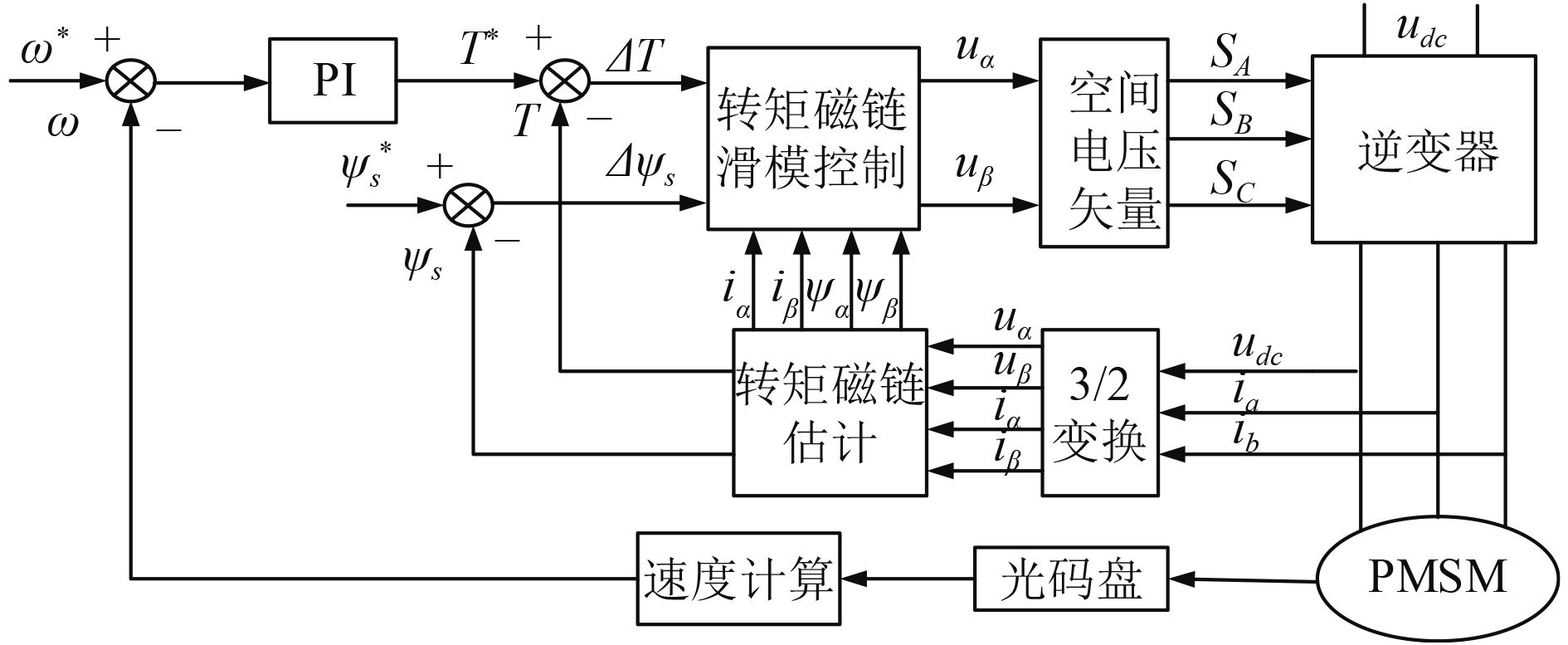
为了验证基于滑模变结构的直接转矩控制系统的控制性能，应用Matlab/Simulink对直接转矩控制策略和基于滑模变结构永磁同步电机控制系统进行仿真研究。根据图1所示的系统控制结构图搭建仿真模型。

电机的仿真实验参数设置如下：电机极对数n_p=4，定子绕组电阻Rs=0.033 5 Ω，直交轴电感分别为L_d=L_q=0.000 47 H，永磁体磁链0.13 Wb，转动惯量J=0.013 kg·m²。

选取永磁同步电机设定转速n*=500 r/min控制进行试验，仿真时间0.2 s，空载启动，0.1 s时加入50 N·m的负载，结合电机的主要性能参数对实验结果分析，验证其控制策略的正确性。涉及到的主要性能参数有转速n，转矩T_e，定子磁链ψ_s等。

图2为传统直接转矩控制和基于滑模变结构直接转矩控制下转速曲线对比。从图中可以看到在0.1 s加入负载后传统直接转矩控制下转速响应较慢，经过一段时间波动后才进入稳定状态，而基于滑模变结构控制下转速响应较快。

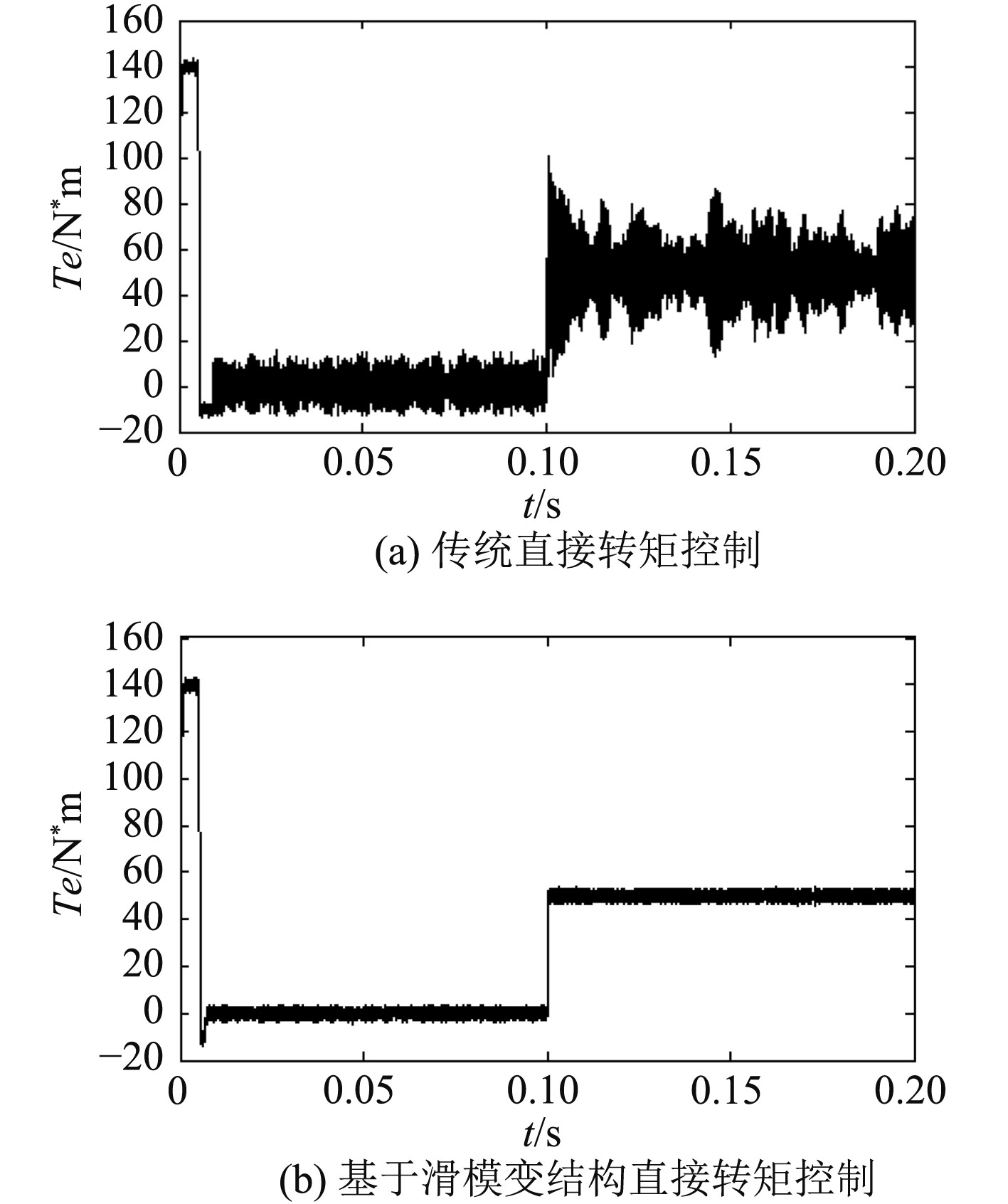
图3为传统直接转矩控制和基于滑模变结构直接转矩控制下转矩曲线对比。可以看到，在滑模变结构应用到直接转矩控制下后，转矩脉动明显减小，0.1 s加入负载后转矩响应迅速，并且很快进入稳定状态，说明了其鲁棒性较好的特点。系统动态性能得到明显改善，且转矩较稳定。

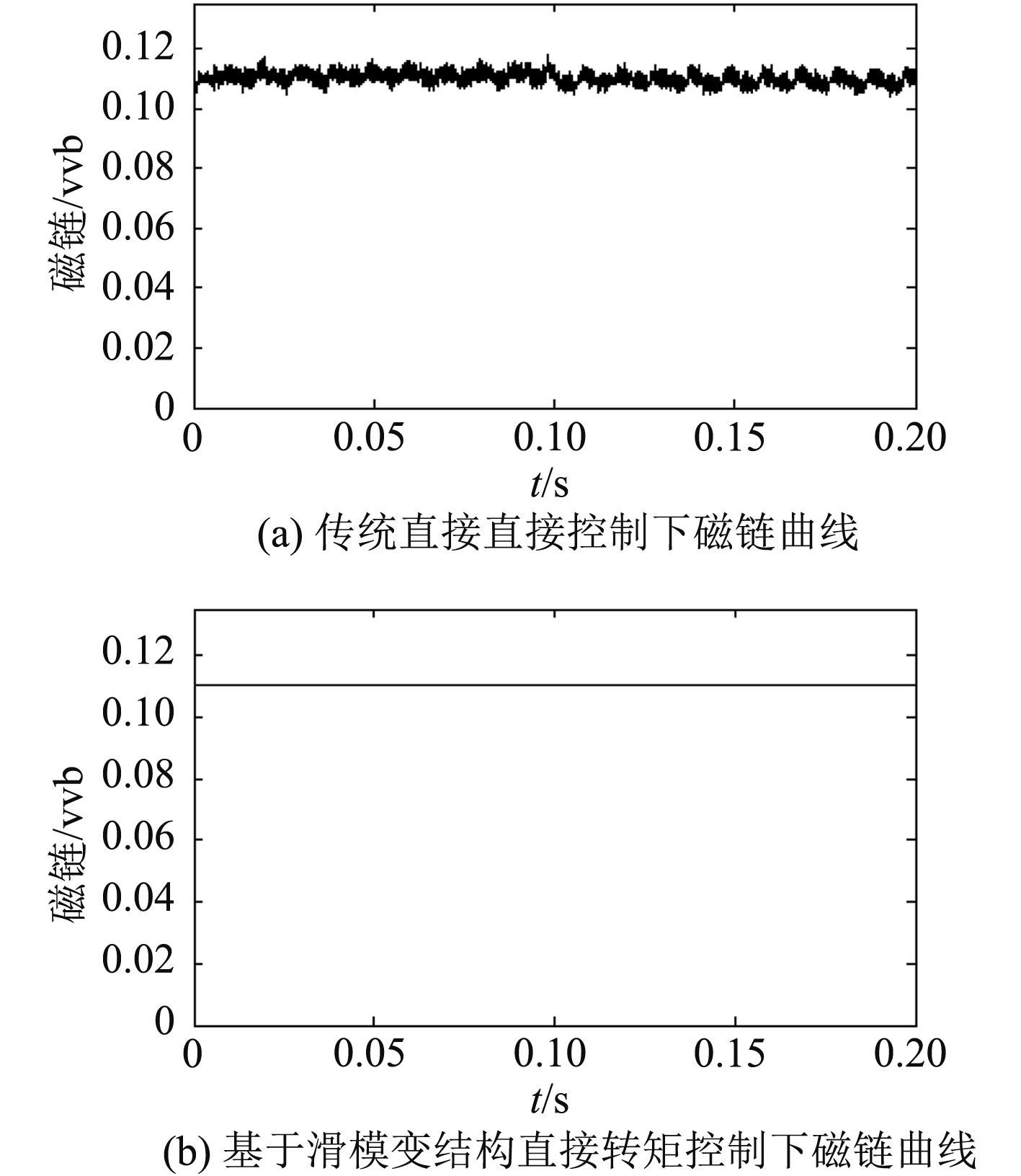
图4 为传统直接转矩控制和基于滑模变结构直接转矩控制下磁链曲线对比。图中看到较传统直接转矩控制策略，引入滑模控制器后定子磁链脉动有很大减小。

4 结　语

本文针对船用永磁同步电机设计了一种基于滑模的直接转矩控制系统。该控制方法用转矩／磁链滑模控制器替代常规直接转矩控制中的磁滞比较器，运用指数趋近律设计控制率，可以有效削弱抖振，克服了常规直接转矩控制转矩和磁链脉动大的缺点，大幅度减小转矩和磁链的脉动，稳定了开关频率，在常规控制方法优点的基础上，增强了鲁棒性。