滤波技术对于船舶的运动控制系统具有非常重要的地位。由一阶波浪导致的船舶高频运动不能够进入到控制系统中去。如果进入控制系统后,会引起推进器做不必要的动作,造成推进器的疲损,并且会消耗大量不必要的燃料[1]。传统的低通或者陷波滤波器会造成相位滞后,降低控制器的性能。卡尔曼滤波器,虽然能够很好地解决这一问题,但是却十分的依赖系统的模型,而且在实船当中,其过程噪声矩阵、初始值、初始误差矩阵也很难确定[2]。所以,本文提出一种基于递推的最小二乘频率估计的改进陷波滤波器,在滤除高频波的同时,又能保证具有很好的相位特性。
1 海浪的高频模型高频波的模型一般用的是线性的波浪模型,该模型能够对一阶波浪运动进行很好的近似[6 – 7]:
|
$h(s) = \frac{{{K_\omega }s}}{{{s^2} + 2\varsigma {\omega _0}s + \omega _0^2}},$
|
(1) |
式中:
将式(1)转化为时域的形式,得
|
$\ddot y(t) + 2\varsigma {\omega _0}\dot y(t) + \omega _0^2y(t) = {K_\omega }\dot \omega (t),$
|
(2) |
转化为状态空间的形式:
|
$\left\{ \begin{array}{l}{{\dot X}_H} = {A_H}{X_H} + {E_H}{w_H},\\[4pt]{Y_H} = {C_H}{X_H}\text {。}\end{array} \right.$
|
(3) |
式中:
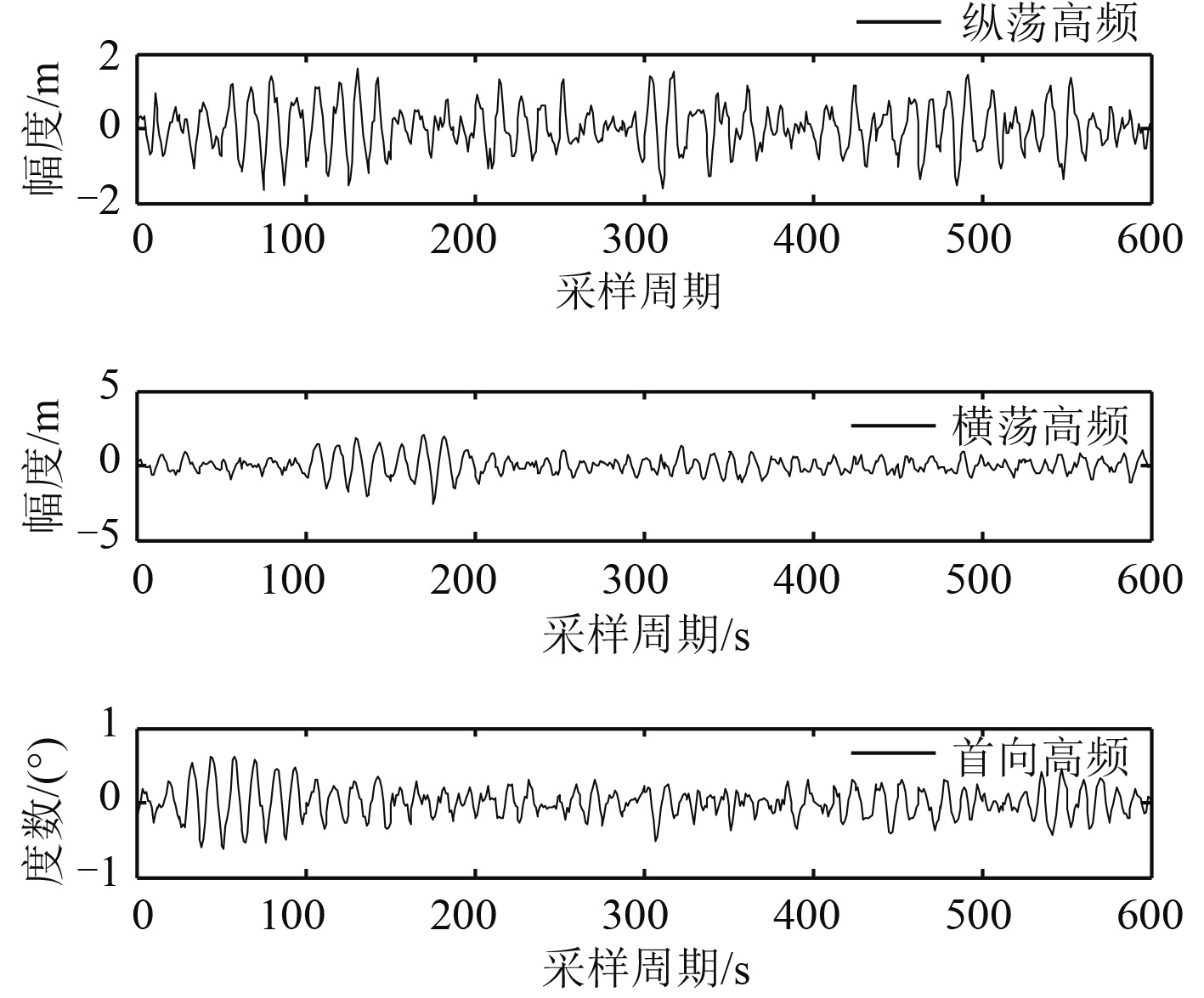
当主导波频 ω0 = 0.5 rad,ζ = 0.1,σω = 0.58 时,高频的输出如图1所示。
|
图 1 高频波浪的输出 Fig. 1 Output of high frequency waves |
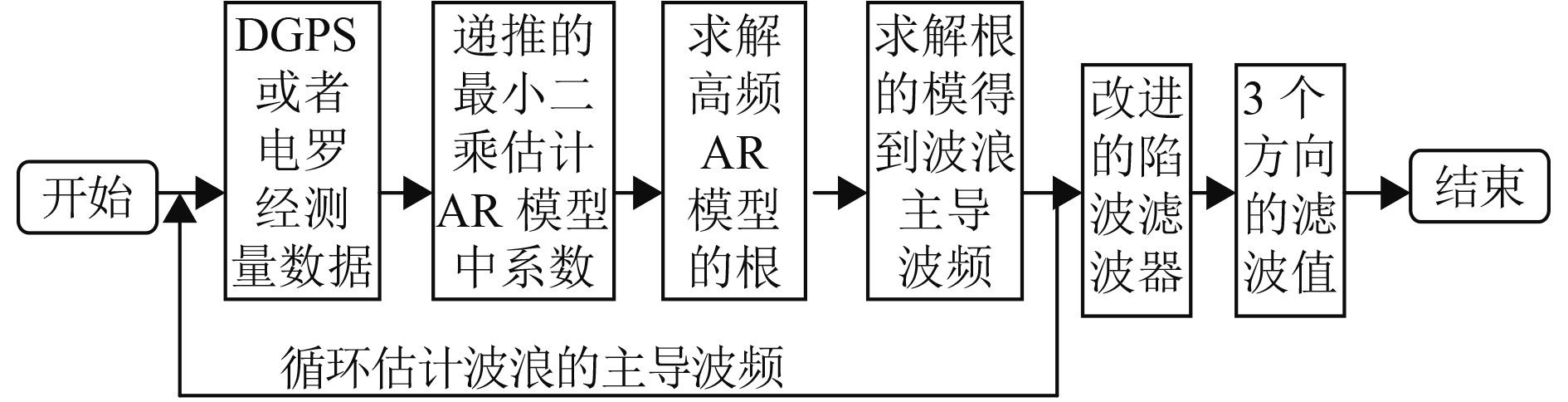
由图2可看到,DGPS 的数据或者电罗经的数据首先通过递推最小二乘估计得到高频海浪 AR 模型中的系数,然后求解 AR 模型,得到海浪的主导波频。接着设置改进的陷波滤波器的陷波频率,最后将每个方向的数据传入到改进的陷波滤波器当中去,得到 3 个方向滤波后的值。
|
图 2 滤波流程图 Fig. 2 Filtering flow chart |
递推的最小二乘估计,虽然算法不是最新的算法,但是并未有任何文献把该方法应用于估计海浪的主导波频。其具体的方法如下:
波浪主导波频的估计可以通过建立一个 AR 模型来估计出来[4]。该随机过程通过白噪声激励产生。
AR 模型的形式如下:
|
$A({z^{ - 1}})y(k) = e(k)\text{。}$
|
(4) |
船舶的总运动方程为:
|
$\psi (s) = {\psi _L}(s) + {\psi _H}(s),$
|
(5) |
其中:ΨH(s)为船舶的高频运动;ΨL(s)为船舶的低频运动。ΨH(s)可以通过一个一阶高通滤波器来得到:
|
${\psi _H}(s) = \frac{{{T_f}s}}{{1 + {T_f}s}}\psi (s)\text{。}$
|
(6) |
其中 Tf 为滤波的时间常数。为了将式(6)表示成 AR 模型的形式,需重新定义一个变量[3]:
|
${\xi _H}(s)\! =\!\! \frac{1}{s}{\psi _H}(s) \!= \!\!\frac{{{T_f}}}{{1 + {T_f}s}}\psi (s) \!=\!\! \frac{{{K_w}}}{{{s^2} + 2\zeta ws + {w^2}}}\omega (s)\text{。}\!\!\!$
|
(7) |
将式(8)与式(5)进行对比,得到:
|
$\begin{array}{l}A({z^{ - 1}}) = 1 + {a_1}{z^{ - 1}} + {a_2}{z^{ - 2}} + {a_3}{z^{ - 3}} = 0,\\[5pt]e(k) = {K_w}w(k)\text{。}\end{array}$
|
(8) |
对 a1,a2,a3 的估计通过带遗忘因子的递推最小二乘估计得到的:
|
$\begin{array}{l}\hat \theta (k) = \hat \theta (k - 1) + K(k)[y(k) - {\phi ^{\rm T}}(k)\hat \theta (k - 1)],\\[5pt]K(k) = \displaystyle\frac{{P(k - 1)\phi (k)}}{{\lambda + {\phi ^T}(k)P(k - 1)\phi (k)}},\\[8pt]P(k) = \frac{1}{\lambda }[I - K(k){\phi ^{\rm T}}(k)]P(k - 1)\text{。}\end{array}$
|
(9) |
其中,
采样时间为 1 s,修改高频海浪模型中主导波频参数,产生如表1所示的 8 段数据。
|
|
表 1 高频波浪数据 Tab.1 Data of high frequency wave |
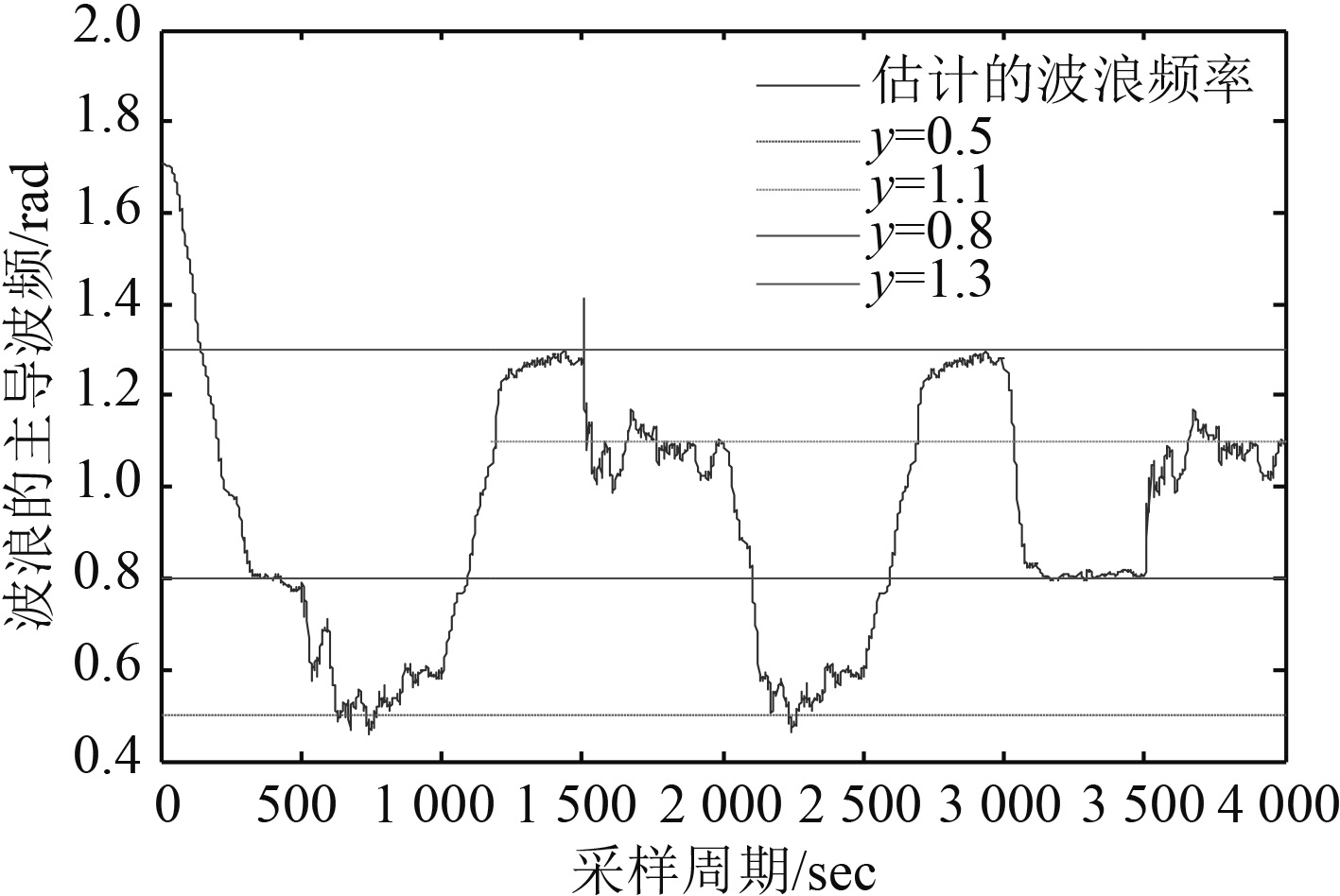
RLS 仿真估计波浪频率的结果如图 3 所示。
|
图 3 递推的最小二乘波频估计 Fig. 3 Recursive least square wave frequency estimation |
从图中可看到,一开始由于初始状态值,初始的误差选取的影响导致波浪频率估计的波动存在误差,波动比较大,但是随着时间的推移,大约在 300 s 之后,波频估计逐渐稳定,面对不断跳变的波频,如在临界点 1 000 s,1 500 s,2 000 s,2 500 s,3 000 s,3 500 s等处均能够达到预期的效果,比较好的跟踪了波浪的频率,可以满足工程应用的需求。
4 改进的陷波滤波器传统的陷波滤波器,虽然能够很好地滤除掉一阶波浪产生的高频运动,但同时也产生了严重的相位滞后,在时域里面的表现就是信号的延时[8 – 9]。为此,针对传统滤波器的缺陷,提出了积分补偿的陷波滤波器。
传统的陷波滤波器的传递函数为:
|
$H(s) = \frac{{{s^2} + {w^2}}}{{{s^2} + kws + {w^2}}} = 1 - \frac{{kws}}{{{s^2} + kws + {w^2}}} = 1 - Q,$
|
(10) |
其中:w 为陷波的频率;ζ 为相对阻尼系数;Q 为带通滤波器。
将 Q 转化为状态空间的形式:
|
$\begin{array}{l}\mathop {{x_1}}\limits^ \bullet = w{x_2},\\\mathop {{x_2}}\limits^ \bullet = - w{x_1} + kw(u - {x_2})\text{。}\end{array}$
|
(11) |
其中:
为了克服传统滤波器相位滞后的缺陷,需要对式(12)进行改进,改进后的状态方程为:
|
$\begin{array}{l}\mathop {{x_1}}\limits^ \bullet = w{x_2},\\\mathop {{x_2}}\limits^ \bullet = - w{x_1} + kw(u - {x_2} - {x_3}),\\\mathop {{x_3}}\limits^ \bullet = aw(u - {x_2} - {x_3})\text{。}\end{array}$
|
(12) |
其中 x3 对传统的陷波滤波器输出起到补偿作用,x3 的大小可以通过 a 的值来调节。
改进滤波器的框图如图 4 所示。

|
图 4 改进的滤波框图 Fig. 4 Improved filter block diagram |
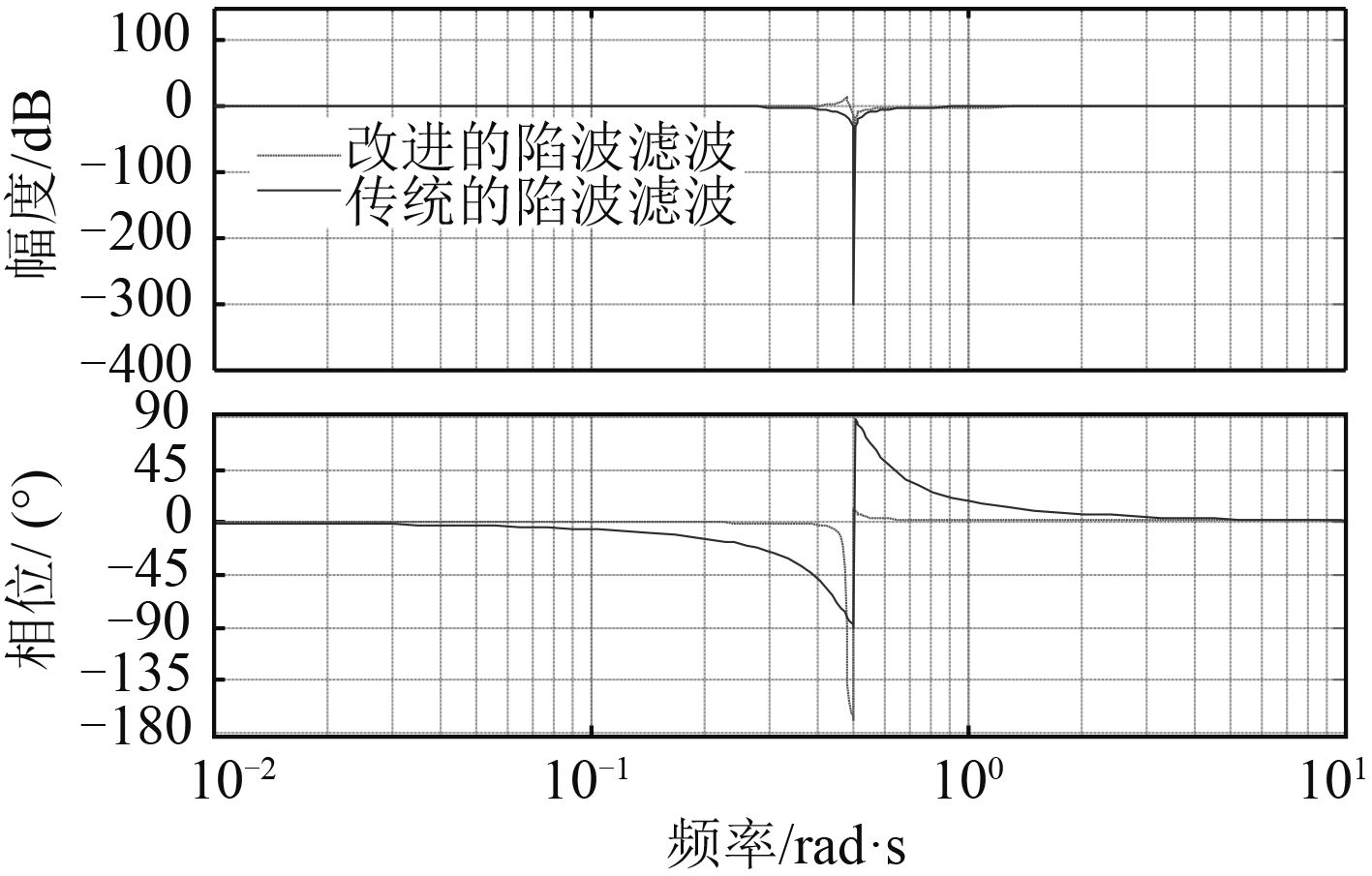
当陷波的频率为 0.5 rad/s,ζ 为 0.1 时,2 种滤波器的 bode 图如图5所示。
|
图 5 改进滤波器的伯德图 Fig. 5 Improved filter Bode diagram |
从伯德图的幅频曲线可看出,滤波器可对波浪进行有效的幅度衰减,从相频曲线图上可看到与传统的滤波器相比较而言,改进的陷波滤波器具有很好的相频特性,信号的相位延迟和超前得到明显的改善。
5 仿真实验以某海工多用途拖轮为对象,利用改进滤波器来进行仿真。开始点在(0 m,0 m),首向值为 0 °,定位点设置在(20 m,20 m),首向值设置为 0 °,主导波频
|
|
表 2 仿真船舶的主要参数 Tab.2 Main parameters of simulation ship |
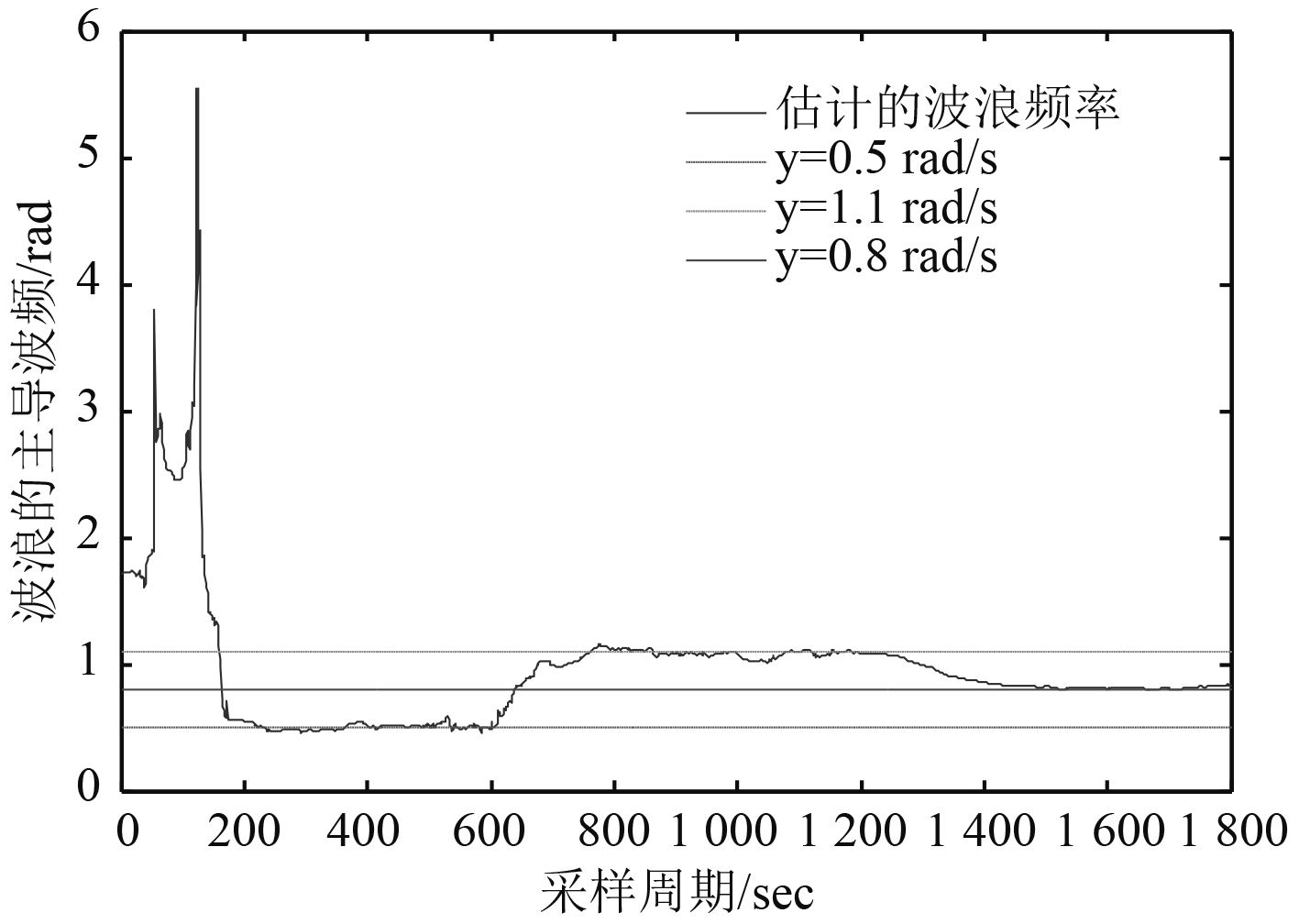
波频估计的结果如图 6 所示。
|
图 6 波频估计 Fig. 6 Wave frequency estimation |
从仿真结果来看,一开始由于初始值和初始误差矩阵的选取造成了波频估计器的不稳定,大约在 180 s 左右稳定下来,结果保持在我们所期望的 0.5 rad/s 左右,接着无论在 600 点处的上升沿还是在 1 200 处的下降沿,都能够很好地追踪到波浪的主导波频。
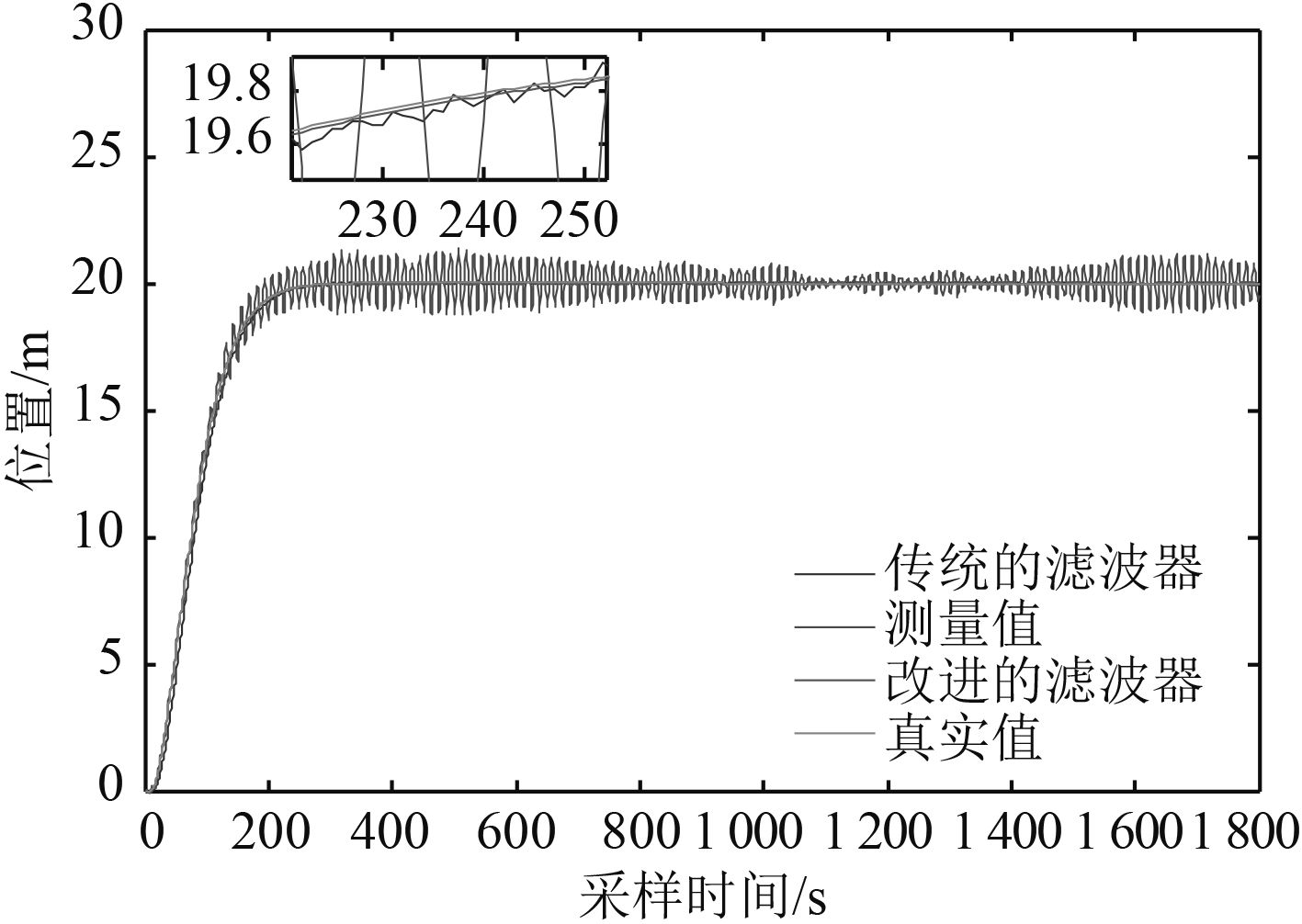
|
图 7 船舶纵荡的对比 Fig. 7 Comparision of the direction of surge |

|
图 8 船舶横荡对比 Fig. 8 Comparision of the direction of sway |
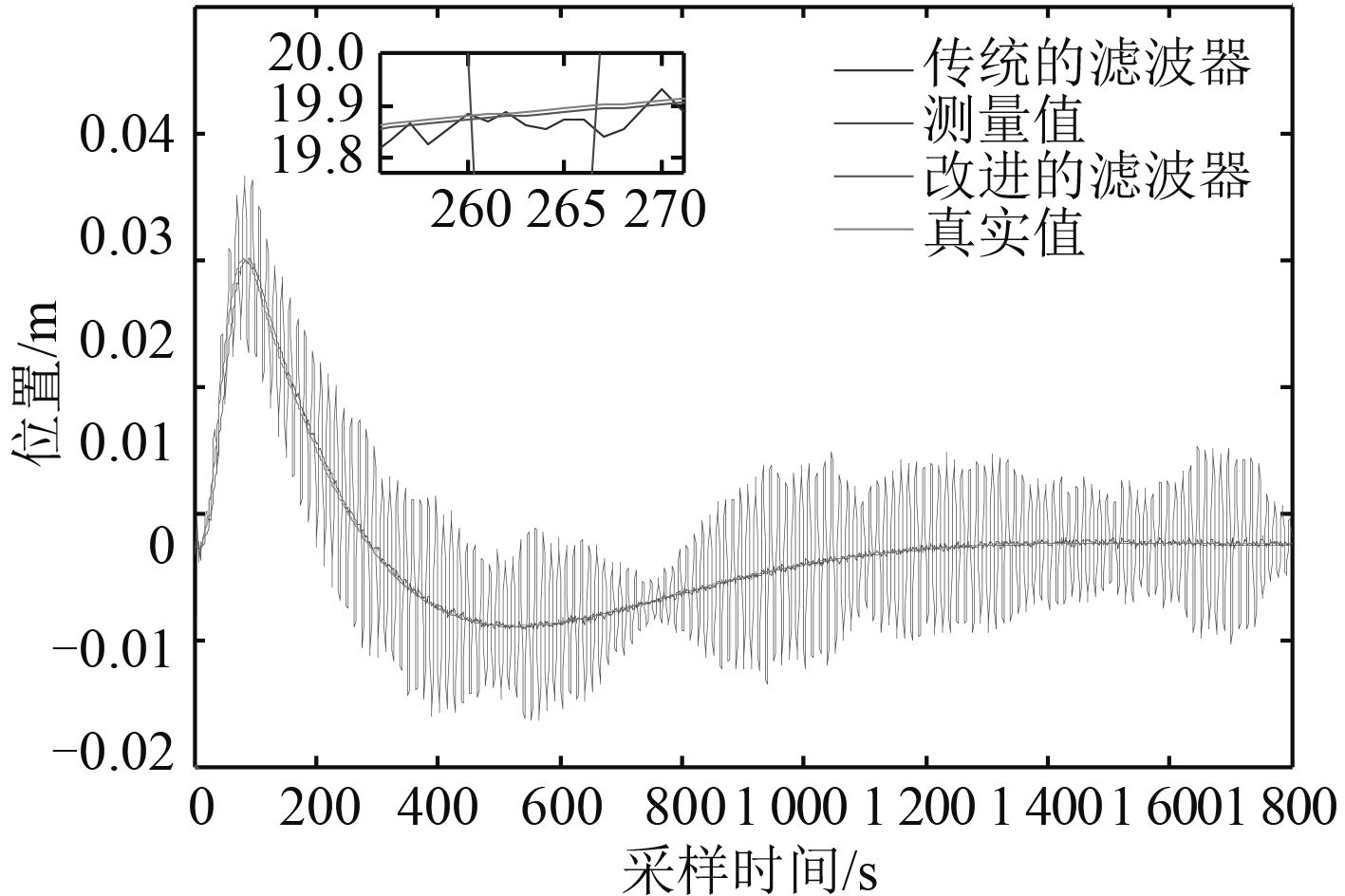
|
图 9 船舶首向对比 Fig. 9 Comparision of the direction of yaw |

|
图 10 船舶行走轨迹对比 Fig. 10 Comparison of ship's walking trajectory |
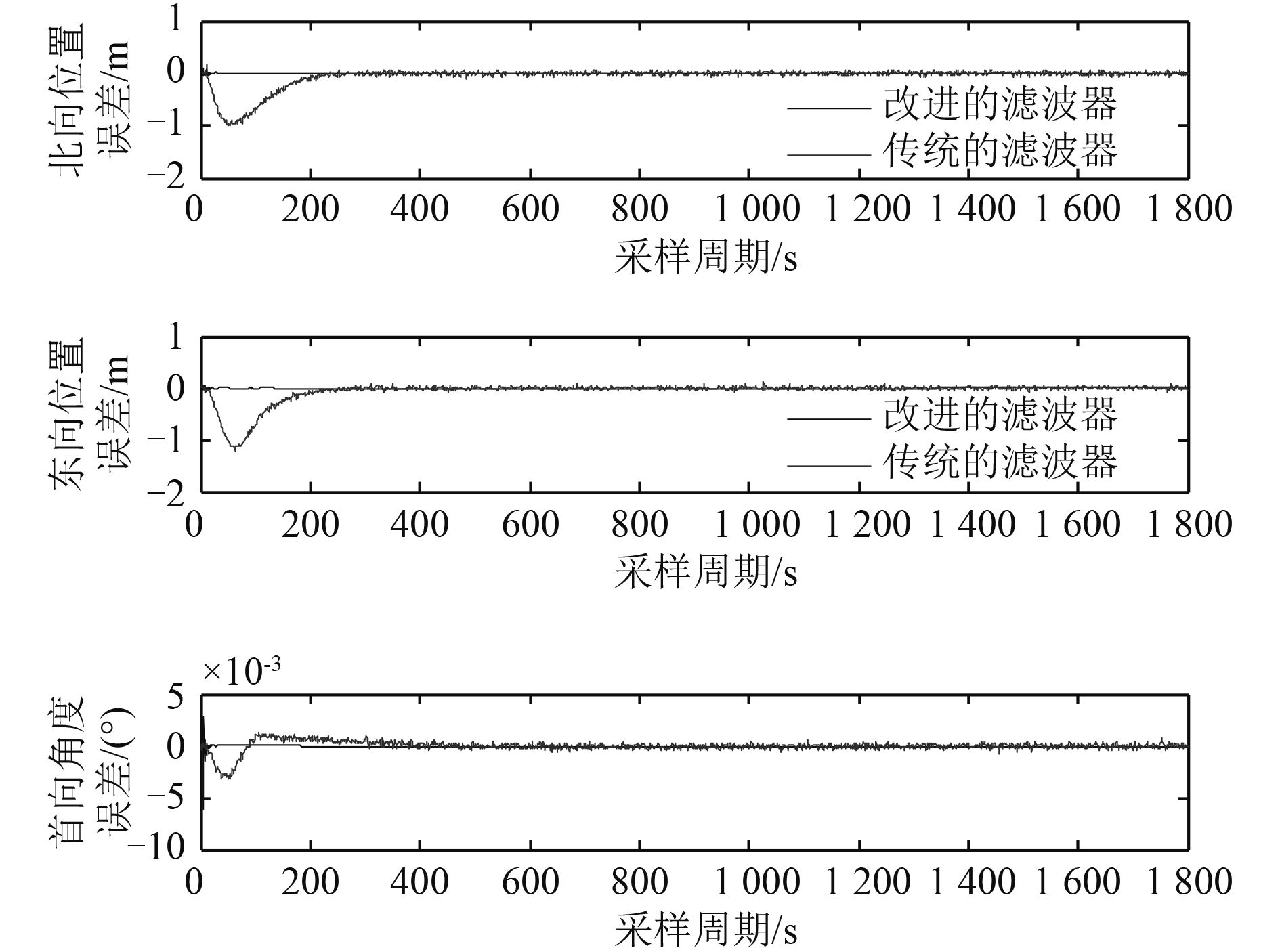
|
图 11 误差对比 Fig. 11 Error contrast |
由图可以看到,船舶的纵荡、横荡和首向3个方向的改进滤波器具有更好的优越性,能够很好地去除高频波浪干扰,使得滤波值更接近真实值。从图 10 中可以看到,与传统的陷波滤波器相比较而言,改进陷波滤波器更加地接近于真实值。从图 11 中可以明显地看出 3 个方向的误差,改进滤波器具有更小的误差。
6 结 语综上所述,本文针对传统陷波滤波器卡尔曼滤波器的缺陷提出了一种不依赖于具体船舶模型的自适应得改进型陷波滤波器。并以某拖轮为仿真对象,进行仿真。仿真的结果表明,用基于递推的最小二乘(RLS)波频估计的改进得陷波滤波器,能够实时的估计出波浪的主导波频,对外界环境有很好的自适应性。与传统的陷波滤波器相比,具有更好的相位特性,解决了由于相位的滞后或者超前导致的时间上的偏差,同时在滤波过程中未涉及船舶的质量矩阵,水动力系数矩阵等参数的计算,所以与扩展卡尔曼相比具有更好的鲁棒性,不依赖于船舶的运动模型。
| [1] | 边信黔, 付明玉, 王元慧. 船舶动力定位[M]. 北京: 科学出版社, 2011. |
| [2] | FOSSENT I. Kalman filtering for positioning and heading control of ships and offshore rigs[J]. IEEE Control Systems, 2009, 29 (6): 32–46. DOI: 10.1109/MCS.2009.934408 |
| [3] | FOSSEN T I. Guidance and control of ocean vehicles[M]. Chichester, UK: John Wiley and Sons, 1994. |
| [4] |
张贤达. 现代信号处理[M]. 北京: 清华大学出版社, 1995.
ZHANG Xian-da. Modern signal processing[M]. Beijing: Tsinghua University Press, 1995. |
| [5] | LOUEIPOURM. Wave filtering and state estimation in dynamic positioning of marine vessels using position measurement[J]. IEEE Transactions on Instrumentation and Measurement, 2015, 64 (12): 3253–3261. DOI: 10.1109/TIM.2015.2459551 |
| [6] |
齐国鹏, 俞孟蕻, 袁伟. 动力定位系统自适应滤波技术[J]. 舰船科学技术, 2013, 35 (10): 96–100.
QIGuo-peng, YUMeng-hong, YUANWei. Research on adaptive filtering techniques in dynamic positioning systems[J]. Ship Science and Technology, 2013, 35 (10): 96–100. DOI: 10.3404/j.issn.1672-7649.2013.10.022 |
| [7] | FOSSEN T I. Marine control systems-guidance, navigation, and control of ships, rigs and underwater vehicles[M]. Norway: Marine Cybernetics, 2002. |
| [8] | TANNURI E A, BRAVIN T T, PESCE C P. Dynamic positioning systems: comparison between wave filtering algorithms and their influence on performance[C]//Proceedings of ASME 2003 22nd International Conference on Offshore Mechanics and Arctic Engineering. Cancun, Mexico: ASME, 2003: 109–117. |
| [9] | FAŸ H. Dynamic positioning systems principles, design and applications[M]. Paris: Editions Technip, 1990. |
 2017, Vol. 39
2017, Vol. 39
