多浮体海上平台可用于各种海洋资源的开发和利用,随着陆地资源枯竭,国际海洋工程界掀起研究超大型浮式结构物的热潮。最早日本研究一种浮箱式海上平台,并通过试验验证海上浮动平台可行性[1, 2]。相比于日本,美国提出半潜式的移动海上移动基地,并进行相关研究[3]。另外新加波[4]、挪威[5]等也从事大型浮式结构的研究。
为了加快我国开发大型海洋浮式结构物的步伐,在国内,一批学者也相继对大型海洋结构物深入研究。吴有生等[6]使用三维线性水弹性力学分析了极大型浮式结构物的运动和连接器的应力响应。宋皓[7]对具有缓变地形的超大型浮体响应使用多重尺度法和常规的有限水深格林函数法势流理论进行分析。徐道临[8]对海上浮动机场动力学建模及非线性动力响应特性分析。李洪仙[9]对系泊多体海上平台非线性动力特性研究进行深入研究。
目前对多浮体海上平台的问题研究,大部分通过模型试验方式,需要投入大量的经费及耗费大量时间。本文利用AQWA软件,基于三维势流理论,对多浮体海上平台水动力响应分析进行深入研究,得到的结论可以为大型海上浮体结构设计提供指导意义。
1 基本理论使用AQWA求解浮体模块的辐射和衍射波浪力时,基于AQWA的理论假设有:1)模块的初速度为0或具有很小的初速度;2)流体无粘性不可压缩且无旋;3)入射规则波的幅值相对波长很小。
围绕浮体模块流域的速度势函数定义为:
|
$\phi (\overrightarrow X ,t) = {a_w}\varphi (\overrightarrow X ){e^{ - i\omega t}},$
|
(1) |
式中:t为时间;i为虚数单位;aw为入射波幅值;ω为波浪频率;
通过线性伯努利方程可以得到水动力压力分布:
|
$P = - \rho \frac{{\partial \phi (\overrightarrow X ,t)}}{{\partial t}} = i\omega \rho \varphi (\overrightarrow X ){e^{ - i\omega t}},$
|
(2) |
式中,ρ为水密度。
使用模块表面的单位法向量n来表示自由度的响应,水动力表达形式可以得到广义形式:
|
${F_m} = - \iint\nolimits_{{S_0}} {P{n_m}} {\rm{d}}S = - i\omega \rho \iint\nolimits_{{S_0}} {\varphi (\overrightarrow X )} {n_m}{\rm{d}}S,$
|
(3) |
式中:S0为模块水下部分的表面;m为自由度。
总的水动力可以表达为:
|
${F_m} = \left[ {({F_{Im}} + {F_{dm}}) + \sum\limits_{k = 1}^6 {{F_{rmk}}{X_k}} } \right],$
|
(4) |
|
$\left\{ {\begin{array}{*{20}{c}}\!\!\!\!\! {{F_{Im}} = - i\omega \rho \iint\limits_{{S_0}} {{\varphi _I}(\overrightarrow X ){n_m}{\rm{d}}S} },\\\!\!\!\!\! {{F_{dm}} = - i\omega \rho \iint\limits_{{S_0}} {{\varphi _d}(\overrightarrow X ){n_m}{\rm{d}}S} },\\\!\!\!\!\! {{F_{rmk}} = - i\omega \rho \iint\limits_{{S_0}} {{\varphi _{rk}}(\overrightarrow X ){n_m}{\rm{d}}S} }{\text{。}}\end{array}} \right.$
|
(5) |
式中:FIm为入射波引起第m自由度波浪力;Fdm为衍射波引起的第m自由度波浪力;Frmk为模块第k自由度单位幅值运动响应引起的第m自由度辐射波浪力。
波浪辐射势函数φrk可以用实部和虚部表示,并代入式(5)中产生附加质量和附加阻尼:
|
$\begin{split}{F_{rmk}} = & - i\omega \rho \iint\limits_{{S_0}} {\left\{ {{\rm{Re}}\left[ {{\varphi _{rk}}(\overrightarrow X )} \right] + i{\mathop{\rm Im}\nolimits} \left[ {{\varphi _{rk}}(\overrightarrow X )} \right]} \right\}{n_m}{\rm{d}}S} = \\ & \omega \rho \iint\limits_{{S_0}} {{\mathop{\rm Im}\nolimits} \left[ {{\varphi _{rk}}(\overrightarrow X )} \right]{n_m}{\rm{d}}S} - \\ & i\omega \rho \iint\limits_{{S_0}} {{\mathop{\rm Re}\nolimits} \left[ {{\varphi _{rk}}(\overrightarrow X )} \right]{n_m}{\rm{d}}S} = {\omega ^2}{A_{mk}} + i\omega {B_{mk}}{\text{。}}\end{split}$
|
(6) |
式中,Amk和Bmk分别为附加质量和附加阻尼。
多个模块组成的动力系统,频域分析的运动方程为:
|
$[ - {\omega ^2}{M} - i\omega {C} + {K}]\cdot{U} = {F}{\text{。}}$
|
(7) |
式中:M,C和K分别是质量矩阵,阻尼矩阵和刚度矩阵;U和F分别是运动响应和外激力矩阵;
|
${H} = {[ - {\omega ^2}{M} - i\omega {C} + {K}]^{ - 1}},$
|
(8) |
所以运动响应可以表示为:
|
${U} = {HF}{\text{。}}$
|
(9) |
值得注意的是,如果式(7)中的外激励只有单位幅值的规则波引起的波浪激力,并且刚度矩阵包括流体和结构刚度,则式(9)被称为完全耦合幅值响应算子(RAOs)。
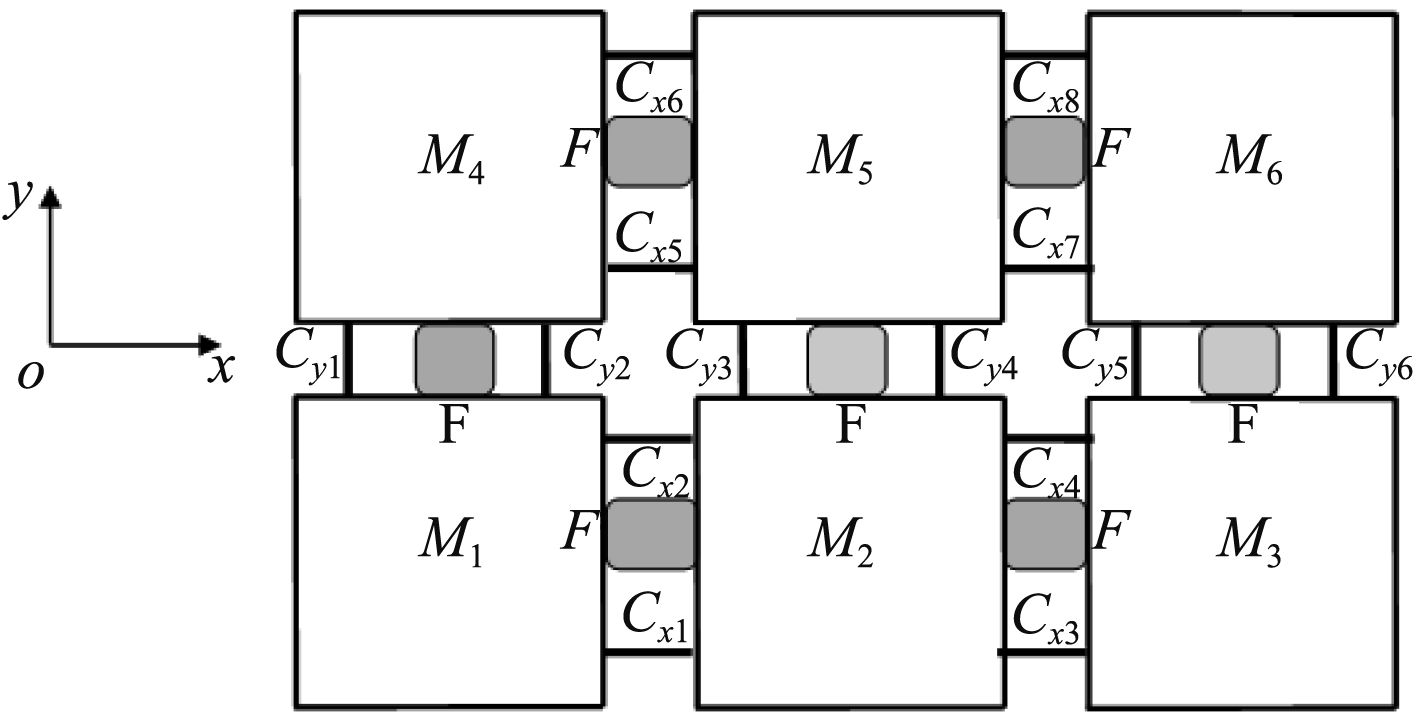
2 计算模型本文计算的海上平台是由6个相同的模块分两排连接组成,每个浮体依序编号M1~M2,缆绳的编号依序Cx1~Cx8和Cy1~Cy6,F表示防撞垫,C为缆绳,如图1所示。
|
图 1 多浮体平台 Fig. 1 Modules-offshore platform |
多浮体模块平台是通过缆绳和防撞垫柔性连接件偶联。缆绳的刚度表示为kc,L0是缆绳的初始长度,缆绳两端连接点的位置为X1(t)和X2(t),所以缆绳的拉力为:
|
${T_c} = \left\{ {\begin{array}{*{20}{c}}{{k_c}(L - {L_0}),L \geqslant {L_0}},\\{\!\!\!\!\!\!\!\!\!\!\!\! 0,\;\;\;\;\;L < {L_0}}{\text{。}}\end{array}} \right.$
|
(10) |
式中,L为缆绳的伸长长度,
防撞垫考虑非线性材料,压缩力定义为如下多项式:
|
${T_F} = \left\{ {\begin{array}{*{20}{c}}{\!\!\! {k_1}\Delta L + {k_2}{{(\Delta L)}^2} + {k_3}{{(\Delta L)}^3},\Delta L \geqslant 0};\\{\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! 0,\;\;\;\;\;\;\;\;\;\Delta L < 0}{\text{。}}\end{array}} \right.$
|
(11) |
式中,kj(j=13)为系数,k1=400 kN/m,k2=300 kN/m,k3=200 kN/m;ΔL为防撞垫压缩量,ΔL=L0–L。
|
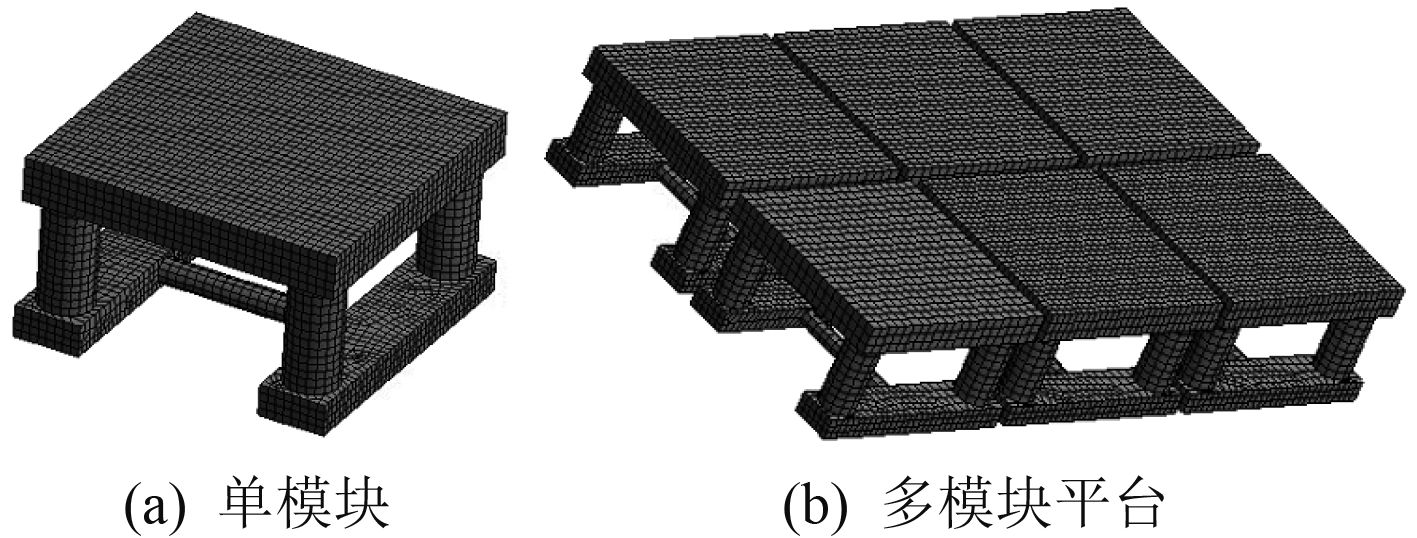
图 2 有限元模型 Fig. 2 Finite element model |
每个模块由1个上体(甲板)、4个支柱(每个舷侧各2个)及3个下体(2个浮筒和1个横梁)组成,如图2(a)所示,图2(b)为多模块网络系统有限元模型,单模块的主要参数如表1所示,表1中Ixx、Iyy和Izz表示转动惯量。
|
|
表 1 单模块的主要参数 Tab.1 The main parameters of single module |
采用JONSWAP谱(γ=3.3)模拟不规则波[10],如式(12)所示。
|
$S\left( \omega \right) = \alpha {g^2}{\omega ^{ - 5}}{\gamma ^{\exp \left[ { - 0.5{{\left( {\frac{{\omega - {\omega _p}}}{{\sigma {\omega _p}}}} \right)}^2}} \right]}}\exp \left[ { - \frac{5}{4}{{\left( {\frac{\omega }{{{\omega _p}}}} \right)}^{ - 4}}} \right],$
|
(12) |
|
$\alpha = \frac{5}{{16}}\left( {\frac{{H_s^2\omega _p^4}}{{{g^2}}}} \right) \cdot \left[ {1 - 0.287\ln \gamma } \right]{\text{。}}$
|
(13) |
式中,ωp为谱峰频率;g为重力加速度;α为广义菲利普常数;σ为谱宽参数;γ为谱峰值参数;HS为有义波高。
本文考虑普通海况,选取HS=3 m,ωP=0.5 rad/s,海洋深度1 000 m。
|
$\sigma = \left\{ {\begin{array}{*{20}{c}}{0.07,\;\;\;\;\;\omega \leqslant {\omega _p}};\\{0.09,\;\;\;\;\;\omega > {\omega _p}}{\text{。}}\end{array}} \right.$
|
(14) |
对于多浮体模块的网络平台,有2个关键参数本文非常关心:其一是连接件的刚度设计如何影响系统动力学行为;其二是随着波浪频率变化导致的系统力学行为。因此本文将关注浮体的幅值响应如何随缆绳刚度和波浪频率变化。现在具体以M2和M5的响应进行讨论。
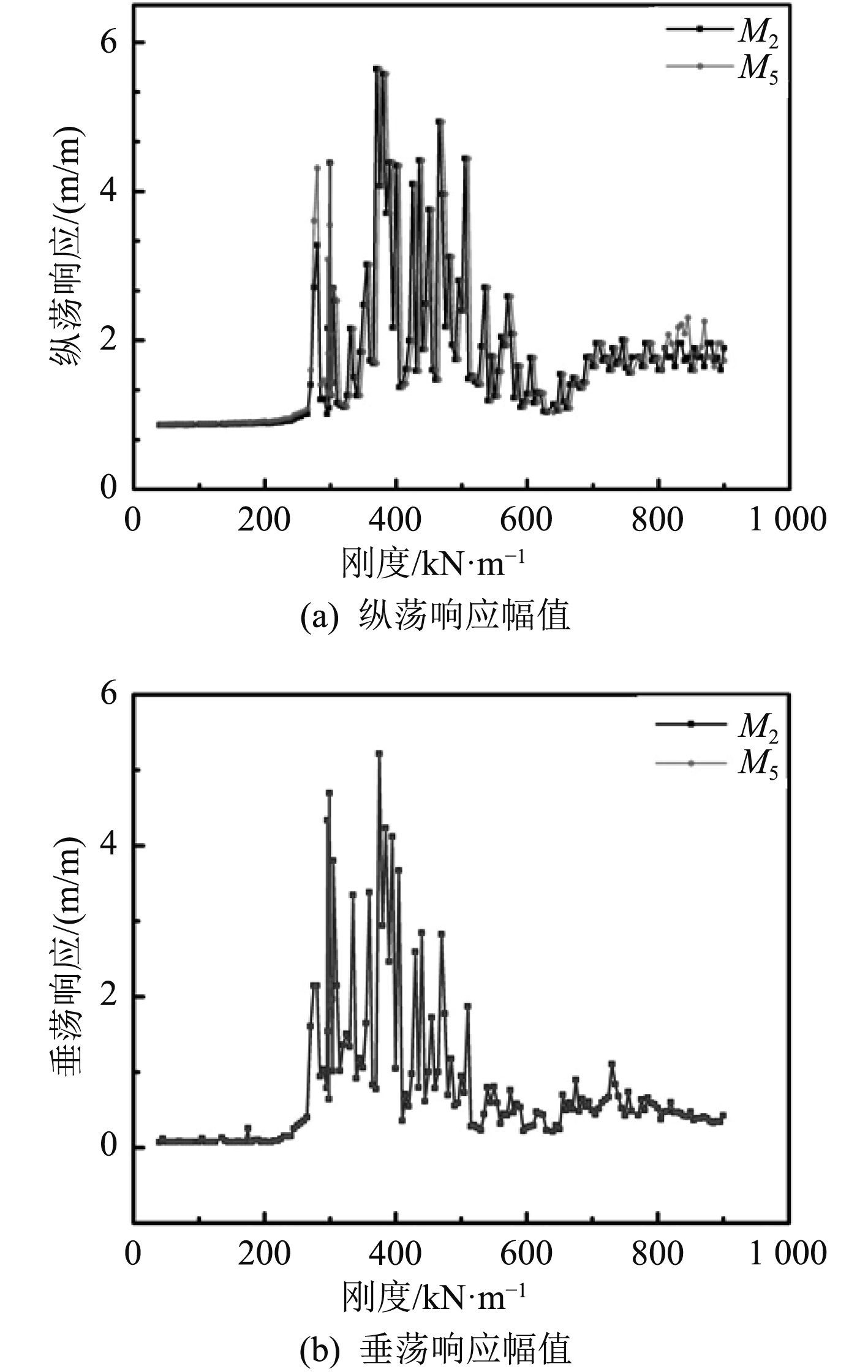
图3是M2和M5浮体响应幅值随缆绳刚度变化规律。其中图3描述浮体的纵荡和垂荡响应幅值随缆绳刚度变化情况,有以下特点:当缆绳刚度小于268 kN/m时,浮体响应幅值比较稳定;随着缆绳刚度的增大,浮体响应出现一个相对大幅值振荡参数区间268 kN/m<kc<697 kN/m,这种跳跃的现象与非线性系统弯曲的共振有关[8];当缆绳刚度大于697 kN/m时,浮体响应幅值较为稳定。
|
图 3 浮体响应幅值随缆绳刚度变化(0°波浪角) Fig. 3 Response amplitude of module changes with the cable stiffness |
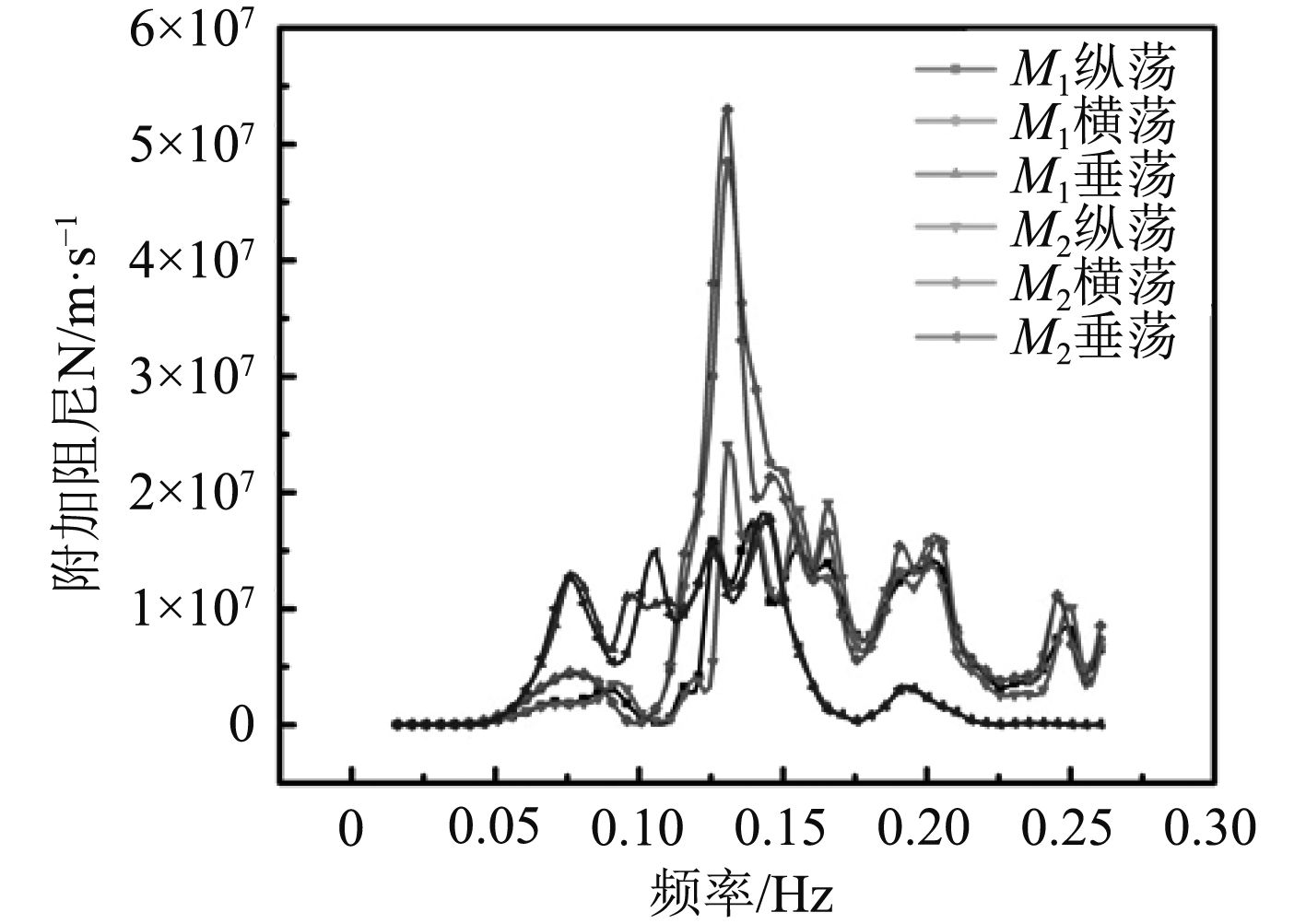
图4是M1和M2模块的附加阻尼随波浪频率的变化,由图可知:横荡的附加阻尼总体大于纵荡和垂荡,这是由于模块水下部分横向面积大于模块水下纵向和垂向面积;两模块附加阻尼随频率先增加后波动递减;低频和高频阶段模块附加阻尼相对较小。
|
图 4 附加阻尼随波浪频率的变化规律 Fig. 4 The variation of additional damping with wave frequency |
图5给出了M2模块所有方位上的幅值响应算子(RAOs)。从图5(a)可以看出,M2模块的横荡幅值随频率变化较小,纵荡和垂荡大体趋势是随频率增加而减少,不过纵荡在0.1~0.3 Hz出现一个波动区间;图5(b)看出,M2模块的纵摇,横摇和首摇随频率先增加,接着在0.1 Hz~0.2 Hz出现波动减小,之后趋于平缓。整体来说,M2模块在高频区域内,响应幅值很小,稳定性良好。

|
图 5 M2的幅值响应算子(0°波浪方位角,kc=500 kN/m) Fig. 5 RAOs of M2 (0° azimuth of wave,kc=500 kN/m) |
本文利用水动力软件AQWA,建立平台的数值仿真计算模型,然后对该平台进行水动力分析,并得到以下结论:
1)浮体响应幅值随连接件刚度变化会出现较大振荡区间现象,这种跳跃的现象与非线性系统弯曲的共振有关,所以在设计连接件刚度时候一定要注意大幅值振荡区间。
2)在低频和高频区域,模块附加阻尼相对较小。
3)得到网络模块在高频区域内,幅值响应较小,稳定性良好。
综上,本文对多浮体网络平台水动力响应分析,获得的分析结果可为网络平台的设计和理论分析提供一定的指导意义。
| [1] | Y KYOZUKA, S KATO, H NAKAGAWA. A Numerical Study on Environmental Impact Assessment of Mega-float of Japan[J]. Marine Structures, 2001, 14 (1): 147–161. |
| [2] | H SUZUKI. Overview of mega-float: concept, design criteria, analysis and design[J]. Marine Structures, 2005, 18 (2): 111–132. DOI: 10.1016/j.marstruc.2005.07.006 |
| [3] | B BHATTACHARYA, R BASU, K MA. Developing target reliability for novel structures: The case of the mobile off shore base[J]. Marine Structures, 2001, 14 (1-2): 37–58. DOI: 10.1016/S0951-8339(00)00024-1 |
| [4] | KOH. The floating platform at the Marina Bay, Singapore[J]. Struct. Eng. Int., 2009, 19 : 33–37. DOI: 10.2749/101686609787398263 |
| [5] | ROGNAAS. Mobile offshore base concepts. Concrete hull and steel topsides[J]. Mar. Struct., 2001, 14 : 5–23. DOI: 10.1016/S0951-8339(00)00019-8 |
| [6] |
吴有生, 杜双兴. 极大型海洋浮体结构的流固耦合分析[J]. 舰船科学技术, 1995 (1): 1–9.
WU Yousheng, DU Shuangxing. Fluid-structure interaction analysis of very large floating structures[J]. Ship Science and Technology, 1995 (1): 1–9. |
| [7] |
宋皓, 崔维成, 刘应中. 底部呈二维缓变情况下超大型浮体水弹性响应的两种计算方法比较[J]. 海洋工程, 2005, 23 (4): 1–8.
SONG Hao, CUI Wei-cheng, LIU Ying-zhong. Comparison of two numerical methods for prediction of hydroelastic responses of VLFS on 2D mild variable bottom[J]. Ocean Engineering, 2005, 23 (4): 1–8. |
| [8] |
徐道临, 卢超, 张海成. 海上浮动机场动力学建模及非线性动力响应特性[J]. 力学学报, 2015, 47 (2): 289–300.
XU Dao-lin, LU Chao, ZHANG Hai-cheng. Dynamic modeling and nonlinear characteristics of floating airport[J]. Chinese Journal of Theo- retical and Applied Mechanics, 2015, 47 (2): 289–300. DOI: 10.6052/0459-1879-14-138 |
| [9] |
李洪仙, 陈衍茂, 巫志文. 系泊多体海上平台非线性动力特性研究[J]. 舰船科学技术, 2016, 38 (10): 52–55.
LI Hong-xian, CHEN Yan-mao, WU Zhi-wen. Nonlinear dynamic characteristics of mooring modules-offshore Platform[J]. Ship Science and Technology, 2016, 38 (10): 52–55. |
| [10] | BERNARD M. 海洋工程水动力学[M]. 刘水庚, 译. 北京: 国防工业出版社, 2012. |
 2017, Vol. 39
2017, Vol. 39
