海洋平台通过推进器推力维持在给定位置的系统称为海洋平台动力定位系统[1],而控制技术作为该系统的核心,一直是研究热点。
韩京清教授提出了一种新型的非线性控制器——自抗扰控制器(Active Disturbance Rejection Controller,ADRC),ADRC 抗扰能力较强且不需知道被控对象的精确模型[2 – 3],其控制性能相对经典 PID 控制有巨大的优越性[4]。在动力定位领域,自抗扰控制已得到了广大学者和科研人员的广泛关注与研究,其中文献[5]是对经典二阶非线性自抗扰控制器的直接应用研究,但其存在着扰动估计能力不足,控制效率与稳定性较低等问题,导致工程实用性不佳;线性自抗扰控制形式较为简单,文献[6]对其做了应用研究,但线性自抗扰的控制性能有所降低。
动态面控制(Dynamic Surface Control,DSC)是从反步法发展起来的一种控制方法。控制效率较高,稳定性好,具有对系统的全局跟踪能力且避免了反步法的计算膨胀问题[7 – 8]。文献[9]率先将其应用于动力定位系统,文献[10]基于智能算法设计了动态面动力定位控制器,动态面控制的问题在于对系统模型依赖较大。
鉴于动态面控制与自抗扰控制各自的优点具有良好的互补性,本文提出引入动态面控制算法同时对自抗扰控制器中的扩张状态观测器以及非线性状态误差反馈控制律进行改造,在提高系统的稳定性与控制效率的同时,增强系统的扰动估计能力。设计出二阶动态面自抗扰控制器(Dynamic Surface Active-Disturbance Rejection Controller,DS-ADRC),并应用于动力定位领域。仿真结果表明,改进后的动力定位控制器具有较好的控制性能,海洋平台定位精度也因此得到了提高。
1 海洋平台动力定位常规自抗扰控制方案 1.1 海洋平台低频运动模型的 2 种形式低速状态下的海洋平台动力定位系统包含纵荡、横荡、首摇 3 个自由度,则可建立其低频数学模型如下[11]:
|
$\left\{ {\begin{array}{*{20}{l}}{{\dot \eta } = {J}(\eta ){\nu }}\text{,}\\{{M\dot \nu} + {D\nu } = {\tau } + {\omega }}\text{。} \end{array}} \right. $
|
(1) |
式中:
|
$\begin{aligned}& { J}(\eta ) = \left[ {\begin{array}{*{20}{c}}{\cos \psi }& { - \sin \psi } & 0 \\{\sin \psi }& {\cos \psi } & 0\\0 & 0 & 1\end{array}} \right]\text{,}\\[6pt]& { M} = \left[ {\begin{array}{*{20}{c}}{m - {X_{\dot u}}} & 0 & 0\\0 & {m - {Y_{\dot v}}} & {m{x_G} - {Y_{\dot r}}}\\0 & {m{x_G} - {Y_{\dot r}}} & {{I_z} - {N_{\dot r}}}\end{array}} \right]\text{,}\\[6pt]& { D} = \left[ {\begin{array}{*{20}{c}}{ - {X_u}} & 0 & 0\\0 & { - {Y_v}} & { - {Y_r}}\\0 & { - {N_v}} & { - {N_r}}\end{array}} \right]\text{。}\end{aligned}$
|
根据平台的长、宽、排水量、吃水深度等参数可求出 M,D 的具体数值,计算公式见文献[12]。
由式(1)可看出,海洋平台各个自由度相互耦合,对模型进行解耦可得:
|
${\ddot \eta } = {{M}_\eta }^{ - 1}(\eta )[{{J}^{ - {\rm{T}}}}(\eta )({\tau } + {\omega }) - {{D}_\eta }{\dot \eta }]\text{,}$
|
(2) |
式中:
设虚拟控制量
|
${\ddot \eta } = {{M}_\eta }^{ - 1}(\eta )[{{J}^{ - {\rm{T}}}}(\eta ){\omega } - {{D}_\eta }{\dot \eta }] + {U}\text{。}$
|
(3) |
跟踪微分器、扩张状态观测器、非线性状态误差反馈控制律构成了自抗扰控制器的 3 个主体部分。
由式(3)可知,海洋平台动力定位系统为二阶被控系统,故本文采用二阶自抗扰控制器。二阶被控系统状态方程表述如下[13]:
|
$\left\{ {\begin{aligned}& {y = {x_1}}\text{,}\\& {{{\dot x}_1} = {x_2}}\text{,}\\& {{{\dot x}_2} = f\left( {{x_1},{x_2},t} \right) + \omega \left( t \right) + bu}\text{。}\end{aligned}} \right.$
|
(4) |
式中:y 为输出;
对照式(3)可知,
适用于二阶系统(4)的自抗扰控制器离散形式如下[13]:
1)跟踪微分器
|
$\left\{ {\begin{array}{*{20}{l}}\!\!\!{{{\dot v}_1} = {v_1} + T{v_2}}\text{,}\\{\begin{array}{*{20}{l}}\!\!\!\!\!\!\!{{{\dot v}_2} = {v_2} + Tfh}\text{,}\\\!\!\!\!\!\!{fh = fhan\left( {{v_1} - v,{v_2},r,h} \right)}\text{。}\end{array}}\end{array}} \right.$
|
(5) |
2)扩张状态观测器
|
$\left\{ {\begin{array}{*{20}{l}}{e = {z_1} - y}\text{,}\\{{{\dot z}_1} = {z_2} - {\beta _{01}}e}\text{,}\\{{{\dot z}_2} = {z_3} - {\beta _{02}}fal\left( {e,{a_1},\delta } \right) + {b_0}u}\text{,}\\{{{\dot z}_3} = - {\beta _{03}}fal\left( {e,{a_2},\delta } \right)}\text{。}\end{array}} \right.$
|
(6) |
3)非线性状态误差反馈控制律
|
$\left\{ {\begin{array}{*{20}{l}}{{e_1} = {v_1} - {z_1}}\text{,}\\{{e_2} = {v_2} - {z_2}}\text{,}\\{{u_0} = {k_1}fal\left( {{e_1},{\alpha _1},\delta } \right) + {k_2}fal\left( {{e_2},{\alpha _2},\delta } \right)}\text{,}\\{u = {u_0} - {z_3}/{b_0}}\text{。}\end{array}} \right.$
|
(7) |
式中:v 为输入;v1 为对 v 进行跟踪;v2 为 v1 的微分;z1,z2,z3 分别为 x1,x2,
常规的自抗扰控制器中的扩张状态观测器扰动估计能力不足,非线性状态误差反馈控制率的控制效率与稳定性较低,为此,本文主要对传统的扩张状态观测器与非线性状态误差反馈控制率进行改进。
2.1 动态面扩张状态观测器的设计引起常规扩张状态观测器扰动估计能力不足的原因是其采取了在分段点 ± δ 处不光滑可导的连续分段函数
为彻底消除非线性函数的影响,须对式(6)进行等价变形,即
|
$\left\{ {\begin{array}{*{20}{l}}{{{\dot z}_1} = {z_2}}\text{,}\\{{{\dot z}_2} = {z_3} + {b_0}u}\text{,}\\{{{\dot z}_3} = - {f_3} - {{\dot f}_2} - {{\ddot f}_1}}\text{。}\end{array}} \right.$
|
(8) |
式中:
1)定义系统(8)的第 1 个子系统
|
${S_1} = {z_1} - {x_1}\text{,}$
|
(9) |
则对 S1 求导可得:
|
${\dot S_1} = {z_2} - {x_2}\text{,}$
|
(10) |
进而有虚拟控制律
|
${\bar u_1} = - {k_1}{S_1} + {x_2}\text{。}$
|
(11) |
使
|
${\tau _1}{\dot x_{1d}} + {x_{1d}} = {\bar u_1}\text{。}$
|
(12) |
2)第 2 个子系统
|
${S_2} = {z_2} - {x_{1d}}\text{,}$
|
(13) |
对 S2 求导得:
|
${\dot S_2} = {z_3} + {b_0}u - {x_{1d}}\text{,}$
|
(14) |
虚拟控制律:
|
${\bar u_2} = - {k_2}{S_2} - {b_0}u + {\dot x_{1d}}\text{。}$
|
(15) |
同样,使
|
${\tau _2}{\dot x_{2d}} + {x_{2d}} = {\bar u_2}\text{,}$
|
(16) |
3)第 3 个子系统
|
${S_3} = {z_3} - {x_{2d}}\text{,}$
|
(17) |
对 S3 求导得
|
${\dot S_3} = \bar u - {\dot x_{2d}}\text{,}$
|
(18) |
最终的实际控制律为
|
$\bar u = - {k_3}{S_3} + {\dot x_{2d}}\text{,}$
|
(19) |
其中:k1,k2,k3,τ1,τ2 为可调参数,且 τ1 > 0,τ2 > 0。
稳定性证明如下:
定义
|
${\dot S_1} = {S_2} + {x_{1d}} - {x_2}\text{,}$
|
(20) |
根据式(11)和式(12)得:
|
${\dot S_1} = {S_2} + {\zeta _1} - {k_1}{S_1}\text{,}$
|
(21) |
同理有
|
$\begin{array}{l}{{\dot S}_2} = {S_3} + {\zeta _2} - {k_2}{S_2}\text{,}\\[5pt]{{\dot S}_3} = - {k_3}{S_3}\text{。}\end{array}$
|
(22) |
由式(10)~式(12)及式(14)~式(16)得:
|
$\begin{array}{c}{{\dot \zeta }_1} = {{\dot x}_{1d}} + {k_1}{{\dot S}_1} - {{\ddot x}_1} = - \displaystyle\frac{{{\zeta _1}}}{{{\tau _1}}} + {g_1}\text{,}\end{array}$
|
(23) |
|
$\begin{array}{c}{{\dot \zeta }_2} = {{\dot x}_{2d}} + {k_2}{{\dot S}_2} + {b_0}\displaystyle\frac{{\partial u}}{{\partial {x_2}}}{{\dot x}_2} + \displaystyle\frac{{{\zeta _1}}}{{{\tau _1}}} = - \displaystyle\frac{{{\zeta _2}}}{{{\tau _2}}} + {g_2}\text{,}\end{array}$
|
(24) |
其中
定义:
|
$\begin{aligned}& {V_{is}} = \frac{{S_i^2}}{2},i = 1,2,3\text{,}\\& {V_{i\zeta }} = \frac{{\zeta _i^2}}{2},i = 1,2\text{,}\end{aligned}$
|
(25) |
根据式(22)~式(24)得:
|
$\left\{ {\begin{aligned}& {{{\dot V}_{is}} = {S_i}({S_{i + 1}} + {\zeta _i} - {k_i}{S_i})=}\\& \;\;\;\;\;\;{ - {k_i}S_i^2 + {S_i}{S_{i + 1}} + {S_i}{\zeta _i},i = 1,2}\text{,}\\& {{{\dot V}_{3s}} = - {k_3}S_3^2}\text{,}\\& {{{\dot V}_{i\zeta }} = - \frac{{\zeta _i^2}}{{{\tau _i}}} + {\zeta _i}{g_i},i = 1,2}\text{,}\end{aligned}} \right.$
|
(26) |
定义 Lyapunov 函数
|
$V = \sum\limits_{i = 1}^3 {{V_{is}}} + \sum\limits_{j = 1}^2 {{V_{j\zeta }}} \text{。}$
|
(27) |
由系统(4)知
|
$\begin{aligned}& \dot V \leqslant - (2 + {\alpha _0})\sum\limits_{i = 1}^3 {S_i^2} + \sum\limits_{i = 1}^2 {[\frac{{2S_i^2 + S_{i + 1}^2 + \zeta _i^2}}{2}} - \\& (1 + \frac{{g_{i\max }^2}}{{2\varepsilon }} + {\alpha _0})\zeta _i^2 + \frac{{g_{i\max }^2\zeta _i^2}}{{2\varepsilon }}\frac{{g_i^2}}{{g_{i\max }^2}}] + \varepsilon \leqslant - 2{\alpha _0}V + 2\varepsilon\text{。} \end{aligned}$
|
(28) |
当
对于式(4)中的二阶系统,结合跟踪微分器的输出 v1,v2,可得动态面非线性状态误差反馈控制律如下:
|
$\left\{ {\begin{array}{*{20}{l}}{{S_4} = y - {v_1}}\text{,}\\{{{\bar u}_3} = - {k_4}{S_4} + {v_2}}\text{,}\\{{\tau _3}{{\dot x}_{3d}} + {x_{3d}} = {{\bar u}_3}}\text{,}\\{{S_5} = {x_2} - {x_{3d}}}\text{,}\\{{u_0} = - {k_5}{S_5} - f({x_1},{x_2},t) - \omega (t) + {{\dot x}_{3d}}}\text{,}\\{u = {u_0} - {z_3}/{b_0}}\text{。}\end{array}} \right.$
|
(29) |
式中:S4,S5 为动态面方程;
由以上分析可知,二阶动态面自抗扰控制器结构如图 1 所示。

|
图 1 二阶动态面自抗扰控制器结构图 Fig. 1 The structure of second-order DS-ADRC |
以某半潜式海洋平台作为控制对象,进行仿真实验。该控制对象参数为:长 114.07 m,宽 78.68 m,排水量 51 624 t,吃水深度 19 m[15]。根据文献[12]的计算公式,可得该平台的质量矩阵和阻尼矩阵分别为:
|
$\begin{array}{l}{M} = \left[ {\begin{array}{*{20}{c}}{6.74 \times {{10}^7}} & 0 & 0 \\0 & {9.15 \times {{10}^7}} & { - 0.608 \times {{10}^7}}\\0 & { - 0.608 \times {{10}^7}} & {1.08 \times {{10}^{11}}}\end{array}} \right]\text{,}\\[6pt]{D} = \left[ {\begin{array}{*{20}{c}}{6.76 \times {{10}^5}} & 0 & 0 \\0 & {5.319 \times {{10}^5}} & { - 1.56 \times {{10}^5}}\\0 & { - 1.56 \times {{10}^5}} & {1.7313 \times {{10}^9}}\end{array}} \right]\text{。}\end{array}$
|
环境干扰设定为:平均风速 vwind = 15 m/s,风向 γwind = 60°,考虑波浪由风引起,故γwave = 60°,流速vcurrent = 1 m/s,流向 γcurrent = 45°。平台初始位置为
在实验条件相同的前提下,本文采用典型的自抗扰与动态面自抗扰 2 种控制策略分别进行控制。对纵荡、横荡、首摇 3 个方向分别设计动力定位控制器并设置控制器参数为:
|
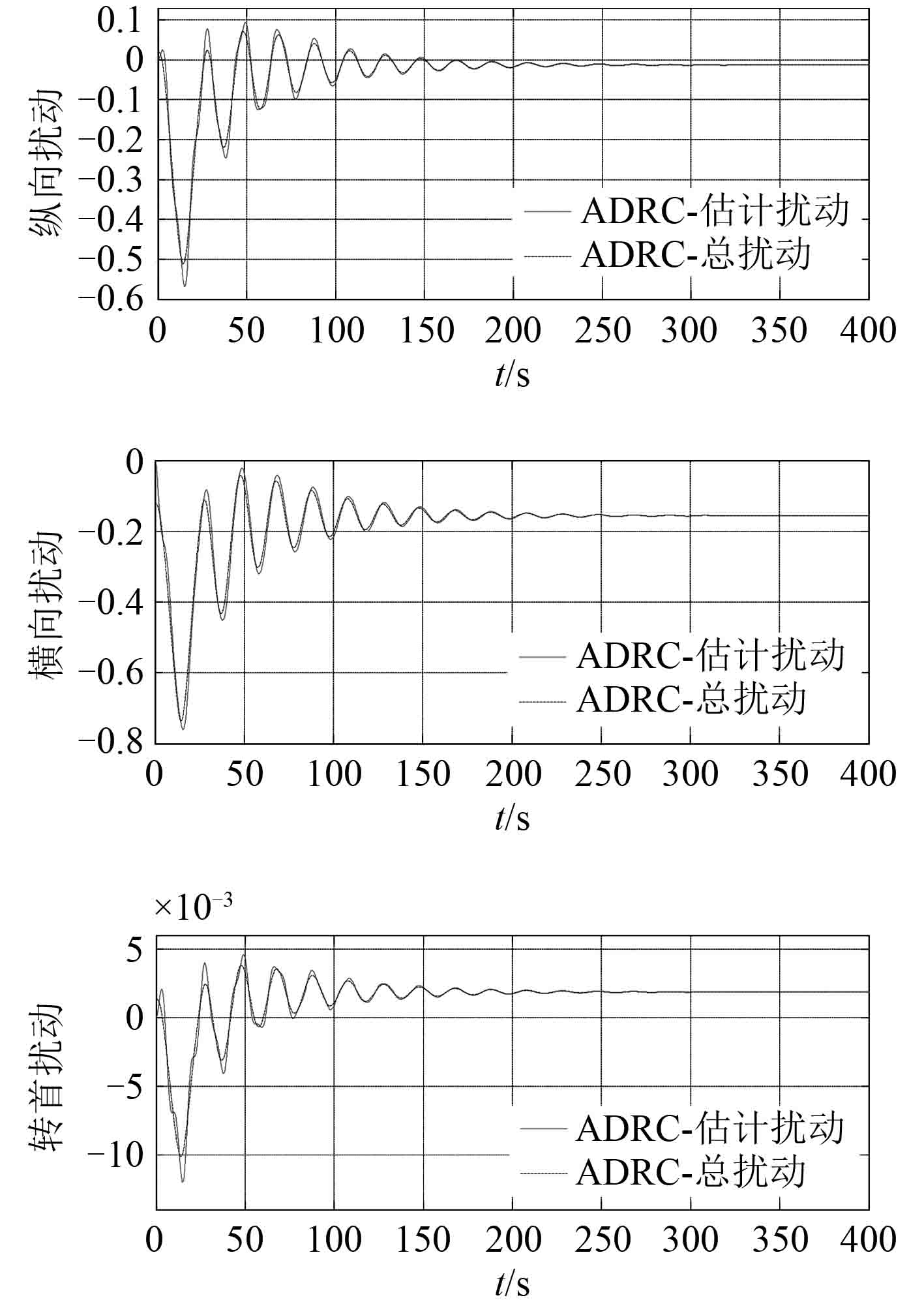
图 2 ADRC 的系统总扰动及估计曲线 Fig. 2 The total disturbance and estimation curves of ADRC |
|
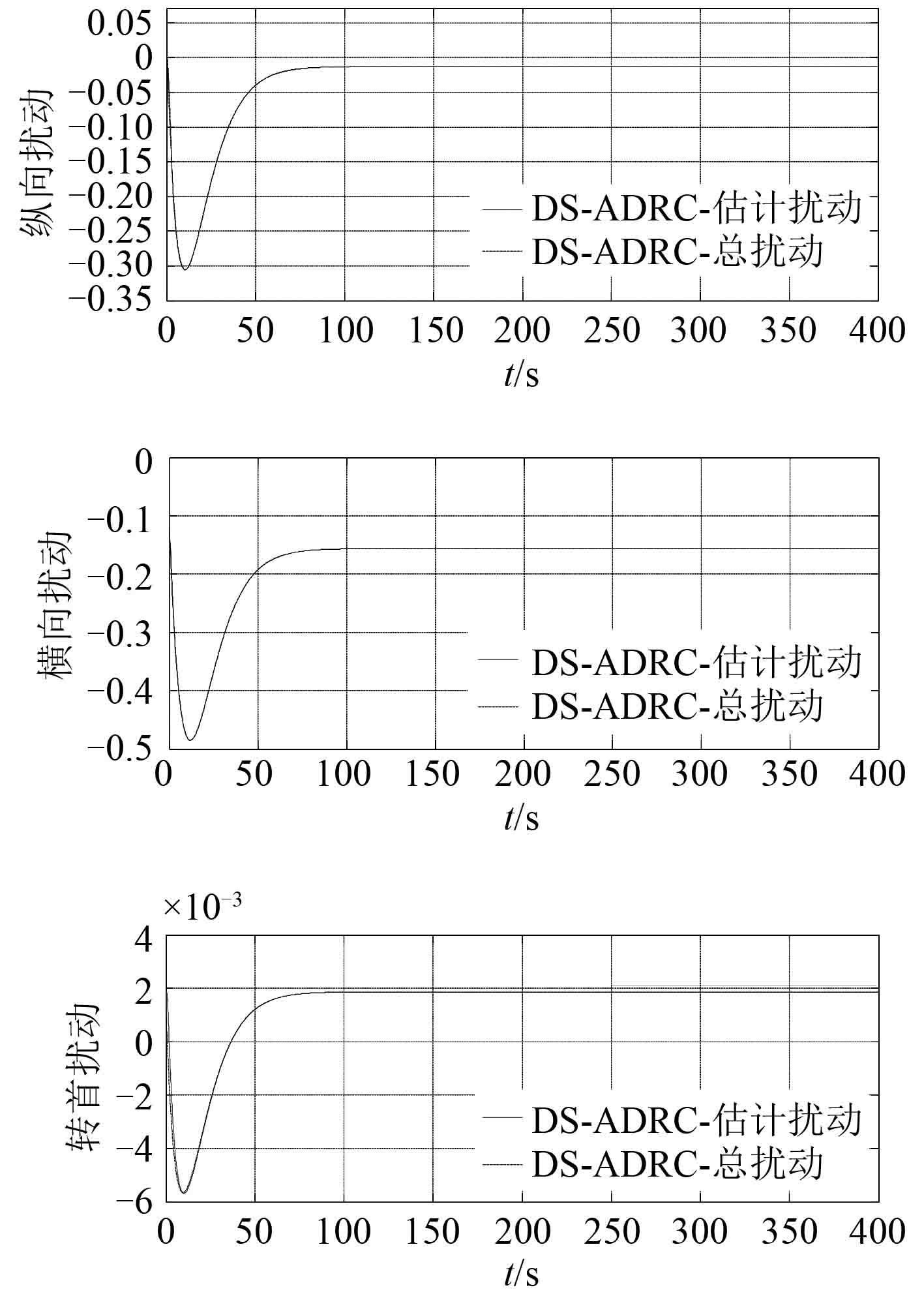
图 3 DS-ADRC 的系统总扰动及估计曲线 Fig. 3 The total disturbance and estimation curves of DS-ADRC |
|
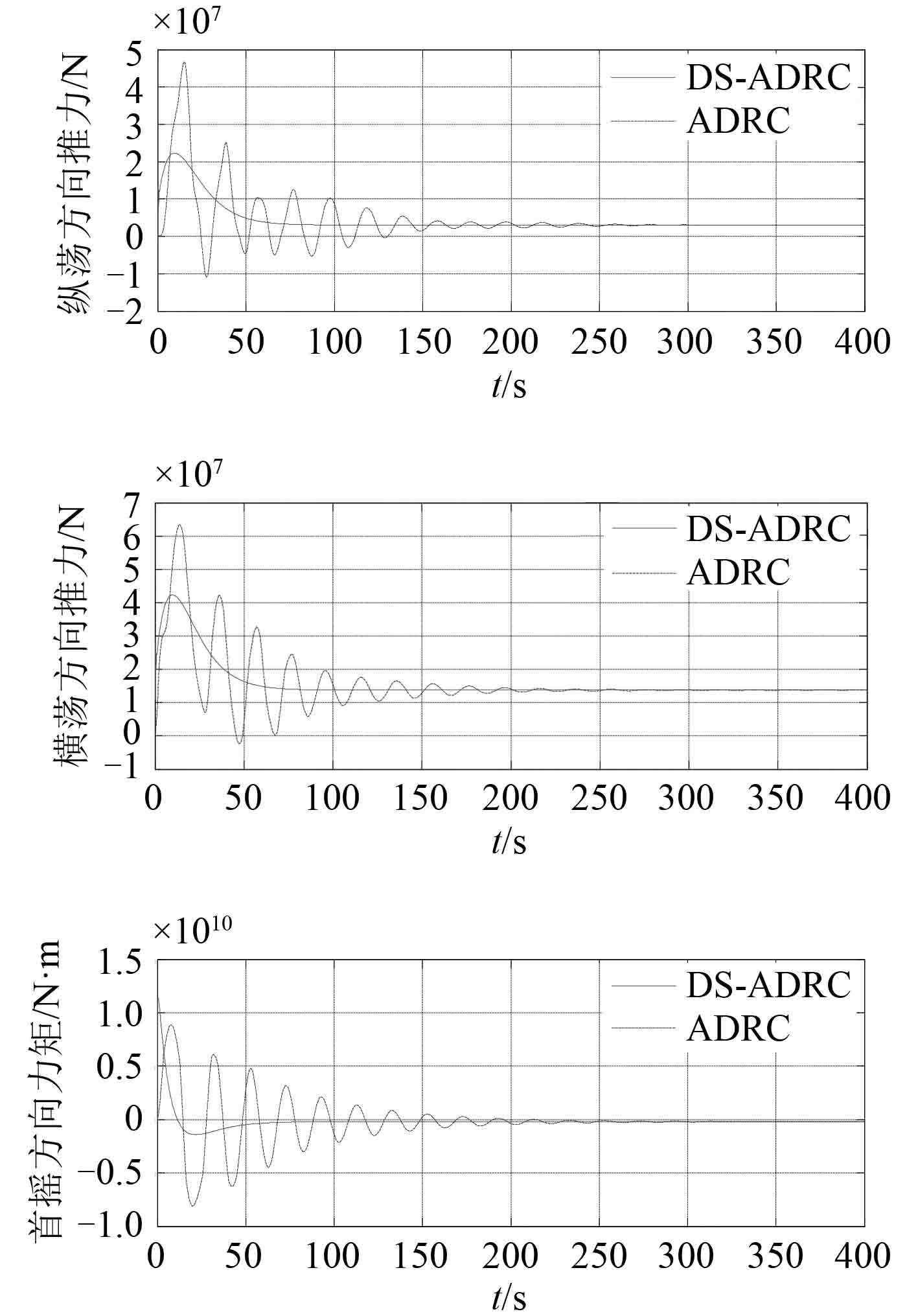
图 4 ADRC 与 DS-ADRC 的控制输出曲线 Fig. 4 The control output curves of ADRC and DS-ADRC |
|
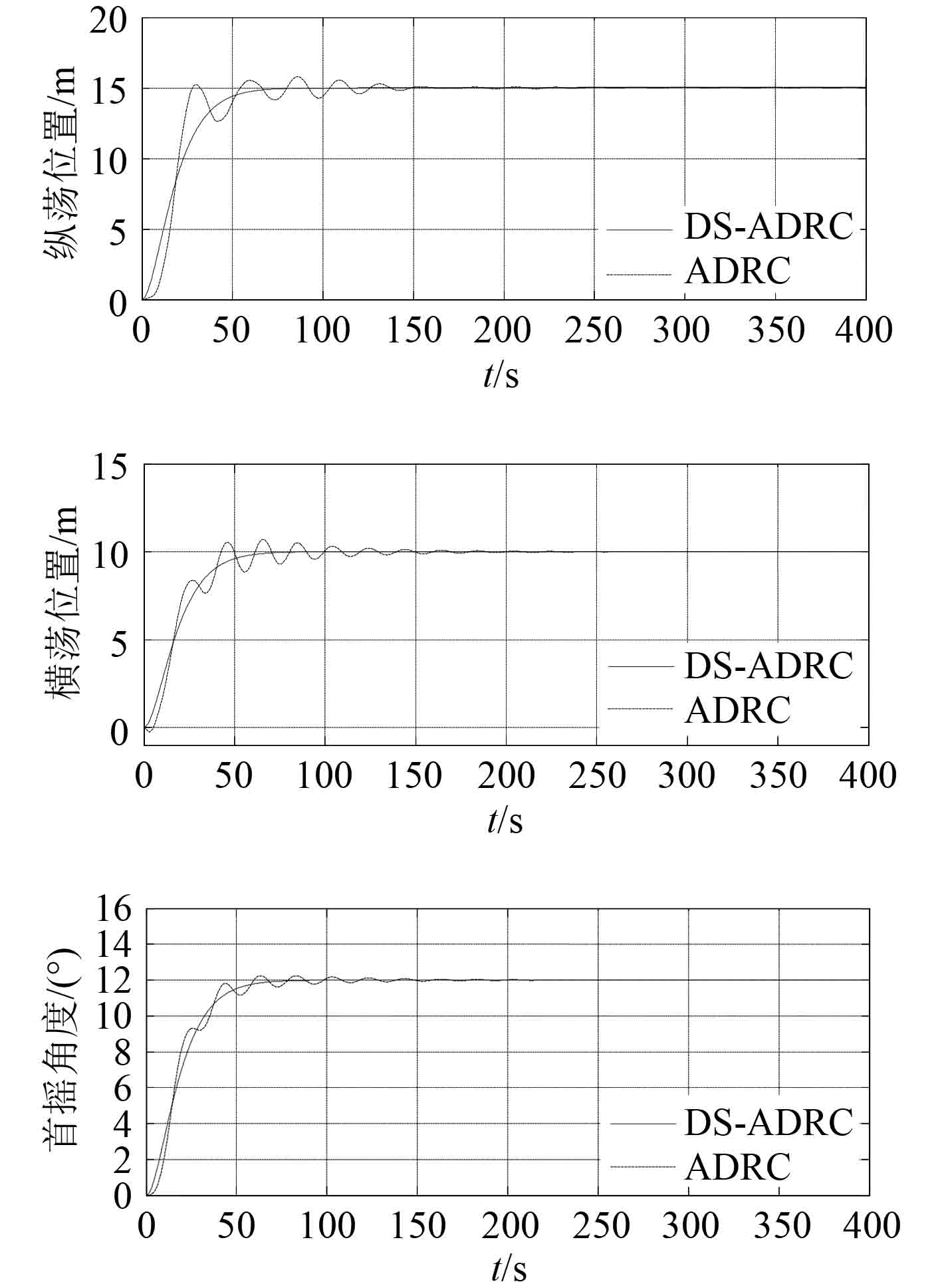
图 5 ADRC 与 DS-ADRC 的位置响应曲线 Fig. 5 The displacement response curves of ADRC and DS-ADRC |
图 2和图 3 分别为 ADRC 与 DS-ADRC 的系统总扰动及估计曲线,图 4 为 ADRC 与 DS-ADRC 的控制输出曲线,图 5 为 ADRC 与 DS-ADRC 的位置响应曲线。
从图 2和图 3 可看出,DS-ADRC 观测出的总扰动与真实值之间除了在零点处出现一些瞬时误差之外,其余各处基本一致,误差明显较 ADRC 小,说明其对扰动的估计能力强于 ADRC。图 4 表明,DS-ADRC 的控制输出波动范围较 ADRC 小,且变化更为平稳,能更快的趋于稳定。说明在 DS-ADRC 作用下的系统抗扰能力和鲁棒性有所提高。从图 5 可看出,2 种控制器均能使输出最终跟踪上设定值,但 DS-ADRC 比 ADRC 更快地稳定于设定值,并且无超调。表明 DS-ADRC 的控制品质与响应特性优于典型的 ADRC。
4 结 语本文在半潜式海洋平台动力定位领域内,以非线性自抗扰控制器为基础,通过引入动态面控制思想对扩张状态观测器和非线性状态误差反馈控制律进行改造,设计出二阶动态面自抗扰动力定位控制器,便于工程实现。仿真结果表明其对扰动的估计能力明显增强,系统的抗扰能力与鲁棒性得到提高,同时其控制品质及响应特性较为优良。改进后的控制器具有较好的控制性能,并实现了动态面自抗扰控制技术在动力定位问题上的应用。
| [1] | 赵志高, 杨建民, 王磊, 程俊勇. 动力定位系统发展状况及研究方法[J]. 海洋工程, 2002, 20 (1): 91–97. |
| [2] | HAN J. Q.. From PID to active disturbance rejection control[J]. IEEE Transactions on Industrial Electronics, 2009, 56 (3): 900–906. DOI: 10.1109/TIE.2008.2011621 |
| [3] | GAO Z. Scaling and bandwidth-parameterization based controller tuning[C]//. Proceedings of the American Control Conference. Denver, USA, 2003: 4989–4996. |
| [4] | 韩京清. 从PID技术到" 自抗扰控制”技术[J]. 控制工程, 2002, 9 (3): 13–18. |
| [5] | 谢洪艳, 谈世哲. 基于ADRC的水面船舶动力定位控制技术及仿真研究[J]. 自动化技术与应用, 2010, 29 (3): 5–7. |
| [6] | 高峰. 船舶动力定位自抗扰控制及仿真的研究[D]. 大连: 大连海事大学, 2013. |
| [7] | SWAROOP D, GERDES J, YIP P, et al. Dynamic surface control of nonlinear systems[C]//. Proceedings of the American Control Conference. Albuquerque, USA, 1997: 3028–3034. |
| [8] | Swaroop D., Gerdes J., Yip P.. Dynamic surface control for a class of nonlinear systems[J]. IEEE Transactions on Automatic control, 2000, 45 (10): 1893–1899. DOI: 10.1109/TAC.2000.880994 |
| [9] | FU M Y, ZHANG A H, XU J L, et al. Robust adaptive dynamic surface path tracking control for dynamic positioning vessel with big plough[C]//. IEEE Oceans-San Diego. San Diego, CA, 2013: 1–6. |
| [10] | 杜佳璐, 杨杨, 胡鑫, 陈海泉. 基于动态面控制的船舶动力定位控制律设计[J]. 交通运输工程学报, 2014, 14 (5): 36–42. |
| [11] | 边信黔, 付明玉, 王元慧. 船舶动力定位[M].北京: 科学出版社, 2011. |
| [12] | 贾欣乐, 杨盐生. 船舶运动数学模型——机理建模与辨识建模[M]. 大连: 大连海事大学出版社, 1999. |
| [13] | 韩京清. 自抗扰控制技术: 估计补偿不确定因素的控制技术[M]. 北京: 国防工业出版社, 2013. |
| [14] | Qi N. M., Qin C. M., Song Z. G.. Improved ADRC cascade decoupling controller design of hypersonic vehicle[J]. Harbin Gongye Daxue Xuebao(Journal of Harbin Institute of Technology), 2011, 43 (11): 34–38. |
| [15] | Liu W., Pang Y. J.. Research on dynamic simulation of DP for a deep watersemi-submersible platform[J]. Mechanical Engineering And Material Science, 2012, 42 : 642–645. |
 2017, Vol. 39
2017, Vol. 39
