船舶航向控制是船舶运动控制的基本内容,它直接影响着船舶的操纵性、安全性和经济性。然而由于船舶具有大惯性、大时滞、非线性等特点,其运动极易受到风、浪、流等强干扰的影响,船速及装载的变化也会造成船舶模型的参数摄动,加之环境参数的严重干扰及测量的不精确性等都使船舶动态产生明显的不确定性[1 – 2]。长期以来,人们一直致力于不确定性非线性系统的鲁棒及自适应控制研究,特别对于存在不确定性干扰的复杂未知系统[3]。由于算法简单,传统的滑模控制方法已经被成功地应用到了船舶航向控制中[4 – 5],但是传统滑模控制中的不连续切换特性会导致抖振现象的出现,这不仅降低了系统的控制精度,使系统的控制性能变差,甚至会严重损坏控制元件。为削弱传统滑模控制中的抖振现象,Levant等[6 – 7]提出一种新型的二阶滑模控制算法。近年来,针对系统的建模不确定性影响,苗保彬等[8]提出一种新颖的船舶航向跟踪控制方法。
本文针对船舶航向运动非线性数学模型,设计了一种基于径向基神经网络逼近的动态面二阶滑模控制器,用径向基神经网络(RBFNN)逼近模型误差,并把二阶滑模控制方法与动态面控制方法相结合,对控制器进行设计。所设计的控制器,保证了船舶航向控制系统中所有信号一致最终有界,并使得跟踪误差任意小。最后,利用Matlab的Simulink仿真工具进行仿真研究,仿真结果验证了所提算法的有效性,并且具有良好的鲁棒性。
1 问题的描述船舶航向控制非线性数学模型中,舵角δ和航向φ的关系可以描述为:
|
$\ddot \varphi + \frac{1}{T}H\left( {\dot \varphi } \right) = \frac{K}{T}\delta + \Delta ,$
|
(1) |
其中:K,T分别为时间增益和时间常数,是船舶前进速度和船长的函数;∆为模型误差;
|
$H\left( {\dot \varphi } \right) = {e_1}\dot \phi + {e_2}{\dot \phi ^3},$
|
(2) |
式中:e1和e2为船舶非线性系数,是实值常数。
定义
|
${\dot x_1} = {x_2},$
|
(3) |
|
${\dot x_2} = {f_2}\left( {{{\bar x}_2}} \right) + \frac{K}{T}u + \Delta {\text{。}}$
|
(4) |
式中:
假设:参考信号xd光滑有界且具有二阶连续有界的导数,即存在一个常数D0>0,使得集合
针对船舶航向控制的非线性数学模型系统设计一种基于反演法的动态面二阶滑模控制器,使闭环系统的所有信号一致最终有界,且使跟踪误差能够任意小。下面给出简要的控制器设计过程。
定义第1个误差面
|
${z_{_1}} = {x_{_1}} - {x_d},$
|
(5) |
|
${\dot z_{_1}} = {x_{_2}} - {\dot x_d}{\text{。}}$
|
(6) |
选取李雅普诺夫候选函数
|
${V_1} = \frac{1}{2}z_1^2,$
|
(7) |
|
${\dot V_1} = {z_1}{\dot z_1}{\text{。}}$
|
(8) |
选择虚拟控制输入
|
$\tau {\dot a_1} + {a_1} = a_1^0,\;\;\;{a_1}\left( 0 \right) = a_1^0\left( 0 \right){\text{。}}$
|
(9) |
其中:
定义滤波器误差
|
${h_1} = {a_1} - a_1^0{\text{。}}$
|
(10) |
定义第2个误差面
|
${z_2} = {x_2} - {a_1},$
|
(11) |
则
|
${\dot z_2} = {\dot x_2} - {\dot a_1}{\text{。}}$
|
(12) |
将式(11)代入到式(6)得
|
${\dot z_1} = {z_2} + {a_1} - {\dot x_d}{\text{。}}$
|
(13) |
考虑到位置跟踪、虚拟控制和滤波误差,选取李雅普诺夫候选函数
|
${V_2} = {V_1} + \frac{1}{2}z_2^2 + \frac{1}{2}h_1^2{\text{。}}$
|
(14) |
由于
|
$\begin{split}\!\!\!\!\! {{\dot V}_2} & = {z_1}({z_2} + {h_1} + a_1^0 - {{\dot x}_d}) + {z_2}({f_2}({{\bar x}_2}) + \frac{K}{T}u + \Delta - {{\dot a}_1}) + \!\!\!\!\! \\& \quad{h_1}(\frac{{ - {h_1}}}{\tau } + {c_1}{{\dot z}_1} - {{\ddot x}_d}) = \\& \quad {z_1}({z_2} + {h_1} + a_1^0 - {{\dot x}_d}) + {z_2}({f_2}({{\bar x}_2}) + \frac{K}{T}u + \Delta - {{\dot a}_1}) + \!\!\!\!\! \\& \quad{h_1}(\frac{{ - {h_1}}}{\tau } + {B_2}){\text{。}}\end{split}$
|
(15) |
其中
结合滑模变结构控制定义,设滑动面为
设计的控制器由2部分组成
|
$u = {u_{st}} + {u_{eq}}{\text{。}}$
|
(16) |
取
|
${u_{st}} = \int { - p{\mathop{\rm sgn}} ({z_2})} - k{\left| {{z_2}} \right|^{0.5}}{\mathop{\rm sgn}} ({z_2}),$
|
(17) |
|
$u_{eq}^* = \frac{T}{K}( - {c_2}{z_2} - {f_2}({\bar x_2}) - \Delta + {\dot a_1}){\text{。}}$
|
(18) |
其中p>0,k>0,c2>0根据连续函数分离技术可知
|
$\Delta = {\bar S_2}\left( {{{\bar x}_2}} \right){A_2}{\bar x_2} = {\bar S_2}\left( {{{\bar x}_2}} \right){\omega _2}{b_2} + {\bar S_2}\left( {{{\bar x}_2}} \right){A_2}{\left[ {{x_d}\,,\,{a_1}} \right]^{\rm T}},$
|
(19) |
式中:
选取
|
$\begin{split}& {z_2}{{\bar S}_2}\left( {{{\bar x}_2}} \right){A_2}{\left[ {{x_d}\,,\,{a_1}} \right]^{\rm T}} \leqslant \lambda _2^{\rm{T}}\left\| {{{\bar S}_2}\left( {{{\bar x}_2}} \right)} \right\|\left| {{z_2}} \right| \leqslant \\& \qquad \tilde \lambda _2^{\rm{T}}\left\| {{{\bar S}_2}\left( {{{\bar x}_2}} \right)} \right\|\left| {{z_2}} \right| + \hat \lambda _2^{\rm{T}}\left\| {{{\bar S}_2}\left( {{{\bar x}_2}} \right)} \right\|\left| {{z_2}} \right|,\end{split}$
|
(20) |
|
$\begin{split}& {z_2}{{\bar S}_2}\left( {{{\bar x}_2}} \right){\omega _2}{b_2} \leqslant \frac{{z_2^2{{\bar S}_2}\left( {{{\bar x}_2}} \right)\bar S_2^{\rm T}\left( {{{\bar x}_2}} \right)\tilde \lambda _2^{\rm{T}}}}{{4r_2^2}} + \\& \qquad\frac{{z_2^2{{\bar S}_2}\left( {{{\bar x}_2}} \right)\bar S_2^{\rm T}\left( {{{\bar x}_2}} \right)\hat \lambda _2^{\rm T}}}{{4r_2^2}} + r_2^2\omega _2^{\rm T}{\omega _2},\end{split}$
|
(21) |
式中,
则选择最终控制器
|
$\begin{split}u & = \int { - p{\mathop{\rm sgn}} ({z_2})} - k{\left| {{z_2}} \right|^{0.5}}{\mathop{\rm sgn}} ({z_2}) + \\& \quad \frac{\rm T}{K}\left( { - {k_2}{z_2} - {f_2}\left( {{{\bar x}_2}} \right) + {{\dot a}_2}} \right) - \\& \quad \frac{\rm T}{K}\left( {\frac{{{z_2}{{\bar S}_2}\left( {{{\bar x}_2}} \right)\bar S_2^{\rm T}\left( {{{\bar x}_2}} \right)\hat \lambda _2^{\rm T}}}{{4r_2^2}} - \hat \lambda _2^{\rm T}\left\| {{{\bar S}_2}\left( {{{\bar x}_2}} \right)} \right\|{\mathop{\rm sgn}} \left( {{z_2}} \right)} \right){\text{。}}\!\!\!\!\end{split}$
|
(22) |
再次选取李雅普诺夫候选函数
|
${V_3} = {V_2} + \frac{1}{2}\tilde \lambda _2^{\rm T}\varGamma _2^{ - 1}{\tilde \lambda _2},$
|
(23) |
式中
|
${\dot V_3} = {\dot V_2} - \tilde \lambda _2^{\rm{T}}\Gamma _2^{ - 1\dot \wedge }{\lambda _2}$
|
(24) |
将式(15)、式(20)、式(21)、式(22)代入式(24),并选择
|
${c_1} \geqslant 1 \! + \! {a_0} \! + \! r_2^2,{r_2} > 0,{c_2} \geqslant \frac{1}{2} \! + \! {a_0} \! + \! r_2^2,\frac{1}{\tau } \geqslant \frac{1}{2} \! + \! \frac{{M_2^2}}{2} \! + \! {a_0}{\text{。}}$
|
得
|
$\begin{array}{l}
{{\dot V}_3} \le - {a_0}z_1^2 + \frac{1}{2} - r_2^2z_1^2 - {a_0}z_2^2 - ({a_0} + \frac{{M_2^2}}{2} - \frac{{B_2^2}}{2})h_1^2 + \\
\frac{{z_2^2{{\bar S}_2}\left( {{{\bar x}_2}} \right)\bar S_2^{\rm{T}}\left( {{{\bar x}_2}} \right)\tilde \lambda _2^{\rm{T}}}}{{4r_2^2}} + r_2^2\omega _2^{\rm{T}}{\omega _2} + \tilde \lambda _2^{\rm{T}}\left\| {{{\bar S}_2}\left( {{{\bar x}_2}} \right)} \right\|\left| {{z_2}} \right| - \\
\tilde \lambda _2^{\rm{T}}{\rm{ }}\Gamma _2^{ - 1\dot \wedge }{\lambda _2} - \frac{K}{{\rm{T}}}\left( {z_2^{\rm{T}}(\int { - p{\rm{sgn}}({z_2})} ) - k{z_2}{{\left| {{z_2}} \right|}^{0.5}}{\rm{sgn}}({z_2})} \right)
\end{array}$
|
(25) |
因为p>0,k>0,所以
|
$\begin{array}{l}
{{\dot V}_3} \le - {a_0}z_1^2 + \frac{1}{2} - r_2^2z_1^2 - {a_0}z_2^2 - ({a_0} + \frac{{M_2^2}}{2} - \frac{{B_2^2}}{2})h_1^2 + \\
\frac{{z_2^2{{\bar S}_2}\left( {{{\bar x}_2}} \right)\bar S_2^{\rm{T}}\left( {{{\bar x}_2}} \right)\tilde \lambda _2^{\rm{T}}}}{{4r_2^2}} + r_2^2\omega _2^{\rm{T}}{\omega _2} + \\
\tilde \lambda _2^{\rm{T}}\left\| {{{\bar S}_2}\left( {{{\bar x}_2}} \right)} \right\|\left| {{z_2}} \right| - \tilde \lambda _2^{\rm{T}}\Gamma _2^{ - 1\dot \wedge }{\lambda _2}
\end{array}$
|
(26) |
选取自适应律
|
${^{\dot \wedge }}{\lambda _2} = {\Gamma _2}\left( {\frac{{z_2^2{{\bar S}_2}\left( {{{\bar x}_2}} \right)\bar S_2^T\left( {{{\bar x}_2}} \right)}}{{4r_2^2}} + \left\| {{{\bar S}_2}\left( {{{\bar x}_2}} \right)} \right\|\left| {{z_2}} \right| - {\sigma _2}\left( {{{\hat \lambda }_2} - \lambda _2^0} \right)} \right),$
|
(27) |
式中:
注意到
|
$\begin{split}{\sigma _2}\tilde \lambda _2^{\rm T}& \left( {{{\hat \lambda }_2} - \lambda _2^0} \right) \leqslant - \frac{{{\sigma _2}\tilde \lambda _2^{\rm T}{{\tilde \lambda }_2}}}{2} + \frac{{{\sigma _2}{{\left( {{\lambda _2} - \lambda _2^0} \right)}^2}}}{2}\\& \leqslant - {a_0}\tilde \lambda _2^{\rm T}\Gamma _2^{ - 1}{{\tilde \lambda }_2} + \frac{{{\sigma _2}{{\left( {{\lambda _2} - \lambda _2^0} \right)}^2}}}{2}{\text{。}}\end{split}$
|
(28) |
其中,
则
|
$\begin{split}& {{\dot V}_3} \leqslant - {a_0}z_1^2 - {a_0}z_2^2 - {a_0}h_1^2 - r_2^2z_1^2 - \\& \quad r_2^2z_2^2 + r_2^2\omega _2^T{\omega _2} - {a_0}\tilde \lambda _2^T\Gamma _2^{ - 1}{{\tilde \lambda }_2} + D{\text{。}}\end{split}$
|
(29) |
其中,
注意到
|
$r_2^2\omega _2^T{\omega _2}\leqslant r_2^2{\left\| {A_2^m} \right\|^2}{\left\| {{{\bar z}_2}} \right\|^2} \leqslant r_2^2{\left\| {{{\bar z}_2}} \right\|^2}\leqslant r_2^2z_1^2 + r_2^2z_2^2,$
|
(30) |
则
|
${\dot V_3} \leqslant - 2{a_0}{V_3} + D \leqslant - 2{a_0}{V_3} + D{\text{。}}$
|
(31) |
由式(31)可得到
|
${V_3} \leqslant \frac{D}{{2{a_0}}} + \left( {{V_3}\left( 0 \right) - \frac{D}{{2{a_0}}}} \right){e^{ - 2{a_0}t}}{\text{。}}$
|
(32) |
显然,当
以大连海事大学远洋教学实习船“育龙”轮为例进行仿真研究,以验证所提控制算法的有效性。
“育龙”轮的参数为:船长126.0 m,船宽20.8 m,满载吃水8.0 m,方形系数0.681,船速7.7 m/s。通过计算得船舶运动非线性数学模型参数K=0.478,T=216,e1=1,e2=30。
在仿真中,选取控制器设计参数c1=8,c2=15,τ=0.01,r2=0.5,Γ2=1,σ2=1,
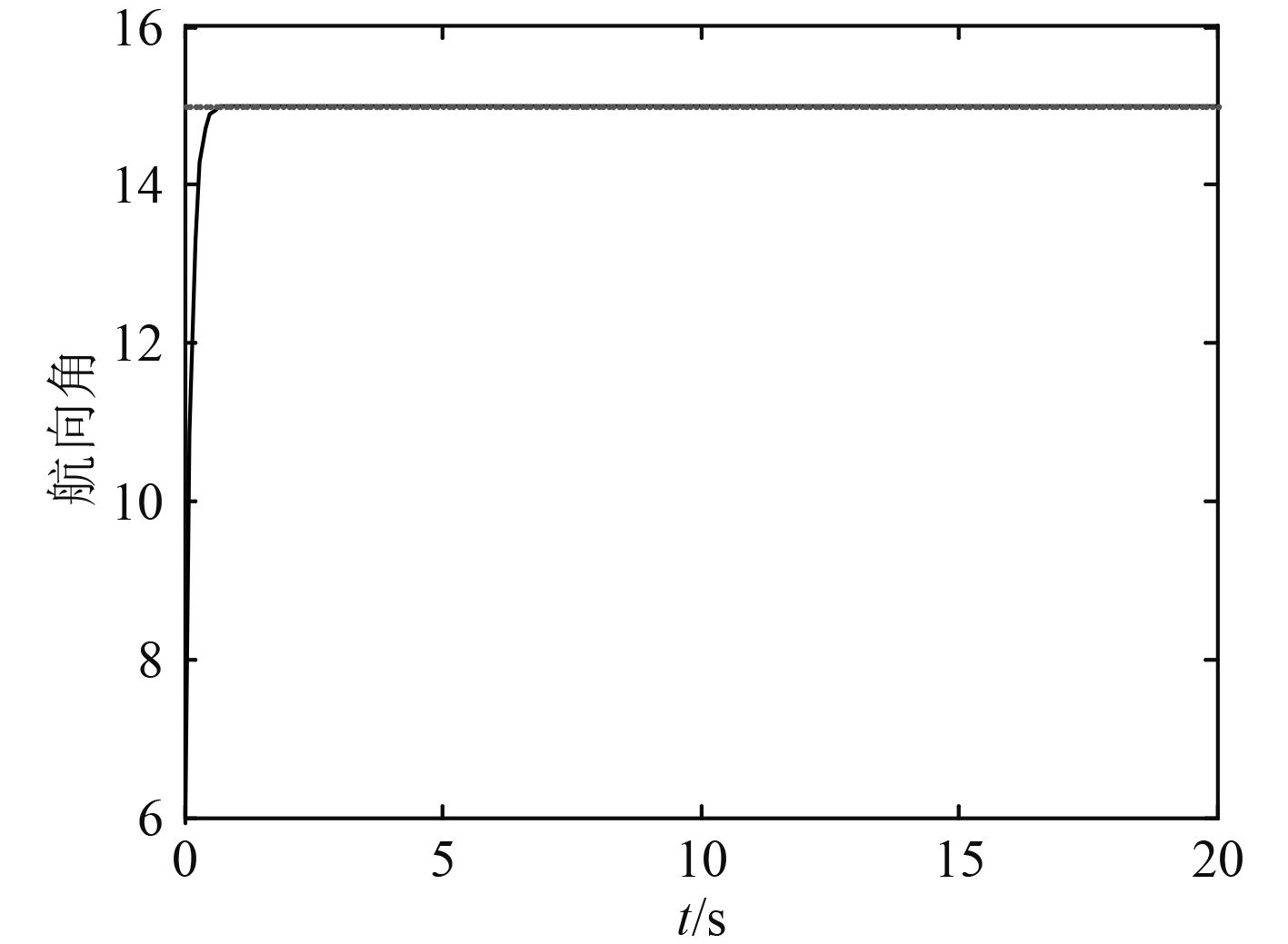
|
图 1 船舶航向历时曲线 Fig. 1 Time response of ship course |
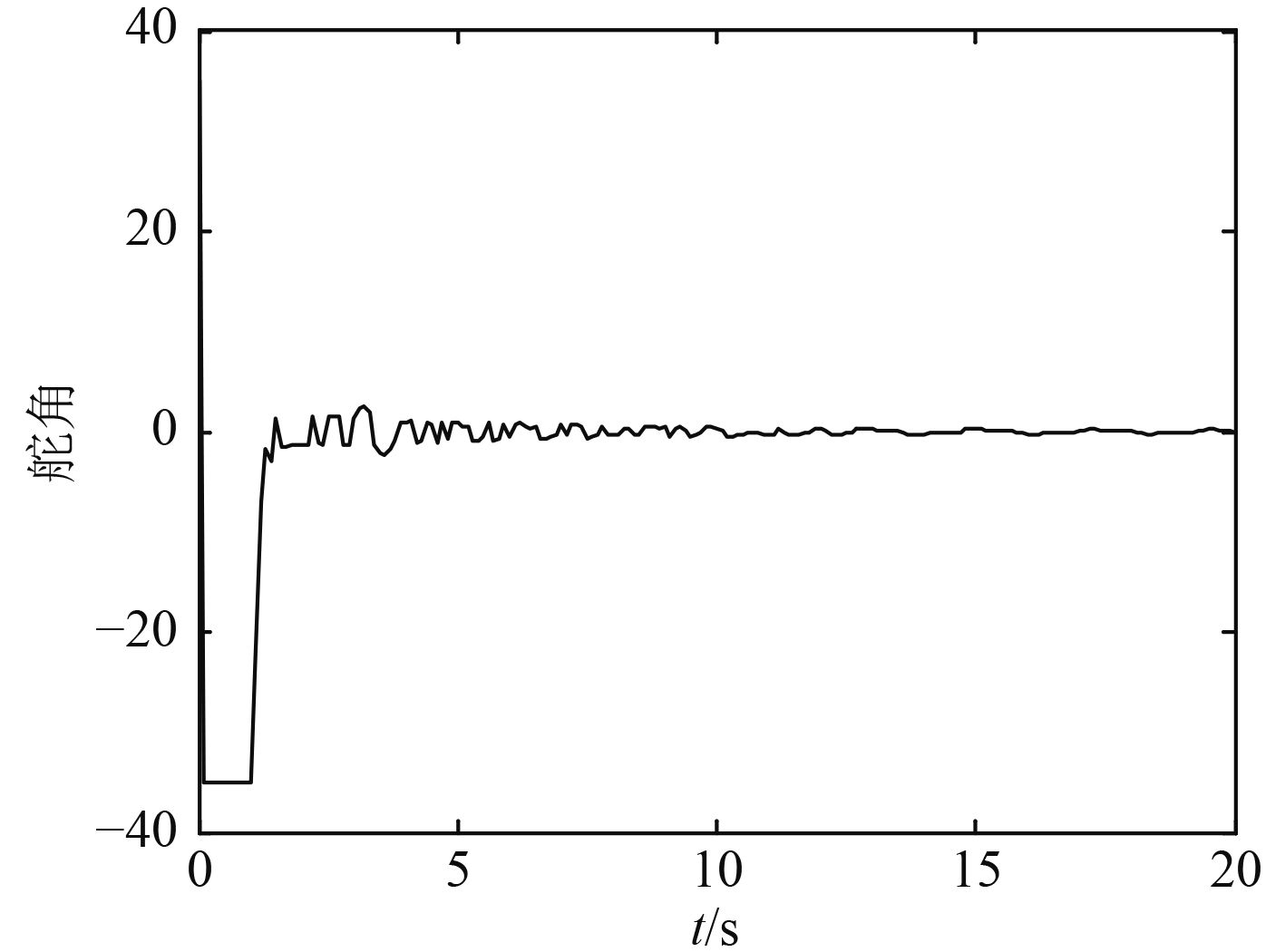
|
图 2 舵角历时曲线 Fig. 2 Time response of rudder angle |
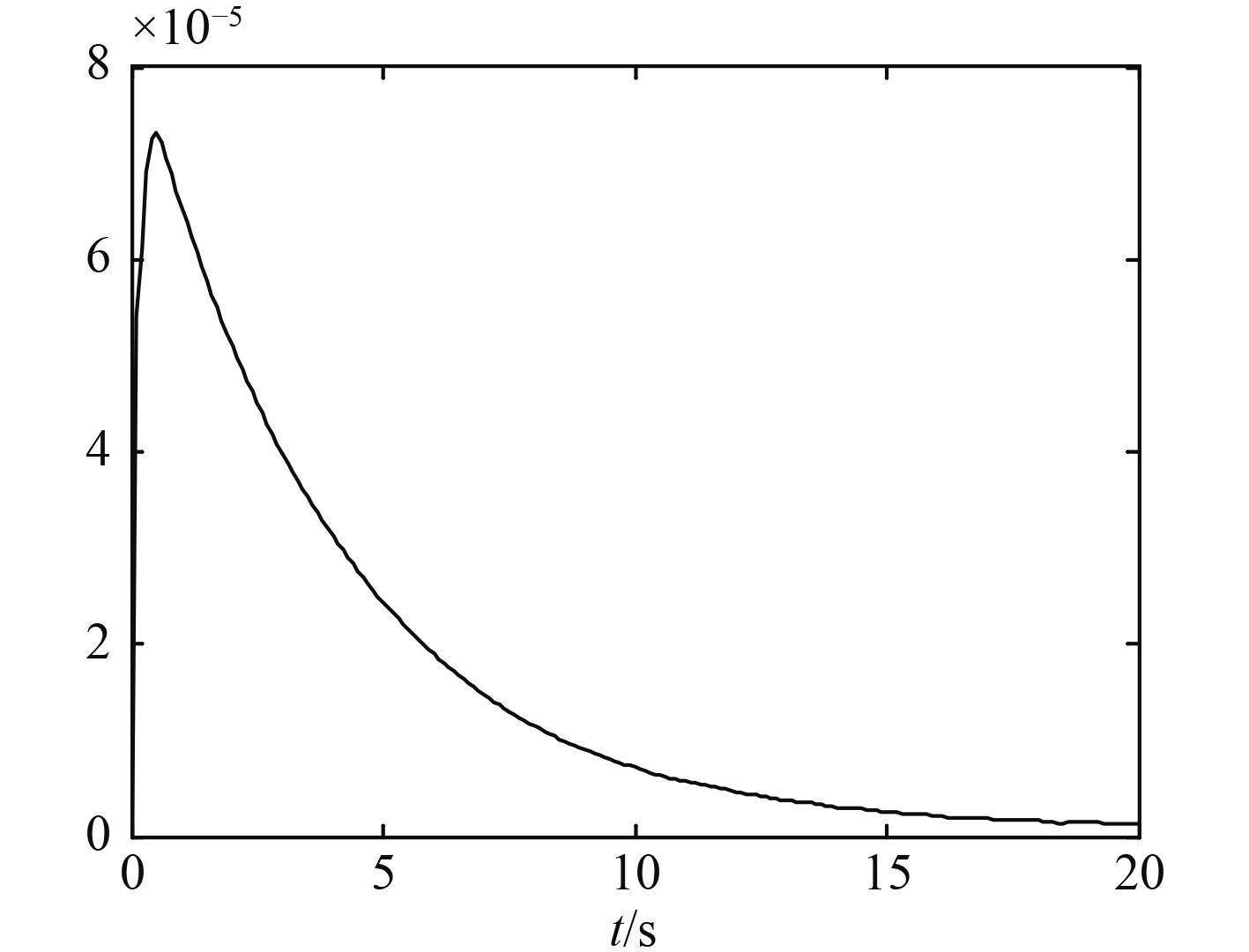
|
图 3
自适应律历时曲线
Fig. 3
Time response of
|
本文在考虑建模不确定性的情况下,针对船舶运动非线性数学模型,采用动态面二阶滑模控制技术和最小学习参数技术,提出了一种新颖的控制方法,在增强了系统鲁棒性的同时,还减少了控制器的计算负担。计算机仿真结果表明了所提算法的有效性。
| [1] | 王林, 陈楠, 高嵬. 基于Backstepping的船舶航向自适应滑模控制[J]. 船电技术, 2012, 32 (4): 16–18. |
| [2] | DU Jia-lu, CHEN Guo. Nonlinear adaptive ship course tracking control based on backstepping and nussbaum gain[C]// IEEE Proceeding of Control Conference 2004, Boston, America. 2004: 6–7. |
| [3] | 卜仁祥, 刘正江, 李铁山. 迭代滑模增量反馈及在船舶航向控制中的应用[J]. 哈尔滨工程大学学报, 2007, 28 (3): 268–272. |
| [4] | GAO X R, HONG B G, XING S W, et al. Designed slide mode controller for ship autopilot with steering gear saturation[C]// 14th International Conference on Algorithms and Architectures for Parallel Processing, 2014, Dalian, China. 2014: 386–395. |
| [5] | WU. Design of Ship Course Control System Based on Backstepping Sliding Mode[J]. Control Engineering of China, 2009, 16 : 52–55. |
| [6] | LEVANT A. Sliding order and sliding ac-curacy in sliding mode control[J]. Interna-tional Journal of Control, 1993, 58 (6): 1247–1263. DOI: 10.1080/00207179308923053 |
| [7] | LEVANT A. Higher-Order Sliding Modes Differentiation and Output-feedback Control[J]. International Journal of Control, 2003, 76 (9-10): 924–941. DOI: 10.1080/0020717031000099029 |
| [8] | 苗保彬, 李铁山, 罗伟林. 基于DSC和MLP的船舶航向跟踪控制[J]. 大连海事大学学报, 2015, 39 (4): 5–8. |
 2017, Vol. 39
2017, Vol. 39
