传统材料在受到冲击载荷的作用下材料将发生压缩变形,一般表现为在垂直于冲击载荷方向上,材料会向冲击部位四周扩散,其宏观变形表现为正泊松比特性。而负泊松比效应的多胞材料由于其具有出众的力学性能、物理性能和可设计性等优点,经常被用在船舶、航天航空、汽车、铁路和军事等重要领域,因而受到广泛的关注[1 – 2]。研究表明胞元微结构(即胞元的拓扑形状)对多胞材料的动力学性能有重要的影响[3],对胞元详尽的分析不但有助于对多胞材料力学响应的深入理解,而且还能为建立新型多胞材料提供理论依据,而探究负泊松比效应下蜂窝结构的动态压缩行为是多胞结构材料动力学性能研究的重要内容之一。
近年来,关于多胞材料冲击动力学性能的研究国内外已经深入展开了研究。对于典型的不同拓扑结构的负泊松比蜂窝结构,Gibson和Ashby[3]结合了大量的实验数据,以六边形单包为理论模型,分析了蜂窝结构的异面和共面变形特性;Zou等[4]讨论了冲击速度对六边形蜂窝材料压缩时前端变形特征的影响,其采用数值模拟的方法研究了六边形蜂窝结构在平面内冲击压缩条件下的动力学响应;Hou等[5]分别研究了在冲击条件和准静态条件下,在压缩过程中六边形铝蜂窝的力学特性;Ruan等[6 – 7]研究了六边形蜂窝材料在面内冲击载荷作用下的力学特性;近些年来,手性蜂窝结构因其具有诸多优点受到国内外学者的广泛关注,手性蜂窝结构的相关研究也得到了进一步开展。1989年Wojciechowski首次提出手性结构的概念[8],2010年,Alderson等[9]研究了三韧带手性蜂窝、四韧带手性蜂窝、六韧带手性蜂窝、反向-三韧带手性蜂窝等在面内弹性模量和泊松比与分网购结构的几何参数的关系;Scarpa等[10]的研究表明,相对于常见的六角蜂窝结构,六韧带手型结构在受到均匀平压时拥有更好的屈曲强度,其研究结果表明,手性结构有出色的静态特性,承受打扰度变形[11],徐时吟等[12]针对中低频段,基于周期结构的Bloch定理以及有限单元法,对六韧带手性结构的能带特性进行理论研究和数值仿真,分析了胞元几何参数对低频带隙的影响,其研究表明手性蜂窝结构具有良好的衰减特性,几何参数对低频带隙有很大的影响,该研究结果对于手性结构及其抗冲击隔振等设计具有重要的参考价值。
在此基础上,本文针对覆盖层空腔形状为负泊松比六韧带手性二维周期性蜂窝结构,建立了其结构的几何模型,进行了面内准静态压缩和低速冲击的力学行为数值仿真分析和研究,其分析结果对于水下舰艇结构的抗冲击设计以及其生命力评估提供一定的参考意义。具体通过非线性有限元软件Abaqus进行建模及仿真,研究了蜂窝覆盖层在不同冲击初速度条件下,施加相同的载荷,分析负泊松比六韧带手性蜂窝覆盖层结构的变形模式,然后对其动态压缩行为以及结构的力学性能进行了相应的解释。
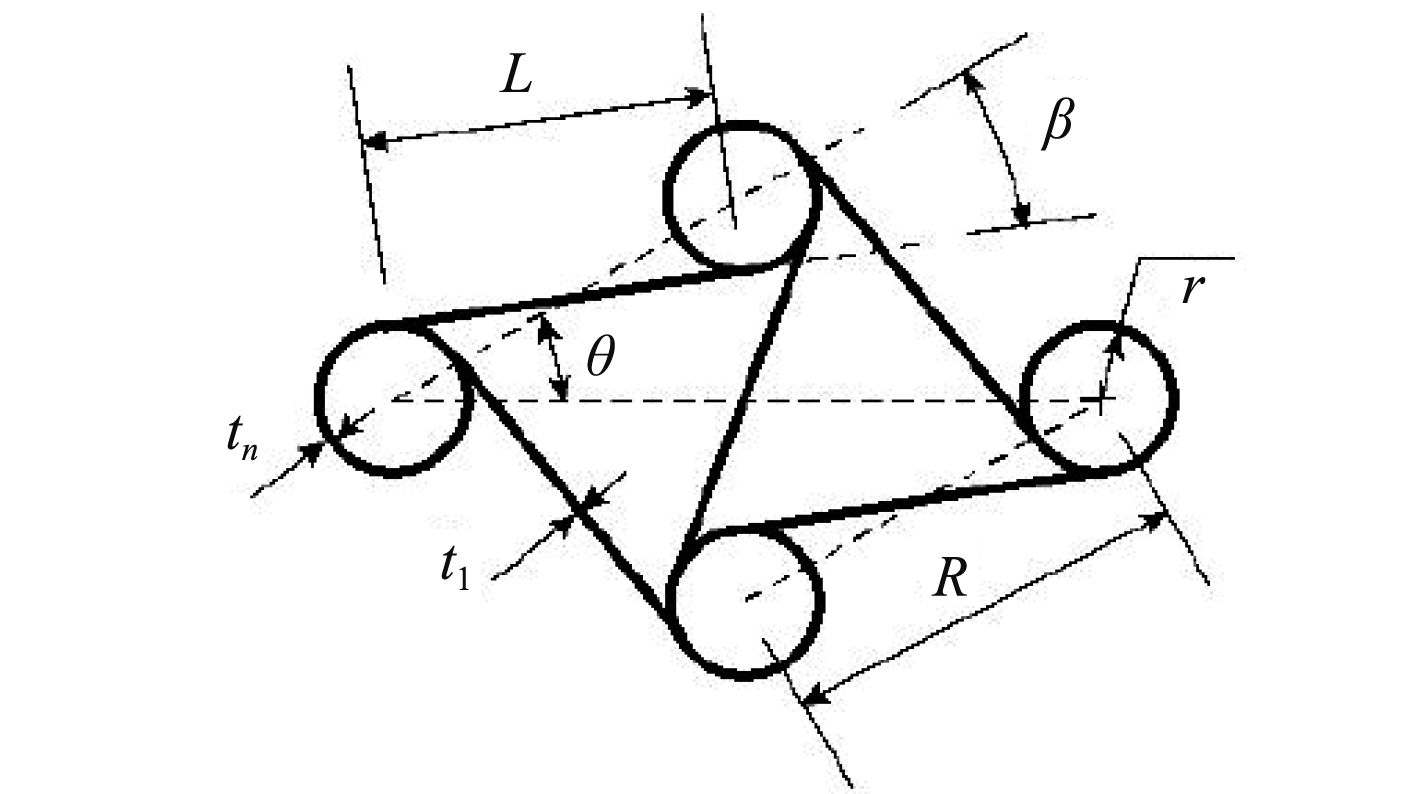
1 六韧带手性蜂窝结构的几何特征由于该结构具有周期性,如图1给出了六韧带手性蜂窝结构的单胞模型示意图,圆环部分为节点,连接相邻圆环且与圆环相切的单元部分称为韧带,根据每个节点所连接的韧带数目,可将手性结构分为三韧带、四韧带和六韧带手性结构。具体几何参数如下:t1为韧带壁厚,θ为相邻节点中心连线之间的夹角,L为韧带长度,r为节点半径,R为相邻两圆环节点之间的距离,β为中心连线与韧带之间的夹角。对于本文所研究的六韧带手性蜂窝结构而言,θ为30°,由简单的几何关系可知,
|
图 1 负泊松比六韧带手性蜂窝结构典型胞元示意图 Fig. 1 Cell diagrammatic sketch of hexachiral honeycomb |
|
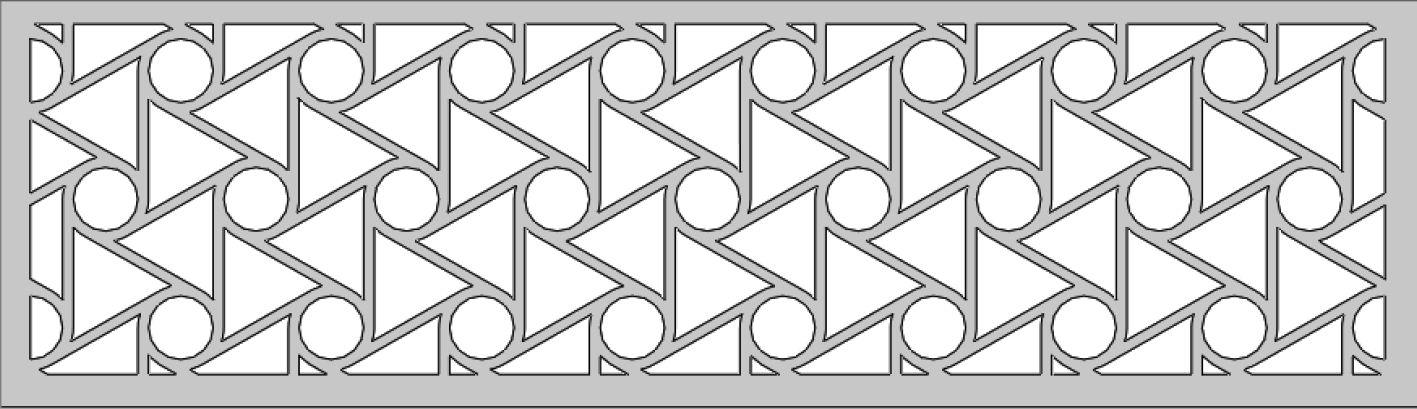
图 2 手性蜂窝结构的计算模型 Fig. 2 Calculating model of hexachiral honeycomb with negative Poission’s ratio |
考虑到覆盖层结构的周期性和计算效率等问题,可以先通过二维模型更容易地揭示其变形特征,图2给出了负泊松比六韧带手性蜂窝覆盖层二维平面有限元模型。覆盖层的宽为66.43 mm,高为19.23 mm,内孔直径为1.5 mm,孔壁为0.5 mm,孔上下边距离1.5 mm,孔周期性分布在橡胶板上。由于橡胶为体积近似且不可压缩的各向同性材料,具有高度的材料非线性,采用超弹性模型来描述其非线性特性。同时考虑到覆盖层在压缩过程中的大变形,故选用Mooney-Rivlin模型拟合的一阶多项式应变势能函数模拟,通过对实验数据的拟合得到相应的超弹性材料常数C10=3.2 MPa,C01=0.8 MPa,D1=0 MPa[13]。为了考察结构的宏观和微观力学性能以及模拟整个覆盖层模型的周期性,在模型左右两侧施加周期性对称边界条件。覆盖层采用4节点四边形双线性减缩积分单元划分(CPE4单元),为了提高有限元计算结果的准确性划分网格尺寸选为0.3 mm,六韧带手性蜂窝结构覆盖层网格单元总数约为6 887个。此外,通过设置胞元内壁自接触可以防止在动态压缩过程中可能发生的穿透现象。由于水下爆炸冲击载荷的复杂性,本文沿用库尔公式,取30 MPa压力为冲击波恒定载荷[14],对蜂窝结构的加载形式为顶端施加恒定均布载荷,且载荷大小为30 MPa,覆盖层结构底端固定。
3 数值计算结果分析与讨论在相同冲击载荷和不同加载初始速度条件下,对负泊松比六韧带手性蜂窝覆盖层结构的瞬态动力学响应特性及能量吸收机理进行了深入的比较分析。加载初速度分别为1 m/s,5 m/s,10 m/s,冲击载荷大小为30 MPa,主要考察的动态压缩性能指标为结构的变形特征、单元节点应力、节点加速度以及能量吸收等。
3.1 不同初速度下覆盖层的变性特征
|
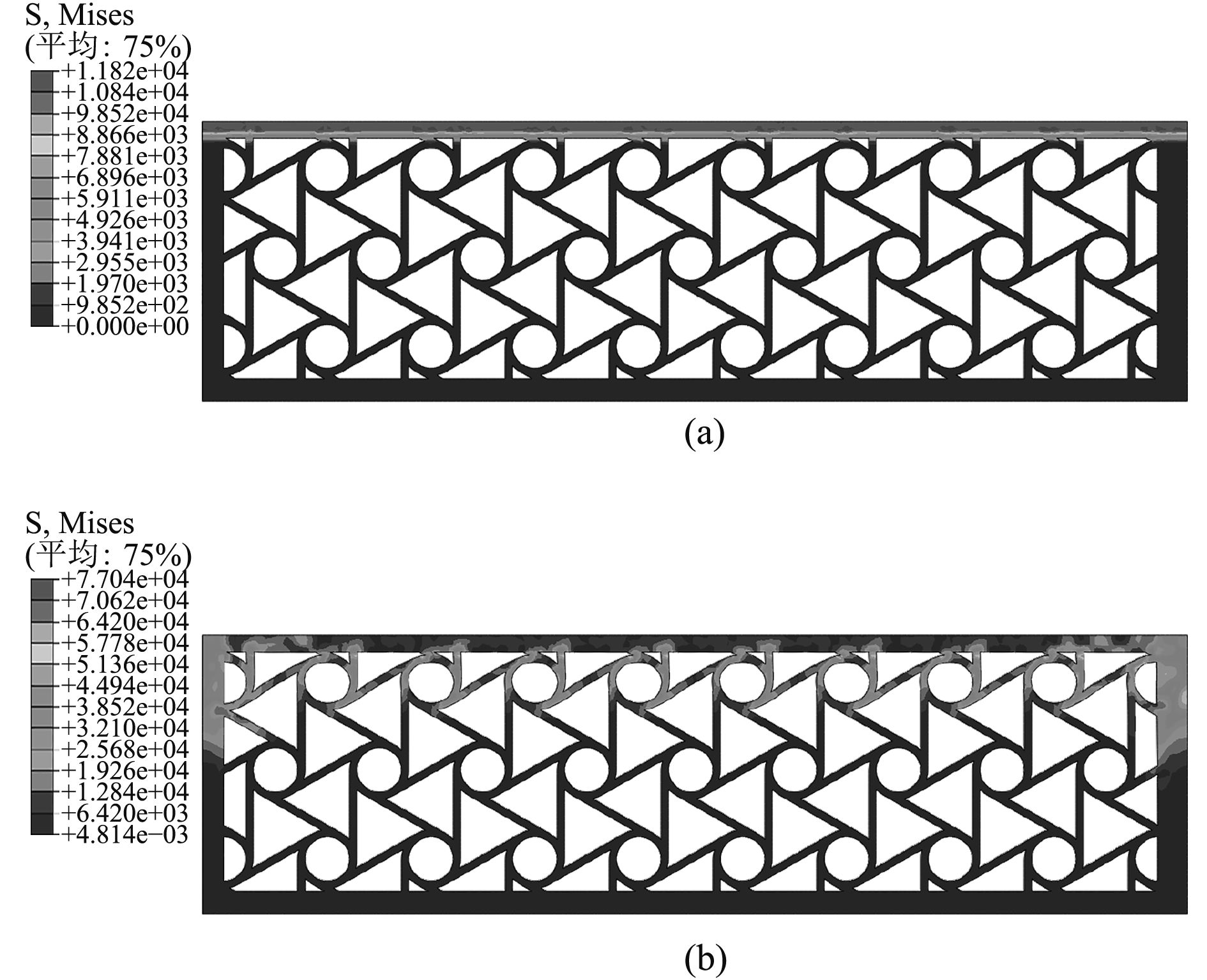
图 3 为覆盖层在1 m/s压缩速度下不同时刻的瞬态响应节点应力云图 Fig. 3 The transient response of node stress at the speed of 1 m/s |
|
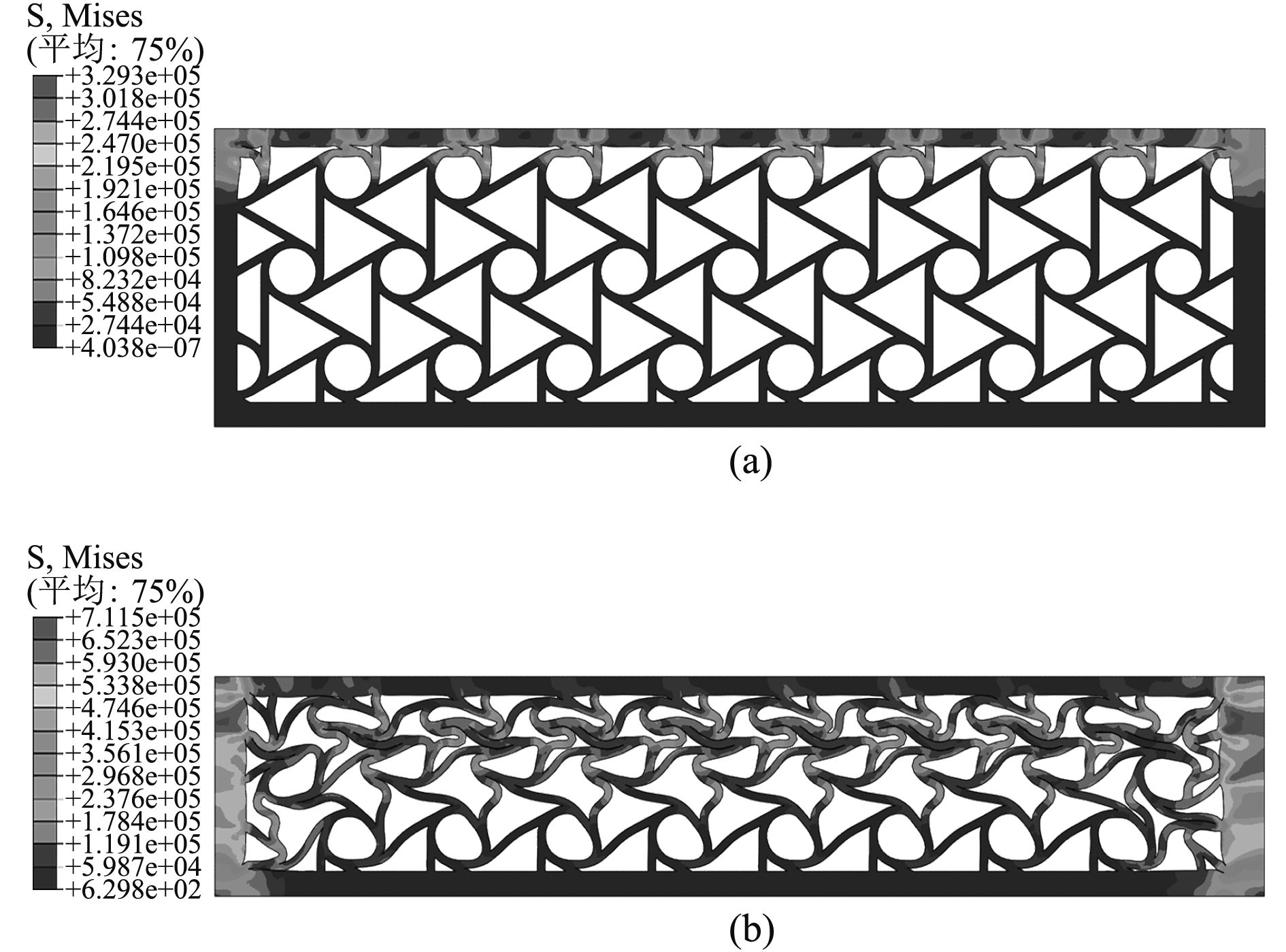
图 4 为覆盖层在5 m/s压缩速度下不同时刻的瞬态响应节点应力云图 Fig. 4 The transient response of node stress at the speed of 5 m/s |
|
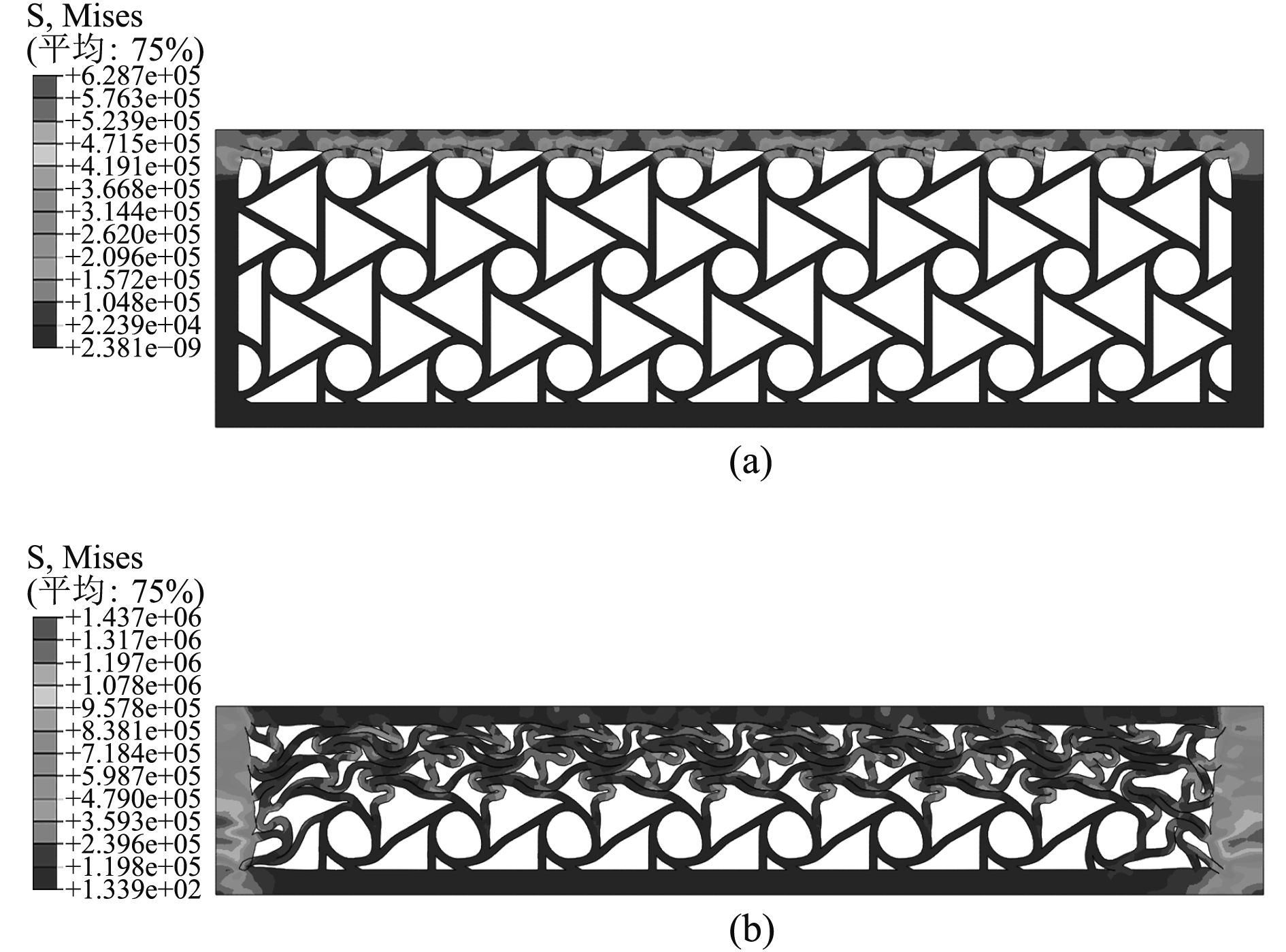
图 5 为覆盖层在10 m/s压缩速度下不同时刻的瞬态响应节点应力云图 Fig. 5 The transient response of node stress at the speed of 10 m/s |
由于本文考察的是水下爆炸冲击载荷,众所周知当动载荷作用在结构上时,加载表面突然获得应力或者质点速度,这种扰动将从结构表面以应力波的形式向前传播,同时考虑到文章中选用的材料是超弹性橡胶材料,对于这种非线性材料,其应变强化逐渐减弱。在初速度为1 m/s低速压缩过程中,由于结构变形程度相对于压缩速度来说变化非常小,因此可将该过程视为准静态压缩,覆盖层结构的变形不太明显。覆盖层受压过程中,冲击端结构先受力,而固定端的结构几乎处于原样,从结构的应力云图可以看出覆盖层结构顶端和底端单元节点应力数值差距较大,表明该覆盖层结构受力有迟滞现象。而随着时间的增加,压缩波由顶端传播到底端,压缩从上向下进行。六韧带手性蜂窝结构受应力波作用后先发生局部变形模式,第1行胞元开始变形,圆环由圆形变为椭圆形,会发现韧带沿着圆环节点发生顺时针旋转再整体向下运动,其宏观变性特征异常明显。随着覆盖层结构压缩量的增大,圆环周围的韧带会慢慢缠绕变形同时发生层状的堆积现象,使得多胞材料进入密实化阶段,直至到达显示动力学设定的时间,整个压缩过程停止。
当冲击初速度为5 m/s时,由于初速度的增加,六韧带手性蜂窝结构的变形程度的变化速度逐渐加快,同时宏观变形特征进一步增强,在相同时刻,覆盖层结构所受的应力有着明显的增加。当施加的初速度继续增大为10 m/s时,覆盖层的压缩行为较低速的动态压缩过程有明显的不同,此时由于初速度的增加幅度较大,惯性效应增强,而靠近载荷加载的一端的韧带和圆环节点被完全压溃,其变形的方式也以一种无序的形式进行,变形主要集中在冲击端,当覆盖层结构被压溃时,六韧带手性蜂窝的孔壁的最后状态也呈现一种无规则形状,而局部变形模式则表现为一层一层的由冲击端向固定端传播。
随着冲击加载速度的增加,变形趋于局部化,而局部变形主要由于惯性效应引起,压缩波在多胞材料中以类似的形式向前扩展来控制胞元的坍塌变形。综合以上3种情况可以发现,在面内冲击载荷作用下,多胞结构冲击方向胞壁的失效机制一般为弹性屈曲或者塑性坍塌:开始阶段材料近似于线性,每个胞元都会沿着对称轴均匀变形,随着应力水平的增加,当结构的局部应力超过胞元壁的弹性屈曲极限,弹性屈曲就会形成,随后进入稳定的平台区,直至材料逐渐压缩密实化。
3.2 不同初速度下单元节点加速度比较分析
|
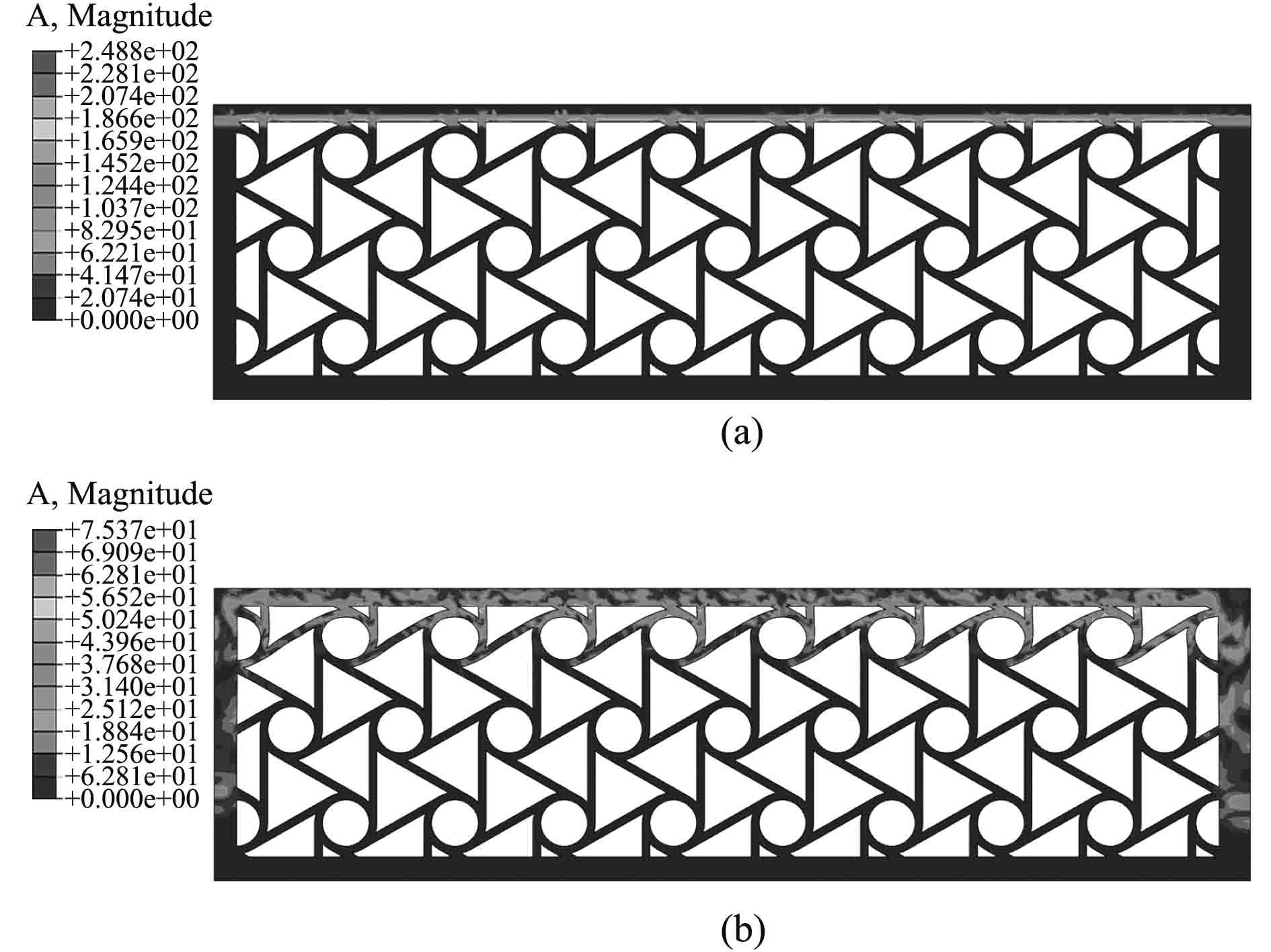
图 6 为覆盖层在1 m/s压缩速度下不同时刻的瞬态响应节点加速度云图 Fig. 6 The transient response of node acceleration under the compression speed of 1 m/s |
|
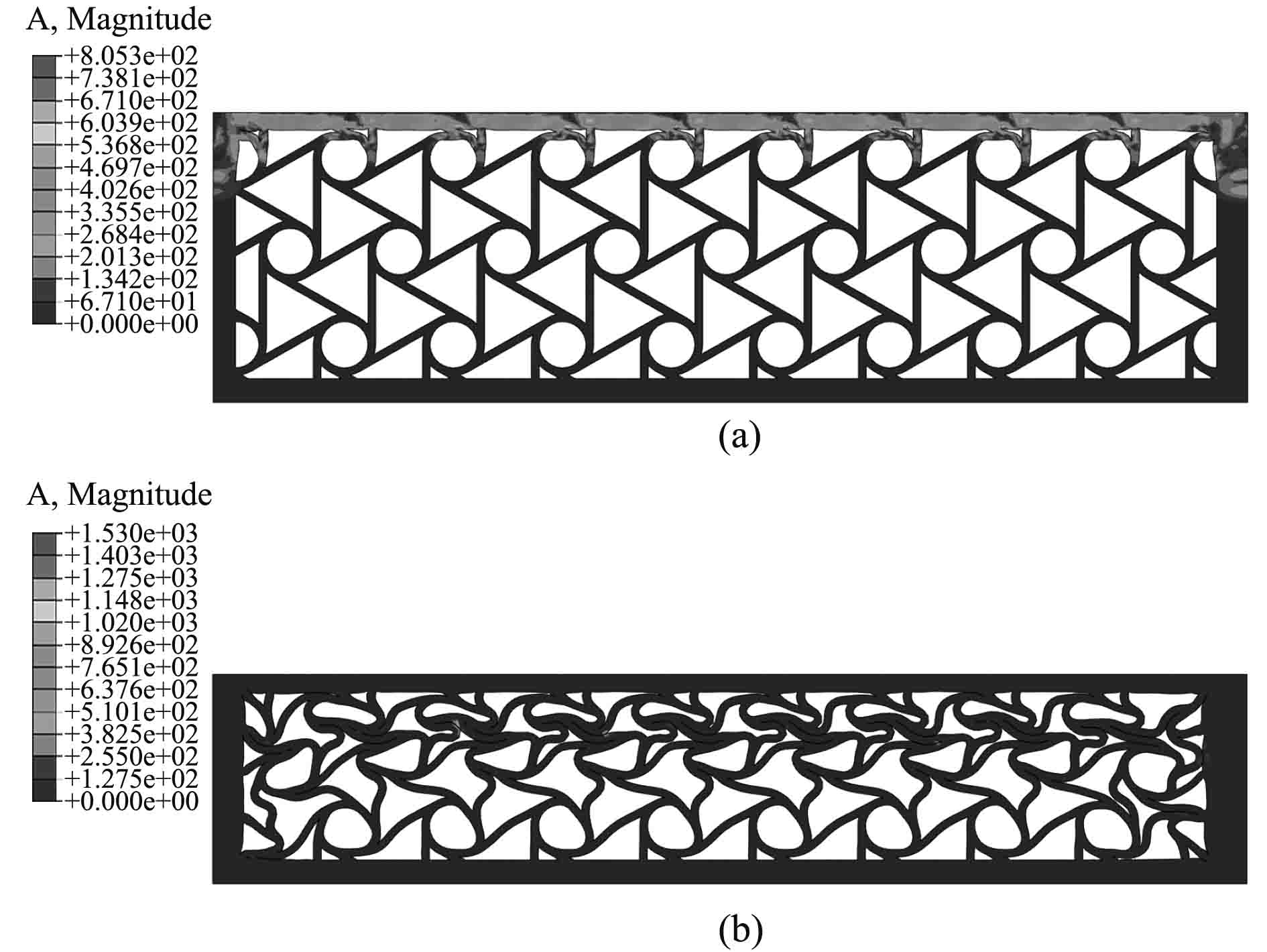
图 7 为覆盖层在5 m/s压缩速度下不同时刻的节点加速度变化云图 Fig. 7 The transient response of node acceleration under the compression speed of 5 m/s |
|
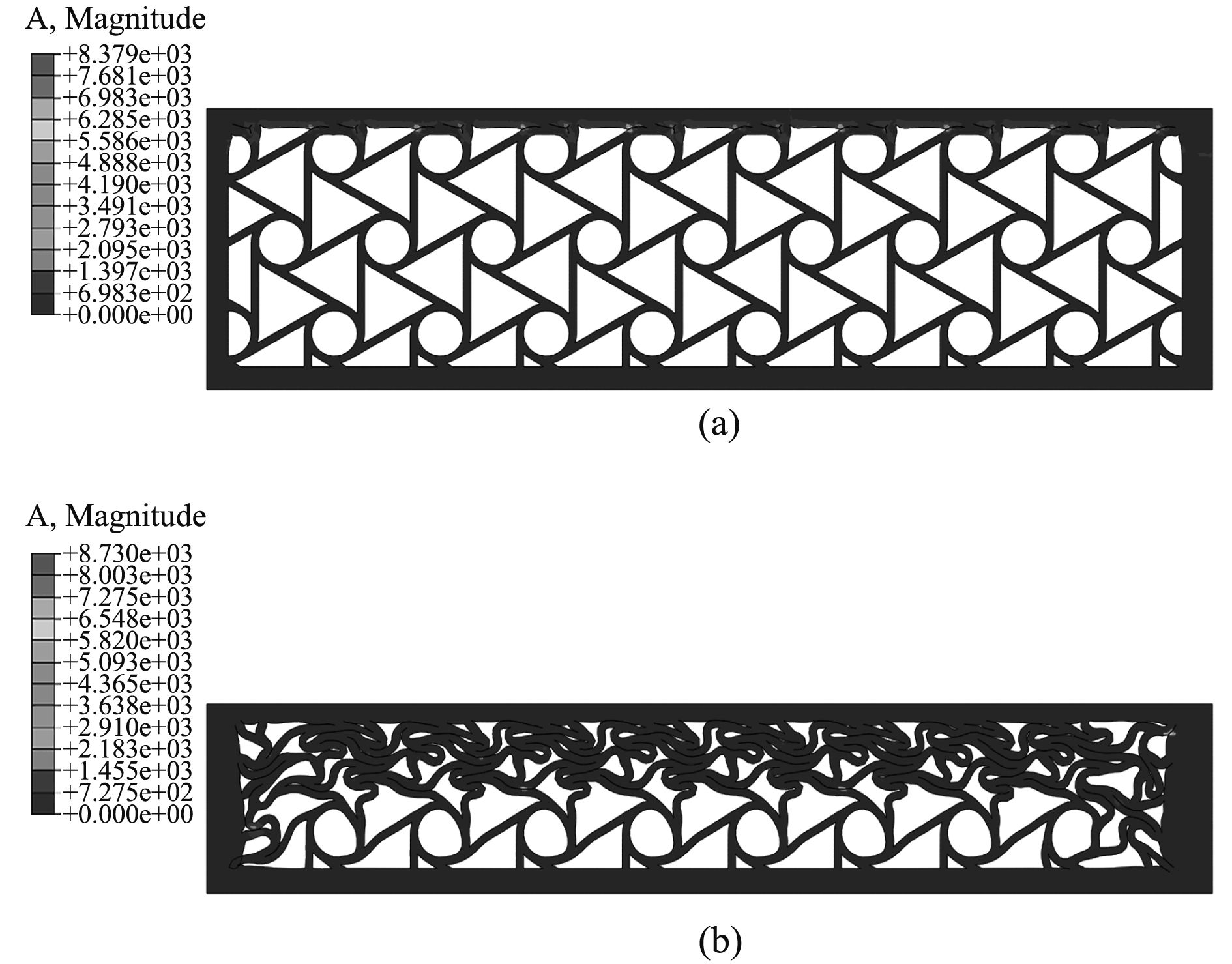
图 8 为覆盖层在10 m/s压缩速度下不同时刻的瞬态响应节点加速度云图 Fig. 8 The transient response of node acceleration under the compression speed of 10 m/s |
图6~图8是3组不同初速度下,不同时刻的六韧带手性蜂窝结构覆盖层瞬态响应下节点加速度云图。可以发现在整个压缩过程中,单元节点的最大加速度不再出现在结构的冲击端或者固定端,而是没有规律性的出现在六韧带手性蜂窝结构的某一孔壁上的某个单元节点上。此外,随着时间的增加,同一初始速度下节点的最大加速度出现的位置也在不断发生变化。总的来说,单元节点的最大加速度出现的地方是变化的,没有规律。
当初始速度为1 m/s时,速度较小,结构的变化较缓慢,在起始阶段,结构的冲击端先接触到应力,顶端的空穴即将发生局部形变,此时加速度云图显示绿色区域(节点加速度较大)范围分布较广,故冲击端的节点加速度较其他地方大,随着应力波的向固定端传播,结构的整体开始动作,蜂窝材料出现局部软化,形成局部变形区,此时加速度较大的地方出现在韧带附近的某处单元节点上,且同样无规律。
当速度为5 m/s时,此时的手性蜂窝结构覆盖层的单元节点在很短时间内的最大加速度的分布与1 m/s相似,但是随着时间的增加,发现最先出现的分布式的云图消失,呈现出来的只是某一区域出现加速度最大值与其他地方不同,而其他地方的节点加速度则大致相近,同时由变形模式可以看出局部变形区的胞元交替变形直至胞元被完全压缩。
随着初速度的进一步增加,当初速度达到10 m/s时,手性蜂窝覆盖层的结构动态响应更加明显,虽然此刻的胞元动态变形模式与前面基本一致,但是由于惯性效应的增加而使得变形主要集中在冲击端,单元节点的最大加速度数值也比前2种情况增加了一个数量级。
由以上分析说明了随着加载速度的增加,结构的单元节点加速度增大,数值呈现出数量级的增加;但是结构大部分区域还是处于较小的加速度,同样说明了此结构即使在较大的载荷作用下,结构整体依然可以保持在一个相对稳定的状态,突显了此结构在抗冲击性能上的优越性,为结构的抗冲击性能提供重要的参考价值。
3.3 不同初速度下结构能量变化比较分析
|
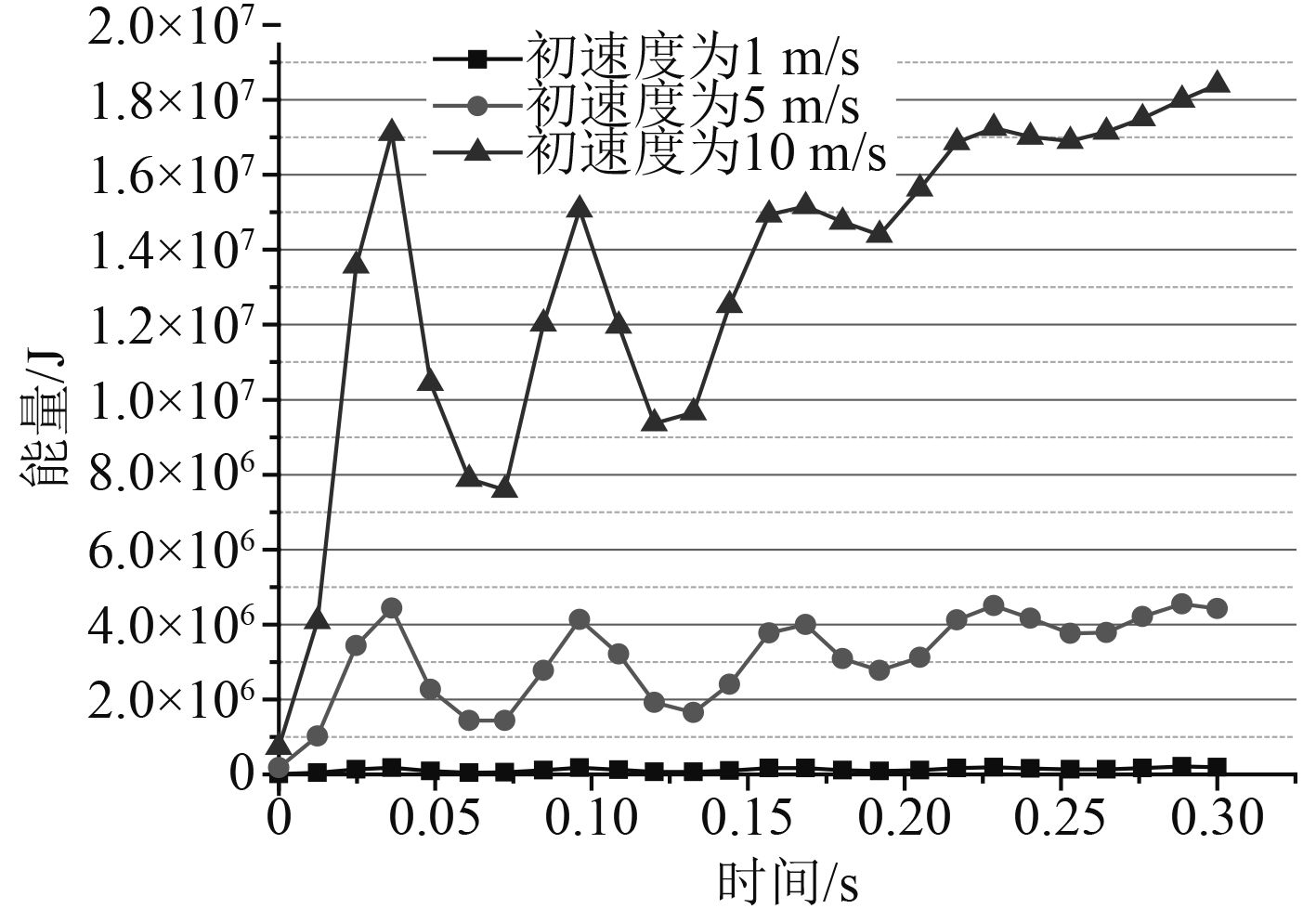
图 9 覆盖层在不同压缩速度下不同时刻结构动能随时间变化曲线图 Fig. 9 The kinetic energy-time curves of coatings under different compression speed |
|
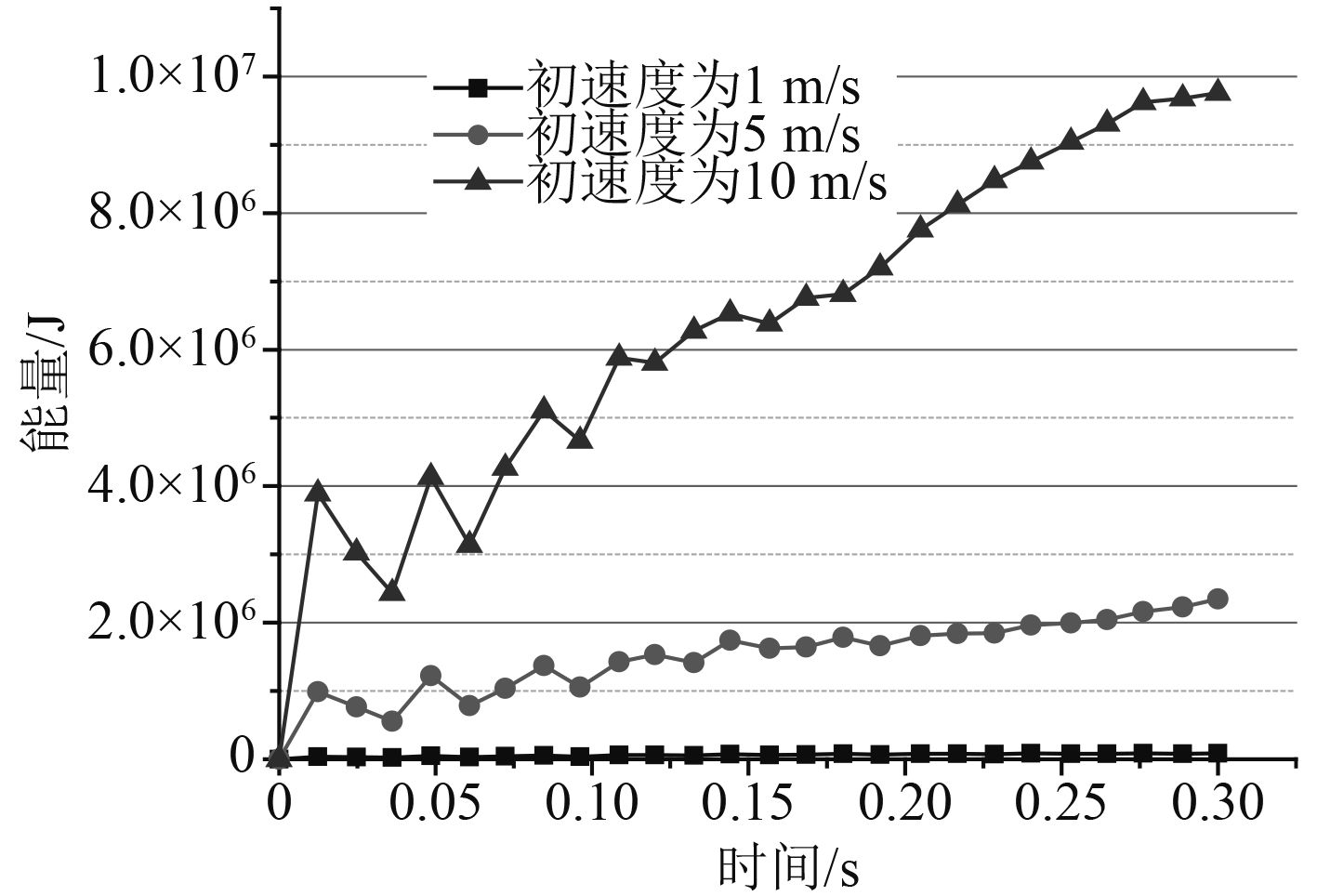
图 10 覆盖层在不同压缩速度下不同时刻结构内能随时间变化曲线图 Fig. 10 The internal energy-time curves of coatings under different compression speed |
图9和图10分别给出了在胞元的边长、壁厚以及尺寸一致,且冲击载荷相同的条件下,负泊松比六韧带手性蜂窝覆盖层结构的动能和内能在不同初始速度下随时间变化的关系。从曲线图中可以看出,手性蜂窝结构覆盖层在不同动态压缩速度下、不同时刻的结构动能和内能不同;在同一初速度、不同时刻下,结构的动能和内能也不尽相同。
具体表现为:在同一时刻、不同初速度下,加载相同的载荷,初速度越大,结构的动能越大,且动能数值先急剧增加然后在一段时间后,动能在一个区间内上下浮动,可以发现,初始速度越大,动能浮动的范围越大,最后再缓慢上升而没有波动现象出现。当初速度较低如1 m/s时,结构的动能数值较小且在一定范围内相对稳定,当速度增大时,刚开始动能会出现小范围的波动现象;当速度进一步增加到10 m/s,动能数值会在较大的范围内波动,同时波动范围跨越的时间也会随之增长。
在3种不同初始速度下,结构储存的内能随时间变化曲线趋势大体相似,内能的数值都是随着时间在不断增加。在较低速度的动态压缩条件下,结构储存的内能效果不明显,而在速度由5 m/s增加到10 m/s时,结构储存的内能随时间变化非常显著,初始速度越大结构的内能变化越大。随着冲击速度的增加,结构表现出来的惯性效应增强,六韧带手性蜂窝结构表现出了相当强的吸能特性,会发现在整个冲击过程中,外界的冲击波能量一部分被手性蜂窝结构胞元的塑性变形耗散掉,另一部分转化为覆盖层结构整体的动能以及其他形式的能量。当此类超弹性负泊松比六韧带手性蜂窝周期结构覆盖层承载爆炸冲击载荷时,施加在此结构上的作用力就会做功,使蜂窝结构孔壁受力变形,会出现弹性屈曲现象,孔壁的弯曲抗力和孔穴的坍塌抗力均提高,随着进一步的压缩,使蜂窝结构达到密实化,通过这样的大变形来吸收大量的能量储存起来,同时也会以其他形式的能量被耗散掉达到非常好的吸能抗冲击的作用。
4 结 语本文基于显示动力学有限元方法,分析比较了负泊松比六韧带手性蜂窝结构的覆盖层,在恒定的爆炸冲击波载荷作用下,3种不同的初速度(分别为1 m/s,5 m/s,10 m/s)对覆盖层动态压缩行为的影响,主要结论如下:
1)六韧带手性蜂窝结构覆盖层在不同的速度下,表现出不同的宏观变形模式或变形特征。低速压缩过程中,可以将其看成准静态静力分析,结构变形缓慢。速度增加以后,圆环孔壁载荷在很短时间内超过弹性屈曲载荷时,圆环节点立即被压溃,覆盖层结构的应力由冲击端向固定端传递。由于惯性效应的作用,会出现局部软化现象,同时会出现一层一层的向固定端传递此种局部变形模式,最后压缩进入密实化阶段。
2)随着压缩速度的改变,单元节点应力、加速度也同时改变,但是结构的力学性能还是具有相似性,随着时间的推移,节点应力及加速度也会有显著的增加,但结构整体依然保持在一个相对稳定的状态。
3)在相同的冲击载荷作用下,初始速度是影响六韧带手性蜂窝结构覆盖层能量吸收的一个重要因素。研究表明,初始速度越大,结构储存的能量越大。
| [1] | PRAWOTO Y. Seeing auxetic materials from the mechanics point of view: A structural review on the negative Poisson’s ratio[J]. Computational Materials Science, 2012, 58 : 140–153. DOI: 10.1016/j.commatsci.2012.02.012 |
| [2] | HOU Y, TAI Y H, LIRA C, et al. The bending and failure of sandwich structures with auxetic gradient cellular cores[J]. Applied Science & Manufacturing, 2013, 49 (3): 119–131. |
| [3] | GIBSON, LORNA J, ASHBY, M. F. Cellular solids: structure and properties [M]. Cambridge University Press, 1999. |
| [4] | ZOU Z, REID S R, TAN P J, et al. Dynamic crushing of honeycombs and features of shock fronts[J]. International Journal of Impact Engineering, 2009, 36 (1): 165–176. DOI: 10.1016/j.ijimpeng.2007.11.008 |
| [5] | HOU B, PATTOFATTO S, LI Y L, et al. Impact behavior of honeycombs under combined shear-compression. Part II: Analysis[J]. International Journal of Solids & Structures, 2011, 48 (5): 698–705. |
| [6] | RUAN D, LU G, WANG B, et al. In-plane dynamic crushing of honeycombs-a finite element study[J]. International Journal of Impact Engineering, 2003, 28 (2): 161–182. DOI: 10.1016/S0734-743X(02)00056-8 |
| [7] | RUAN D, LU G. In-plane static and dynamic properties of aluminum honeycombs[J]. Australian Journal of Mechanical Engineering, 2006, 3 (1). |
| [8] | WOJCIECHOWSKI K W. Two-dimensional isotropic system with a negative poisson ratio[J]. Physics Letters A, 1989, 137 (s1-2): 60–64. |
| [9] | ALDERSON A, ALDERSON K L, ATTARD D, et al. Elastic constants of 3-, 4- and 6-connected chiral and anti-chiral honeycombs subject to uniaxial in-plane loading[J]. Composites Science & Technology, 2010, 70 (7): 1042–1048. |
| [10] | SCARPA F, BLAIN S, LEW T, et al. Elastic buckling of hexagonal chiral cell honeycombs[J]. Composites Part A: Applied Science & Manufacturing, 2007, 38 (2): 280–289. |
| [11] | SPADONI A, RUZZENE M. Numerical and experimental analysis of the static compliance of chiral truss-core airfoils[J]. Journal of Mechanics of Materials & Structures, 2007, 2 (5): 965–981. |
| [12] |
徐时吟, 黄修长, 华宏星. 六韧带手性结构的能带特性[J]. 上海交通大学学报, 2013, 17 (2): 167–172.
XU Shiyin, HUANG Xiuchang, HUA Hongxing. Study on the band structure of hexagonal chiral structures[J]. Journal of Shanghai Jiaotong University, 2013, 17 (2): 167–172. |
| [13] |
肖锋. 舰艇抗冲防护覆盖层水下抗爆机理及实验研究[D]. 上海: 上海交通大学, 2013.
XIAO Feng. Shock resistance and experimental study of the coatings on warship subjected to underwater explosion[D]. Shanghai: Shanghai Jiao tong University, 2013. |
| [14] | 库尔. 水下爆炸[M]. 北京: 国防工业出版社, 1960. |
 2017, Vol. 39
2017, Vol. 39
