0 引 言

船舶在服役期内受到载荷和海水的影响，产生疲劳和腐蚀损伤。随着时间推移，这2种损伤可能累积到很危险的程度。总纵强度是反映船体结构总强度的重要指标，疲劳裂纹的扩展和腐蚀的加重会使船体梁有效剖面模数减小，从而降低总纵抗弯强度，使船的可靠性随时间降低。对此，国内外学者已经做了不少研究；Guedes Soares^[1]用上穿率法对疲劳和腐蚀共同作用下的船体梁时变可靠性进行分析；魏东等^[2]考虑了腐蚀与疲劳损伤分析里船舶的总纵极限强度和可靠性；廖国红^[3]以油船为例，定量考虑疲劳腐蚀对可靠性的影响；黄文波^[4]构造了一种新的时变可靠性表述形式；寇雄^[5]考虑疲劳和腐蚀，使用二阶可靠度方法计算了一艘油船的时变可靠性；施兴华^[6]基于随机过程理论，结合并联系统可靠性分析方法计算了某舰船时变可靠性；李尧^[7]定量分析腐蚀和疲劳计算某船体瞬时可靠性。

以上研究均没有考虑检测维修的影响，而实际上在船舶服役期内定期进行检测，若发现危险构件会进行维修，从而提高船舶的可靠性。对此，周明砚^[8]以某散货船为例计算船体梁时变可靠性时初步考虑了维修因素的影响；李典庆^[9]以受腐蚀损伤的船体构件为例，提出了最优检测及维修策略；Dong Y^[10]在进行船舶风险评估时也考虑了疲劳裂纹的检测维修对于风险水平的更新。目前学术界在维修因素对时变可靠性的影响方面研究较少。

本文以某疏浚船为例，在考虑疲劳和腐蚀损伤的基础上，补充了相应的检测维修方法，计算船舶时变可靠性，并在以往研究的基础上进一步探讨了检测精度及维修更换标准对时变可靠性的影响。

1 载荷分析 1.1 静水弯矩

Soares和Moan根据大量货船的航行数据对静水弯矩进行了统计，认为静水弯矩服从正态分布^[11]。周明砚在对某散货船进行时变可靠性分析时，考虑到船舶的静水弯矩随载况及某载况下航行时间等因素影响，将静水弯矩在时间域内模型化为Poisson矩形脉冲过程，对于每一个单独载况，静水弯矩峰值的累积概率分布在中垂状态下用Raileigh分布拟合，在中拱状态下取为指数分布^[8]。本文算例中的疏浚船载况和持续时间也是波动的，此处同样使用该分布模型。在营运期内静水弯矩最大值的累积概率分布函数和关键参数可表示为：

${F_{{M_S}}} = \exp \left\{ { - \exp \left[ { - {\alpha _S}\left( {{X_S} - {\beta _S}} \right)} \right]} \right\},$

(1)

$\begin{array}{*{20}{l}}{{\alpha _S} = \displaystyle\frac{{2\sqrt {\ln \left( {{\nu _S}{T_0}} \right) \cdot \ln \left( {{\nu _S}T} \right)} }}{{{M_{S0}}}}}&\!\!\!\!\!\!\!\!{,\;{\beta _S} = {M_{S0}}\sqrt {\displaystyle\frac{{\ln \left( {{\nu _S}T} \right)}}{{\ln \left( {{\nu _S}{T_0}} \right)}}} }&\!\!\!\!\!\!\!\!{\text{,中垂}};\\{{\alpha _S} = \displaystyle\frac{{\ln \left( {{\nu _S}{T_0}} \right)}}{{{M_{S0}}}}}&\!\!\!\!\!\!\!\!{,\;{\beta _S} = {M_{S0}}\displaystyle\frac{{\ln \left( {{\nu _S}T} \right)}}{{\ln \left( {{\nu _S}{T_0}} \right)}}}&\!\!\!\!\!\!\!\!{\text{,中拱}}{\text{。}}\end{array}$

(2)

式中： ${\nu _S}$ 为静水弯矩的平均到达率； ${M_{S0}}$ 为船龄 ${T_0} = 20a$ 的最大静水弯矩，可由下式表示：

${M_{S0}} = \left\{ \begin{array}{l}\!\!\! - 0.065{C_W}{L^2}B\left( {{C_B} + 0.7} \right) \!\!\!\!\!\!\!\!\!\! \\\!\!\!{C_W}{L^2}B\left( {0.1225{\rm{ - }}0.015{C_B}} \right) \!\!\!\!\!\!\!\!\!\!\end{array} \right.\begin{array}{*{20}{c}}{\text{,中垂}},\\{\text{,中拱}}{\text{。}}\end{array}$

(3)

式中：L为船长；B为船宽；C_B为方形系数；C_W为波浪系数，

${C_W}\!\! =\!\! \left\{ {\begin{array}{*{20}{l}}\!\!\! {10.75 - {{\left( {\left( {300 - L} \right)/100} \right)}^{3/2}}},&{100 < L \leqslant 300};\\\!\!\! {10.75},&{300 < L \leqslant 350};\\\!\!\! {10.75 - {{\left( {\left( {L - 350} \right)/150} \right)}^{3/2}}},&{L > 350}{\text{。}}\end{array}} \right.$

(4)

1.2 波浪弯矩

波浪弯矩的大小主要取决于波浪的作用，包括垂向弯矩、水平弯矩和扭矩。本文分析基于总纵强度，且引起疲劳裂纹扩展的应力主要由垂向弯矩引起，故这里只考虑垂向弯矩。

短期波浪弯矩可以模型化为平稳Gauss随机过程，对于窄带Gauss随机过程，其峰值分布服从Raileigh分布。波浪弯矩的长期预报建立在短期预报的基础上，一般认为长期波浪弯矩可以模型化为Poisson过程^[3]，由极值分析可知，在营运期内波浪弯矩最大值的累积概率分布和关键参数可表示为：

${F_{{M_W}}} = \exp \left\{ { - \exp \left[ { - {\alpha _W}\left( {{X_W} - {\beta _W}} \right)} \right]} \right\},$

(5)

${\alpha _W} = \frac{{\ln \left( {{\nu _W}{T_0}} \right)}}{{{M_{W0}}}},{\beta _W} = {M_{W0}}\frac{{\ln \left( {{\nu _W}T} \right)}}{{\ln \left( {{\nu _W}{T_0}} \right)}}{\text{。}}$

(6)

式中： ${\nu _W}$ 为波浪弯矩的平均到达率； ${M_{W0}}$ 为船龄 ${T_0} = 20a$ 的最大波浪弯矩，

${M_{W0}} = \left\{ \begin{array}{l} - 0.11{C_W}{L^2}B\left( {{C_B} + 0.7} \right),\\0.19{C_W}{L^2}B{C_B},\end{array} \right.\begin{array}{*{20}{c}}{\text{中垂}}\text{；}\\\,{\text{中拱}}{\text{。}}\end{array}$

(7)

2 剖面模数的时变模型

在计算总纵强度时需计算上甲板或船底的剖面模数，本文算例中上甲板剖面模数较小，比较危险，故下文提及的剖面模数均指上甲板剖面模数。船体梁剖面模数与剖面内构件的尺寸及其在剖面上分布的位置有关。在船舶服役期内，认为构件在剖面上位置不变，构件抵抗总纵弯矩的有效尺寸会随着疲劳裂纹的扩展和腐蚀的影响而折减。

2.1 腐蚀的影响

对于新造船舶，由于采用防腐涂层，其腐蚀过程分为2个阶段：第1阶段，由于涂层保护，构件不发生腐蚀；第2阶段，失去涂层保护后，腐蚀导致构件厚度减小。由于腐蚀而导致的构件厚度的折减量表达为^{[3, 6, 8]}：

$r(t) = c(t - {t_0}), $

(8)

式中：t₀为防腐涂层的有效保护时间，本文取5年。系数c为平均年度腐蚀率，是随机变量，廖国红的研究中将其作为正态分布，对于甲板、舷侧、船底不同位置给出均值和变异系数^[3]。

2.2 疲劳的影响 2.2.1 疲劳裂纹扩展

本文主要考虑焊接结构的裂纹扩展，认为结构中预先存在初始裂纹，裂纹从腹板和面板的焊接处产生，然后分别在腹板和面板上扩展，根据Paris公式，裂纹扩展的速度 ${\rm d}a/{\rm d}n$ 与裂纹尖端的应力强度因子范围 $\Delta K$ 有关^[7-8]。

$\frac{{{\rm d}a}}{{{\rm d}n}} = C{(\Delta K)^m}, $

(9)

$\Delta K = SY(a)\sqrt {π a}{\text{。}} $

(10)

其中：a为裂纹尺寸，n为循环次数，C和m为材料的裂纹扩展参数。由于一般船用钢材为中等强度碳锰结构钢，本文算例参考周明砚文中取值，m取3.07，C服从对数正态分布^[8]。 $Y\left( a \right)$ 为几何修正系数，是裂纹尺度的函数，还和裂纹形状、结构尺度、裂纹处的应力状态等有关，研究中常为计算简便，取1^{[3, 7-8]}，S为交变应力范围。

通过对Paris公式积分可得裂纹尺寸随时间变化的关系如下^[11]：

$a(t) = {\left[ {a_0^{1 - m/2} + \left( {1 - \frac{m}{2}} \right)C{S^m}{Y^m}{π ^{m/2}}{f_L}t} \right]^{1/(1 - m/2)}}{\text{。}}$

(11)

式中：a₀为初始裂纹尺寸，f_L为应力循环频率，等于波浪弯矩的平均到达率 ${\nu _W}$ 。

裂纹尺寸随时间变化的均值和方差分别为：

$\begin{split}E\left[ {a\left( t \right)} \right] = & \left[ {{{\left\{ {E\left[ {{a_0}} \right]} \right\}}^{1 - m/2}} + \left( {1 - m/2} \right) } \right.\times\\ &{\left. {E\left[ C \right]E\left[ {{S^m}} \right]{Y^m}{π ^{m/2}}{f_L}t} \right]^{1/(1 - m/2)}}{\text{。}}\end{split}$

(12)

$\begin{aligned}\sigma _{a\left( t \right)}^2 \!=\! & {\left[ \! {\frac{{{{\left\{ {E\left[ {{a_0}} \right]} \right\}}^{\left( { - m/2} \right)}}a\left( t \right)}}{{{{\left\{ {E\left[ {{a_0}} \right]} \right\}}^{1 - m/2}} \!+\! \left( {1 \!-\! m/2} \right)E\left[ C \right]E\left[ {{S^m}} \right]{Y^m}{\pi ^{m/2}}{f_L}t}}} \! \right]^2} \!\!\! \sigma _{{a_0}}^2 \!+\! \\ & {\left[ {\frac{{E\left[ \! C \right]E\left[ {{S^m}} \right]{Y^m}{π ^{m/2}}}}{{{{\left\{ {E\left[ {{a_0}} \right]} \right\}}^{1 - m/2}} \!+\! \left( {1 \!-\! m/2} \right)E\left[ C \right]E\left[ {{S^m}} \right]{Y^m}{π ^{m/2}}{f_L}t}}} \! \right]^2} \!\!\! \sigma _S^2 \!+\! \\ & {\left[ {\frac{{E\left[ \! {{S^m}} \right]{Y^m}{π ^{m/2}}{f_L}ta\left( t \right)}}{{{{\left\{ {E\left[ {{a_0}} \right]} \right\}}^{1 - - m/2}} \!+\! \left( {1 \! -\! m/2} \right)E\left[ C \right]E\left[ {{S^m}} \right]{Y^m}{π ^{m/2}}{f_L}t}}} \! \right]^2} \!\!\! \sigma _C^2{\text{。}}\end{aligned}$

(13)

2.2.2 交变应力范围

由波浪弯矩诱导的交变应力范围S的长期分布可以用Weibull分布描述^[8]：

$\begin{array}{*{20}{c}}{{f_S}\left( S \right) = \displaystyle\frac{{\xi \ln {N_L}}}{{S_L^\xi }}{S^{\xi - 1}}\exp \left( { - \displaystyle\frac{{{S^\xi }}}{{S_L^\xi }}\ln {N_L}} \right)}\!\!\!\!\!\!\!&{,0 \! \leqslant \! S \! < \!\!\! }\end{array} \! + \infty {\text{。}}\!\!\!\!\!\!\!\!$

(14)

其中 $\xi $ 是形状参数，一般对船舶进行疲劳分析时取1^[8]，N_L为服役期内应力循环总次数，S_L为最大应力范围，可以表示为：

${S_L} = \frac{{{M_W}\left( H \right) - {M_W}\left( S \right)}}{W}\text{。}$

(15)

式中： ${M_W}\left( H \right)$ ， ${M_W}\left( S \right)$ 分别为船舶在中拱和中垂状态下的最大波浪弯矩。由公式可知，不同位置处的剖面模数不同，要对S_L分别进行计算。计算的S方差表达式如下：

$\sigma _S^2 = {\left( {\frac{{S_L^\xi }}{{\ln {N_L}}}} \right)^2}\left\{ {\varGamma \left( {\frac{2}{\xi } + 1} \right) - {{\left[ {\varGamma \left( {\frac{1}{\xi } + 1} \right)} \right]}^2}} \right\}{\text{。}}$

(16)

由于计算中用到应力范围S的m次幂，计算可得：

$E\left( {{S^m}} \right) = \frac{{S_L^m}}{{{{\left( {\ln {N_L}} \right)}^{m/\xi }}}}\varGamma \left( {\frac{m}{\xi } + 1} \right){\text{。}}$

(17)

2.3 船体梁剖面模数

由于疲劳和腐蚀的共同作用，船体构件的尺寸相应折减。假设腹板的初始高度和时变高度分别为h₀， $h(t)$ ；面板的初始宽度和时变宽度分别为b₀， $b(t)$ ；板的初始厚度和时变厚度分别为s₀， $s(t)$ 。疲劳裂纹和腐蚀对构件尺寸的折减可以表示为：

$h(t) = {h_0} - a(t),$

(18)

$b(t) = {b_0} - a(t),$

(19)

$s(t) = {s_0} - r(t){\text{。}}$

(20)

按折减后的构件尺寸重新计算剖面模数，可以发现，剖面模数是一个和时间有关的随机变量，已有的研究中通常将其作为正态分布函数^{[8, 11]}，本文也将其作为正态分布的随机变量。

3 时变可靠性

船体梁极限状态函数可以表达为：

$g(t) = {C_U}{\sigma _y}W(t) - {C_S}{M_S}(t) - {C_W}{M_W}(t),$

(21)

式中：C_U为抗弯强度不确定因子； ${\sigma _y}$ 为材料的许用应力； $W(t)$ 为剖面模数； ${C_S}$ 为静水弯矩不确定因子； ${M_S}$ 为静水弯矩； ${C_W}$ 为波浪弯矩不确定因子； ${M_W}$ 为波浪弯矩。考虑船处于中拱或中垂状态的可能性相同，分别计算出中拱中垂状态下的条件失效概率 ${f_1}(t)$ 和 ${f_2}(t)$ ，船整体的失效概率为二者的平均值，则船的时变可靠度可以表示为：

$r(t) = 1 - \left( {{f_1}(t) + {f_2}(t)} \right)/2\text{。}$

(22)

4 检测维修更新

船舶在服役期内要定期接受检测，本文考虑每5年检测一次。一旦发现构件严重受损，则对其进行维修或更换。对于疲劳裂纹和腐蚀这2种损伤，分别对应不同的检测维修方法。

4.1 疲劳裂纹检测维修

裂纹的检测一般基于探测方法和构件上的实际尺寸。理论上，每种探测技术都存在一个检测临界值，即检测过程中将发现所有大于或等于裂纹检测临界值的裂纹。该检测过程可用下式描述：

$a(t) \geqslant {a_c},$

(23)

式中：a_c为裂纹检测临界值，体现了检测方法的精度， $a(t)$ 为检测时某裂纹的尺寸。一旦发现裂纹，就对其修理，使其恢复到初始尺寸a₀。

4.2 腐蚀板件检测维修

船体板的腐蚀状态通过在若干有代表性的点处测量板厚来评估，如果由于腐蚀导致板厚折减量超过某一阈值，通常要求换一块新板。关于更换的标准，一般采取最小允许板厚或最小允许板厚折减量比率的形式。本文采用最小允许板厚折减量比率方法，认为当测到板的厚度减小到初始板厚的一定比率时，更换为新板。该检测过程可以用下式表示：

$s(t) \leqslant {p_c}{s_0}\text{。}$

(24)

式中： $s(t)$ 为测到的板厚，s₀为初始板厚，p_c为最小允许折减量比率，体现了板件更换标准。Paik建议对甲板板、船底板和纵向舱壁板， ${p_{c1}}$ 取0.8，对于舷侧板和横向舱壁板， ${p_{c2}}$ 取0.75^[12]。

4.3 考虑检测维修的计算流程图

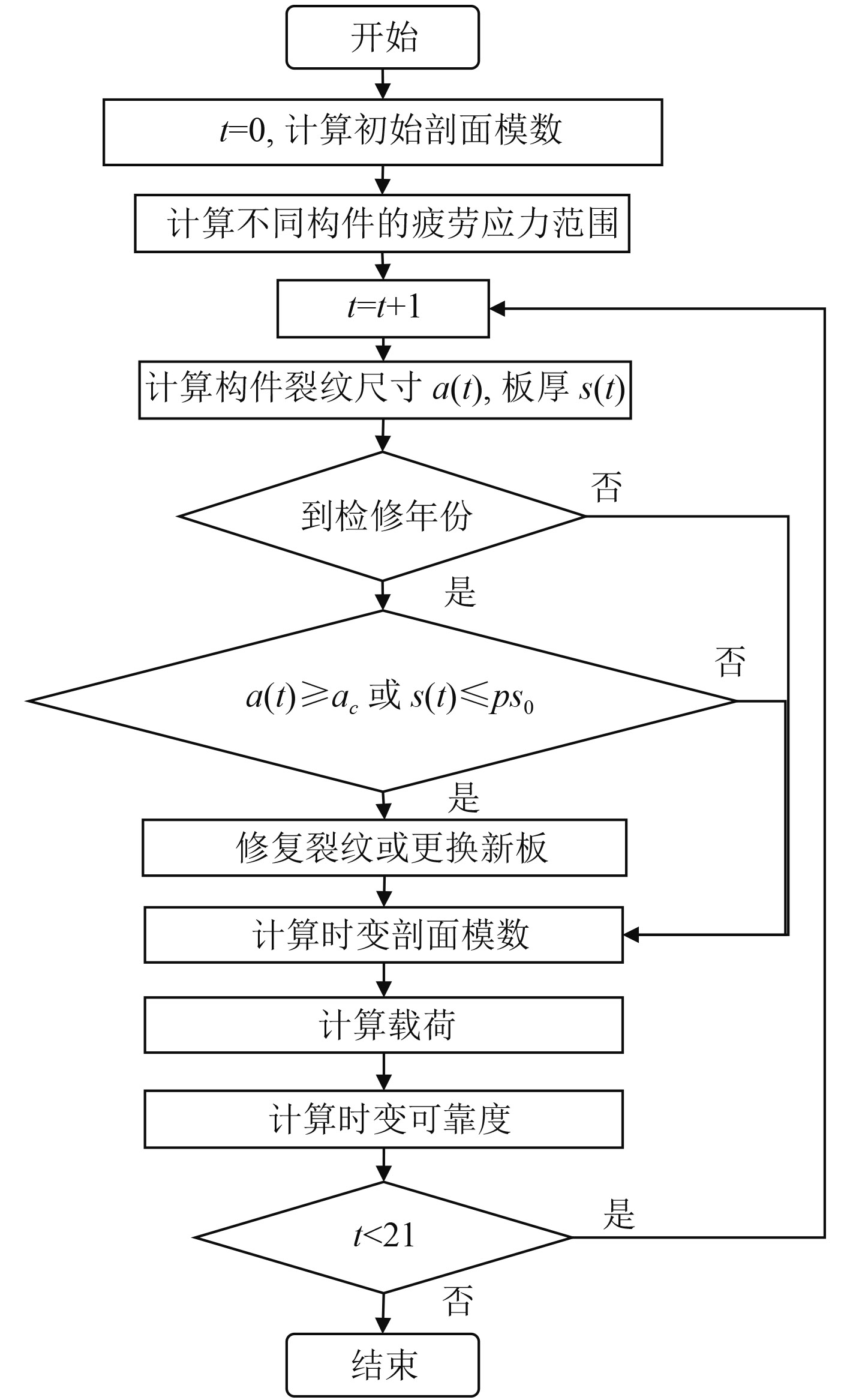
综合疲劳和腐蚀损伤，并考虑了检测维修因素的影响后，对船体梁的时变可靠性计算流程如图1所示。

5 算　例

根据上述流程图，在Matlab中编写计算程序，并应用程序对某疏浚船的时变可靠性进行分析。

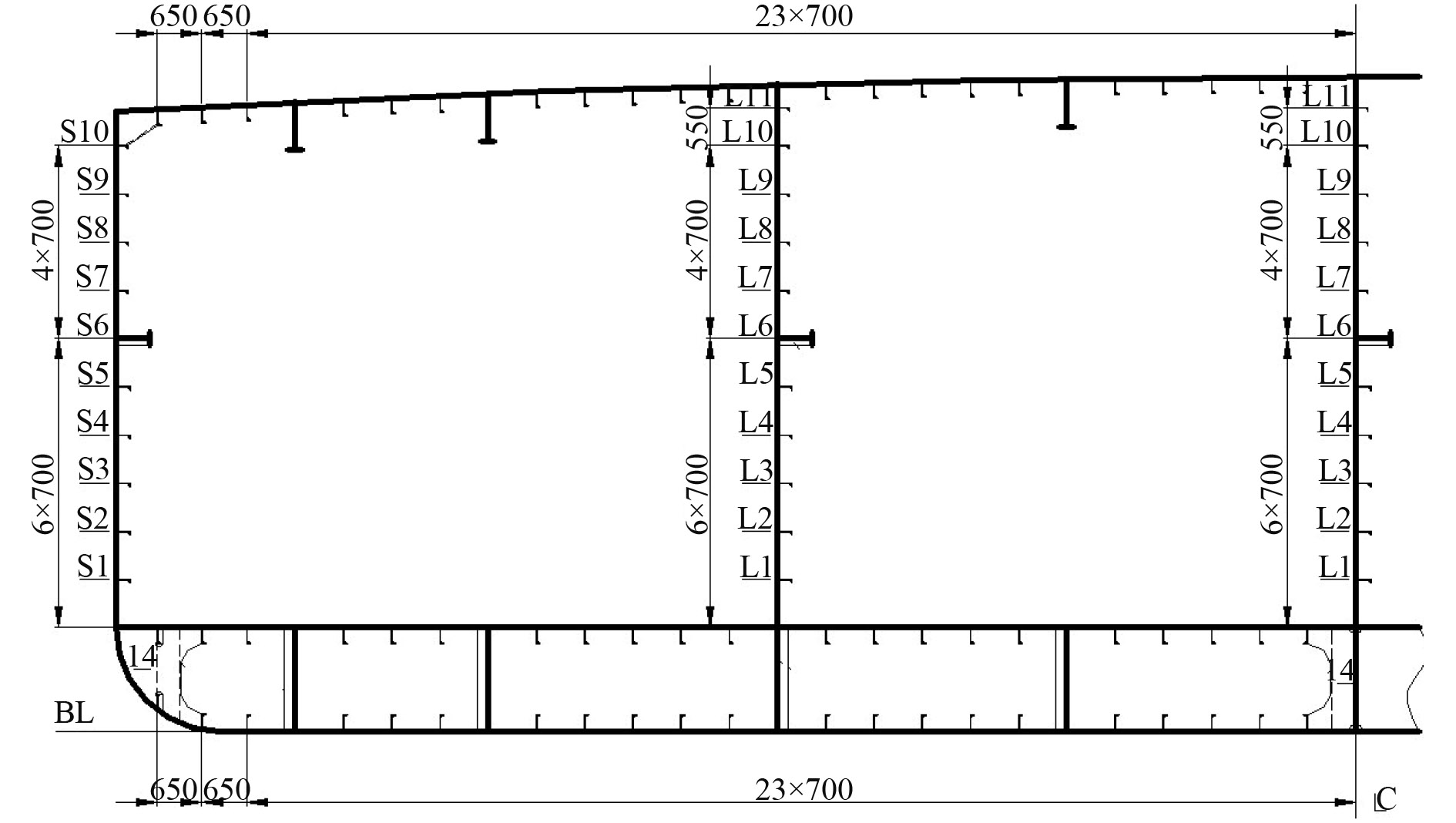
5.1 主要参数

本文以某200方抓斗式疏浚船为算例进行计算，主尺度如表1所示。疏浚船的中横剖面如图2所示。中横剖面中各构件的型号和尺寸如表2所示。

计算过程中还涉及到很多随机变量，各变量具体的描述如表3所示。

5.2 计算结果

1）只考虑疲劳损伤

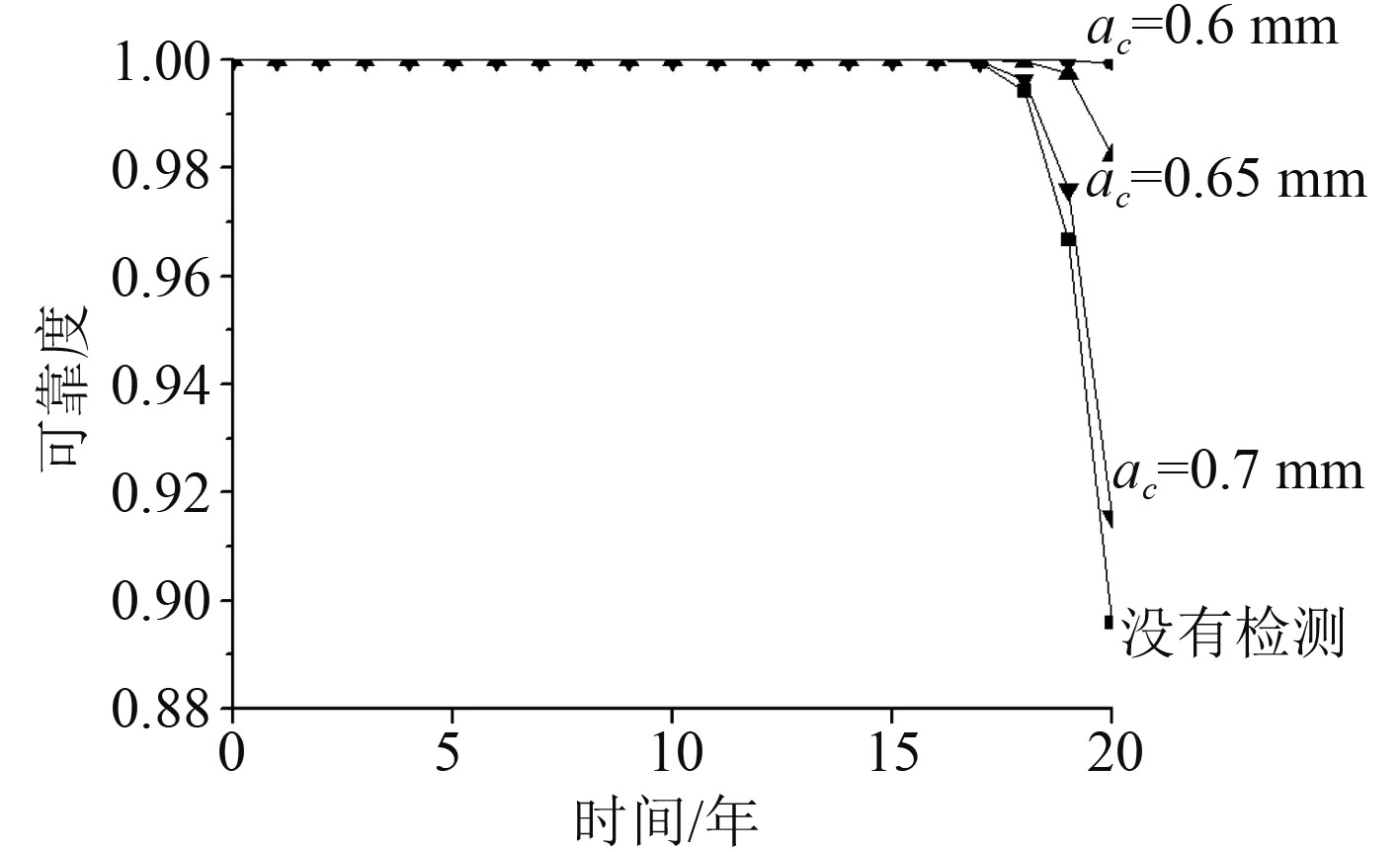
分别计算没有检测维修以及考虑检测维修因素时的时变可靠性。其中在考虑检测维修因素时，裂纹检测临界尺寸a_c分别取0.6 mm，0.65 mm，0.7 mm。计算结果如图3所示。

由图3可见，没有检测时，疲劳损伤在服役前期及中期对时变可靠度几乎没有影响，在服役末期造成时变可靠度的下降，在第20年可靠度降为0.9。考虑检测维修因素后，整体趋势不变，但时变可靠度得到一定恢复，且裂纹检测临界尺寸越小，时变可靠度曲线下降越小。

2）只考虑腐蚀损伤

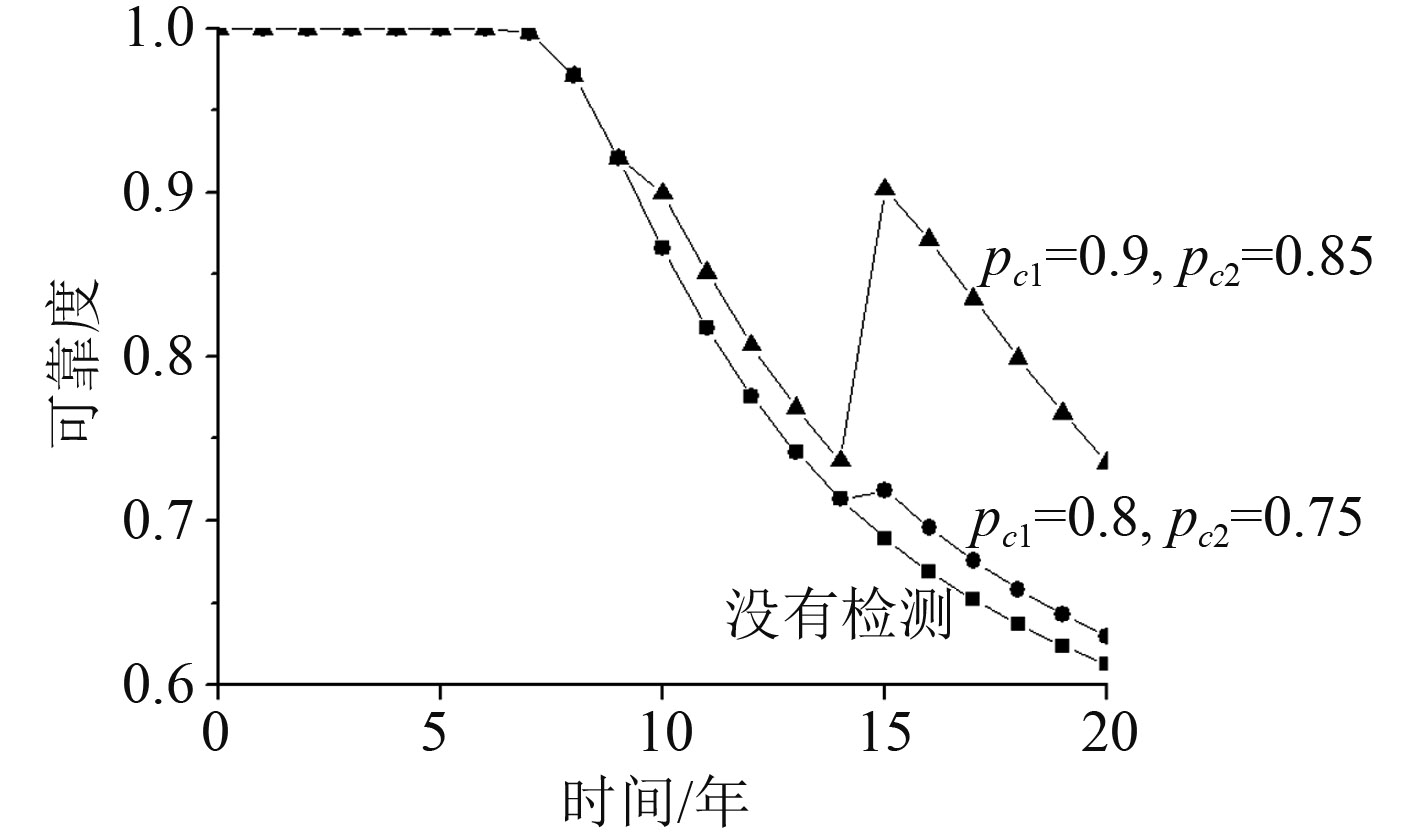
分别计算没有检测维修以及考虑检测维修因素时的时变可靠性。其中在考虑检测维修因素时，腐蚀板件更换标准分别取 ${p_{c1}} = 0.8,{p_{c2}} = 0.75$ ，以及 ${p_{c1}} = 0.9$ ， ${p_{c2}} = 0.85$ 。计算结果如图4所示。

观察图4发现，没有检测时，过了腐蚀保护期第5年后，船体梁时变可靠度快速下降。考虑腐蚀板件的检测和更换后，对时变可靠度有一定恢复作用。本算例中，第1种标准即Paik推荐的取值下，只在第15年的检测后使时变可靠度得到一定恢复。本文选取的第2种标准中最小允许折减量比率p_c高于第1种标准，结果显示分别在第10年和第15年的检测后都使时变可靠度得到一定恢复，整体时变可靠度高于第一种标准。

3）疲劳及腐蚀损伤影响比较

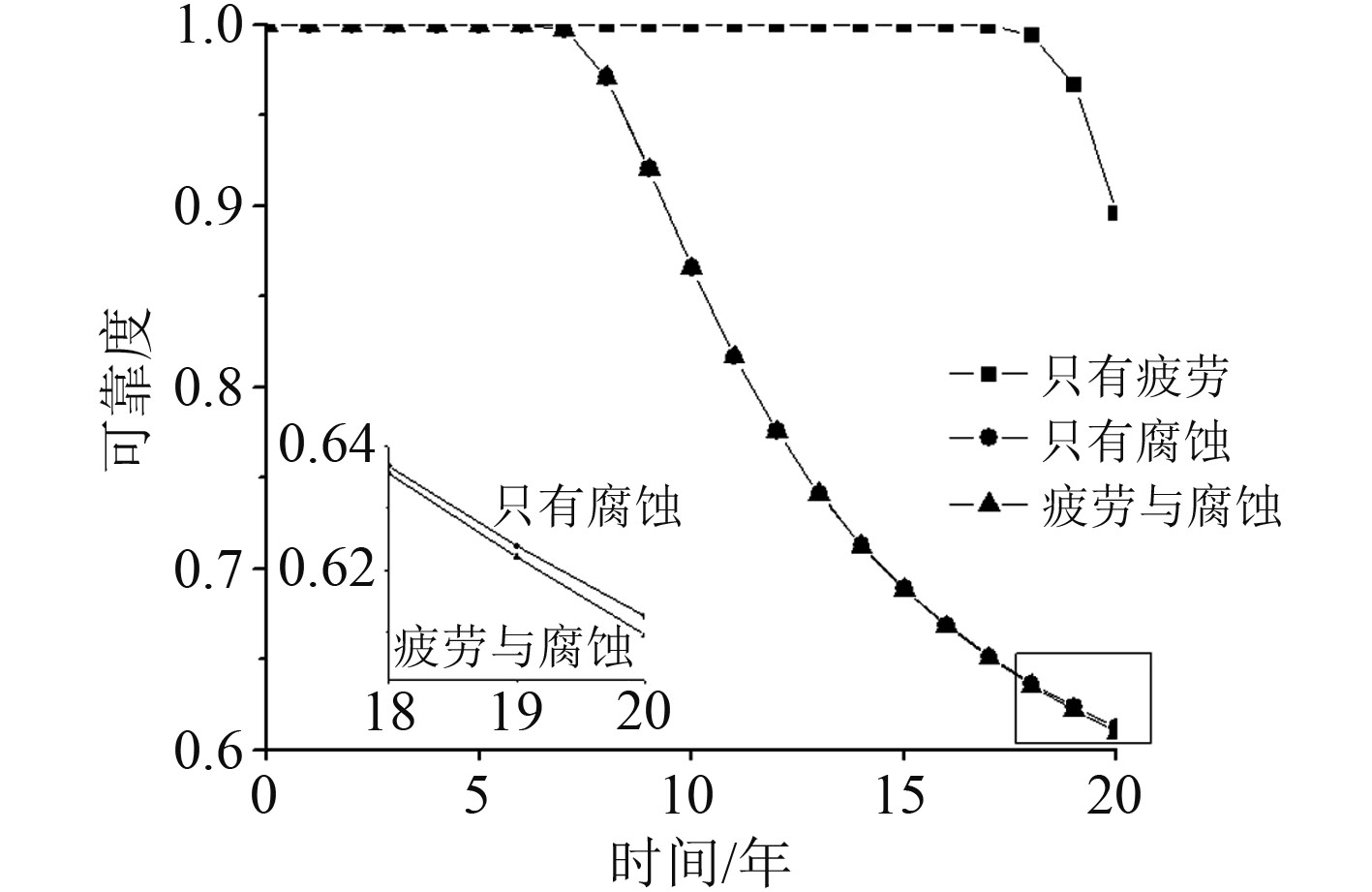
无检测状态下，只考虑疲劳或腐蚀以及综合考虑2种损伤情况下的时变可靠度如图5所示。

由图5可见，只考虑疲劳损伤时的曲线下降不多，而只考虑腐蚀损伤的曲线与综合考虑2种损伤的曲线都下降较多，且非常接近。可见，在本算例所采用的疲劳裂纹和腐蚀假设下，腐蚀是导致船体梁时变可靠度降低的主要因素。

4）考虑检测维修更新的时变可靠度分析

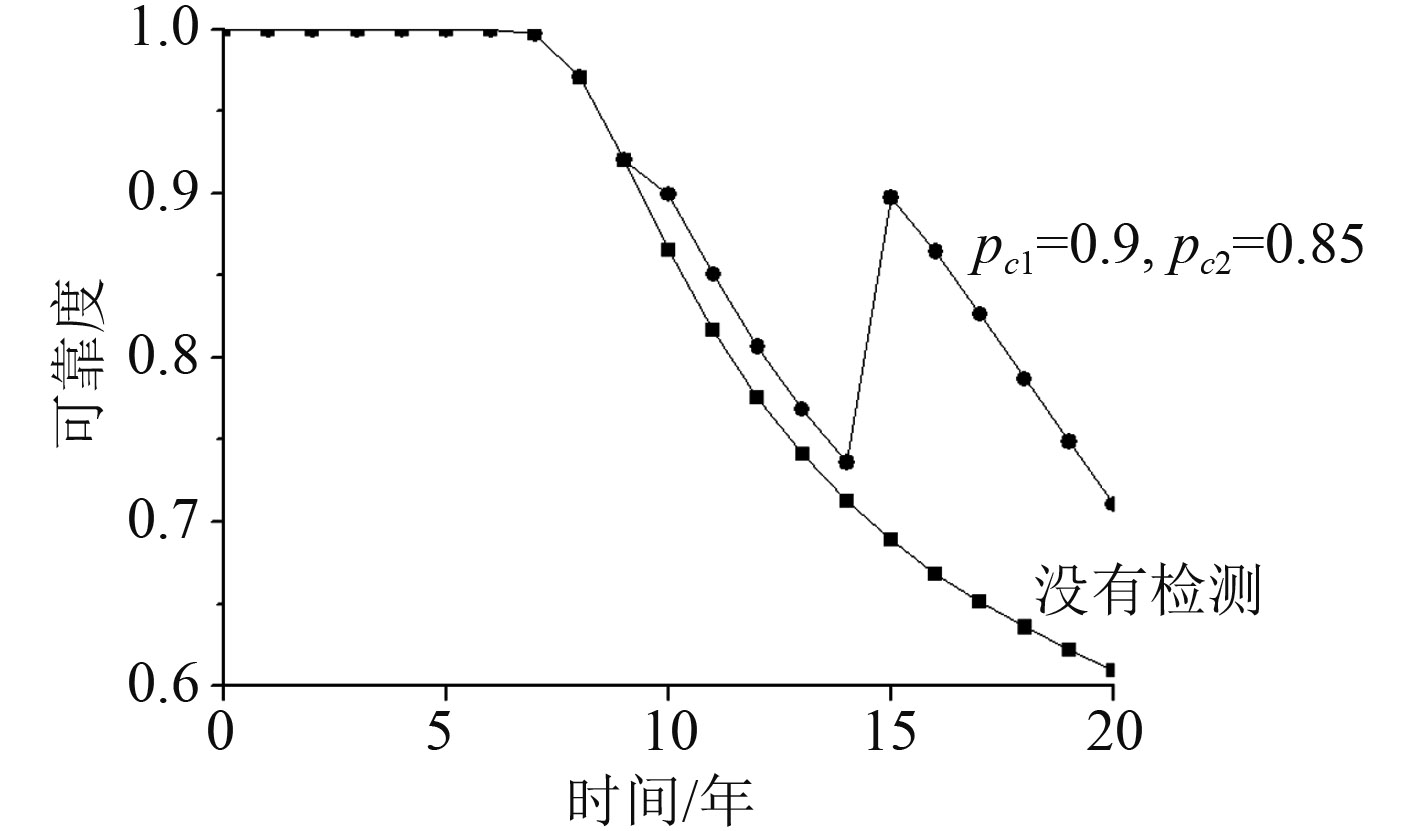
综合考虑疲劳和腐蚀损伤以及检测维修的影响，将裂纹检测临界尺寸a_c取0.6 mm，腐蚀板件更换标准取为 ${p_{c1}} = 0.9,{p_{c2}} = 0.85$ ，则时变可靠度曲线如图6所示。

由图6可见，与没有检测的情况相对比，考虑检测维修后在第10年的检测后时变可靠度得到一定恢复，在第15年的检测后时变可靠度得到更大程度的恢复。曲线整体走势与只考虑腐蚀损伤，并采用 ${p_{c1}} = 0.9$ ， ${p_{c2}} = 0.85$ 这种更换标准时一致，结合图5的结论，进一步证明本算例中，腐蚀是影响时变可靠度的主要因素。

由以上结果可见，在本文算例中，疲劳裂纹和腐蚀损伤随时间累积均会引起船体梁时变可靠度降低，其中疲劳裂纹的影响主要在服役后期体现，腐蚀的影响从过了涂层保护年限后开始有明显的体现，并且是主要影响因素；而对裂纹和腐蚀板件的检测更新能恢复船舶的可靠度，恢复的效果与检测精度和构件更换标准有关，检测精度越高，腐蚀板件最小允许折减量比率越大，则时变可靠度恢复效果越好；时变可靠度在第5年的检修后没有改变，在第10年的检修后得到较小程度恢复，在第15年时得到更大程度恢复。

6 结 语

本文定量考虑了疲劳裂纹和腐蚀对于船舶结构的损伤，并考虑了检测维修对于裂纹的修复和腐蚀板件更换的影响，以某疏浚船为例分析了时变可靠性。可见：

1）疲劳裂纹和腐蚀损伤随时间累积均会引起船体梁时变可靠度降低。其背后的力学机理是疲劳裂纹造成构件有效宽度或高度的折减，腐蚀损伤造成构件有效厚度的折减，这2种损伤使船体梁剖面模数随时间减小，从而降低时变可靠度。本文算例中腐蚀是时变可靠度降低的主要因素，可能是因为腐蚀比裂纹对剖面模数的折减量更大。本文中假定焊接处有初始裂纹，随时间在腹板和面板上扩展，没有考虑非焊接结构的裂纹以及初始裂纹的不同尺寸，有一定局限性，后续可进一步研究多种裂纹及多种初始尺寸的情况。

2）对裂纹和腐蚀板件的检测更新能恢复船舶的可靠度。本文对检测维修主要分析了检测精度、维修更换标准、对时变可靠度的恢复作用这几个方面。本文假定裂纹一旦被发现就修复以及对腐蚀板件的检测质量高，从而由结果发现时变可靠度恢复的效果与裂纹检测精度和腐蚀板件最小允许折减量比率有关，即越容易发现损伤，在越小的损伤允许范围内进行修复，则时变可靠度恢复效果越好。但这也意味着检测维修费用的增加，后续可以进一步研究考虑经济效益的最优检测维修方案。

3）本文假定检测维修间隔为5年，算例中实际对恢复时变可靠度起到作用的是第10年和第15年的检修，这主要由于防腐涂层保护作用，5年之后才出现较明显的构件损伤，从而被检测维修；并且第15年的检修的恢复作用大于第10年，可能由于第10年时少量构件达到维修标准，而到第15年时更多的构件达到维修标准而得到修复。此外本文中检测维修5年间隔的假定有一定局限性，后续可以进一步研究不同检测间隔对时变可靠性的影响，优化检测维修计划。