2. 中国人民解放军92941部队,辽宁 葫芦岛 125000
2. No. 92941 Unit of PLA, Huludao 125000, China
水雾技术在城市建筑、工业制造、农业生产、火灾救援等方面都有着广泛的应用。城市建筑建造和拆除中可运用水雾除尘技术缓解环境压力;工业生产中有关于水雾技术降温减阻,避免高温引发火情;工业生产利用水雾灌溉和湿润空气;火灾求援中水雾可以蒸发降温,控制火情和有效抑制二次伤害。有研究表明水雾对抑制爆炸强压力冲击也有着积极的作用,并且水雾可以蒸发吸收热量和抑制火灾的发生[1],因此水雾作为抑爆的介质有着理想的应用前景。
在以煤矿瓦斯抑爆应用为代表的弱冲击波与液滴相互作用特性方面已有较多研究,G.Jourdan[2]从实验和数值模拟两方面研究了直径约为120 um、250 um、500 um的密集液滴对Ma在1.1~1.8的冲击波的衰减作用。Schwer[3]和Thomas[4]的研究证实了在爆炸中使用喷水抑爆可以使大液滴破碎成细小雾滴,直接导致冲击波的衰减,减缓或熄灭冲击波作用后续化学反应,稀释爆炸后气体密度,防止产生二次爆炸或者次生火灾。Lane[5 – 7]观察了弱冲击波(马赫数MS=1.05~1.28)作用下的液滴(直径d=1~2 mm)的变形和破碎过程。M.Jalaal[8]指出We数约为20~80的水滴的破碎过程包括:液壁刺穿生成、破洞的消散、网状液带的形成、液带的扩散和分离、形成稳定液滴碎片等一系列现象,并指出破碎液滴平均尺寸随着奥托斯数的增加而减小的结论。总之,与层状多相介质类似,冲击波在液滴表面也会发生入射和反射,导致液滴的压缩;冲击波在液滴背表面的反射,将导致液滴的破碎、飞散,而破碎液滴与空气介质的切向速度差将导致气液界面的不稳定,并使液滴进一步破碎和雾化[9 – 10]。根据层状介质的思想,舰船遭受到反舰武器攻击发生舱内爆炸前,采取在舱室内部喷洒水雾的方式,可以达到抑制冲击波和衰减其强度的作用。
为进一步探讨水雾对舰船舱内爆炸强冲击波的耗散作用与机理的规律,本文采用动态非线性有限元方法,拟对同等喷雾体积条件下不同喷雾尺寸液滴之间的抑爆差异,从而分析处喷雾大小和密度对抑制冲击波作用的影响。本文对各工况环境中,液滴的直径不同但总体积比相同,对比分析各工况下冲击波比冲量的衰减情况。
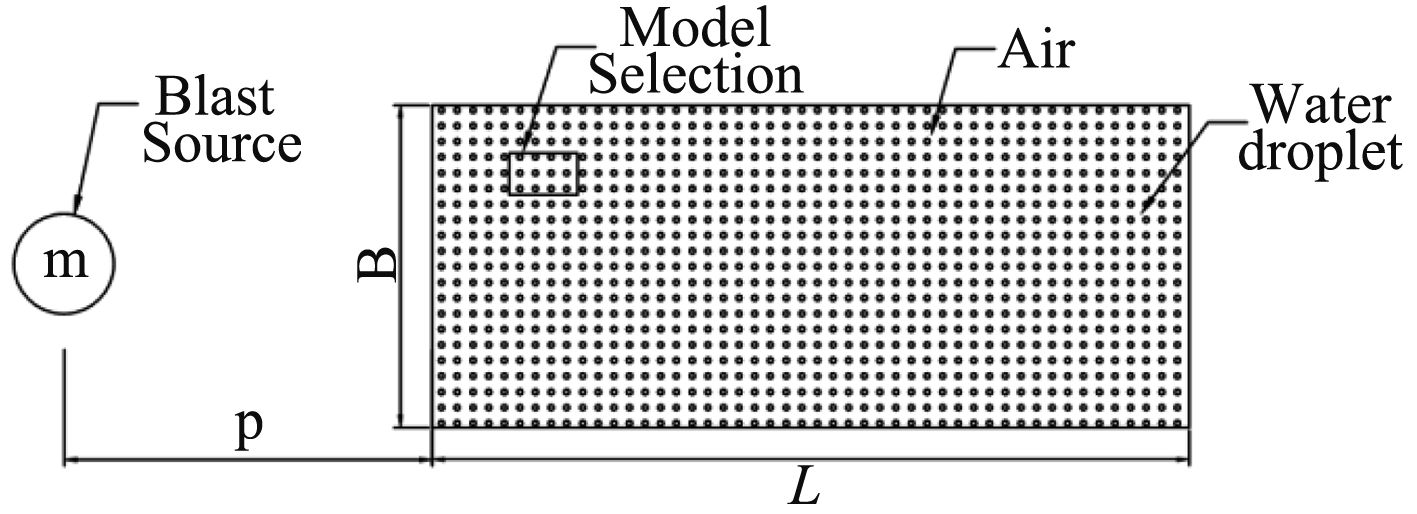
1 模型建立根据水雾抑爆的思想,舰船遭受到反舰武器攻击发生舱内爆炸前,采取在舱室内部喷洒水雾的方式,以达到抑制冲击波和衰减其强度的作用,宏观模型如图1所示。在进行有限元仿真时,可选取其中的若干液滴建立二维平面模型(见图2),二维模型能够有效模拟平面内液滴破碎,直观反映模型内部的压力变化历程以及液滴的形态变化及位置改变。
|
图 1 水雾抑爆宏观模型 Fig. 1 Macromodel of mist explosion suppression |
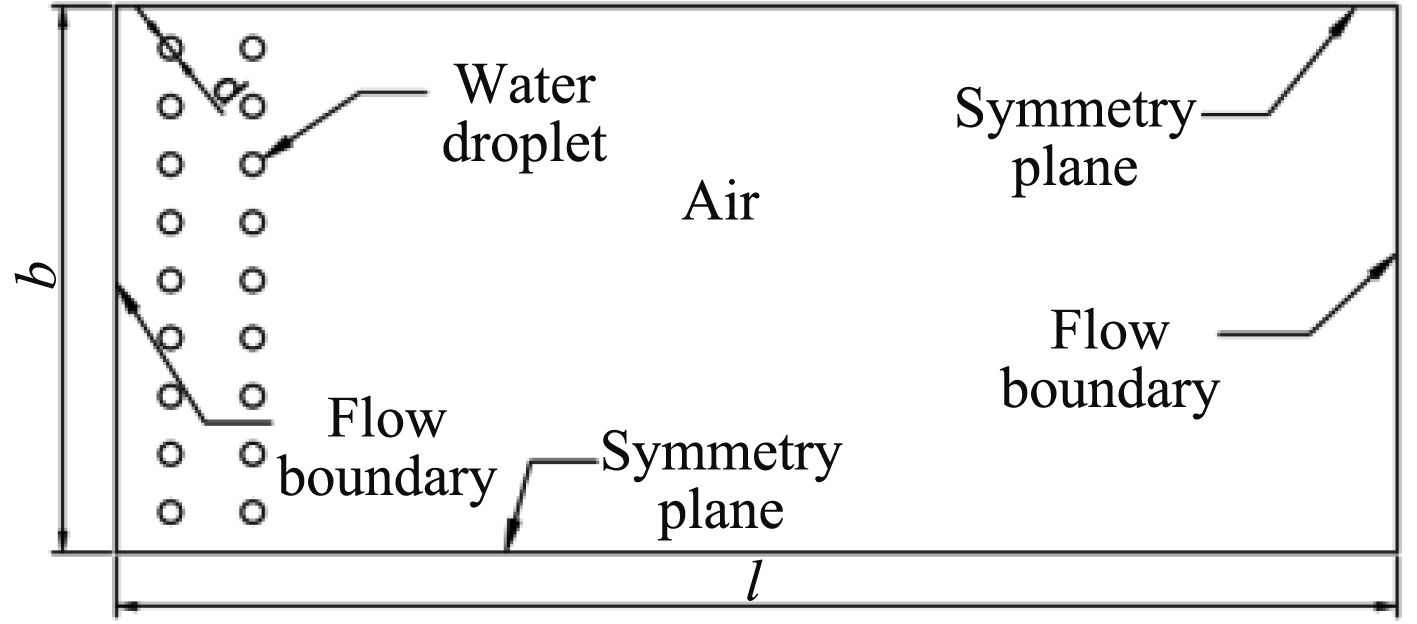
|
图 2 液滴模型 Fig. 2 Micromodel of multi-row droplets |
爆炸源产生的冲击波成球形向外扩散,冲击波以弧形冲击波作用于整个模型空间,由于其空间极小,对于二维液滴单元,冲击波作用相当于是平面波。运用有限元软件LS-Dyna建立平面模型,欧拉域长l =4 cm,宽b = 2 cm,液滴直径d。欧拉域上下边界均采用对称边界设置,以减小模型内比冲量的损失,前后边界为自由流入流出边界,保证冲击波可以正常作用于液滴。在欧拉域前距离为P的位置放置TNT当量为m的爆炸源。
模型中空气采用NULL材料模型及线性多项式状态方程描述:
|
$P = {C_0} + {C_1}\mu + {C_2}{\mu ^2} + {C_3}{\mu ^3} + ({C_4} + {C_5}\mu + {C_6}{\mu ^2})E, $
|
(1) |
式中:P为压力;E为单位体积内能,取2.525 × 10 5 J/m3;μ = ρ/ρ0-1,ρ/ρ0为实际密度与标准密度之比;空气密度取1.225 kg/m3;C0~C6为多项式方程系数,当线性多项式状态方程用于理想气体模型时,C0 = C1 = C2 = C3 = C6 = 0,C4 = C5 = γ-1,γ=Cp/Cv为气体的热容比,取γ = 1.4。
液滴采用Gruneisen状态方程描述:
|
$\begin{split}P & = \frac{{{\rho _0}{C^2}\mu [1 + (1 - {\gamma _0}/2)\mu - {\mu ^2}{a_{\rm{m}}}/2]}}{{[1 - ({S_1} - 1)\mu - {S_2}{\mu ^2}/(1 + \mu ) - {S_3}{\mu ^3}/{{(\mu + 1)}^2}]}} + \\& \quad ({\gamma _0} + {a_m}\mu ){E_{\rm{V}}},\mu > 0,\end{split}$
|
(2) |
|
$P = {\rho _0}{c_l}^2\mu + ({\gamma _0} + {a_m}\mu ){E_{\rm{V}}},\;\;\;\mu < 0{\text{。}}$
|
(3) |
式中:Gruneisen系数γ0 = 0.493 4,体积修正系数am =1.393 7;S1 = 2.56,S2 = –1.986,S3 = 0.226 8;EV为单位体积内能,初始能量为E0 = 9.182 × 10 5J;μ=ρ/ρ0-1。此处,冲击波在水中的速度为1 484 m/s,初始相对体积V0=1.0。
2 等体积比液滴对冲击波衰减分析不同尺寸液滴的We(Weber数)和Oh(Ohnesorge数)均不同,且其对液滴破碎变形有着决定性的作用,其中,We表示惯性力和表面张力之比,Oh表示粘性力和表面张力之比[11]。为研究液滴直径对冲击波衰减的影响,在二维模型中,建立如表1所示工况下的模型组,模型内部液滴体积比相同。不同尺寸液滴在冲击波作用下的破碎和抛散存在形态存在差异,因此对冲击波的衰减作用也不尽相同,本文拟定量计算出表1工况下冲击波的衰减率。
|
|
表 1 计算工况 Tab.1 Working condition of calculations |
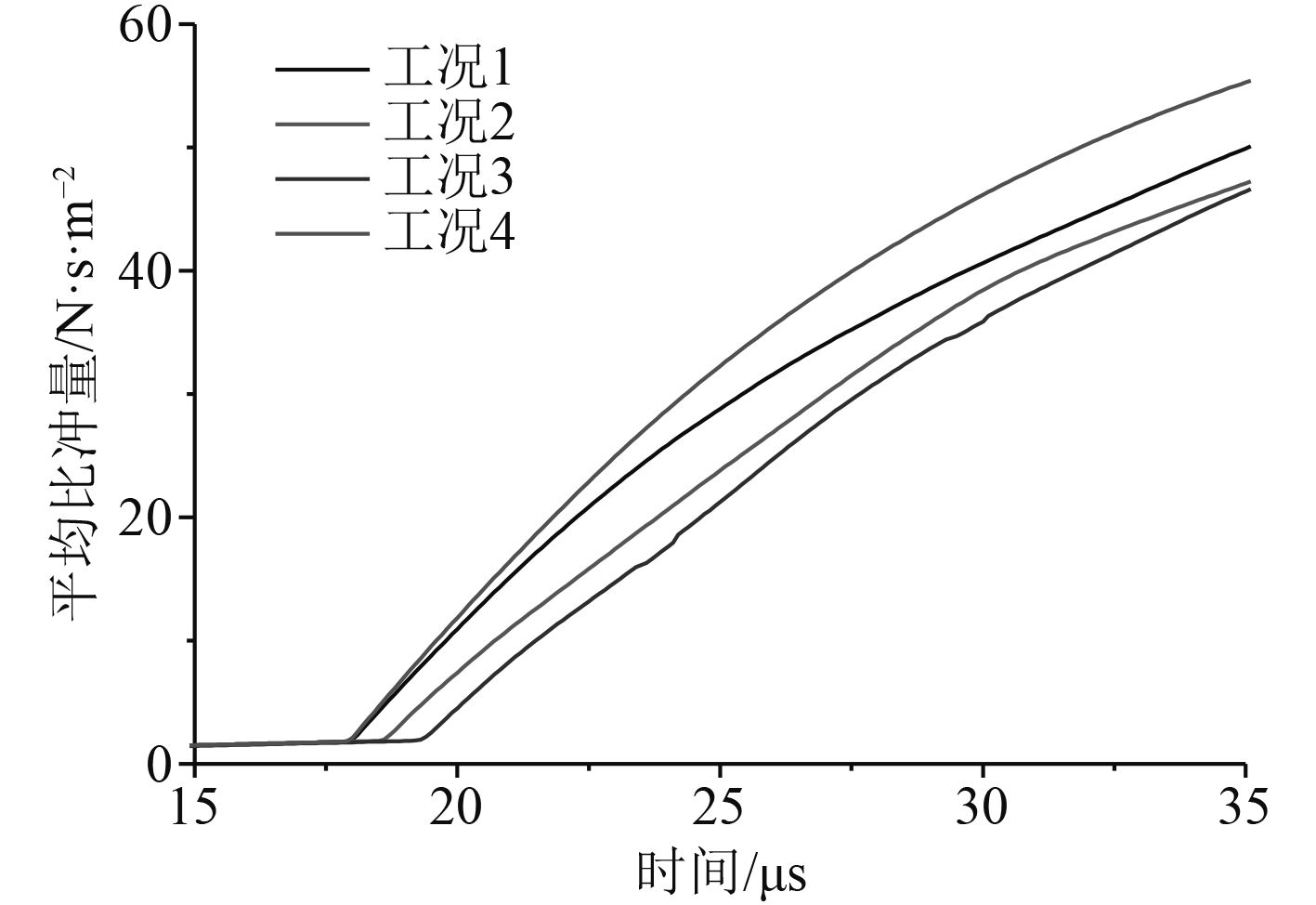
冲击波作用于液滴以后,液滴对冲击波的传播和扩展有着阻碍作用,因此液滴的存在对冲击波的破坏性也有衰减作用。为研究液滴大小对冲击波衰减作用的影响,本节对比研究相同液滴总体积比下的几组模型,液滴数目有3,9和18,对比模型末端测量点在相同作用时间段内的平均比冲量。如图3所示为0.1 kg装药在0.2 m爆距条件下各模型末端平均比冲量,由于液滴内部高压导致的比冲量在35 μs后迅速增大,此处只选取35 μs时刻前比冲量对比。
|
图 3 等体积比工况比冲量曲线 Fig. 3 Specific impluse curve of same volume |
如图3所示,在前18~35 μs时间段内,比冲量变化曲线值呈现明显的规律性,随着时间的推移各组模型比冲量均逐渐增大,且增长率递减;各组有液滴模型比冲量均小于无液滴模型,说明液滴阻碍的冲击波的作用;在相同液滴总体积比条件下,液滴数目越多其比冲量数值越小,可见分散的小液滴对冲击波的衰减作用明显强于集中的大液滴。
由表2可知,20~35 μs时段末端平均比冲量及其衰减率,可知在各时间点处均有工况3比冲量小于工况2,工况2小于工况1,衰减率呈现相反的规律。由表中数据可知,假如仅考虑正压作用某一时段,液滴对冲击波的衰减作用非常显著,而实际上液滴对冲击波的衰减效果远没有如此理想。得到真实的衰减率数据,需要在整个正压作用时长上考虑此问题。
|
|
表 2 比冲量数据表 Tab.2 Data of specific impluse |
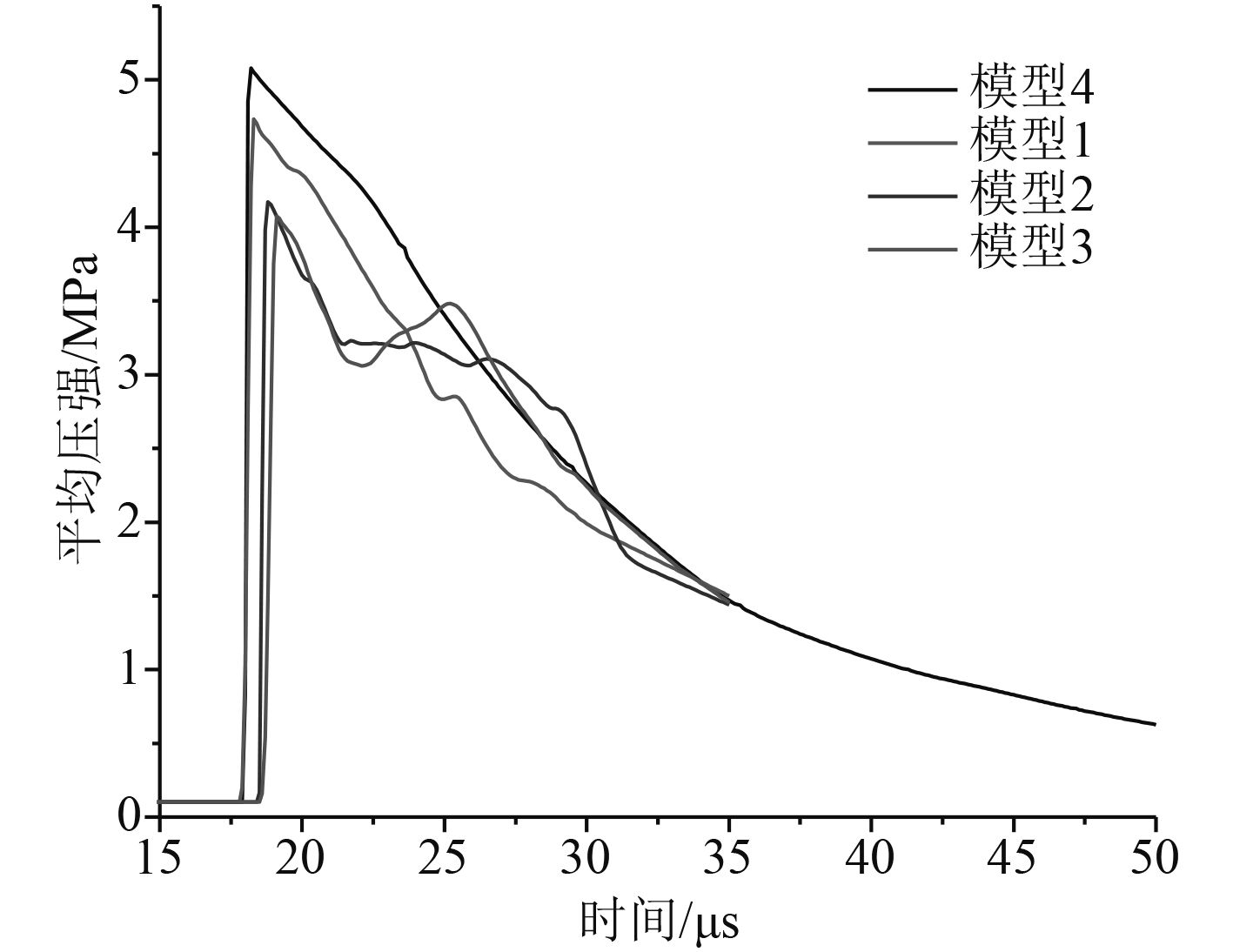
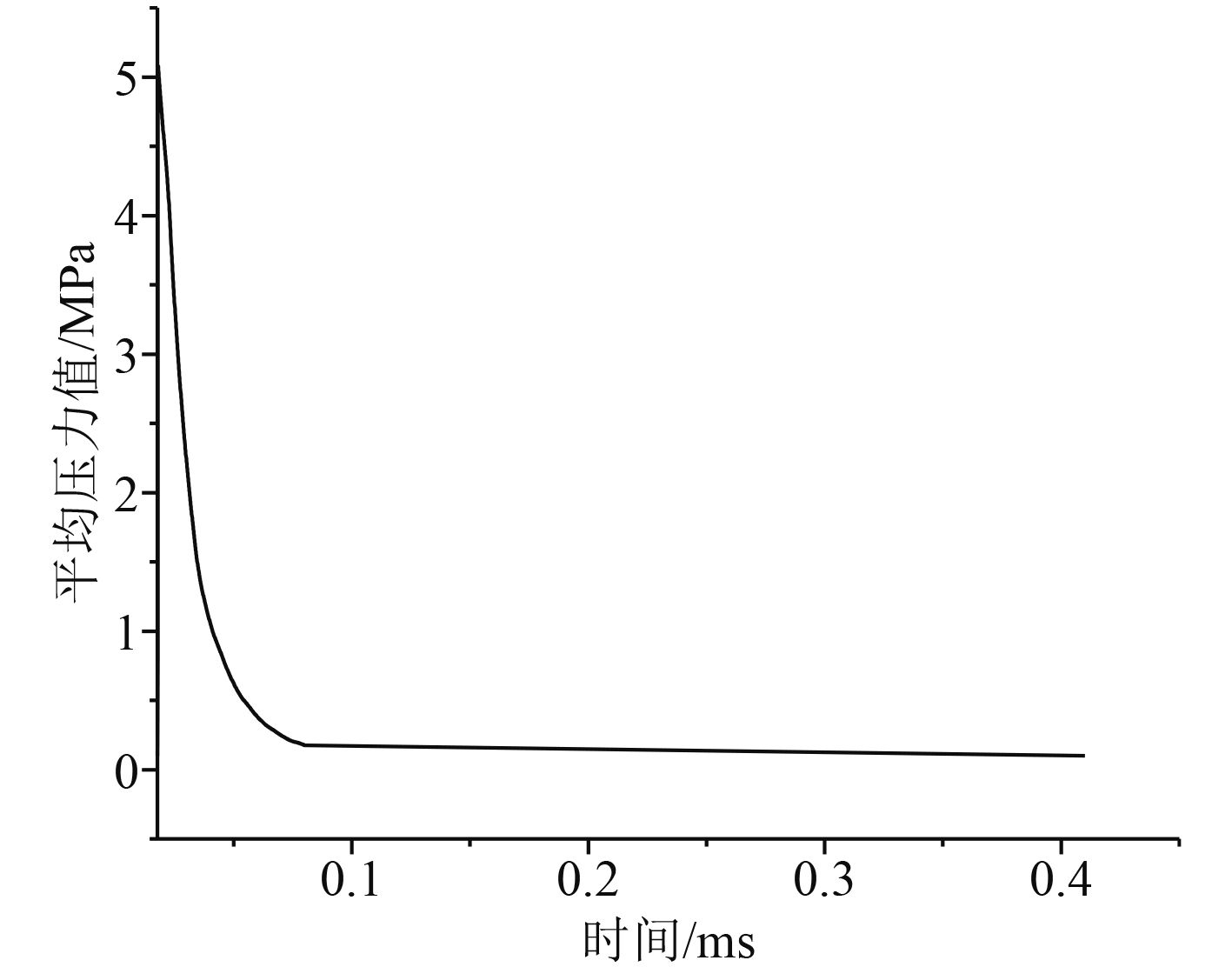
为得到比冲量宏观的衰减率,在整个正压作用时间内采用粗略估算的方法,将液滴达到测量点后的时间段内的压强曲线用无液滴模型代替。模型内的液滴在约35 μs时刻陆续接触测量处,如图4所示为各模型该时段内测量压力曲线,正压作用时间为0.411 ms,无液滴模型压力曲线图见图5。此处在计算宏观衰减率时将有液滴模型35~411 μs时段用无液滴曲线代替,得到如表3所示数据。
|
图 4 测量压力曲线图 Fig. 4 Measuring pressure curve |
|
图 5 无液滴压力曲线图 Fig. 5 Pressure without droplet |
|
|
表 3 各弥散程度衰减率表 Tab.3 Attenuation rate of different dispersion degree |
由表3可知,在二维平面内相同液滴体积比条件下,液滴尺寸对比冲量衰减有相应的影响。在此模型环境中,液滴尺寸小而分散的工况中对冲击波的衰减强于液滴尺寸大而集中的工况,即冲击波的衰减随着液滴越为分散则越为显著。然而实际环境中的爆炸和二维模拟有较大的差异,易知三维条件下衰减率将明显减小。
3 机理分析水雾对冲击波的衰减作用,从能量和动力学的角度分析都有充分的理论依据:1)能量的角度来看,冲击波在传播的过程中,气动力推动液滴加速,液滴逐渐发生变形破碎和抛散,此过程中冲击波能量会有一部分转化为液滴的动能,因此冲击波的强度和能量会发生衰减。液滴尺寸小,则其更易被气动力加速,故能量转化的效率更高,其冲击波衰减率更大。2)动力学角度来看,弥散的小液滴和空气形成了气液两相混合介质,液滴与空气接触面形成2种介质的传递界面,冲击波在到达每一个界面时必然会发生透射、反射、绕射、衍射等现象,在界面传递的过程中必然发生能力形式的转化。更小的液滴尺寸对应的两相介质混合更为充分,则其介质传递界面的面积和也更大,故小尺寸液滴会有更大的衰减率。
4 结 语本文通过有限元分析的方法,在单层网格内建立冲击波作用于同体积比不同尺寸分布的液滴模型,对液滴阻碍冲击波作用的规律进行分析总结,得到结论如下:
1)液滴的存在对冲击波有一定的削弱作用,且在液滴总体积比相同条件下,液滴数目多的工况比冲量衰减更大,可知分散的小液滴对冲击波的衰减作用强于集中的大液滴。
2)0.1 kgTNT在0.2 m爆距产生的冲击波在二维模型中,液滴体积比为2.21×10–3时液滴数为3时冲击波衰减2.06%,液滴数为9时冲击波衰减3.14%,液滴数为18时衰减3.39%。
| [1] | GRANT G, BRENTON J, DRYSDALE D. Fire suppression by water sprays, Prog. Energy Combust. Sci. 2000, 26: 79–130. |
| [2] | JOURDAN G, BIAMINO L, MARIANI C. Attenuation of a Shock Wave Passing through a Cloud of Water Droplets[J]. Shock Waves, 2010 (20): 285–296. |
| [3] | SCHWER D, KAILASANATH K. Blast mitigation by water mist: Mitigation of confined and unconfined and unconfined blasts[J]. Navy research laboratory report, NRL/MR/6410-06-89762006. |
| [4] | THOMAS G O. On the conditions required for explosion mitigation by water sprays[J]. Trans. I. Chem. E.: Part B Process Saf. Environ. Prot. 2000, 78: 339-354. |
| [5] | WIERZBA A, TAKAYAMA K. Experimental investigation of the aerodynamic breakup of liquid drops[J]. AIAA, 1988, 26 (15): 1329–1335. |
| [6] | Gel’fand B. Destruction of Gryogenic Liquid Drops by Shock Waves[J]. SSSR, 1972, 26 (6): 1313–1316. |
| [7] | Gel’fand B E, GUBIN S A, KOGARKO S M. Various forms of drop fractionation in shock waves and their special characteristics[J]. Inzh. Fiz, 1974, 27 (2): 119–126. |
| [8] | M. Fragmentation of Falling Liquid Droplets in Bag Breakup Mode[J]. International Journal of Multiphase Flow, 2012 (47): 115–132. |
| [9] |
岳中文, 颜事龙, 刘锋. 液体抛撒初期水雾运动速度的实验研究[J], 安徽理工大学学报(自然科学版), 2006, 26(1): 61–63.
YUE Zhong-yan, YAN Shi-long, LIU Feng. An experimental study on veloctity of mist at initial stage of liquid dispersal[J]. 2006, 26(1): 61–63. |
| [10] |
李斌. 激波驱动下液体与固体抛撒的实验研究[D], 南京: 南京理工大学, 2012.
LI Bin. Experimential study on the disperisal of liquid and solid particles induced by shock wave[D]. Nanjing: Nanjing University of Science and Technology, 2012. |
| [11] |
王超, 吴宇, 施红辉, 等. 液滴在激波冲击下的破裂过程[J]. 爆炸与冲击, 2016, 36 (1): 129–134.
WANG Chao, WU Yu, SHI Honghui, et al. Breakup process of a droplet under the impact of a shock wave[J]. Explosion and Shock Waves, 2016, 36 (1): 129–134. DOI: 10.11883/1001-1455(2016)01-0129-06 |
 2017, Vol. 39
2017, Vol. 39
