船舶在外力作用下偏离其平衡位置而倾斜,当外力消失后,能自行恢复到原来平衡位置的能力,叫做船舶稳性[1]。船舶稳性是船舶最主要的航行性能之一,是确保船舶安全航行的基本保障。对于船舶经济安全的运营有重要的意义。目前国内的配载仪对稳性的计算大多基于装载手册数据,不考虑纵倾的影响,这导致计算的精度不足。
目前船舶静水中稳性的计算,主要有4类算法:
第1类是牛顿迭代法。赵晓非[2]、桑松[3]将船舶稳性计算转化为求解优化问题,成功实现了在自由纵倾状态下船舶的稳性曲线计算方法,运用牛顿迭代法将其转化为线性化方程组进行求解。孙承猛[4]在此基础上引入差商代替导数的思想来求解雅可比矩阵。牛顿迭代法收敛速度较快,但是该方法需要的船舶参数较多,特别是在大横倾状态下船舶水线面发生很大变化,导致求取船舶参数变复杂。
第2类是优化法。马坤[5]将自由纵倾下最小功原理的优化问题釆用非线性规划中的惩罚函数法进行迭代求解,对计算自由纵倾下的稳性问题进行了简化。优化法对于求解参数的设定要求较高,若设置不合理可能造成迭代过多,收敛缓慢。
第3类是有限元分析法。令波[6]基于船舶三维模型,通过有限元分析计算稳性。有限元分析法需要划分大量的网格,计算量较大,实时性较差。
第4类是表面元法。程智斌[7]、Radwan[8]采用表面元法计算船舶的稳性。这种方法是把船舶的表面分解成许多小的表面单元,从而算出某倾角下的回复力矩。表面元法提出用静压力解决稳性问题的新思路,但同时涉及大量面元的计算,计算量大。
考虑到程序的实时性,本文选用牛顿迭代法求解船舶稳性方程组。目前配载仪的程序对于稳性的计算都基于CPU编写,由于功耗和散热的限制,单CPU已经达到了4 GHz左右的时钟极限[9]。CPU被设计用来运行单个复杂的运算,GPU被设计用来进行高密度的简单并行计算。GPU通过成千上万的线程来隐藏延迟,实现高速运算,单个线程的计算在GPU上运行效率很低[10]。CPU的设计宗旨是在单个CPU单元上对数据进行处理,而由于GPU上集成了成百上千处理单元,因此GPU并行计算能力大于CPU。现在的GPU如GTX 1080有2 560个CUDA核心,浮点计算能力为8.9 TFLOPS,而八核心的CPU I7 5960X的浮点计算能力仅为354 GFLOPS。现在GPU能够提供强大的计算能力,并且具有较高的存储带宽。
如今GPU已经被大量应用于通用计算领域,如固体力学计算、分子动力学计算、飞行器优化设计等。如果将牛顿迭代法求解船舶稳性方程组的过程并行化,通过GPU强大的浮点运算并行能力,则可大大加快散货船配载仪中稳性计算的效率。
1 基于CGAL的船舶数据库建立CGAL(Computational Geometry Algorithms Library,计算几何算法库)[11]以C++库的形式提供高效、可靠的几何算法。CGAL提供计算几何相关的数据结构和算法,如三角剖分、Voronoi图、多边形、几何处理和凸包算法等。
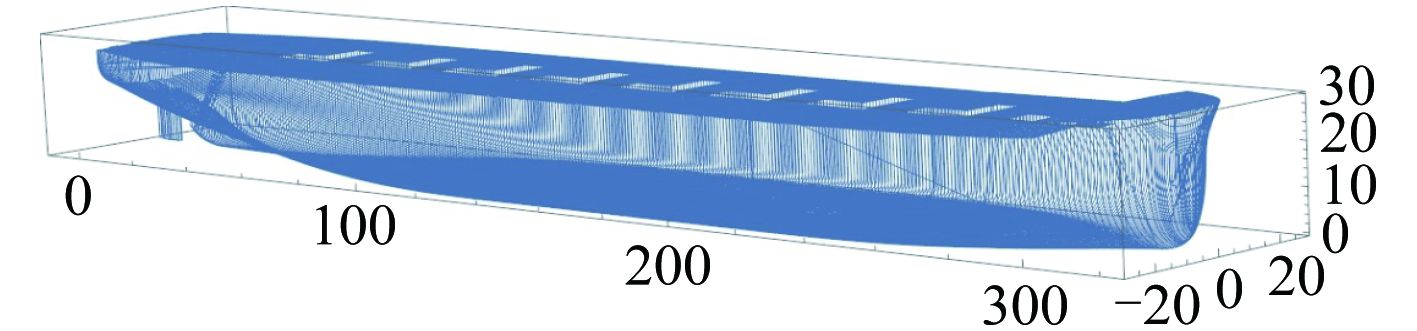
本文利用CGAL几何算法库中的切片模块,沿船长方向依次切割船舶三维型表面,得到船舶每个肋位处横剖面的型值数据。通过使用CGAL几何算法库中的切片功能,可得到任意浮态下船舶横剖面封闭环上点的三维坐标,如图1所示。x轴船首方向为正,y轴左舷方向为正。考虑到船壳版的存在,需要对船舶每个横剖面进行大小为平均板厚的等距偏移,来得到外板数据,具体的过程见参考文献[12]。
|
图 1 散货船SHANDONG REN HE型表面横剖面示意图 Fig. 1 Molded surface transverse sections of bulk carrier SHANDONG REN HE |
按照文献[2],设船舶排水量为P,海水密度为
|
$\left\{ \begin{array}{l}Mxz = VYB - \frac{P}{\rho }YG\text{,}\\Myz = VXB - \frac{P}{\rho }XG\text{,}\\Mxy = VZB - \frac{P}{\rho }ZG\text{,}\end{array} \right.$
|
(1) |
式中,V为排水体积;XB,YB,ZB为船舶浮心的纵向、横向和垂向坐标。
定义基平面和水线面大圆弧相交顶角α的球面二角形:
|
$\cos \alpha = 1/\sqrt {1 + {{\tan }^2}\theta + {{\tan }^2}\varphi }{\text{。}} $
|
(2) |
船舶由任意浮态,等体积的倾斜某个指定角度α1时,设倾斜船舶功的函数为T,稳性求解可以表达为在约束条件下求函数T的极值问题,函数T的极值点由下列方程确定:
|
$\left\{ \begin{array}{l}f_1 = V - V0 = 0\text{,}\\[4pt]f_2 = (1 \!+\! \tan \theta \tan \theta_0 \!+\! \tan \varphi \tan \varphi_0)\cos \alpha \cos \alpha_0 \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,-\! \cos \alpha_1 \!=\! 0\text{,}\\[4pt]f_3 = Mxz(tan\varphi - tan\varphi_0) - Myz(\tan \theta - \tan \theta_0)\text{,}\\[4pt] - Mxy(\tan \theta tan\varphi_0 - tan\varphi \tan \theta_0) = 0\text{。}\end{array}\!\!\! \right.$
|
(3) |
式中:θ,φ分别为横倾角和纵倾角;V0为初始排水体积;θ0,φ0分别为初始横倾角和纵倾角;α0为初始基平面和水线面大圆弧相交顶角。α1为最终水线面和初始水线面夹角。
引入向量表示:
|
${{F(x)}} = \left( \begin{array}{l}f_1(x)\\f_2(x)\\f_3(x)\end{array} \right),{{x}} = \left( \begin{array}{l}T_m\\\tan \theta \\\tan \varphi \end{array} \right),{{0}} = \left( \begin{array}{l}0\\0\\0\end{array} \right)\text{。}$
|
(4) |
式中:Tm为船中吃水。
使用牛顿法得到线性化方程:
|
$F'({x_k})\Delta {x_k} + F({x_k}) = 0\ (k = 0,1,2,...){\text{。}}$
|
(5) |
解线性方程组:
|
$\begin{split} & \left( {\begin{array}{*{20}{c}}{\displaystyle\frac{{\partial f_1}}{{\partial T_m}}}&{\displaystyle\frac{{\partial f_1}}{{\partial \tan_\theta }}}&{\displaystyle\frac{{\partial f_1}}{{\partial \tan_\varphi }}}\\{\displaystyle\frac{{\partial f_2}}{{\partial T_m}}}&{\displaystyle\frac{{\partial f_2}}{{\partial \tan_\theta }}}&{\displaystyle\frac{{\partial f_2}}{{\partial \tan_\varphi }}}\\{\displaystyle\frac{{\partial f_3}}{{\partial T_m}}}&{\displaystyle\frac{{\partial f_3}}{{\partial \tan_\theta }}}&{\displaystyle\frac{{\partial f_3}}{{\partial \tan_\varphi }}}\end{array}} \right) \cdot \left( \begin{array}{l}\delta {T_{mk}}\\\delta \tan {\theta _k}\\\delta \tan {\varphi _k}\end{array} \right) +\\ &\left( \begin{array}{l}f_1({T_{mk}},\tan {\theta _k},\tan {\varphi _k})\\f_2({T_{mk}},\tan {\theta _k},\tan {\varphi _k})\\f_3({T_{mk}},\tan {\theta _k},\tan {\varphi _k})\end{array} \right) = {{0}}{\text{。}}\end{split}$
|
(6) |
式中:δTm,δtanθk,δtanφk为设置精度。
按照船舶静力学原理,式(6)的雅克比矩阵为:
|
$\left(\! {\begin{array}{*{20}{c}}\!\!\!\!\!\! S&{SY_F}&{SX_F}\\\!\!\!\!\!\! 0&\begin{array}{l}\cos \alpha_0\cos \alpha \left[ {} \right. \tan\theta_0 - \tan\theta {\cos ^2}\alpha \\ \cdot (1 + \tan\theta \tan\theta_0 + \tan \varphi \tan \varphi_0)\left. {} \right]\end{array}&\begin{array}{l}\cos \alpha_0\cos \alpha \left[ {} \right.\tan \varphi_0 - \tan\varphi {\cos ^2}\alpha \\ \cdot (1 + \tan\theta \tan\theta_0 + \tan \varphi \tan \varphi_0)\left. {} \right]\end{array}\\\begin{array}{l}\!\!\!\!\!\! SY_F(\tan\varphi -\\ \!\!\!\!\!\! \tan\varphi_0) - SX_F(\tan\theta - \tan\theta_0)\\ \!\!\!\!\!\! - SZ_F(\tan\theta \tan\varphi_0 - \tan\varphi \tan\theta_0)\end{array}&\begin{array}{l}I_x(\tan\varphi - \tan\varphi_0) - I_{xy}(\tan\theta - \tan\theta_0)\\ - (I_x \tan\theta + I_{xy} \tan\varphi + SY_FT_m)(\tan\theta \tan\varphi_0\\ - \tan\varphi \tan\theta_0) - (M_{yz} + M_{xy} \tan\varphi_0)\end{array}&\begin{array}{l}I_{xy}(\tan\varphi - \tan\varphi_0) - I_y(\tan\theta - \tan\theta_0)\\ \!\!\!\!\!\!\!\! - (I_y \tan\varphi + I_{xy} \tan\theta + SX_FT_m)\\ \!\!\!\!\!\! (\tan\theta \tan\varphi_0 - \tan\varphi \tan\theta_0) -\\ (M_{xz} + M_{xy} \tan\varphi_0)\!\!\!\!\!\end{array}\end{array}} \!\!\!\!\!\right){\text{。}}$
|
(7) |
式中:S为水线面在基平面上的投影面积;XF,YF,ZF为船舶漂心的纵向,横向和垂向坐标;水线面对Ox轴的面积惯性矩为Ix;水线面面积S对于通过该水线面漂心F的横轴的纵向惯性矩为ILF;S的惯性积为Ixy。
总复原力臂L为:
|
$\begin{split}L = & \cos \alpha \left\{ {{{\left[ {\left( {X_B - X_G} \right)\tan \theta - (Y_B - Y_G)\tan \varphi } \right]}^2}} \right.+ \\ & {\left[ {(Y_B - Y_G) + (Z_B - Z_G)\tan \theta } \right]^2} +\\ &\left[ {(X_B - X_G)} \right. + (Z_B - Z_G)\tan \varphi {\left. {} \right]^2}{\left. {} \right\}^{1/2}}{\text{。}}\end{split}$
|
(8) |
将船体坐标转换到船中后,按照文献[13]给出的倾斜水线面一般式方程为:
|
$x\tan \varphi + y\tan \theta - z + T_m = 0{\text{。}}$
|
(9) |
设水线面左舷曲线为p(x),右舷曲线为s(x)。水线面在基平面上投影的面积S为:
|
$S = \int_{x_0}^{x_n} {{\rm{d}}x\int_{s(x)}^{p(x)} {{\rm{d}}y} } = \int_{x_0}^{x_n} {\left( {p(x) - s(x)} \right){\rm{d}}x}\text{。}$
|
(10) |
式中:x0,xn分别为船首尾到z轴距离。
漂心F(XF,YF,ZF)的坐标为:
|
$X_F = \frac{{\int_{x_0}^{x_n} {\left( {p(x) - s(x)} \right) \cdot x{\rm{d}}x} }}{S},$
|
(11) |
|
$Y_F = \frac{{\int_{x_0}^{x_n} {{{\left( {p(x) - s(x)} \right)}^2}{\rm{d}}x} }}{{2S}},$
|
(12) |
|
$\begin{split}{l}&Z_F = \displaystyle\frac{1}{S}\int_{x_0}^{x_n} {\left( {(x \cdot \tan \varphi + T_m) \cdot } \right.} \left[ {p(x) - s(x)} \right]{\rm{ + }}\\&\;\;\;\;\;\;\;\;{\displaystyle\frac{1}{2} \cdot {\rm{tan}}\theta \cdot {{\left[ {p(x) - s(x)} \right]}^2}}{\rm{d}}x{\text{。}}\end{split} $
|
(13) |
水线面对Ox轴,Oy轴的面积惯性矩Ix,Iy为:
|
$I_x = \frac{1}{3}\left( {\int_{x_0}^{x_n} {p{{(x)}^3}{\rm{d}}x} - \int_{x_0}^{x_n} {s{{(x)}^3}{\rm{d}}x} } \right),$
|
(14) |
|
$I_y = \int_{x_0}^{x_n} {{x^2}p(x){\rm{d}}x} - \int_{x_0}^{x_n} {{x^2} \cdot s(x){\rm{d}}x}{\text{。}} $
|
(15) |
|
$I_{LF} = I_y - S \cdot {X^2}_F,$
|
(16) |
|
$I_{xy} = \frac{1}{2}\left( {\int_{x_0}^{x_n} {x \cdot p{{(x)}^2}{\rm{d}}x} + \int_{x_0}^{x_n} {x \cdot s{{(x)}^2}{\rm{d}}x} } \right){\text{。}}$
|
(17) |
水线面参数的计算可以先计算每个肋位处微元参数,再通过梯形积分法沿船长方向积分求出。类似的,可以用梯形法近似求取其他船舶参数。
2.2.2 排水体积和浮心的计算排水体积
|
$V = \int_{x_0}^{x_n} {As{\rm{d}}x}, $
|
(18) |
式中AS为距离z轴x处的横剖面面积。
船舶浮心坐标B(XB,YB,ZB)为:
|
$X_B = \frac{{M_yO_z}}{V} = \frac{{\int_{x_0}^{x_n} {x_aA_s{\rm{d}}x} }}{V},$
|
(19) |
|
$Y_B = \frac{{M_xO_z}}{V} = \frac{{\int_{x_0}^{x_n} {y_aA_s{\rm{d}}x} }}{V},$
|
(20) |
|
$Z_B = \frac{{M_xO_y}}{V} = \frac{{\int_{x_0}^{x_n} {z_aA_s{\rm{d}}x} }}{V}{\text{。}}$
|
(21) |
式中:Myoz,Mxoz和Mxoy分别为排水体积对中站面、中线面和基平面的静矩;xa,ya,za分别为距z轴x处的横剖面的形心纵向,横向和垂向坐标。
2.3 基于CUDA的程序设计NVIDIA公司为了推动GPU在大规模高性能计算领域里的发展,在2006年11月推出为通用并行计算开发的CUDA通用并行计算架构,由于它的编程方便与并行性能高的特点,充分利用了CPU和GPU各自的优点,实现CPU/GPU联合执行,使得并行计算得到更快的发展[10]。
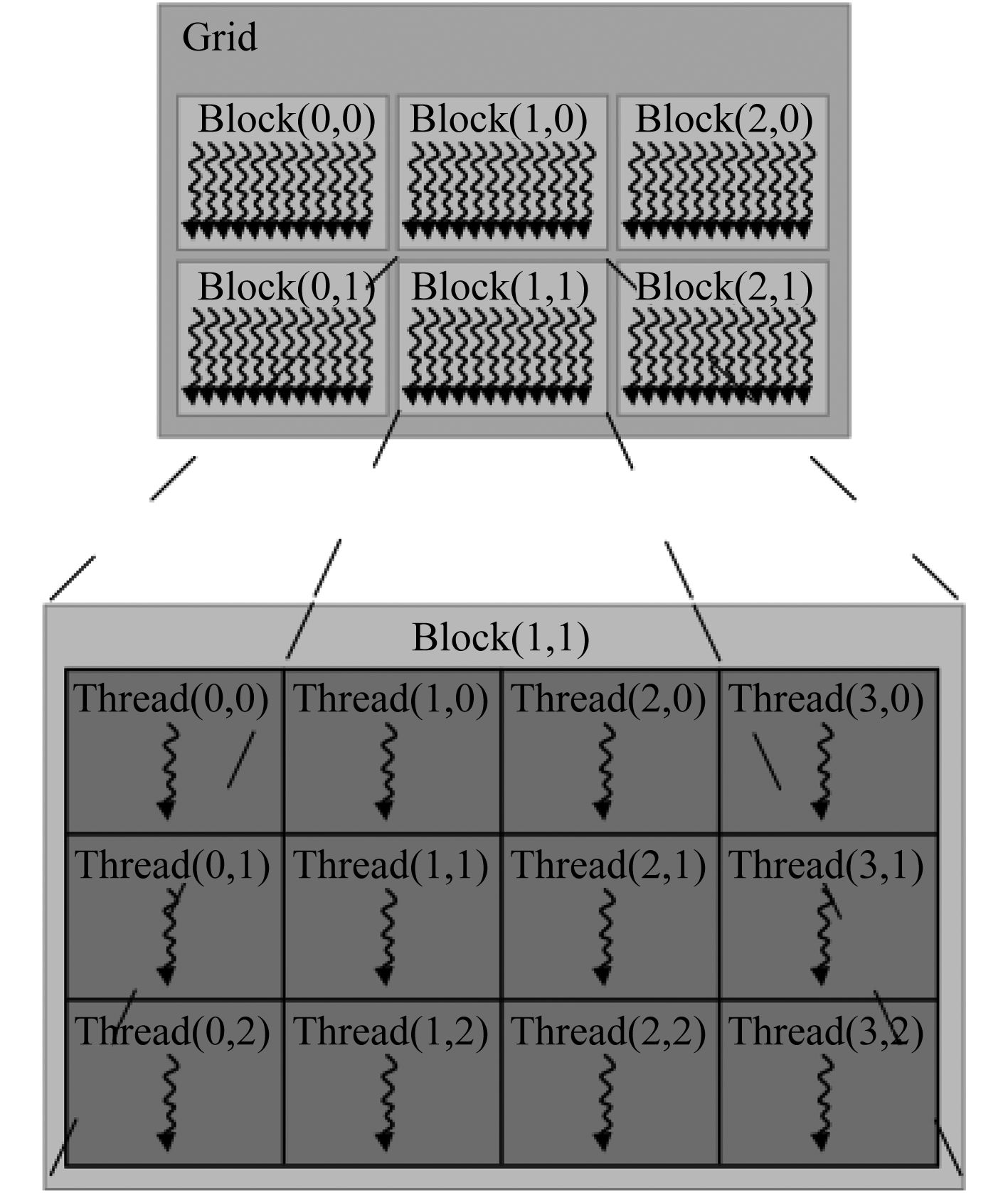
在GPU中,CUDA的并行结构由网格(grid)-块(block)-线程(thread)的结构组成。其结构如图2所示。CUDA将问题分解成线程块的网格,每块包含多个线程,执行相同的代码。每个块可以被分配到任意一个处理器核心以并行或串行方式执行。
|
图 2 CUDA并行结构示意图[14] Fig. 2 CUDA structure diagram |
CUDA在编译时,会将CPU代码和GPU代码分开编译。程序从主机端的CPU代码开始执行,当执行到GPU代码时,调用内核函数,并将代码切换到GPU。当内核函数执行完后,设备代码被切换到CPU端,继续执行代码。
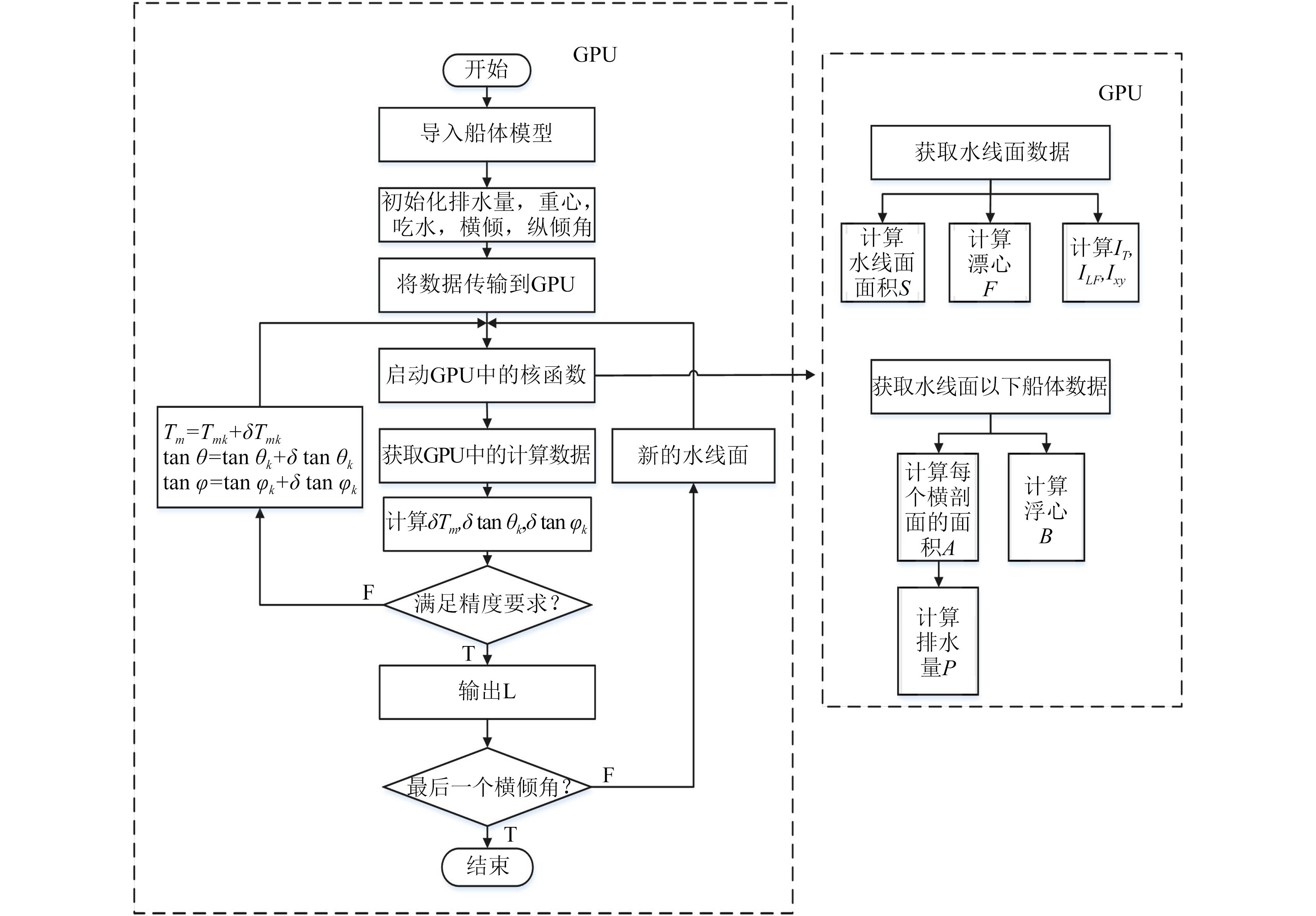
本文用C++语言,使用CUDA 7.5编写了船舶稳性计算程序,其流程如图3所示。首先对所有切割肋位处的横剖面进行等距偏移得到外板的离线数据;然后将外板的离线数据发送到GPU,在迭代过程中,外板数据一直储存在显存中。
|
图 3 稳性计算流程图 Fig. 3 Stability calculation flowchart |
由船舶初始浮态得到船舶初始船中吃水、横倾角及纵倾角,从而确定初始水线面;依次与水线面求交得到水线面数据和水下部分横剖面数据;现在船舶数据可以分为2个部分,求解雅可比矩阵的所需的静水力参数可以同步并行计算。
考虑到求解船舶稳性方程组的数据量很小,不适合使用GPU处理,将GPU中的静水力系数值传回CPU,计算雅各比矩阵系数求解稳性方程组;若满足精度要求则输出该倾角下的复原力臂值,接着进行下一个倾角的力臂计算;否则确定新的水线面继续迭代。
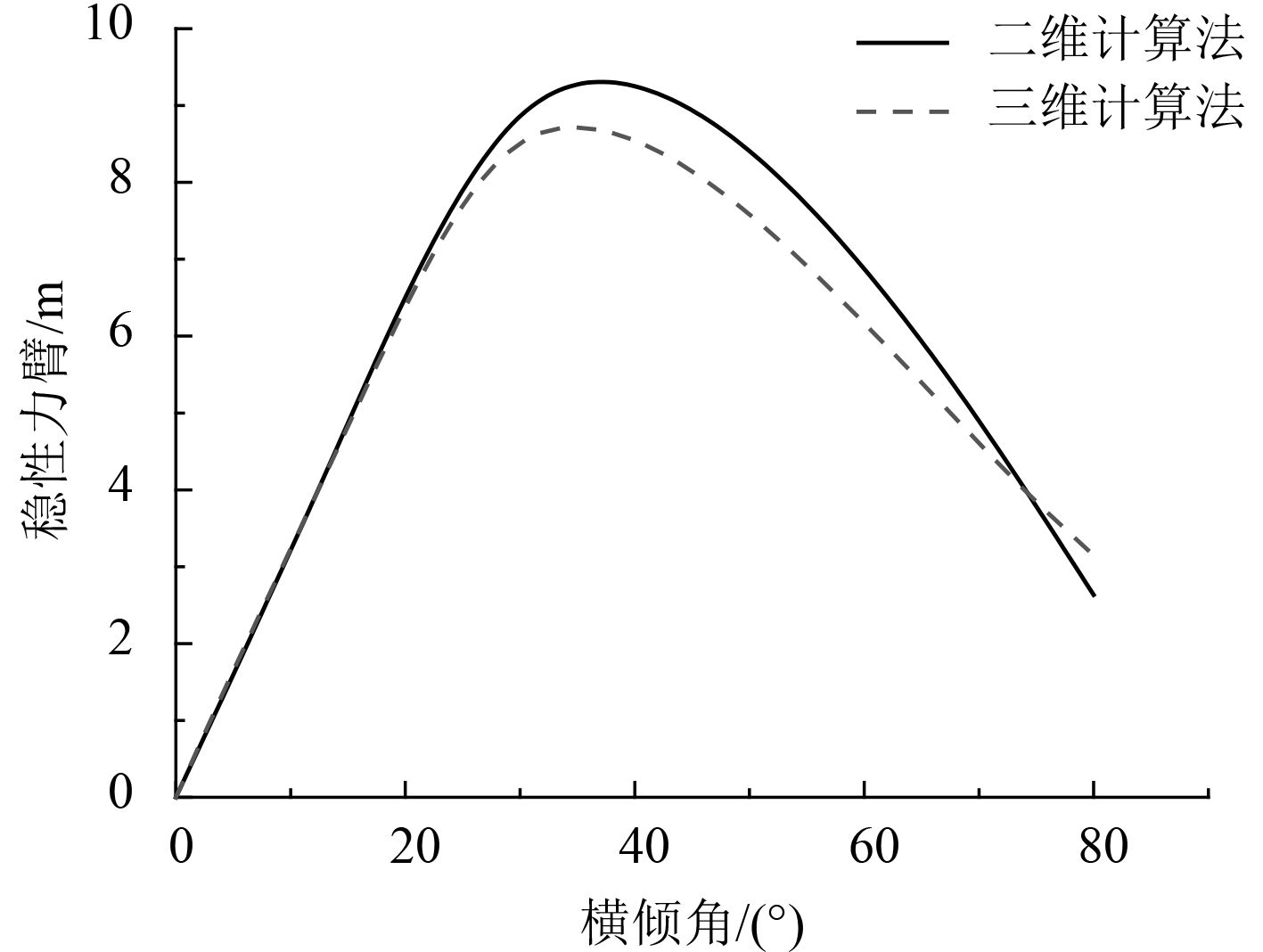
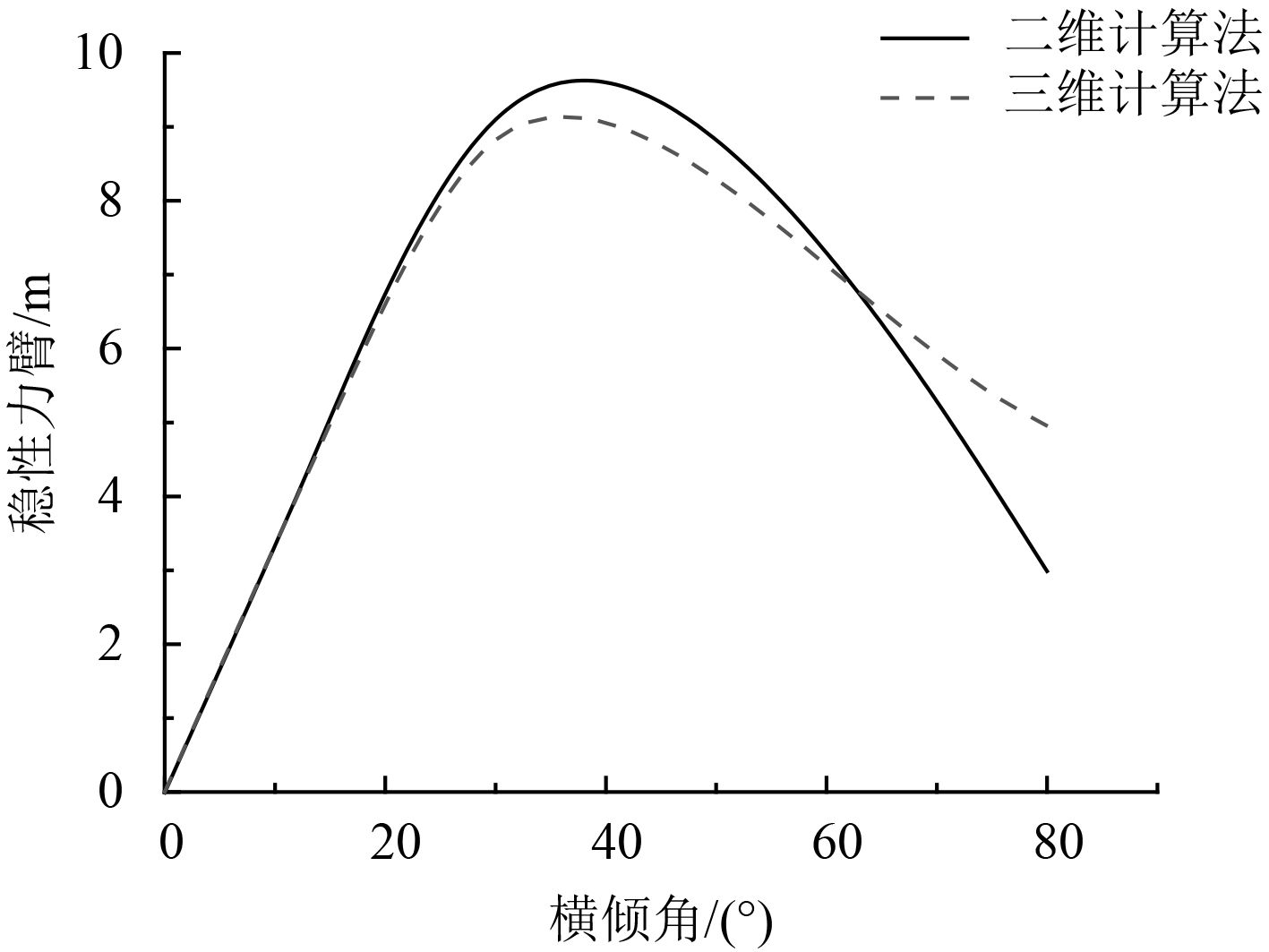
3 算 例以散货船SHANDONG REN HE为例,平均板厚为0.021 m,分别设计CPU和GPU处理的程序,计算回复力臂值,设置步长为5°,计算区间0°到80°。根据计算结果绘制复原力臂曲线。用本文计算结果与二维数值计算方法的计算值进行对比,结果如图4~图6所示。可以看到在横倾初期2种计算方法结果相差较小。在横倾角超过60°~70°时,计算结果相差较大,主要原因在于在该种载况下,横倾角已经超过进水角,本文的计算方法已经包含舱盖等船体上部计算数据,与二维计算法计算结果相比存在一定误差。

|
图 4 压载出港稳性力臂对比图 Fig. 4 Comparison of GZ during ballast condition at DEP |
|
图 5 压载途中稳性力臂对比图 Fig. 5 Comparison of GZ during ballast condition in MID |
|
图 6 压载到港稳性力臂对比图 Fig. 6 Comparison of GZ during ballast condition at ARR |
本文基于船舶三维型表面模型及CGAL几何算法库中的切片模块建立了船舶三维基础数据库,在此数据库基础上,通过CUDA并行加速,实现了船舶稳性的实时计算,可得到如下结论:1)船舶三维型表面模型来源于船舶设计软件,是船舶真实数据,计算精度较高;2)以散货船SHANDONG REN HE为例,对多个典型载况进行计算,验证了本文算法的准确性。
| [1] | 盛振邦, 刘应中. 船舶原理[M]. 上海交通大学出版社, 2003. |
| [2] |
赵晓非, 蔡伟科. 船舶稳性计算优化方法研究[J]. 中国造船, 1987 (02): 88–94.
ZHAO Xiao-fei, CAI Wei-ke. An Optimization Methodforthe Calculation of Ships Stability Curves[J]. Shipbuilding of China, 1987 (02): 88–94. |
| [3] |
桑松, 徐学军. 浮式结构物完整稳性优化计算原理[J]. 上海交通大学学报, 2009 (10): 1568–1572.
SANG Song, XU Xue-jun. Optimization Calculational Principle on Intact Stability of Floating Structures[J]. Journal of Shanghai Jiaotong University, 2009 (10): 1568–1572. DOI: 10.3321/j.issn:1006-2467.2009.10.011 |
| [4] |
孙承猛, 刘寅东. 一种船舶最小稳性和自由浮态计算的改进算法[J]. 中国造船, 2007 (03): 1–4.
SUN Cheng-meng, LIU Yin-dong. An Improved Algorithm for Calculating Ship’s Minimum Stability and Free Floatation[J]. Shipbuilding of China, 2007 (03): 1–4. DOI: 10.3969/j.issn.1000-4882.2007.03.001 |
| [5] |
马坤, 张明霞, 纪卓尚, 等. 非线性规划法计算船舶稳性[J]. 中国造船, 2003 (02): 83–86.
MA Kun, ZHANG Ming-xia, JI Zhou-shang, et al. Application of Nonlinear Programming to Calculation of Ship Stability Curve[J]. Shipbuilding of China, 2003 (02): 83–86. |
| [6] | 令波. 浮性与完整稳性的直接计算法[D]. 武汉: 华中科技大学, 2013. |
| [7] | 程智斌, 魏建志, 曾宏军. 计算破损船舶稳性的表面元法[J]. 海军工程大学学报, 2002 (4): 41–44. |
| [8] | RADWAN A M. A different method to evaluate the intact stability of floating structures[J]. Marine Technology and Sname News, 1983, 20 (1): 21–25. |
| [9] | COOK S. CUDA programming: a developer’s guide to parallel computing with GPUs[M]. Newnes, 2012. |
| [10] | KIRK D B, Wen-mei W H. Programming massively parallel processors: a hands-on approach[M]. Newnes, 2012. |
| [11] | The Computational Geometry Algorithms Library[EB/OL]. [2016-8-19]. http://www.cgal.org. |
| [12] |
王智洲, 孙霄峰, 尹勇, 等. 基于三维设计数据的船舶湿面积计算[J]. 船舶工程, 2016, 38 (05): 5–8.
WANG Zhi-zhou, SUN Xiao-feng, YIN Yong, et al. Ship’s Wetted Surface Calculation Based on 3D Design Data[J]. Ship Engineering, 2016, 38 (05): 5–8. |
| [13] | 张明霞. 基于NURBS曲面的船舶破舱稳性计算方法研究[D]. 大连理工大学, 2002. |
| [14] | NVIDIA. CUDA programming guide V 7.5[Z]. 2015. |
 2017, Vol. 39
2017, Vol. 39
