2. 中国船舶及海洋工程设计研究院,上海 200011
2. Marine Design and Research Institute of China, Shanghai 200011, China
FPSO需要在目标海域长期作业,在服务期内,FPSO(特别是不具备自航功能的FPSO)很有可能遭遇极端的载荷情况。出于安全考虑,目前的规范都将FPSO的设计环境条件定为100年一遇,因此,如何准确地确定FPSO的设计载荷是FPSO设计评估中的重点。
目前有大量的规范可以对在不限定航线的波浪条件下运营的船舶的设计载荷进行计算,但是由于运营方式的不同,其计算载荷不能直接用于FPSO的结构设计与强度评估。为使基于不限定航线波浪条件下的船舶载荷计算规范能用于FPSO的设计与评估,美国船级社引入了环境烈度因子对用于计算不限定航线船舶的载荷的规范公式进行了修正[1]。本文基于钢质海船建造和入级规范[2],参照浮式生产装置建造入级规范[3]中的相关规定,采用环境烈度因子对文献[2]中的公式进行修正,并作为某30万吨FPSO评估载荷的计算公式。同时,为避免复杂、耗时的全船有限元模型建立工作,文中采用薄壁梁理论[4 – 5]对该FPSO的船体梁剪切强度进行校核。
1 环境烈度因子的定义环境烈度因子分为α因子和β因子2种。α因子主要用来修正无限定航线条件下运营船舶(即基于规范)与长期作业于指定海域装置(FPSO)之间的预期疲劳强度;β因子主要用来修正用于创建船体梁强度、单独构件尺寸方程的动载荷分量,也用于修正船体强度分析的载荷以及一些辅助性的力如由位于主甲板及其以上的设备运动产生的力。本文主要讨论β因子的运用,β因子的定义如下[3]:
|
$\beta = \frac{{{L_S}}}{{{L_U}}},$
|
(1) |
式中:LS为在特殊作业场地海况下的动载荷极值,场地自存重现期为100年;LU为基于北大西洋无限航区海况条件下的动载荷极值,重现期为25年。
根据ABS船级社关于FPSO的规范,有13个关于动载荷分量的环境烈度因子,见表1。
|
|
表 1 动载荷分量环境烈度因子 Tab.1 The ESFs of component of dynamic loads |
环境烈度因子计算要点在于LS和LU的确定,采用基于三维线性势流理论[6]的波浪载荷直接计算软件COMPASS-WALCS-BASIC对二者进行计算。
2.1 LS的计算设置文章计算FPSO的作业海域为南海,工作水深为103 m,计算航速为本0 kn,其余参数设置参见文献[7 – 8]。
2.2 LU的计算设置基于北大西洋无限航区海况条件下的动载荷极值LU,系指计算相应环境条件下的长期预报极值。LU为动载荷成分在无限航区海况下的极值响应,与LS的计算过程相似,通过基于波浪谱和波浪散布图的长期预报方法[6]得到。
需要注意的是:1)水深。LU是针对无限航区海域,计算LU时的计算水深应取为无限水深;2)海浪谱。对于LU对应的无限航区或开放海域,推荐使用双参数PM谱,文中采用ISSC推荐的双参数PM谱;3)海况散布图。对于无限航区,采用IACS推荐的NO. 34北大西洋波浪散布图[8]。
2.3 环境烈度因子计算根据上述方法,可以计算出各装载工况下的LS和LU,即可得到不同动载荷分量的ESF。各载况下不同动载荷分量的环境烈度因子ESF见表2。为了防止ESF值过小,不足0.5的按0.5取[8]。
|
|
表 2 各载况下FPSO环境烈度因子 Tab.2 The ESFs of FPSO under different loading conditions |
根据文献[2],本文主要对FPSO的船体梁纵向强度—船体梁弯曲强度与船体梁剪切强度—进行评估,故实际用到的环境烈度因子为βVBM和βVSF。
3.1 弯曲强度校核作用于FPSO的载荷分为垂向静水弯矩与垂向波浪弯矩2部分,静水弯矩由装载手册提供,垂向波浪弯矩环境烈度因子修正后的公式决定,见式(2),单位为kNm。
|
${M_{ws}} = - {k_1}{\beta _{VBM}}{C_1}{L^2}B\left( {{C_b} + 0.7} \right) \times {10^{ - 3}}\text{,}\;\;\text{中垂,}$
|
(2) |
|
${M_{wh}} = - {k_2}{\beta _{VBM}}{C_1}{L^2}B{C_b} \times {10^{ - 3}}\text{,}\;\;\;\;\;\text{中拱}\text{。}$
|
(3) |
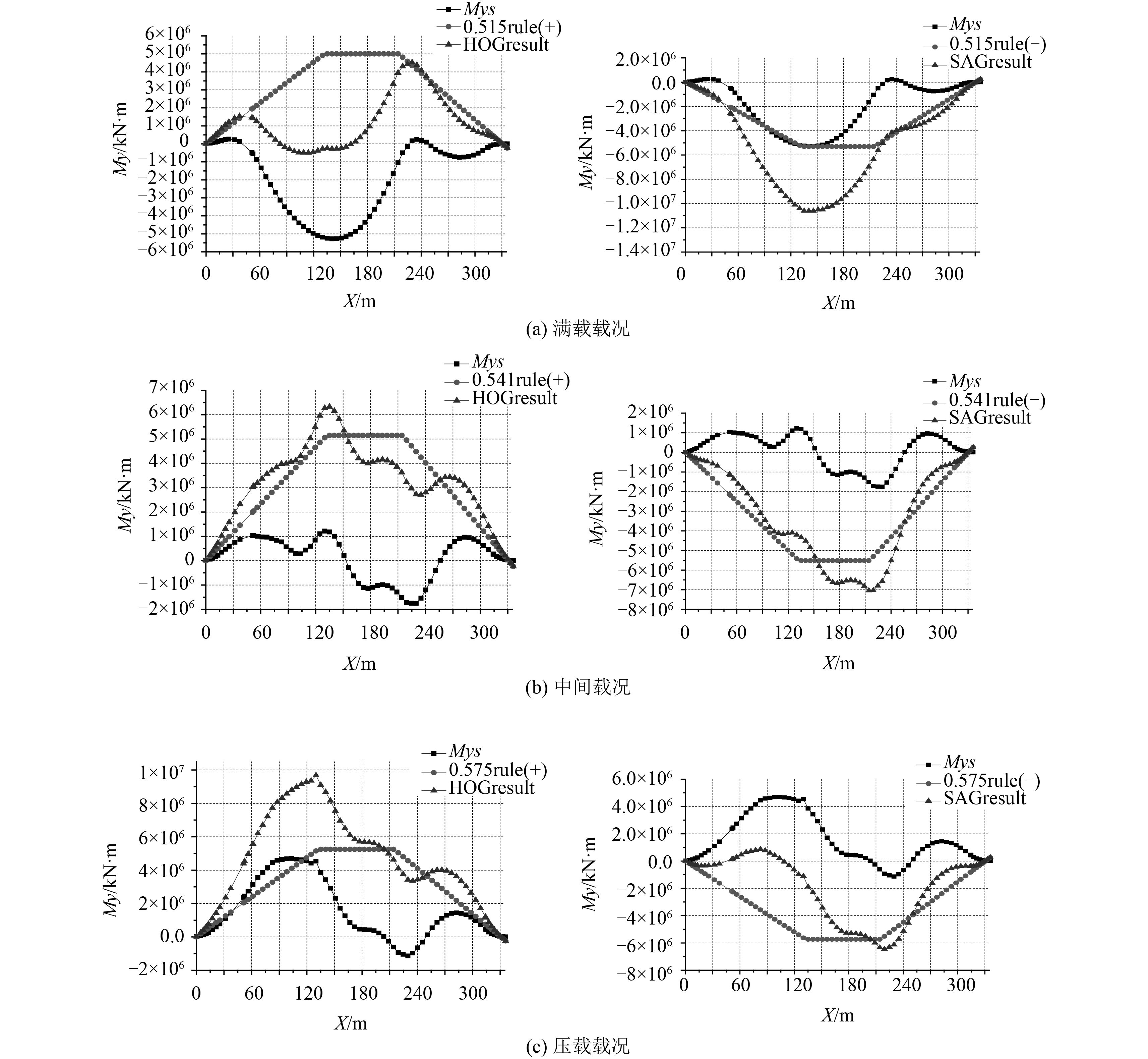
各载况下中垂和中拱工况的合成载荷如图1所示。由图1得到各载况下最大合成弯矩作用剖面位置及作用载荷,见表3。
|
图 1 中拱/中垂静水弯矩与波浪弯矩分布图 Fig. 1 The bonding moment of hogging and sagging |
|
|
表 3 各载况最大合成弯矩作用剖面 Tab.3 The section bearing maximum resultant bending moments |
根据文献[2]规定,船体梁校核应满足下列要求:
船体梁0.4 L区域的剖面模数应不小于下式计算值
|
$SM = {M_t}/{f_p}\text{。}$
|
(4) |
式中:Mt为总弯矩,垂向静水弯矩与垂向波浪弯矩之和,kN·m;fp为名义许用弯曲应力,为175 000 kN/m2
同时,视计算环境烈度因子值的大小,垂向波浪弯矩作用下的船体梁最小剖面模数应不小于表4中的值。
|
|
表 4 各ESF下的最小船体粱剖面模数 Tab.4 The minimum hull girder section modulus under different βVBM |
式中:SMsvr最小船体梁剖面模数,见文献[2]。
目标FPSO采用高强度钢的区域为甲板,船底,舷侧外板甲板边线向下3.2 m、基线向上3.2 m的舷侧板,纵舱壁从甲板边线向下4.395 m、基线向上4.95 m的纵舱壁板。高强钢等级为H36,屈服极限为
弯曲强度校核结果见表5。
|
|
表 5 弯曲强度校核结果 Tab.5 The check results of bending strength |
由表5可知弯曲强度校核满足要求。
3.2 剪切强度校核同弯曲强度校核相同,FPSO剪切强度校核作用载荷包含静水剪力与垂向波浪剪力。静水剪力由装载手册提供,垂向波浪剪力环境烈度因子修正后的规范公式决定,见式(4),单位为kN。
|
${F_{wp}} = + k{\beta _{VSF}}{F_1}{C_1}LB\left( {{C_b} + 0.7} \right) \times {10^{ - 2}}\left( + \right),$
|
(5) |
|
${F_{wn}} = - k{\beta _{VSF}}{F_2}{C_1}LB\left( {{C_b} + 0.7} \right) \times {10^{ - 2}}\left( - \right)\text{。}$
|
(6) |
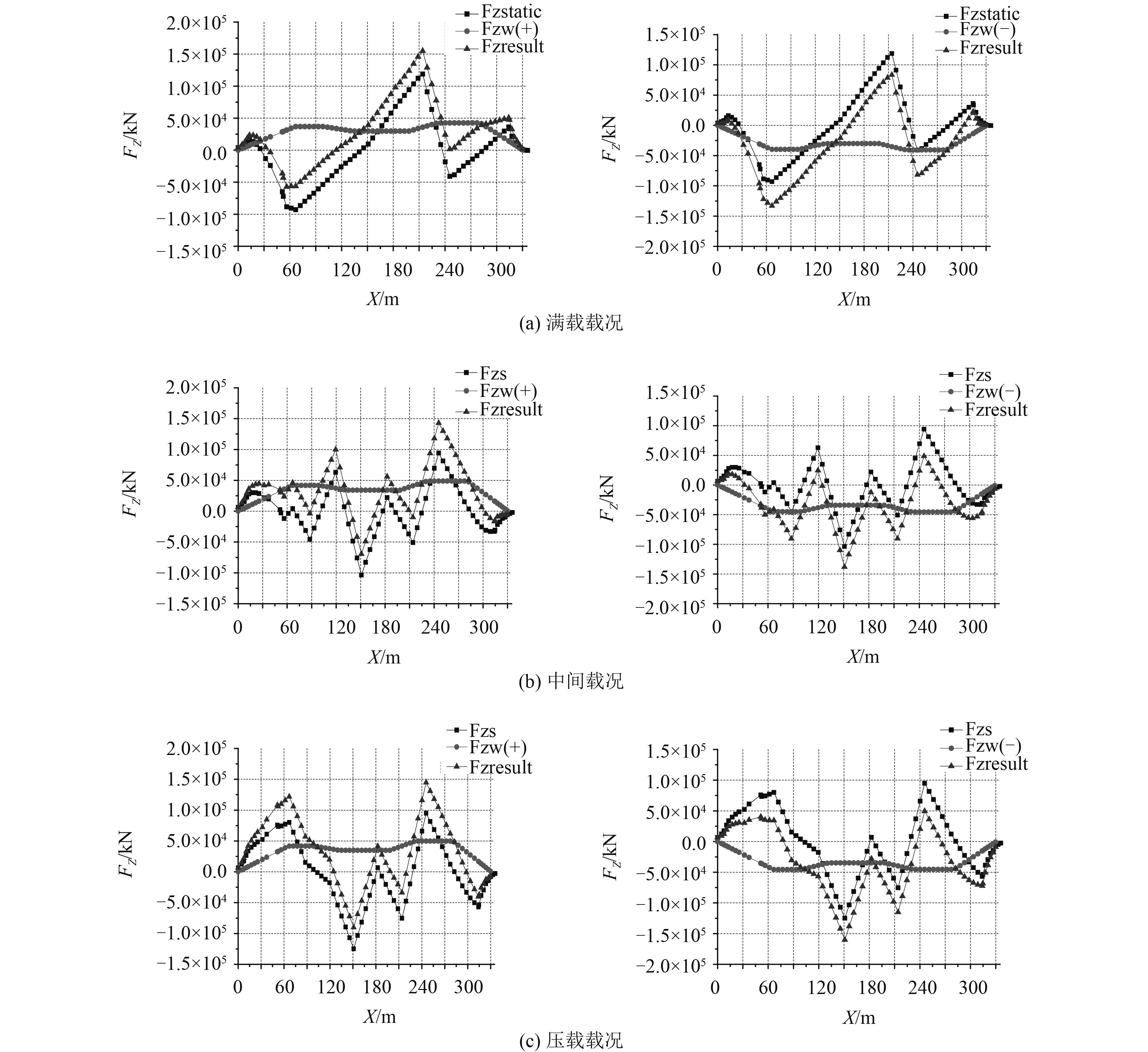
各载况下垂向波浪剪力分别为正、负工况时的合成载荷如图2所示。
|
图 2 中拱/中垂静水剪力与波浪弯矩分布图 Fig. 2 The shear force of hogging and sagging |
由图2得到各载况下危险剖面所在位置及作用载荷。按照文献[2]规定,船体梁剪切强度校核应满足下列要求:
计算所得剪应力应大于下值
|
${f_s} = 110\;000\;{\rm{kN/}}{{\rm{m}}^{\rm{2}}},$
|
(7) |
需要注意的是目标FPSO具有2道连续纵舱壁,其横剖面属于多腔室闭口薄壁杆件,见图3,利用薄壁梁理论[4 – 5]计算剖面剪应力,剪切强度校核结果见表6。由表6可知剪切强度满足要求。

|
图 3 目标FPSO三舱段模型图 Fig. 3 The three cargo hold model |
|
|
表 6 剪切强度校核结果 Tab.6 The check results of shearing strength |
不引入环境烈度因子修正,直接应用文献[2]中的公式进行强度校核的结果见表7和 表8。
|
|
表 7 未经ESF修正弯曲强度校核结果 Tab.7 The check results of bending strength with no application of ESFs |
|
|
表 8 未经ESF修正剪切强度校核结果 Tab.8 The check results of shearing strength with no application of ESFs |
可知在采用ESF修正时,剪切强度校核复合要求;弯曲强度虽然满足文献[2]中3-2-1/3.7.1(a)要求,但不满足文献[2]中3-2-1/3.7.1(b)的规定,故不满足要求。
经ESF修正与未经ESF修正的强度评估结果见表9 和 表10。
|
|
表 9 ESF修正与否的弯曲强度校核结果比较 Tab.9 The comparison of bending strength between the results corrected by ESFs and that not |
|
|
表 10 ESF修正与否的剪切强度校核结果比较 Tab.10 The comparison of shearing strength between the results corrected by ESFs and that not |
可以看出,在弯曲强度校核中未经ESF修正时,计算所得的规范要求剖面模数相对修正结果偏大最小10.95%,最大至18.91%;规范要求的船中最小剖面模数相对修正结果偏大约17.6%。在剪切强度校核时,未经ESF修正的剪应力计算结果相对修正结果偏大达28.91%。
4 结 语文章基于文献[2 – 3]的相关规定,采用未经ESF修正和ESF修正后规范公式计算某FPSO的设计载荷,在此基础上,利用薄壁梁理论对其船体梁强度进行校核,结论如下:
1) 船体梁弯曲强度校核,未经ESF修正的计算结果相对修正后计算所得的规范要求剖面模数偏大10.95%~18.91%;规范要求的最小剖面模数前者偏大17.6%左右;
2) 船体梁剪切强度校核时,未经ESF修正的计算结果相对修正后的计算结果偏大14.28%~28.91%;
3) 相对有限元计算,采用薄壁梁理论可以快速、有效计算船体梁闭型舱室的剪切强度。
采用环境烈度因子方法可以基于现有规范公式,快速、有效地确定FPSO的设计载荷,并对其进行结构设计与评估,简单易于实现,是FPSO设计评估的一种有效方法。在评估船体梁闭型舱室的剪切强度时,为避免繁重的建模任务量,可以利用薄壁梁理论对剪切强度进行评估。
| [1] | 赵春田, 王艳芳. 用动载荷因子法进行FPSO船体强度的设计和评估[J]. 中国造船, 2002, 43 (S): 132–143. |
| [2] | ABS. ABS rules for building and classing steel vessels[M]. 2016: 42–56. |
| [3] | ABS. ABS Rules for building and classing floating production installations[M]. 2016, 98–449. |
| [4] | 杨代盛. 船体强度与结构设计[M]. 北京: 国防工业出版社, 1981: 41–61. |
| [5] | 陈伯真, 胡毓仁. 薄壁结构力学[M]. 上海: 上海交通大学出版社, 1998. |
| [6] | 戴仰山, 沈进威, 宋竞正. 船舶波浪载荷[M]. 北京: 国防工业出版社, 2007: 23–113. |
| [7] |
刘成名, 李洛东, 孙政策. FPSO 环境烈度因子应用分析[J]. 船海工程, 2014, 43 (6): 1671–7953.
LIU Chengming, LI Luodong, SUN Zhengce, et al. Application analysis of FPSO environmental severity factors[J]. SHIP & OCEAN ENGINEERING, 2014, 43 (6): 1671–7953. |
| [8] | 中国船级社. 海上浮式装置入级规范[M]. 北京: 人民交通出版社, 2014: 2-79–2-188. |
 2017, Vol. 39
2017, Vol. 39
