造成船舶海难的事故种类繁多,有碰撞、进水、搁浅、火灾、沉没等,海难给人员生命和财产带来巨大的损失,某些情境例如油船破损还会给海洋环境带来严重的破坏。因此,对船舶受损后的生存能力、浮态情况进行研究具有重要的现实意义。
船舶的破损进水过程一般分为3个阶段:破损产生之后水从破口涌入船内称为瞬时进水阶段,水从内部开口浸入未破损的舱室,称为连续进水(递进进水)阶段,最终船舶没有倾覆或者在该阶段没有沉没,将得到最后的稳定阶段。在瞬时进水阶段船舶可能达到比之后连续进水和稳定阶段更大的横倾角,造成船舶倾覆,这对进水过程的瞬态时域模拟提出了要求。对船舶破舱进水过程的时域模拟是解决船舶破损沉没时间预报、可供救援时间预报、救援措施选择等挑战的有效方式。
对于船舶破舱稳性与进水的时域模拟研究已进行20余年。发生在1987年的Herald of Free Enterprise客滚船倾覆事件和1994年Estonia ferry沉没事件强调了船舶破舱稳性的重要性,促使对于此问题的研究加速。
Spouge[1]对于European Gateway客滚船的倾覆进行了分析探讨,首次提出了“对称舱室的瞬时非对称进水”。Santos and Guedes[2]应用了6自由度时域模拟了滚装船的瞬时进水过程,在进水舱室中用大的流动障碍物模拟瞬时不对称进水,整个过程假定液面水平。Zhiliang Gao等[3]用一种N-S方程求解器结合VOF方法模拟了固定状态下客滚船进水,并用该方法测试了二维和三维的溃坝模拟问题。李佳[4]采用伯努利方程的准静态法求解了自由漂浮状态下不考虑外流体域的船舶进水过程。曹雪雁[5]采用SPH法对于三维船舶破舱进水特性进行了模拟研究。刘强[6]基于Fluent平台局部网格重构动网格技术和用户自定义函数(UDF)进行了对进水以及二维舱室耦合运动的模拟,并探讨了空气压缩性对于进水过程的影响。上述方法均未对三维实船对象在自由漂浮状态下的破舱流动特性、船体与水的横摇耦合运动进行时域模拟研究。
本文对三维客滚船破舱进水过程时域模拟的方法进行探讨。应用STAR-CCM+计算软件对三维客滚船计算模型进行了破舱进水的时域模拟。采用VOF法模拟进水过程的自由液面,且首次采用重叠网格技术结合STAR-CCM+ DFBI (Dynamic Fluid Body Interaction)模块实现对于三维客滚船实体在破损进水过程中的6-DOF运动模拟。
1 数值模拟的理论基础 1.1 控制方程本文的理论基础是三维不可压缩的粘性流体瞬态运动方程,流体的密度和粘性系数为常数。
质量守恒方程(连续性方程):
|
$\frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}} + \frac{{\partial w}}{{\partial z}}{\rm{ = }}0{\text{,}}$
|
(1) |
式中:u,v,w为速度矢量v沿着x,y,z轴3个方向的速度分量。
动量守恒方程(运动方程):
|
$\rho \frac{{d\nu }}{{dt}} = \rho F - gradp + \mu {\nabla ^{\rm{2}}}v{\text{,}}$
|
(2) |
式中:F为质量力;p为压强;μ为流体动力粘度。
有限体积法是在控制体积内对一般形式的控制微分方程的积分,即是求解积分形式的守恒方程。
|
$\begin{split}&\int_V \!\! {\frac{\partial }{{\partial t}}\left( {\rho \phi } \right){\rm{d}}v + } \!\! \int_V {div\left( {\rho v\phi } \right){\rm{d}}}v =\\&\;\;\;\;\;\;\;\;\;\;\;\;\;\;\int_V {div\left( {\Gamma grad\phi } \right){\rm{d}}v + } \!\! \int_V {S{\rm{d}}v} {\text{。}}\end{split}$
|
(3) |
式中:ϕ为通用变量;V为控制体积;Γ为广义扩散系数;S为广义源项。
1.2 VOF方法VOF(Volume of fluid)方法的基本原理是通过研究网格单元中流体和网格体积比函数F来确定自由面,追踪流体的变化,而非追踪自由液面上质点的运动。VOF方法可以处理自由面重入等强非线性现象,所需计算时间短、存储量少。
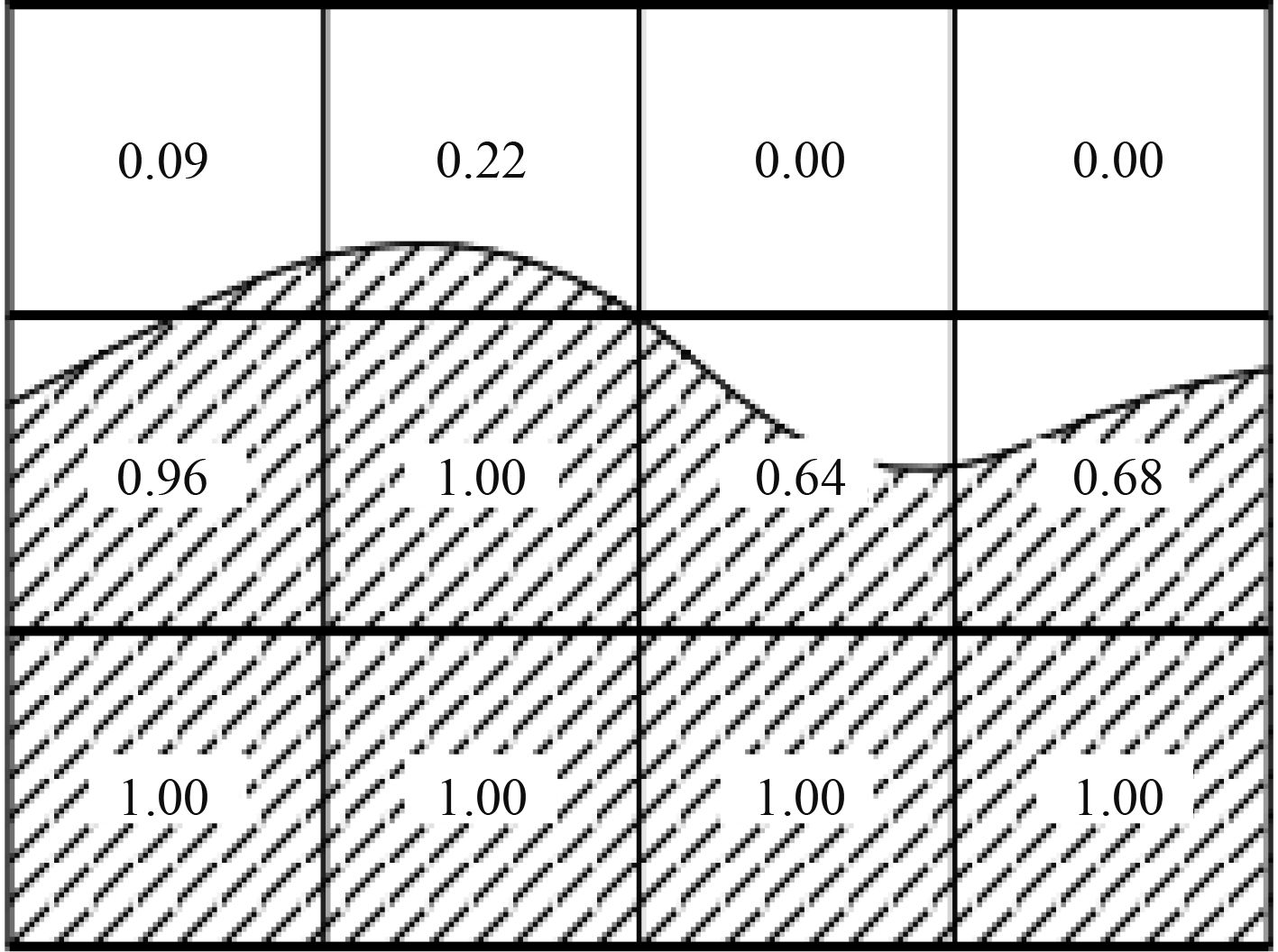
如图1所示,VOF方法中若体积比函数F=1,则说明该单元全部为指定相流体所占据;若F=0,则该单元为无指定相流体单元;当0<F<1时,则该单元称为交界面单元。
1.3 重叠网格(Overset Grid)动网格处理技术Overset grid技术[8 – 9]是将复杂的流动区域分成几个几何边界较为简单的子区域,各个子区域之间的计算网格独立生成,彼此存在重叠或覆盖关系。流场信息通过插值在重叠区域的边界上进行交换和匹配。
重叠网格逻辑关系简单,对流场计算精度高、效率高、壁面粘性模拟能力强。重叠网格技术可以使得计算更容易执行和自动参数化:单组网格可以对应多重配置,网格质量不受位置和方向影响,边界条件易于设置等;又有对复杂运动模拟的可能性:不必预先设定路径,路径可以相互交叉。
2 计算模型尺寸本文模拟对象为某1 600客的客滚船,船体主要参数如表1所示。
|
|
表 1 1 600 RoRo主尺度信息 Tab.1 Principal dimension information for 1 600 RoRo |
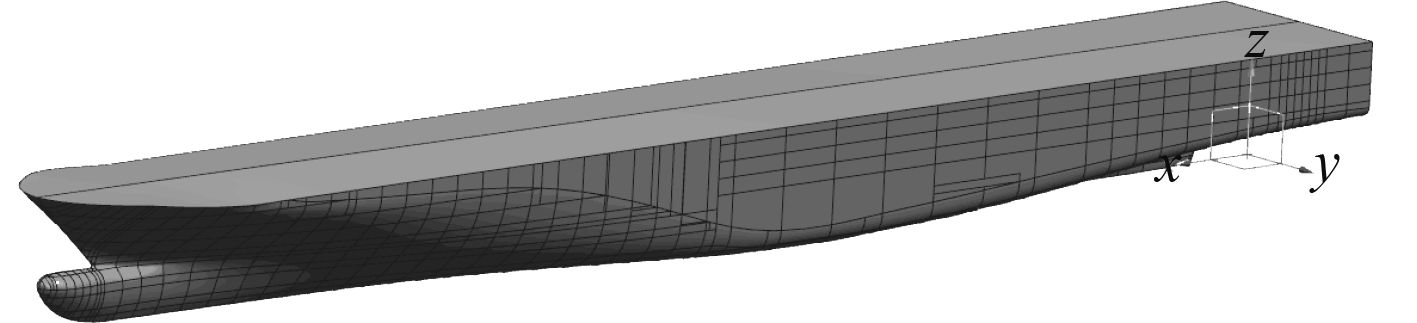
建立完整船体几何模型见图2。计算坐标系的原点位于船体尾垂线、中心线与基线的交点,X轴向首为正,Y轴向左舷为正,Z轴向上为正。
|
图 2 完整船体几何模型 Fig. 2 Geometry model of intact ship |
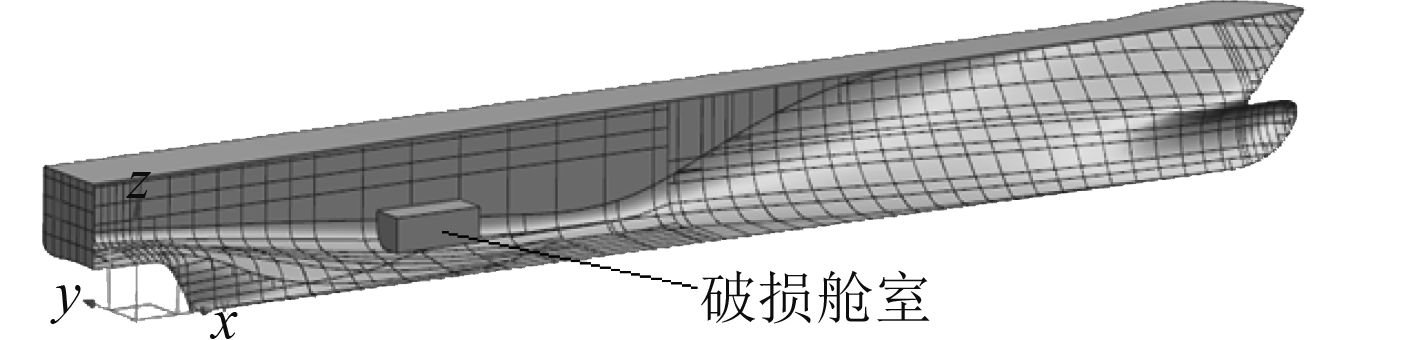
破损舱室为船舶左侧一个全部在水线之下的机舱R6.2。示意图见图3,相关参数见表2。
|
图 3 破损舱室 Fig. 3 Damaged compartment |
|
|
表 2 破损舱室信息 Tab.2 Information for damaged compartment |
设计破口为长度与舱室长度一样均为13.6 m(x=48 ~61.6 m),高度为0.96 m(z=4.44 ~5.4 m),位于舱室侧壁上方的长方形破口。

|
图 4 破口 Fig. 4 Opennig |
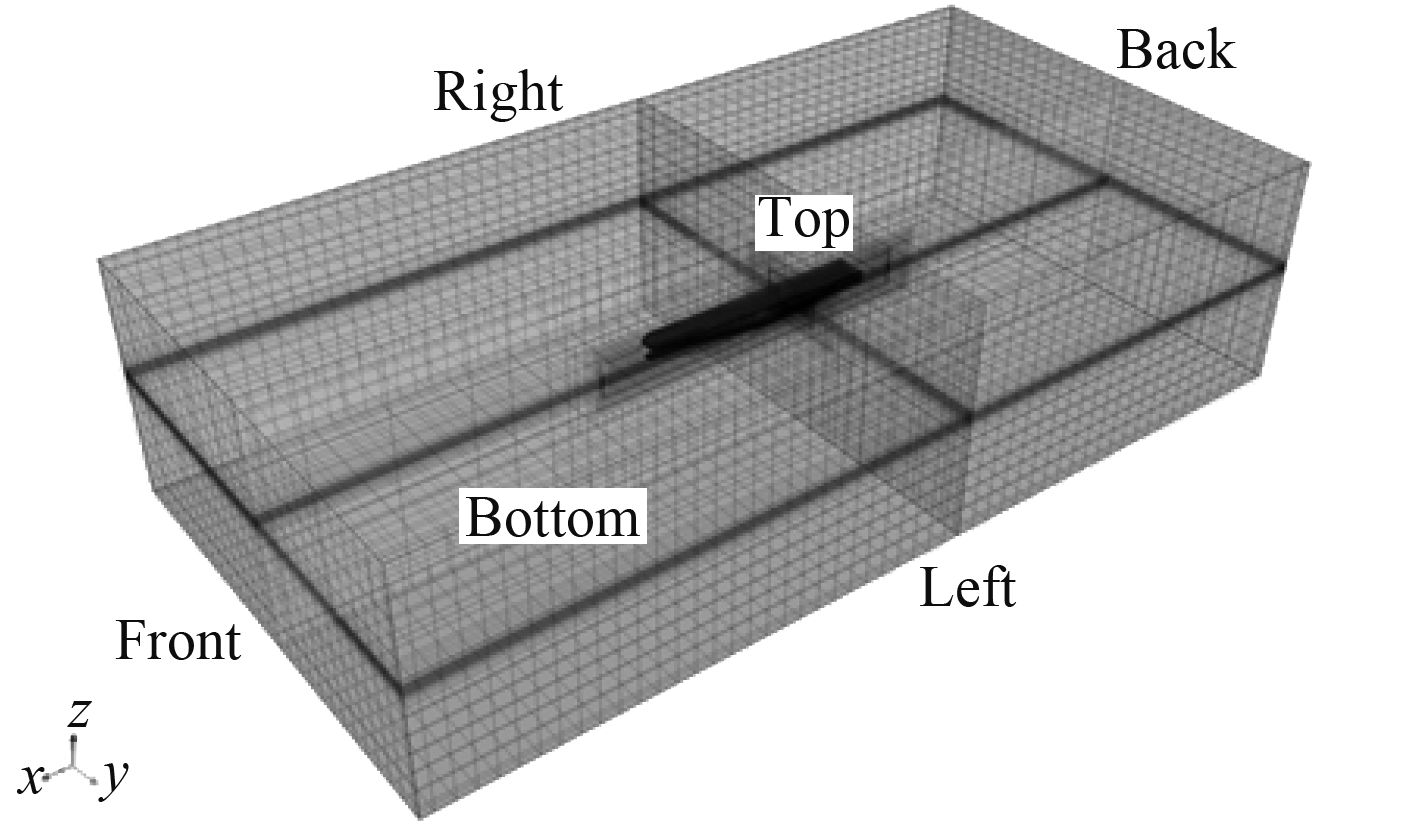
将建立的几何面网格信息导入STAR-CCM+后,需要对其进行面的检查、修补,例如去除自由边、穿刺面等,进行面网格重构以满足后续体网格生成和计算的模型质量要求。此次计算采用质量较高的切割体网格(Trimmed Cell),整个计算域即背景网格区域,如图5所示,计算域内作横、纵两剖面(x=55 m和y=10 m)以展示计算区域内部的体网格情况。
|
图 5 整个计算域的网格配置概览 Fig. 5 Sketch of mesh arrangement in the whole computational domain |
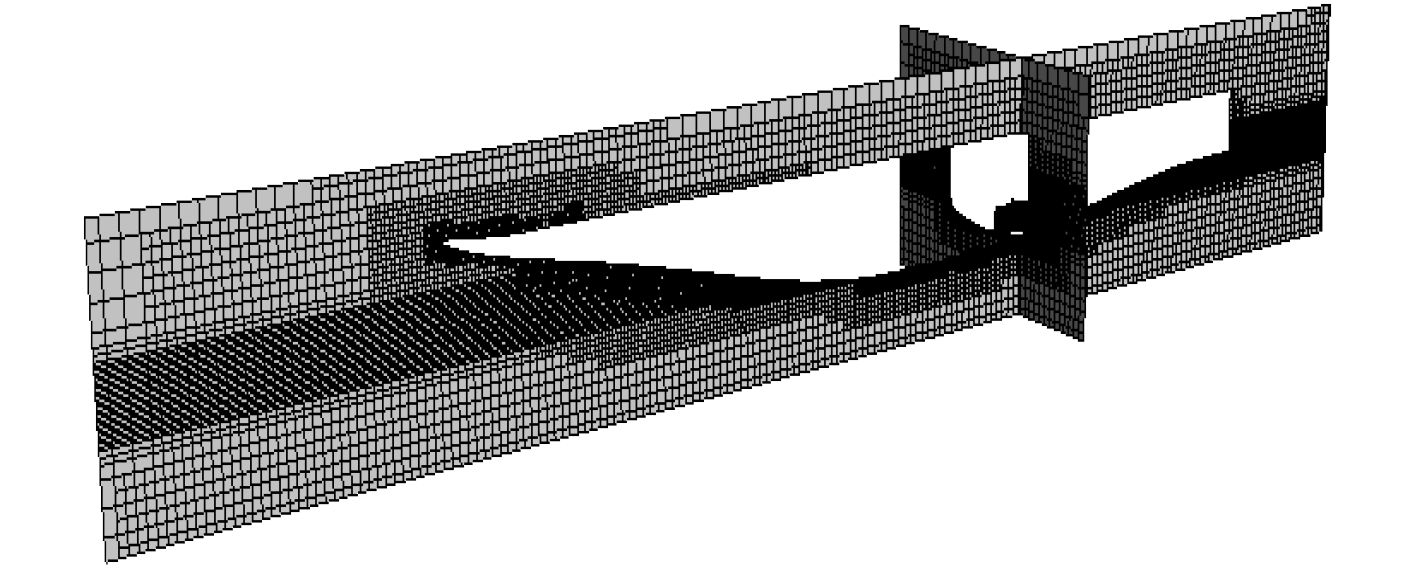
数值模拟的计算精度和计算量与网格密切相关,因此生成一套合适的网格用于计算显得十分重要。此处根据计算区域的重要性,对于不同区域建立疏密有别的网格。背景网格基本尺寸(Base Size)为15 m,重叠网格区域网格基本尺寸为3 m。对于背景网格区域,在近重叠网格区域处、近水线面处作了网格加密;对于重叠网格区域,如图6和图7所示,在船体周围、近水线面处和破舱内及周围区域作了不同程度的网格控制加密,其中破口周围区域的六面体网格尺寸为0.1 m。
|
图 6 重叠网格区域内部网格 Fig. 6 Mesh in overset region |

|
图 7 破口处网格细节 Fig. 7 Detail of mesh around opening |
最终生成网格数量:背景网格区域444 448,重叠网格区域2 957 687(其中破口舱室内及周围外域加密网格数约147万)。
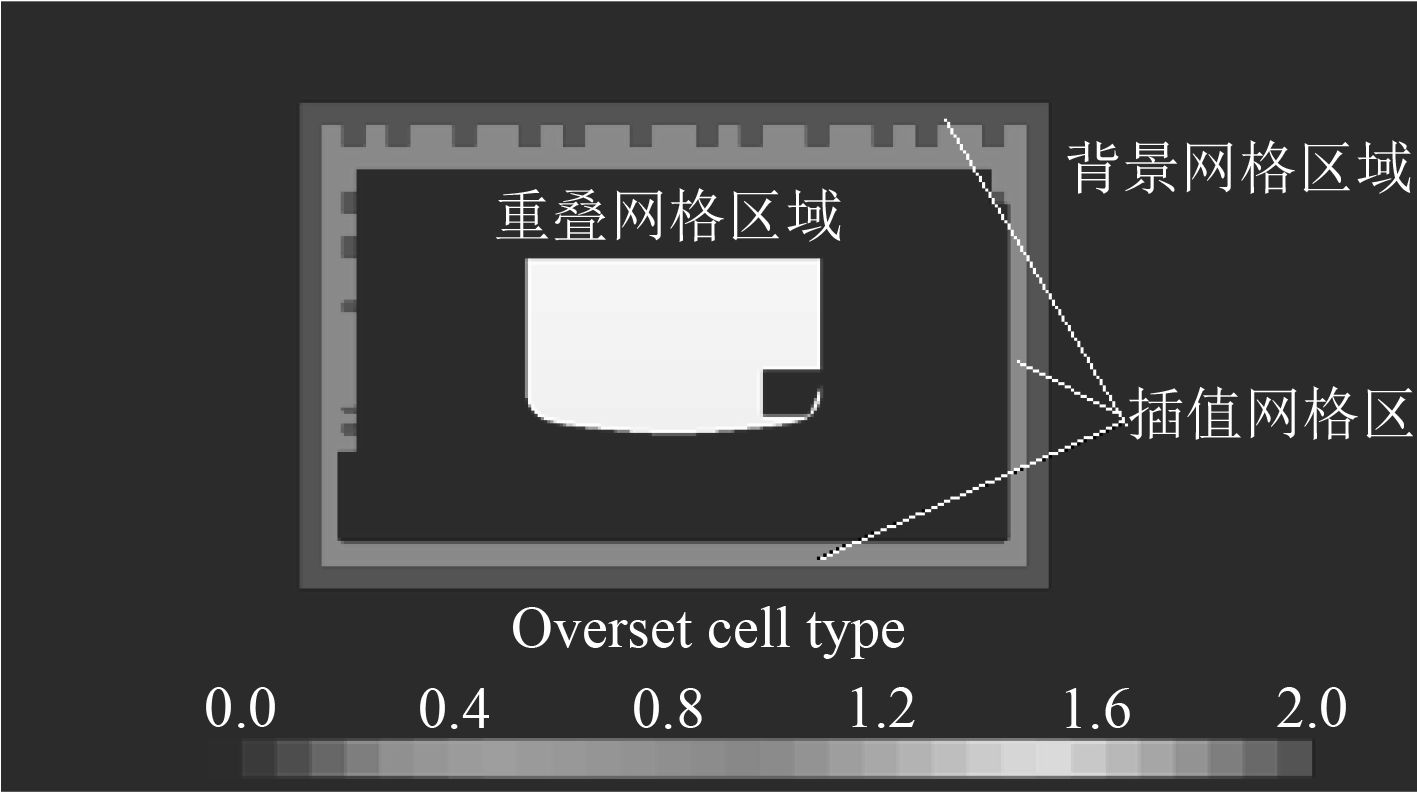
图8为初始横倾角=0°状态下横截面中重叠网格和背景网格的插值网格区域示意图。
|
图 8 初始状态插值区域 Fig. 8 Interpolation region of initial condition |
计算采用隐式非定常(Implicit Unsteady)下的欧拉多相流(Eulerian Multiphase)计算模型,选用应用较多的k-epsilon湍流模型,船体在运动中视为不可变形刚体,不计空气压缩性。
对于边界条件的设置,背景网格前、后边界面设置为壁面(wall),上、下、左边界面设置为速度入口(Velocity Inlet),右边界面设置为压力出口(Pressure Outlet)。具体采用STAR-CCM+中的场函数(Field Function)功能,指定速度入口的Volume Fraction函数、速度值,压力出口的Volume Fraction函数、压力值,控制计算中边界处多相流分布和速度、压力值分布。对于多相流的初始化设置,采用类似的自定义场函数方法进行。客滚船初始吃水5.323 m,无横倾。
求解采用一阶时间离散,并根据最大流动速度的预估和舱内网格尺寸要求,取隐式计算时间步长为0.005 s。
4 模拟计算与结果分析 4.1 计算结果

|
图 9 各时刻自由液面示意图 Fig. 9 Sketch of free surface of different time |
|
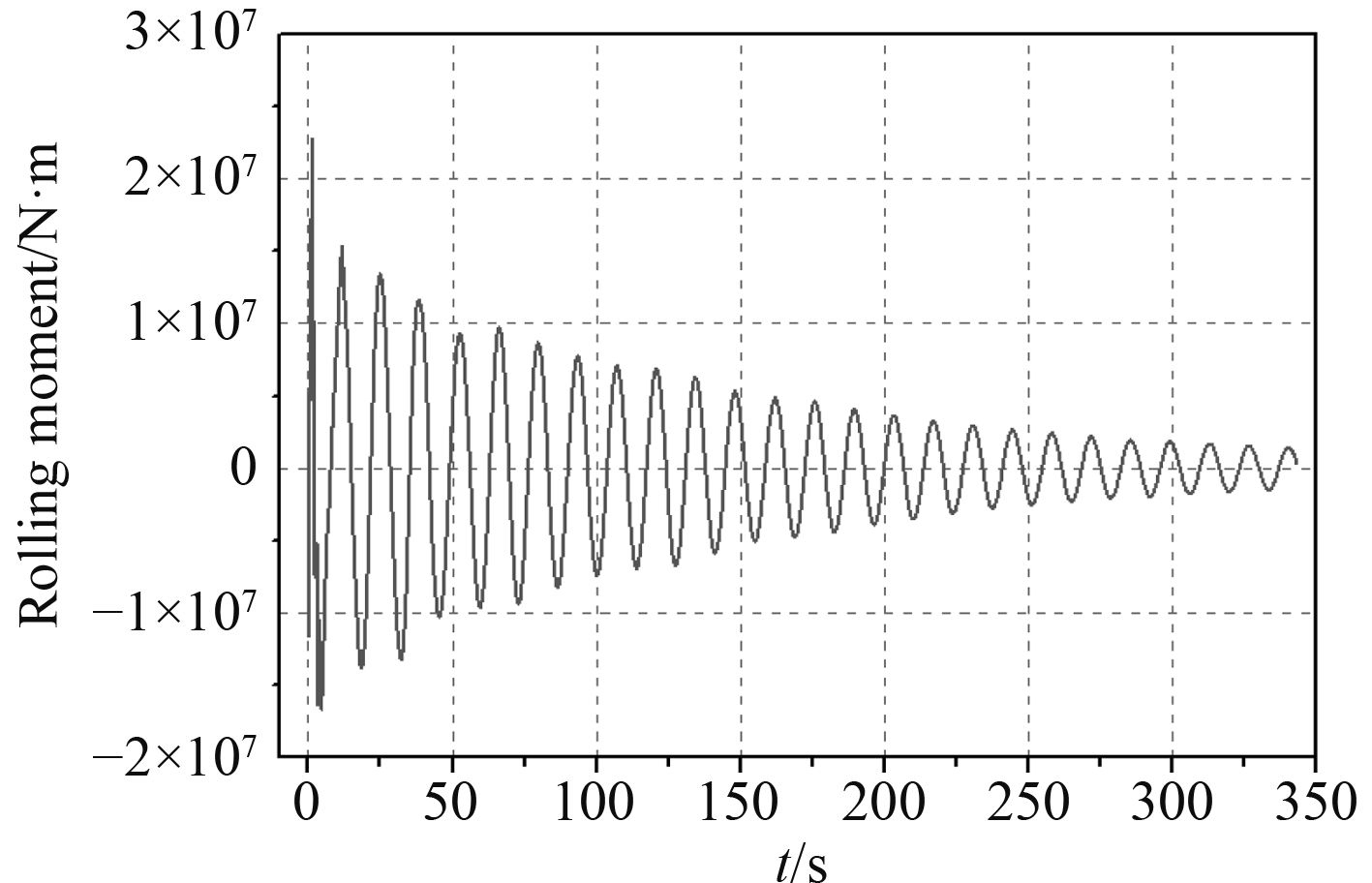
图 10 船舶横倾力矩时历曲线 Fig. 10 Rolling moment curve |
|
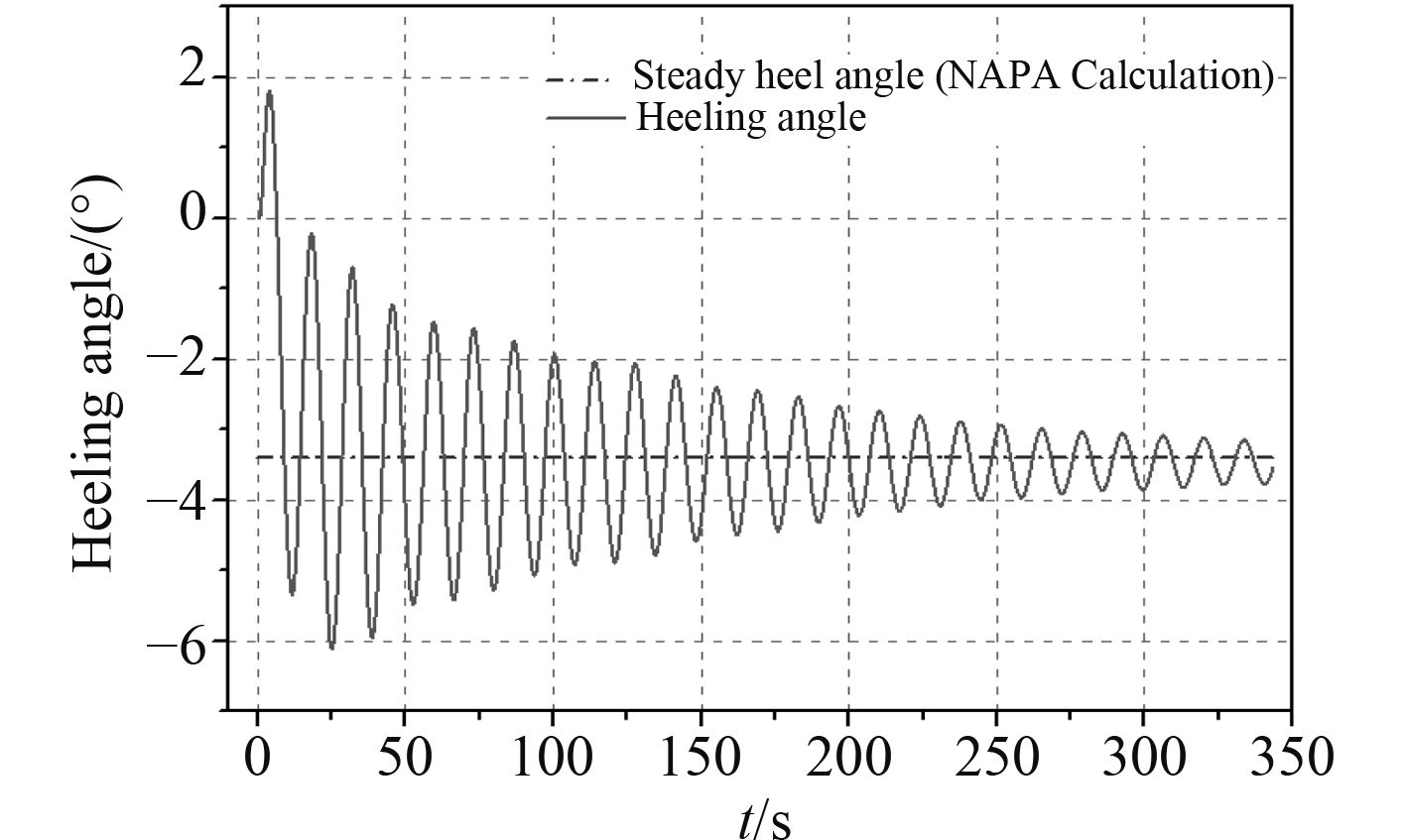
图 11 船舶横倾角时历曲线 Fig. 11 Rolling angle curve |
NAPA软件稳性模块的计算精度得到了各大船级社和设计公司的肯定,将其作为验证工具,结果可信。NAPA计算船舶浮态的方法是假定舱内液面均为水平的准静态方法。由NAPA稳性模块计算得到此客滚船在R6.2单舱室破损情况下最终船舶横倾角为3.4°,吃水增加0.039 m。
如数值模拟结果图9所示,在瞬时进水过程中,可以看到破口水柱射流、进水冲击舱底并溅开、舱内自由液面的波动等瞬态现象;在进水后期,由于进水速度减小,液面趋于平稳,呈近似准静态过程。如图10和图11所示,船舶受到的横倾力矩在初始进水时候非线性波动很大,随后以0为平衡位置呈阻尼衰减正弦趋势。最大瞬时横倾角在第2次波谷值t=25 s处出现,大小为6.12°,是最终稳态横倾角的1.8倍。随着横摇时间增加,船体围绕横摇角–3.4°作阻尼衰减横摇。初始2个波峰之间时间间隔为14.18 s,2个波谷之间时间间隔为13.43 s,整个计算过程横摇周期值约为13.9 s,略大于按照杜埃尔公式估算的完整船舶固有横摇周期12.65 s。
5 结 语本文以STAR-CCM+为软件平台,首次运用重叠网格动网技术在自由漂浮的三维客滚船实体瞬时非对称破舱进水时域模拟中。在模拟研究中,为了提高数值运算的效率且保证计算精度,对重叠区域和背景区域进行疏密有别的网格划分;根据破舱进水过程的物理特点,对边界条件进行合理的设置,选择隐式非定常求解和0.005 s的时间步长。
在与传统准静态结果比较中发现,在船舶不对称进水过程中,瞬时横倾角可能会达到最终稳态横倾角的近两倍。在最终未沉没的情况下,船舶进水中后期阶段以最终稳态为平衡点作阻尼衰减横摇。本研究结果为船舶破舱进水过程的分析提供了一种新的技术路线,通过STAR-CCM+对破舱进水时流体运动情况和船舶浮态进行模拟分析,其结果可为破舱船舶的救援时间预报、救援计划制定和新船设计方案提供数据参考依据,也为后续更复杂的船舶破舱问题研究打下基础。
| [1] | SPOUGE J R. The technical investigation of the sinking of the Ro-Ro ferry EUROPEAN GATEWAY [J]. Transactions of RINA, 1985, 127: 49–72. |
| [2] | SANTOS T A, GUEDES SOARES C. The influence of obstructions on the transient asymmetric flooding of roro ships[C]// 7th International Conference on stability of ships and ocean vehicles. |
| [3] | GAO Zhiliang, VASSALOS D, GAO Qiuxin. Numerical simulation of water flooding into a damaged vessel's compartment by the volume of fluid method[J]. Ocean Engineering, 2010, 37 : 1428–1442. DOI: 10.1016/j.oceaneng.2010.07.010 |
| [4] |
李佳. 船舶破舱浸水的横摇运动时域计算及破舱稳性研究[D]. 上海: 上海交通大学, 2009.
LI Jia. Time domain calculation of damaged ship floating and study of damage stability [D]. Shanghai: Shanghai Jiaotong University, 2009. |
| [5] |
曹雪雁, 明付仁, 张阿漫. 船舶破损进水特性的SPH三维模拟研究[C]//第十六届中国海洋(岸)工程学术讨论会论文集, 2013.
CAO Xue-yan, MING Fu-ren, ZHANG A-man. The SPH 3D simulation study of ship damage and flooding character[C]//The 16th Chinese Ocean Engineering Seminar Collectred Papers, 2013. |
| [6] |
刘强, 段文洋. 舰船破舱进水过程的时域模拟[J]. 舰船科学技术, 2012, 3 (34): 45–49.
LIU Qiang, DUAN Wen-yang. Time-domain simulation of the flooding process of damaged warships[J]. Ship Science and Technology, 2012, 3 (34): 45–49. |
| [7] | FERZIGER J H, PERIC M. Computational methods for fluid dynamics[M]. Berlin: Springer, 1996. |
| [8] | ZHANG Z, ZHAO F, LI B. Numerical calculation of viscous free-surface flow about ship hull[J]. Journal of ship mechanics, 2002, 6 (6): 10–7. |
| [9] | SUHS N E, ROGERS S E, DIETZ W E. PEGASUS 5: An automated pre-processor for overset-gnd CFD[R]. AIAA-2002–3186, 2002. |
 2017, Vol. 39
2017, Vol. 39