在潜艇的概念设计中,潜艇的水动力性能是评价潜艇设计的一个重要指标。因此对于潜艇周围流场的测量和数值仿真,以及后续的水动力性能预报,在潜艇概念设计过程中很重要。潜艇一般有2对尾舵和1对首舵或围壳舵。在很多情况下,安装在潜艇上的首操纵面不可或缺。首操纵面可以独立控制纵倾和潜深。对于在无纵倾情况下进行潜水或者上浮操作时,首操纵面必需[1]。
为了有助于未来先进潜艇的设计,DARPA对Suboff模型进行了一系列实验,让研究者与数值结果进行比较。许多研究者使用数值模拟来研究轴对称的光艇模型以及带各种附体模型的流场。Yang[2]计算在高雷诺数下,带有螺旋桨或者不带螺旋桨以及带各种不同附体的轴对称光艇模型周围的流场。Bull[2]使用不同的求解器、湍流模型和网格拓扑结构研究Suboff AFF-1和AFF-8周围的粘性流场。Yang[4]使用Baldwin-Lomax湍流模型模拟Suboff AFF-1和AFF-8在不同攻角下的尾流。Bensow[3]使用大涡模拟方法,研究Suboff AFF-1和AFF-8周围的流动,并且和实验数据进行对比。张楠[4]模拟了带附体时的潜艇绕流,进行艇型的数值优化研究。邓峰[5]基于CFD对水下回转体高速运动阻力进行预报,实验与数值仿真计算吻合较好。
刘明静[6]对带首舵和带围壳舵潜艇的流场进行数值模拟,结果表明在采用较好的流线型指挥室的情况下,采用首舵形式有利于尾部伴流场的均匀性。赵鹏伟[9]基于湍流强度和耗散率对潜艇尾流进行模拟。
但是绝大部分研究并没有考虑首操纵面的影响。舵安装在首部或者围壳处对整艇影响不同。本文使用数值仿真方法来研究舵安装在首部和围壳处的水动力性能,来流速度为5.93 kn和16 kn。在研究带有舵的模型前,先对Suboff和DTMB舵进行数值模拟验证。然后对带舵模型进行研究,并对仿真结果以及结果产生的原因进行了详细讨论和分析。
1 控制方程和RNG k-ε湍流模型对于不可压缩粘性湍流,使用RANS方程和RNG k-ε来封闭方程。在控制方程中[7],不可压缩流体连续性方程如下:
|
$\frac{{\partial \overline {{u_i}} }}{{\partial x}} = 0,$
|
(1) |
RANS方程有如下形式:
|
$\rho \frac{{\partial \overline {{u_i}} }}{{\partial t}} + \rho \overline {{u_j}} \frac{{\partial \overline {{u_i}} }}{{\partial t}} = - \frac{{\partial \bar p}}{{\partial {x_i}}} + \mu \frac{{{\partial ^2}\overline {{u_i}} }}{{\partial {x_i}\partial {x_j}}} - \rho \frac{{\partial \overline {{{u'}_i}{{u'}_j}} }}{{\partial {x_j}}} + \rho \overline {{f_i}}, $
|
(2) |
湍动能方程:
|
$\frac{{\partial \left( {{\rm{\rho k}}} \right)}}{{\partial t}} + \frac{{\partial \left( {{\rm{\rho k}}\overline {{u_i}} } \right)}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left[ {{a_k}{\mu _{eff}}\frac{{\partial k}}{{\partial {x_j}}}} \right] + {G_k} - \rho \varepsilon ,$
|
(3) |
湍动能耗散方程:
|
$\frac{{\partial \left( {{\rm{\rho }}\varepsilon } \right)}}{{\partial t}} + \frac{{\partial \left( {{\rm{\rho }}\varepsilon \overline {{u_i}} } \right)}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left[ {{a_\varepsilon }{\mu _{eff}}\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right] + \frac{{{C_{1\varepsilon }}}}{k}{C_{2\varepsilon }} - \rho \frac{{{\varepsilon ^2}}}{k},$
|
(4) |
其中:
本研究不带首舵或围壳舵的模型是全附体Suboff模型。Suboff模型的详细尺寸见文献[8]。安装在首部或围壳处的舵来自文献[9]。舵由于安装在Suboff模型上,将其缩放至平均弦长
本文中的系数全部无因次化。舵的阻力、升力系数表达式如下所示:
阻力系数
|
${C_d} = \frac{{{F_d}}}{{\frac{1}{2}\rho {v^2}A}},$
|
(5) |
升力系数
|
${C_l} = \frac{{{F_l}}}{{\frac{1}{2}\rho {v^2}A}},$
|
(6) |
系数定义中,A是中纵剖面投影面积。
Suboff带舵模型的阻力、升力、力矩系数定义如下:
阻力系数
|
${C_d} = \frac{{{F_d}}}{{\frac{1}{2}\rho {v^2}S}}\text{,}$
|
(7) |
升力系数
|
${C_l} = \frac{{{F_l}}}{{\frac{1}{2}\rho {v^2}S}}\text{,}$
|
(8) |
力矩系数
|
${C_m} = \frac{M}{{\frac{1}{2}\rho {v^2}SL}}\text{。}$
|
(9) |
式中:S为Suboff带舵模型的湿表面积。力矩中心点坐标为在潜艇轴线上(0,2.178,0) ,L为艇长。
|
|
表 1 舵的参数 Tab.1 The main parameter of the rudder |
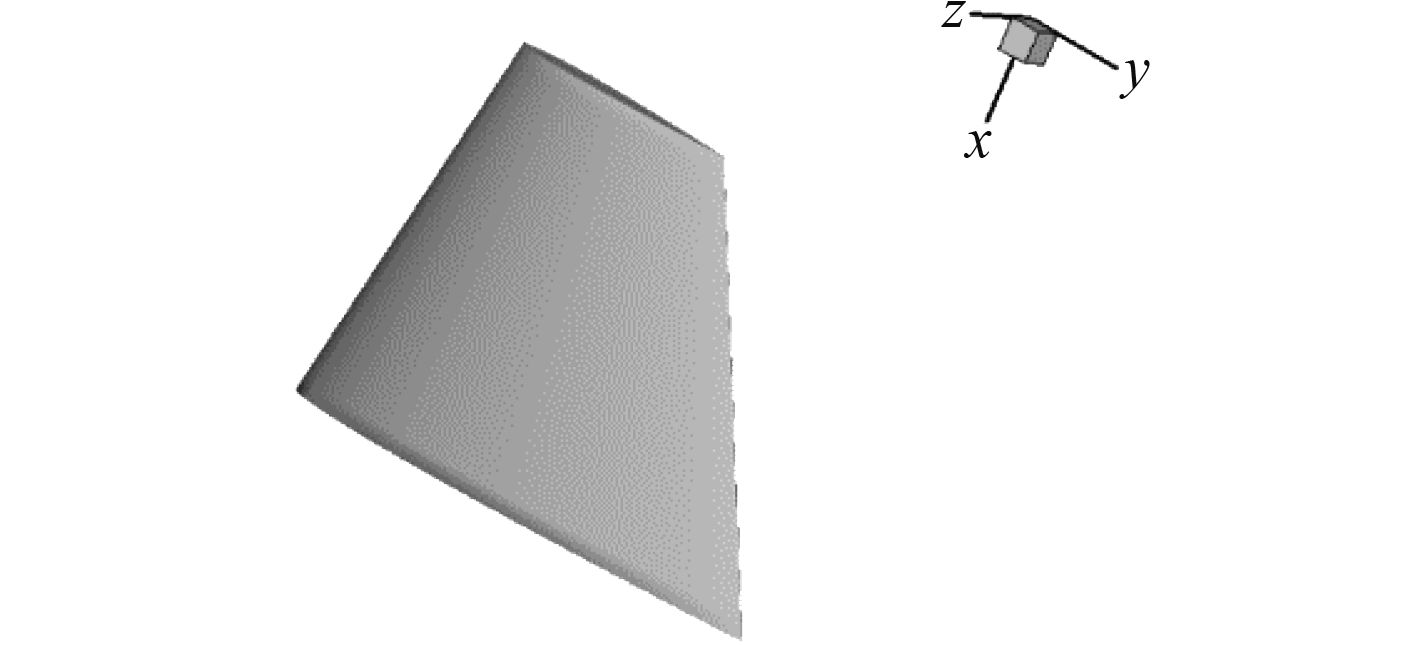
|
图 1 舵外形 Fig. 1 The figure of the rudder |
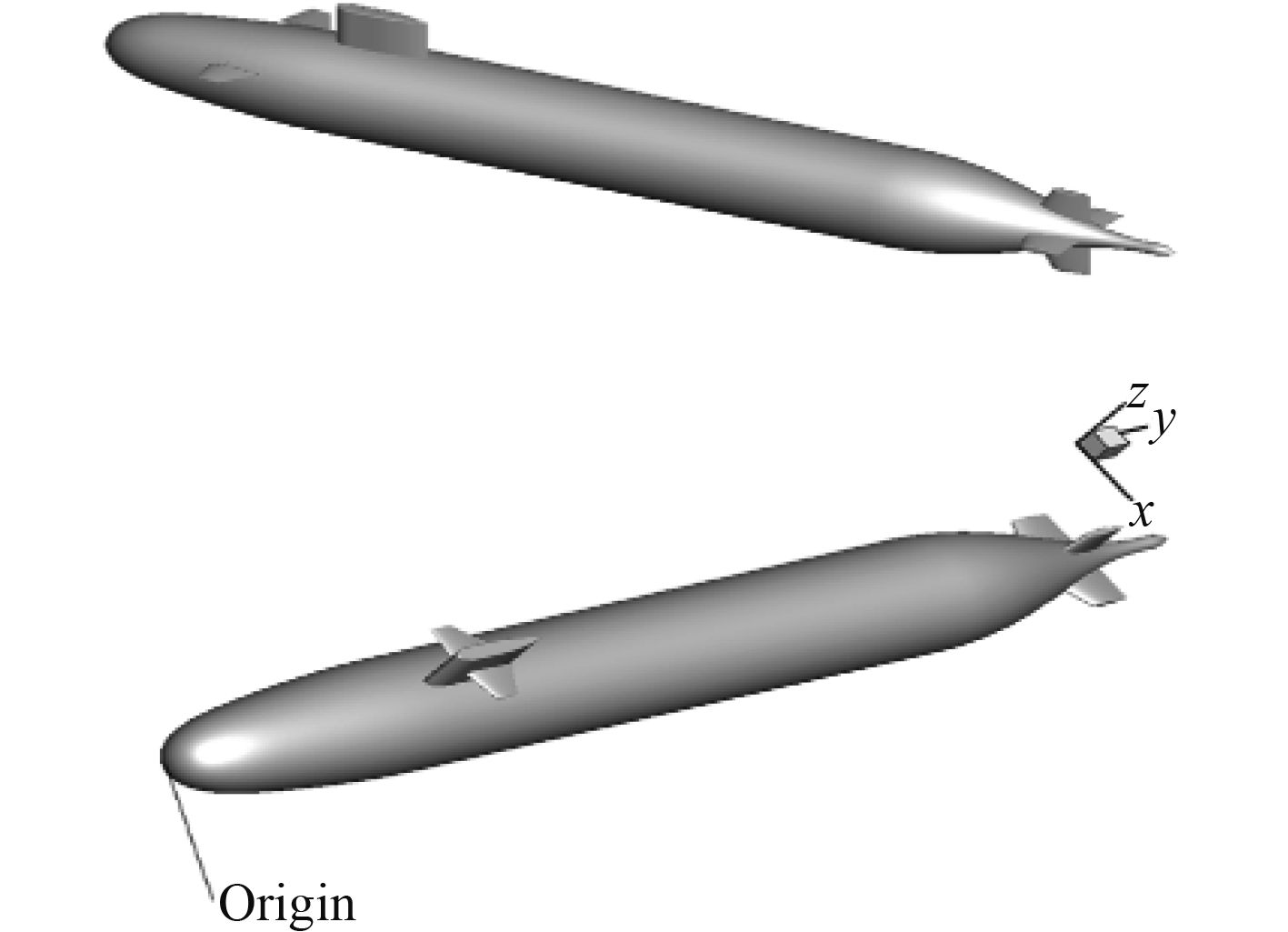
|
图 2 Suboff+首舵和Suboff+围壳舵 Fig. 2 SUBOFF+bow rudder and SUBOFF+sail rudder |
计算域和边界条件如图3所示,计算域为圆柱体,长5L(L为Suboff全长),直径为10 d(d为Suboff最大直径)。中心轴与艇体中心轴重合,进流面距离首部1 L,出流面距离尾部为3 L。
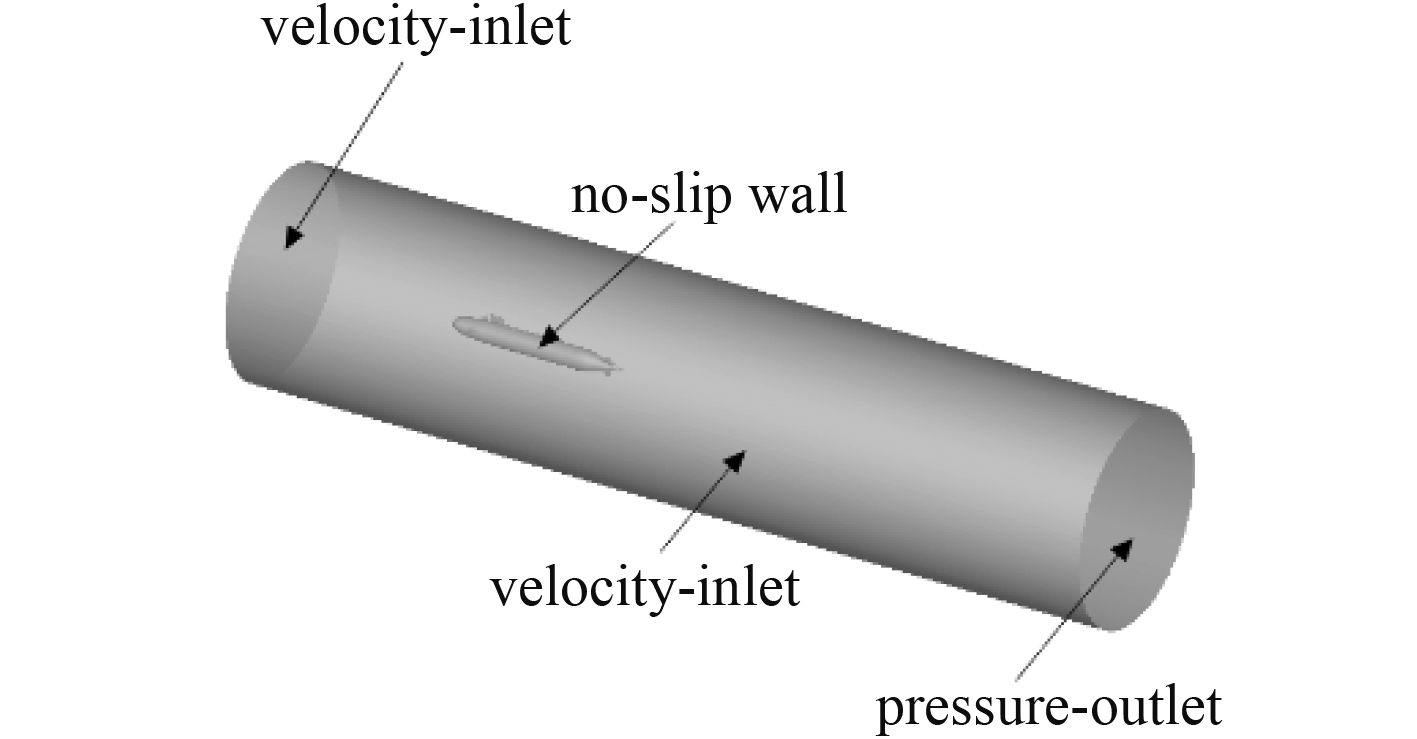
|
图 3 计算流域图以及边界条件 Fig. 3 Computational domain and boundary condition |
坐标轴系统:来流沿着y轴正向,升力方向沿着z轴,纵倾力矩沿着x轴。数值模拟使用有限体积法,RNG k-ε湍流模型。压力方程使用标准格式进行离散化。动量方程、湍流动方程和雷诺应力运输方程使用二阶迎风格式进行离散化。
2.3 数值方法验证和网格独立性在计算带舵模型前,对数值模拟方法进行验证。使用Suboff模型和舵模型来进行验证,计算结果与实验数据[9 – 10]进行比较。数值模拟使用结构化网格,为了有效模拟近壁面的流动,壁面处采用边界层网格加密。无量纲化的从第1层网格到壁面的距离y+,平均值为40。
根据网格独立性验证,最后选择400万网格作为后续研究的基本网格。带首舵的Suboff潜艇模型总网格量为744万,带围壳舵的Suboff潜艇模型总网格量为798万。安装围壳舵和首舵后,尽量保证网格分布和边界层与基本网格一致。400万网格Suboff在16 kn下总阻力为677.6 N,与实验数据675.6 N误差为0.3%。舵平均弦长为0.145 m,来流为16 kn,雷诺数为1.193×106。舵数值模拟的升力系数、阻力系数和实验数据吻合良好。不过应该注意文献[9]强调舵模型安装在平板上,因此有效展弦比近似为几何展弦比的2倍。
3 计算结果和分析 3.1 首舵和围壳舵升阻力特性分析数值仿真的来流速度分为低速5.93 kn和高速16 kn。由于首舵、围壳舵在来流速度为5.93 kn和16 kn时的阻力、升力系数变化规律相同。因此只给出来流速度为16 kn时,围壳舵和首舵阻力、升力的计算结果对比如图4示。因此下面用来进行分析的结果取自16 kn时的计算结果。
首舵和围壳舵的阻力系数相差较小。围壳舵的升力比首舵的升力大,最大相对增量为53.4%,此时攻角为–5°。围壳舵安装在围壳上,围壳平坦的中部面和围壳舵一起组成反映面,也即产生镜面效应。这导致围壳舵的实效展弦比近似为几何展弦比的2倍。在失速角前,翼的展弦比越大,升力系数越大,因为展弦比越大,相比低展弦比翼型,可以更加有效抑制横向流动。
在翼遭遇翼地效应以及维持不变的升力系数,上洗、下洗以及梢尾涡减弱。由于梢尾涡的减弱,处在翼地效应中的翼将会表现出好像展弦比增大一般。翼处在翼地效应中和不处在翼地效应中的升力与攻角关系如图5所示。失速角的下降和翼型有关。但是一般有几度。由于展弦比较小,下洗严重。导致低展弦比翼的有效攻角减下,从而倾向于在更大角度失速,相比较于大展弦比翼。围壳舵有效展弦比的增加以及由于艇体和围壳舵之间产生的轻微翼地效应,使得围壳舵的失速与首舵和敞水舵相比提前。

|
图 4 阻力、升力系数比较,v=16 kn Fig. 4 Comparison of drag, lift coefficient, v=16 kn |
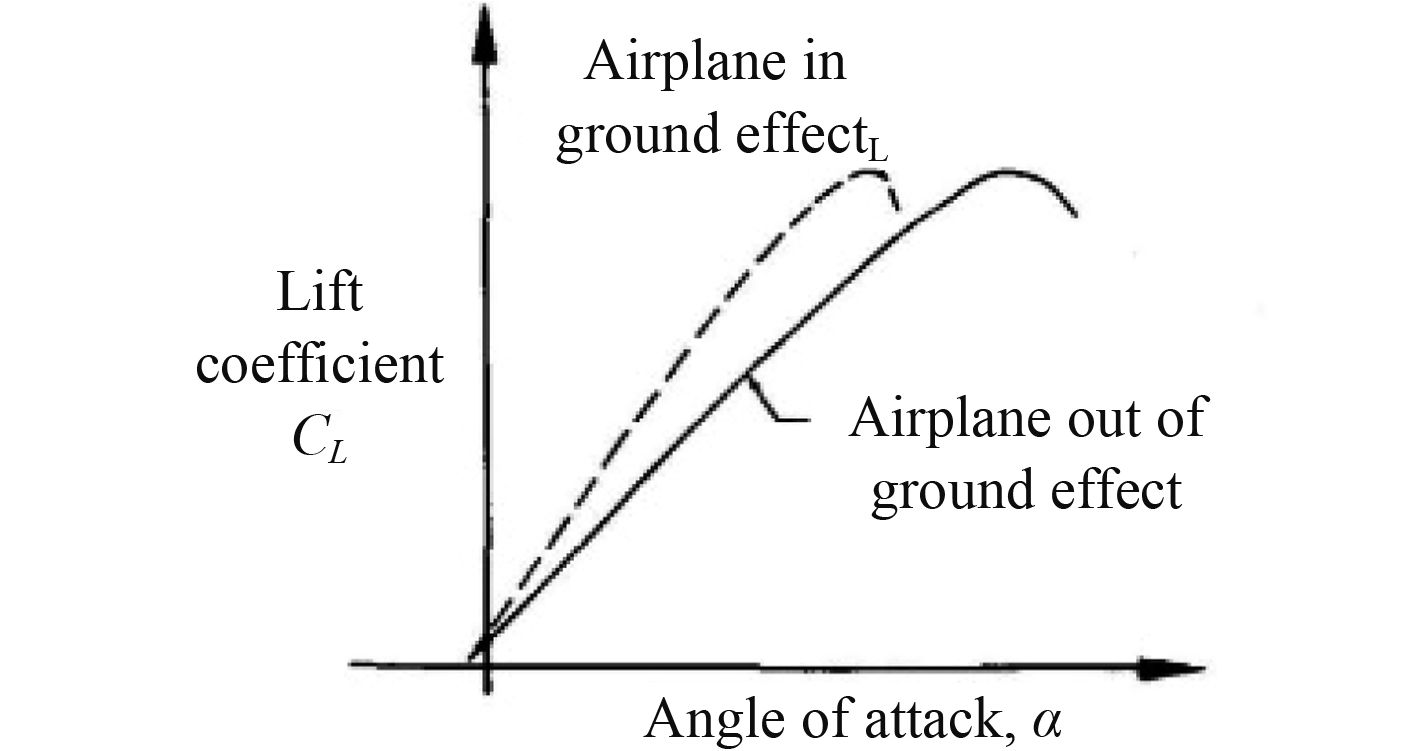
|
图 5 翼有无翼地效应的升力和攻角关系 Fig. 5 The wing in and out of ground effect |
总阻力、总升力、总力矩计算结果的对比如图6~图7所示。由于来流速度5.93 kn和来流速度16 kn的变化规律基本相同。接下来的分析使用来流速度为16 kn时的结果。
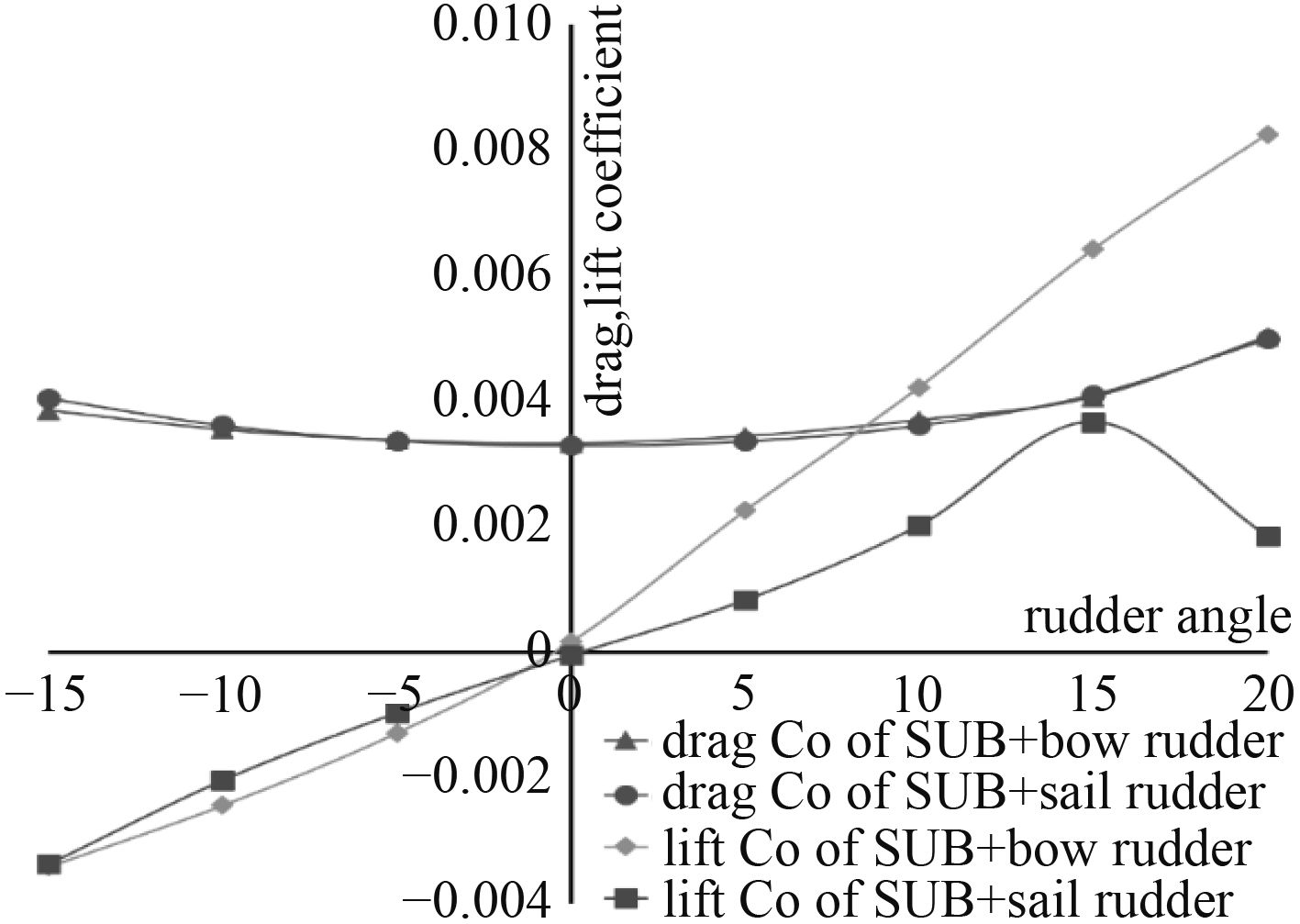
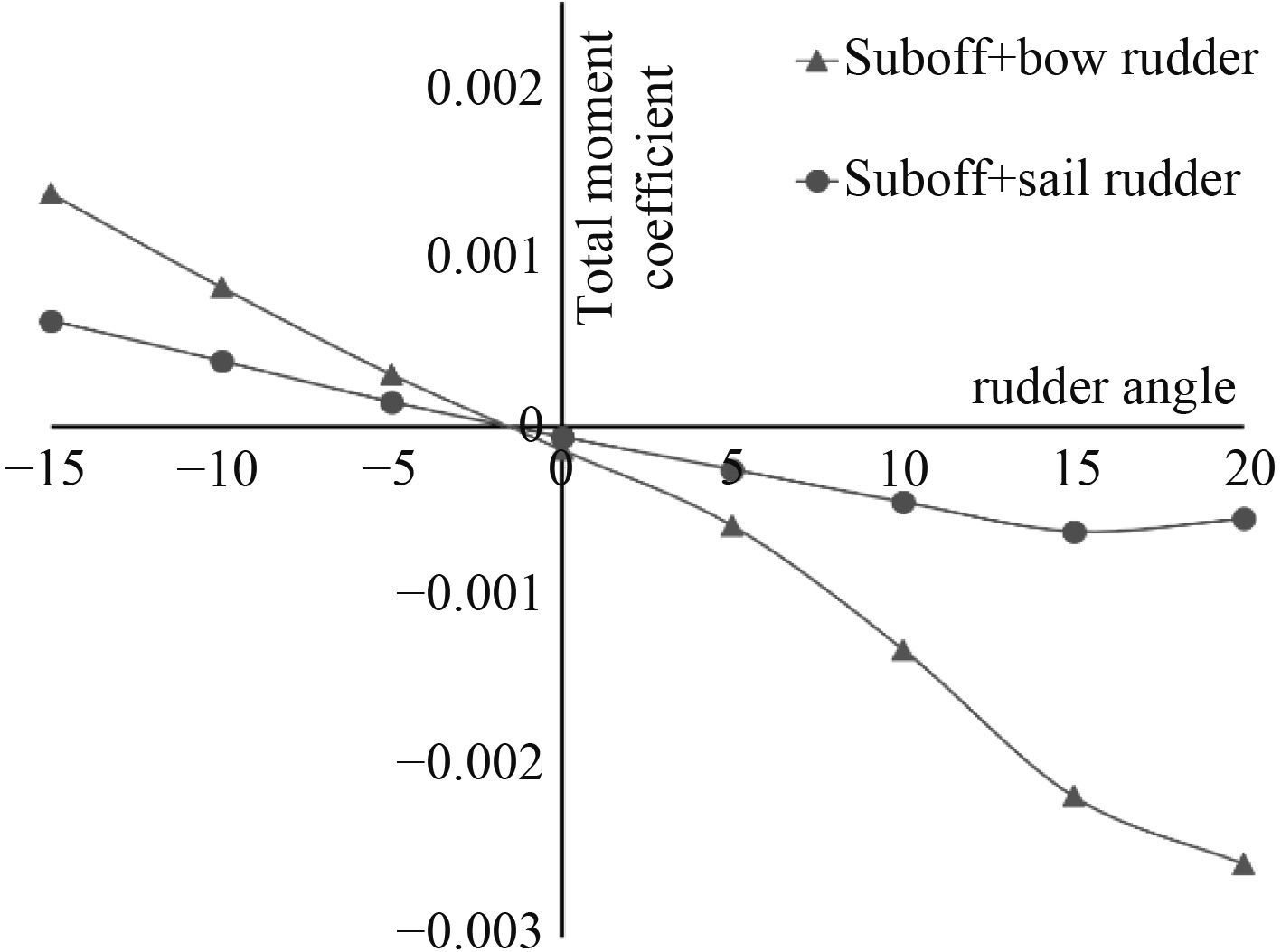
Suboff带围壳舵模型的总阻力和Suboff带首舵模型的总阻力相差很小。Suboff带首舵模型的总升力、总力矩比Suboff带围壳舵模型的总升力、总力矩大。当舵角为5°时,升力最大相对增量为171.5%,
当来流速度为5.93 kn时,带首舵潜艇水动力导数
|
图 6 总阻力、总升力系数对比,v=16 kn Fig. 6 Comparison of total drag, lift coefficient, v=16 kn |
|
图 7 总力矩系数对比,v=16 kn Fig. 7 Comparison of total moment coefficient, v=16 kn |
接下来将从转舵对光艇压力分布以及尾流场影响来分析转首舵时总升力比转围壳舵时总升力大的原因。升力主要由于压差产生,由于粘性产生的升力非常小且基本相同。由上述讨论可知,围壳舵升力比首舵升力大。
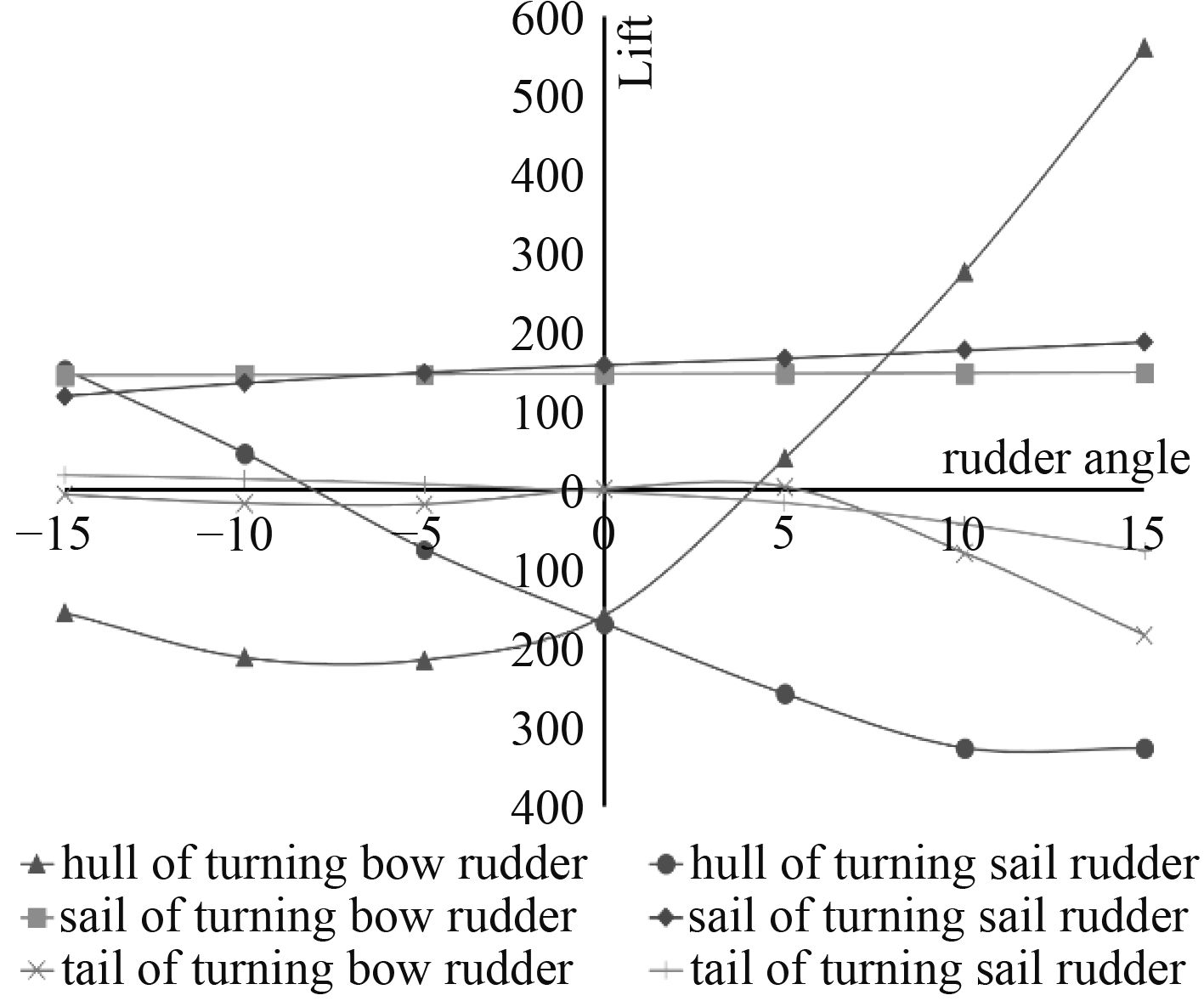
转首舵时光艇体、围壳和尾翼的升力和转围壳舵时光艇体、围壳和尾翼的升力的比较如图8所示。光艇体的升力随着围壳舵舵角的增加减小。当首舵舵角为负值时,光艇体的升力变化较小,当舵角为正值时,光艇体的升力随着舵角的增加而增加,这是首舵安装位置,对光艇的影响表现出不对称极其明显。
|
图 8 光艇体、围壳和尾翼的升力,v=16 kn Fig. 8 Lift of hull, sail, tail, v=16 kn |
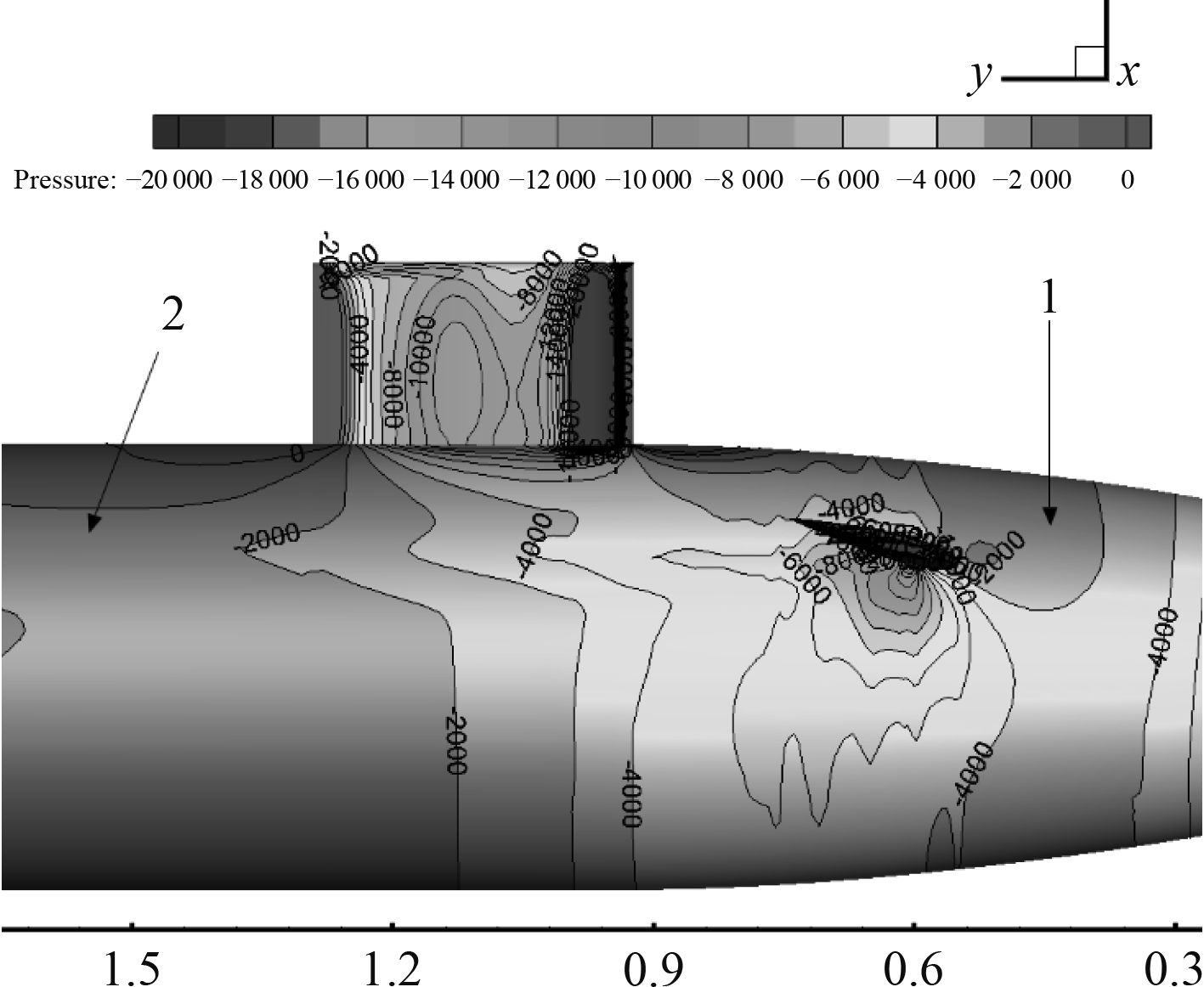
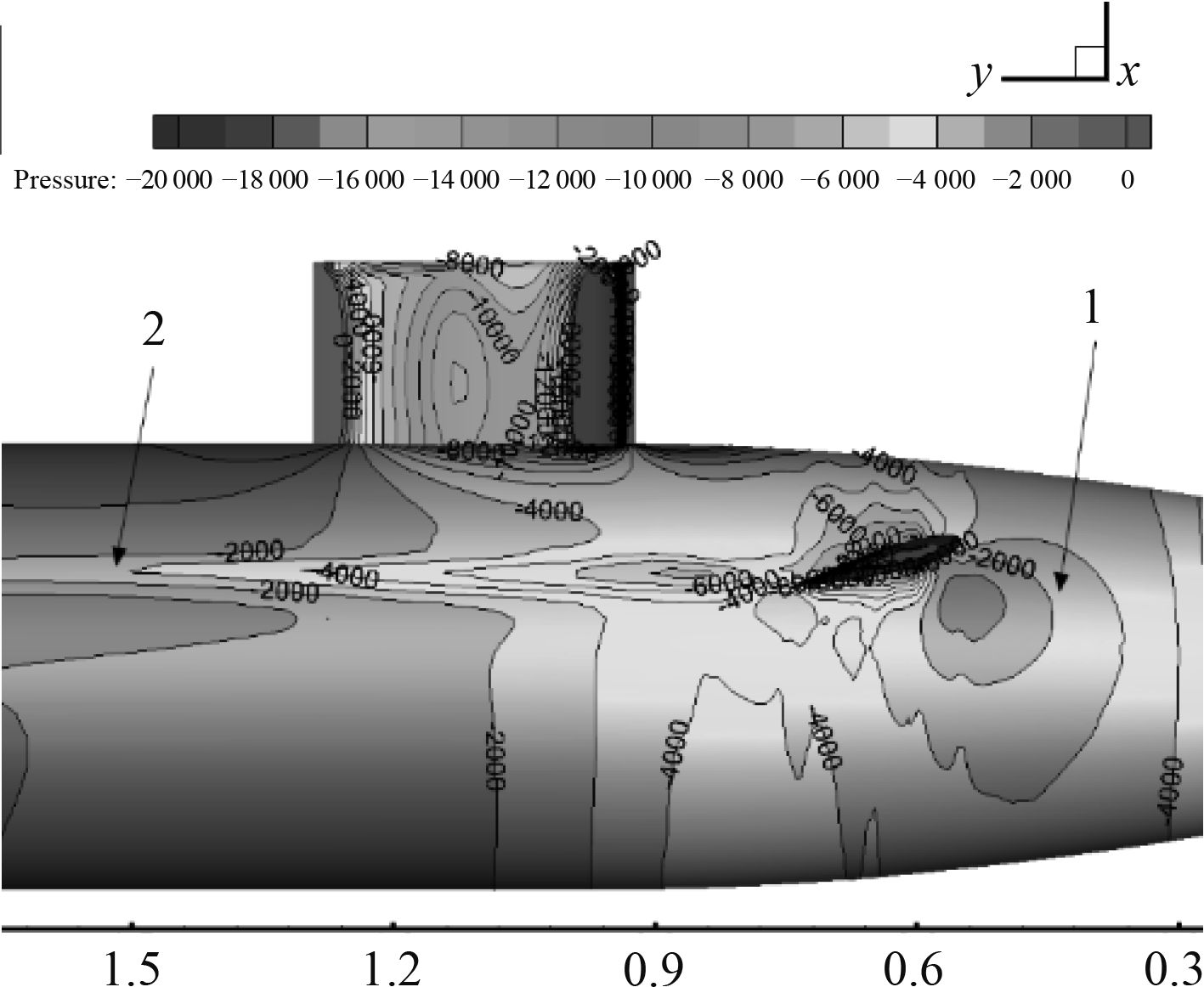
图9和图10显示当首舵舵角为–15°~15°艇体表面压力分布。图9和图10中艇体1、2处压力都表现出明显的变化。首舵舵角为–15°时,1处的压力变化产生负升力。2处压力变化产生正升力。这导致首舵舵角为–15°时光艇体升力和首舵舵角为0°时光艇体升力相对变化较小。首舵舵角为15°时,1处的压力变化产生正升力。2处压力变化产生正升力。这导致首舵舵角为15°时光艇体升力比首舵舵角为0°时光艇体升力大。15°时光艇体升力相对于0°时光艇体升力增大254%,且是从负升力变为正升力。
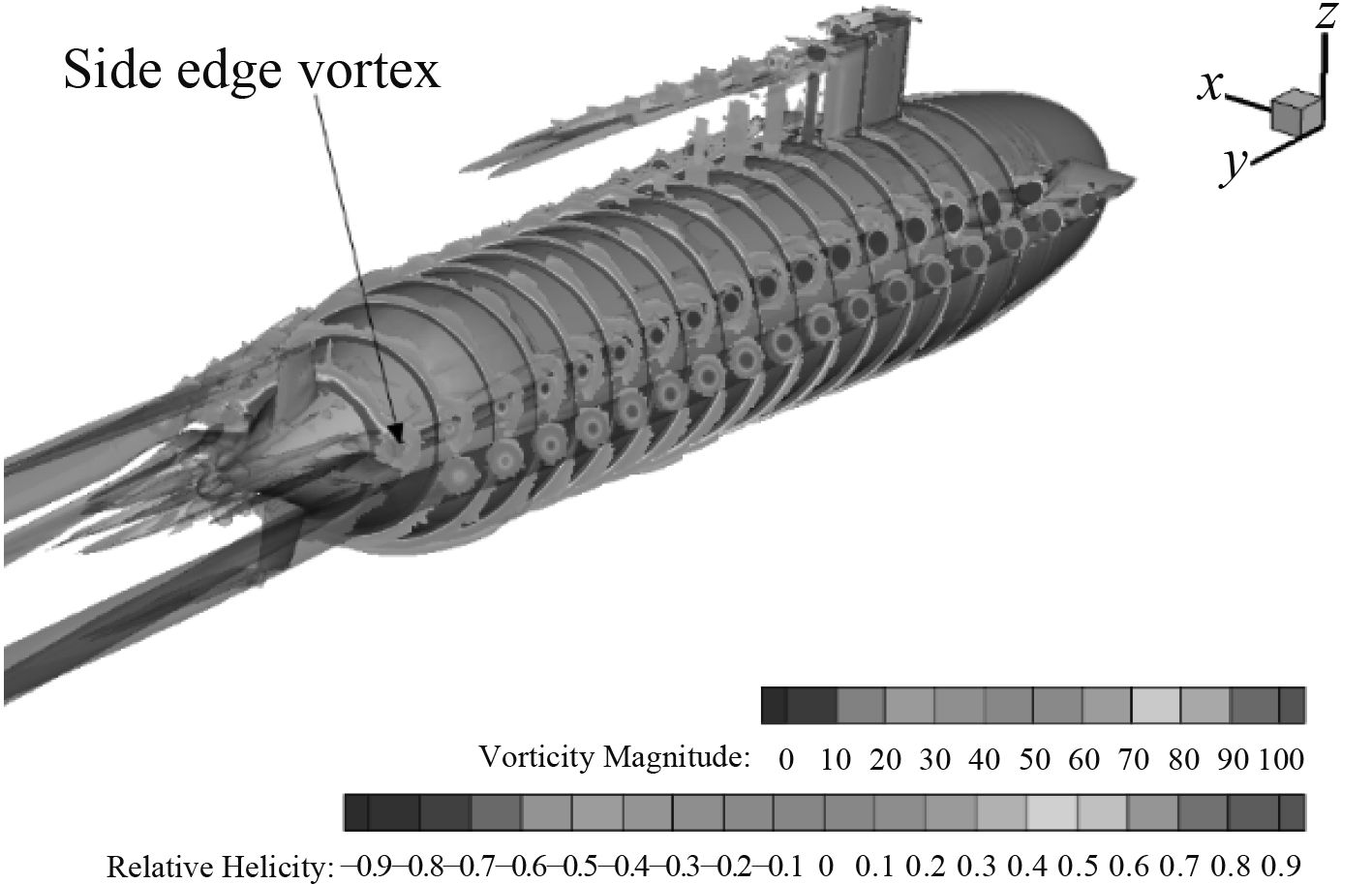
图9和图10中2处都有沿艇长方向的的压力变化,图10中2处压力变化尤其明显。图11显示当首舵舵角为15°时的涡结构。切面用涡强度进行染色。一系列涡强度的切面可以很好地反映首舵由于转角度产生的侧缘涡的发展过程。随着舵角增大,上表面和下表面的压差变大,下洗翻卷运动更加严重。因此侧缘涡延伸更远。首舵根弦面产生的侧缘涡贴近艇体表面,从而导致图10中2处压力明显的变化。
由于围壳舵所在安装位置,正负角度对光艇影响有略微不同,差异不明显。选取围壳舵舵角为15°进行分析。图12显示艇体表面压力分布,此时围壳舵舵角15°。图12中,围壳舵表现为引导来流冲击光艇与围壳交界处,引起1处压力发生及其明显的变化。2处压力变化,也是由于围壳舵转角度所产生的侧缘涡引起的。涡结构图如图13示,由于围壳舵离艇体相对较远,侧缘涡对艇体表面压力影响相对较小。1处的压力变化产生负升力,且1处压力变化在升力变化中占据主导地位。2处压力变化产生正升力。从而当围壳舵舵角为15°时,压力变化表现为光艇体产生更大负升力。
|
图 9 Suboof+首舵模型压力分布,舵角为–15° Fig. 9 Pressure distribution of the Suboof+ bow rudder model, bow rudder angle –15° |
|
图 10 Suboof+首舵模型压力分布,舵角为15° Fig. 10 Pressure distribution of the Suboof+ bow rudder model, bow rudder angle 15° |
|
图 11 涡结构,首舵舵角为15°,Q准则涡量等值面,Q=80 Fig. 11 Vortex structure, bow rudder angle 15°, iso-surface of Q-Criteria atQ=80 |

|
图 12 Suboof+围壳舵模型压力分布,舵角为15° Fig. 12 Pressure distribution of the Suboof+ sail rudder model, sail rudder angle 15° |

|
图 13 涡结构,围壳舵舵角为15°,Q准则涡量等值面,Q=80 Fig. 13 Vortex structure, sail rudder angle 15°, iso-surface of Q-Criteria atQ=80 |
围壳、尾翼的升力变化相对光艇体的变化较小。但是值得注意尾翼在首舵舵角和尾舵舵角为15°时产生了相对较大的负升力。尾水平舵较大负升力产生的原因均为首舵或者围壳舵转角后,产生的侧缘涡,发展到尾部引起的,现选取首舵转角15°情况进行分析。围壳舵转角15°,分析情况类似。
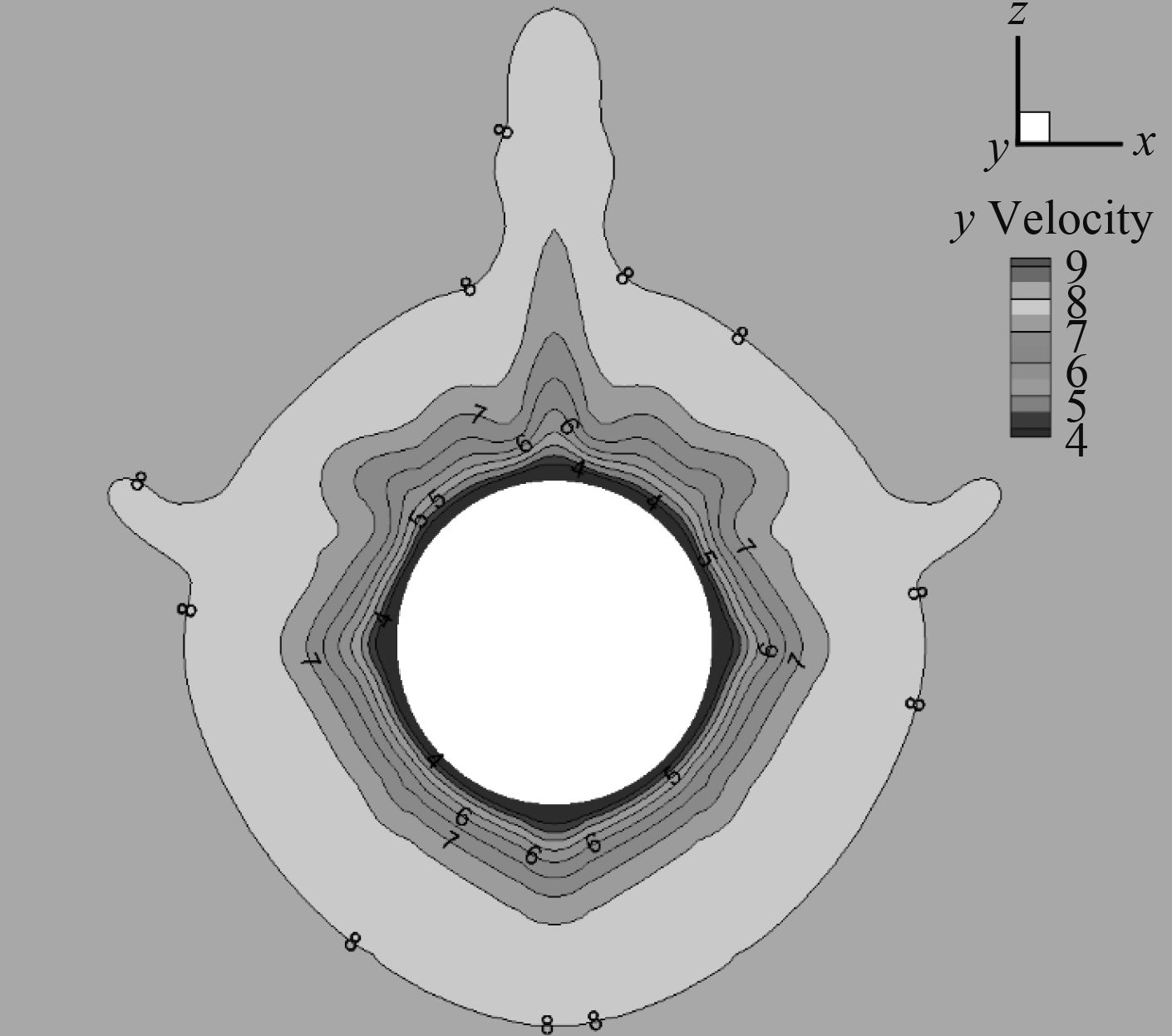
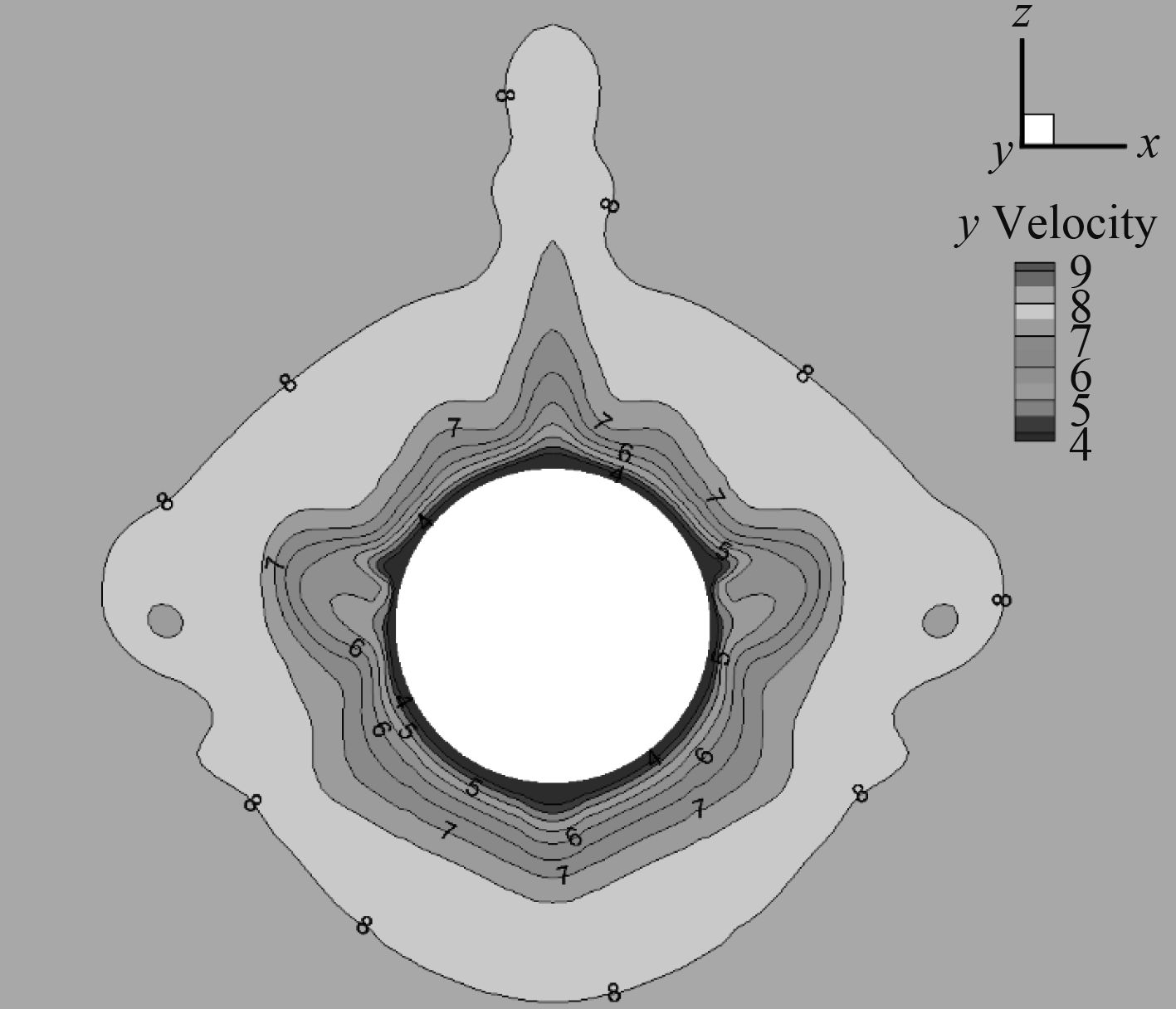
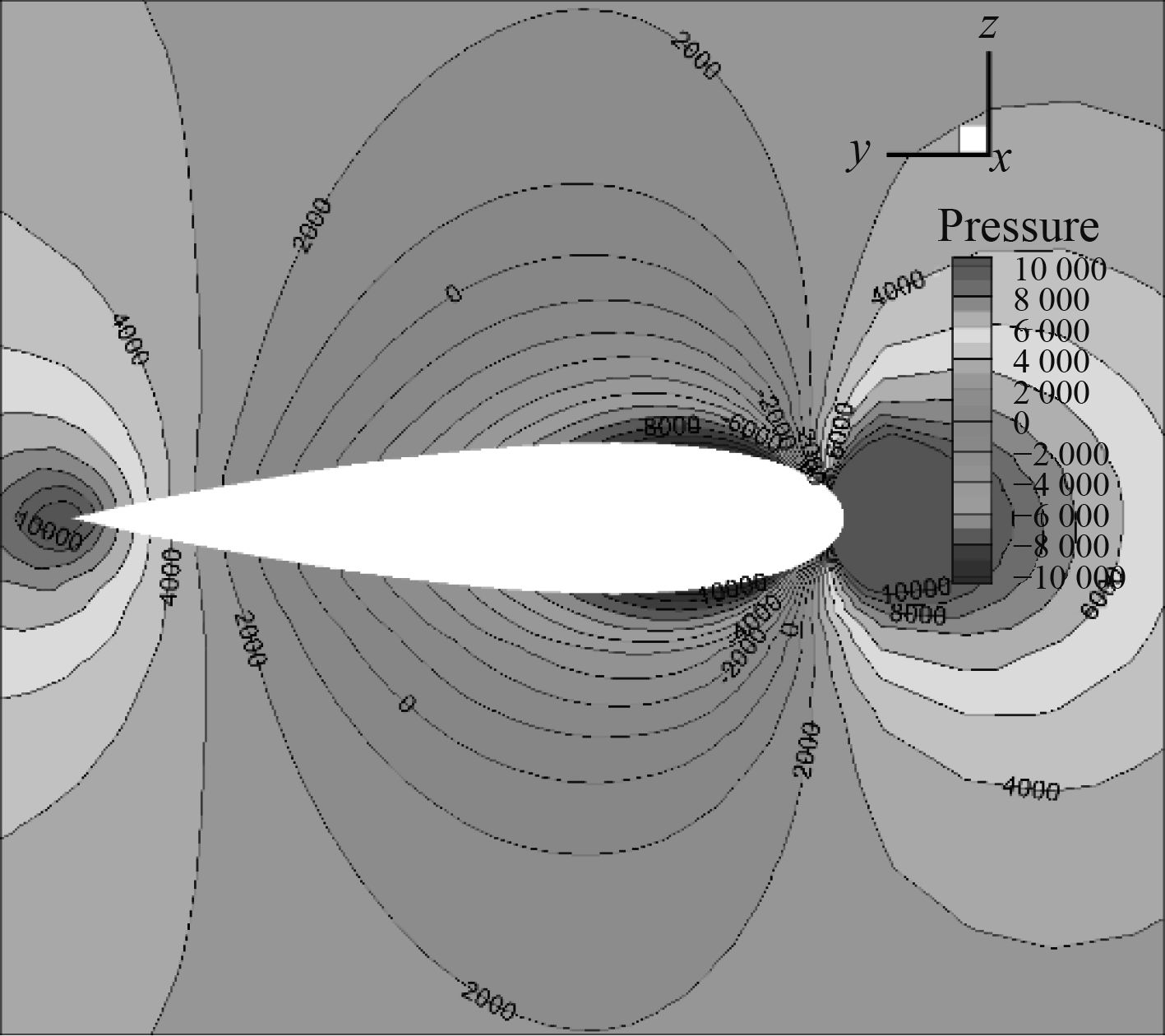
图14和图15为y=3.8 m切面Y方向速度等值线图,当首舵舵角为0°和15°时。2个图表明改变首舵舵角明显改变了水平尾翼前的的流场。图16显示切面(x=–0.2 m)在水平尾翼附近的Y方向速度分布,当首舵舵角为0°和15°时。图16表明水平尾翼周围Y方向速度发生变化,尤其是上表面周围变化明显。图17和图18显示切面(x=–0.2 m)在水平尾翼周围压力分布,当首舵舵角为0°和15°时。图17和图18对比表明上表面的压力发生明显改变。从而压力差产生,产生负升力。
图11显示当首舵舵角为15°时的涡结构。从图中可以看出首舵产生的侧缘涡改变了尾部流场,对于水平尾翼有直接影响。侧缘涡导致了水平尾翼周围Y方向速度分布发生了改变,从而压力发生改变,产生压力差,最后产生负升力。
虽然围壳舵的升力比首舵升力大。在各种因素综合作用下,转首舵时Suboff+首舵模型的总升力比在转围壳舵时Suboff+围壳舵模型的总升力大。
|
图 14 y=3.8 m切面轴向速度等值图,首舵舵角为0° Fig. 14 Axial velocity contour at y=3.8 m, bow rudder angle 0° |
|
图 15 y=3.8 m切面轴向速度等值图,首舵舵角为15° Fig. 15 Axial velocity contour at y=3.8 m, bow rudder angle 15° |

|
图 16 2D切面(x=–0.2 m)水平尾翼周围Y 方向速度分布 Fig. 16 2D slice (x=–0.2 m) Y Velocity distribution around horizontal tail |
|
图 17 2D切面(x=–0.2 m) 水平尾翼周围压力度分布,首舵舵角为0° Fig. 17 2D slice (x=–0.2 m) pressure distribution around horizontal tail, bow rudder angle 0° |

|
图 18 2D切面(x=–0.2 m) 水平尾翼周围压力度分布,首舵舵角为15° Fig. 18 2D slice (x=–0.2 m) pressure distribution around horizontal tail, bow rudder angle 15° |
将Suboff和DTMB舵的仿真结果与实验数据进行对比,验证本文所使用的CFD方法可靠。接下来研究将舵安装在潜艇不同位置。计算结果显示围壳舵升力比首舵升力大,是由于围壳和围壳舵构成的反映面模型(即镜面效应)以及翼地效应造成的。
转首舵和围壳舵对于艇体压力分布有显著影响。转首舵对于总的升力有正面影响,而转围壳舵对于总的升力有负面影响。因此转首舵时总升力比转围壳舵时总的升力大。首舵和围壳舵产生的侧缘涡对于尾部流场也有较大影响,直接体现在对于水平尾翼周围流场的影响,当围壳舵和首舵舵角为15°时,水平尾翼产生相对较大的负升力。
| [1] | BURCHER R, RYDILL L J. Concepts in submarine design [M]. Cambridge University Press, 1995. |
| [2] | BULL P. The validation of CFD predictions of nominal wake for the SUBOFF fully appended geometry[C]//21st Symposium on Naval Hydrodynamics, June. 1996: 1061–1076. |
| [3] | BENSOW R, PERSSON T, FUREBY C, et al. Large eddy simulation of the viscous flow around submarine hulls[C]//25th ONR Symposium on Naval Hydrodynamics. 2004. |
| [4] |
张楠, 沈泓萃, 姚惠之. 潜艇阻力与流场的数值模拟与验证及艇型的数值优化研究[J]. 船舶力学, 2005, 01 : 1–13.
ZHANG Nan, SHEN Hong-cui, YAO Hui-zhi. Validation of numerical simulation on resistance and flow field of submarine and numerical optimization of submarine hull form[J]. Journal of Ship Mechanics, 2005, 01 : 1–13. DOI: 10.3969/j.issn.1007-7294.2005.01.001 |
| [5] |
邓峰, 戴余良, 陈志法, 等. 基于CFD的水下回转体高速运动阻力预报精度影响研究[J]. 舰船科学技术, 2016, 38 (03): 22–26.
DENG Feng, DAI Yu-liang, CHEN Zhi-fa, et al. Research on resistance forecast accuracy of high-speed underwater revolving object based on CFD[J]. Ship Science and Technology, 2016, 38 (03): 22–26. |
| [6] |
刘明静, 马运义, 吴军. 潜艇艏舵绕流场的数值模拟[J]. 中国舰船研究, 2010, 05 : 40–43.
LIU Ming-jing, MA Yun-yi, WU Jun. Numerical Simulation on the Flow Around Fore Hydroplane of Submarine[J]. Chinese Journal of Ship Research, 2010, 05 : 40–43. DOI: 10.3969/j.issn.1673-3185.2010.04.009 |
| [7] | YAKHOT V, ORSZAG S A. Renormalization-group analysis of turbulence[J]. Physical review letters, 1986, 57 (14): 1722. DOI: 10.1103/PhysRevLett.57.1722 |
| [8] | GROVES N C, HUANG T T , CHANG M S. Geometric characteristics of DARPA (Defense Advanced Research Projects Agency) SUBOFF Models (DTRC Model Numbers 5470 and 5471)[R]. David Taylor Research Center Bethesda md Ship Hydromechan-ICS DEPT, 1989. |
| [9] | WHICKER L F, FEHLNER L F. Free-stream characteristics of a family of low-aspect-ratio, all-movable control surfaces for application to ship design[R]. David Taylor Model Basin WASHINGTON DC, 1958. |
| [10] | LIU H L, HUANG T T. Summary of DARPA SUBOFF experimental program data[R]. Naval Surface Warfare Center Card-erock DIV BETHESDA MD Hydromechanics Direc-Torate, 1998. |
| [11] | HURT H H. Aerodynamics for naval aviators [M]. Skyhorse Pub. 1965. |
 2017, Vol. 39
2017, Vol. 39
