2. 高新船舶与深海开发装备协同创新中心,上海 200240
2. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai 200240, China
潜水器是探索深海的重要工具,目前研究人员对于开发新型高性能深潜器的需求日益突出。而作为深潜器结构中核心部分的水下耐压结构,对其优化设计,探寻新的耐压结构的最优拓扑形式有着重大的应用价值。在传统的耐压结构的设计中,形成了在浅水中采用圆柱形耐压壳,在深水中采用球形耐压壳的固定观念。如我国 7 000 m 载人深潜器“蛟龙”号的耐压结构部分就选用了钛合金球形耐压壳。但随着科学技术的发展与复合材料的应用,这些传统的观念被打破。在 2009 年,由美国伍兹霍尔海洋研究所研制的“海神”号无人潜水器成功到达了马里亚纳海沟的 10 902 m 深处[1]。而为了实现“海神”号的最轻化,同时保证足够的结构强度,其耐压结构选用了质量轻、强度高的陶瓷材料,并且其形状不再是传统的球形,而是圆柱形的耐压壳。目前,国外开展了基于复合材料的耐压结构优化设计研究,由于复合材料的轻质,未来基于复合材料的耐压结构将成为潜器设计的重要发展方向。
|
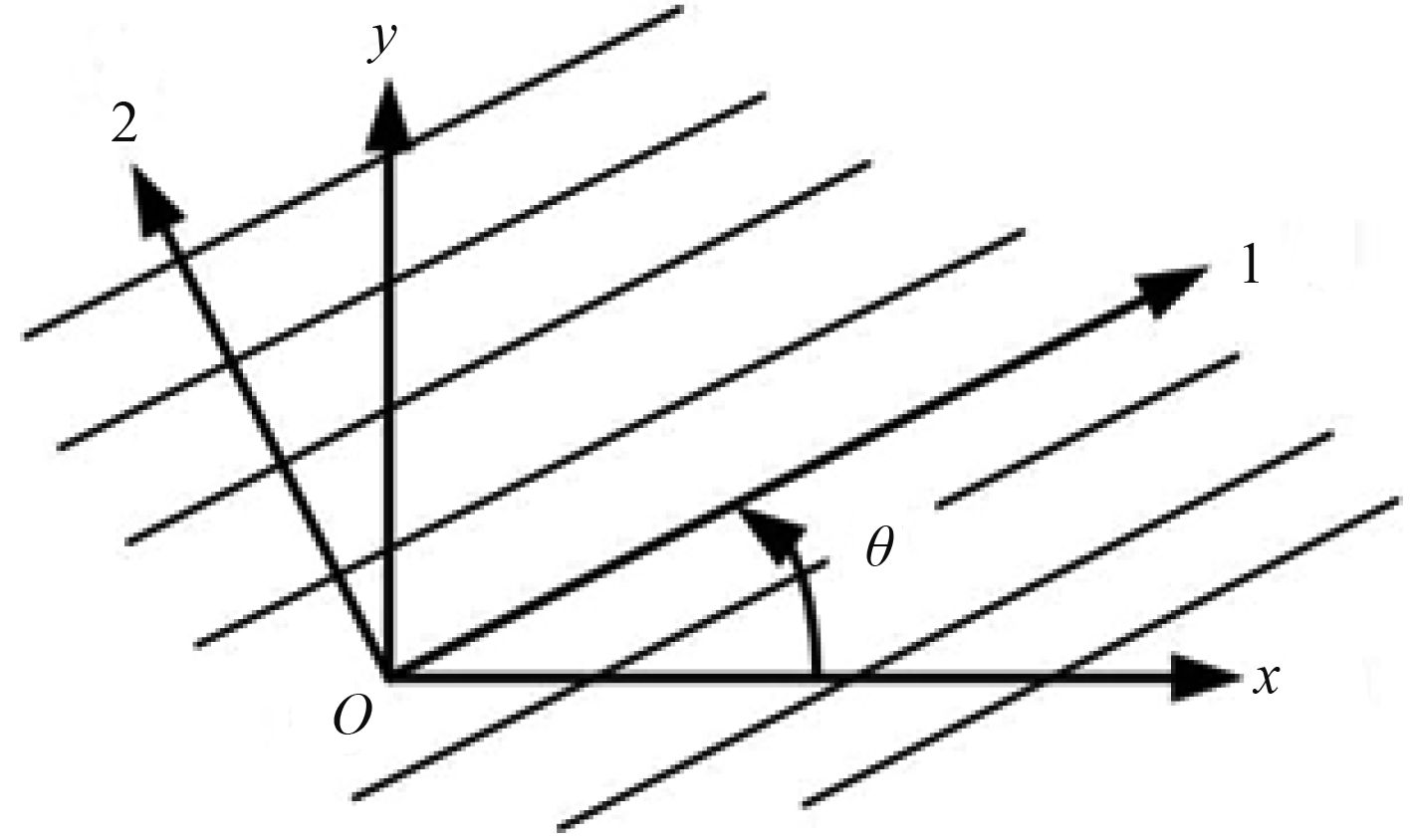
图 1 材料主向坐标系与自然坐标系 Fig. 1 Principle coordinate system of material and natural coordinate system |
通过陶瓷材料在 11 000 m“海神”号深潜器的应用可以发现,复合材料的使用造成了水下耐压结构的巨大改变,而为了能探究复合材料究竟对于耐压结构的设计产生如何的影响,就需要一种方法能够计算基于复合材料的结构设计模型。采用拓扑优化方法,能够直观地模拟材料的最优分布,对于探寻基于复合材料的耐压结构最优拓扑形式有着重要的参考意义。
1 复合材料拓扑优化设计拓扑优化最开始产生于 20 世纪初的 Michell 桁架[2]的设计中,之后在 1988 年 Bendsoe 与 Kikuchi[3]在连续结构设计中提出均匀化方法后得到了快速发展,并且延伸到诸多其他学科领域中。在拓扑优化的方法中,均匀化方法和变密度法[3 – 7]作为最具代表性的方法被广泛地应用,而在两者之中,变密度法由于其插值模型在算法上更易实现,是更具有工程应用前景的一种拓扑优化方法。密度法插值模型的基础是由 Mlejnek 与 Schirrmacher[8]提出的一种对结构材料密度的幂次惩罚模型,他们通过在 0 – 1 的离散结构优化问题中引入连续设计变量,并加入中间密度的惩罚项,将问题转变为连续结构优化问题。之后,Sigmund 与 Bendsoe[9 – 10]提出了一种基于正交各向同性材料的密度幂指数形式的变密度插值方法(SIMP),它将单元密度与材料的弹性模量之间建立起联系,从而减少了设计变量,简化了优化过程。虽然拓扑优化方法已经被应用在了很多工程设计中,但其中很少有关于拓扑相关载荷的优化。与固定载荷的优化问题不同,在拓扑相关载荷的优化设计中,载荷的方向与位置处于随着结构边界变化而改变,如何确定拓扑相关载荷作用的加载面是解决这类问题的关键。在 Maute 与 Ramm[11]提出的等值线概念的基础上,Hammer 与 Olhoff[12]引入了1条等体积密度曲线来作为加载面。而 Du 与 Olhoff[13]提出了一种修正的等值线技术,在其文章中,还讨论了载荷灵敏度与周边单元的关系,并指出单元内的加载面只受到相邻单元的密度的影响,从而大大减少了灵敏度分析的计算量。在以往的拓扑优化研究中,被优化的结构多是各向同性材料,有关复合材料的拓扑优化的研究很少。相比于传统的各向同性材料,复合材料由于其自身的强度高、刚度大等特点,将复合材料用于拓扑优化中,可能会出现未知的特殊效果。而为了能解决基于复合材料的拓扑优化问题,Lee 等[14]修改了拓扑优化中的单元刚度矩阵,以此来适应正交各向异性材料的情况。在拓扑优化过程中,为了避免拓扑优化中出现多孔材料、棋盘格、网格依赖性等数值不稳定的现象,同时保证优化的效果及效率,往往需要用到灵敏度过滤技术。Sigmund 提出了一种距离加权的灵敏度过滤方法,它能有效地消除大部分数值不稳定的现象,但它往往不能得到完全离散的优化结果。为了获取清晰的边界,有很多不同的灵敏度过滤公式被引入拓扑优化问题中,包括 Borrvall 提出的修正的灵敏度过滤方法,平均灵敏度过滤方法,考虑密度梯度的灵敏度过滤方法[15 – 17]等。对于不同的优化问题,能达到最佳过滤效果的方法往往也不会完全相同,因此,在拓扑优化中需要寻找适合的灵敏度过滤方法。本文的研究是基于文献[14]将 SIMP 模型应用于复合材料拓扑优化的思路,推导复合材料的等效单元刚度矩阵,来实现复合材料的拓扑优化。并且将此方法用于水下耐压结构的最优拓扑形式的探究中,分析复合材料对于拓扑优化结果的影响。
2 拓扑优化数学模型本文从最简单的结构拓扑优化问题开始研究,即在给定体积约束下使得结构具有最小的柔顺度。设有给定的设计区域 Ω,将其离散成 N 个有限单元,根据 SIMP 模型,对于各向同性材料[18],每个单元具有相对密度
|
${E_e} = E\left( {{\rho _e}} \right) = \rho _e^p{E_0},0 \leqslant {\rho _e} \leqslant 1,e = 1, \cdots ,N\text{。}$
|
(1) |
式中:E0 为固体材料的弹性模量;p 为惩罚系数,在本文中取为 3。
在这个设计问题中,连续体结构最小柔顺度的优化模型为:
|
$\begin{aligned}\mathop {\min }\limits_\rho {\rm{: }}C\left( {\rho} \right) =& \displaystyle {{{U}}^{\rm T}}{{KU}} = \sum\limits_{e = 1}^N {{u}_e^{\rm T}{{k}_e}{{u}_e}}\text{,} \\& {\rm{s}}{\rm{.t}}{\rm{. : }}{{F = KU}}\text{,}\\& {\rm{: }}V\left( \rho \right)/{V_0} = volf\text{,}\\& {\rm{: 0 < }}{\rho _{\min }} \leqslant {\rho _e} \leqslant 1\text{。}\end{aligned}$
|
(2) |
式中:ρ 为单元相对密度构成的矩阵;K,F 和 U 分别为总体刚度矩阵、载荷矩阵和位移矩阵;ue 为单元的位移矩阵;
使用 SIMP 模型来求解式(2),原本基于离散变量的设计问题转化为基于连续变量的优化问题。本文使用等值线方法[12 – 13]作为边界搜索方法来寻找拓扑变化相关的压力加载面,而由于设计变量数目多,采用移动渐近线方法(MMA)[19]来求解更新设计变量。本文采用平均灵敏度过滤方法[16]与考虑密度梯度的敏度过滤方法[17]相结合的灵敏度过滤方法。
3 复合材料的单元刚度矩阵本文研究基于纤维增强型复合材料层合板的拓扑优化问题,由于复合材料层合板的厚度相较于长宽很小,故可以将其视为平面应力板。坐标系的设定如图 1 所示,图中坐标系 1和2 为材料主向坐标系,而坐标系 x – y 为自然坐标系;θ 表示坐标轴 x 与坐标轴 1 的夹角,以沿着逆时针方向为正。
|
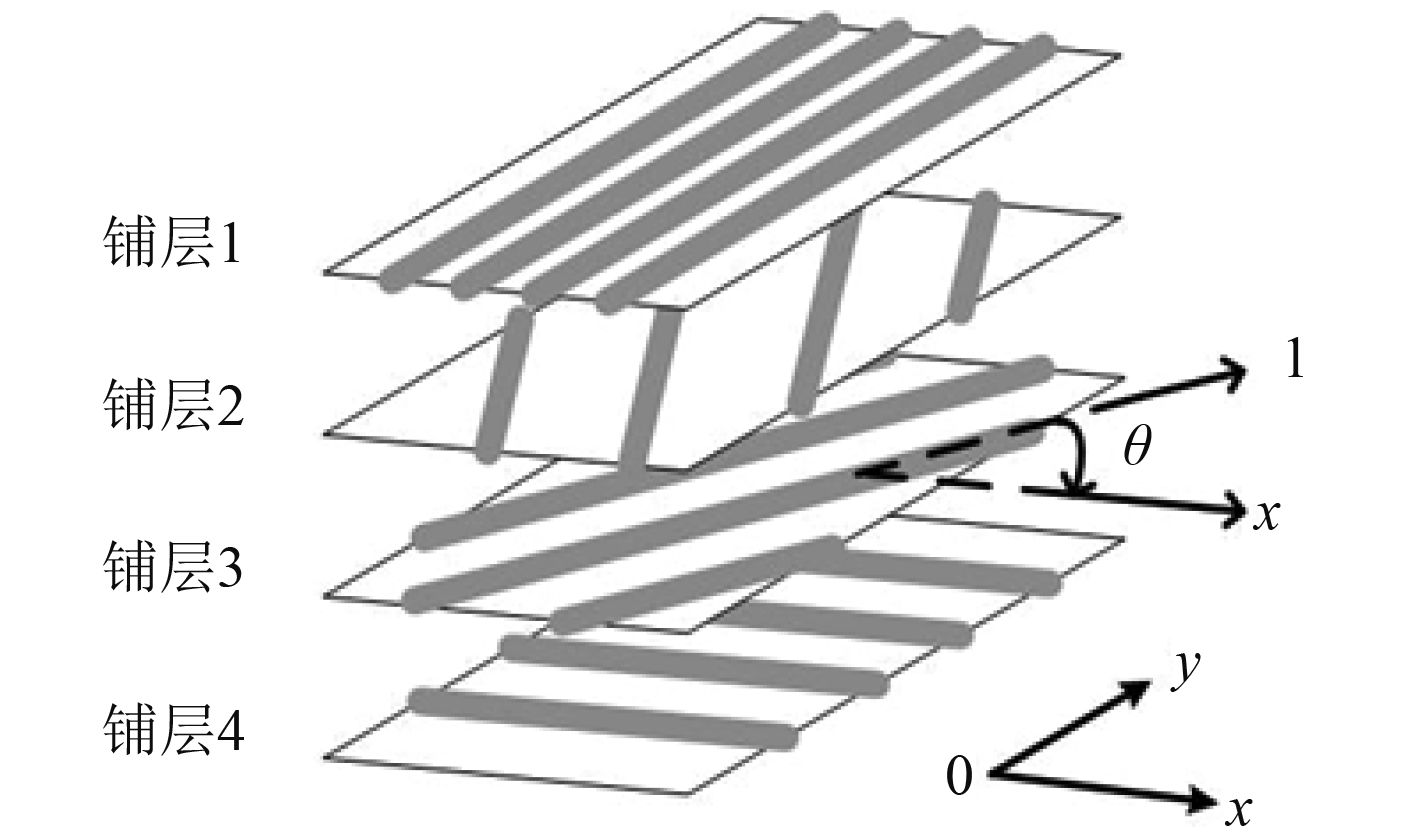
图 2 复合材料铺层模型 Fig. 2 A model laminated with composite material |
根据材料力学相关知识,则正交各向异性材料的弹性矩阵为:
|
${{D}} = \left[ {\begin{array}{*{20}{c}}{\displaystyle\frac{{{E_1}}}{{1 - {\nu _{12}}{\nu _{21}}}}}&{\displaystyle\frac{{{\nu _{12}}{E_2}}}{{1 - {\nu _{12}}{\nu _{21}}}}}&0\\[10pt]{\displaystyle\frac{{{\nu _{21}}{E_1}}}{{1 - {\nu _{12}}{\nu _{21}}}}}&{\displaystyle\frac{{{E_2}}}{{1 - {\nu _{12}}{\nu _{21}}}}}&0\\[8pt]0&0&{{G_{12}}}\end{array}} \right]\text{,}$
|
(3) |
式中:E1 和 E2 分别为沿着 1 方向和 2 方向的材料弹性模量;v12 和 v21 为1 方向和 2 方向之间的泊松比;G12 为材料主向坐标系下的剪切模量。
式(3)的材料弹性矩阵是在材料主向坐标系下的形式,通过坐标变换,则在自然坐标系下的转换后的弹性矩阵可记为:
|
$\bar { D} = { T D}{\left( { T} \right)^{\rm{T}}}\text{,}$
|
(4) |
其中T 为坐标变换矩阵,其表达式为:
|
${{T}} = \left[ {\begin{array}{*{5}{c}}{{\rm {cos}}^2\theta }\quad\quad\quad {{\rm {sin}}^2\theta }\quad\quad\quad{2{\rm sin}\theta {\rm cos}\theta }\\{{\rm sin}^2\theta }\quad\quad\quad{{\rm cos}^2\theta }\quad\quad{ - 2{\rm sin}\theta {\rm cos}\theta }\\{ - {\rm sin}\theta {\rm cos}\theta }\quad\quad{{\rm sin}\theta {\rm cos}\theta }\quad\quad{{\rm cos}^2\theta - {\rm sin}^2\theta }\end{array}} \right]\text{。}$
|
(5) |
在本文的数值分析中,选择二维线性等参单元作为基本单元。则为了计算单元内某个点的位移,其计算公式为:
|
$\begin{array}{l}\left\{ \begin{array}{l}u\\v\end{array} \right\}{\rm{ = }}\left[ \begin{array}{l}{N_1}\;\;\;0\;\;\;{N_2}\;\;\;0\;\;\;{N_3}\;\;\;0\;\;\;\;{N_4}\;\;\;0\;\;\;\\\;0\;\;\;\;{N_1}\;\;\;0\;\;\;\;{N_2}\;\;\;0\;\;\;{N_3}\;\;\;0\;\;\;{N_4}\end{array} \right]\text{,}\\[10pt]\left\{ \begin{array}{l}{u_1}\\{v_1}\\{u_2}\\{v_2}\\{u_3}\\{v_3}\\{u_4}\\{v_4}\end{array} \right\}{\rm{ = }}\sum {{N_i}{d_i}} = Nd\text{。}\end{array}$
|
(6) |
式中:Ni 为拉格朗日插值函数,di 为单元节点的位移分向量,
|
${N_i} = \left[ {\begin{array}{*{20}{c}}{{N_i}}&0\\0&{{N_i}}\end{array}} \right]\text{,}{\rm{ }}{d_i} = \left\{ {\begin{array}{*{20}{c}}{{u_i}}\\{{v_i}}\end{array}} \right\}\text{,}{\rm{ }}(i = 1,2,3,4)\text{,}$
|
(7) |
进而自然坐标系下的应变矢量 ε 可表示为:
|
$\varepsilon = { L N}d = { B}d = \mathop \sum \nolimits^{ {L}} { N_i}{d_i}\text{,}$
|
(8) |
其中:
|
${{L}} = \left[ {\begin{array}{*{20}{c}}{\displaystyle\frac{\partial }{{\partial {\rm{x}}}}}&0\\[10pt]0&{\displaystyle\frac{\partial }{{\partial {\rm{y}}}}}\\[10pt]{\displaystyle\frac{\partial }{{\partial {\rm{y}}}}}&{\displaystyle\frac{\partial }{{\partial {\rm{x}}}}}\end{array}} \right]\text{,}$
|
(9) |
则将自然坐标系下的应力矢量 σ 定义为:
|
${\bf{\sigma }} = {{\bar { D}\varepsilon }}\text{,}$
|
(10) |
对于弹性材料,单元应变能的表达式可以表示如下:
|
$U = \frac{1}{2}\int {\int_A {{\varepsilon ^{\rm{T}}}\sigma {\rm{d}}A = \frac{1}{2}d} } \left( {\int {\int_A {{{ B}^{\rm{T}}}\overline { D} {\rm{ }}{ B}dA} } } \right)d = \frac{1}{2}{d^{\rm{T}}}{ K}d\text{,}$
|
(11) |
其中:
|
$ K = \int_{ - 1}^1 {\int_{ - 1}^1 {{{ B}^{\rm{T}}}{{\bar { D} B}}{\rm{det}}{{J}}{\rm{d}}\xi {\rm{d}}\eta } }\text{,} $
|
(12) |
式中J 为雅可比矩阵,其行列式 det J 为:
|
${\rm{det}}{ J} = \left| {\begin{array}{*{20}{c}}{\displaystyle\frac{{\partial {\rm{x}}}}{{\partial {\rm{\xi }}}}}&{\displaystyle\frac{{\partial {\rm{y}}}}{{\partial {\rm{\xi }}}}}\\[10pt] {\displaystyle\frac{{\partial {\rm{x}}}}{{\partial {\rm{\eta }}}}}&{\displaystyle\frac{{\partial {\rm{y}}}}{{\partial {\rm{\eta }}}}}\end{array}} \right|\text{。}$
|
(13) |
根据复合材料力学,可以推出等效单元刚度矩阵为:
|
${ K} = \frac{1}{n}{\rm{ }}\sum\limits_{i = 1}^n {{{ K}_i}} \text{。}$
|
(14) |
其中:Ki 为自然坐标系下第 i 个铺层的刚度矩阵,可以由式(12)计算得到;n 为层合板的总铺层数。
4 灵敏度分析本文采用的 MMA 方法是基于梯度的优化算法,优化问题中的目标函数和约束对设计变量的灵敏度分析不能忽略。Wang 等[20]在其关于距离正规化水平集方法(DRLSE)应用于压力加载面搜索算法的文章中,提到了相应的灵敏度分析。本文采用的是等值线方法作为压力加载面搜索算法,因此本文的灵敏度分析与 Wang 的方法略有不同。
在本文研究的优化问题中,设计变量为单元的相对密度
|
$\frac{{\rm{d}}}{{{\rm{d}}{\rho _e}}}\left[ {C\left( {{U}\left[ {{\rho _e}} \right],{\rho _e}} \right)} \right] = \frac{{\partial C}}{{\partial {\rho _e}}} + \frac{{\partial C}}{{\partial {U}}}\frac{{\partial {U}}}{{\partial {\rho _e}}}\text{。}$
|
(15) |
根据平衡方程以及灵敏度关系式,采用伴随法[21]对
|
$\frac{{{\rm{d}}C}}{{{\rm{d}}{\rho _e}}} = - p{\rho ^{p - 1}}{E_0}{u}_e^{\rm T}{k}_e^0{{u}_e} + 2{{U}^{\rm T}}\frac{{\partial {F}}}{{\partial {\rho _e}}}\text{。}$
|
(16) |
式中,
|
$\frac{{\partial {F}}}{{\partial {\rho _e}}} = \frac{{\partial {F}}}{{\partial {{x}_f}}}\frac{{\partial {{x}_f}}}{{\partial {\rho _e}}} \approx \frac{{{\Delta _e}{F}}}{{\Delta {\rho _e}}}\text{,}$
|
(17) |
其中:
|
$\begin{split}\Delta eF = & F\left( {{x_f}\left( {{\rho _1},...,{\rho _e} + \Delta {\rho _e},...,{\rho _N}} \right)} \right) - \\& F\left( {{x_f}\left( {{\rho _1},...,{\rho _e},...,{\rho _N}} \right)} \right)\text{。}\end{split}$
|
(18) |
式中:xf 为加载面与单元边界交点的坐标矩阵;
本文所计算的算例为基于复合材料的拓扑优化问题,所采用的材料为纤维增强型复合材料,其铺层模型如图 2 所示。并且根据不同的算例,本文将选用不同的灵敏度过滤技术来获得更好的优化结果。
|
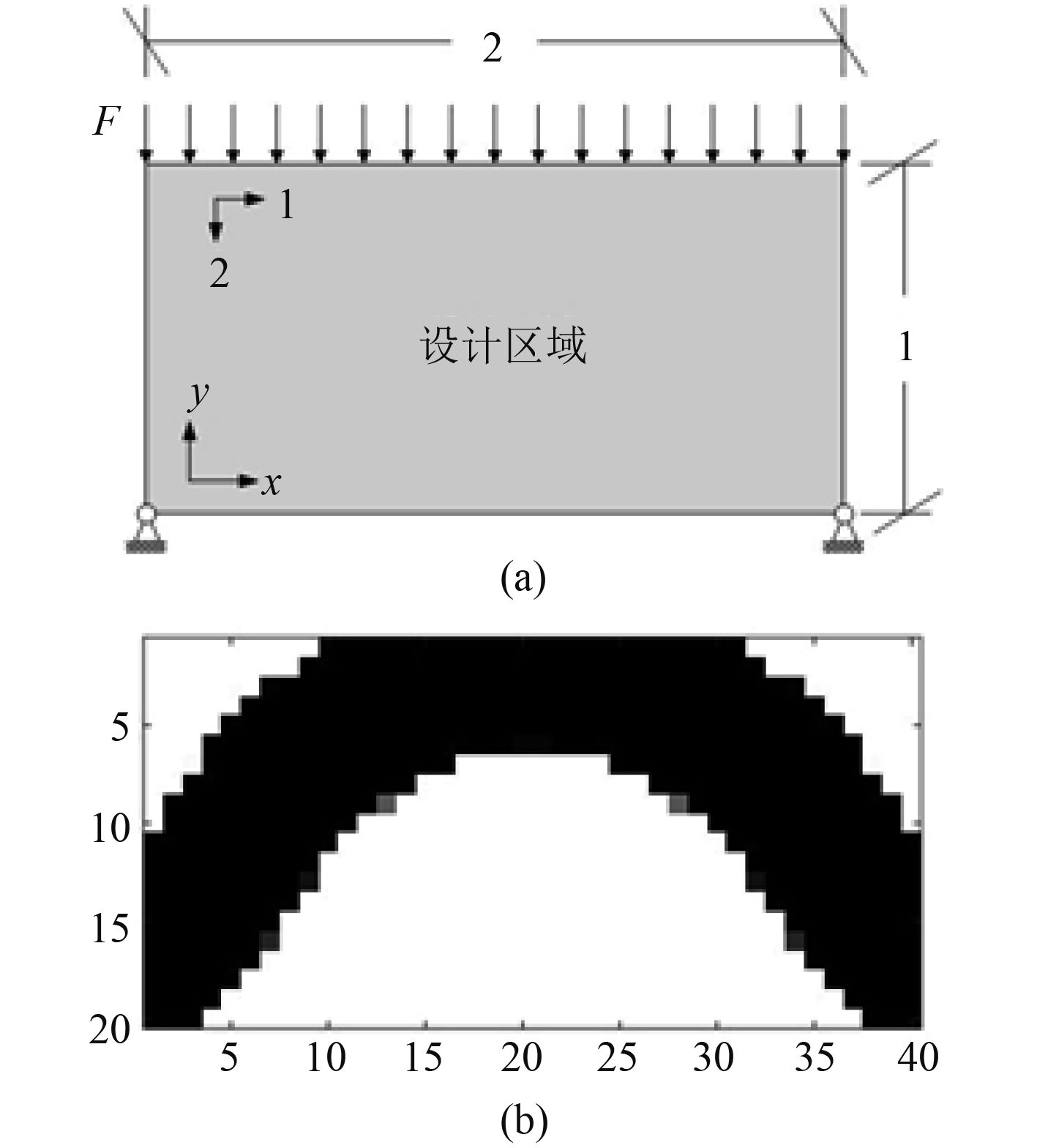
图 3 各向同性情况下,外部受压的桥形结构计算模型及优化结果 Fig. 3 Bridge-like structure with isotropic material subjected to pressure loading |
作为承受压力载荷的结构优化问题中的经典算例,本文选择外部受压的桥形结构优化设计作为第一个算例,用以验证推导的复合材料的单元刚度矩阵的可靠性,并研究复合材料对于拓扑优化结果的影响。初始的设计区域以及边界约束条件如图 3(a) 所示,长方形设计区域的长宽分别为 2 m 和 1 m,顶端受到方向垂直向下大小为 2 MPa 的均布压力载荷的作用,长方形设计区域的底边 2 个顶点固支。假设材料的弹性模量分别为

|
图 4 三种铺层形式下的桥形结构优化结果 Fig. 4 Optimal results of bridge-like structure with laminate composites |
在此算例中,平均灵敏度过滤方法[16]被用来消除计算中的数值不稳定现象。优化结果如图 3(b),整体结构的最小柔顺度为 271.358 6 J。对比文献[13]中的结果,本文的计算结果与其非常相似。
为进一步研究复合材料对于拓扑优化结果的影响,假设材料的弹性模量分别为 E1 = 2 100 GPa,
|
|
表 1 复合材料铺层形式 Tab.1 Three cases of different layups for the laminate composites |
表 1 中所列的 3 种铺层形式的优化结果如图 4 所示。图 4(a) 为铺层 i 的计算结果,结构的最小柔顺度为 66.854 5 J,图像与图 3(b) 中的各向同性材料的优化结果相似,并且同样为左右对称结构;图 4(b) 为铺层 ii 的计算结果,结构的最小柔顺度为 84.607 2 J,优化后的图像虽然仍然是桥形结构,但桥形结构不再是左右对称,左半桥相较于右半桥更宽,桥形的顶部稍向右侧偏移;图 4(c) 为铺层 iii 的计算结果,结构的最小柔顺度为 84.607 2 J,优化后的结构最小柔顺度与铺层 ii 的结果完全相同,并且图像与图 4(b) 互为镜像。

|
图 5 静水压下耐压结构的计算模型 Fig. 5 Computing model for underwater structure subjected to hydrostatic pressure |
从上述结果中可发现,基于复合材料的拓扑优化结果与基于各向同性材料的结果存在着差异,优化结果中实体单元(即黑色单元)的分布与复合材料铺层的角度有关。当某种复合材料铺层的角度相互关于 90° 对称(如表 1 铺层 i)时,优化结果呈左右对称;当 2 种铺层形式的角度分别关于 0° 对称(如表 1 铺层 ii 与铺层 iii)时,2 个优化结果镜像对称。
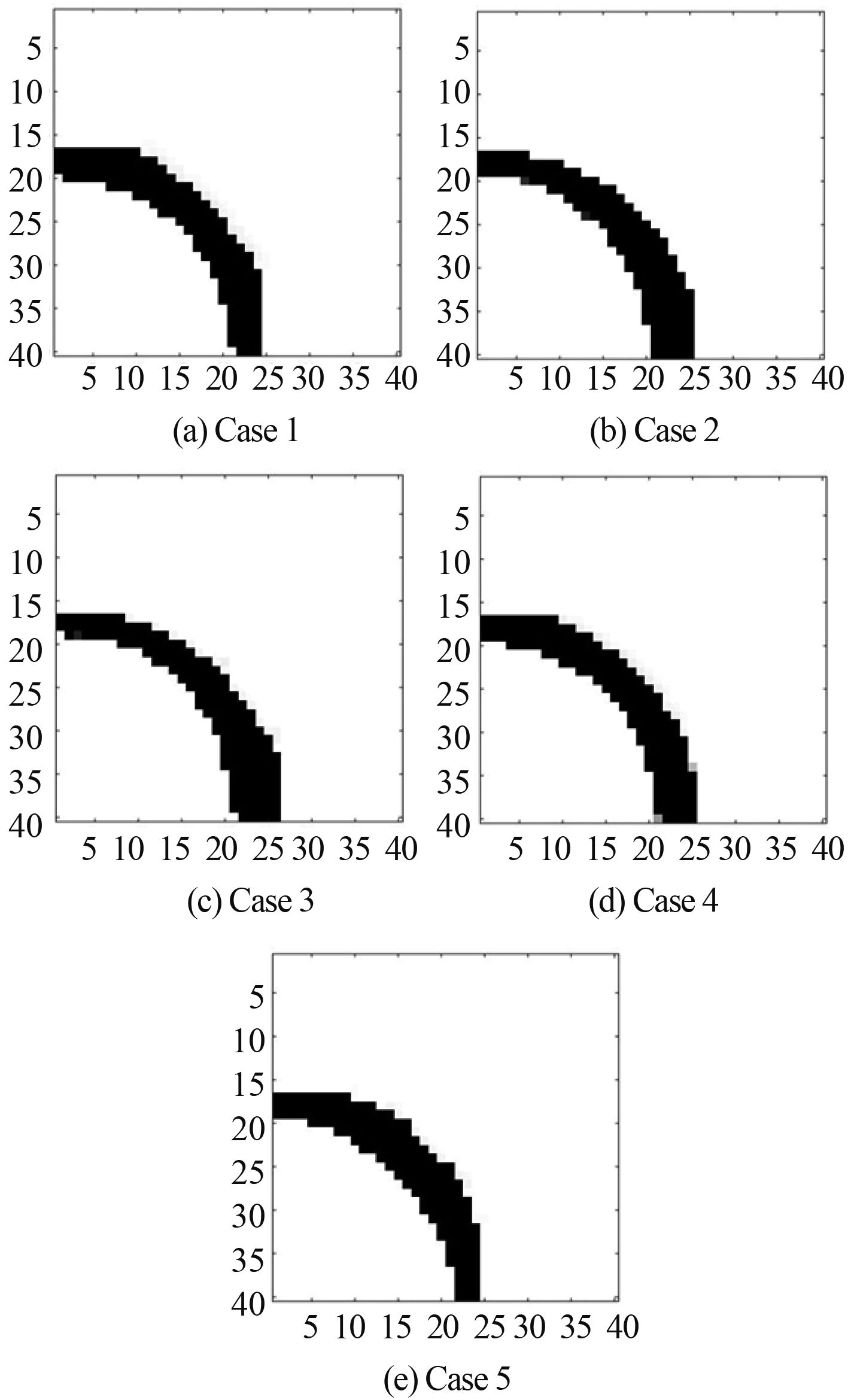
5.2 静水压下耐压结构的优化设计水下耐压结构作为潜水器中的重要结构,其优化设计一直是一项引人关注的课题。在本算例中,仅考虑从结构的刚度方面进行优化设计,忽略诸多其他因素。则简化后的耐压结构的优化设计模型及其尺寸、边界条件等如图 5(a) 所示,正方形的设计区域四周受到静水压力,静水压大小为 2 MPa,并且在正方形 2 条对称轴上添加四处约束,使得对称轴上的点仅能沿中心线方向移动。各向同性材料及复合材料的材料参数均与 5.1 节中的设定相同,实体材料占总设计区域的体积分数设为 10%。考虑到图 5(a) 中的优化模型及边界条件的对称性,如图 5(b) 取 1/4 模型作为优化对象,并离散成 40 × 40 个正方形单元。本例中,采用平面应变假设,并且分2步进行灵敏度过滤:第 1 步,选择平均灵敏度过滤方法 [16];第 2 步,选择考虑密度梯度的灵敏度过滤方法[17],其中取 α = 0.1。表 2 所列为计算的所有材料及铺层情况。
|
图 6 静水压下的耐压结构优化结果 Fig. 6 Optimal results of underwater structure subjected to hydrostatic pressure |
|
|
表 2 考虑的各向同性材料及复合材料铺层的情况 Tab.2 Cases of isotropic material and laminate composites considered |
图 6 所示为各向同性材料及其他几种复合材料铺层形式下的耐压结构优化结构。图 6(a) 为各向同性材料的优化结果,其最终的柔顺度为 229.283 8 J,最优拓扑形式接近 1/4 圆环,此结果与 Zheng 等[22]的优化结果的形状非常相似;图 6(b) ~ 图 7(e)分别为对应表 2 中 Case 2~Case 5 的不同铺层方式的拓扑优化结果,优化后的最终柔顺度分别为 119.757 2 J,89.078 6 J,56.572 8 J,78.051 2 J,而从形状上看,这些结果都接近 1/4 圆环,但是铺层角度的不同会导致圆环宽度产生差异。Case 2~Case 5 的复合材料的铺层方式的相似之处为都拥有 0° 铺层,而不同之处为另一个铺层(以下称为“第2铺层”)的角度不同。从图 6(b) 和图 6(c) 中可以看到,1/4 圆环靠近 0° 轴的一侧的宽度明显大于靠近 90° 轴的一侧,而相应的 2 种铺层方式中,第 2 铺层的角度分别为 10° 和 30°,都比较接近 0°;图 6(d) 显示的结果中,圆环各处的宽度相对均匀,与图 6(a) 的优化结果比较接近,这说明对于图 5(b) 的优化问题,(0°/60°)s 这种铺层方式的效果与各向同性材料相似;从图 6(e) 可以发现,此时的 1/4 圆环关于 45° 的对角线对称,并且圆环中段的宽度大于两端,在这种情况下,完整模型的最优拓扑形式应为圆柱,在沿着铺层主向的方向上(即 0° 与 90° 方向),圆柱的厚度最小,而沿着斜对角线方向(即 45° 与 135° 方向),圆柱的厚度最大。
|
图 7 内部铰支的空心耐压结构的计算模型 Fig. 7 Computing model for underwater structure with initial void and inside simply-supported constraints |
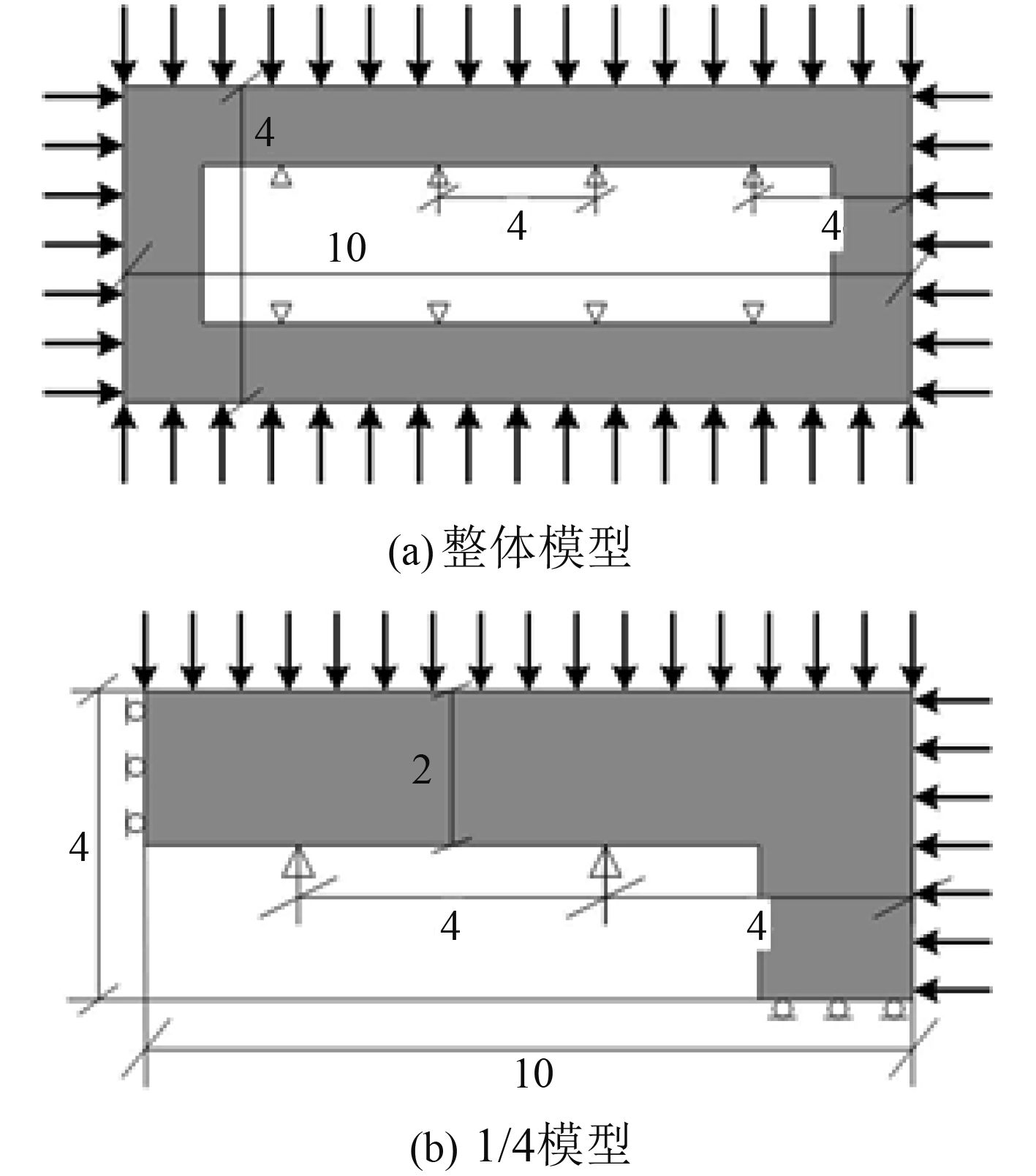
在实际应用中,耐压结构往往需要预留一定的内部空间用于容纳物品或者人,因此,对于空心耐压结构的优化设计对于耐压壳体的设计具有一定的现实参考意义。与 5.2 节中设计区域为完整的正方形区域不同,本例中在长方形设计区域中间预留出一个小的长方形空白区域,同时考虑内部受约束的情况。设计模型及尺寸、边界条件如图 7(a) 所示,设计区域为灰色部分,设计模型的四周受到静水压力,静水压力大小为 2 MPa,并且在模型内部 8 处铰支(即限制相应点出的垂直位移与水平位移)。计算模型的材料参数与 5.1 节的设定相同,实体材料占整个长方形区域的 35%。如图 7(b),取 1/4 模型作为优化对象,相应的尺寸及边界条件如图所示,将其离散成 100 × 40 个正方形单元。灵敏度过滤分2步进行:第 1 步,选择平均灵敏度过滤方法 [16];第 2 步,选择考虑密度梯度的灵敏度过滤方法[17],其中取 α = 0.1。本例所计算的所有材料及铺层情况同表 2。
|
图 8 不同情形下内部铰支的耐压结构的优化结果 Fig. 8 Optimal results of underwater structure with initial void and inside simply-supported constraints |
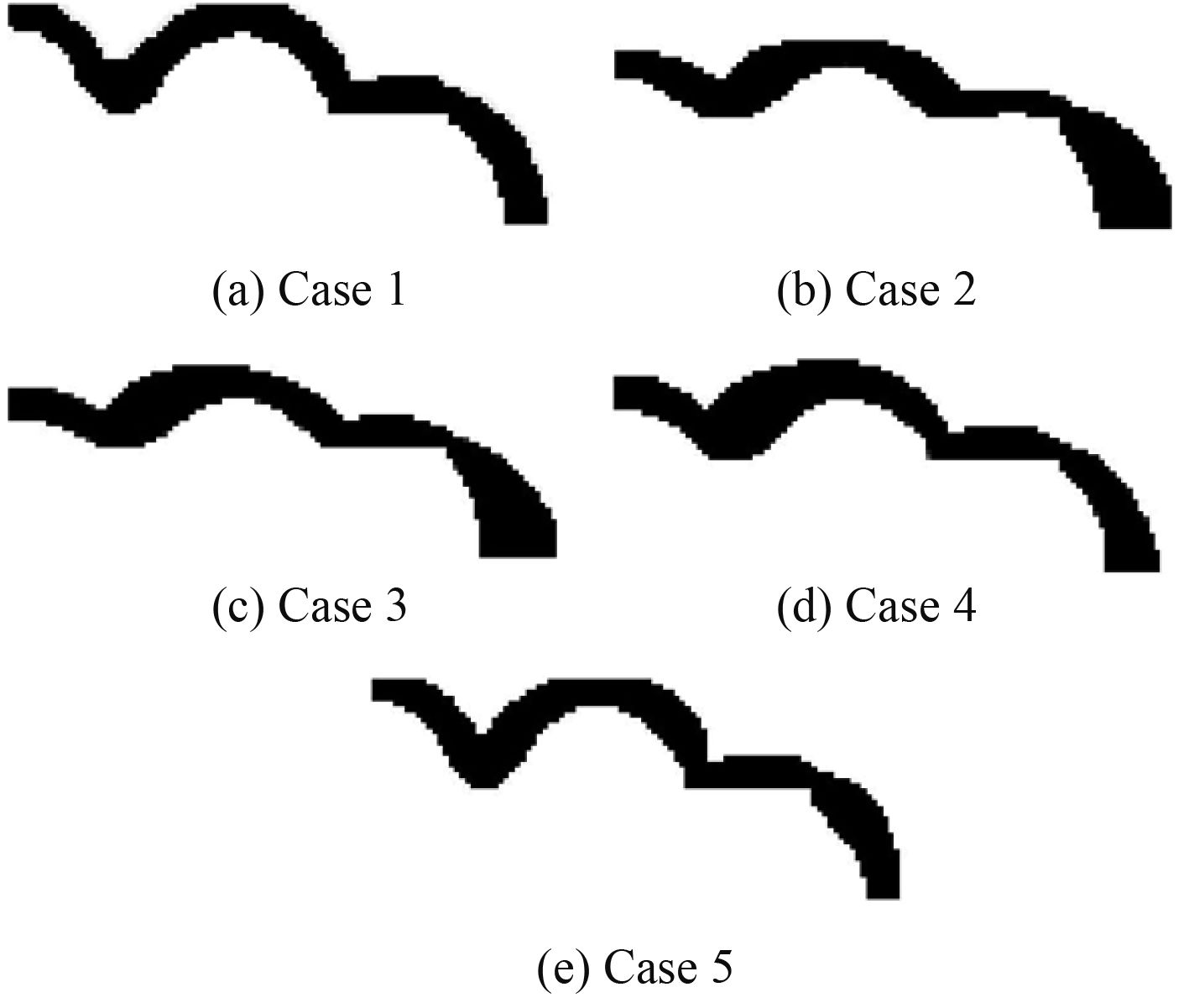
图 8 所示为对应于表 2 所示的不同情形下的优化结果。图 8(a) 为基于各向同性材料的优化结果,其最终的柔顺度为 2 887.186 5 J,由此 1/4 模型的优化结果可以推测出完整模型的最优拓扑形式应为一个多球交接的连续壳体结构,此结果与 Wang[20]的计算结果非常相似;图 8(b) ~ 图8(e) 分别对应于表 2 中 Case 2~Case5 的优化结果,最终的柔顺度分别为 1 492.517 3 J,1 092.020 4 J,869.415 1 J,999.741 1 J,这些拓扑形式大体上都有着类似于各向同性情况的结构,但在局部结构的细节上又存在着差异。比较这些结果可以发现,第 2 铺层角度越接近 0°,优化结果中拱形的高度越低,而拱的两边的宽度差越小;随着第 2 铺层角度的增大,结构的最小柔顺度值先逐渐变小,达到某一角度后柔顺度值出现回升;而在优化结果中,拱形两边的宽度差随角度的增大而增大;同时,如果第 2 铺层的角度为 90°(即 Case 5),其最优拓扑形式基本与各向同性的情况相同,拱形两边的宽度差异也不大。另外,从图 7(a) 中可以推断,这种内部铰支的空心耐压结构的最优拓扑形式可能会在壳体连接处出现应力集中的情况,进而可能导致结构的失效。而根据图 8(b)~ 图8(d) 的结果,可以提出猜想:选择合适铺层的复合材料作为此种耐压结构的主材料,对应的最优拓扑形式的壳体连接处更平缓,可能会减少应力集中出现的情况。
|
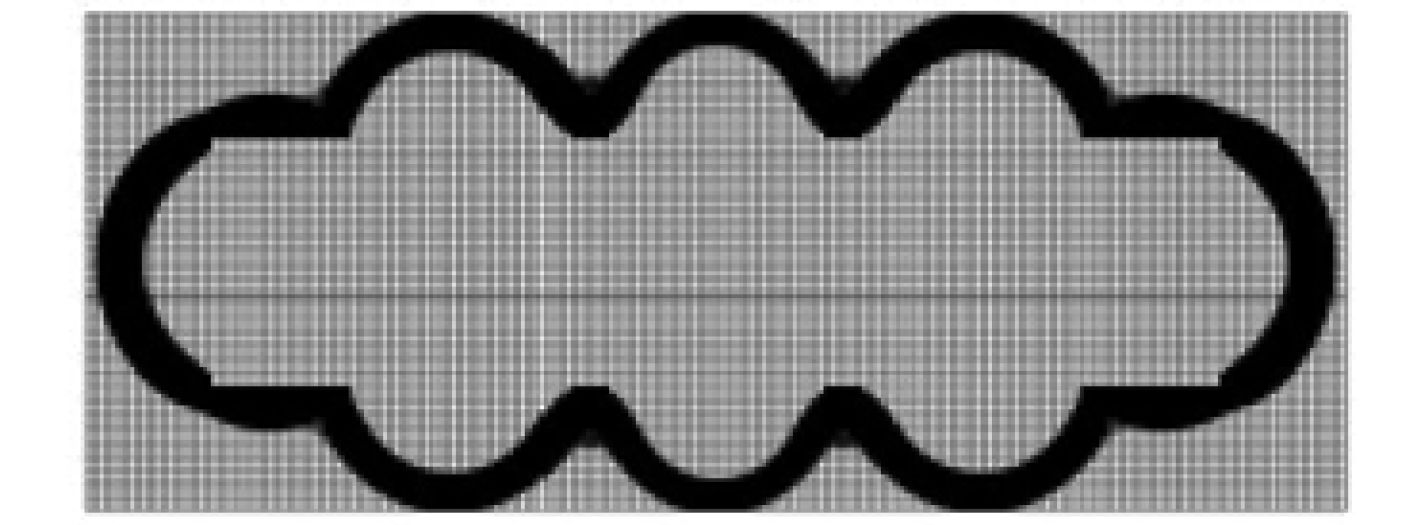
图 9 材料各向同性多球铰支的耐压结构 Fig. 9 Optimal results of multiple intersecting spherical pressure hull with isotropic material |

|
图 10 MIT 提出的多球交接耐压结构模型 Fig. 10 Conceptual model of multiple intersecting spherical pressure hull |
图 9 是王存福[23]于 2014 年提出的通过拓扑优化发现的多球铰接模型,通过本节的优化模型可以发现,图 8 中各向同性材料的结果的拓扑形式与图 9 一致,说明了本文方法的有效性,但随着铺层的变化,其优化结构也发生了一定的变化,说明复合材料的应用对于未来深潜器耐压结构新形式的探索具有重要的工程意义。图 10 为 MIT 水下潜器设计团队[24]给出的一种多球交接耐压壳体模型图,该概念的提出说明在未来多球交接模型讲有着广阔的应用前景,本文优化结构拓展至三维将给出不同铺层状态下的多球交接耐压结构形式,对于发展该种耐压结构的设计具有指导意义。
6 结 语本文通过推导复合材料的等效刚度矩阵,并结合 SIMP 模型,等值线方法以及平均敏度方法与考虑密度梯度的灵敏度过滤方法,实现了对在拓扑相关载荷作用下,基于复合材料的拓扑优化问题的研究。在本文中,计算分析了 3 个算例:外部受压的经典桥形结构优化算例,静水压作用下的耐压结构优化设计算例,以及内部铰支的空心耐压结构优化设计算例。可以得出以下几个结论:
1)对于同一个优化设计问题,采用复合材料得到的优化结果与采用各向同性材料得到的结果在结构大体上相似,但局部结构会存在差异;
2)复合材料的铺层方式不同,优化结果也可能不同:如果是非对称铺层,优化结果很可能出现不对称的结构;如果 2 种铺层方式完全相反,两者的优化结果可能会是互成镜像;
3)对于有2个铺层的复合材料,铺层角度的变化,会改变实体材料的分布,对最优拓扑形式产生较大影响;
4)对于静水压作用下的耐压结构及空心耐压结构,复合材料的应用有可能消除或削弱原优化结果中的应力集中等不良现象。本文的研究只是对基于复合材料的拓扑优化在水下耐压结构设计上的初步应用,诸如基于复合材料的三维拓扑优化问题,以及更多形式的耐压结构设计问题等都是值得进一步探究的课题。
| [1] | BOWEN A D, YOERGER D R, TAYLOR C, et al. The Nereus hybrid underwater robotic vehicle for global ocean science operations to 11, 000m depth [C]// Oceans. 2008: 1–10. |
| [2] | MICHELL A G M. The limit of economy of material in frame structures[J]. Philosophical Magazine Ser, 1904, 8 : 589–597. DOI: 10.1080/14786440409463229 |
| [3] | BENDSOE M P, KIKUCHI N. Generating optimal topologies in structural design using a homogenization method[J]. Computer Methods in Applied Mechanics & Engineering, 1988, 71 (2): 197–224. |
| [4] | SUZUKI K, KIKUCHI N. A homogenization method for shape and topology optimization[J]. Computer Methods in Applied Mechanics and Engineering, 1991, 93 (3): 291–318. DOI: 10.1016/0045-7825(91)90245-2 |
| [5] | BENDSOE M P. Optimal shape design as a material distribution problem[J]. Structural Optimization, 1989, 1 (4): 193–202. DOI: 10.1007/BF01650949 |
| [6] | ZHOU M, ROZVANY G I N. The COC algorithm, Part II: Topological, geometrical and generalized shape optimization[J]. Computer Methods in Applied Mechanics & Engineering, 1991, 89 (1-3): 309–336. |
| [7] | SIGMUND O. On the Design of Compliant Mechanisms Using Topology Optimization[J]. Mechanics of Structures & Machines, 1997, 25 (4): 493–524. |
| [8] | MLEJNEK H P, SCHIRRMACHER R. An engineer’s approach to optimal material distribution and shape finding[J]. Computer Methods in Applied Mechanics & Engineering, 1993, 106 (1-2): 1–26. |
| [9] | SIGMUND O. Design of material structures using topology optimization [D]. Denmark: Technical University, 1994. |
| [10] | BENDSOE M P, SIGMUND O. Material interpolation schemes in topology optimization[J]. Archive of Applied Mechanics, 1999, 69 (9): 635–654. |
| [11] | MAUTE K, RAMM E. Adaptive topology optimization[J]. Structural Optimization, 1995, 10 (2): 100–112. DOI: 10.1007/BF01743537 |
| [12] | HAMMER V B, OLHOFF N. Topology optimization of continuum structures subjected to pressure loading[J]. Structural and Multidisciplinary Optimization, 2000, 19 (2): 85–92. DOI: 10.1007/s001580050088 |
| [13] | DU J, OLHOFF N. Topological optimization of continuum structures with design-dependent surface loading-Part I: new computational approach for 2D problems[J]. Structural and Multidisciplinary Optimization, 2004, 27 (3): 151–165. DOI: 10.1007/s00158-004-0379-y |
| [14] | LEE D, SHIN S, TUAN L A, et al. Computational MATLAB-based optimal design of laminated composite plates [C]// Proc. 5th European Conference of Computer Science, Recent Advances in Information Technology. Geneva, Switzerland, 2014. |
| [15] | BORRVALL T. Topology optimization of elastic continua using restriction[J]. Archives of Computational Methods in Engineering, 2001, 8 (4): 351–385. DOI: 10.1007/BF02743737 |
| [16] | SIGMUND O. Morphology-based black and white filters for topology optimization[J]. Structural and Multidisciplinary Optimization, 2007, 33 (4): 401–424. |
| [17] |
龙凯, 傅晓锦. 考虑密度梯度的敏度过滤方法[J]. 计算机辅助设计与图形学学报, 2014, 26 (4): 669–674.
LONG Kai, FU Xiao-jin. Sensitivity filtering method considering density gradient[J]. Journal of Computer-Aided Design & Computer Graphics, 2014, 26 (4): 669–674. |
| [18] |
张维声, 孙国, 郭旭. 基于水平集描述的结构拓扑与构件布局联合优化新方法[J]. 工程力学, 2013, 30 (7): 22–27.
ZHANG Wei-sheng, SUN Guo, GUO Xu, et al. A level set-based approach for simultaneous optimization of the structural topology optimization and the layout of embedding structural components[J]. Engineering Mechanics, 2013, 30 (7): 22–27. |
| [19] | SVANBERG K. The method of moving asymptotes—a new method for structural optimization[J]. International Journal for Numerical Methods in Engineering, 1987, 24 (2): 359–373. DOI: 10.1002/(ISSN)1097-0207 |
| [20] | WANG Cun-fu, ZHAO Min, GE Tong. Structural topology optimization with design-dependent pressure loads[J]. Structural and Multidisciplinary Optimization, 2015 : 1–14. |
| [21] | MICHALERIS P, TORTORELLI D A, VIDAL C A. Tangent operators and design sensitivity formulations for transient non-linear coupled problems with applications in elastoplasticity[J]. International Journal for Numerical Methods in Engineering, 1994, 37 (14): 2471–2500. DOI: 10.1002/(ISSN)1097-0207 |
| [22] | ZHENG B, CHANG C J, GEA H C. Topology optimization with design-dependent pressure loading[J]. Structural and Multidisciplinary Optimization, 2009, 38 (6): 535–543. DOI: 10.1007/s00158-008-0317-5 |
| [23] | 王存福. 水下耐压壳体拓扑优化设计方法探究[D]. 上海: 上海交通大学, 2013. |
| [24] | http://web.mit.edu/12.000/www/m2005/a2/finalwebsite/equipment/manned/hull.shtml. |
 2017, Vol. 39
2017, Vol. 39

