在一些光学系统中使用了大口径透镜,为了减轻重量,部分光学系统的透镜选用了塑料材料,如PMMA(聚甲基丙烯酸甲酯)。PMMA具有透射率高、重量轻、易于加工等特点。理论上该种材料的透光率可以达到90%以上[1]。在某光学系统中使用了PMMA作为透镜材料,受材料特性影响,该透镜的焦距在温度变化时会发生变化。特别是在低温环境下,其焦距变化量引起系统光学指标发生较大改变,不能满足使用要求。因此,需将该塑料透镜放置在密闭腔体内,在低温时采取加热措施,保证该透镜在36 ℃及以上的环境中工作。本文根据传热原理设计了一种密闭腔体,通过建立该腔体加热的数学模型对该腔体进行加热分析计算。本文开展了该腔体的加热试验,不仅验证了建立的计算模型,同时还证明了设计的密闭腔体能实现所需的加热功能,可满足塑料透镜的工作环境要求。
1 密闭腔体结构及加热设计 1.1 热传导方式传热是物质在温度差作用下所发生的热量传递过程。无论在一个物体内部还是在一些物体之间,只要存在温差,热量就将以某一种或某几种方式自发地从高温处传向低温处[2]。根据传热机理的不同,热量传递有3种基本方式:热传导(导热)、热对流、热辐射。物体通常以2种形式发射辐射能量,即热辐射和光辐射。任何高于绝对零度的物体都具有热辐射能力[3, 4]。
为了实现低温下加热塑料透镜,本文设计一种密闭腔体,该腔体使用加热电阻作为热源加热其内部的透镜,从而提高腔体内塑料透镜的温度。
1.2 腔体设计受制于透镜形状以及外形尺寸限制,腔体为矩形腔体。为增加加热效果,加热电阻分为两边布置,加热电阻安装在小型散热器上,同时,两边各放置一个小风机使散热器散发出来的热量尽快均匀分布在腔体内。在两边放置温度传感器作为测温元件,对腔体内温度进行反馈。如果腔体内温度达到要求,则使加热电阻停止工作,从而实现加热电阻的供电控制。
该密闭腔体外形及内部元件示意图如图1所示。

|
图 1 密闭腔体外形及内部元件示意图 Fig. 1 Sketch of closed cavity’s shell and interior component |
为了确保加热效果,降低散热效率,腔体设计成气密结构。使用光学窗口对腔体密封。同时,在小型散热器以及透镜座与腔体外壳连接处使用非金属材料隔开,避免热源以及被加热的透镜元件通过腔体外壳传热到外界。
2 加热分析计算本次加热分析计算主要内容为:建立腔体加热的数学模型,得到低温下加热温度与加热时间的关系。
2.1 腔体加热的数学模型腔体加热时间由加热所需能量与电阻器所能提供的能量决定。
2.1.1 加热腔体所需的能量。在环境温度为T1时,将腔体温度加热到T2需要的能量可以用式(1)表示:
|
${Q_{\rm{1}}} = {Q_a} + {Q_b} + {Q_c} + {Q_d} + {Q_e} + {C_1} \cdot ({T_2} - {T_1})\text{,}$
|
(1) |
其中,Qa为加热腔体内金属材料所需的能量,Qb为加热腔体内透镜材料所需的能量。为了简化计算模型,加热腔体内除金属、透镜及气体外的其他固体所需要的能量用Qc表示。Qd为加热腔体内气体所需的能量。Qe为耗散的能量。由于此腔体形状复杂,计算中有较多参数使用估算,因此增加C1修正此数学模型。
1)物体传热计算
向金属、透镜及其他固体传递热量可用式(2)进行计算:
|
$Q = c \cdot m \cdot ({T_2} - {T_1})\text{,}$
|
(2) |
式中:m为物体的质量;c为比热容。T1及T2为传热前后物体的温度,方便起见,下文使用
|
${Q_a} = {c_1} \cdot {m_1} \cdot \Delta T\text{,}$
|
(3) |
|
${Q_b} = {c_2} \cdot {m_2} \cdot \Delta T\text{,}$
|
(4) |
|
${Q_c} = {c_3} \cdot {m_3} \cdot \Delta T\text{,}$
|
(5) |
其中,c1为金属的比热,m1为金属的质量;c2为透镜材料的比热,m2为透镜材料的质量;c3为其他物体综合比热,m3为其他物体的总质量;
2)气体传热计算
向气体传递热量,热量Q可用式(6)计算:
|
$Q = \frac{m}{M} \cdot c \cdot ({T_2} - {T_1})\text{,}$
|
(6) |
式中:m为气体的质量;M为气体的摩尔质量;c为气体的热容。
气体质量m可由式(7)计算:
|
$pV = \frac{m}{M} \cdot R \cdot {T_0}\text{,}$
|
(7) |
其中:p为腔体内气体的气压;V为腔体内气体的体积。
由式(6)与式(7)可得,
|
${Q_d} = \frac{{{p_N}{V_N}}}{{R{T_0}}} \cdot {c_N} \cdot \Delta T\text{。}$
|
(8) |
由于腔体内为氮气,pN为氮气压强,VN为氮气体积,cN为氮气热容。
3)耗散能量计算
腔体中气体与外界气体温度不同,此时腔内气体会通过中间的壳体向腔外气体传递热量,这种热量传递称为对流换热。本腔体的耗散能量即为对流换热损失的能量。影响该种热量传递的因素很多[5],完整、精确考虑各种因素极其困难。根据牛顿冷却定律,可用式(9)近似计算对流换热;
|
$\varPhi = hA\Delta {T_d}\text{,}$
|
(9) |
式中:A为表面面积;
本腔体中,前后两面为5 mm的K9玻璃,竖直放置;两侧为3 mm厚的铝板,竖直放置;上下为3.5 mm厚的铝板,水平放置。由于腔体内表面与外表面形状复杂,厚度不一,材料也不单一,以上厚度值及材料均为近似。
因此,本腔体对流换热的热流密度可由式(10)计算:
|
$\varPhi = {h_1}{A_1}\Delta {T_d} + {h_2}{A_2}\Delta {T_d} + {h_3}{A_3}\Delta {T_d}\text{,}$
|
(10) |
式中:h1,h2,h3分别为不同放置方式的对流系数;A1,A2,A3分别为各个放置的表面的面积;
|
$\begin{split}{Q_e} = \int_0^{{t_{\text{总}}}} {\Phi {\rm d}t} =& \int_0^{{t_{\text{总}}}} {({h_1}{A_1}\Delta {T_d} + {h_2}{A_2}\Delta {T_d} +}\\ &{ {h_3}{A_3}\Delta {T_d}){\rm d}t}\text{,} \end{split}$
|
(11) |
其中,t总指加热所需的总时间。由于
|
${Q_e} = \frac{1}{2}({h_1}{A_1} + {h_2}{A_2} + {h_3}{A_3})\Delta T \cdot t\text{。}$
|
(12) |
由于非金属材料与壳体的接触面积很小,通过非金属材料耗散到壳体的热量忽略不计。
腔体内通过内部风扇形成的气体对流循环以及镜座与栅格之间热传导实现能量传递,具有良好的气体对流条件。
针对此密闭腔体,通过以上计算,加热腔体所需的能量由式(13)表示:
|
$\begin{split}{Q_{\rm{1}}} = & {c_1} \cdot {m_1} \cdot \Delta T + {c_2} \cdot {m_2} \cdot \Delta T + {c_3} \cdot {m_3} \cdot \Delta T + \\ &\frac{{{p_N}{V_N}}}{{R{T_0}}} \cdot {c_N} \cdot \Delta T + \frac{1}{2}({h_1}{A_1} + {h_2}{A_2} + {h_3}{A_3})\Delta T \cdot t + \\ &{C_1}\! \cdot \!\Delta T \!=\! ({c_1} \!\cdot \! {m_1} \!+\! {c_2} \!\cdot \!{m_2} \!+\! {c_3} \cdot {m_3} \!+ \!\frac{{{p_N}{V_N}}}{{R{T_0}}} \cdot {c_N}\! + \\ &\frac{1}{2}({h_1}{A_1} + {h_2}{A_2} + {h_3}{A_3}) \cdot t + {C_1})\Delta T\text{。}\end{split}$
|
(13) |
电阻器提供的能量:
|
${Q_2} = {c_t} \cdot P \cdot {t_{\text{总}}}\text{。}$
|
(14) |
式中:P为电阻器的输出功率;ct为电阻器与金属铝的热传导效率。
2.1.3 加热时间与加热温度之间的关系式当加热到指定温度,腔体达到热平衡后,
|
$\begin{split}{c_t} \cdot P \cdot t = & ({c_1} \cdot {m_1} + {c_2} \cdot {m_2} + {c_3} \cdot {m_3} + \frac{{{p_N}{V_N}}}{{R{T_0}}} \cdot {c_N} + \\ &\frac{1}{2}({h_1}{A_1} + {h_2}{A_2} + {h_3}{A_3}) \cdot t + {C_1})\Delta {T_1}\text{,}\end{split}$
|
(15) |
得到:
|
$t \!=\! \frac{{({c_1}\! \cdot \!{m_1} \!+\! {c_2} \!\cdot \!{m_2}\! +\! {c_3} \!\cdot \!{m_3}\! +\! \displaystyle\frac{{{p_N}{V_N}}}{{R{T_0}}} \!\cdot\! {c_N}\! +\! {C_1})\Delta T}}{{{c_t} \cdot P - \displaystyle\frac{1}{2}({h_1}{A_1} + {h_2}{A_2} + {h_3}{A_3})\Delta T}}\text{。}\!\!\!\!$
|
(16) |
可见,加热时间是温差的函数。
2.2 特定腔体加热所需时间计算本文设计的密闭腔体的信息如下:环境温度范围:–28 ℃~+65 ℃;腔体内镜座及栅格材料为铝,重量1.01 kg;腔体内柱面镜重量为0.3 kg,菲涅尔镜重0.35 kg,材料为PMMA及PC;腔体内部空间尺寸(394×241×54)mm3;腔体内充氮气。
可得到以下参数:
铝的比热c1=908 J/(kg·K),质量m1=1.01 kg;PMMA及PC材料的比热c2=1 470 J/( kg·K),质量m2=0.65 Kg;其他物体总质量约为m3=0.06 kg。腔体内氮气的体积VN≈0.005 13 m3,R=8.31 J/(mol·K)。设氮气为理想气体且在标准状态,即压力为1个标准大气压,pN=1.013×105 Pa,T0=273.15K;所选电阻器总功率为P=200 W。
同一种气体在不同过程中有不同的热容,常用的是等容过程和等压过程中的热容。由于腔体的体积不发生变化,应适用等容过程的条件。由于理想气体的定容摩尔热容只与分子的自由度有关,与气体的温度无关,因此氮气的热容cN=20.8 J/(mol·K)。
对流系数h的单位为W/m2·K,根据传热位置及热流方向,对流相关的参数取值详细如下:
|
$\begin{aligned}& {h_1} = 1.77{\left( {\Delta T} \right)^{1/4}};{A_1} = 0.2159\;{{\rm{m}}^2};\\ & {h_2} = 2.49{\left( {\Delta T} \right)^{1/4}};{A_2} = 0.0213\;{{\rm{m}}^2};\\ & {h_3} = 1.31{\left( {\Delta T} \right)^{1/4}};{A_3} = 0.0213\;{{\rm{m}}^2}\text{。}\end{aligned}$
|
以上参数可总结成表1。
|
|
表 1 设计的密闭腔体参数表 Tab.1 Parameters table of designed closed cavity |
将以上参数代入式(16),得到:
|
$t = \frac{{(1876.842 + 0.03 \times {c_3} + {C_1})\Delta T}}{{200{c_t} - 0.2315\Delta {T^{5/4}}}}\text{。}$
|
(17) |
其中,c3为其他物体的比热容,由于材料组成复杂,范围应在800~1 500 J/(kg·K)选择;ct为电阻器与金属铝的热传导效率,从0.01~0.99选取;C1为修正系数,其绝对值应不能太大,与
由以上计算可知,加热时间是温差的函数。我们可以通过3次加热试验,测量不同
试验装置如图2所示。

|
图 2 密闭腔体加热试验装置 Fig. 2 Heating experiment device of designed closed cavity |
该装置包括:密闭腔体,温度试验箱,腔体控制盒以及秒表等。温度试验箱能够提供–28 ℃~35 ℃±1 ℃的恒定气温。腔体控制盒能够控制密闭腔体的加热通断,且能实时显示腔体内的温度。
3.3 加热试验过程加热试验分为以下3个步骤:
步骤1 将腔体放置在温箱内,控制温箱温度到指定温度T1并记录;
步骤2 待达到指定温度后,应保持温箱温度一定时间,保证密闭腔体充分冷却,其温度与温箱温度一致,本次腔体的冷却时间设定为30 min;
步骤3 待腔体内外均降至温箱的温度,通过腔体控制盒控制密闭腔体开始加热,同时使用秒表记录开始时间t1;腔体加热至指定温度T2时,记录加热完成时的时间t2,计算本次加热的总时间t总=t2–t1。
3.4 加热试验结果及分析本次加热试验的试验温度T1区间为–28~35 ℃,T2为36 ℃,因此
试验结果如表2所示。
|
|
表 2 不同ΔT下的加热时间数据表 Tab.2 Data of heating time in different ΔT |
选取(
|
$t = \frac{{1849.3 \times \Delta T}}{{110 - 0.2315\Delta {T^{5/4}}}}\text{。}$
|
(18) |
至此,密闭腔体加热时间与加热温度的函数关系式已经得到。为了验证此关系式,本文绘制了加热时间理论值与实际值随加热温度的变化曲线,如图3所示。
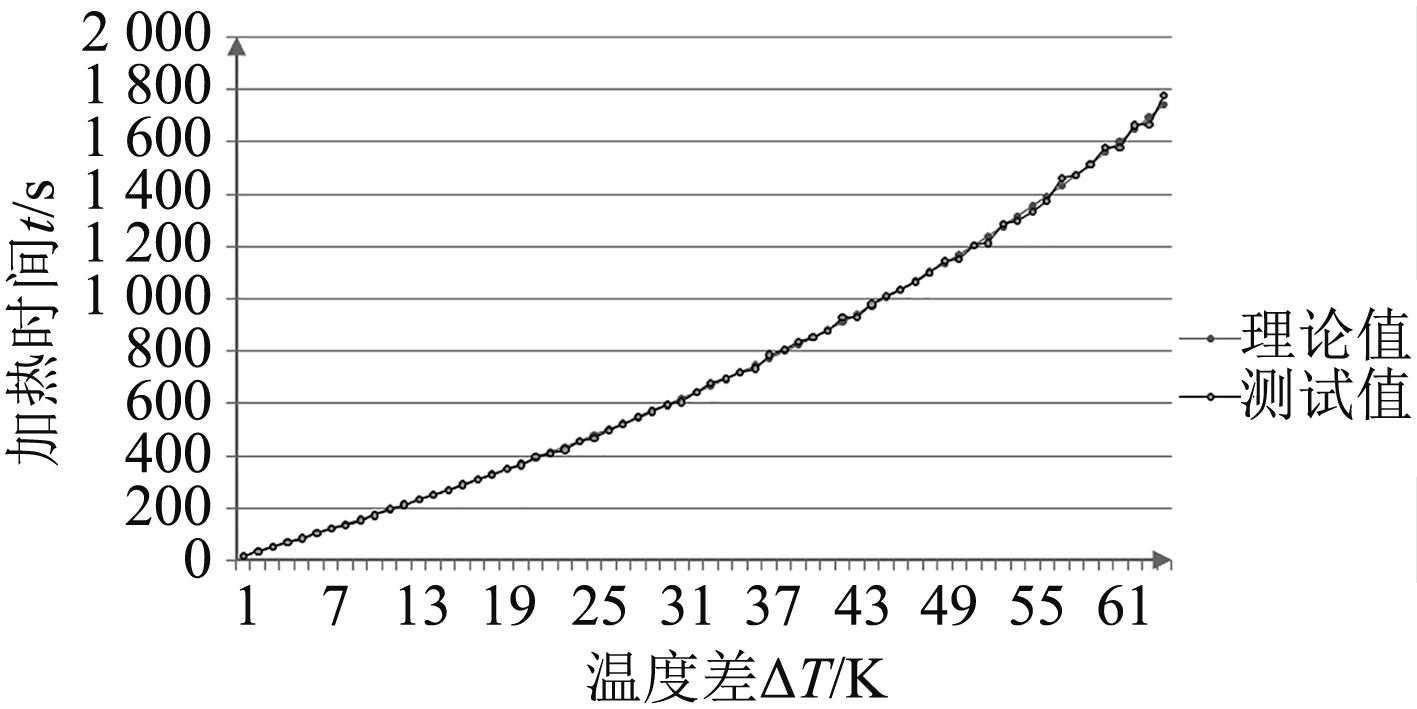
|
图 3 加热时间理论值与实际值随加热温度的变化曲线图 Fig. 3 Curve of heating time theory value change with actual value along with heating temperature |
用
为了满足部分光学系统塑料透镜的工作环境要求,本文根据传热原理设计并分析计算了一种密闭腔体,并开展了该腔体的加热试验。试验证明,该密闭腔体能够在30 min左右将腔体内温度从–28 ℃加热到36 ℃,从而改善塑料透镜的工作环境,保证透镜光学参数的稳定性。该密闭腔体实用有效,应用于某光学系统后取得了良好的效果。虽然本文只针对特定腔体进行了加热分析与试验,但是此加热分析与计算的方法具有一定的普适性,研究方法可应用到其他的研究对象。
| [1] |
韩延民. 太阳能高倍聚光能量传输利用理论及试验研究[D]. 上海: 上海交通大学, 2008.
HAN Yan-min. Theoretical and experimental study on transmisson and utilization of high concentrated solar energy[D]. Shanghai: Shanghai Jiao Tong University, 2008. |
| [2] |
赵镇南. 传热学[M]. 北京: 高等教育出版社, 2002.
ZHAO Zhen-nan. Heat transfer science[M]. Beijing: Higher Education Press, 2002. |
| [3] |
赵惇殳. 电子设备热设计[M]. 北京: 电子工业出版社, 2009.
ZHAO Dun-shu. Thermal design of electronic equipments[M]. Beijing: Publishing House of Electronics Industry, 2009. |
| [4] |
邱成悌, 赵惇殳, 蒋全兴. 电子设备结构设计原理(修订本)[M]. 南京: 东南大学出版社, 2007.
QIU Cheng-ti, ZHAO Dun-shu, JIANG Qian-xing. Structure design principle of electronic equipments(revision) [M]. Nanjing: Southeast University Press, 2007. |
| [5] |
范宏昌. 热学[M]. 北京: 科学出版社, 2003.
FAN Hong-chang. Calorifics[M]. Beijing: Science Press, 2003. |
 2017, Vol. 39
2017, Vol. 39
