随着科学技术的飞速发展,船舶领域也在不断发展。很多新型微小、高密度、宽频谱、大功率的电子元器件不断应用于船舶中,使得狭小的工作空间布满了电磁干扰信号,严重影响到船舶的正常工作。最有效的方法是提高电子设备的电磁兼容性,现代船用行程传感器在充满电磁干扰的环境下,其输出信号的信噪比很低,多数有用信号均被电磁干扰而湮没,而船舶系统对于行程传感器的输出信号具有非常高的精度要求,故船用行程传感器的信号降噪势在必行。本文基于常用除噪、降噪算法原理,对船舶行程传感器开展了一系列的电磁干扰信号仿真研究。
1 小波降噪算法 1.1 小波降噪原理小波变换是一种时间-频率的变化算法,其定义是对不同尺度a作用下的待分析信号x(t)基于基本小波函数Ψ(t)为位移τ的内积:
|
$W{T_x}\left( {a,\tau } \right) = \frac{1}{{\sqrt a }}\int_{ - \infty }^{ + \infty } {x\left( t \right){\Psi ^ * }\left( {\frac{{t - \tau }}{a}} \right)} {\rm d}t,a > 0\text{,}$
|
(1) |
其中,小波变换时间t的频率分辨率动态变化,低频时频率宽度非常窄,而高频处时间范围很小。
设含噪信号s(k),则
|
$s\left( k \right) = f\left( k \right) + e\left( k \right);k = 0,1, \cdot \cdot \cdot ,n - 1\text{。}$
|
(2) |
其中:s(k),f(k),e(k)分别表示含噪信号,有用信号,噪声信号;故小波变换可获得2部分小波系数,分别是有用信号f(k)和噪声信号e(k)相对应的小波系数
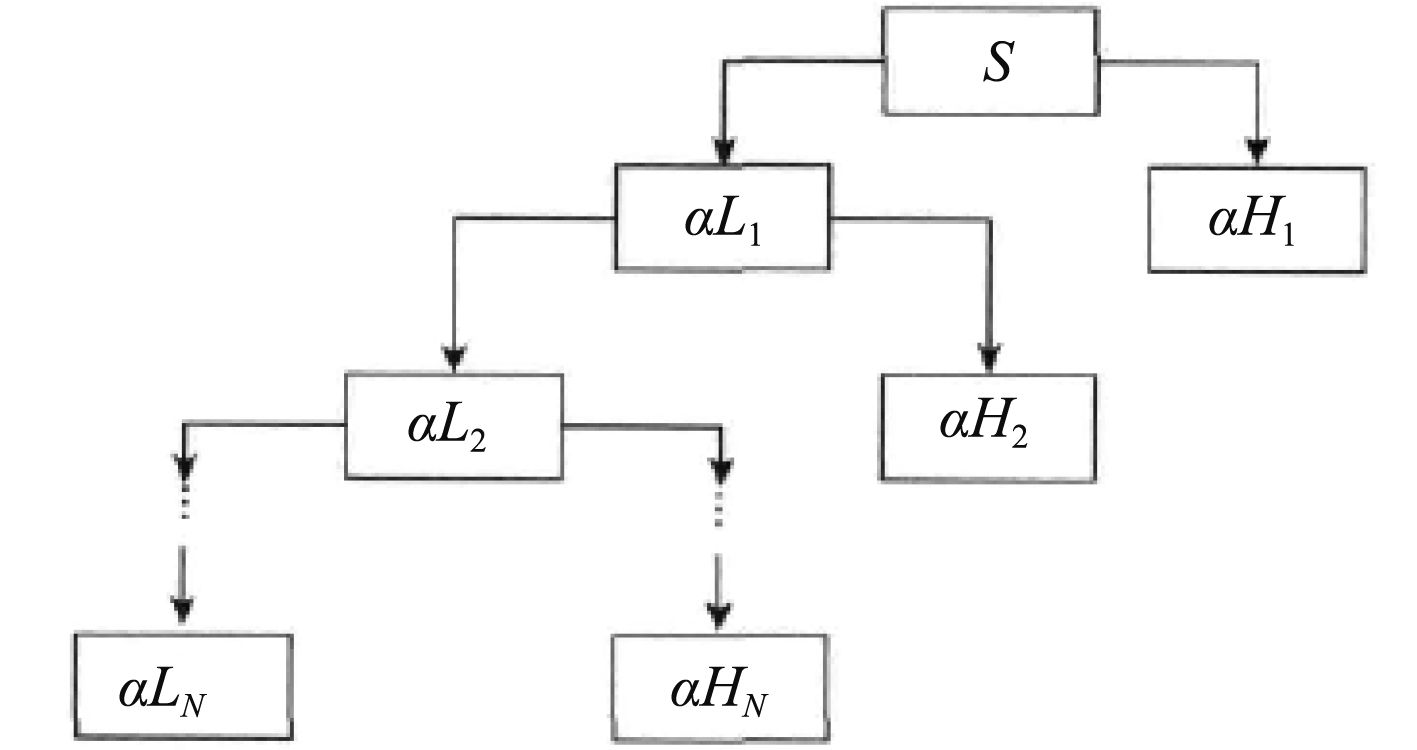
小波变换分析可借助2个互补滤波器把噪声信号解析为近似和细节2部分内容,其中近似部分代表高尺度、低频率信号部分,细节信号代表低尺度、高频率信号部分[1]。近似部分可持续解析到第N层,见式(3),分解过程如图1所示。
|
$S = a{L_N} + a\sum\limits_{i = 1}^N {{H_i}} \text{。}$
|
(3) |
|
图 1 噪声信号近似部分的N层分解 Fig. 1 The N layer decomposition of noise signal approximation |
由分解过程可以发现,低频或高频部分也包含了噪声信号,可以适当调整小波变换系数,小波变换将抑制噪声部分的频率,即可对输出信号进行降噪处理,实现抑制噪声干扰的目标。因单独使用硬阈值和软阈值均存在某些缺点,故本文选用软硬阈值折中的方式进行降噪处理,软硬阈值折中定义为:
|
$\left\{ {\begin{array}{*{20}{c}}{\mathop {{{\hat \omega }_{j,i}} = }\limits_{sign\left( {{w_{j,i}}} \right)\; \cdot }}\\0,\end{array}} \right.\begin{array}{*{20}{c}}{ \left( {\left| {{w_{j,i}}} \right|} \right),} & {\left| {{w_{j,i}}} \right| \geqslant \lambda }\\{} & {\left| {{w_{j,i}}} \right| < \lambda }\end{array},0 \leqslant \alpha \leqslant 1\text{。}$
|
(4) |
其中:
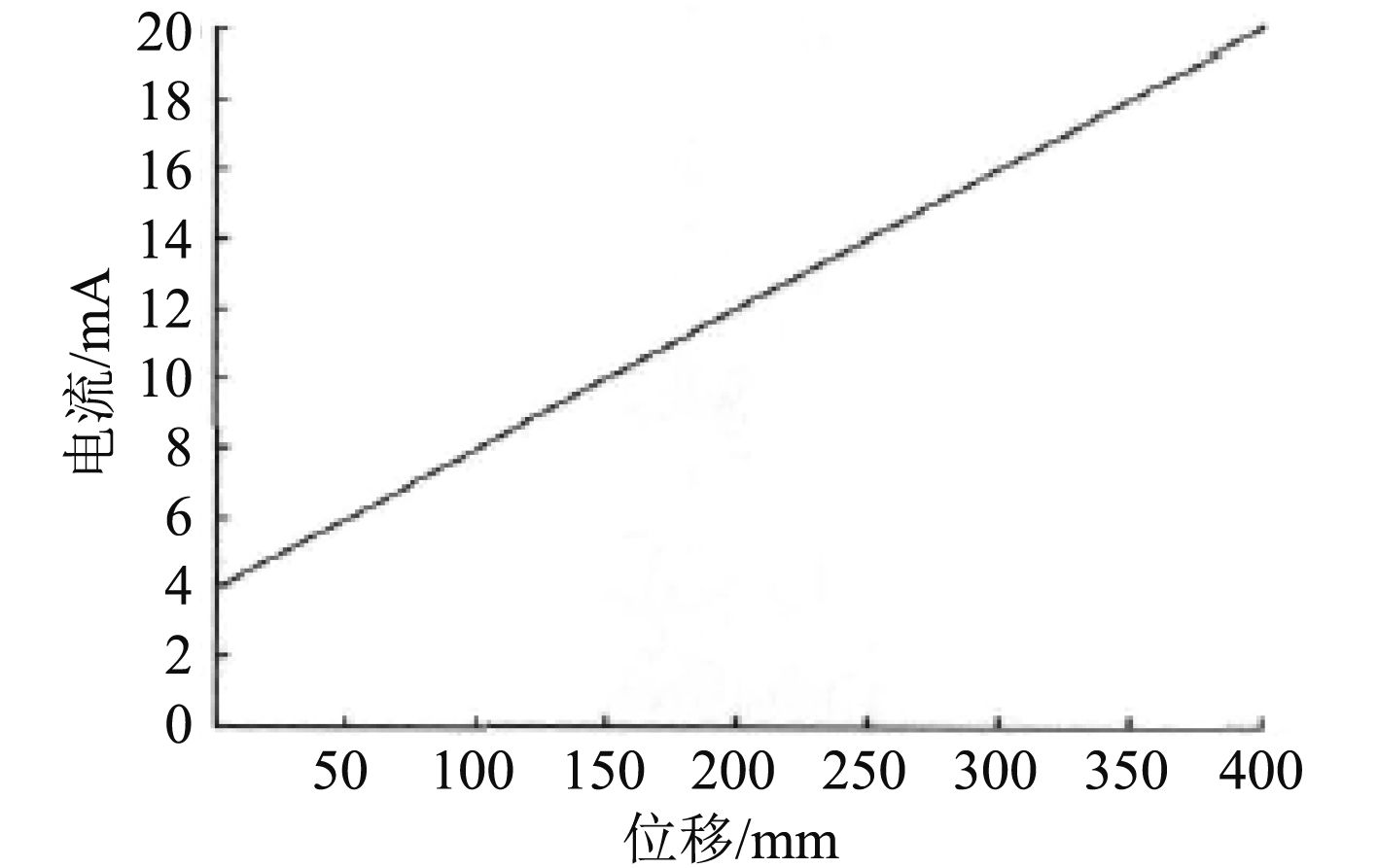
通常海航中的船用行程传感器规格均为0~400 mm量程、LVDT型的差动变压器位移传感器。该传感器配套于位移变送器,使得输出电流信号可达4~20 mA,输出信号和量程的理想关系如图2所示。
|
图 2 传感器输出信号和量程的关系 Fig. 2 Relationship between output signal and range of sensor |
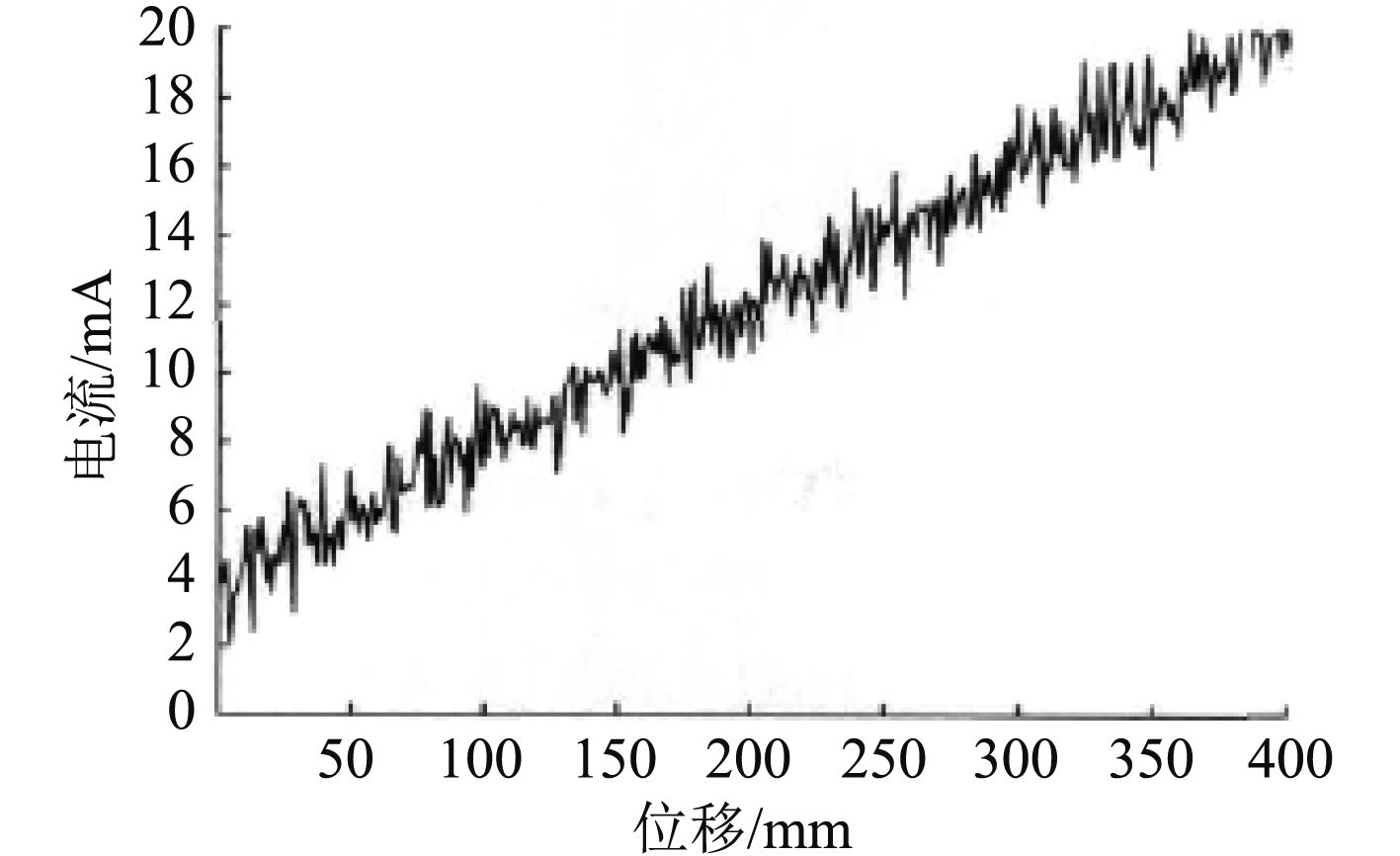
因海航中船用行程传感器始终处于恶劣环境下工作,受到电磁波的干扰非常严重,故在信号仿真过程中设定信噪比为2,含噪声的输出信号和量程关系详见图3所示。
|
图 3 加噪后输出信号和量程的关系 Fig. 3 The relationship between output signal and range after adding noise |
1)选取合适的小波函数
本文小波函数选用了世界闻名的小波分析学者Ingrid Daubechies创造的symlet小波函数,即symN函数,其中N表示小波分解阶数。symN小波函数基于dbN小波函数开展了一系列改进处理,在dbN小波的基础上新增了近似对称形式,dbN小波函数只有N=1外的明确表达形式,但其他尺度可通过尺度函数获得,尺度函数见式(5):
|
$\Psi \left( k \right) = \sum\limits_k {{g_k}\varphi \left( {2t - k} \right)} \text{。}$
|
(5) |
式中:φ(t)为尺度函数;gk为权重;gk随N值变化而变化。
2)信号降噪仿真图
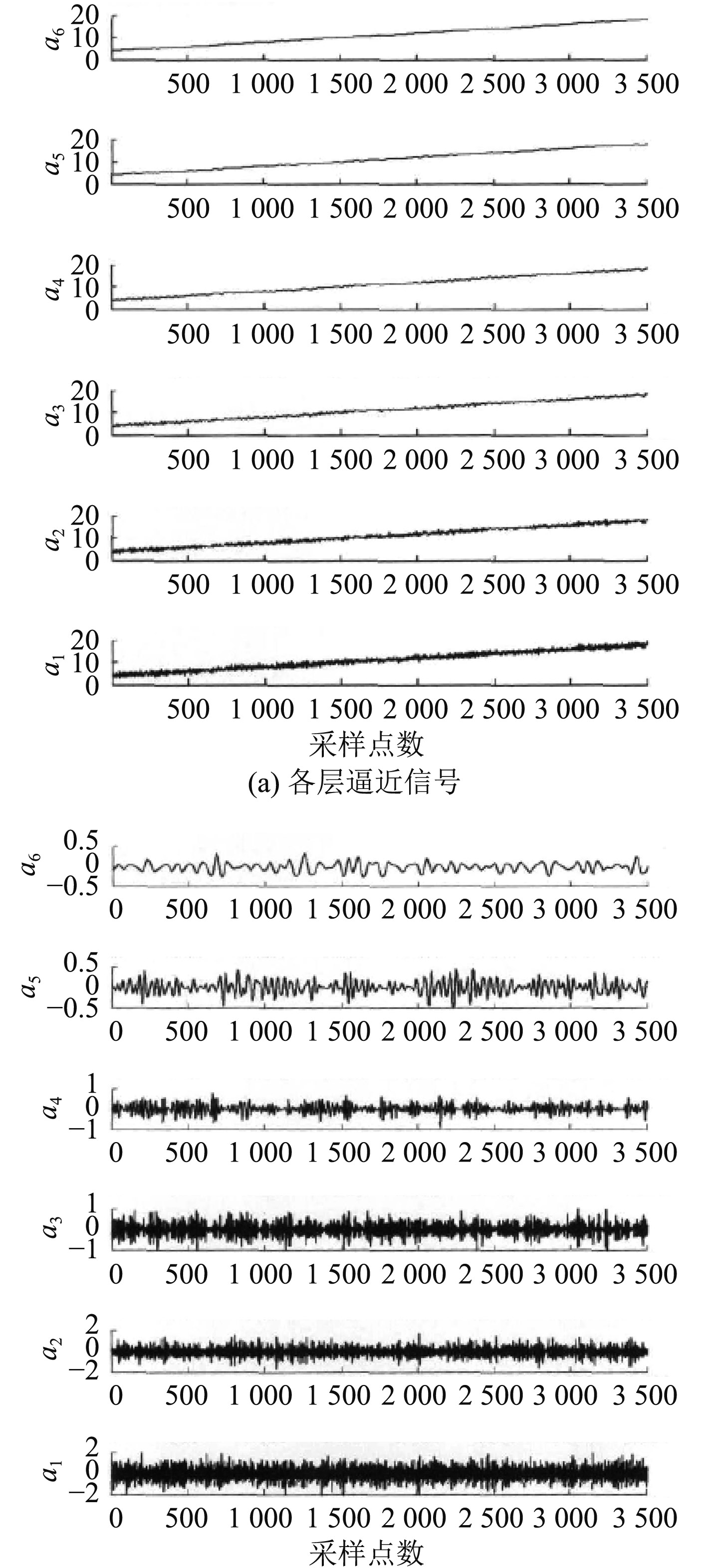
本文基于sym8小波函数对图3所示的含噪信号开展分解处理,仿真获得各层逼近信号和细节信号,详见图4。由图4(a)发现,随着分解层数N的增长,信号分解越来越明确、精准,噪声对其影响越来越低,当N=6时,输出信号基本可以精准重构。
|
图 4 小波分解后的信号降噪图 Fig. 4 Signal noise reduction after wavelet decomposition |
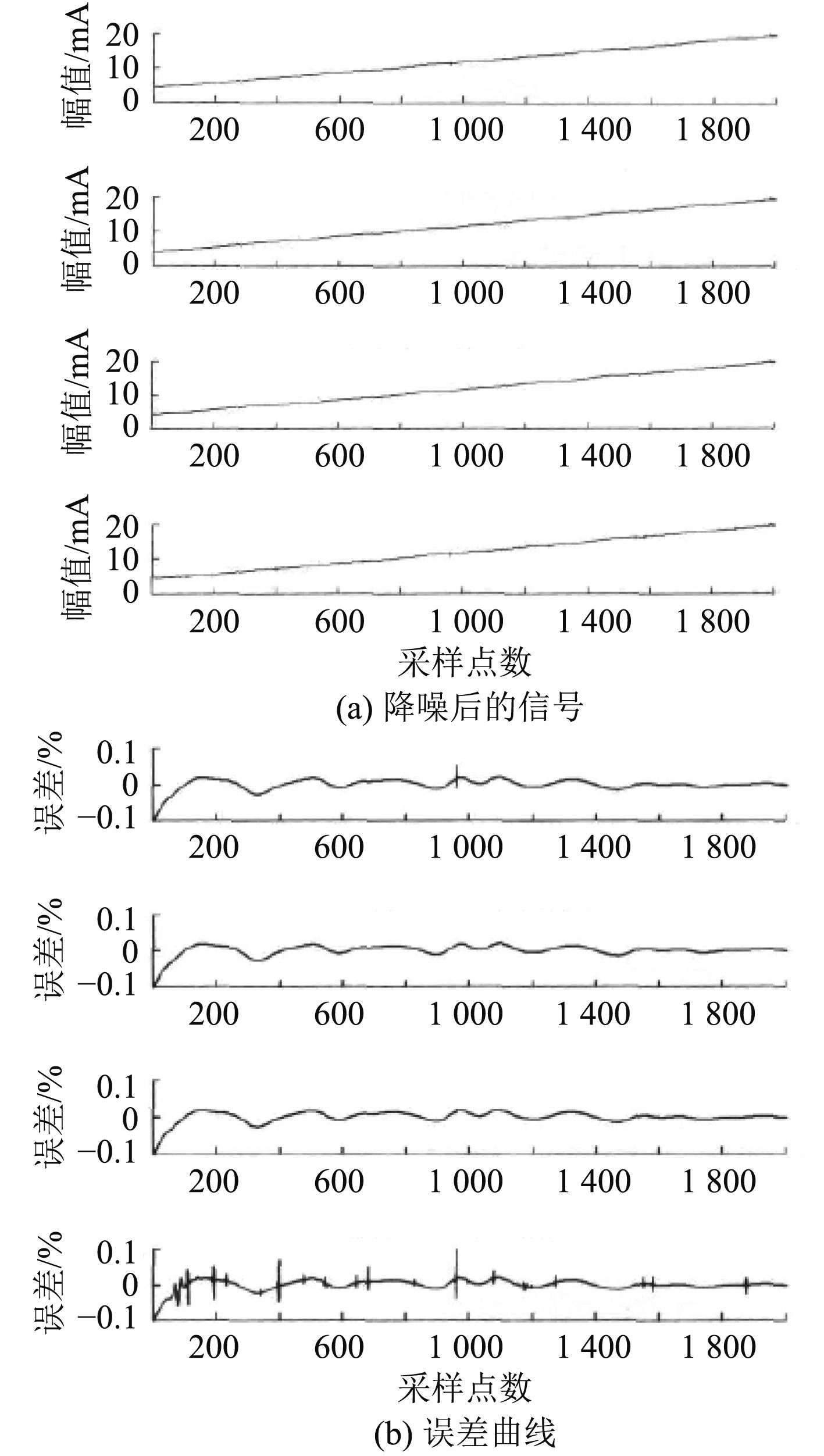
图5是行程传感器输出信号利用小波降噪处理后得到的信号曲线和误差曲线。借助sym8小波函数对含噪信号分解处理到6层后,选用了4种阈值规则进行降噪处理,分别是固定式阈值、无偏似然估计阈值、启发式阈值及极值原理选取阈值等,通过比较来选择最佳的阈值规则[2]。
|
图 5 小波函数降噪处理所得信息曲线和误差曲线 Fig. 5 The information curve and error curve of wavelet denoising |
由图5仿真结果发现,通过heursure阈值规则选定的阈值,其降噪效果最佳,获得信号误差最低,误差不超过0.05%。因此,本实验中选择的最佳阈值规则是heursure阈值,以此来进行信号降噪处理。
1.4 仿真验证由采样实验发现,行程传感器输出信号的有用信号均湮没在电磁噪声干扰环境里。把借助示波器获得的采样信号导入Matlab工作区域,开展信号的小波函数降噪处理过程。实验结果发现,通过对信号的逐层分解,随着分解层数越多,信号将越靠近实际信号,当分解到第6层时获得的信号已非常接近实际信号。通过小波降噪处理后,噪声信号被有效消除,除了刚开始误差约达到20%外,其后误差均在不断降低。通过比对理想信号和降噪后获得的信号,借助式(6)可以准确得到理想信号和降噪后信号的误差均值:
|
$e = \frac{1}{n}\sum\limits_{i = 1}^n {\sqrt {{{\left( {{{y'}_i} - {y_i}} \right)}^2}} } \text{,}$
|
(6) |
式中:n为采样点数;y'表为小波降噪处理得到的输出信号;y为理想输出信号。
当n取值2 000时,计算可得误差均值是0.3%。因此借助软硬阈值折中法对输出信号实施小波降噪处理后,船用行程传感器的电磁噪声干扰信号得到明显抑制。
2 相位差计算算法相位差计算算法主要思想是:信号接收线圈的 2 组差分线圈绕制过程中,其物理位差等同于超声波半波长,这就造成 2 组线圈信号采集时产生了约180°的相位差,故 2 组线圈采集的有用信号也将产生约180°的相位差[3]。基于此思想,可通过一种改进后得到的加窗傅里叶函数来得到信号相位计算公式,从而得到有用信号,除去不符合相位关系的噪声信号。设 2 组线圈的离散信号分别是S1,S2,相应的参数数量是50 000个。因离散信号个数有限,为降低频谱能量的泄漏,可选用窗函数进行信号的分析处理。对离散信号S1、S2分析采取加窗傅里叶变换处理,窗函数设为W。由于窗函数特征和窗的形状和宽度直接相关,故窗函数需符合窗谱主瓣和窗谱最大旁瓣的相对幅度尽量小的特点。对比可得,本实验选用的窗函数为布莱克曼窗,参数个数K1为200,公式如下:
|
$W\left( j \right) = 0.42 - 0.5\cos \left( {\frac{\pi }{{100}}j} \right) + 0.08\cos \left( {\frac{{2\pi }}{{100}}j} \right)\text{,}$
|
(7) |
其中,j=1,2,3,…,K1。
离散信号S1和S2对应的相位公式是:
1)S1实部:
|
${S_{1Rc}} = \sum\limits_{i = 1}^{{K_2}} {\sum\limits_{j = 1}^{{K_1}} {{S_1}\left( {i + j} \right)} } {}^ \circ \cos \left( {\frac{{2\pi }}{{{T_1}}}{}^ \circ i} \right){}^ \circ W\left( j \right)\text{,}$
|
(8) |
其中,i= 1,2,3,…,50 000;K1为窗函数参数个数;K2为S1参数个数和K1参数个数的差。
S1虚部:
|
${S_{1{\mathop{\rm Im}\nolimits} }} = \sum\limits_{i = 1}^{{K_2}} {\sum\limits_{j = 1}^{{K_1}} {{S_1}\left( {i + j} \right)} } {}^ \circ {\rm sim}\left( {\frac{{2\pi }}{{{T_1}}}{}^ \circ i} \right){}^ \circ W\left( j \right)\text{。}$
|
(9) |
其中,T1代表相关参数,结合实际信号特征,得
|
$\tan {\theta _1} = \frac{{{S_{1{\mathop{\rm Im}\nolimits} }}}}{{{S_{1Rc}}}}\text{。}$
|
2)S2实部:
|
${S_{2Rc}} = \sum\limits_{i = 1}^{{K_2}} {\sum\limits_{j = 1}^{{K_1}} {{S_2}\left( {i + j} \right)} } {}^ \circ \cos \left( {\frac{{2\pi }}{{{T_1}}}{}^ \circ i} \right){}^ \circ W\left( j \right)\text{,}$
|
(10) |
S2虚部:
|
${S_{2{\mathop{\rm Im}\nolimits} }} = \sum\limits_{i = 1}^{{K_2}} {\sum\limits_{j = 1}^{{K_1}} {{S_2}\left( {i + j} \right)} } {}^ \circ sim\left( {\frac{{2\pi }}{{{T_1}}}{}^ \circ i} \right){}^ \circ W\left( j \right)\text{,}$
|
(11) |
对应相位角θ2为:
|
$\tan {\theta _2} = \frac{{{S_{2{\mathop{\rm Im}\nolimits} }}}}{{{S_{2Rc}}}}\text{,}$
|
由此可得,两差分线圈的相位差为
|
$\left| {{\theta _1} - {\theta _2}} \right| = \left| {\arctan \left( {\frac{{{S_{1{\mathop{\rm Im}\nolimits} }}{S_{2Rc}} - {S_{1Rc}}{S_{2{\mathop{\rm Im}\nolimits} }}}}{{{S_{1{\mathop{\rm Im}\nolimits} }}{S_{2Rc}} - {S_{1Rc}}{S_{2{\mathop{\rm Im}\nolimits} }}}}} \right)} \right|\text{。}$
|
(12) |
借助改进的加窗傅里叶变换对电磁噪声干扰环境中输出信号的相位差进行处理,通过简单的反三角函数可以得到输出信号的相位差,最终输出时,若相位差为180°,则该信号将保留,否则置0,上述过程即为通过布莱克曼窗函数的简单三角函数获得离散信号相位差计算过程。需注意,相位差算法的基础条件是相位宽度符合180°±15°,在满足相位宽度情况下,加窗函数处理得到的有用周期信号可能有信号缺失的问题,稍微增大相位差范围,如相位宽度为180°±20°范围内,会出现造成加强的现象。针对此问题,充分考虑所得数据的特性,故给出综合算法对加噪信号进行降噪处理。
3 综合算法通过仿真实验结果可知,无论是单独选用小波软硬阈值降噪算法还是相位计算算法在进行输出信号的降噪处理时,都有某些不足之处:
1)小波软硬阈值降噪算法处理信号时,当分级层数很低时,其信号降噪效果非常不好,当分解层数太高时会发生有用信号失真问题;
2)相位差算法处理信号时,会出现降噪效果不好的问题。因此本文基于2种算法原理,充分结合各种算法的特点,设计形成了一种综合算法,即对 2 组线圈采集获得的输入信号先利用小波软硬阈值降噪算法进行降噪处理,后再通过相位差计算算法对输出信号进行降噪处理。由于综合算法相比较2种单一算法在信号降噪处理时,过程更复杂,若参数还和2种单一算法处理时相同,将造成严重的信号失真。因此,适当调整综合算法参数:1)小波降噪分解层数为5层;2)相位差算法的相位宽度范围180°±30°。随机从采集数据中选取500组,采用上述包含自适应算法在内的4种降噪算法对输出信号进行降噪处理,对比结果详见表1。由结果可知,通过综合算法降噪处理的原始信号,其数据的良好率显著上升,且有用信号失真率明显降低,得到有效控制。
|
|
表 1 4种降噪算法的处理结果对比 Tab.1 Comparison of processing results of 4 noise reduction algorithms |
综上所述,综合降噪算法可以大大提高行程传感器输出信号的降噪效率,降低电磁干扰噪声信号对行程传感器有用信号的干扰,提高船用行程有用信号的获取,保障船舶的顺利航行。
| [1] | 张伟, 师奕兵, 卢涛. 小波神经网络在无线随钻测量系统在泥浆信号检测中的应用研究[J]. 电子测量与仪器学报, 2008 (6): 98–101. |
| [2] | 乐波, 刘忠, 古天祥. 一种低信噪比线性调频脉冲信号参数提取方法[J]. 电子测量与仪器学报, 2008 (5): 76–79. |
| [3] | 胡柏青, 魏峥, 王伯雄. 强噪条件下基于小波降噪的陀螺仪声信号处理方法[J]. 传感技术学报, 2008 (6): 81–84. |
 2017, Vol. 39
2017, Vol. 39
