矢量水听器是一种能够探测水声振速、加速度等矢量信号的传感器[1],其低频指向性好,空间增益高,较传统声压水听器及其基阵体积更小[2-3]。根据工作原理的不同,矢量水听器可分为压差式和同振式[4],其中,同振式矢量水听器可直接测量声场中的质点振速,本身不产生明显的声场畸变,且性能参数稳定,已被广泛用于声呐浮标系统、拖曳阵低噪声测量等领域[5]。
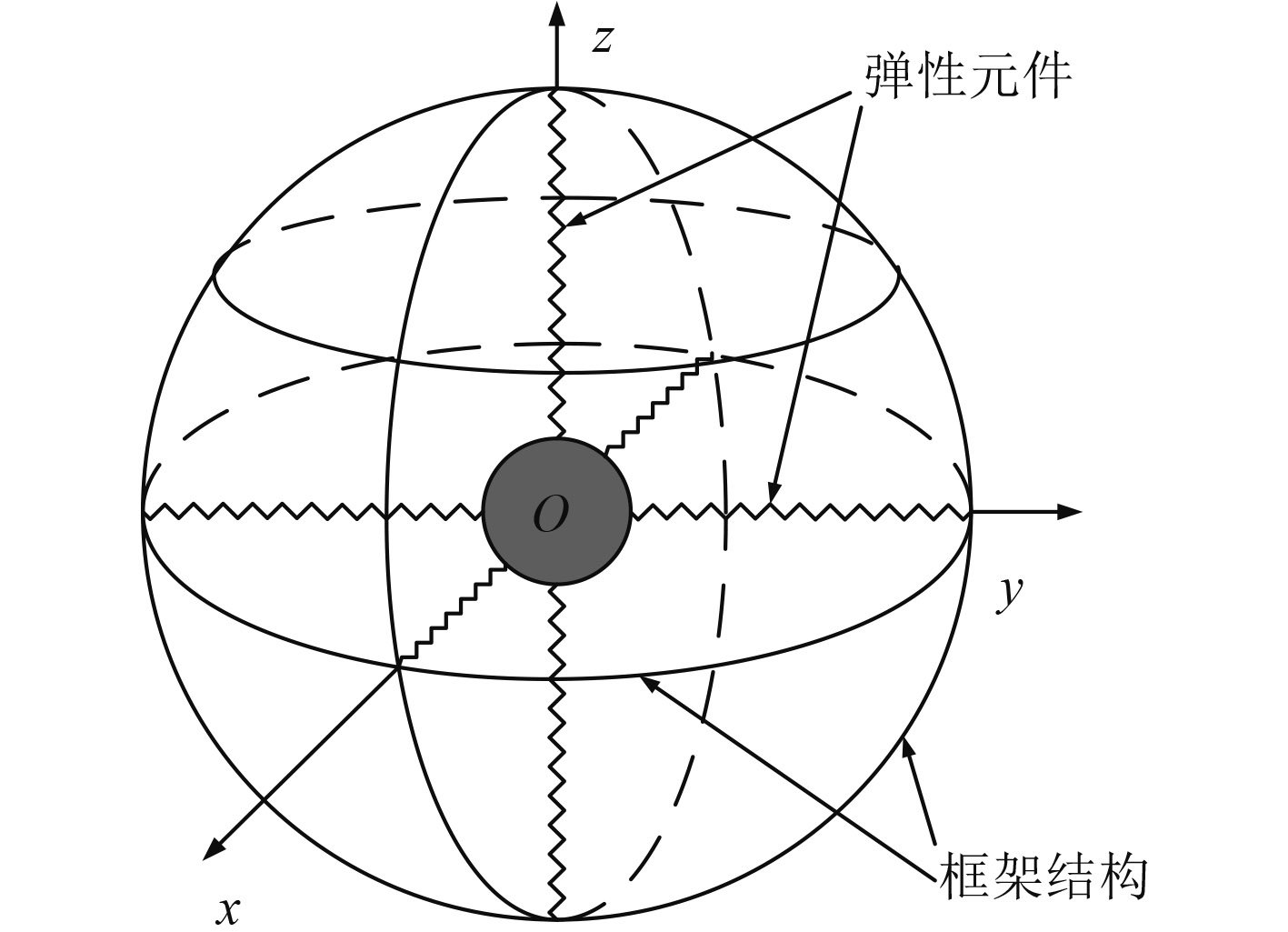
工作时,同振式矢量水听器一般通过弹性元件悬挂安装于大质量框架之上[6](见图1)。外围框架悬挂系统能效隔离工作平台振动对水听器的影响并保证其时间平均位置[7, 8],但也使其难以应用于深水炸弹、鱼水雷等空间有限的小尺寸工作平台。
本文通过分析压电加速度计幅频特性,获得一种中心位置固定的悬挂方案,研究具有该新型悬挂系统矢量水听器的基本结构设计,并对其性能进行仿真分析,为下一步工程应用提供一定理论依据。
|
图 1 同振球型矢量水听器悬挂示意图 Fig. 1 Schematic diagram of the resonant-sphere type vector hydrophone |
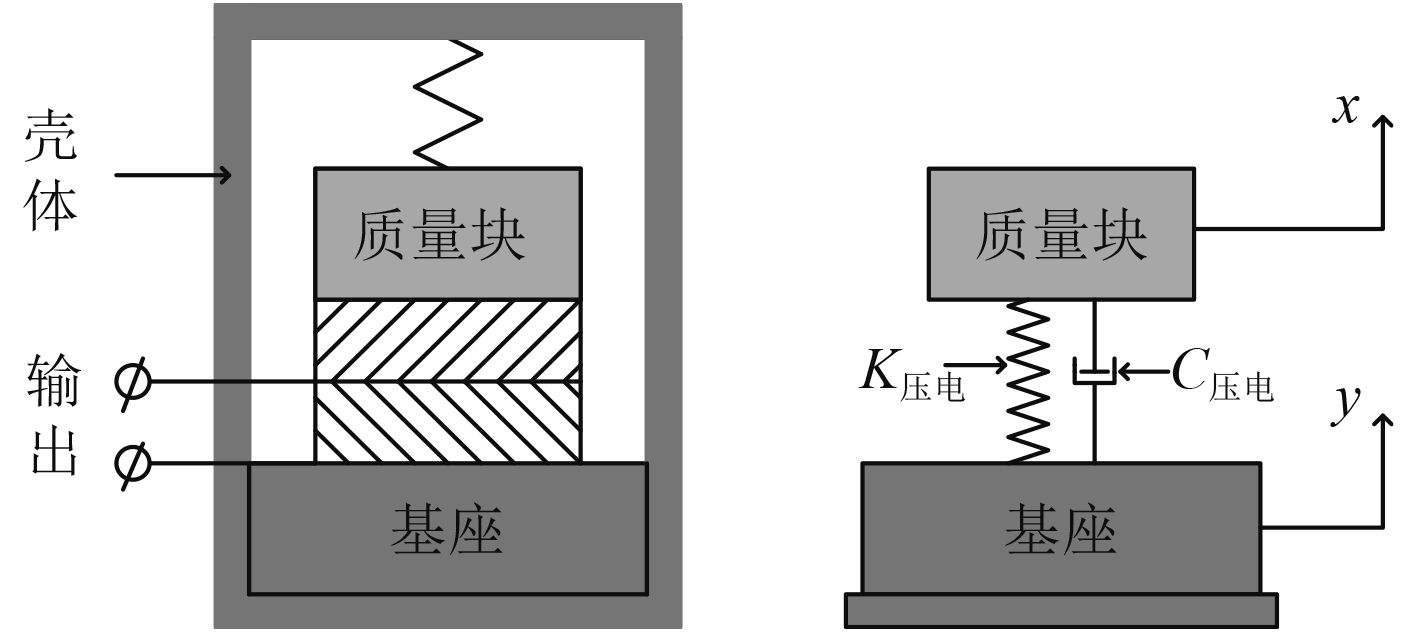
将压电加速度计简化为由集中阻尼器C、弹簧K和集中质量m构成的二阶单自由度系统,通过研究其频率特性,获得新型悬挂系统的设计思路。如图2所示,传感器感受到振动体加速度时的运动方程式为:
|
$m\frac{{{{\rm d}^2}x}}{{{\rm d}{t^2}}} + c\left( {\frac{{{\rm d}x}}{{{\rm d}t}} - \frac{{{\rm d}y}}{{{\rm d}t}}} \right) + k\left( {x - y} \right) = 0\text{。}$
|
(1) |
式中,y为壳体的绝对位移,x为质量块的绝对位移。
|
图 2 加速度计简化模型 Fig. 2 Simplified model of accelerometer |
令ωn和ζ分别为加速度计固有频率和阻尼比,y0为壳体的位移幅值,ω为壳体的振动角频率,Ur为该振动系统稳态振动位移的幅值,可求得压电加速度计的幅频特性表达式及其对应曲线为:
|
$A\left( \omega \right) = \frac{{{U_r}}}{{{y_0}}} = \frac{{{{\left( {\frac{\omega }{{{\omega _n}}}} \right)}^2}}}{{\sqrt {{{\left[ {1 - {{\left( {\frac{\omega }{{{\omega _n}}}} \right)}^2}} \right]}^2} + {{\left[ {2\zeta \frac{\omega }{{{\omega _n}}}} \right]}^2}} }}\text{。}$
|
(2) |

|
图 3 加速度计外壳与内部质量块相对位移幅频特性曲线(ζ=0.1) Fig. 3 Relative displacement amplitude frequency characteristic curve of the shell and mass of the accelerometer (ζ=0.1) |
可见弹性元件的结构在不同频率的外部激励下会出现3种运动状态:当激励频率远低于结构固有共振频率时,整个系统刚度可控,外壳和内部质量块一前一后地协同动作;随着频率增加,在系统共振频率附近,内部质量块的运动严重偏离,出现数倍于激励值的位移;频率远高于系统共振频率时,系统惯性锁死,内部质量块相对外部激励而言将保持原地不动。
根据此结论可设计一种新型悬挂方案,即用刚性支柱代替加速度计内部质量块,并将水听器通过支柱与工作平台相连。
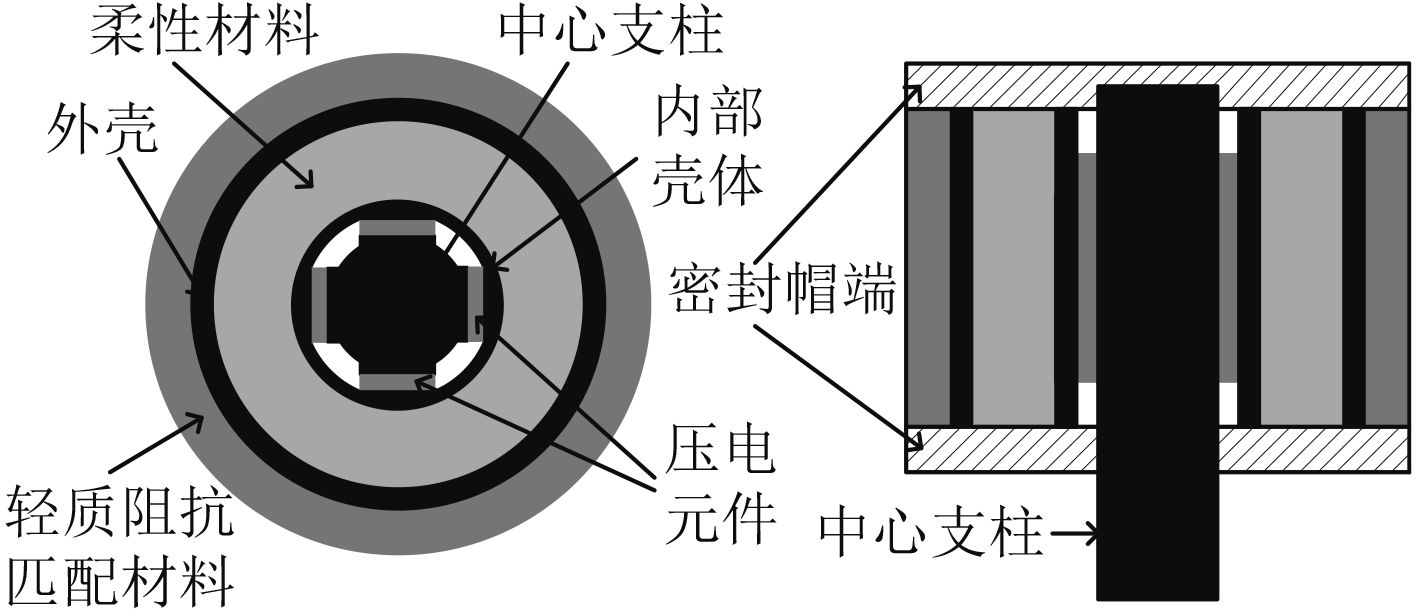
2 新型矢量水听器设计方案具有中心固定结构的矢量水听器如图4所示。水听器外壳需满足中性浮力,可采用压电陶瓷材料,用以测量声压信息;柔性材料层使用柔顺系数大的橡胶材料;内壳采用密度较小的刚性金属;内壳通过4块对称的压电陶瓷元件固定于中心支柱之上。
|
图 4 中心固定式矢量水听器结构示意图 Fig. 4 Schematic diagram of the structure of the center fixed vector hydrophone |
工作时,水听器通过中心支柱安装于工作平台之上。在声波激励下,外壳便产生与声质点同幅同相的振动,同时柔性材料层将该振动传递给内壳,并耦合到压电元件上,压电元件内外表面便产生了比例于中性浮力外壳振动的电信号。同样,此电信号也与周围水质点的振动成比例。
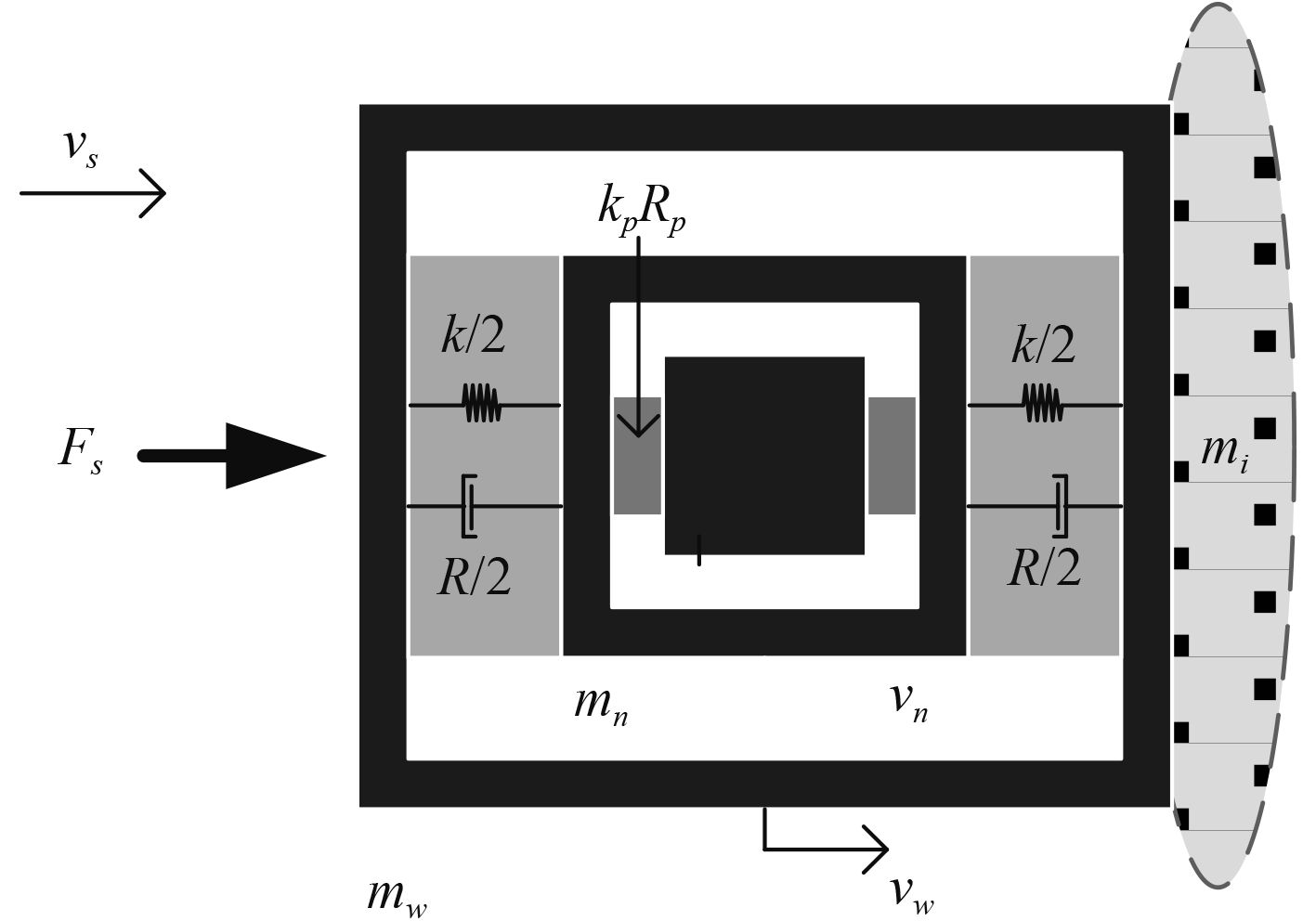
3 性能仿真与分析建立新型矢量水听器的一维振速通道简化模型(见图5)。其中,vs,vw和vn分别为水质点、外壳和内壳的振速;mw,mn,ms和mi分别为外壳质量、内壳质量、水听器排开水柱质量和共振质量;k,R,kp和Rp分别为柔性材料层和压电元件的刚度和阻尼;
|
图 5 一维振速通道简化模型 Fig. 5 Simplified model of one dimensional velocity channel |
系统动力学回路方程为
|
$\left\{ \begin{aligned}& {F_s} = {v_w}\left[ {R + \frac{k}{{j\omega }} + j\omega \left( {{m_i} + {m_w}} \right)} \right] + {v_n}\left[ { - R - \frac{k}{{j\omega }}} \right],\\& 0 \!=\! {v_w}\left[ { - R - \frac{k}{{j\omega }}} \right] \!+\! {v_n}\left[ {R \!+\! \frac{k}{{j\omega }} \!+\! \left( {{R_p} \!+\! j\omega {m_n} \!+\! \frac{{{k_p}}}{{j\omega }}} \right)} \right]\text{。}\end{aligned} \right.$
|
(3) |
由此可求得振速通道压电元件电压输出eoc与质点振速vs的关系式为
|
$\frac{{{e_{oc}}}}{{{v_s}}} \approx R{\left( {1 + \frac{k}{{{k_p}}}} \right)^{{\rm{ - }}1}}\left( {\frac{{ - {h_{33}}{t_p}}}{{c_{33}^D}}} \right),$
|
(4) |
式中,h33、
对于该水听器,其外壳、内壳与柔性材料层组成的振动系统,具有与前述加速度计模型相同的共振特性,其共振频率决定着水听器工作频率的下限ωl,此处由柔性材料层刚度、水听器所排开水柱质量及其共振质量共同决定。压电元件作为一种弹性材料,与内壳耦合产生共振,决定了水听器的工作频率上限ωh。2个频率限制条件如下所示:
|
${\omega _l} = \sqrt {\frac{k}{{{m_s} + {m_i}}}} ,\;\;\;\;{\omega _h} = \sqrt {\frac{{{k_p}}}{{{m_n}}}}\text{。}$
|
(5) |
|
|
表 1 分析水听器理论模型所用参数列表(mm) Tab.1 The list of parameters used in the analysis of the theoretical model of hydrophone |
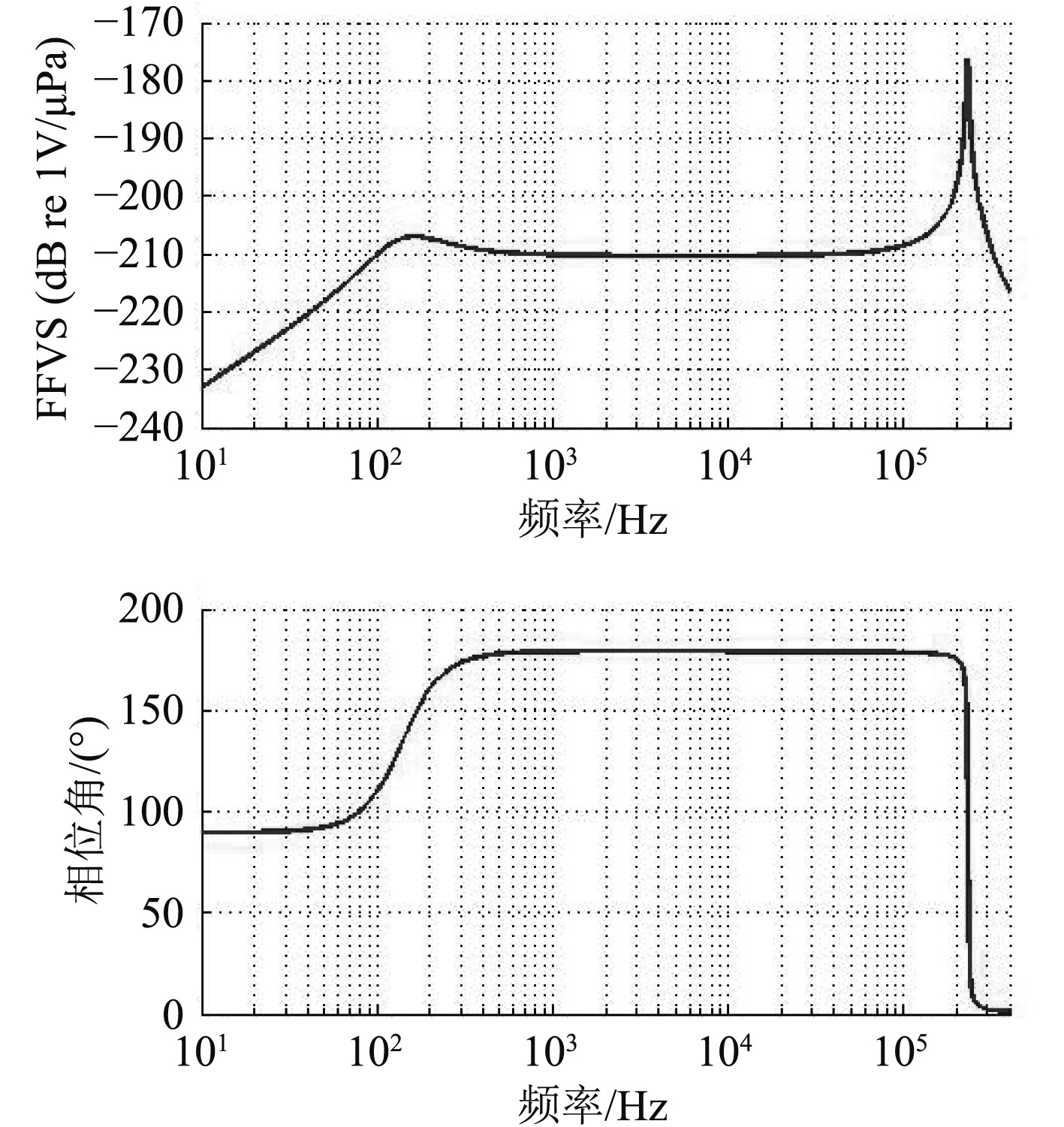
在满足中性浮力的基础上,给定一组结构参数(见表1),对压电元件的开路电压在全部工作频段内进行仿真计算,得到自由场声压灵敏度和相位特性曲线,如图6所示。由图可知,2个频率限制条件决定水听器稳定工作的频段范围;电压响应相位角输出与质点振速保持180°的偏置,体现了该种结构设计的惯性特征。
将给定的结构参数和材料参数代入(4)式计算水听器振速灵敏度为
|
${M_u} = \frac{{{e_{oc}}}}{{{v_s}}} \approx {\rm{ - 45}}{\rm{.20 V}}/{\rm{m}} \cdot {{\rm{s}}^{{\rm{ - 1}}}}\text{。}$
|
(6) |
用分贝表示时,振速通道灵敏度为:
|
$\begin{split}{M_{uL}} = & 20\log \left[ {{M_u}\left( {\frac{1}{{\rho c}}} \right)/{{\left( {{M_e}} \right)}_o}} \right] = \\& - 209.3 \; {\rm{dB}} \; {\rm{re 1V}}/{\rm{\mu Pa}}\text{。}\end{split}$
|
(7) |
仿真计算结果表明,该新型矢量水听器在工作频段内(此处约1~30 kHz),振速通道等效电压响应约为–209 dB,幅度波动小于0.2 dB,其相位角约为180°,角度波动小于0.3°,可满足水下声场振速信息的测量要求。
|
图 6 通频带内振速通道响应曲线 Fig. 6 Channel response curve of the frequency band |
本文通过研究压电加速度计幅频特性,获得了一种新型悬挂系统设计方案,给出了采用该新型悬挂方案的矢量水听器的结构设计,并对其性能进行了仿真研究。结果表明:1)中心固定式矢量水听器的结构设计能够实现声场中声压与质点振速信息的直接测量;2)中心固定内置式悬挂系统,可有效缩小水听器外部体积,适合水下小尺寸平台的安装使用;3)在工作频段内(此处约1~30 kHz),水听器振速通道等效电压响应约为–209 dB,幅度波动小于0.2 dB,其相位角约为180°,角度波动小于0.3°;
中心固定式矢量水听器结构紧凑、安装方便,可有效扩展矢量水听器的应用空间并提高其性能与使用的方便性,对于增强水下平台的声探测能力有重要意义。但是由于悬挂系统的特殊性,使得水听器工作频率下限较高,不利于水下目标的远程测量。一方面可进一步研究改善水听器结构设计,另一种可行改善方法是构建空间阵列式的矢量阵,通过设定接收单元的接收距离,实现远程水下目标的低频探测[10]。
| [1] |
孙贵青, 李启虎. 声矢量传感器研究进展[J]. 声学学报, 2004, 29 (6): 481–490.
SUN Guiqing, LI Qihu. Progress of study on acoustic vector sensor[J]. Chinese Journal of acoustics, 2004, 29 (6): 481–490. |
| [2] | 杨德森, 洪连进. 矢量水听器原理及应用引论[M]. 北京: 科学出版社, 2009, 1–2. |
| [3] |
张椿, 陈斌, 田忠仁. 三维同振式矢量水听器设计[J]. 声学与电子工程, 2009, 46 (4): 5–7.
ZHANG Chun, CHEN Bin, TIAN Zhongren. Design of three dimensional co-vibration vector hydrophone[J]. Acoustic and electronic engineering, 2009, 46 (4): 5–7. |
| [4] |
孙贵青. 矢量水听器检测技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2001.
SUN Gui-qing. Research on technology of detection vector hydrophone[D]. Harbin: Harbin Engineering University, 2001. |
| [5] |
陈洪娟, 杨士莪, 王智元, 等. 同振式矢量传感器设计方法的研究[J]. 声学技术, 2005, 24 (2): 80–83.
CHEN Hongjuan, YANG Shie, WANG Zhiyuan, et al. Research on the design method of the co-vibration vector sensor[J]. Chinese Journal of acoustics, 2005, 24 (2): 80–83. |
| [6] |
张俊. 潜标平台下的矢量水听器悬挂系统声学性能影响研究[D]. 哈尔滨: 哈尔滨工程大学, 201.
ZHANG Jun. Study on the influence of acoustic performance of submerged buoy system under the platform of the vector hydrophone suspension[D]. Harbin: Harbin Engineering University , 201. |
| [7] |
贾志富. 三维同振型矢量水听器的特性及其结构设计[J]. 应用声学, 2001, 20 (4): 15–20.
JIA Zhifu. Characteristics and structural design of three-dimensional co-vibrati0n vector hydrophone[J]. Application of acoustic, 2001, 20 (4): 15–20. DOI: 10.11684/j.issn.1000-310X.2001.04.005 |
| [8] |
时胜国, 杨徳森. 弹性元件对同振型振速水听器的影响[J]. 应用声学, 2004, 23 (5): 21–26.
SHI Sheng-guo, YANG De-sen. Elastic element influence on the vibration velocity hydrophone[J]. applied acoustics, 2004, 23 (5): 21–26. DOI: 10.11684/j.issn.1000-310X.2004.05.008 |
| [9] | MCCONNELL J A. Practical experiences with inertial type underwater acoustic intensity probes[J]. JASA, 2002, 27 (8): 19–21. |
| [10] |
石杰, 相敬林, 陈韶华. 间距可调的小尺寸空间十字阵对水下低频声源的被动定向[J]. 探测与控制学报, 2006, 28 (5): 12–15.
SHI Jie, XIANG Jinglin, CHEN Shaohua. The passive orientation of the small size space cross array with adjustable pitch to underwater acoustic source[J]. Journal of detection and control, 2006, 28 (5): 12–15. |
 2017, Vol. 39
2017, Vol. 39
