声呐是目前海洋勘探与目标探测的主要设备,随着海洋活动的愈加频繁,水下充斥着各种来源不明的声发射源,这些声呐源发射各种不同的信号,但是这些信号存在着高度的相似,导致无法鉴别其来源,信息安全的重要性成为水下活动的关键问题[1]。
当前声呐信号的鉴别方法主要为结合数字水印技术的研究,当前声呐信号鉴别最新的方法是基于数字水印技术的信号鉴别,通过检测接收信号中是否含有水印鉴别其身份。Mobasseri B G和Lynch R S等先后于2008年和2010年针对主动声呐信号的鉴别提出分别用短时傅里叶变换(STFT)和离散余弦变换(DCT)进行水印嵌入[2-3]。但是算法比较复杂而且没有充分考虑到海洋信道多途、衰减以及多普勒频移等因素。又在2011年提出信道相关特性对水印声呐的影响以及利用嵌入水印提高探测性能等方法[4]。在声呐信号的鉴别中已经研究出现的算法,虽然已经将信道衰减以及多普勒等因素考虑在内,但是嵌入水印之间的脉冲干扰对检测的影响仍然没有得到改善,水印在信道中的鲁棒性较差并且也严重影响鉴别精度。可见检测精度和水印鲁棒性这2个方面的提高对声呐信号的鉴别有着至关重要的意义,本文就这2个方面进行研究,并且发现分数阶傅里叶变换(FRFT)有着较好的时频特性,结合此基础提出了基于(FRFT)的数字水印声呐鉴别算法。
分数阶傅里叶变换可以看作是傅里叶变换的一种广义的形式,近年来在信号处理方面获得了广泛的关注,它融合了信号在时域和频域的特性,此方法的应用最先出现在数字图像水印中,并且具有较好的效果,文献[5-6]为水印在图像中的应用,在本文将水印嵌入到声呐信号的分数阶傅里叶变换中,在水印的嵌入中所取FRFT(分数阶傅里叶变换)的幂次作为自由度,同时也作为嵌入密钥,不仅增强了水印的安全性同时也增加了水印的鲁棒性。
1 基于FRFT的声呐数字水印嵌入原理 1.1 理论基础FRFT作为傅里叶变换的一种广义形式,它可以解释为信号在时频平面内坐标轴绕原点逆时针旋转任意角度后构成的分数阶傅里叶变换域上的表示方法。如果信号的傅里叶变换可看成将其在时间轴上逆时针旋转π/2到频率轴上的表示,则FRFT可以看成将信号在时间轴上逆时针旋转角度α到μ轴上的表示(μ轴被称为分数阶Fourier域),信号x(t)的分数阶Fourier变换(FRFT)定义为:
|
${X_\alpha }(u) = \{ {F^u}[X(t)]\} (u) = \int_{ - \infty }^{ + \infty } {X(t){K_\alpha }} (t,u){\rm{d}}t\text{,}$
|
(1) |
式中FRFT的变换核
|
${K_\alpha }(t,u) = \left\{ \begin{array}{l}\sqrt {\displaystyle\frac{{1 - j\cot (\alpha )}}{{2\pi }}} \exp (j \displaystyle\frac{{{t^2} + {u^2}}}{2} \times \\\cot (\alpha ) - tu\csc (\alpha ))\;\;\;\;\;\;\;\;\;\;\;\alpha \ne n\pi \\\delta (t - u)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\alpha = 2n\pi \\\delta (t + u)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\alpha = (2n + 1)\pi \end{array} \right\}\text{,}$
|
(2) |
式中:α=pπ/2为FRFT的旋转角度;Fα为α阶的分数阶傅里叶算子符号。其逆变换为:
|
$x(t) = \int_{ - \infty }^{ + \infty } {{X_\alpha }(u){K_\alpha }} (t,u){\rm{d}}t\text{。}$
|
(3) |
当p=1(α=π/2)时,FRFT就退化为传统的傅里叶变换,当变换阶数接近于1时反应的是频域特性,当变换阶数接近于0时候反应的是时域特性。
1.1.1 分解法离散分数傅里叶变换所谓分解方法是指根据FRFT(分数阶傅立叶变换)的表达式,将FRFT分解为信号的卷积形式,从而利用FFT来计算FRFT。文中利用由Bultheel A等提出的分解型快速算法[7],非常适合于对信号进行实时的FRFT数值计算。但是这种快速算法的运算机理决定了在进行FRFT数值计算之前必须先对原始信号进行量纲归一化处理。采用量纲归一化的离散分数阶Fourier变换定义为:信号的时域区间为
|
$\Delta x = \sqrt {\Delta t\Delta f}\text{,} \;\;x = t/s\text{,}\;\;\;v = fxs\text{,}$
|
(4) |
则区间可归一化为
分阶傅里叶变换可以重写为:
|
$\begin{split}& {X_p}(u) = {A_\alpha }\exp [j\pi {u^2}\cot \alpha ] \times \\& \int_{ - \infty }^{ + \infty } {x(t)\exp [j\pi {t^2}\cot \alpha ]} \exp [ - j2\pi ut\csc \alpha ]{\rm{d}}t\text{,}\end{split}$
|
(5) |
其中
|
$\begin{array}{l}0 < \left| \alpha \right| < \pi \\{A^\alpha } = \exp [j(P - 1)\pi /4]/\sqrt {\left| {\sin \alpha } \right|} ,\alpha = P\pi /2\text{。}\end{array}$
|
由上述式子分数阶傅里叶变换可分为:
1)信号与线性调频函数的相乘,
2)傅里叶变换(变元乘以尺度系数csc α),
3)再与线性调频函数相乘,
4)乘以一复数因子。
最后归一化之后的表达式为:
|
$\setcounter{equation}{6}\begin{aligned}& {X_P}(\displaystyle\frac{m}{{2\Delta x}}) = \displaystyle\frac{{{A_\alpha }}}{{2\Delta x}}\sum\limits_{n = - N}^N {\exp [\displaystyle\frac{{j\pi (\cot \alpha ){m^2}}}{{{{(2\Delta x)}^2}}} - \displaystyle\frac{{j2\pi (\csc \alpha )mn}}{{{{(2\Delta x)}^2}}} + } \\& \displaystyle\frac{{j\pi (\cot \alpha ){n^2}}}{{{{(2\Delta x)}^2}}}]x(\displaystyle\frac{n}{{2\Delta x}}) =\\& \displaystyle\frac{{{A_\alpha }}}{{2\Delta x}}[\exp \frac{{ - j\pi \tan \frac{\alpha }{2}{m^2}}}{{{{(2\Delta x)}^2}}}]X\sum\limits_{n = - N}^{n = N} {\exp [\displaystyle\frac{{j\pi (\csc \alpha ){{(m - n)}^2}}}{{{{(2\Delta x)}^2}}}]} \times \\& [\exp \displaystyle\frac{{ - j\pi \tan \frac{\alpha }{2}{m^2}}}{{{{(2\Delta x)}^2}}}]x(\displaystyle\frac{n}{{2\Delta x}})\text{。}\\& {A^\alpha } = \exp [j(P - 1)\pi /4]/\sqrt {\left| {\sin \alpha } \right|}\text{,} \\& \alpha = P\pi /2\text{,}\;\;N = {(\Delta x)^2}\text{,}\;\;\;0.5 \leqslant p \leqslant 1.5\text{。}\end{aligned}$
|
(6) |
具体计算时首先对信号样本进行2倍插值,经过式(6)计算之后,在对其结果进行2倍插值得到分数阶傅里叶变换的N个样本值,虽然上述p的值为0.5~1.5,但是利用分数阶傅里叶变换的周期性和相加性可以推广到所有阶次的分数阶傅里叶变换。
1.2 声呐数字水印嵌入系统通过在信号的分数阶傅里叶变换域中嵌入具有鲁棒性的水印实现FRFT系数的修改,其中鲁棒性水印的来源主要是高斯随机序列,结合信号在分数阶傅里叶变换的系数特性,选择合适的水印位置,通过计算检测统计量进行检测。
1.2.1 水印生成水印序列的选取一般要求具有较好的自相关特性,高斯序列满足这一要求并且其自相关函数具有冲激函数的特点。由高斯分布的随机序列构成的水印具有很好的鲁棒性。高斯噪声具有能量均匀、相关性强的特点。研究表明利用随机序列作为水印进行嵌入,不会影响信号的整体性能[8]。检测时若在某一偏移处存在明显的峰值,超过了设定的阈值,则说明水印存在,可以通过改变设定的阈值来改变水印的鲁棒性,此方法相比其他水印方法突出了鲁棒性,检测算法也比较简单。因此,采用随机序列作为水印序列是较好的选择。本文产生的是复随机序列,2个高斯随机序列的组合为复随机序列,产生均值为0,方差为1的高斯序列,长度均为M,R1和R2,组成一个复随机序列
在载体信号进行水印嵌入之前要进行预处理,首先对声呐波形x(t)进行取样得到离散点,取样点为N对应的离散值产生离散信号X:
|
$X = \{ x(n),n = 1,2...,N\} \text{,}$
|
(7) |
利用伪噪声发生器产生2个长度均为M,分别服从(0,σ1)和(0,σ2)的随机序列R1和R2,组成一个复随机序列
对产生的离散信号X进行分解法分数阶离散傅里叶变换,自由度为p,在研究基础上自由度的选择在[0,1]范围内[5],得到分数阶傅里叶变换系数
|
$S_i^w = {S_i} + {\rm{a}}W = {\rm{a}}(R_1 + jR_2),i = L + 1,...L + M\text{。}$
|
(8) |
其中a为嵌入强度。
嵌入之后进行自由度为–p的分数阶傅里叶变换得到水印之后的信号。
1.2.3 水印嵌入准则水印声呐并不影响声呐信号的连续性以及带宽,嵌入的水印如若带来超出声呐本身的额外能量是不希望的,水印声呐能量由如下的表达式表示:
|
${E_{xw}} = \int {{x^2}(t){\rm{d}}t\;} + {k^2}\int {{w^2}} (t){\rm{d}}t + k\int {x(t)w(t){\rm{d}}t} \text{。}$
|
(9) |
其中K为水印强度。
由式可以看出嵌入的水印为非水印的声呐附加了能量,其中嵌入强度产生的SWR(信号水印比)在15~25 dB范围内,仿真环境中的SNR为10~15 dB的噪声,SWR最低为15 dB,其能量低于背景噪声,并且水印和声呐非相关,所以嵌入的水印能量对声呐没有实际的影响。
水印嵌入同样也受到水印能量的分布约束,水印嵌入主要是为了提高声呐源的鉴别精度,信号在时频域中,水印可以嵌入在瞬时频域(IF)内部,线性调频信号的(IF)的分布呈现线性特征,水印也可以嵌入在(IF)之外但是在时频域内,水印嵌入在(IF)内,它可以有效地隐藏在(IF)之下,但是需要较小的SWR(较强的水印)以便检测,嵌入在(IF)之外若达到相同的检测效果则需要较高的SWR,水印则比较弱。
1.2.4 水印检测方法本文采用的算法为Bultheel A等提出的分解型快速算法[7],使用该算法进行FRFT数值运算时会产生一定的误差[9]。为了进行有效的检测,选择合适的检测统计量,水印的检测通过计算检测统计量d并与预先确定的一个阈值比较来完成。检测统计量d由下式计算:
|
$\begin{split}d \!= &\!\!\! \sum\limits_{i \!=\! L + 1}^{i = L + M} \!\!\!{[R_{1i} \!-\! jR_{2i}]} S_i^{(a)} \!=\!\!\! \sum\limits_{i = L + 1}^{i = L + M} \!\!\! {[R_{1i} \!-\! jR_{2i}][{S_i} \!\!+\!\! a(R_{1i} \!\!+\!\! R_{2i})]} \!= \\[7pt] & a \!\! \sum\limits_{i = L + 1}^{i = L + M} \!\! {[R_{1i}^2 + R_{2i}^2]} + \!\! \sum\limits_{i = L + 1}^{i = L + M} {[{S_i}R_{1i} - j{S_i}R_{2i}]} \text{,} \end{split}$
|
(10) |
式中,
|
$E(d) = aM(\sigma _1^2 + \sigma _2^2)\text{,}$
|
(11) |
对于没有嵌入水印的信号,则有:
|
$E(d) = 0\text{。}$
|
(12) |
而在2种情况下,d的方差相同,即通常嵌入水印的FRFT系数的数量M非常大(可达数百个),因此,有水印和无水印2种情况下|d|的值将会相差很大,这种方法当设定适当的阈值,可以很好地将水印检测出来。鉴于FRFT不可避免地会对系数带来一定的误差,使|d|的实际值小于理论值,且不同的变换角度引起的误差也不尽相同,根据经验,在应用中,阈值稍小于|d|/2。仿真结果也验证了其有效性。
2 仿真分析本文的仿真在如表1中模拟的仿真环境中进行,主要是通过不同水印序列,不同的变换阶数检测器的响应对水印进行测试以及在变换阶数相同时不同SNR(信噪比)下检测响应曲线进行分析,本文同时也对水印容量的2个相关变量嵌入强度以及嵌入水印比进行了分析。
首先说明仿真中出现的SWR
|
$SWR = 10\lg \frac{{{\text{载体信号的功率}}}}{{{\text{嵌入水印的功率}}}}\text{。}$
|
表1为仿真环境的说明,以及线性调频信号的仿真参数说明。
|
|
表 1 仿真参数 Tab.1 Simulation parameters |
|
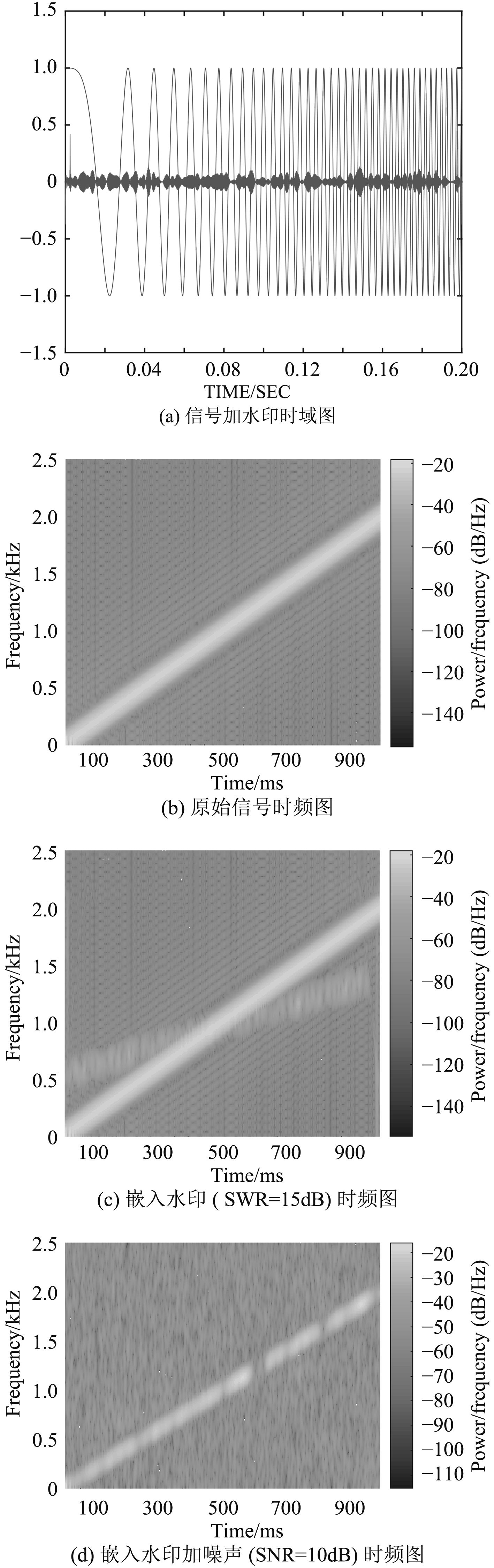
图 1 时频图 Fig. 1 Time frequency diagram |
如上仿真分析时频图表示,图1(a)为当变换阶数为0.8,嵌入水印强度为0.3时的信号与水印时域图。图1(b)为原始载体时频图,比较图1(c)和图1(d)对比看出水印被噪声隐藏具有不可见性,图1(c)可以看出水印嵌入靠近(IF)瞬时频带带宽内,瞬时频率(IF)带宽是指信号存在于时频域分布范围内,通过上述4个图可看出线性调频信号时频特性不受水印影响。
2.2 水印容量根据上述参数,本文的检测阈值根据嵌入水印检测统计量d的模值选取,检测阈值设置为0.3。仿真中使用了51个高斯随机序列,其中序号为第25个的水印序列为本文中嵌入的水印,其余序列产生密钥均不同于正确水印,并且对不同的变换阶数也进行了测试,仿真结果如图2所示。

|
图 2 不同水印序列和阶数的检测 Fig. 2 Detection of different watermark sequence and order |
从图2(a)和图2(b)可以看出来只有在水印序号为第25个时才会正确检测出来,并且只有在变换阶数正确的条件下才会检测出水印,水印序列“种子”的基础上增加了另外一个密钥变换阶数。增加了水印的安全性。
|
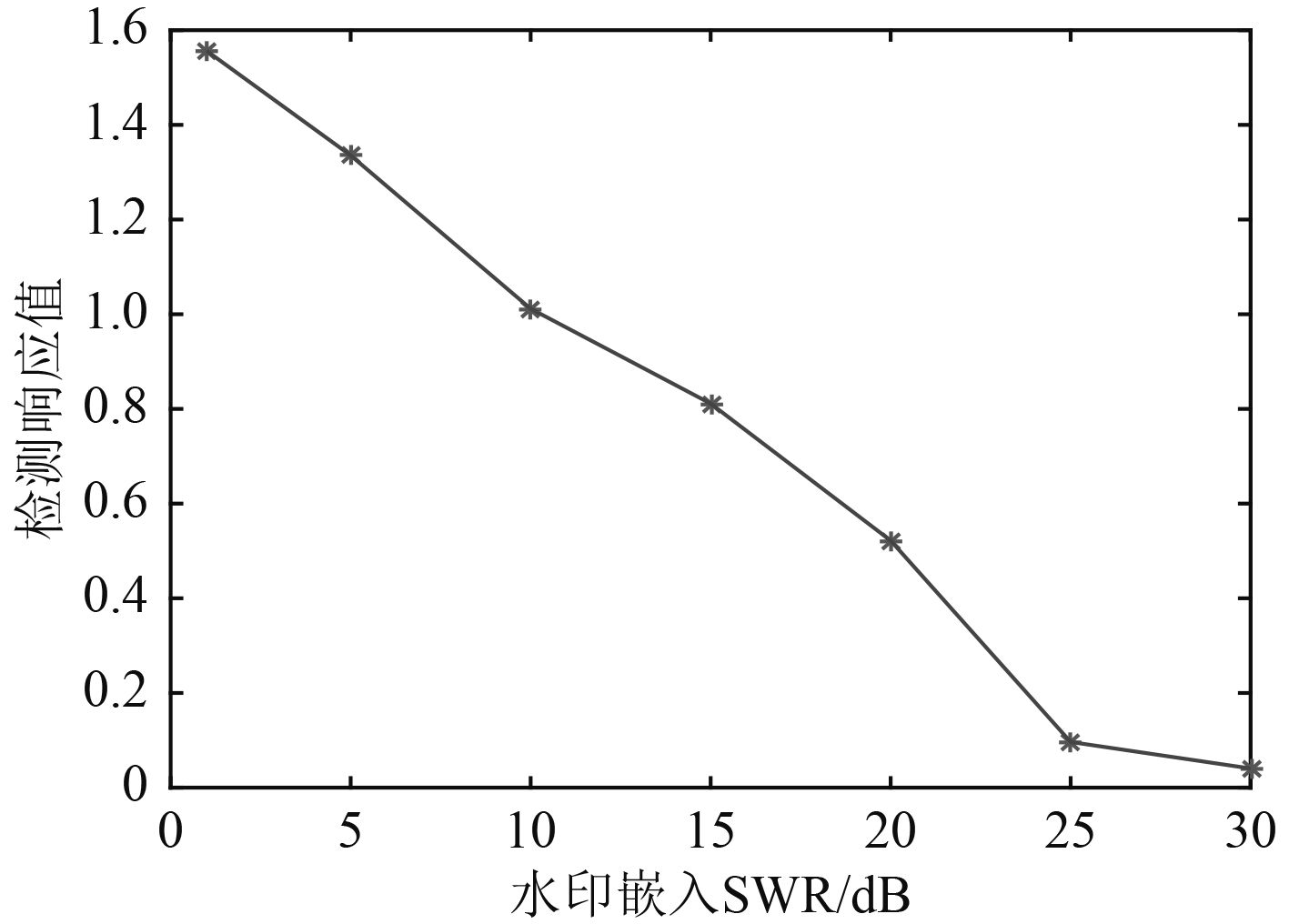
图 3 不同SWR的检测器响应 Fig. 3 Detector response of different SWR |
|
|
表 2 嵌入强度和SWR对比数据 Tab.2 Contrast data of embedding strength and SWR |
由图3可以得到,水印嵌入强度在较大时,经过计算水印嵌入强度为3.03时此时的SWR趋于数值0,已经达到极限值,当水印强度为0.1时,SWR数值达到30,但是此时的检测响应值已经低于检测阈值,如果嵌入强度较低就会出现虚警。上述可以得出SWR在10~18 dB较为合适,当SWR过小时如图1(a)为水印嵌入强度为0.5的信号与水印时域图。嵌入水印为高斯序列,通过式(10)可以看出水印序列长度对检测器响应值有一定的影响,当水印序列长度变化时检测响应值变化如下。

|
图 4 不同水印长度检测器响应 Fig. 4 Detector response of different watermark length |
如图所示,所得结果符合式(10)理论结果,本文水印嵌入长度选取为400。若水印序列长度过大时候,会对信号本身产生影响。图4和图3两者的原理相同,图4是当变换阶数一定时,嵌入强度K一定,随着嵌入序列的增加水印SWR在减小,同时和图3表达一致,图4主要是用于选取适合的序列长度。
2.3 P阶数的选择和水印鲁棒性分析

|
图 5 不同变换阶数对应的信噪比检测器响应 Fig. 5 Response of signal to noise ratio detectors with different transform orders |
从图5(a)和图5(d)可知,信噪比从5 dB到25 dB变化,并且变换阶数p取值为0.2,0.4,0.6,0.8。图5中加入噪声均为不同方差均值为0的高斯噪声,由图中可以看出随着信噪比的增加,检测响应值愈来愈大,当信噪比较小时,若选择的阶数也较小,检测响应值接近阈值如图5(a),根据变换阶数,在变换阶数选择为0.8时检测响应值产生较大的差值,易区分于无水印检测值,减少出现虚警概率。水印在不同变换阶数中加入高斯噪声,随着高斯噪声方差的增大,水印检测响应值虽然接近检测阈值,但是还不至于出现虚警,综合图5(a)到图5(d),SNR的数值即使为5 dB其检测响应值依然大于所设定的检测阈值,所以虚警出现的概率极低,并且阈值选取恰当的情况下可以严格控制虚警状况的发生。所以它在检测方面体现出优越性,由此可以得出在给定SNR的情况下,为达到更好的检测效率选取合适的阈值以及变换阶数就可以达到,此方法选取的检测阈值偏高,还可以看出该鉴别方法在水印有较高的水印鲁棒性性能下可以得到较高的检测精度。
通过上述仿真分析表明在不知道变换阶数以及水印相关参数时,基本上无法检测到是否含有水印,也无法鉴别信号,较强的鲁棒性使得通过设置不同参数来破坏已经嵌入的水印很困难。因此此方法在声呐信号鉴别中的安全性得到保证,鲁棒性也得到进一步提高。
3 结 语本文利用分数阶傅里叶变换(FRFT)作为工具,利用其随着变换阶次连续增大展示出信号从时间域逐步变换到频率域的所有特征[10]并且利用分数阶傅里叶变换良好的时频域特性[11],设计了一种基于FRFT的声呐鉴别方法,将水印嵌入到信号的FRFT域,不同变换阶数以及复随机序列的水印的嵌入提高了该算法的安全性和鲁棒性,通过对算法的鲁棒性,水印容量以及变换阶数的选择进行分析。实验结果表明基于FRFT的数字水印算法的声呐信号鉴别具有优于其他算法的鲁棒性和检测效率。
| [1] | 金聪. 数字水印理论与技术[M]. 北京. 清华大学出版社, 2008. |
| [2] | MOBASSERI B G, LYNCH R S, CARTER G C. Information embedding in sonar for authentication and identification[J]. IEEE Aerospace Conference Proceedings, 2008 : 1–5. |
| [3] | MOBASSERI B G, LYNCH R S. Sonar authentication performance evaluation under realistically simulated undersea channels[J]. Proceedings of SPIE-The International Society for Optical Engineering, 2010, 7678 : 76780R–76780R-10. |
| [4] | MOBASSERI B G, LYNCH R S, CHAKILAM N. Watermarking sonar waveforms using knowledge of channel coherence[C]// Oceans. IEEE, 2010: 1–8. |
| [5] |
平先军, 陶然, 等. 一种新的分数阶傅立叶变换快速算法[J]. 电子学报, 2001, 29 (3): 406–408.
PING Xian-jun, Tao-ran Si-yong, et al. A new fast algorithm of fractional Fourier transform[J]. Electronic journal, 2001, 29 (3): 406–408. |
| [6] | 王娟峰. 基于分数阶Fourier域图像特征的数字水印算法研究[D]. 郑州: 郑州大学, 2007. |
| [7] | BULTHEEL A, SULBARAN H E M. Computation of the fractional Fourier transform[J]. Applied & Computational Harmonic Analysis, 2004, 16 (3): 182–202. |
| [8] | 许文丽, 王命宇, 马君. 《数字水印技术及应用》[M]. 北京. 电子工业出版社 2013. |
| [9] | 程雪. 基于分数阶傅里叶变换的数字水印技术研究[D]. 南京: 南京理工大学, 2009. |
| [10] | PEI S C, DING J J. Fractional Fourier transform, wigner distribution, and filter design for stationary and nonstationary random processes[J]. Signal Processing IEEE Transactions on, 2010, 58 (8): 4079–4092. DOI: 10.1109/TSP.2010.2048206 |
| [11] |
朱健东, 赵拥军. 线性调频连续波信号的周期分数阶Fourier变换检测与估计[J]. 电子与信息学报, 2013, 35 (8): 1827–1833.
ZHU Jian-dong, ZHAO Yong-jun. Detection and estimation of linear frequency modulated continuous wave signal in periodic fractional Fourier transform[J]. Journal of Electronic and Information Science, 2013, 35 (8): 1827–1833. |
 2017, Vol. 39
2017, Vol. 39
