2. 中国人民解放军92635部队,山东 青岛 266000
2. No. 92635 Unit of PLA, Qingdao 266000, China
在海洋环境中,由于传播信道中海洋介质随机散射及信道的多途、频散等水声环境效应,使得水中目标辐射噪声信号波形发生畸变,从而改变接收端信号的频谱特征。为研究水中目标辐射噪声通过水下声信道传播后噪声特征的变化规律,需要分析表征目标辐射噪声典型特征参数的变化。描述目标辐射噪声的特征参数包括目标辐射噪声的基频、谐波振幅及各阶谐波的信噪比[1]。水下目标辐射噪声中的谐波分量包含了反映目标自身本质特性的信息,能否有效提取目标谐波特征关系到目标类型识别的效果。
为此,本文提出了一种水声目标辐射噪声谐波特征提取算法,结合仿真信号与实测数据进行对比,验证了该算法的可行性。
1 水声目标辐射噪声信号模型目标辐射噪声由宽带噪声与多个正弦信号组成,可表示为[2]:
|
$\begin{split}r(t) = & s(t) + n(t)=\\& \sum\limits_{h = 1}^H {{A_h}} \cos (2\pi h\gamma t + {\varphi _h}) + n(t)\end{split}\text{。} $
|
(1) |
其中,H为谐波阶数,Ah和φh为第h阶谐波分量的振幅和相位,γ为基频,与目标的引擎转速等参数有关,因此可将r(t)表示为
由于引擎速度的变化,多普勒频移以及传播环境的影响,被动声呐接收到的信号与目标实际辐射的噪声信号不同。由于基频时变,将γ表示为
|
$\begin{split}r(t,\theta ) = & s(t,\theta ) + n(t)=\\& \sum\limits_{h = 1}^H {{A_h}} \cos (2\pi h\gamma (t)t + {\varphi _h}) + n(t)\end{split}\text{。}$
|
(2) |
被动声呐接收信号是频率时变的连续波信号,在信号处理前须对其进行采样。利用短时傅里叶变换(STFT)按一定窗口长度滑动,并计算每个窗内数据的傅里叶变换,得到信号频率随时间变化关系[3]。假设时间窗的长度足够小,则窗内数据对应的频率变化可近似忽略,即
|
$S(f,{\theta _k}) = \sum\limits_{h = 1}^H {\frac{{{A_h}}}{2}} \sin {\mathop c\nolimits} [\pi (f - h{\gamma _k})]\text{,}$
|
(3) |
假设
|
${R_{ko}}(m\Delta f,{\theta _k}) \!=\! \frac{2}{{{N_S}}}\sum\limits_{n = - {N_S}/2}^{{N_S}/2 - 1} {{r_k}} ({t_k} \!\!+\! n\Delta t,{\theta _k}){e^{ - jm2\pi \Delta fn\Delta t}}\text{。}\!\!$
|
(4) |
其中
水下目标谐波特征提取算法的总体思路。主要分为 3 个步骤:
步骤 1 计算信号频谱与梳状滤波器的频率响应间的互相关,完成对基频的估计;
步骤 2 利用卡尔曼滤波器跟踪基频量测随时间的变化,得到基频的最优估计;
步骤 3 利用基频的最优估计,提取相应谐波的振幅信息。
2.1 基频估计方法由式(3)可知,目标辐射噪声的频谱可表示为一组在tk时刻基频为γk的sinc函数的加权和,利用该模型构建梳状滤波器的频率响应为:
|
$\begin{split}{C_{mp}} =& S({f_m},{\theta _k}|{\gamma _k} = {\zeta _p},{A_h} = 2)=\\& \sum\limits_{h = 1}^H {\sin {\mathop c\nolimits} \left[ {\pi ({f_m} - h{\zeta _p})} \right]}\text{。}\end{split}$
|
(5) |
在此假设所有谐波的振幅相等,而Cmp是矩阵
对于均值分别为
|
$\rho \left( t \right) = \frac{{E\left[ {\left( {X\left( t \right) - {\mu _x}\left( t \right)} \right)\left( {Y\left( t \right) - {\mu _y}\left( t \right)} \right)} \right]}}{{\sqrt {E\left[ {{{\left( {X\left( t \right) - {\mu _x}\left( t \right)} \right)}^2}} \right]E\left[ {{{\left( {Y\left( t \right) - {\mu _y}\left( t \right)} \right)}^2}} \right]} }}\text{,}$
|
(6) |
ρ(t)取值在[–1,1]间。要估计tk时刻接收信号
|
${\hat \rho _{pk}}({\zeta _p},{t_k}) = \frac{{\sum\nolimits_{fm} {({C_{mp}} - {\mu _C}){R_k}({f_m},{\theta _k})} }}{{\sqrt {\sum\nolimits_{fm} {{{({C_{mp}} - {\mu _C})}^2}} } \sqrt {\sum\nolimits_{fm} {{R_k}{{({f_m},{\theta _k})}^2}} } }}\text{。}$
|
(7) |
其中
利用式(7)计算
|
${\hat{ \varGamma }}_k^ - = {{F}}{{\hat{ \varGamma }}_{k - 1}} \text{,}\;\;\;{{P}}_k^ - = {{F}}{{{P}}_{k - 1}}{{F}^{\rm T}} + {{Q}} \text{。}$
|
(8) |
其中F是状态转移矩阵,Q是过程噪声协方差。利用k时刻量测zk,通过式(9)进行状态更新得到k时刻的状态估计
|
$\left\{ \begin{aligned}& {K_k} = {{P}}_k^ - {{{H}}^{\rm T}}{({{HP}}_k^ - {{{H}}^{\rm T}} + {{R}})^{ - 1}}\\& {{{\hat{ \varGamma }}}_k} = {\hat{ \varGamma }}_k^ - + {K_k}({{\bf{z}}_k} - {{{\rm H}\hat \Gamma }}_k^ - )\\& {{{P}}_k} = ({{I}} - {K_k}{{H}}){{P}}_k^ - \end{aligned} \right.$
|
(9) |
其中Kt是k时刻的卡尔曼滤波增益,R是量测噪声协方差矩阵,H为量测矩阵。在下一时刻,将当前时刻的状态估计值反馈到预测方程中,并且重复式(8)和(9)的预测更新过程,最终得到所有时刻的均值和误差协方差的滤波估计,形成频率跟踪航迹。
2.2.2 基频跟踪算法借鉴近似的匀速运动模型,基频频率变化跟踪,即
|
$\left\{ {\begin{array}{*{20}{l}}{{{{\varGamma }}_k} = {{F}}{{\bf{\varGamma }}_{k - 1}} + {{{w}}_k}}\text{,}\\{{{{\varGamma }}_k} = {{[{\gamma _{KF,k}},{{\dot \gamma }_{KF,k}},{\rho _{KF,pk}}]}^{\rm T}}}\text{,}\\{{{F}} = \left[ {\begin{array}{*{20}{c}}1 & 1 & 0\\0 & 1 & 0\\0 & 0 & 1\end{array}} \right]}\text{,}\\{{{{w}}_k} \sim N({{0}},{{Q}})}\text{。}\end{array}} \right.$
|
(10) |
其中
|
$\left\{ {\begin{array}{*{20}{l}}{{{{z}}_k} = {{H}}{{{\varGamma }}_k} + {v_k}}\text{,}\\{{{{z}}_k} = {{[{{\hat \gamma }_k},{{\hat \rho }_{pk}}]}^{\rm T}}}\text{,}\\{{{H}} = \left[ {\begin{array}{*{20}{c}}1 & 0 & 0\\0 & 0 & 1\end{array}} \right]}\text{,}\\{{v_k} \sim N(0,R)}\text{。}\end{array}} \right.$
|
(11) |
其中zk为频率
|
${{Q}} = \left[ {\begin{array}{*{20}{c}}{{Q_\gamma }} & 0 & 0\\0 & {{Q_{\dot \gamma }}} & 0\\0 & 0 & {{Q_\rho }}\end{array}} \right]\text{,}\;\;\;{{R}} = \left[ {\begin{array}{*{20}{c}}{{R_\gamma }} & 0\\0 & {{R_\rho }}\end{array}} \right]\text{。}$
|
(12) |
实际上,过程噪声或量测噪声的大小蕴含了利用该模型进行状态估计时的可信度。
2.2.3 基频跟踪逻辑卡尔曼滤波需要一个初始的状态估计,跟踪过程需要航迹起始和结束的逻辑判断[7]。首先设置相关系数门限λγ,对每个快拍对应的相关系数
|
$({z_k} - H\hat \Gamma _k^ - ){(HP_k^ - {H^{\rm T}} + R)^{ - 1}}{({z_k} - H\hat \Gamma _k^ - )^{\rm T}} < {\chi ^2}\text{。}$
|
(13) |
则该观测量与航迹相关,χ2度量的是每个测量频率和卡尔曼滤波预测得到频率的差,χ2值越小,表明测量频率和预测频率越接近。当有多个观测频率满足上述关系式时,最小χ2值对应的频率为预测频率。
2.3 谐波特征提取实际中,卡尔曼滤波输出可能有多条航迹,每条航迹是
|
${\bf{\psi }}\left[ k \right] = \sqrt {\frac{1}{L}\sum\limits_{k = 1}^L {{{\left| {{\rho _{KF,pk}}\left[ k \right]} \right|}^2}} } \text{。}$
|
(14) |
其中k为航迹号,
谐波特征是目标的“声音指纹”。由于航迹
按照式(1)模拟生成被动声呐的接收信号,谐波数为5,宽带噪声的功率为5。假设所有谐波振幅相等均为1,且信号时长有限,而噪声与信号时长相等。信号采样频率为8 kHz,采样点数为65 536,信号基频在[5,65] Hz间服从均匀分布。仿真参数见表1。
|
|
表 1 仿真参数 Tab.1 Simulation parameters |
|
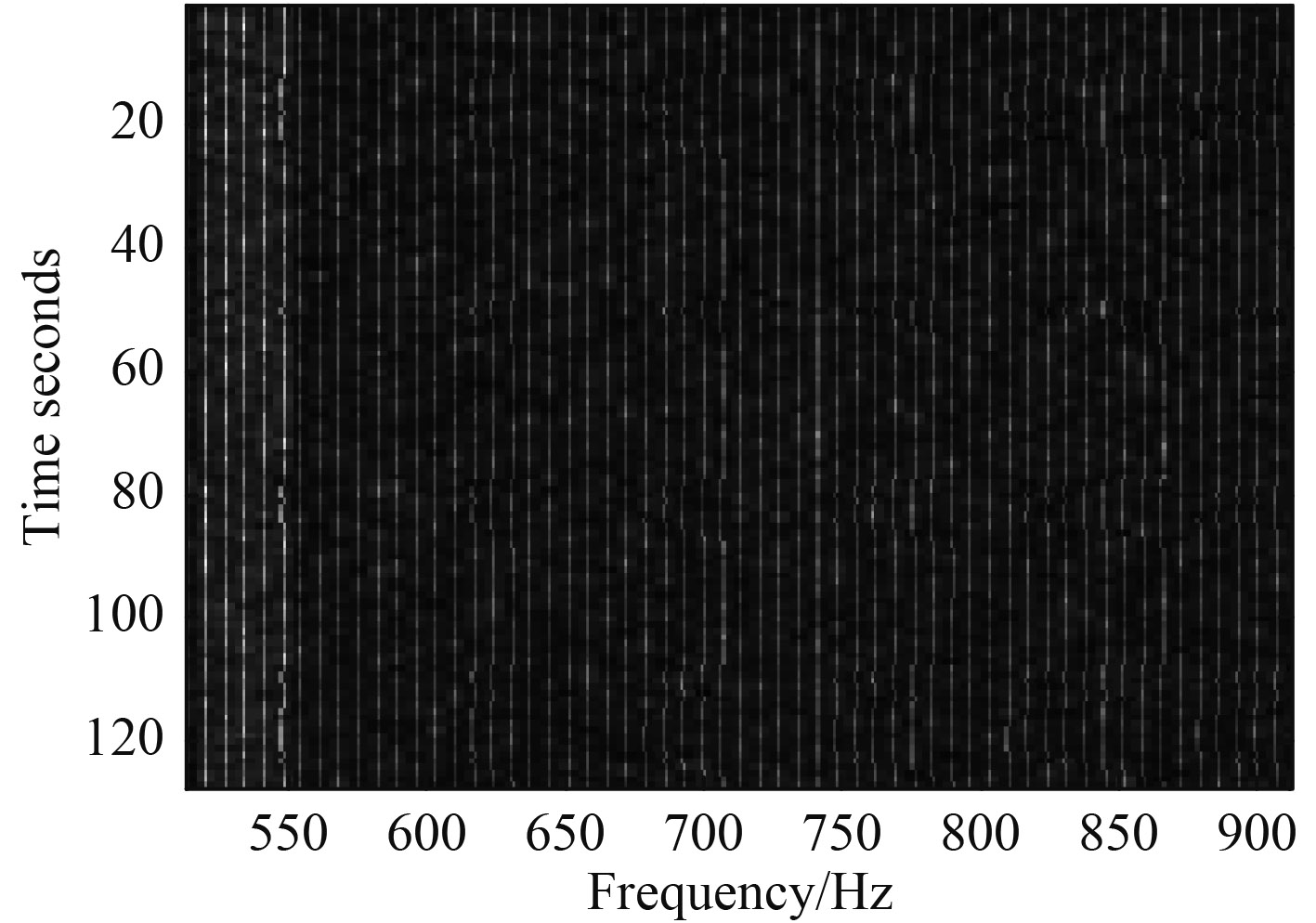
图 1 基频跟踪在谱图上的投影 Fig. 1 Projection of fundamental frequency tracking on the spectrogram |

|
图 2 各阶谐波与背景噪声的相对振幅特性 Fig. 2 The relative amplitude characteristics of harmonics and background noise |
图1给出的是一个段时长8.192 s的目标噪声对应的声谱图,为便于显示,X轴截选显示500~900 Hz范围内频率。图2给出了各阶谐波与背景噪声的相对振幅特性,每根谱线给出的是各阶谐波的相对振幅,每个峰值周围的背景噪声用实线表示,图中所有谐波分量全部可见。图1中基频在整个航迹跟踪范围内有一些微小变化。在频率[500,550] Hz范围内,基频跟踪在谱图上的投影明显更亮一些,说明在这个范围内
谐波特征是目标的“声音指纹”。每个目标自身辐射噪声对应的“声音指纹”都是由其引擎转速、汽缸数、齿轮齿数比、叶片数量等参数决定。本文提出了一种基于最大似然估计和卡尔曼滤波理论的目标辐射噪声谐波特征的提取与分析算法,经验证该算法的稳健性较好,且提取的谐波信息包含了反映目标自身本质特性的信息,可进一步用于不同类型的水下目标识别。
| [1] | 李启虎. 数字式声呐设计原理[M]. 合肥: 安徽教育出版社, 2003: 141–142. |
| [2] | P. Radiated noise characteristics of a modern cargo ship[J]. Acoust. Soc. Am, 2000, 107 : 118–129. DOI: 10.1121/1.428344 |
| [3] | 胡广书. 现代信号处理教程[M]. 第1版. 北京: 清华大学出版社, 2004: 52–58. |
| [4] | 孙即祥. 现代模式识别[M]. 长沙: 国防科技大学出版社, 2008: 73–75. |
| [5] | KIM S, HOLMSTROM L, MCNAMES J. Multiharmonic tracking using marginalized particle filters[C]//in Proceedings of the 30th Annual International Conference of the IEEE, 2008, August 20–25, 29–33. |
| [6] | 何友, 王国宏, 陆大金, 等. 多传感器信息融合及应用[M]. 第2版. 北京: 电子工业出版社, 2007: 13–20. |
| [7] | LAWRENCE M W. Ray Theory Modeling Applied to Low-Frequency Acoustic Interaction with Horizontally Stratified Ocean Bottoms[J]. Acoustic. Soc. Am., 1985, 78 (2): 125–133. |
 2017, Vol. 39
2017, Vol. 39
