0 引　言

船舶操纵响应模型在船舶操纵性研究中占有重要地位。自野本谦作通过Z形试验求取K，T的标准算法提出后^[1]，各国的船舶操纵性研究者都乐于用Z形操舵试验来确定K，T，以评价船舶的操纵性能。用系统辨识的方法来获取K，T简单、快速、准确。辛元欧等通过自然回归离散模型的最小二乘法建立了一阶和二阶KT非线性的连续模型^[2]；邹早建等利用分步辨识的方法对一阶和二阶非线性KT方程的参数进行了辨识^[3]；罗伟林结合船模自航模试验，应用岭回归方法，辨识了一类非线性的船舶操纵运动数学模型并且进行了操纵运动预报^[4]。文献[2-3]在辨识时对原始数据采用差分的方法处理，误差较大。本文利用积分方法获取样本数据，以使辨识的准确性有所提高。

1 系统辨识

系统辨识^[5]是在系统的输入和输出数据基础上，建立一个与所测系统等价的数学模型的理论和方法，包括确定模型结构和估计模型参数两部分。系统辨识方法应用于船舶操纵运动建模已经有近40年的历史。经典的辨识方法由于其本身的局限性已经逐渐被淘汰，智能算法因其对初值要求不高，不要求系统具有连续性等优势而兴起，差分进化法就是其中一种。

1.1 差分进化法简介

Rainer Storn和Kenneth Price于1995年共同提出了一种基于群体进化的算法^[6] ，即差分进化法（Differential Evolution，DE），目的是求解切比雪夫多项式拟合问题。DE最大的特点就是可以记忆个体最优解并且在种群内共享信息，即利用群体内个体间的竞争与合作来求解优化问题，它基于实数进行编码，具有保留精英个体的思想，实质是一种贪婪遗传算法。整体结构上与其他进化算法类似，由变异、交叉和选择3个基本操作构成。标准差分进化法主要包括4个步骤^[7]。

1）生成初始群体

在n维空间里随机生成满足约束条件的M个个体，实施措施如下：

${x_{ij}}(0) = ran{d_{ij}}(0,1)(x_{ij}^U - x_{ij}^L) + x_{ij}^L,$

(1)

其中， $x_{ij}^U$ 和 $x_{ij}^L$ 分别为第j个染色体的上界和下界， $ran{d_{ij}}(0,1)$ 是[0，1]之间的随机小数。

2）变异操作

从群体中随机选择3个个体 ${x_{{p_1}}}$ ， ${x_{{p_1}}}$ 和 ${x_{{p_1}}}$ ，且 $i \ne {p_1} \ne {p_2} \ne {p_3}$ ，则基本的变异操作为

${h_{ij}}(t + 1) = {x_{{p_1}j}}(t) + F({x_{{p_2}j}}(t) - {x_{{p_3}j}}(t)),$

(2)

如果无局部优化问题，变异操作可写为

${h_{ij}}(t + 1) = {x_{bj}}(t) + F({x_{{p_2}j}}(t) - {x_{{p_3}j}}(t))\text{。}$

(3)

其中， ${x_{{p_2}j}}(t) - {x_{{p_3}j}}(t)$ 为差异化向量，此差分操作是差分进化算法的关键；F为变异因子；p₁，p₂，p₃为随机整数，表示个体在种群中的序号； ${x_{bj}}(t)$ 为当前种群中最好的个体。由于式（3）借鉴了当前种群中最好的个体信息，可加快收敛速度。

3）交叉操作

交叉操作是为了增加群体的多样性，具体操作如下：

${v_{ij}}(t + 1) = \left\{ \begin{array}{l}{h_{ij}}(t + 1),rand\;\;{l_{ij}} \text{≤} CR,\\{x_{ij}}(t),rand\;\;{l_{ij}} > CR \text{。}\end{array} \right.$

(4)

其中，rand l_ij为[0，1]之间的随机小数；CR为交叉概率，CR∈[0，1]。

4）选择操作

为了确定 ${x_i}(t)$ 是否成为下一代的成员，实验向量 ${v_i}(t + 1)$ 和目标向量 ${x_i}(t)$ 对评价函数进行比较：

${x_i}(t + 1) = \left\{ \begin{array}{l}{v_i}(t + 1),f({v_{i1}}(t + 1),...,{v_{in}}(t + 1))\\ < f({x_{i1}}(t),...,{x_{i2}}(t)),\\{x_{ij}}(t),f({v_{i1}}(t + 1),...,{v_{in}}(t + 1))\\ \text{≥} f({x_{i1}}(t),...,{x_{i2}}(t))\text{。}\end{array} \right.$

(5)

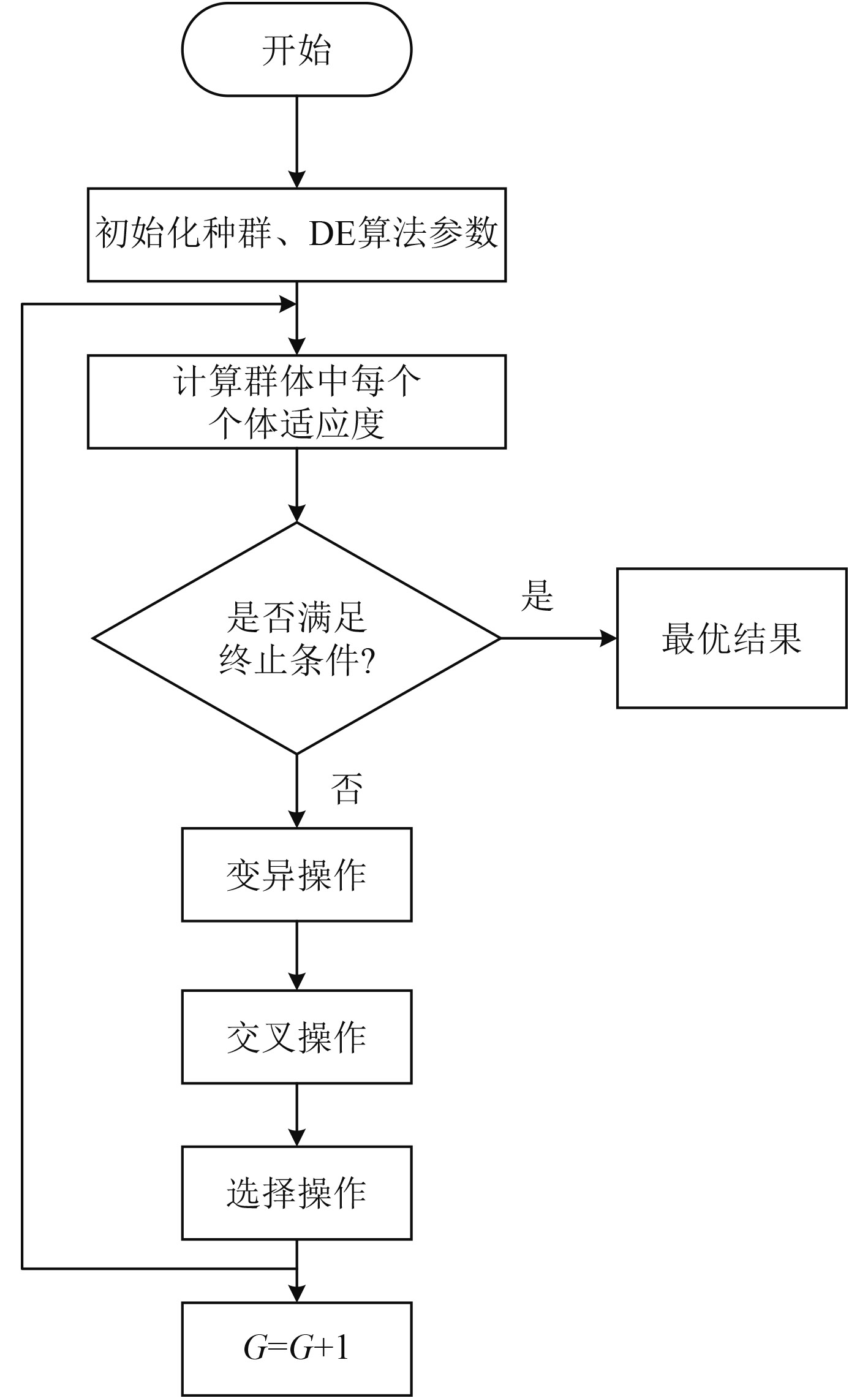
反复执行步骤2~步骤4操作，直到达到最大迭代次数G，差分进化基本运算流程如图1所示。

1.2 参数相消现象及平行处理法

在辨识过程中，可能出现参数相消或者同时漂移现象^[8]，使辨识的精度大大降低。因为，模型中每个方程可能包含多个参数，例如同时辨识2个参数A和B，由于计算中的最优化要求，A和B可能同时偏离真值，使得目标函数达到最小。克服参数相消是获得较准确的辨识结果的基础，分步辨识法和平行处理法^[9]都可以有效抑制参数相消。文献[3]运用了分步辨识的方法，但过程较为繁琐，本文采用平行处理法，简单而且有效。

Gelb（1974）年指出，系统所观测到的信息越多，辨识的结果就越准确。所以增加观测器无疑是一个好方法。如果选择2个观测器，它们互相独立，如：

观测器1

${y_1} = x + {\sigma _1},$

(6)

观测器2

${y_2} = x + {\sigma _2}\text{。}$

(7)

2个观测器各自的误差分别为 $E({y_1}) = \sigma _1^2$ ， $E({y_2}) = $ $\sigma _2^2$ 。

将 $\hat y$ 写成2个观测器的加权和，即

$\hat y = {k_1}{z_1} + {k_2}{z_2},$

(8)

由无偏估计的要求，有

${k_2} = 1 - {k_1},$

(9)

不妨设

${k_1} = \frac{{\sigma _2^2}}{{\sigma _1^2 + \sigma _2^2}},{k_2} = \frac{{\sigma _1^2}}{{\sigma _1^2 + \sigma _2^2}},$

(10)

那么

$\begin{split}E(\hat y) & = E({k_1}{y_1} + {k_2}{y_2})\\ & = k_1^2E({y_1}) + k_2^2E({y_2})\\ & = k_1^2\sigma _1^2 + k_2^2\sigma _2^2\\ & = \displaystyle\frac{{\sigma _2^4}}{{{{(\sigma _1^2 + \sigma _2^2)}^2}}} \cdot \sigma _1^2 + \frac{{\sigma _1^4}}{{{{(\sigma _1^2 + \sigma _2^2)}^2}}} \cdot \sigma _2^2\\ & = \displaystyle\frac{{\sigma _1^2\sigma _2^2}}{{\sigma _1^2 + \sigma _2^2}}\text{。}\end{split}$

(11)

因为 $E(\hat y)$ 小于 $E({y_1})$ ， $E({y_2})$ 的任一个，所以式（11）所表示的 $\hat y$ 比2个观测器中的任何一个都要好。由此可以看出，相比于单一观测器的模型，多观测器的模型能得到更好的估计结果。

平行处理法不但可以提高参数辨识的精度，还可以改善参数相消现象。因为在平行处理过程中，要辨识的参数个数并没有变化，但是所使用的数据却并不相同，不同的数据对参数的辨识均做出贡献，这样对相互抵消有所抑制。在处理时，既可以2组不同的观测数据，也可以用同一组观测数据在不同相位条件下的值来进行参数平行处理辨识。

2 操纵运动响应方程

船舶在广阔水域中航行，最关心的是航向问题，因此需要研究船舶的首向角对操舵的响应，这在自动操舵系统中尤为重要。一般的船舶首摇响应线性方程形式如下：

${T_1}{T_2}\ddot r + ({T_1} + {T_2})\dot r + r = K\delta + K{T_3}\dot \delta ,$

(12)

式（12）对分析航向稳定性很方便，也称为二阶线性KT方程。

1957年野本谦作用自动调节原理的方法，分析式（12）后提出了其简化形式，在操作不是很频繁的情况下，式（12）可近似用下式代替：

$T\dot r + r = K\delta \text{。}$

(13)

式中： $T = {T_1} + {T_2} - {T_3}$ 。

式（13）称为一阶KT方程，也称作野本方程。系数K，T具有鲜明的物理意义：K为回转性指数，能表征船舶回转性能的好坏；T为应舵指数，表示转首对操舵响应的快慢。式（13）在求解和分析问题时非常方便，所以得到了广泛的应用。本文的待辨识参数即为一阶和二阶非线性操纵响应方程中K，α，T（T₁，T₂，T₃）。

3 操纵运动响应方程的辨识

为了进行参数辨识，首先需要获得样本数据。从式（12）和式（13）中可以看出，在进行辨识时，除了用到首向角和舵角的数据外，还要用到首向角速度及其一、二次微分形式还有转舵角速度，但是这些数据无法直接测得。文献[2-3]均采用差分的方法，本文提出采用积分的方法，2种方法均可以获得所需的样本，不同的是，差分过程要在辨识前进行，而积分过程则在辨识过程中进行。

3.1 差分处理

在对数据进行差分处理时，一般采用的方法是向前差分格式，但其精度要低于中心差分^[10]格式，因此这里以中心差分格式为说明，各阶中心差分格式为：

$r(k) = [\psi (k + 1) - \psi (k - 1)]/(2h),$

(14)

$\dot r(k) = [\psi (k + 1) - 2\psi (k) + \psi (k - 1)]/{h^2},$

(15)

$\ddot r(k) = [\psi (k + 2) - 2\psi (k + 1) + 2\psi (k - 1) - \psi (k - 2)]/(2{h^3}),$

(16)

$\dot \delta (k) = [\delta (k + 1) - \delta (k - 1)]/(2h)\text{。}$

(17)

文献[3]中提出的分步辨识方法如下：

1）由小舵角回转试验辨识K；

2）固定K，由大舵角回转试验辨识α；

3）固定K和α，由大舵角Z形试验辨识T（T₁，T₂，T₃）；

4）用中舵角Z形试验验证辨识结果的准确性。

3.2 积分处理

对于一阶非线性操纵响应方程，需进行如下计算：

$\left\{ \begin{aligned}& \dot r = (K\delta - r - \alpha {r^3})/T,\\& r = \int_0^t {\dot r(t){\rm{d}}t}, \\& \psi = \int_0^t {r(t){\rm{d}}t} \text{。}\end{aligned} \right.$

(18)

对于二阶非线性操纵响应方程，计算如下：

$\left\{ \begin{aligned}& \ddot r = [K\delta + K{T_3}\dot \delta - ({T_1} + {T_2})\dot r - r - \alpha {r^3}]/({T_1}{T_2}),\\& \dot r = \int_0^t {\ddot r(t){\rm{d}}t}, \\& r = \int_0^t {\dot r(t){\rm{d}}t}, \\& \psi = \int_0^t {r(t){\rm{d}}t} ,\\& \delta = \int_0^t {\dot \delta (t){\rm{d}}t} \text{。}\end{aligned} \right.$

(19)

$\dot r$ ，r，ψ，δ的初始值由试验数据直接或者差分得到。通过积分运算最终能得到首向角ψ的变化曲线，并作为目标向量与试验值作比较。由于积分过程在辨识过程中进行，无需对试验数据做过多处理即可开始辨识。采用平行处理法可以一次辨识多个参数，无需分步进行，所以大大简化了辨识流程。

3.3 不同方法辨识结果的比较

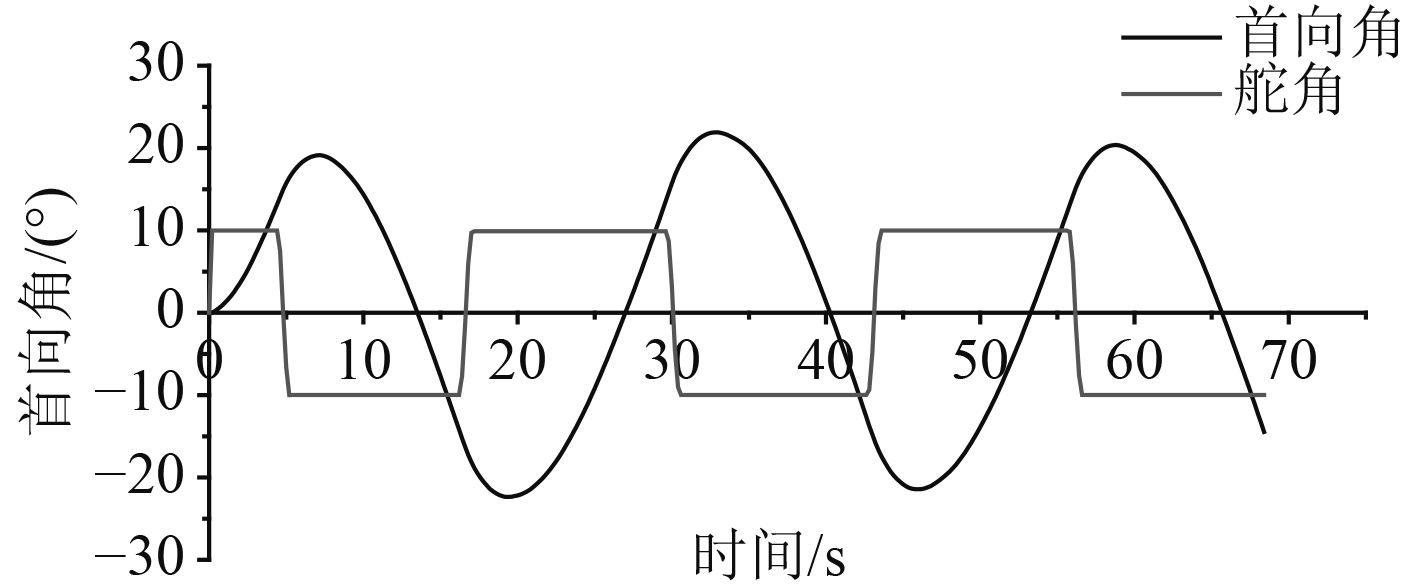
本文所涉及的船模试验包括一系列的回转试验和Z形试验，积分法在不同工况下的辨识结果均要好于差分法。图2是自航模试验中10°/10°Z形运动首向角变化曲线，以此为例来对比二者的辨识结果。

分别用文献[3]中的差分法和本文提出的积分法辨识一阶和二阶非线性响应方程中的参数，辨识结果如表1所示。

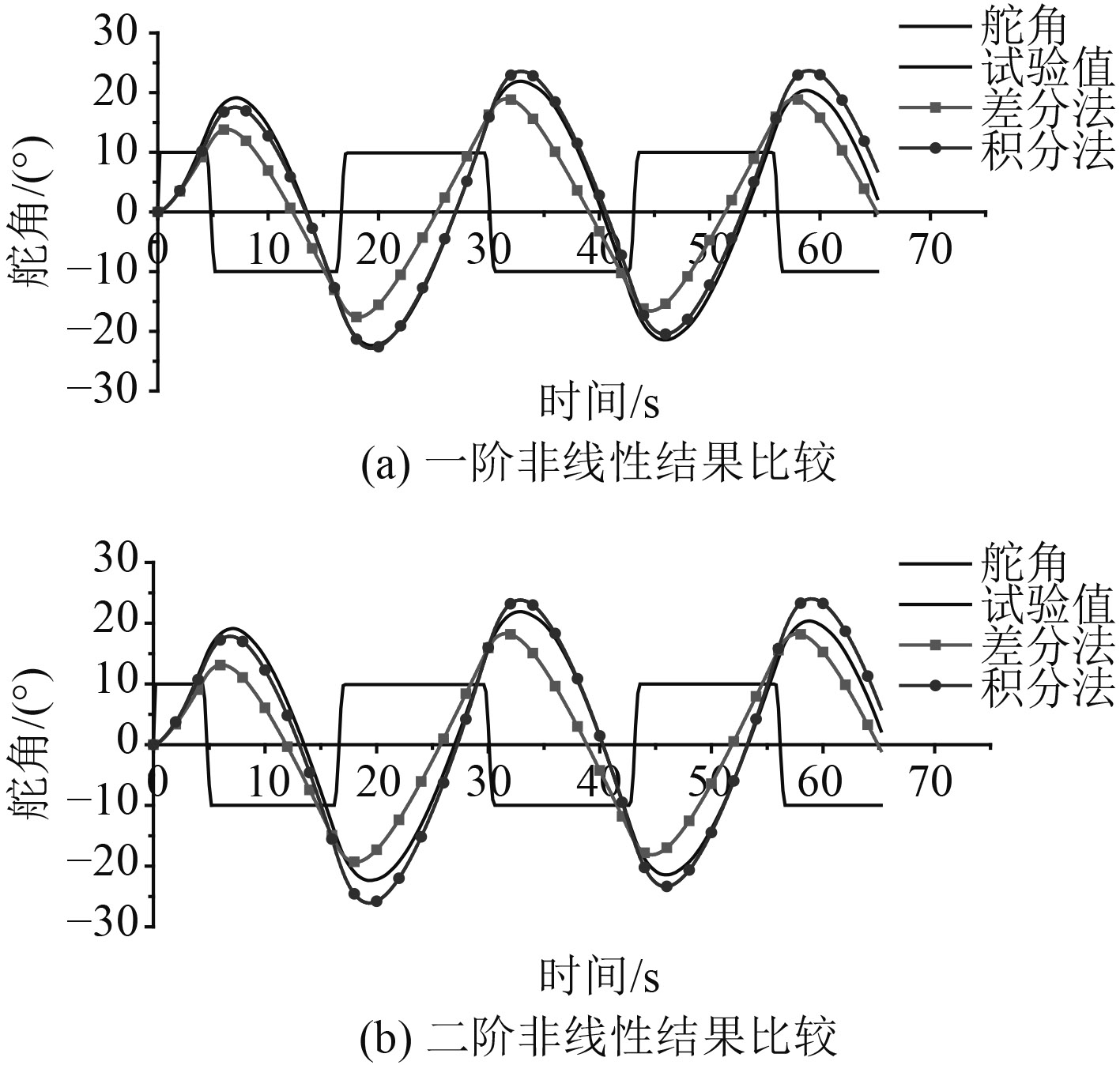
为了验证辨识结果的准确性，将以上结果带到一阶线性操纵响应方程中，模拟船舶10°/10°Z形运动，模拟结果如图3所示。

从图中可以看出，利用积分的方法获得的样本数据辨识的结果要远好于通过差分方法得来的结果。

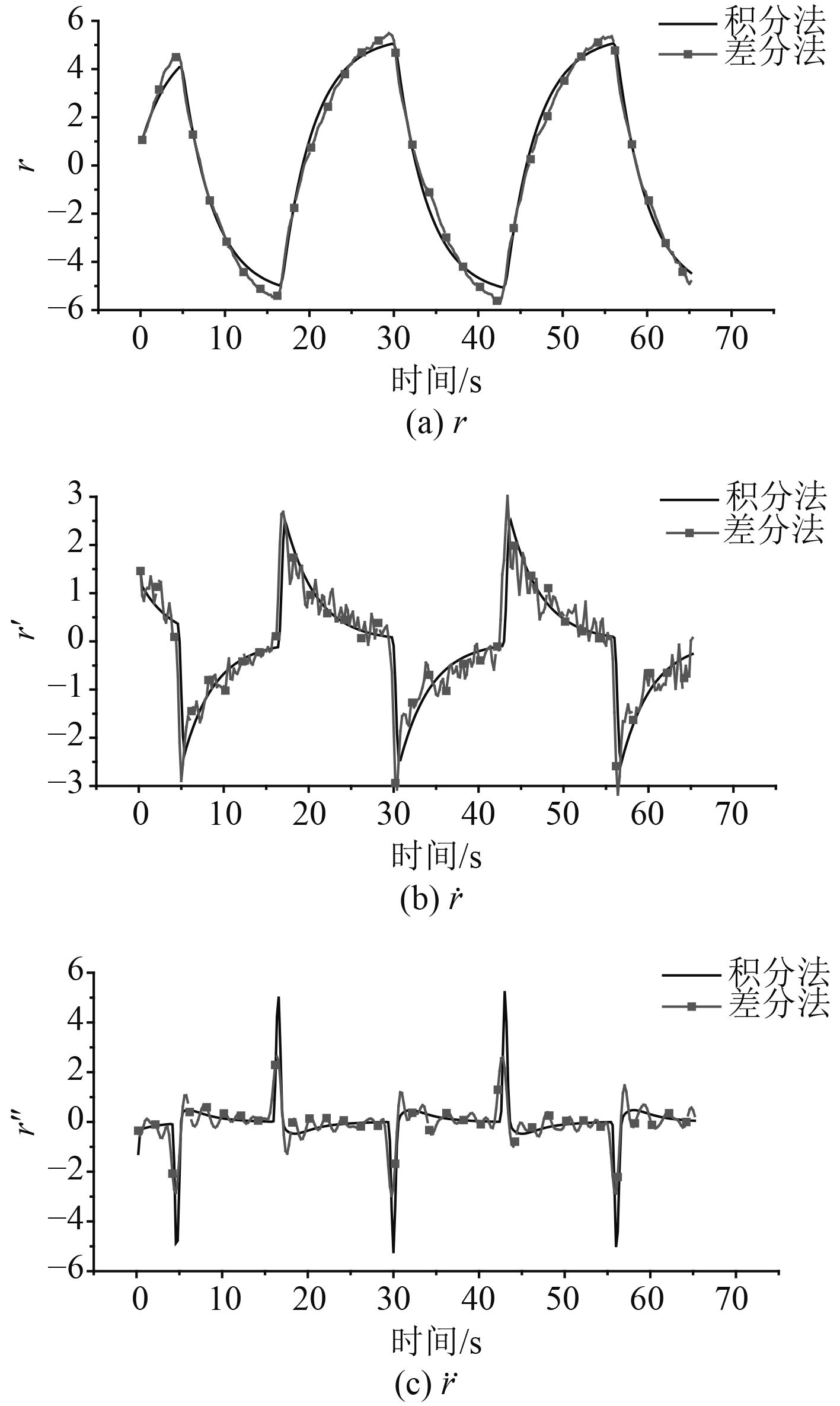
3.4 误差分析

利用差分方法计算r时已经产生了一定的误差，但是为了得到 $\dot r$ ， $\ddot r$ 等数据，又对差分后的结果进行差分，误差逐渐积累，从而导致辨识结果的不准确。图4用来比较分别用差分和积分的方法获得的r， $\dot r$ ， $\ddot r$ 。

从图中可以看出，2种方法的差异在计算r时尚不明显；但当计算 $\dot r$ 时已经差别很大；计算 $\ddot r$ 时差异更加明显。

4 结　语

本文改进了系统辨识过程中样本数据的获得途径，变差分为积分，从而避免了差分过程造成的误差。将辨识结果与差分处理的辨识结果以及野本手算法作比较，证明积分方法获得的样本数据更准确，能有效提高辨识精度。另外，在处理参数相消问题上采用平行处理法，可以一次辨识多个参数，简化了辨识流程。