2. 天津大学,天津 300072
2. Tianjin University, Tianjin 300072, China
根据不同的海域和海况条件,目前世界上的FPSO主要采用以下3种系泊方式:单点系泊系统、多点系泊系统以及动力定位系统。在世界上环境条件最恶劣的三大海域(北海、墨西哥湾和南中国海),几乎所有的FPSO都配置内转塔式单点系泊系统。虽然南中国海由于风浪流等环境参数极为恶劣,环境条件的方向性不明显,但内转塔式单点系泊系统在南中国海具有多年安全生产的经验,因此其成为了南中国海FPSO定位的唯一选择。内转塔式单点系泊系统承担着FPSO定位、油气水生产及信号传输功能,并使FPSO具有了风向标效应,这样FPSO能够随着风浪流进行360°回转,且在各种风浪流作用下FPSO的受力最小。
我国8艘在南海服役的FPSO均采用转塔式单点系泊方式[1],但在台风过程中,都曾发生过系泊系统损伤的事故。对于单点系泊系统来说,某一个设计参数的变化有可能会对整个系泊系统的刚度特性产生极大的影响,从而影响系统动力响应特性。因此在单点设计分析阶段,有必要对系泊系统进行参数敏感性分析。本文以南海某内转塔式FPSO系泊系统为研究对象,如图1所示,对其系泊系统相关参数,进行敏感性分析。

|
图 1 内转塔式单点系泊系统形式示意图 Fig. 1 The structure type of STP |
FPSO一般是由船体与系泊缆、立管等组成的多体耦合系统。通常系泊系统响应的分析采用准静力分析以及动力分析2种方法。准静力分析忽略系泊缆的质量、阻尼以及动力效应。但随着水深的逐步增加,这些被忽略的因素对系统响应造成的影响开始逐步显现,而动力分析恰恰可以弥补这些不足[2]。此外,浮体运动主要受系统的惯性、阻尼、回复刚度以及环境载荷影响,而浮体的运动则是引发系泊系统响应的主要因素,因此系泊系统与浮体之间相互影响,其求解并不能完全独立。基于这些因素,当前普遍采用的分析方法是时域耦合动态分析方法。
1.1 系泊系统耦合时域响应分析运动方程FPSO时域运动控制方程如下式所示:
|
$\begin{split}\left[ {{m_{ji}} + {A_{ji}}(\infty )} \right] & {{\ddot x}_i}\left( t \right) + \int_0^t {{r_{ji}}\left( {t - \tau } \right){{\dot x}_i}\left( t \right){\rm{d}}\tau } + \\& {D_{ji}}{{\dot x}_i}\left( t \right) + {c_{ji}}x\left( t \right) = F_{waj}^{\left( 1 \right)}\left( t \right) + F_{waj}^{\left( 2 \right)}\left( t \right) + \\& F_{wij}^{}\left( t \right) + F_{cuj}^{}\left( t \right) + F_{morj}^{}\left( t \right)\text{。}\end{split}$
|
(1) |
式中,
FPSO所受风流载荷按照OCIMF[3]给出的计算公式计算,船体所受的波浪载荷通常采用三维势流理论进行计算,由于FPSO在水平面内的运动属于低频运动,而差频力会产生低频激励,容易引发系统共振,因此系泊系统分析中通常关注二阶力中的差频成分。时域分析中,二阶低频波浪载荷通常需要计算二阶波浪载荷传递函数(QTF)获得,通常采用Newman近似方法近似计算。
1.2 计算模型相关参数本文以南海某油田服役中的某内转塔式单点系泊FPSO为研究对象,其作业水深为100 m,相关主尺度如表1所示。
|
|
表 1 南海某FPSO主尺度 Tab.1 The main particulars of FPSO in the South China Sea |
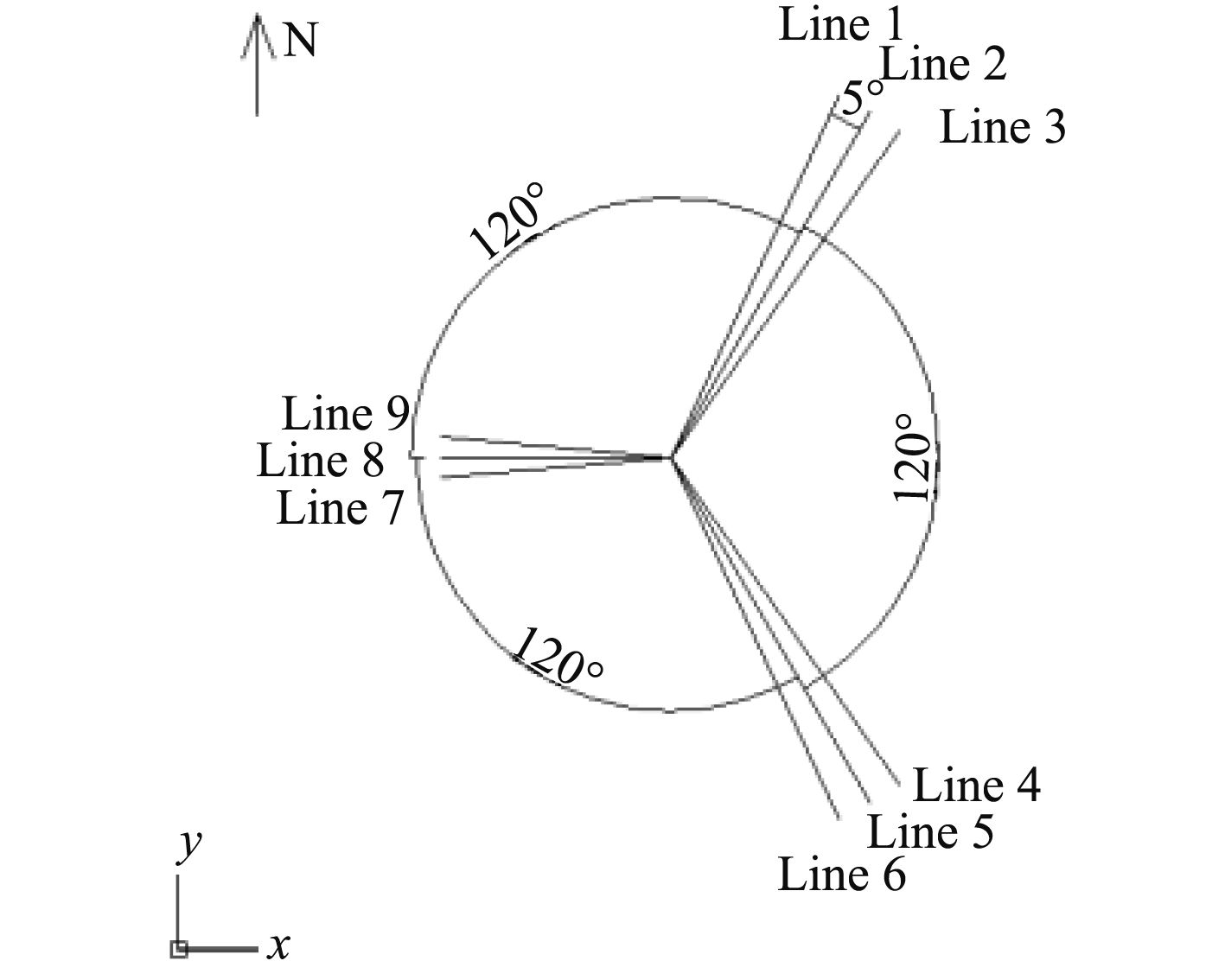
FPSO系泊系统布置如图2所示,由3组、每组3根系泊缆组成。组与组之间的夹角为120°,夹角为5°。每根系泊缆由钢缆与锚链组成,各段参数见表2,其中长缆的LCS、短缆的UCS1段与海底相连,长、短缆的UWS段与内转塔相连。由于计算采用动态方法,将考虑系泊缆的动力特性,因此按照规范[4 – 5]选取系泊缆的水动力系数,如表3所示。
|
|
表 2 系泊缆相关参数 Tab.2 The parameters of mooring lines |
|
|
表 3 系泊缆水动力参数 Tab.3 The dynamic parameters of mooring lines |
|
图 2 系泊系统布置示意图 Fig. 2 The layout of mooring system |
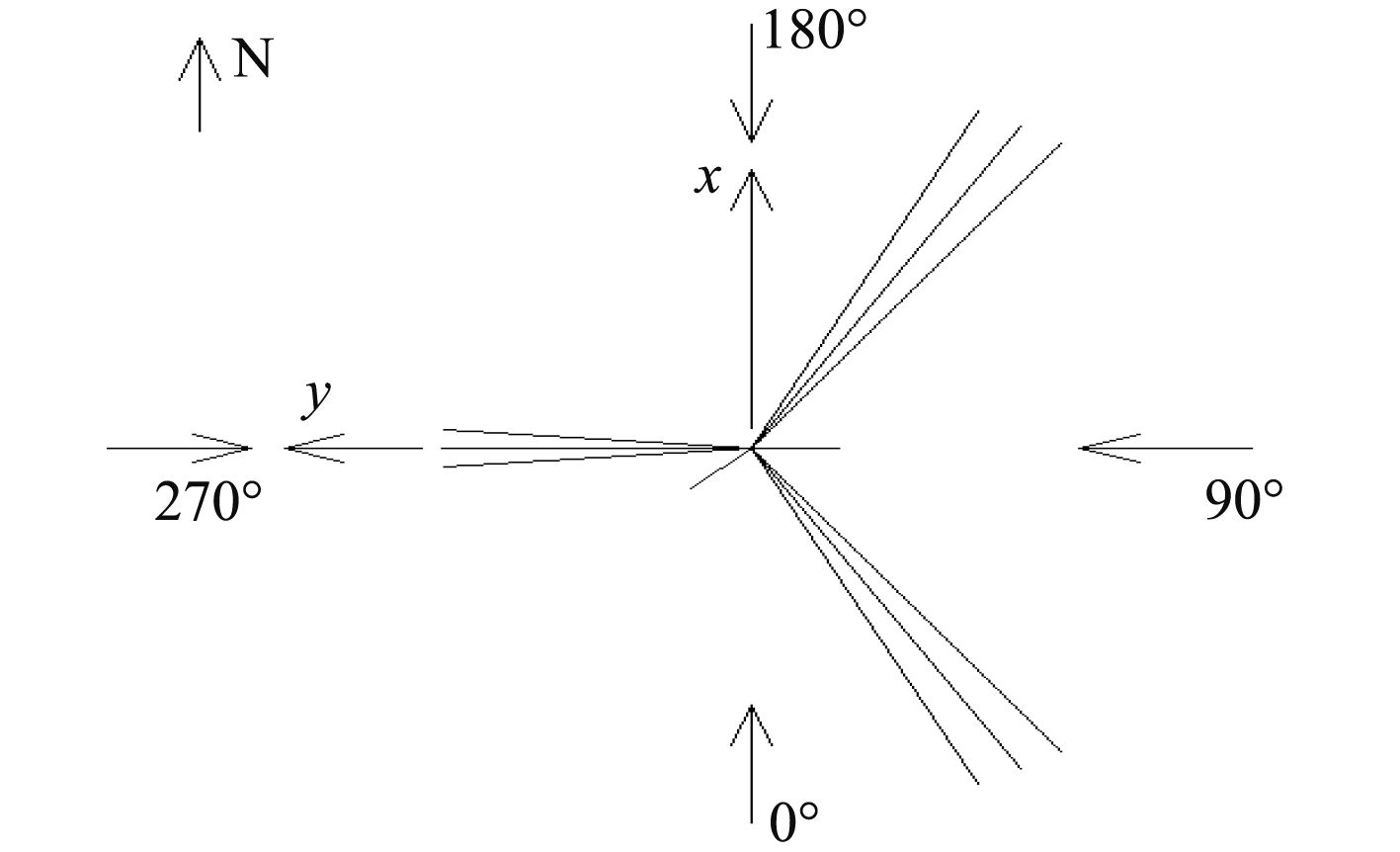
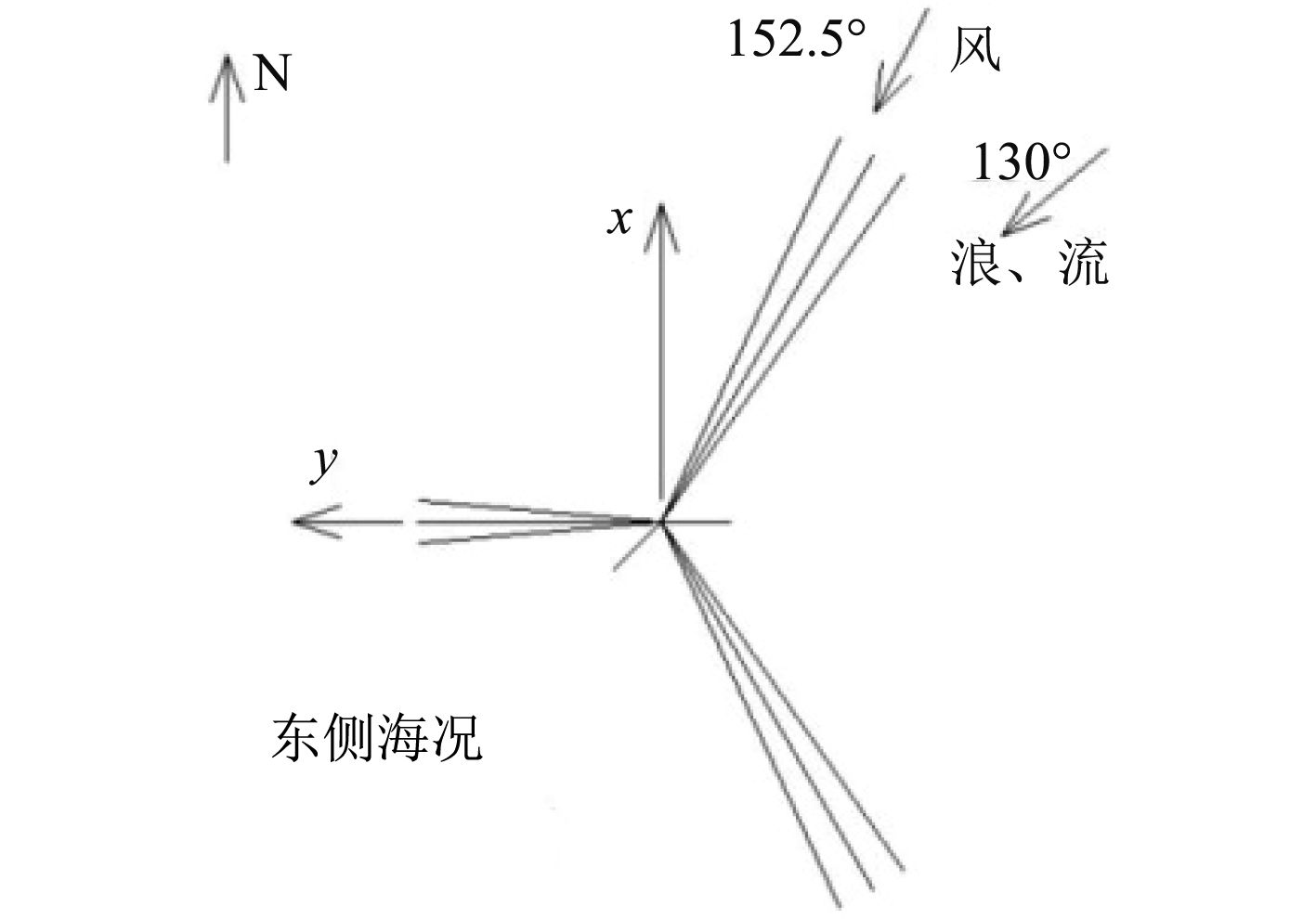
坐标系统和浪向定义如图3所示。单点是采用百年一遇环境条件不解脱标准设计的,波浪谱为JONSWAP谱,风谱采用NPD风谱,海流处理为定常流,具体环境条件参数如表4,方向示意图如图4所示。
|
图 3 坐标系及环境载荷方向定义 Fig. 3 The definition of coordinate and environment condition |
|
|
表 4 环境条件参数 Tab.4 The parameters of environment condition |
|
图 4 环境载荷方向示意图 Fig. 4 The direction of environment condition |
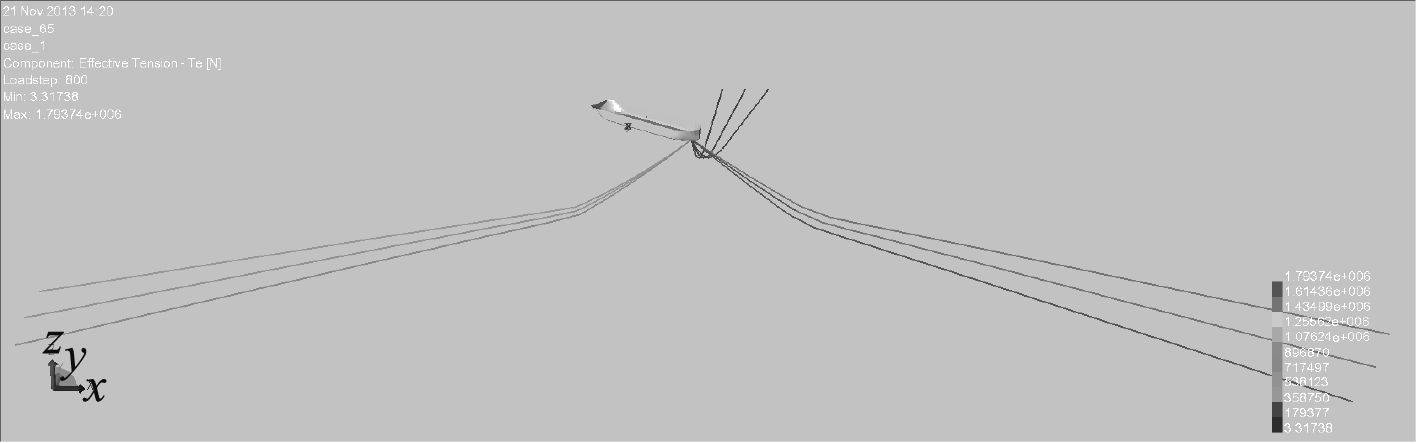
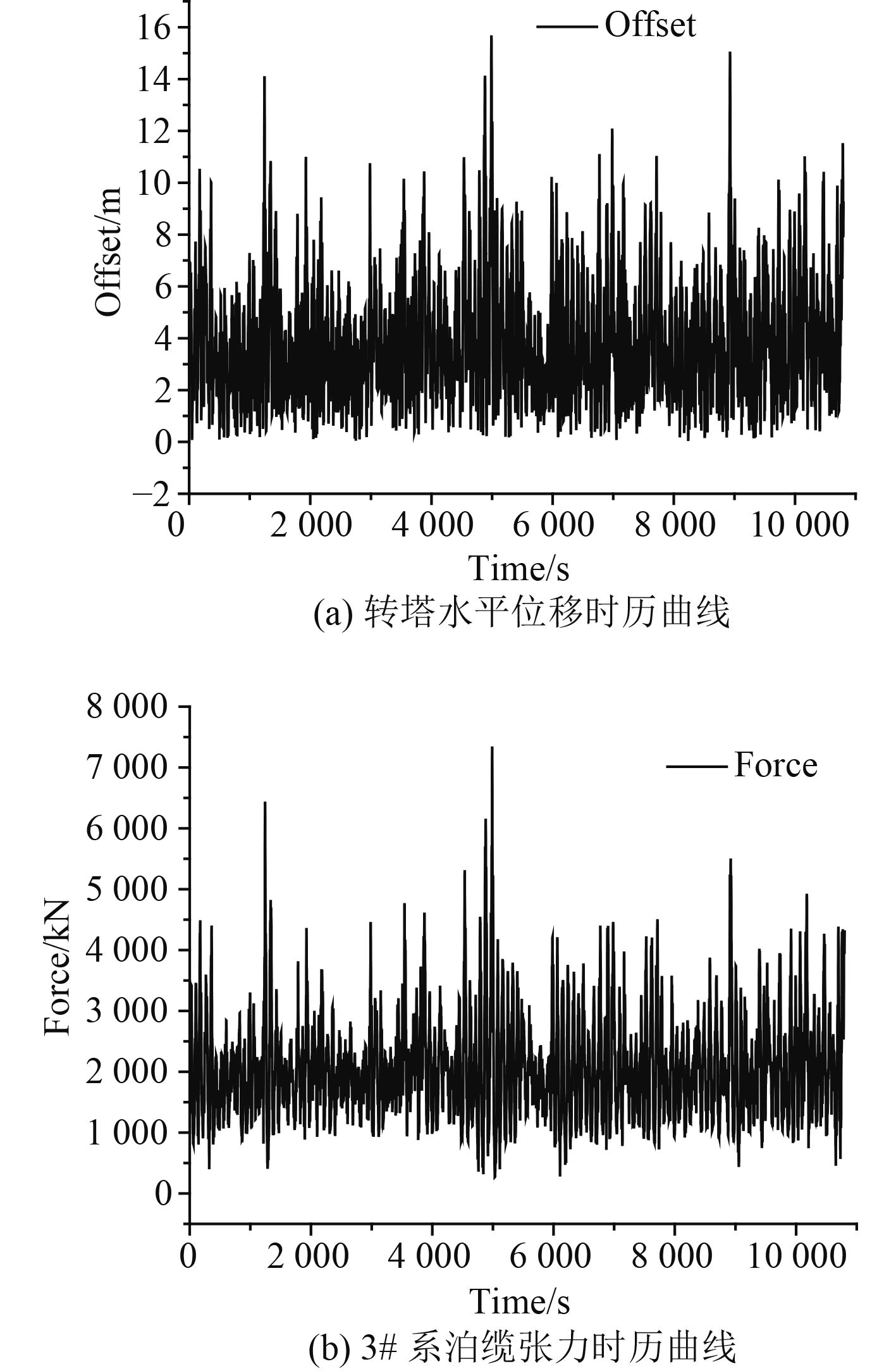
对于内转塔式单点系泊FPSO,各系泊缆的张力以及转塔位移大小是衡量一套单点系统好坏的重要指标,对系泊缆设计参数研究对FPSO的系泊系统设计具有一定的参考价值。计算时采用SESAM软件中的DeepC模块进行系泊系统与FPSO之间的时域耦合动力分析,模型如图5所示,计算各系泊缆的张力以及转塔水平面内位移的时间历程响应曲线,结果形式如图6所示。
|
图 5 DeepC耦合分析模型 Fig. 5 The couple analysis model of DeepC |
|
图 6 时间历程响应曲线 Fig. 6 The time history curve |
由于波浪谱、风谱转化的波面升高以及风速的时历曲线是随机的,因此在计算时参考BV规范[4]进行,即每个计算工况选取若干不同的随机种子数,随机生成不同的环境载荷的时间历程,并将不同的随机种子数的时域计算结果得到该工况下的预报值,具体如下所示:
|
${S_D} = {S_M} + a{S_S},$
|
(2) |
|
${S_M} = \frac{1}{n}\sum {{S_k}} ,$
|
(3) |
|
${S_S}^2 = \frac{1}{{n - 1}}\sum {{{\left( {{S_k} - {S_M}} \right)}^2}}\text{。} $
|
(4) |
式中:Sk为各次计算得到的极值;n为模拟次数;SM为样本均值;SS为样本标准差;SD为响应预报值;a的取值参考规范取值。由于敏感性分析的目的是为了寻找参数变化引起的响应变化的规律,因此综合考虑时间成本与计算精度,每次计算随机种子数取5。
2 系泊系统设计参数敏感性分析 2.1 敏感性分析参数影响内转塔系泊系统刚度的因素主要包括以下3点:系泊缆材料、系泊缆重量以及系泊缆预张力。系泊缆材料的影响因素主要考虑系泊缆材料自身抗拉刚度的变化,系泊缆的重量主要从系泊缆配重块重量以及系泊缆成分配比角度进行考虑,而影响系泊缆预张力最主要的因素是系泊缆自身长度与导缆孔到锚点之间距离,因此本文也将从以上几个方面对该内转塔单点系泊系统进行敏感性分析。
2.2 内转塔系泊系统敏感性衡量指标与基准 2.2.1 敏感性衡量指标对于转塔式系泊系统一个重要的动力响应参数就是系泊缆的最大张力,当系泊缆张力超过其最小破断张力时,将有可能发生断裂,从而对系统的定位能力以及安全性产生巨大的影响。而在实际工程中,通常将安全系数定义为系泊缆最小破断张力与系泊分析中得到的系泊缆最大张力的比值。规范[12]规定完整系泊状态下,动态方法模拟计算得到的安全系数须大于1.67。
此外,对于内转塔系泊系统来说,转塔上不仅挂载了系泊缆,此外其作为连接生产平台与FPSO的装置,还起到了输送原油、水以及电力的作用,因此转塔上还连接着立管、复合电缆等设备,而这些管线不仅对于张力有一定的要求,其对于内转塔在水平面内的位移也有着相关要求,因此转塔的位移也是敏感性分析的一个重要指标。
综上所述,本文以系泊缆的最小安全系数以及转塔最大水平面内位移作为衡量指标。
2.2.2 敏感性分析基准敏感性分析是一个对比的过程,因此在分析的过程中应确定某一种作为基准的状态。本文以满载工况的FPSO在百年一遇环境条件下的动力响应作为基准,结果如表5所示。
|
|
表 5 敏感性分析基准状态计算结果 Tab.5 The results of sensitive analysis’s basic condition |
本内转塔系泊系统主要有锚链、钢缆2种主要材料构成,因此通过改变这2种材料抗拉刚度的大小,从而研究系泊系统材料对系泊系统刚度的影响。
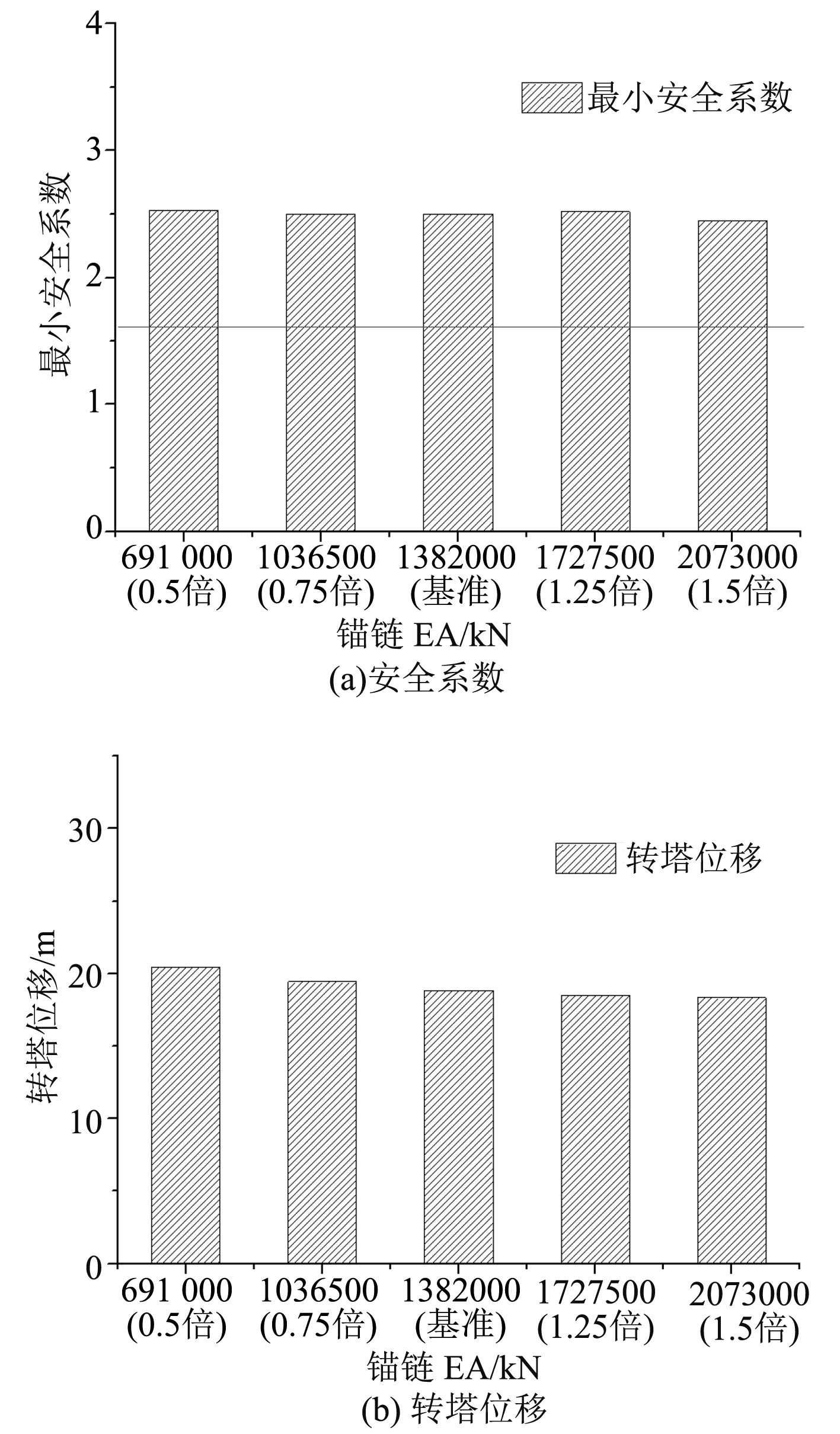
2.3.1 锚链刚度的敏感性分析为分析系泊缆锚链刚度对系泊系统响应的影响,分别计算锚链轴向刚度减小50%,25%,增加25%,50%的系泊系统主要响应。图7为锚链刚度的敏感性分析结果。从分计结果来看,系泊缆的安全系数变化不大,但转塔位移随着刚度的增加,位移值变小。
|
图 7 锚链EA敏感性分析 Fig. 7 The sensitive analysis of EA about chain |
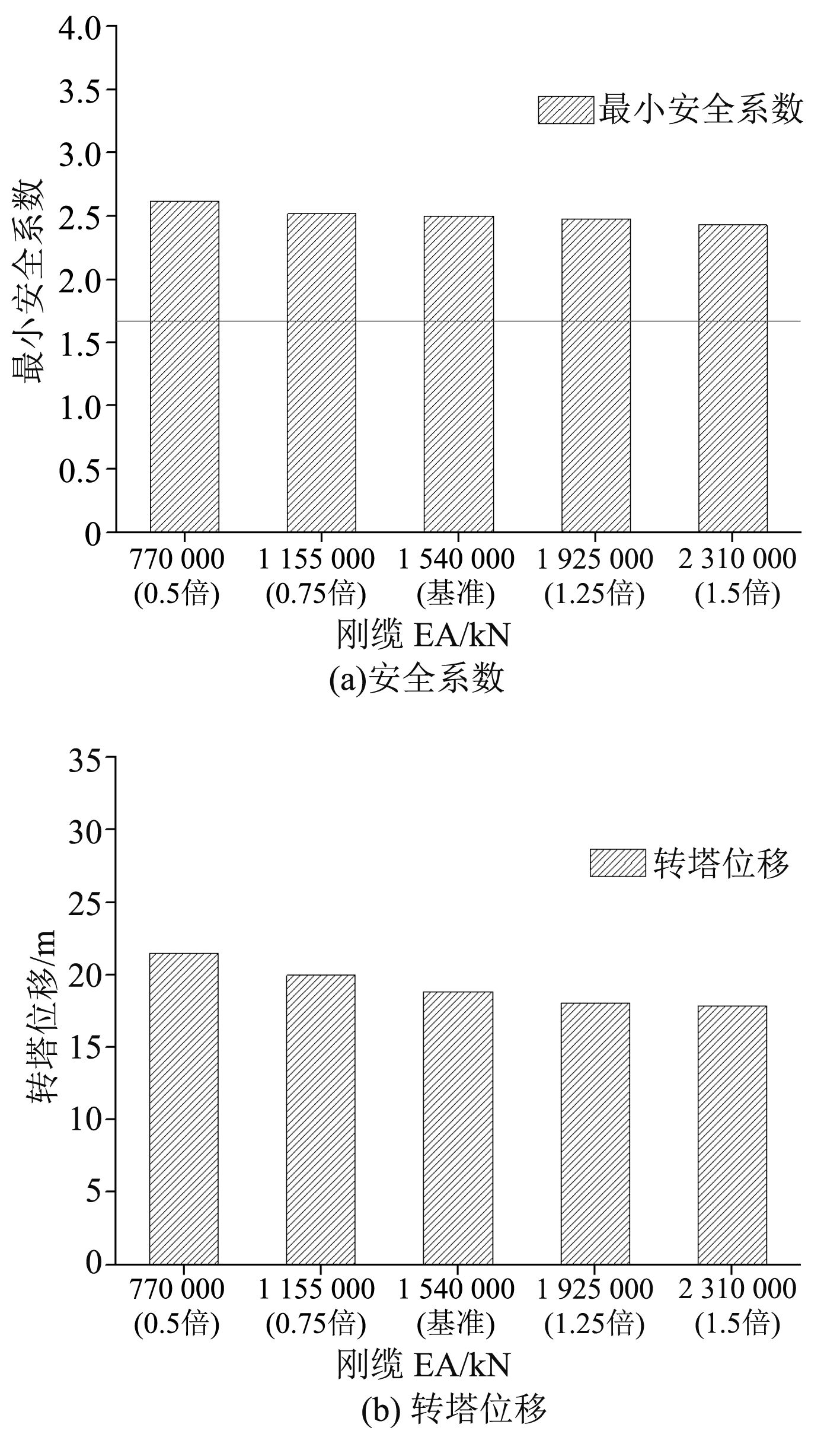
为分析钢缆刚度对系泊系统的影响,同样分别计算钢缆轴向刚度减小50%,25%,增加25%,50%的系泊系统主要响应。图8为钢缆刚度的敏感性分析结果。从分析结果来看,系泊缆的安全系数变化不大,但转塔位移随钢缆刚度的增加而减小。
|
图 8 钢缆EA敏感性分析 Fig. 8 The sensitive analysis of EA about wire |
长、短系泊缆中包含长度相同的加有配重块的一段锚链,称之为配重段,即UCS2段。改变配重段系泊缆的单位长度重量,分析其对系泊系统响应的影响。从实际设计角度考虑,配重段悬挂配重块的位置有限,且配重块容易丢失,因此考虑重量减少的情况,以模拟配重块丢失。由于设计中每根长缆上挂有12块配重块,短缆上挂有6块配重块,因此计算每根系泊缆上的配重块丢失17%,33%,50%,67%,83%以及100%的情况,图9为其分析结果。从分析结果来看,转塔位移与系泊缆安全系数均随着配重块的丢失数量的增多而增大。

|
图 9 配重段重量敏感性分析 Fig. 9 The sensitive analysis of clump weight |
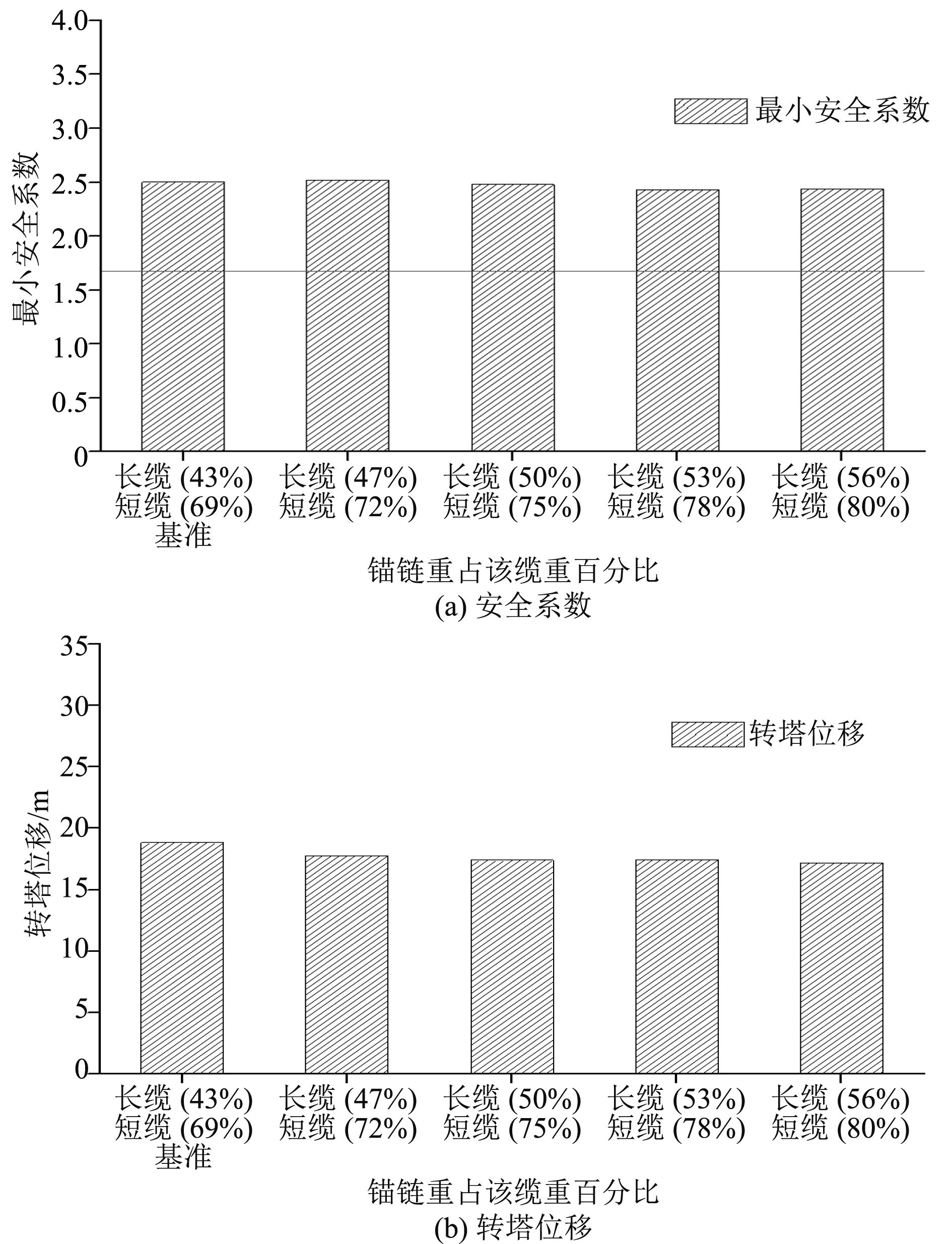
重力式系泊锚链重量是提供回复刚度的主要因素,因此在各系泊缆长度不变的条件下,通过调节UCS3段以及UWS段长度,增大锚链重量所占比例,进行敏感性分析,结果如图10所示。由于锚链所占比例增加,系泊缆重量增大,回复刚度增大,转塔位移呈减小趋势,安全系数总体上呈减小趋势。
|
图 10 锚链重量所占比例敏感性分析 Fig. 10 The sensitive analysis of the ration of chain weight |
由于配重段(UCS2)湿重是上部锚链最大的,因此通过调节UCS段中UCS2段长度所占比例,进行敏感性分析。由于UCS3段长度仅10 m,因此仅分析UCS2段靠近导缆孔的端点位置不变、另一端伸长或缩短,UCS1段随之相应变化,保证系泊缆总长不变的情况,结果如图11所示。从分析结果来看,改变配重段在系泊缆中所占位置与比例,对系泊系统响应的影响并不明显。
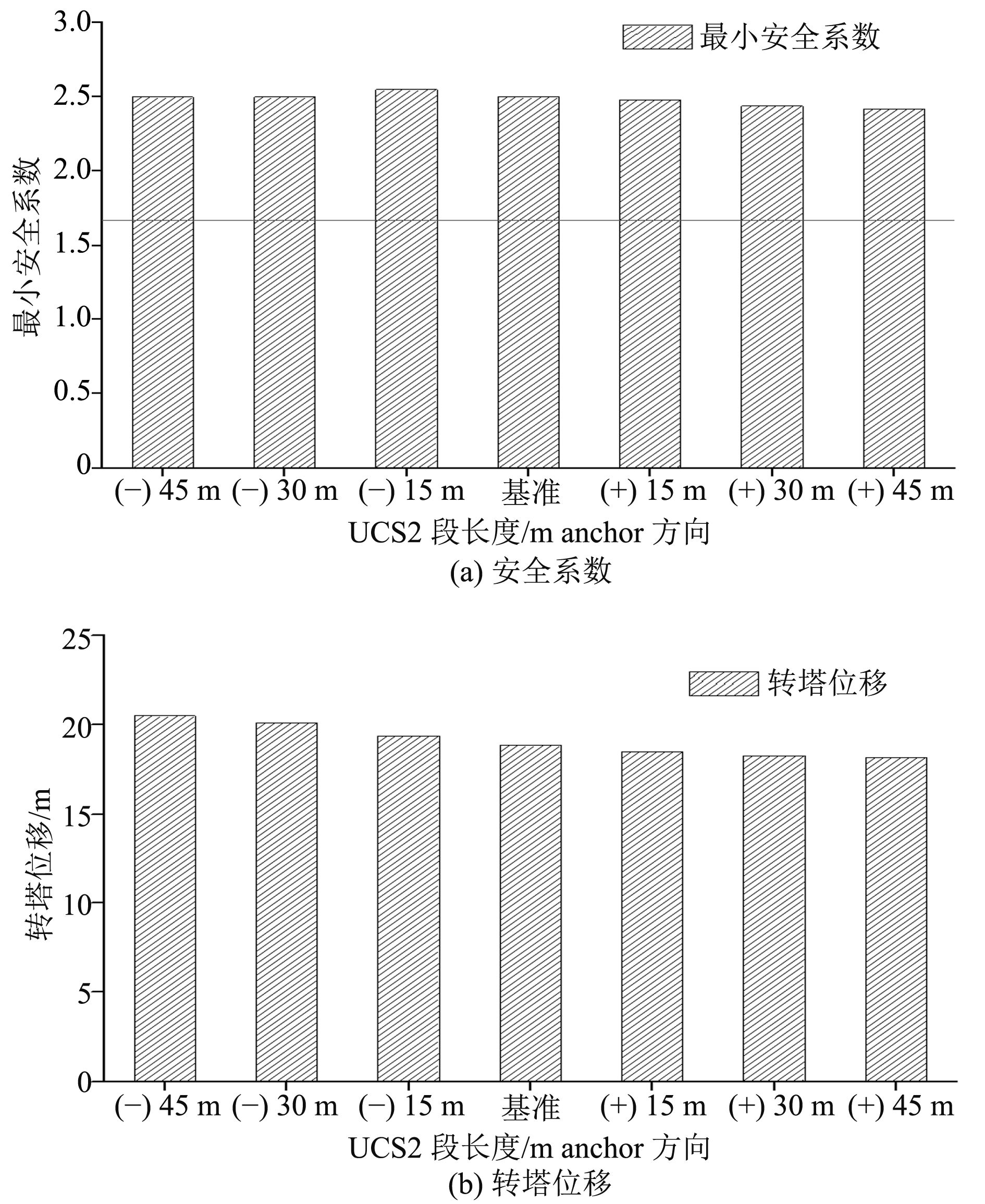
|
图 11 上部锚链成分配比敏感性分析 Fig. 11 The sensitive analysis of the ration of upper chain weight |
改变UWS段长度,分别计算钢缆长度加减5 m、10 m情况下系泊系统动力响应特性,分析其对系泊系统响应的影响,结果如图12所示。从结果中明显看出,系泊系统响应对UWS段长度变化非常敏感。这是由于系泊缆长度的变化,将会引起预张力的变化,从而引起系泊刚度的显著变化。
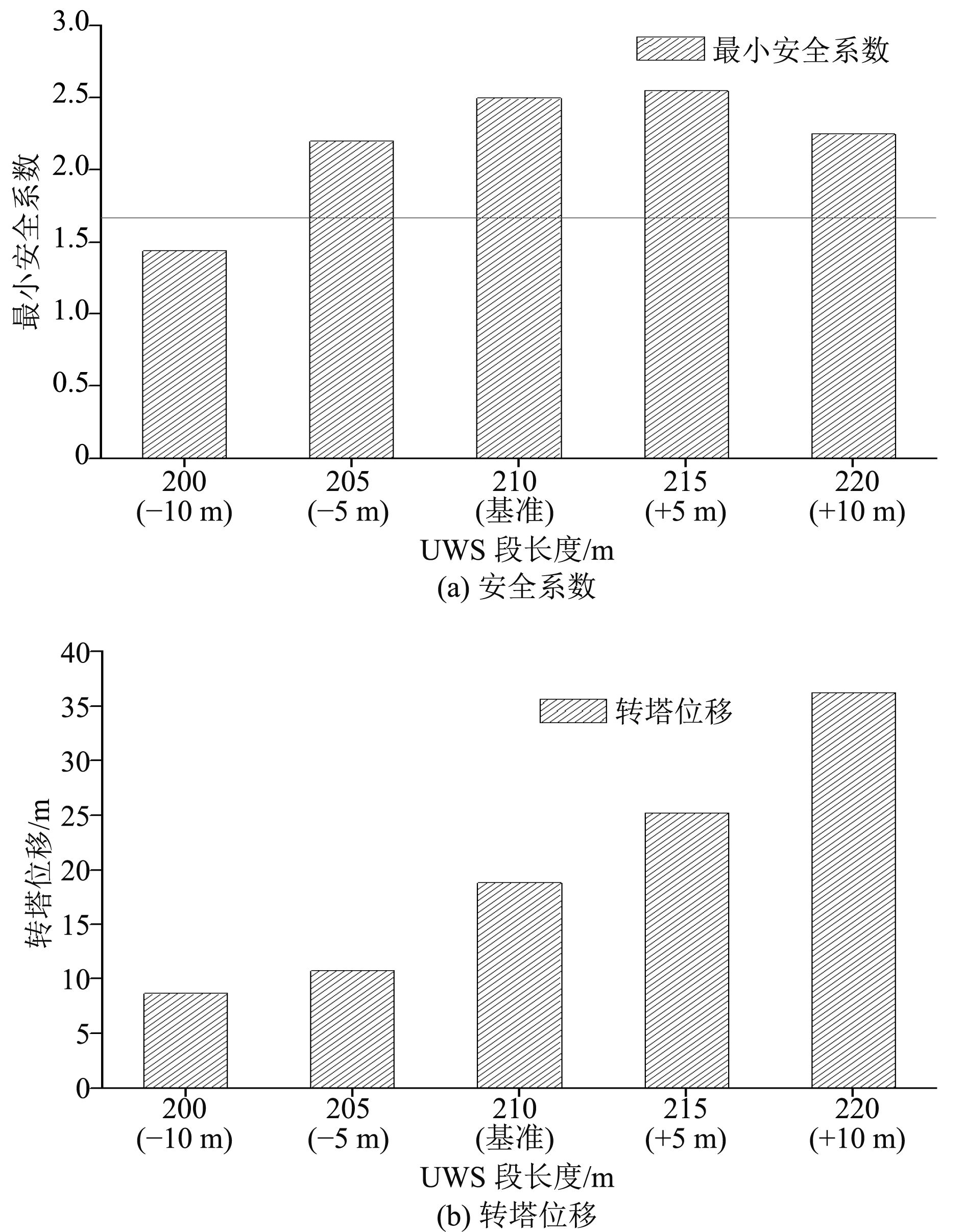
|
图 12 系泊缆长度敏感性分析 Fig. 12 The sensitive analysis of mooring line length |
系泊系统安装时容易产生误差,因此通过改变锚点位置,分析其对系泊系统响应的影响,结果如图13所示。(+)表示锚点远离转塔位置,(–)表示靠近转塔位置。
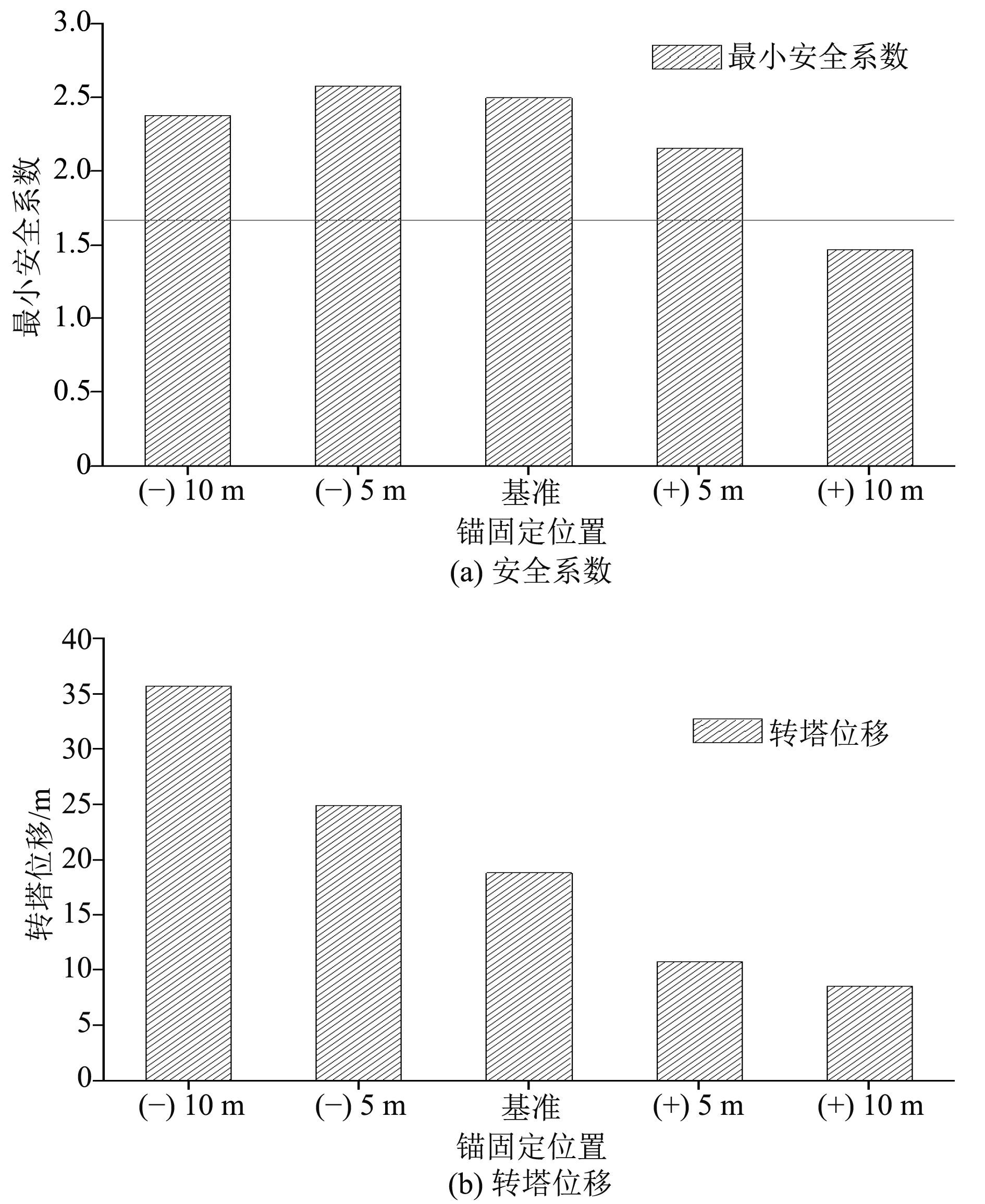
|
图 13 锚固点位置敏感性分析 Fig. 13 The sensitive analysis of anchor position |
在系泊缆长度不变的情况下,锚固点位置的移动导致系泊缆的形态发生变化,从而影响系泊缆上的预张力,从而导致系泊系统的回复刚度发生变化。
2.6 小结从上述计算结果中不难看出,系泊系统动力响应对于系统材料相关参数的敏感性,无论从安全系数角度还是转塔位移角度来看,都是钢缆刚度大于锚链刚度;对于系统重量相关参数的敏感性,当配重块丢失量超过50%时,将对系泊系统动力响应产生较大的影响,而且系统重量相关参数的影响对于转塔位移要比安全系数显著;而系泊系统动力响应对于系泊缆的预张力最为敏感,微小的参数变化将会导致系统动力响应的剧烈变化。因此系泊系统敏感性参数中系泊系统预张力影响最大,因此在设计中应重点关注系泊缆长度、锚点位置、配重块重量。
3 结 语本文通过FPSO、系泊缆和立管多体时域耦合分析方法,对内转塔式单点系泊的FPSO进行了系泊系统的敏感性分析。通过系泊系统参数的敏感性分析,得出系泊系统响应的变化规律:
1)系泊缆材料相关参数中,配重段重量是影响系泊系统响应的主要因素。配重段部分连接的配重块对于调节系泊系统的刚度具有较大影响,改变配重块的重量,可以有效改变系泊缆的刚度;
2)系泊缆长度、位置参数中,锚点位置与系泊缆长度的变化将会大幅影响系泊缆的预张力,使得系泊刚度变化很大,从而严重影响系泊系统的动力响应,因此在系泊系统安装中应合理的选择锚固点和系缆长度;
3)单点系泊系统动力响应对系泊缆长度、锚固点位置非常敏感,对配重段的重量较为敏感。
| [1] | 吴家鸣. FPSO 的特点与现状[J]. 船舶工程, 2012, 2 . DOI: 10.3969/j.issn.1000-6982.2012.01.031 |
| [2] | 郑成荣, 范菊, 缪国平, 等. 深水 FPSO 时域耦合动力分析[J]. 水动力学研究与进展: A 辑, 2012, 27 (4): 376–382. |
| [3] | OCIMF. Prediction of Wind and Current Loads on VLCCs[M]. London: WITHERBY & CO. LTD, 1994. |
| [4] | VERITAS B. NR 493 Classification of mooring systems of permanent offshore units[J]. NT, 2004. |
| [5] | VERITAS D N. Offshore Standard DNV-OS-E301 Position Mooring[J]. 2008. |
 2017, Vol. 39
2017, Vol. 39
