水面无人艇(unmanned surface vehicle,USV)在海洋科研、海洋开发和军事领域具有极其广泛的应用前景,已经成为国内外智能化装备的研究方向之一。文献[1]总结了USV的历史、研究现状以及发展趋势。目前已有多种水面无人艇应用于军事、科研等领域,其中以美国的SPAR-TAN和以色列的Protector为典型代表。
国内外不少学者对USV避碰问题经行了相应研究,并取得了较好的成果。王敏捷等利用模糊近域图避障方法进行了避障研究;Caccia等针对海洋-大气研究的需要开发了Sesamo号双体型USV,基于视线(line-of-sight,LOS)规划算法设计了具有自主避碰能力USV系统;Casalino等利用分层思想把USV的实时危险规避分为静止障碍物规避,运动障碍物规避和反应式规避,并分层讨论了规避策略。
目前国内外的USV避碰研究为水面无人艇避碰提供了一定的参考,然而这些方法运用的前提大多是将USV视为质点,并没考虑其操纵运动特性,而且忽略外界条件对USV航行的影响,然而,在相当复杂的水域环境中,USV在智能避碰的同时,还会受到风浪流的影响,所以这种理想化的思想对于USV在实际水域上航行避碰的借鉴价值是有限的。因此,水面无人艇避碰不仅要考虑静态障碍物的智能避碰,还需要考虑动态障碍物情况下的智能避碰。
本文在海事避碰规则的基础上,考虑水面无人艇的操纵运动模型(MMG模型)和运动数学模型,以及动态障碍物的运动情况,通过实时改变USV的航速和航向,成功的实现水面无人艇在运动情况下的动态障碍物的智能避碰。
1 USV运动环境模型建立水面无人艇在海面上行驶过程中,会遇到动态障碍物的阻碍,并且考虑到USV体积小、速度快等特点,在行驶中会碰到横倾、首摇等现象。因此为了保障水面无人艇的安全行驶,必须考虑USV的避碰规则和运动环境模型的建立。
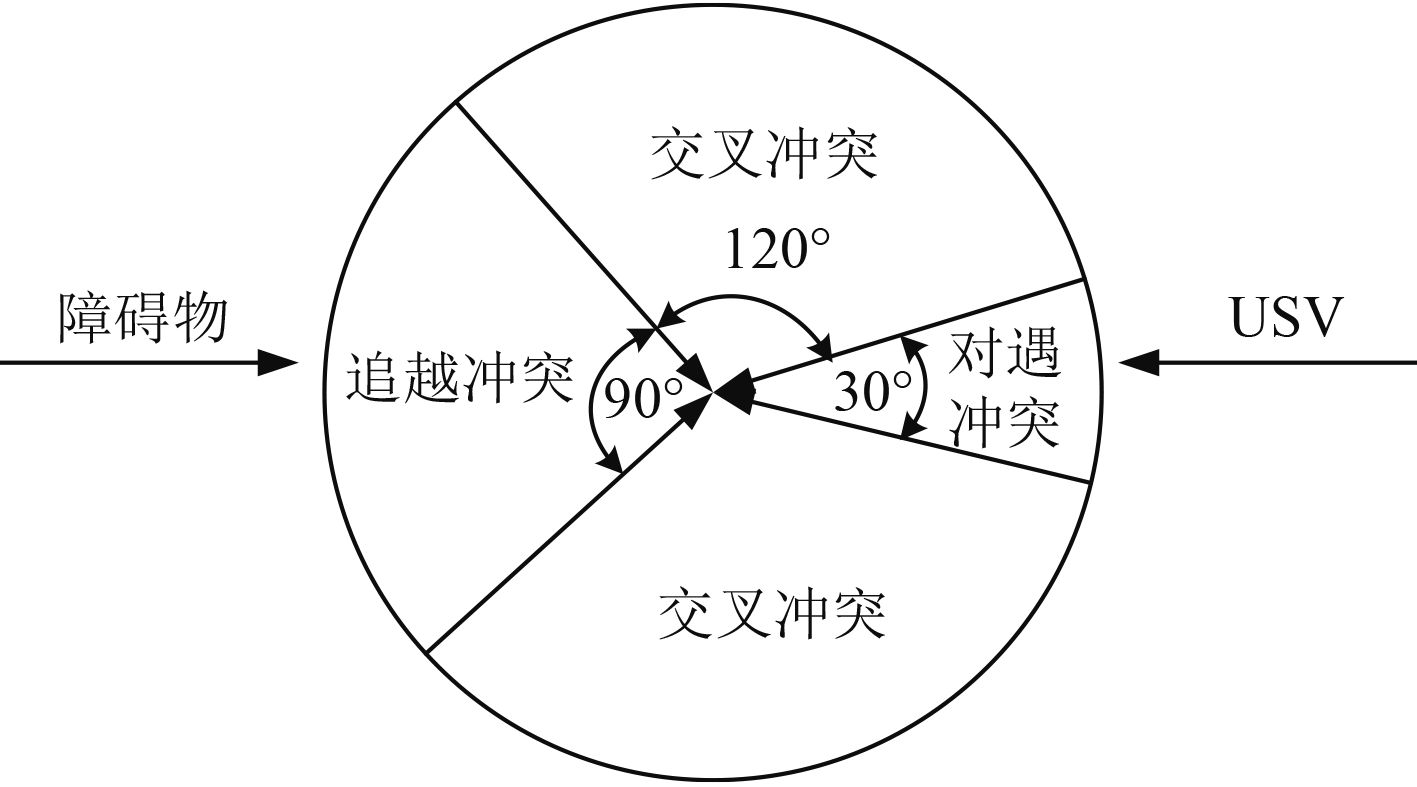
1.1 避碰规则公约按照《国际海上避碰规则公约》,将船舶互见中构成避碰危险时的局面分为以下3类(见图1)。
对遇:USV与动态障碍物航向角度差∆θ满足|180–∆θ|<15°,USV应向其右方转向,从障碍物的左方通过。
追越:USV与动态障碍物航向角度差∆θ满足|∆θ|<45°,USV应向其左舷转向,从障碍物的左方通过。
交叉:USV与动态障碍物航向角度差∆θ满足45°≤|∆θ|≤165°,USV要从障碍物后方航行。
|
图 1 海事避碰规则划分图 Fig. 1 Maritime regulations for preventing collisions plans |
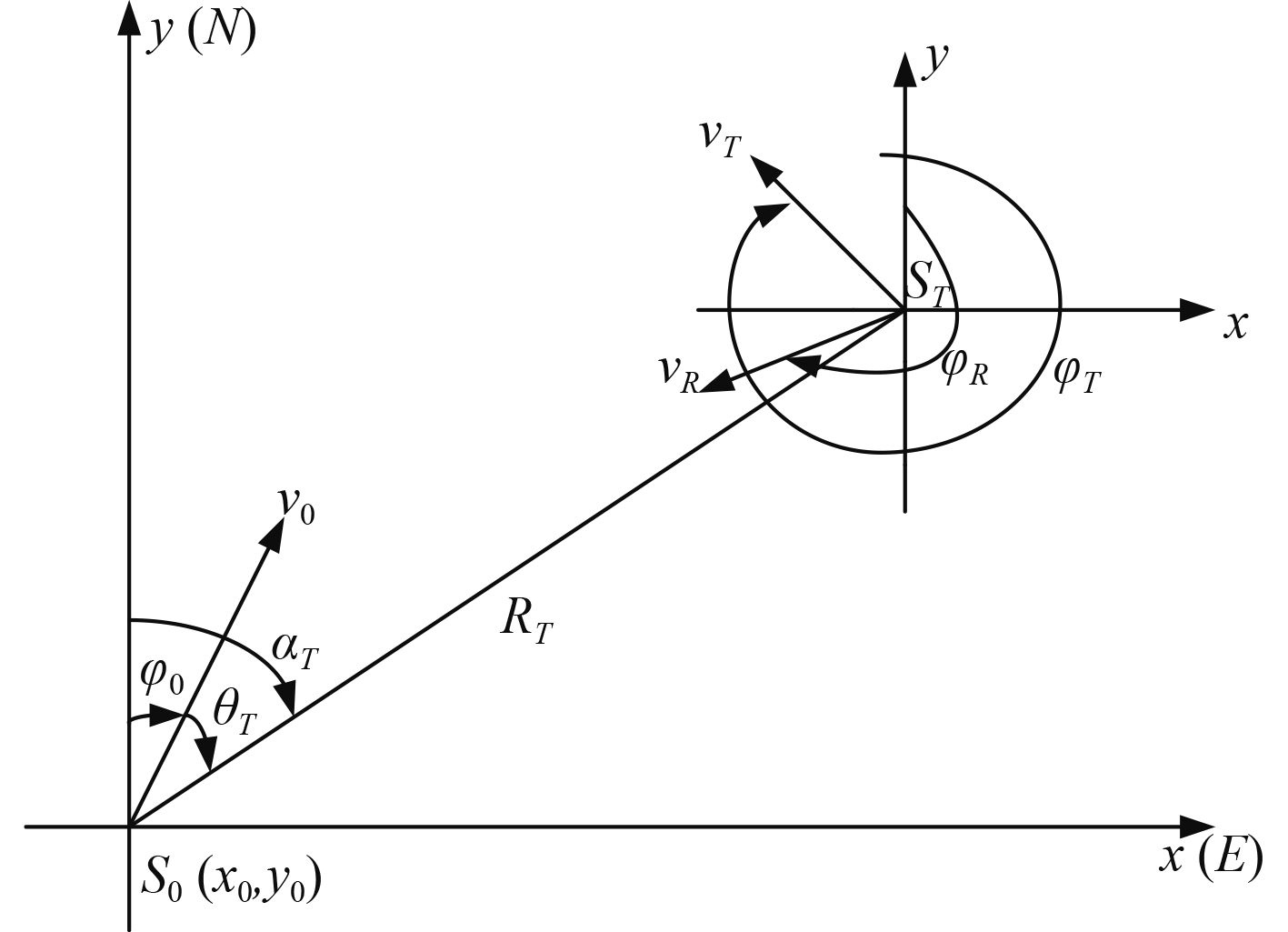
为了实现USV较好的动态智能避碰效果,必然要对USV和动态障碍物的相关参数进行计算分析,根据参数分析结果对水面无人艇实施相应的措施,因此,需要在坐标系下进行相应的计算(见图2)。
|
图 2 USV与动态障碍物运动模型 Fig. 2 Motion model of USV and dynamic obstacles |
图2中,S0是USV的当前位置,以航速v0、首向φ0前行(在海洋环境中,水面无人艇简化为一个点)。其中:
|
$\begin{array}{l}{v_0} = \sqrt {v_{x0}^2 + v_{y0}^2} \text{,} \\{\phi _{\rm{0}}} = \arctan \displaystyle\frac{{{v_{x0}}}}{{{v_{y0}}}} + \alpha \text{,} \\\alpha = \left\{ {\begin{array}{*{20}{c}}{{{\rm{0}}^{\rm{o}}}},\\{{{180}^{\rm{o}}}},\\{{{180}^{\rm{o}}}},\\{{{360}^{\rm{o}}}},\end{array}} \right.\;\;\;\;\begin{array}{*{20}{c}}{if:{v_{x0}} \geqslant 0,{v_{y0}} \geqslant 0}\text{;}\\{if:{v_{x0}} \leqslant 0,{v_{y0}} \leqslant 0}\text{;}\\{if:{v_{x0}} \geqslant 0,{v_{y0}} \leqslant 0}\text{;}\\{if:{v_{x0}} \leqslant 0,{v_{y0}} \geqslant 0}\text{。}\end{array}\end{array}$
|
ST是动态障碍物的位置,以航速vT、首向φT前行。其中:
|
$\begin{array}{l}{v_T} = \sqrt {v_{xT}^2 + v_{yt}^2} \\{\phi _T} = \arctan \displaystyle\frac{{{v_{xT}}}}{{{v_{yT}}}} + \alpha \end{array}$
|
式中α同上。障碍物相对USV的相对运动速度为vR、相对速度的航向为φR。则
|
$\begin{array}{l}v{}_R = \sqrt {v_{xR}^2 + v_{yR}^2} \text{,}\\{\phi _R} = \arctan \displaystyle\frac{{{v_{xR}}}}{{{v_{yR}}}} + \alpha \text{。}\end{array}$
|
USV与动态障碍物之间的相对距离RT为
|
${R_T} = \sqrt {{{\left( {{x_T} - {x_0}} \right)}^2} + {{\left( {{y_T} - {y_0}} \right)}^2}} \text{。}$
|
障碍物相对USV的真方位为αT,水面无人艇相对动态障碍物的真方位为α0,以及动态障碍物的相对方位θT和障碍物与水面无人艇航向交叉角CT。
|
$\begin{array}{l}{\alpha _T} = \arctan \displaystyle\frac{{{x_T} - {x_0}}}{{{y_T} - {y_0}}} + \alpha\text{,} \\{\alpha _0} = \arctan \displaystyle\frac{{{x_0} - {x_T}}}{{{y_T} - {y_0}}} + \alpha\text{,} \\{\theta _T} = {\alpha _T} - {\phi _0}\text{,}\\{C_T} = {\phi _T} - {\phi _0}\text{。}\end{array}$
|
通过上面公式可以得到无人艇与障碍物的最近会遇距离DCPAT和无人艇与障碍物的最小会遇时间TCPAT为
|
$\begin{array}{l}DCP{A_T} = {R_T} \cdot \sin \left( {{\phi _R} - {\alpha _T} - \pi } \right)\text{,}\\TCP{A_T} = {R_T} \cdot \cos \left( {{\phi _R} - {\alpha _T} - \pi } \right)/{v_R}\text{。}\end{array}$
|
而USV与动态障碍物的碰撞危险度ρ与DCPAT和DCPAT有较大关系,因此可以通过结合DCPA和TCPA来衡量碰撞危险度ρ。
|
$\rho = {\left( {a \cdot DCP{A_T}} \right)^2} + {\left( {b \cdot TCP{A_T}} \right)^2}\text{。}$
|
式中a,b为加权值,是通过统计得到的数值。通常情况下,当右戚来船时,a取5,b取0.5;当左戚来船时,a取5,b取1。由此可以看出,当ρ越小,USV和障碍物之间越危险。
2 水面无人艇操纵运动模型为了研究基于操纵运动特性的水面无人艇智能避碰问题,需要对水面无人艇的操纵性运动模型进行分析,即需要对水面无人艇进行运动建模,从而完成USV在受力情况下的智能避碰问题。
作用于水面无人艇上的力包括艇体、螺旋桨、以及舵上受到的流体力。按照力产生的性质进行分类,艇体上受到的流体力和力矩可分为惯性类及粘性类流体力和力矩。因此,作用于艇体上的流体力和力矩可表示为:
|
$\left\{ {\begin{array}{*{20}{c}}{X = {X_I} + {X_H} + {X_P} + {X_R}}\text{,}\\{Y = {Y_I} + {Y_H} + {Y_P} + {Y_R}}\text{,}\\{N = {N_I} + {N_H} + {N_P} + {N_R}}\text{。}\end{array}} \right.$
|
其他I为惯性类流体力和力矩;H,P,R为作用在艇体,螺旋桨,舵上的流体动力与力矩。
本文采用MMG分离建模的思想,把作用于水面无人艇上的力和力矩分流体动力、主动力、外力。假定质量为m的水面无人艇,重心G处的速度向量为
|
$\left\{ {\begin{array}{*{20}{c}}{\sum {\overline F } = m\displaystyle\frac{{{\rm{d}}\overline {{V_G}} }}{{{\rm{d}}t}}}\text{,}\\[8pt]{\sum {\overline M } = m\displaystyle\frac{{{\rm{d}}\overline {{H_G}} }}{{{\rm{d}}t}}}\text{。}\end{array}} \right.$
|
式中:
本文主要研究USV水平面上的运动。在USV做平面运动过程中,对于涉及其运动及其操纵控制的问题,主要考虑的运动变量是前进速度u,横移速度v,转首角速度r,因此可以将USV的运动简化为三自由度的运动问题。
|
$\left\{ {\begin{array}{*{20}{c}}{m\left( {\dot u - rv - {x_G}{r^2}} \right) = \sum X }\text{,}\\{m\left( {\dot v + ru - {x_G}{r^2}} \right) = \sum Y }\text{,}\\{{I_{ZZ}}\dot r + m{x_G}\left( {\dot v + ru} \right) = \sum N }\text{。}\end{array}} \right.$
|
在水面无人艇模拟交通时,其运动状态有3种:定常运动、转向运动和变速运动。因此,水面无人艇的运动模型主要包括定常运动模型、转向运动模型和变速运动模型。
3.1 定常运动模型定常运动模型是指水面无人艇在航向和航速都不变的情况下的运动数学模型。假设当前USV的平面坐标位置为
|
$\left\{ {\begin{array}{*{20}{c}}{x = {x_0} + v \cdot \cos \phi \cdot t}\text{,}\\{y = {y_0} + v \cdot \sin \phi \cdot t}\text{。}\end{array}} \right.$
|
转向运动模型是指水面无人艇保持航速不变,只改变航向的运动。假设当前USV的平面坐标位置为
|
$\left\{ {\begin{array}{*{20}{c}}{x = {x_0} + \int_0^1 {0.9v\cos \phi \left( t \right){\rm{d}}t} }\text{,}\\{y = {y_0} + \int_0^1 {0.9v\sin \phi \left( t \right){\rm{d}}t} }\text{。}\end{array}} \right.$
|
|
$\phi \left( t \right) = k{\delta _0}\left[ {t - \left( {T + \frac{{{t_1}}}{2} + \frac{{{T^2}}}{{{t_1}}}\left( {{e^{{t_1}/T}} - 1} \right){e^{ - t/T}}} \right)} \right]\text{,}$
|
式中:k,T为操纵性指数;δ0为操控角,一般取10°~15°;t表示时刻,s;t1表示操控舵的时间,一般取为2.5 s。
3.3 变速运动模型如果USV在对遇或者超越过程中,仅转向无法避免碰撞时,需要采用变速运动模型,其运动方程为:
|
$v = {v_1} + \left( {{v_0} - {v_1}} \right) \cdot \exp \left( { - \frac{{k \cdot t}}{{m + {m_x}}}} \right){\text{。}}$
|
其中:v0为变速前的速度;v1为终速度;m+mx为前进方向的虚质量;m为USV的质量;mx为附加质量;k为USV的阻力系数。
如果以上3种运动模型依然无法避免碰撞的话,则必须立即停止USV的前行。
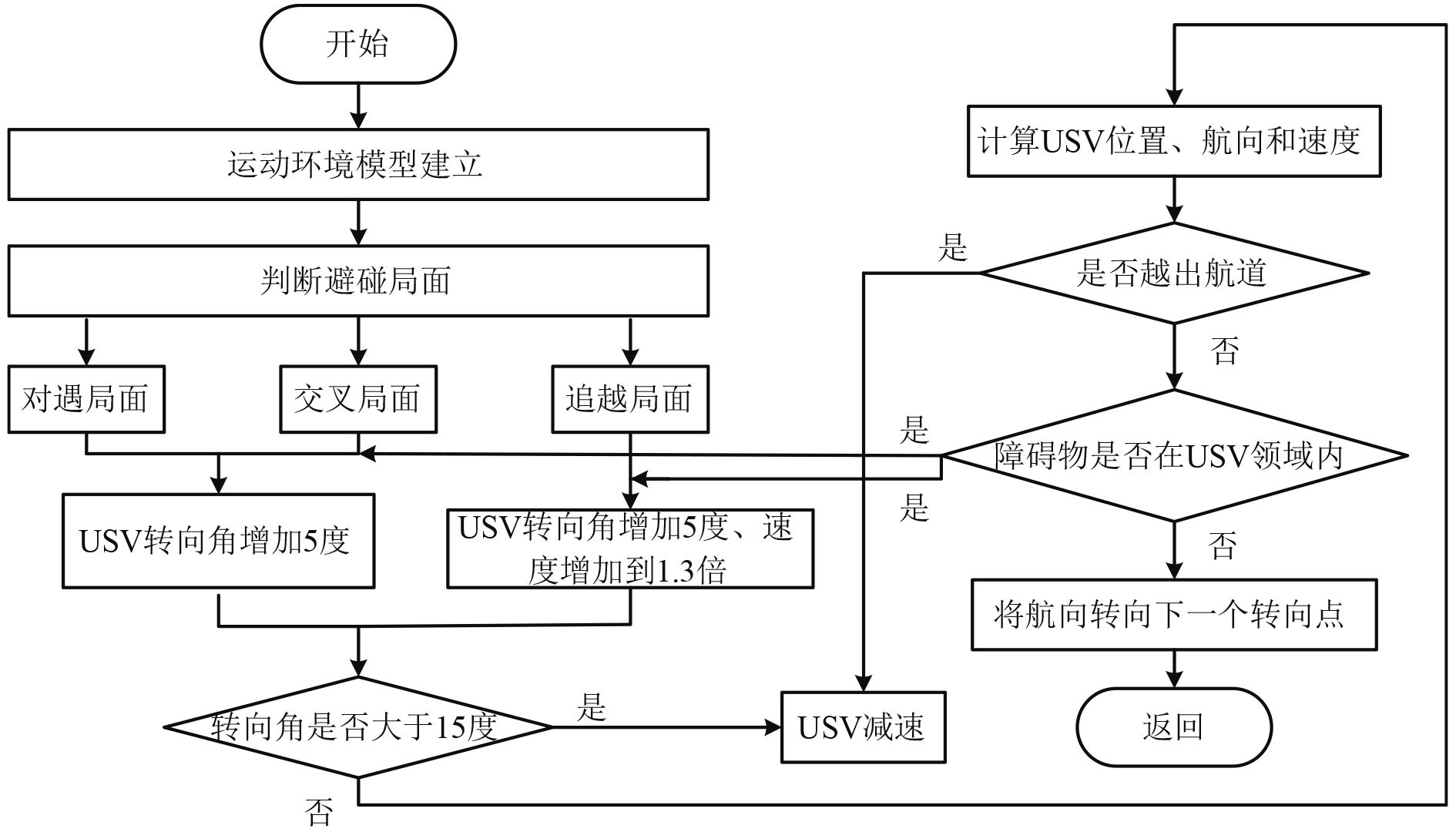
3.4 USV动态避碰流程图本文中,USV动态避碰是基于无人艇操纵运动模型,通过判断USV的碰撞危险局面,然后选择避碰模型,从而实现USV的动态智能避碰。具体流程图如图3所示。
|
图 3 动态避碰流程图 Fig. 3 Dynamic collision avoidance flowchart |
步骤1 初始化USV的位置和速度,建立运动环境模型。
步骤2 判断USV与动态障碍物的碰撞危险局面。
步骤3 通过得到的碰撞局面,进行USV的转向角操作,如果是对遇或者交叉局面,则仅仅增加转向角;如果是追越局面,不仅要增加转向角,还要增加速度。
步骤4 判断转向角是否大于15°,如果是则减速航行;如果不是则计算USV航向、航速和位置。
步骤5 继续判断USV是否越出轨道,是则减速,否则判断动态障碍物是否在USV领域内,如果在领域范围内,继续增加转向角或速度,不在领域内则转向下一个转向点。
步骤6 最后成功实现USV动态智能避碰,继续航行。
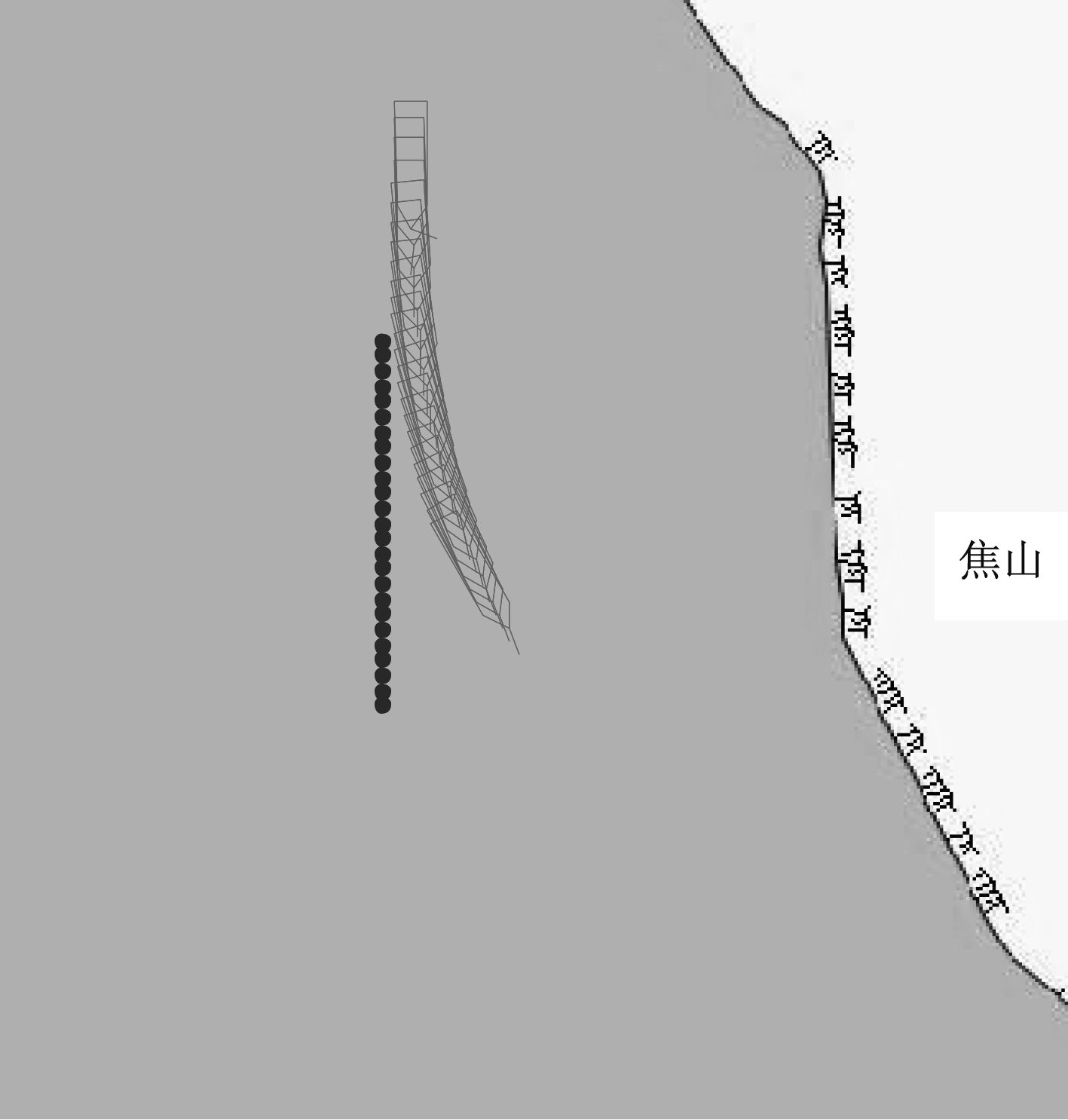
4 仿真实验结果与分析为验证该动态智能避碰方法的有效性,现使用软件Matlab2012a进行仿真,背景图采用镇江焦山风景区长江水域图。图中浅色部分代表USV,深色部分代表动态障碍物。
4.1 对遇局面避碰仿真图生成水面无人艇和动态障碍物,无人艇的初始中心坐标为(125,237),障碍物的初始坐标为(125,160)。考虑USV操纵运动模型,通过智能避碰模型对动态障碍物进行避碰。USV提前获取动态障碍物信息,当进入危险领域时,开始避碰,如图4所示。
|
图 4 对遇局面动态智能避碰仿真图 Fig. 4 Dynamic intelligent collision avoidance simulation map on situation |
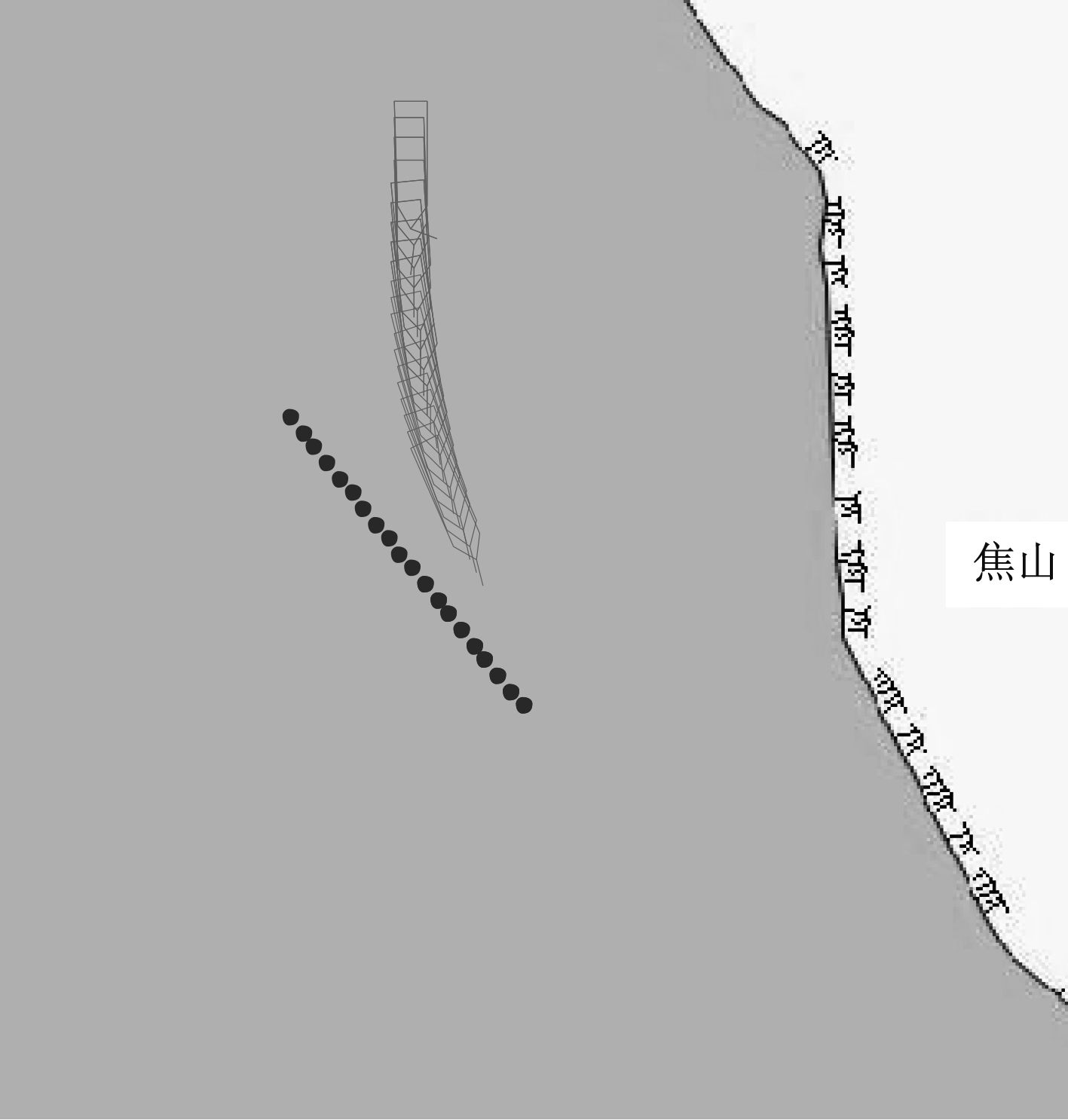
生成水面无人艇和动态障碍物,无人艇的初始中心坐标为(125,237),障碍物的初始坐标为(175,160)。考虑USV操纵运动模型,通过智能避碰模型对动态障碍物进行避碰。USV提前获取动态障碍物信息,当进入危险领域时,开始避碰,如图5所示。
|
图 5 交叉局面动态智能避碰仿真图 Fig. 5 Dynamic intelligent collision avoidance simulation map cross situation |
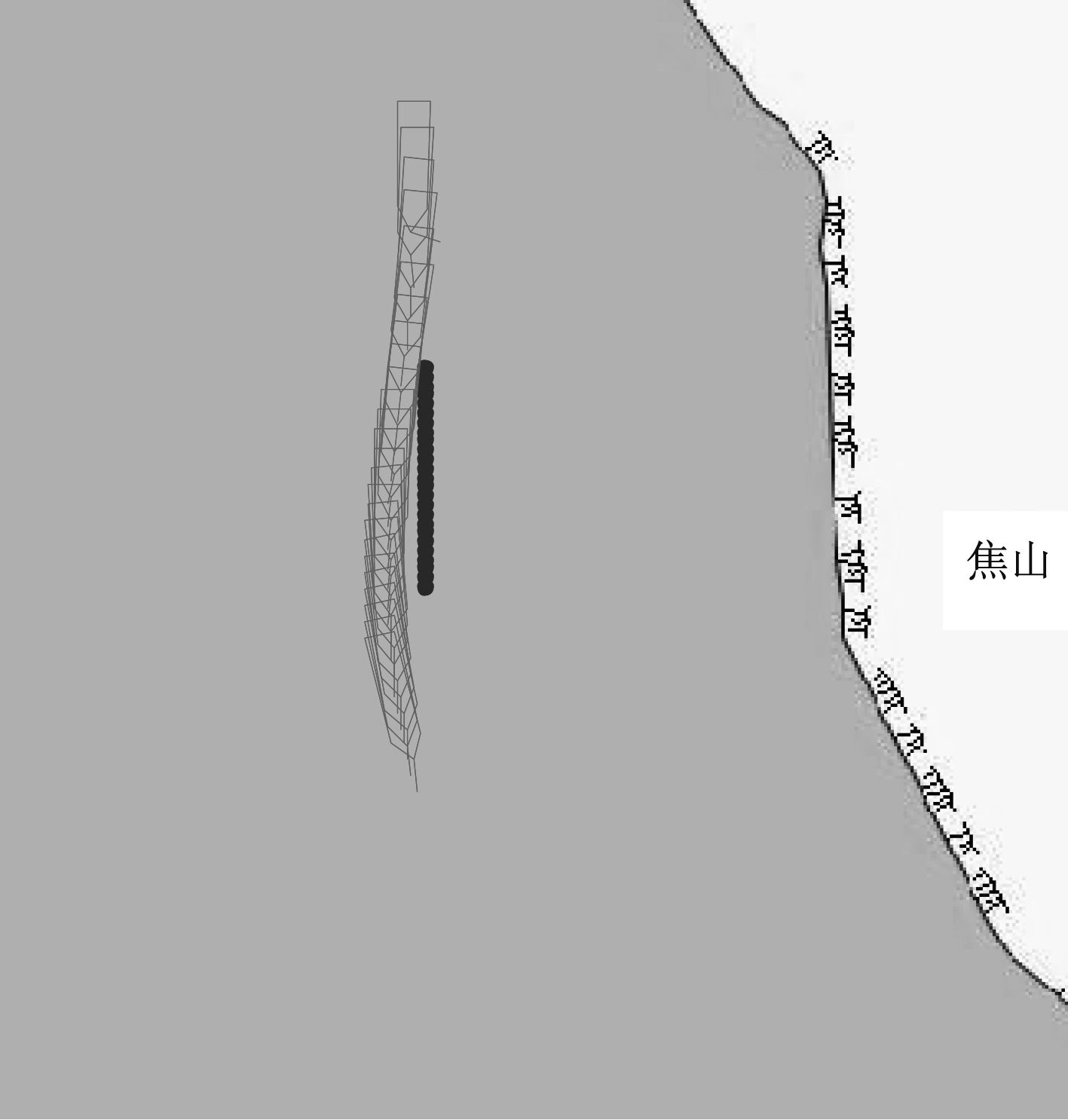
生成水面无人艇和动态障碍物,无人艇的初始中心坐标为(125,237),障碍物的初始坐标为(125,190)。考虑USV操纵运动模型,通过智能避碰模型对动态障碍物进行避碰。USV提前获取动态障碍物信息,当进入危险领域时,开始避碰,如图6所示。
|
图 6 追越局面动态智能避碰仿真图 Fig. 6 Dynamic intelligent collision avoidance simulation map overtaking situation |
本文通过考虑USV操纵运动模型,采用USV智能避碰模型,通过分析USV与动态障碍物的相对位置和相对速度关系,改变USV的速度和航向,实现了水面无人艇对动态障碍物的智能避碰。通过建立USV自动避碰决策仿真系统,证明了该智能避碰方法的有效性、高效性和实用性。
| [1] |
庄佳园, 张国成, 苏玉民. 水面无人艇危险规避方法[J]. 东南大学学报, 2013, 43 (SⅠ): 126–130.
ZHUANG Jia-yuan, ZHANG Guo-cheng, SU Yu-min. USV hazard workaround[J]. Southeast University learned journal, 2013, 43 (SⅠ): 126–130. |
| [2] |
吴博, 熊勇, 文元桥. 基于速度障碍原理的无人艇自动避碰算法[J]. 大连海事大学学报, 2014, 40 (2): 13–16.
WU Bo, XIONG Yong, WEN Yuan-qiao. Based on the principle of USV speed barrier automatic collision avoidance algorithm[J]. Dalian Maritime University, 2014, 40 (2): 13–16. |
| [3] |
茅云生, 宋利飞, 向祖权. 水面无人艇多船障碍智能避碰[J]. 大连海事大学学报, 2015, 41 (4): 8–13.
MAO Yun-sheng, SONG Li-fei, XIANG Zu-quan. USV more water obstacle boat intelligent collision avoidance[J]. Dalian Maritime University, 2015, 41 (4): 8–13. |
| [4] |
王哲. 无人艇自动避碰策略的研究[D]. 大连: 大连海事大学, 2013.
WANG zhe. USV automatic collision avoidance strategy research[D], Dalian: Dalian Maritime University, 2013. |
| [5] |
吴博. 基于操纵运动特性的海事无人艇自主避碰算法研究[D]. 武汉: 武汉理工大学, 2014.
WU bo. Autonomous collision avoidance algorithm based on maneuvering characteristics marine USV[D]. Wuhan: Wuhan University of Technology, 2014. |
| [6] | YAN Rujian, PANG Shuo, SUN Hanbing, et al. Development and missions of unmanned surface vehicle[J]. Journal of Marine Science and Application,, 2010, 9 (4): 451–457. DOI: 10.1007/s11804-010-1033-2 |
| [7] | CACCIA M, BIBULI M, BONO R, et al. Basic navigation, guidance and control of an unmanned surface vehicle[J]. Autonomous Robots, 2008, 25 (4): 349–365. DOI: 10.1007/s10514-008-9100-0 |
| [8] |
陈超, 唐坚. 基于可视图法的水面无人艇路径规划设计[J]. 中国造船, 2013, 54(1): 129–135.
CHEN chao, TANG jian. Based on water law USV can view route planning[J]. Shipbuilding of China, 2013, 54(1): 129–135. |
 2017, Vol. 39
2017, Vol. 39
