顺浪航行是船舶,尤其是中小型船舶大风浪中航行优选的航法,以其往往能减轻摇荡和动力响应的影响。然而,进一步的研究和海上实践表明,顺浪航行的船舶可能陷入纯稳性损失、参数横摇和骑浪/横甩等不利局面[1]。
所谓纯稳性损失,是指船舶顺浪航行时,由于船体较长时间处于水线面变化的状态,以及动水压力场变化等因素的作用,致使船舶静稳性降低的情况。当前,IMO正在制定船舶第2代完整稳性衡准[2],“纯稳性损失”是完整稳性失效模式之一,是航海界、造船界密切关注的课题。
现有的纯稳性损失的研究一般采用以下2种方法:
1)水池试验法:优点是更加贴近海上实际;缺点是试验的次数、船型等受经费的约束较大[3 – 5];
2)计算法:优点是适用性比较好,不受时空等限制;缺点是计算繁琐,至少要计算4个自由度的摇荡,并且所计算的水动力受到诸多约制,譬如傅汝德-克里洛夫(Frude-Krylov)力和斯密斯(Smith)效应,误差较大[6 – 8]。
针对以上情况,本文根据Ю.И.涅查耶夫[9]基于28艘渔船和运输船船模水池试验给出的顺浪航行纯稳性损失计算方法(以下简称涅法),提出切合实用需求的扩展模式。涅法的优势是描述了顺浪航行船舶船体和波浪间复杂的耦合作用,计算结果有较高的可信度;缺点是适用面太窄,难以用于水面舰艇及其他类型的船舶。扩展模式拓宽了涅法的适用范围,并且实现了该算法的程序化,生成了便捷的实用化软件。
本文最后借助CFD方法和一般的理论计算法[10],验证了船舶顺浪航行纯稳性损失扩展模式计算结果的可信度。
1 涅法数模化本文优选涅法作为扩展模式的基础,涅法基于28艘渔船和运输船船模水池试验,以曲线和图表等形式计算了顺浪航行船舶骑浪时船中处于波峰和波谷2种情况下的稳性力臂增量
在横倾角小于60°的范围内,力臂增量
|
$\Delta l\left( \theta \right) = B\left[ {\phi \left( {\frac{h}{\lambda };\theta } \right) + \sum\limits_{m = 1}^{14} {{A_m}{f_m}\left( \theta \right)} } \right],$
|
(1) |
式中:
|
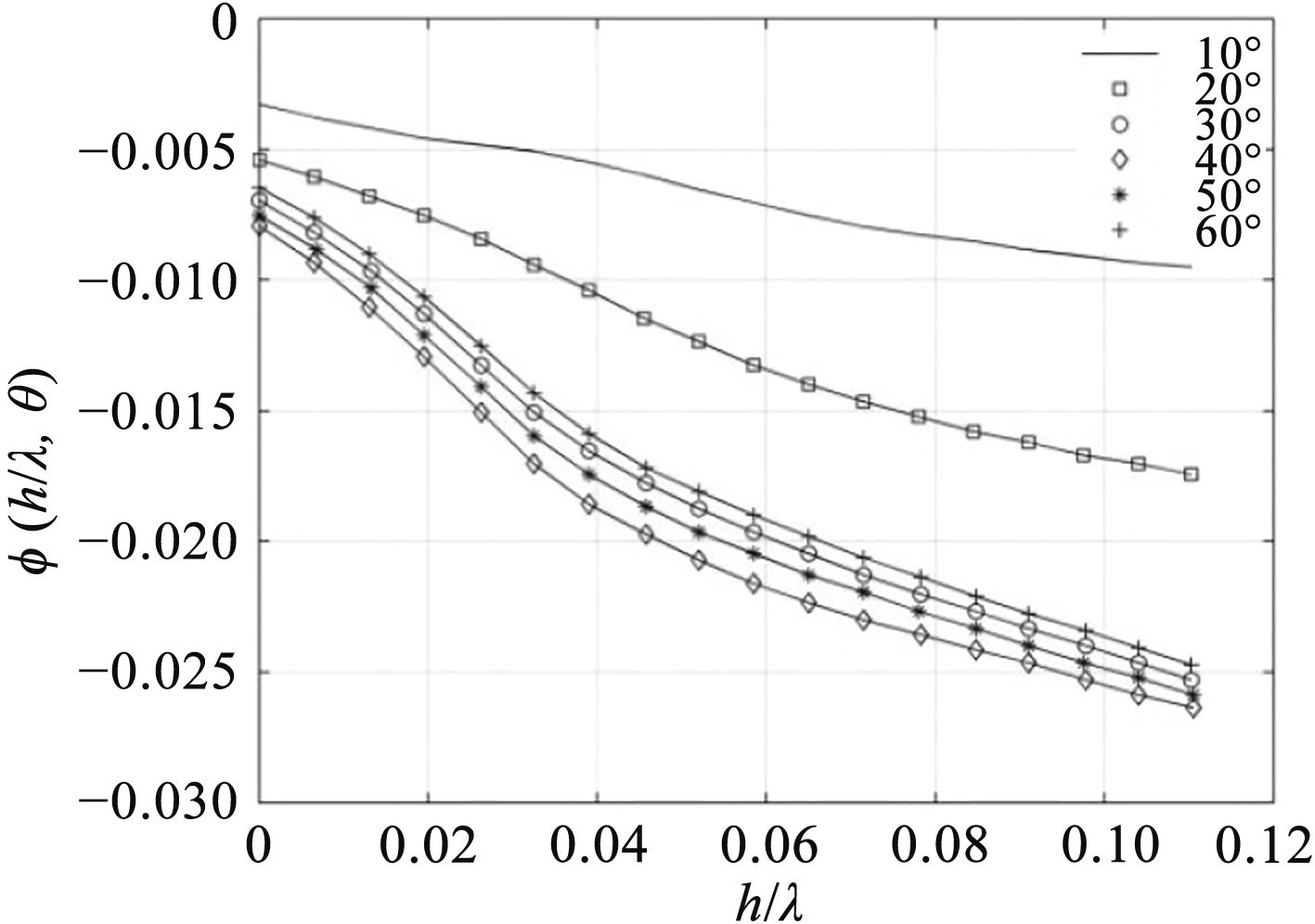
图 1 随浪在波峰时稳性力臂增量函数 Fig. 1 The stability arm increment function on the peak in following waves |
|
$\left\{ \begin{aligned}&\phi \left( {\frac{h}{\lambda };10} \right) = - 3428.6{\left( {\frac{h}{\lambda }} \right)^5} \!\!\!+ 975.93{\left( {\frac{h}{\lambda }} \right)^4} \!\!\!- 93.86{\left( {\frac{h}{\lambda }} \right)^3} \!\!\!+ \\&\quad \quad\quad\;\;\;\;3.487{\left( {\frac{h}{\lambda }} \right)^2} - 0.102\frac{h}{\lambda } - 0.0033, \\ & \phi \left( {\frac{h}{\lambda };20} \right) = - 987.25{\left( {\frac{h}{\lambda }} \right)^5} \!\!\!+\! 125.58{\left( {\frac{h}{\lambda }} \right)^4} \!\!\!+\! 13.448{\left( {\frac{h}{\lambda }} \right)^3} \!\!\!- \\&\quad \quad\quad\;\;\;\;2.0048{\left( {\frac{h}{\lambda }} \right)^2} - 0.0752\frac{h}{\lambda } - 0.0054, \\ & \phi \left( {\frac{h}{\lambda };30} \right) = 6481.2{\left( {\frac{h}{\lambda }} \right)^5} \!\!\!- 2059.7{\left( {\frac{h}{\lambda }} \right)^4} \!\!\!+ 229.69{\left( {\frac{h}{\lambda }} \right)^3}\!\!\! - \\&\quad \quad\quad\;\;\;\;9.4139{\left( {\frac{h}{\lambda }} \right)^2} - 0.117\frac{h}{\lambda } - 0.007, \\ & \phi \left( {\frac{h}{\lambda };40} \right) = 7592.9{\left( {\frac{h}{\lambda }} \right)^5} \!\!- 2395.7{\left( {\frac{h}{\lambda }} \right)^4} \!\!+ 262.6{\left( {\frac{h}{\lambda }} \right)^3} - \\&\quad \quad\quad\;\;\;\;10.1932{\left( {\frac{h}{\lambda }} \right)^2} - 0.1461\frac{h}{\lambda } - 0.008, \\ & \phi \left( {\frac{h}{\lambda };50} \right) = 7782.4{\left( {\frac{h}{\lambda }} \right)^5} \!\!\!- 2428.3{\left( {\frac{h}{\lambda }} \right)^4} \!\!\!+\! 264.996{\left( {\frac{h}{\lambda }} \right)^3} \!\!\!- \\&\quad \quad\quad\;\;\;\;10.5842{\left( {\frac{h}{\lambda }} \right)^2} - 0.1152\frac{h}{\lambda } - 0.0076, \\ & \phi \left( {\frac{h}{\lambda };60} \right) = 6813.3{\left( {\frac{h}{\lambda }} \right)^5} \!\!\!- 2163{\left( {\frac{h}{\lambda }} \right)^4} \!\!\!+ 242.0232{\left( {\frac{h}{\lambda }} \right)^3} \!\!\!-\\& \quad \quad\quad\;\;\;\;10.1331{\left( {\frac{h}{\lambda }} \right)^2} - 0.0974\frac{h}{\lambda } - 0.0065\text{。}\end{aligned} \right.$
|
(2) |
上述数模化之后的函数图象与原图基本重合,误差可以忽略。
式中:B为船宽;h和
|
$\left\{ \begin{aligned}& {A_1} = \displaystyle\frac{L}{B} \!-\! {\left( {\frac{L}{B}} \right)_0},\!\begin{array}{*{20}{c}}\!\!\!\!\!\!\!{}&{{A_2} = \displaystyle\frac{B}{T} \!-\! {{\left( {\frac{B}{T}} \right)}_0},\!\begin{array}{*{20}{c}}\!\!\!\!\!\!\!{}&{{A_3} = \displaystyle\frac{H}{T} - {{\left( {\frac{H}{T}} \right)}_0}},\!\end{array}}\end{array}\\& {A_4} =\!\! x - {x_0},\!\!\! \begin{array}{*{20}{c}}{}{{A_5} = \varphi - {\varphi _0},\!\!\! \begin{array}{*{20}{c}}{}{{A_6} = Fr - F{r_0},\!\! \;\begin{array}{*{20}{c}}{}{{A_7} = A_1^2}, \end{array}}\end{array}}\end{array}\\& {A_8} = A_2^2,\begin{array}{*{20}{c}}{}&{{A_9} = A_3^2,\!\begin{array}{*{20}{c}}{}&{{A_{10}} = A_5^2,\!\begin{array}{*{20}{c}}{}&{{A_{11}} = A_6^2},\!\end{array}}\end{array}}\end{array}\\& {A_{12}} = {A_2}{A_3},\!\begin{array}{*{20}{c}}{}&{{A_{13}} = {A_2}{A_4},\!\begin{array}{*{20}{c}}{}&{{A_{14}} = {A_1}{A_6}}\text{。}\end{array}}\end{array}\end{aligned}\!\!\! \right.\!\!\!$
|
(3) |
式中:L为船长;T为船的吃水;H为干舷;x为垂向棱形系数;
|
$\left\{ \begin{aligned}& {\left( {\displaystyle\frac{L}{B}} \right)_0}{\rm{ = }}4.820, \begin{array}{*{20}{c}}{}&{{{\left( {\displaystyle\frac{B}{T}} \right)}_0}{\rm{ = 2}}.{\rm{67}}0}, \end{array}\\& {\left( {\displaystyle\frac{H}{T}} \right)_0}{\rm{ = }}1.300, \begin{array}{*{20}{c}}{}&{{x_0}{\rm{ = }}0.700}, \end{array}\\& {\varphi _0}{\rm{ = 0}}{\rm{.692}}, \begin{array}{*{20}{c}}{}&{F{r_0}{\rm{ = }}0.280}\text{。}\end{array}\end{aligned} \right.$
|
(4) |
按照上述方法最后只能得到6个固定角度的值,为了扩展这一局限性,本文用函数拟合的方法将最后的6个点扩展成1条曲线,可以求得60°以内的任意度数的值。
2 扩展适用范围基于28艘渔船和运输船船模水池试验顺浪航行骑浪状态纯稳性损失计算法,其优势是计及了船体与水体之间复杂的耦合动态响应;它的不足之处是适用范围过窄,具体参数约束见表1。
为拓宽其适用范围,使其适用于包括舰体细长、航速高的水面舰艇之类的船舶,本文提出了扩展算法,思路如下:
1)骑浪状态舰艇纯稳性损失的计算,取决于A1~A14等参数,可归结为
2)设每一参数对纯稳性损失的影响权重相同;
3)超过表1所述适用范围的船舶,其参数值如大于范围上限则扩展值为负值,小于下限则扩展值为正值。
|
|
表 1 某舰艇6个参数与试验规定标准船模的偏差 Tab.1 Deviation between a naval vessel and the standard ship model in six parameter |
扩展公式如下:
|
$\begin{split}{l}&\left( {1 - K} \right) \cdot \Delta l\left( \theta \right) = \\&\left( {1 - K} \right) \cdot B\left[ {\phi \left( {\displaystyle\frac{h}{\lambda };\theta } \right) + \sum\limits_{m = 1}^{14} {{A_m}{f_m}\left( \theta \right)} } \right],\end{split}$
|
(5) |
式中,K为修正系数。
|
$K = \sum\limits_i^6 {\frac{1}{6}} \left( {\frac{{{M_i} - {M_{0i}}}}{{{M_{0i}}}}} \right)\text{。}$
|
(6) |
其中,Mi为舰艇实际参数值;
以某型舰为例,进行扩展计算。该舰与标准船模的差值见表1。
表1数据代入式(3)求得K为:
|
$\begin{aligned}K & {\rm{ = }}\frac{1}{6}\left( {\frac{{9.1 - 4.820}}{{4.820}} + \frac{{3.45 - 2.670}}{{2.670}} + \frac{{0.399 - 0.280}}{{0.280}}} \right)=\\ & 0.268,\\ & 1 - K = 0.732\text{。}\end{aligned}$
|
即
为使上述计算模式不仅适用于多类船舶顺浪航行骑浪状态的纯稳性损失计算,而且适用于非骑浪状态,本文参考有关文献[9],提出适用于船舶顺浪航行任意航态纯稳性损失的扩展近似算法;
|
$\Delta l{\left( \theta \right)_t} = \frac{1}{2}\left[ {\Delta l{{\left( \theta \right)}_f} + \Delta l{{\left( \theta \right)}_g}} \right]\cos \left( {{\omega _e}t - \varepsilon } \right){\text{。}}$
|
(7) |
式中:
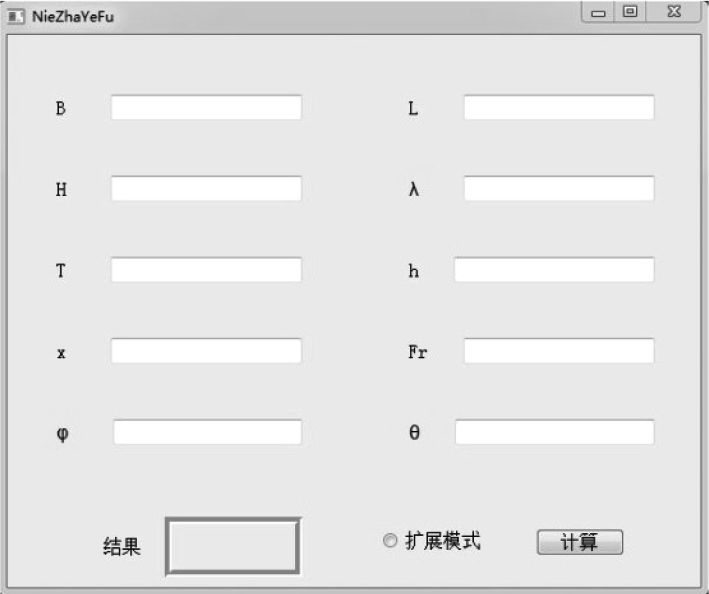
本文采用Qt语言对算法进行编程实现,最终生成软件的计算界面如图2所示。
该界面需要输入船型参数、波浪参数、傅汝德数以及横倾角等10个参数。参数输入之后选择“扩展模式”,再点“计算”按钮,程序就会按照扩展模式算法给出结果;如果不选“扩展模式”直接点“计算”程序就会按照原算法给出结果。最后的结果会直接显示在软件的“结果”对应的方框中。
程序内部的计算流程:
1)判断“扩展模式”是否被选择,若是,修正超范围参数后转步骤2;若否,且存在超范围参数则报输入错误并退出程序,参数皆符合范围则转步骤2;
|
图 2 扩展模式界面 Fig. 2 Interface of extended mode |
2)根据涅查耶夫算法分别计算10°,20°,30°,40°,50°,60°对应的纯稳性损失,如果“扩展模式”被选中,则按照第2节的思路对这6个值进行修正,转步骤3;否则,直接转步骤3;
3)对步骤2得到的6个点做函数拟合,根据输入的
本文借助基于CFD的舰艇骑浪状态下纯稳性损失计算和一般的理论计算法的结果与涅法扩展模式进行对比,比较结果如图3所示。

|
图 3 三种稳性计算方式结果对比图 Fig. 3 Contrast diagram of three different methods of stability calculation |
从图中可以看出,扩展模式得到的结果与CFD法和计算法基本一致。CFD方法作为一种前沿的计算比较精确的方法,其结果已经基本可以达到与水池试验等效的程度,因此为进一步确认准确度,表2列出了扩展模式法和一般计算法跟CFD试验法的比对误差值。从中可以得出:扩展模式法更加接近CFD试验结果,其准确性得到证明。
|
|
表 2 CFD试验、扩展模式法和计算法结果对比表 Tab.2 Comparison table of CFD test, extended mode method and calculation method |
通过分析对比可以看出,本文提出的扩展模式法能够适应细长舰艇的要求,并能够扩展到任意顺浪航行航态,计算简洁且精度较高,优于一般的纯计算的方法,为船舶顺浪纯稳性损失的计算提供了一种新的模式。
| [1] | 中国船舶重工集团第七〇二研究所, 等. 工信部高技术船舶项目——船舶第二代完整稳性衡准技术研究建议书[R]. 中国船舶重工集团第七〇二研究所, 2012. |
| [2] |
顾民, 鲁江. IMO第二代完整稳性衡准评估技术进展综述[J]. 中国造船, 2014, 55 (4): 185–193.
GU Min, LU Jiang. Review on the progress of IMO second generation of complete stability assessment techniques[J]. Shipbuilding of China, 2014, 55 (4): 185–193. |
| [3] | 顾民, 王田华, 鲁江, 等. 波浪中纯稳性丧失试验和数值研究[C]// 第二十七届全国水动力学研讨会文集(下册), 2015. |
| [4] | 顾民, 鲁江, 兰波, 等. 波浪中船舶横摇复原力变化试验和数值研究[C]// 中国造船工程学会船舶力学学术委员会第八次全体会议文集, 2014. |
| [5] | 邱敏芝. 船舶随浪稳性与航行安全性研究[D]. 哈尔滨: 哈尔滨工程大学, 2008. |
| [6] |
马坤, 甘鄂, 谢微. 船舶纯稳性丧失薄弱性衡准样船计算分析[J]. 中国造船, 2015, 56 (S1): 193–200.
MA Kun, GAN E, XIE Wei. Calculation and analysis of ship’s pure stability loss[J]. Shipbuilding of China, 2015, 56 (S1): 193–200. |
| [7] |
胡开业, 丁勇, 聂芳. 基于NURBS方法的船舶随浪航行纯稳性损失研究[J]. 中国造船, 2015 (S1): 29–36.
HU Kai-ye, DING Yong, NIE Fang. Study on pure stability loss of ship with wave navigation based on NURBS method[J]. Shipbuilding of China, 2015 (S1): 29–36. |
| [8] | Proposed amendments to part B of the 2008 IS code to assess the vulnerability of ships to the pure loss of stability failure mode[R]. The Correspondence Group, IMO SDC_ISCG, 2014. |
| [9] | A. H. 霍洛季夫, A. H. 什梅列夫. 船舶耐波性和在波浪上的稳定措施[M]. 北京: 国防工业出版社, 1980. |
| [10] | 黄衍顺, 林欣. 船舶在随浪中的稳性计算[C]// 第五届船舶耐波性学术讨论会论文集, 1991. |
| [11] | 李积德. 舰船耐波性[M]. 哈尔滨: 哈尔滨船舶工程学院出版社, 1992. |
 2017, Vol. 39
2017, Vol. 39
