炸药在空气中爆炸时,形成高温、高压的爆轰产物,并不断向外膨胀,膨胀气体前沿形成一压缩空气层,压缩空气层向四周传播,最终形成空气冲击波[1 – 2]。舰船除了受到水下爆炸冲击波的破坏,空中爆炸,特别是近距离的爆炸所形成的冲击波对舰船防护结构的破坏一直受到人们的高度关注。在各学者对空中爆炸对防护结构破坏的研究中,空气冲击波是重点研究的载荷形式。因其复杂性,过去对空中爆炸的研究主要以实验数据为主,然而研究结果受到实验条件等因素的限制。近年来,随着计算机科学技术的不断发展,数值模拟方法在爆炸领域中的应用也日趋成熟。大型通用非线性有限元软件MSC.DYTRAN,AUTODYN,LS-DYNA已经被广泛的应用于爆炸等国防和民用工程领域[3]。不少学者针对影响空中爆炸数值模拟结果的因素已经做出了比较详尽的讨论。归纳起来,文献[4]对比了各学者根据实验结果总结出的经验公式,根据对比结果总结出了合理的冲击波超压峰值与比例关系的表达式,并利用数值模拟计算结果和经验公式进行对比。文献[5]对网格密度、药量、空气状态方程调整对计算结果的影响做出了详尽的对比分析。上述讨论未对无反射边界条件进行讨论分析,本文试图利用LS-DYNA软件探讨无反射边界条件对空中爆炸超压峰值的影响。
1 空中爆炸冲击波的数值模拟 1.1 条件及参数选择 1.1.1 材料参数1)空气
假设空气为无粘性理想气体,冲击波的膨胀为等熵绝热过程。选择LS-DYNA中的*MAT_NULL材料模型,*EOS_LINEAR_POLYNOMIAL状态方程模拟空气。*EOS_LINEAR_POLYNOMIAL状态方程表达式为:
|
$p = {c_0} + {c_1}\mu + {c_2}{\mu ^2} + {c_3}{\mu ^3} + \left( {{c_4} + {c_5}\mu + {c_6}{\mu ^2}} \right){e_0}\text{,} $
|
(1) |
其中:
|
|
表 1 空气状态方程及材料的参数值 Tab.1 Eos and material parameters of air |
2)炸药
TNT炸药采用LS-DYNA中的*MAT_HIGH_EXPLOSIVE_BURN材料模型和*EOS_JWL状态方程进行模拟。*EOS_JWL状态方程表达式为:
|
$p = {A_1}\left( {1 - \frac{\omega }{{{R_1}V}}} \right){e^{ - {R_1}V}} + {B_1}\left( {1 - \frac{\omega }{{{R_2}V}}} \right){e^{ - {R_2}V}} + \frac{{\omega E}}{V}\text{,} $
|
(2) |
其中:p为压力;V0为相对体积;E为炸药单位体积的内能;A1,B1,R1,R2以及
|
|
表 2 TNT炸药材料模型参数 Tab.2 TNT material parameters |
|
|
表 3 JWL状态方程参数 Tab.3 JWL parameters |
1)选取50 kg的球形装药在空气中爆炸,坐标原点为装药中心和爆炸中心;根据对称性原则,建模计算均选取1/8域作为计算对象;模型采用cm-g-μs的单位制,球形炸药的半径为19.4 cm;定义空气和炸药为Euler单元;
2)根据文献[5],药包边长长度与单元边长长度之比λ应大于等于2;取λ为4时,单元尺寸为5 cm;
3)在模型对称面处取对称边界条件,即对称面法向位移取为0;为模拟无限空域中炸药的爆炸,其余各面取为无反射边界条件;
4)采用Ansys16.1/LS-DYNA求解器;
5)选取对称面边界处距爆心不同位置的点作为测点。
1.2 数值模拟实例取空气域的尺寸大小为
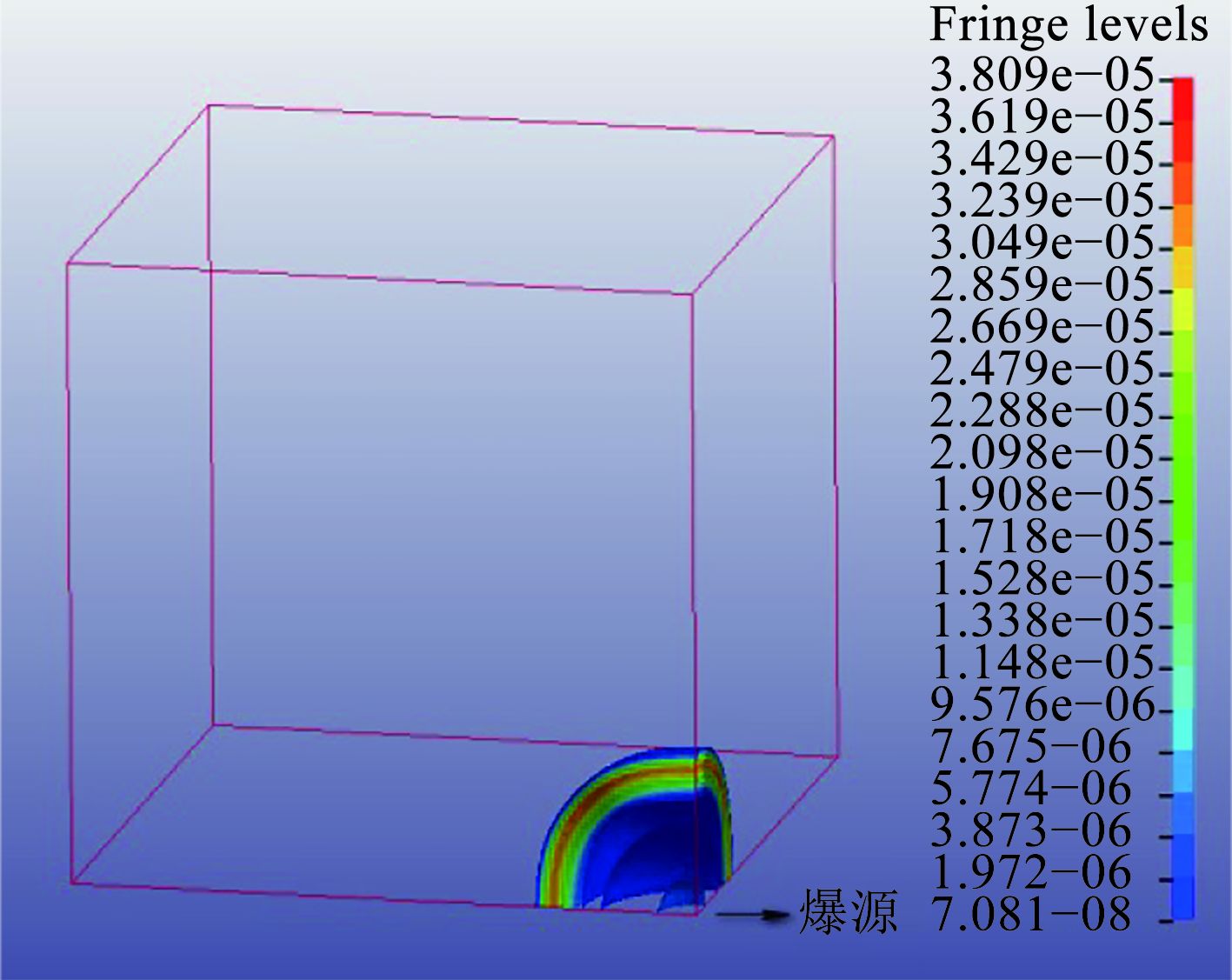
|
图 1 某时刻超压分布 Fig. 1 Distribution of over-pressure |
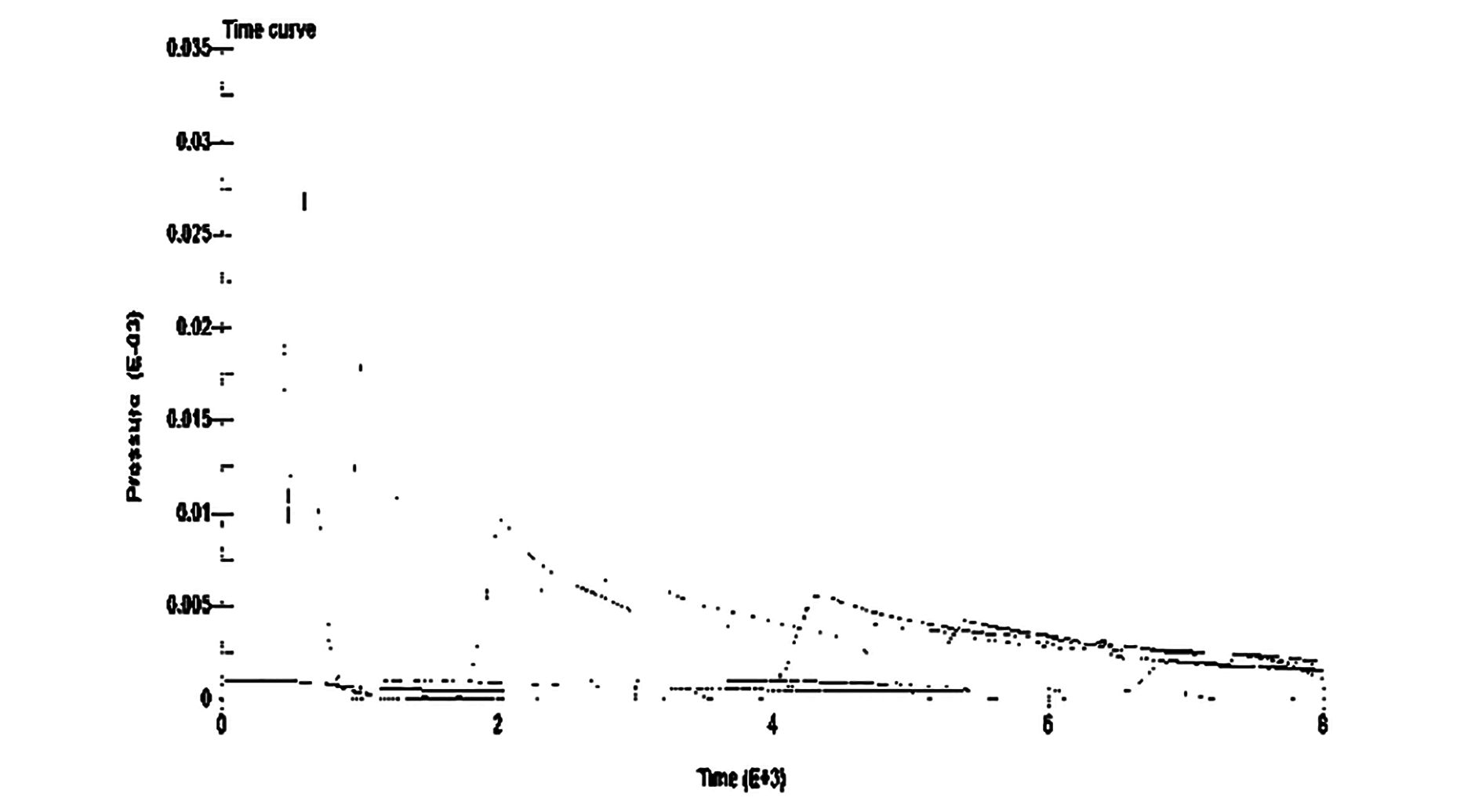
|
图 2 不同测点处的超压随时间变化曲线 Fig. 2 Time history of over-pressure |
文献[4]总结了各学者关于空中爆炸超压峰值的经验公式,提出了能更准确地描述冲击波超压峰值与比例距离的关系,其表达式为:
|
${P_{so}} = \left\{ \begin{array}{l}\displaystyle\frac{{0.084}}{Z} + \frac{{0.27}}{{{Z^2}}} + \frac{{0.7}}{{{Z^3}}},Z \leqslant1 \text{;} \\[10pt]\displaystyle\frac{{0.076}}{Z} + \frac{{0.255}}{{{Z^2}}} + \frac{{0.65}}{{{Z^3}}},1 < Z \leqslant 15 \text{。} \end{array} \right.$
|
(3) |
Henrych(1979)学者的经验公式在空中爆炸研究中应用广泛,其经验公式的表达式为[1]:
|
$P{}_{so} \!=\! \left\{\!\!\!\! \begin{array}{l}\displaystyle\frac{{1.40717}}{{\rm{Z}}} \!+\! \frac{{0.55397}}{{{Z^2}}} \!-\! \frac{{0.03572}}{{{Z^3}}} \!+\! \frac{{0.000625}}{{{Z^4}}}\text{,} \\[7pt] 0.05 \leqslant Z \leqslant 0.3\text{;} \\[7pt]\displaystyle\frac{{0.61938}}{Z} - \frac{{0.03262}}{{{Z^2}}} + \frac{{0.21324}}{{{Z^3}}},0.3 \leqslant \!Z \leqslant\! 1\text{;} \\[7pt]\displaystyle\frac{{0.0662}}{Z} + \frac{{0.405}}{{{Z^2}}} + \frac{{0.3288}}{{{Z^3}}},1 \leqslant Z \leqslant 10\text{。} \end{array} \right.\!\!\!\!\!\!\!$
|
(4) |
式中:Z为比例距离,定义为
|
$Z = R/{W^{1/3}}\text{;} $
|
(5) |
R为测点与爆心之间的距离,m;W为等效TNT药量,kg。
选取文献[6 – 7]中的实验数据,将LS-DYNA计算结果和经验公式、实验数据进行比较。
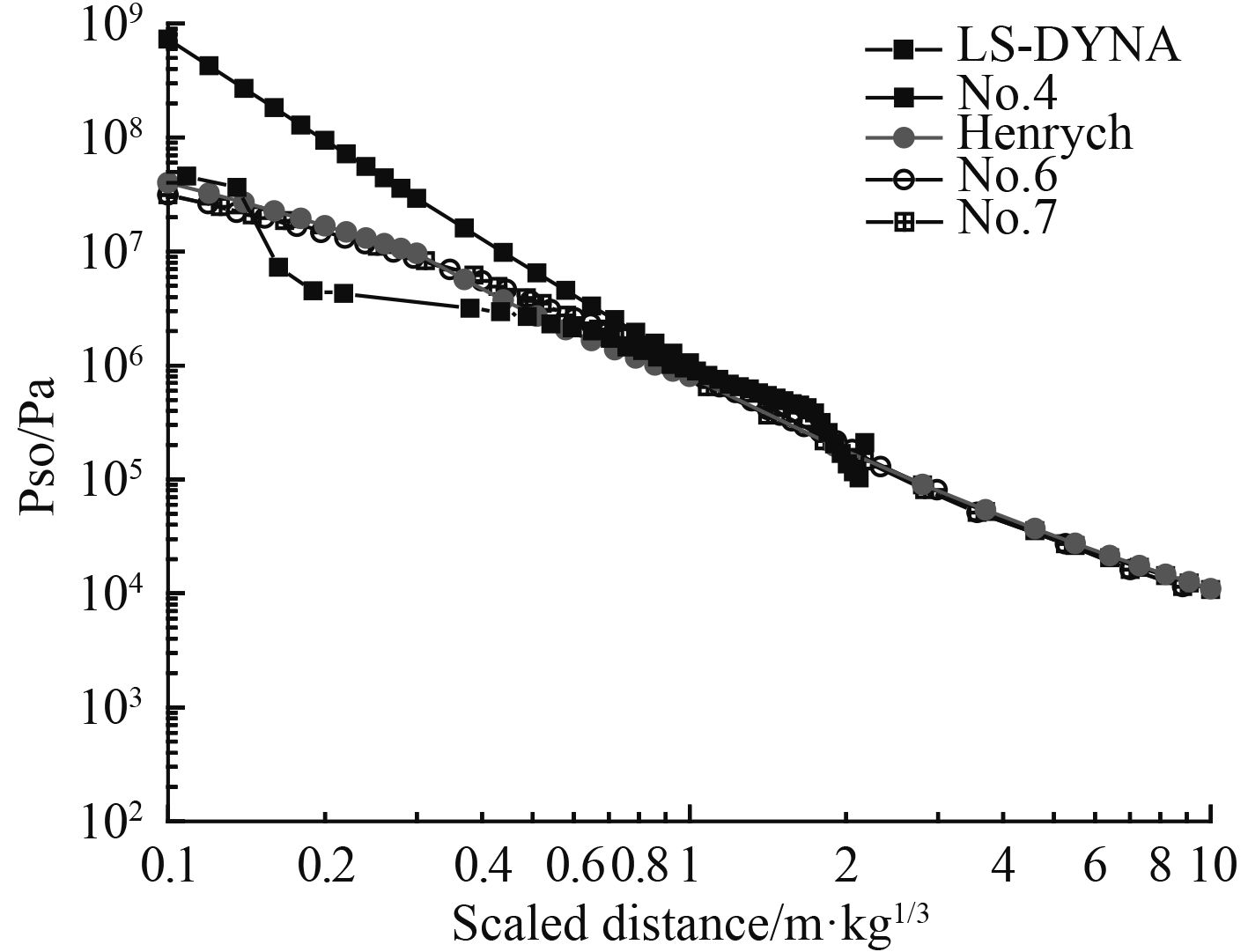
|
图 3 文献[4, 6 – 7] 及Henrych公式超压峰值与比例距离关系 Fig. 3 Over-pressure to scaled distances in papers[4, 6 – 7] and Henrych equations |
对于有限空域模拟无限空域的数值模拟问题,通常采用的方法是利用无反射边界条件实现这种近似的模拟,这样可以节省计算时间提高计算效率。但是,利用有限空域和无反射边界条件来模拟,与真实的无限空域的计算结果是否一致,仍值得探讨。下文利用有限的工况,对无反射边界对超压峰值影响范围进行分析探讨。
根据上一节的分析结果可以看出,上一节选择的数值模拟各条件参数在比例距离范围为0.4~2.0(m/kg1/3)时计算较准确,可以作为参数及条件的选择标准。利用上述所用的空气和炸药的材料参数和状态方程,选取50 kg球形TNT炸药作为爆炸源、5 cm的六面体单元进行网格划分、1/8模型作为模拟对象,并在对称面设置对称边界条件,其余各面设置无反射边界条件进行模拟,其中所有工况均采用Ansys16.1/LS-DYNA求解器。一共建立下述5种计算模型:6×6×6m,8×8×8m,10×10×10m,12×12×12m,14×14×14m工况分别为1~5。图为这5种模型探讨不同比例距离下的超压峰值与上节16×16×16m模型计算结果差异,从而分析无反射边界条件对计算结果的影响。
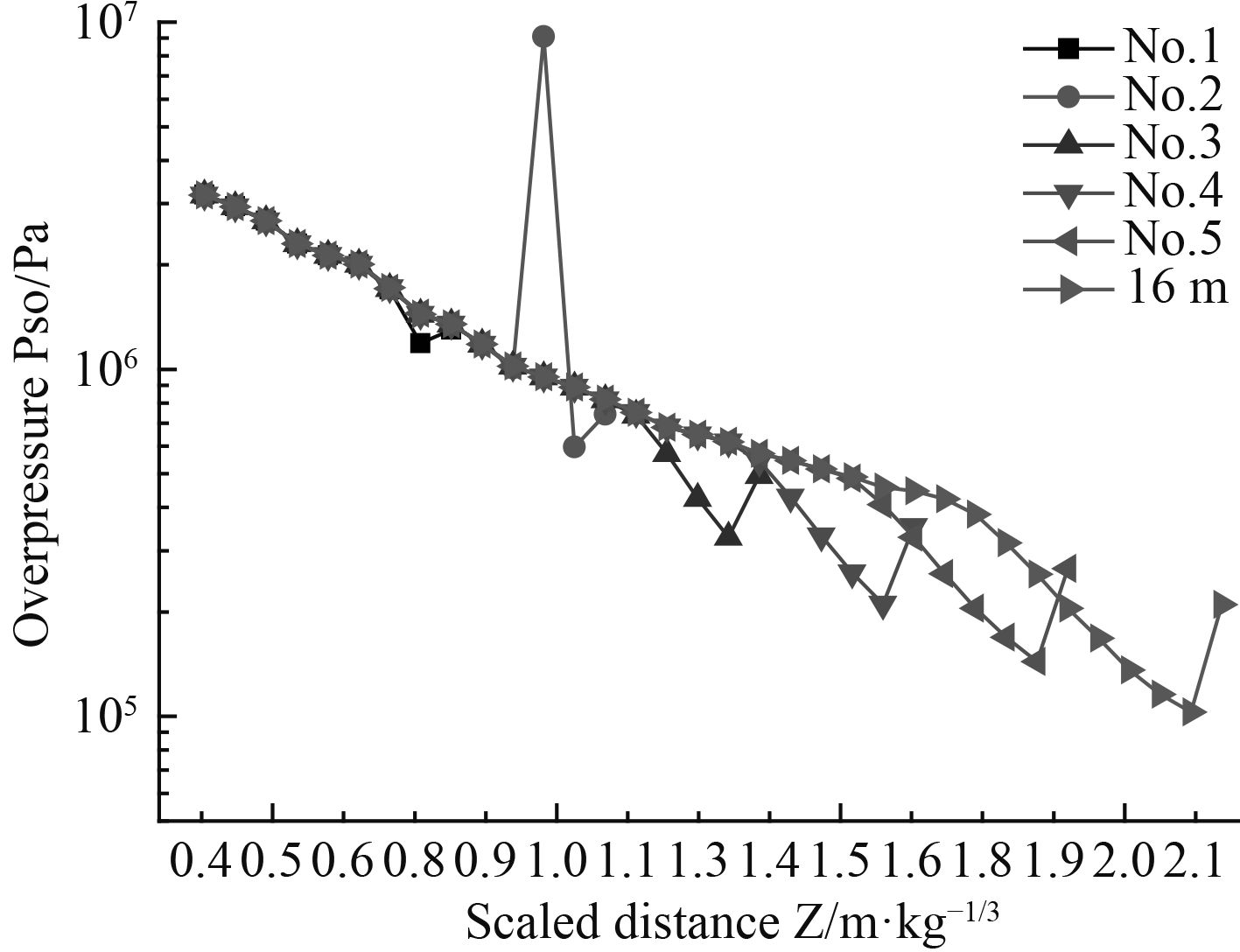
|
图 4 工况1~工况5与16×16×16m模型计算结果比较 Fig. 4 Comparison among conditions 1 to 5 and model of 16m |
图4显示,工况1-工况5在比例距离为0.4~0.7(m/kg1/3)范围内,超压峰值与16×16×16 m模型计算结果基本一致;工况1在比例距离为0.7~0.8(m/kg1/3)范围内峰值超压误差较大。工况2~工况5在比例距离为0.4~0.9(m/kg1/3)范围内,超压峰值与16×16×16 m模型计算结果基本一致;工况2在比例距离为0.9~1.1(m/kg1/3)范围内峰值超压误差较大;工况3-工况5在比例距离为0.4~1.1(m/kg1/3)范围内,超压峰值与16×16×16 m模型计算结果基本一致;工况3在比例距离为1.2~1.4(m/kg1/3)范围内峰值超压误差较大;工况4~工况5在比例距离为0.4~1.4(m/kg1/3)范围内,超压峰值与16×16×16 m模型计算结果基本一致;工况4在比例距离为1.4~1.6(m/kg1/3)范围内峰值超压误差较大;工况5在比例距离为0.4~1.5(m/kg1/3)范围内,超压峰值与16×16×16 m模型计算结果基本一致;在比例距离为1.5~1.9(m/kg1/3)范围内峰值超压误差较大。
图5 ~ 图9,在比例距离Z为0.4~2.0(m/kg1/3)时,工况1-工况5与16×16×16 m模型计算结果的相对误差ei。

|
图 5 工况1超压峰值的相对误差 Fig. 5 Relative error of condition 1 |
|
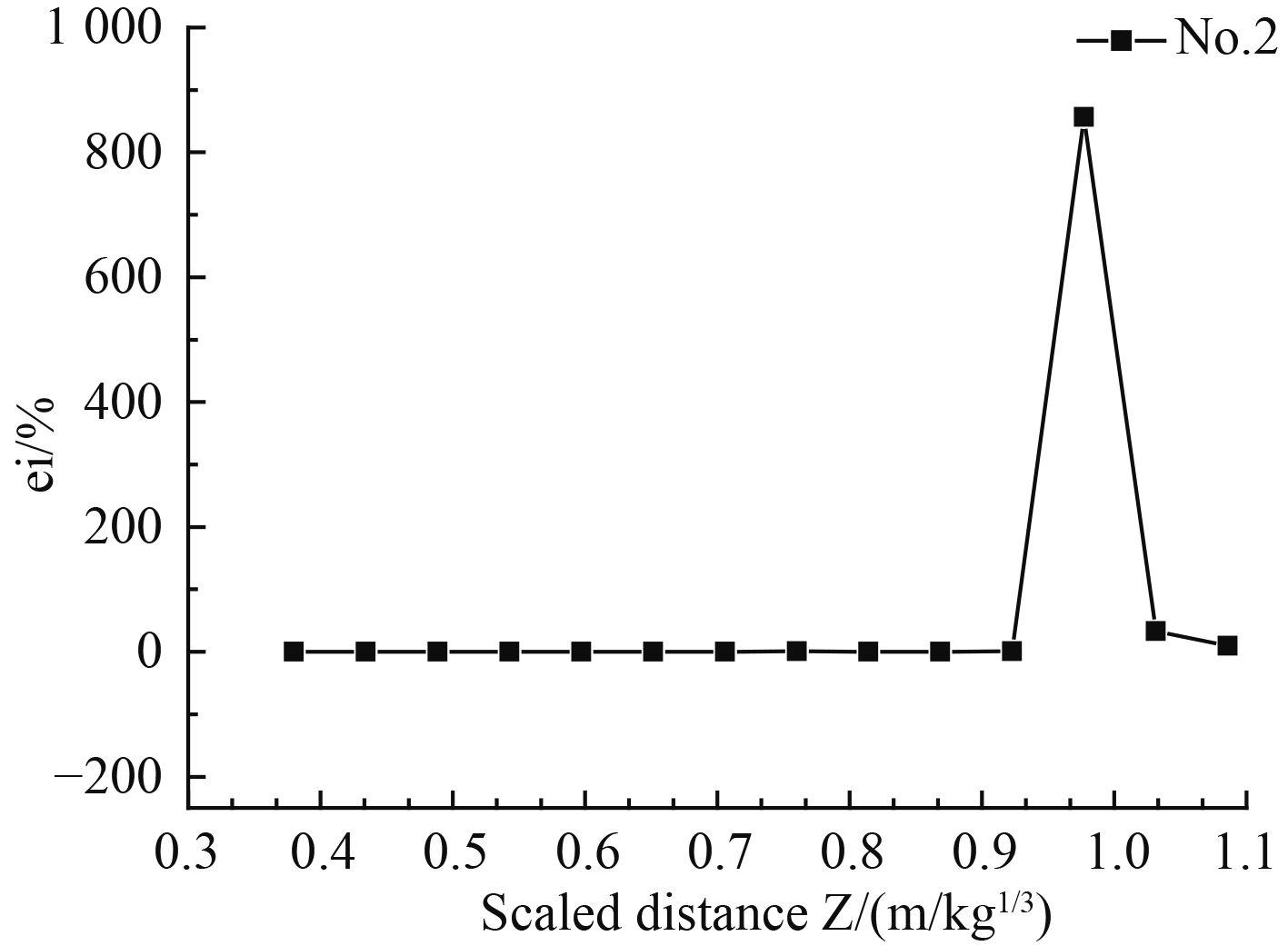
图 6 工况2超压峰值的相对误差 Fig. 6 Relative error of condition 2 |
|
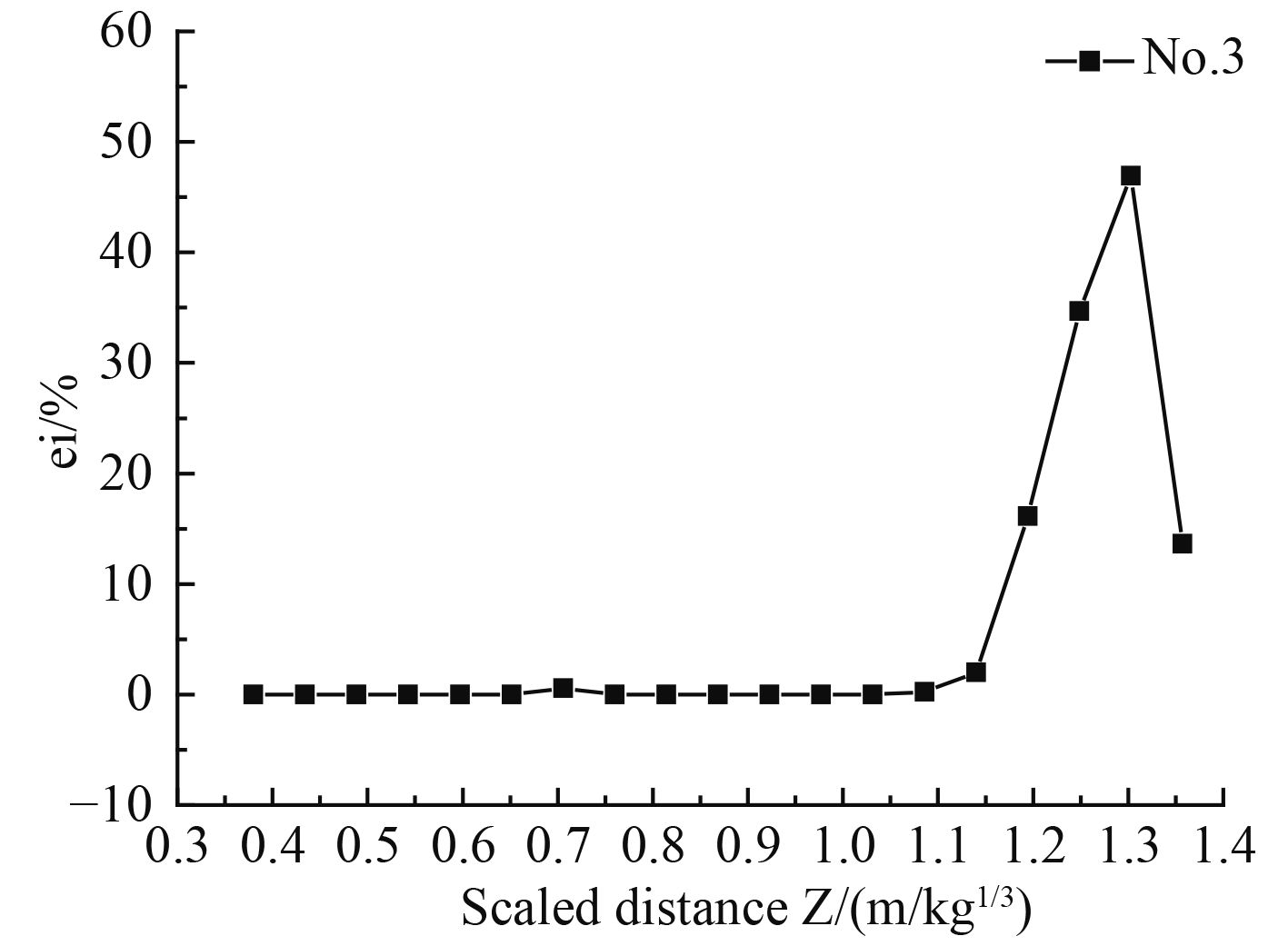
图 7 工况3超压峰值的相对误差 Fig. 7 Relative error of condition 3 |
|
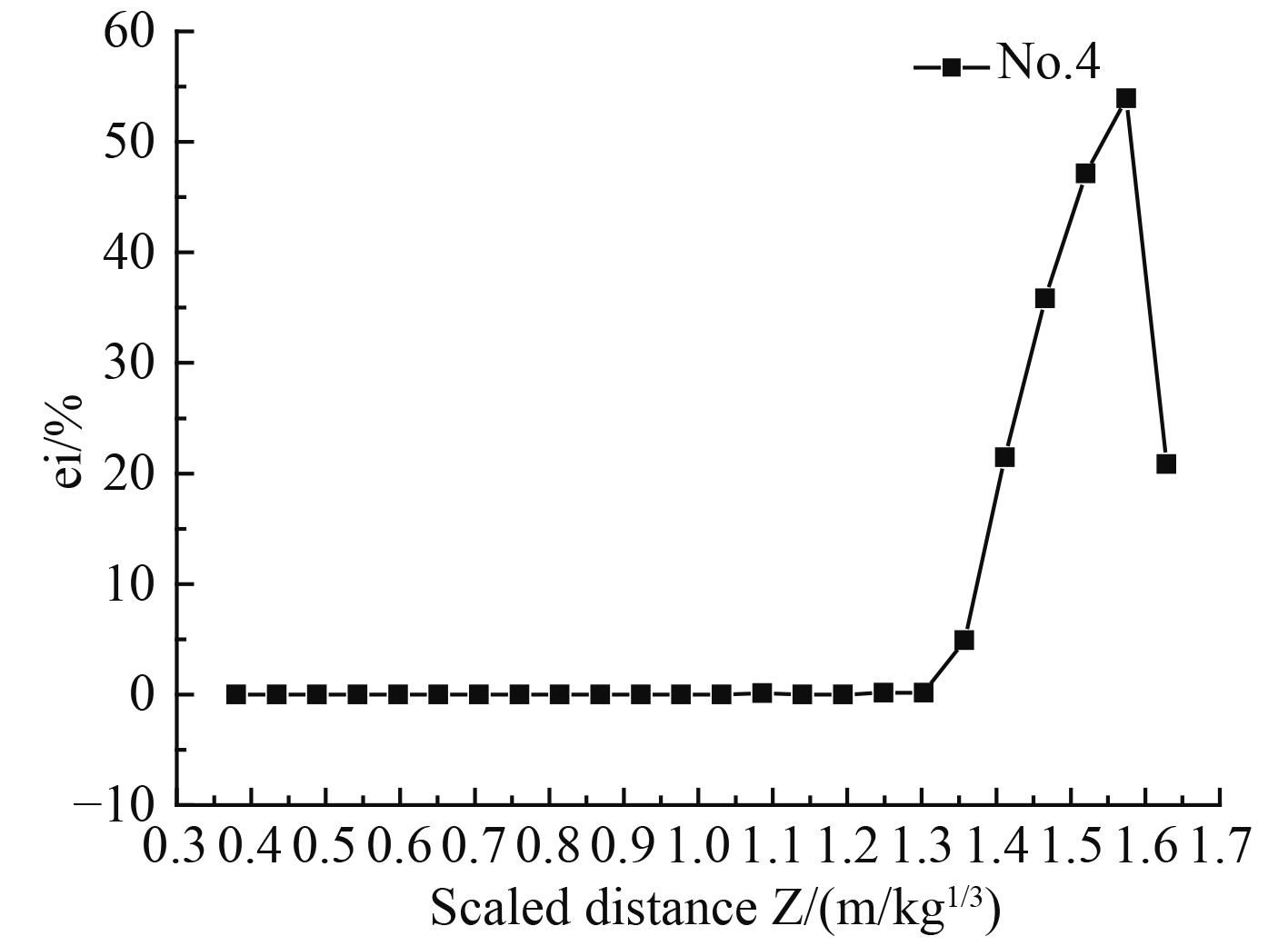
图 8 工况4超压峰值的相对误差 Fig. 8 Relative error of condition 4 |
|
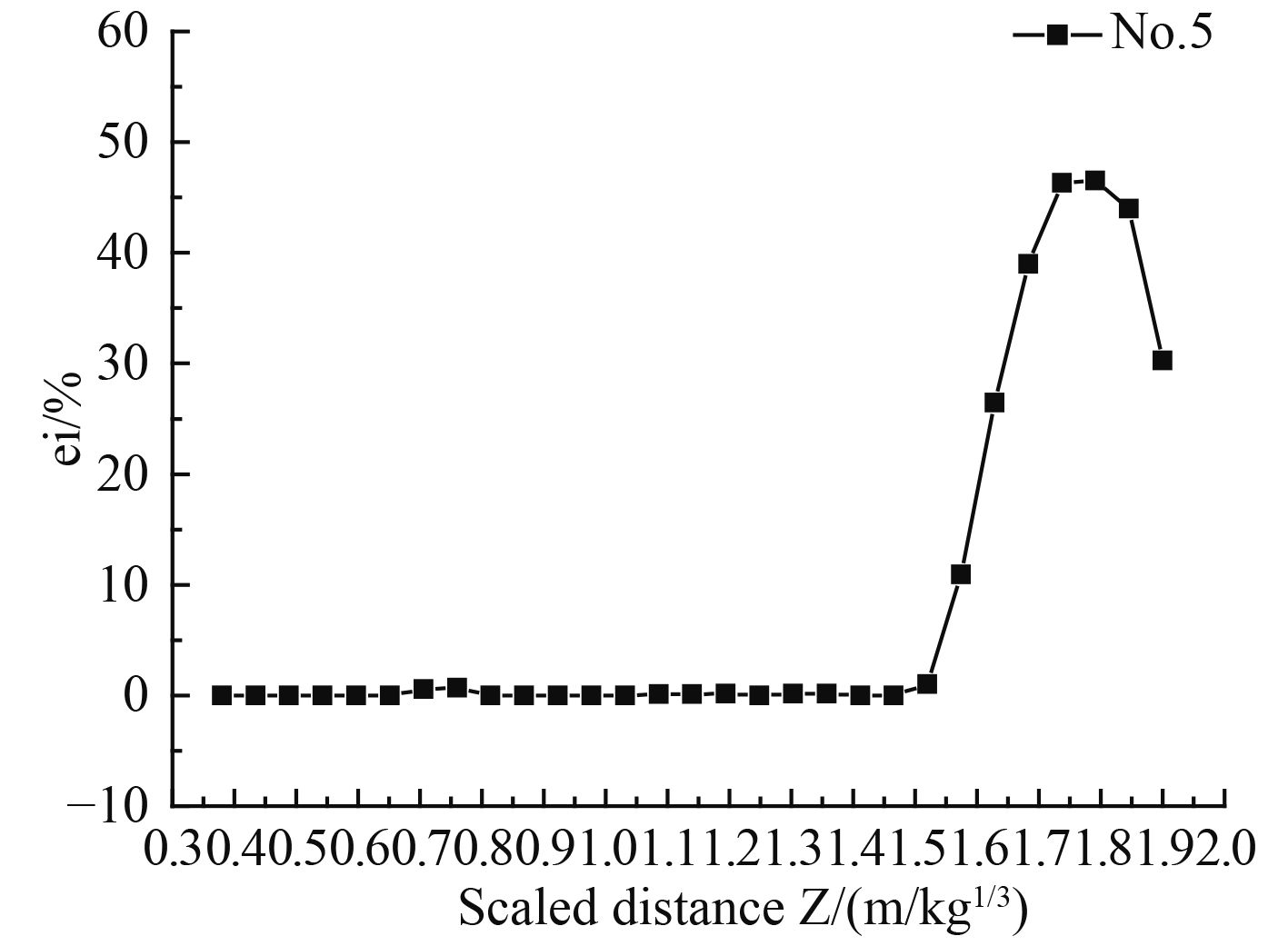
图 9 工况5超压峰值的相对误差 Fig. 9 Relative error of condition 5 |
根据上述计算结果,对比可得到如表4。
|
|
表 4 不同工况下的比例距离及误差大于5%比例距离范围 Tab.4 Scaled distances in different conditions and scaled distances of errors more than 5% |
从图5~图9、表4可以看出,相对误差大于5%的位置均靠近无反射边界条件位置,说明无反射边界条件会影响附近位置的超压峰值的模拟精度。分析可能原因,无反射边界附近存在能量损失,边界附近能量不守恒导致峰值超压值与实际情况存在较大的差距。从表4分析可知,误差大于5%的比例距离范围占所空气域比例距离范围的比例,从工况1到工况5分别为14.80%,15.60%,16.18%,16.56%,17.37%,随着空气域比例距离的增大,误差大于5%的比例距离范围也随之增大。分析知,空中爆炸随着距离的增大,超压峰值呈指数衰减,当超压峰值衰减到一定程度时,受到无反射边界条件的影响也随之增大,因此空气域的增大,使无反射边界条件影响的区域也增加。随着空气域的进一步增加,误差大于5%的比例距离范围是否收敛仍值得探讨。
图5显示,在比例距离0.4~0.81(m/kg1/3)范围内,0.4~0.69(m/kg1/3)内的超压峰值比较准确,说明模型尺度增大1.17倍能保证考察范围超压峰值的准确性;图6显示,在比例距离0.4~1.09(m/kg1/3)范围内,0.4~0.92(m/kg1/3)内的超压峰值比较准确,说明模型尺度增大1.18倍能保证考察范围超压峰值的准确性;图7显示,在比例距离0.4~1.36(m/kg1/3)范围内,0.4~1.14(m/kg1/3)内的超压峰值比较准确,说明模型尺度增大1.19倍能保证考察范围超压峰值的准确性;图8显示,在比例距离0.4~1.63(m/kg1/3)范围内,0.4~1.36(m/kg1/3)内的超压峰值比较准确,说明模型尺度增大1.20倍能保证考察范围超压峰值的准确性;图9显示,在比例距离0.4~1.90(m/kg1/3)范围内,0.4~1.57(m/kg1/3)内的超压峰值比较准确,说明模型尺度增大1.21倍能保证考察范围超压峰值的准确性。
从上述分析可以看出,为保证考察范围的准确性,模型尺度应随着考察范围的增加而增加,当考察范围比例距离每增加约0.22(m/kg1/3)时,模型尺度的倍数约增加0.01倍。随着考察范围超压峰值的增大,模型尺度与考查范围的比例由1.17倍增加至1.21倍。因此,针对模型尺度小于16×16×16 m的情况,模型尺度与考察范围的比例约1.2倍时,可减小无反射边界条件对考察范围的影响,这为较大模型的建模计算提供了一定的指导。
3 结 语1)LS-DYNA对于空中爆炸的数值模拟具有较高的精度,利用上述参数建立模型能很好的计算空中爆炸的超压峰值,超压峰值的计算结果与实验结果和经验公式误差较小,说明上述参数的选取合理。
2)对比各个工况的实验结果可以看出,无反射边界条件会影响附近位置超压峰值模拟的精度,影响范围随着空气域的增加也逐渐变大;随着考察范围超压峰值的增大,模型尺度与考查范围的比例也逐渐增大。
3)针对模型尺度小于16×16×16 m的情况,模型尺度与考察范围的比例约1.2倍时,可减小无反射边界条件对考察范围的影响。
| [1] | 亨利奇 J. 熊建国. 译. 爆炸动力学及其应用[M]. 北京: 科学出版社, 1987. |
| [2] | 李翼祺, 马素贞. 爆炸力学[M]. 北京: 科学出版社, 1992. |
| [3] | 时党勇, 李裕春, 张胜民. 基于ANSYS/LS-DYNA8.1 进行显示动力分析[M]. 北京: 清华大学出版社, 2005. |
| [4] | 杨鑫, 石少卿, 程鹏飞. 空气中TNT爆炸冲击波超压峰值的预测及数值模拟[J]. 爆破, 2008, 25 (1): 15–18, 31. |
| [5] | 卢红琴, 刘伟庆. 空中爆炸冲击波的数值模拟研究[J]. 武汉理工大学学报, 2009, 31 (19): 105–108. DOI: 10.3963/j.issn.1671-4431.2009.19.029 |
| [6] | Department of the Army Washington DC. Structures to Resist the Effects of Accidental Explosions[R]. ADA951601, Washington DC: Department of the Army, 1969. |
| [7] |
贝克 WE. 江科, 译. 空中爆炸[M]. 北京: 原子能出版社, 1982.
BAKER W E. Engineering design handbook: explosions in air part one[M]. JIANG Ke, Translated. Beijing: Atomic Energy Press, 1982. |
 2017, Vol. 39
2017, Vol. 39
