2. 武汉第二船舶设计研究所,湖北 武汉 430205
2. Wuhan Second Ship Design and Research Institute, Wuhan 430205, China
舰船表面存在着诸多不同形式的开孔,这些开孔的存在会使原本光滑船体的流动噪声显著增大,因此,针对舰船开孔水动力噪声采取控制措施具有十分重要的意义。表面开孔附近流体会呈现丰富的流体力学现象。开孔处存在部分内流与外流交换,在孔壁面处存在流体附着、脱落、分离及尾迹流的相互干涉。流场的高度非定常性会产生各种尺度的旋涡及湍流引发的脉动,作用于艇体外表面导致压力波动,破坏表面湍流附面层内的流动进而形成流动噪声。依据Lighthill流动声学理论以及Powell[1]的涡声理论,开孔中的涡流导致孔壁面的压力脉动,是典型的偶极子型声源,同时脱落涡及孔内漩涡将产生四极子噪声。部分学者将开孔内流噪声问题简化为空腔流动发声问题,并主要集中于压力脉动及声辐射方面。Rossiter等[2]提出了空腔振荡的流声共振反馈模型,并提出一个半经验公式用于预测振荡频率。
随着计算机科学的发展和计算流体动力学/计算气动声学(CFD/CAA,Computational Fluid Dynamics/Computational Aeroa-coustics)理论的进步,准确模拟复杂流场及相应声场现象成为可能,学者们针对开孔流动或流动噪声进行了一定的研究。张楠等[3]采用RANS模拟了带有 2 种不同形式流水孔潜体的内外流场,主要分析了流水孔引起的阻力增量。赖焕新等[4]采用大涡模拟-声学比拟相结合的方法研究三维开式空腔的非定常可压缩过流及其相关的气动声学问题。李晓东等[5]求解二维非定常雷诺平均N-S方程,采用频散相关保持格式及无反射边界条件计算了空腔的流激振荡发声现象,通过与实验对比验证了声辐射指向性的正确。耿冬寒等[6]为了研究空腔产生的水动力噪声,对气动声学理论与研究方法进行了分析,确定了大涡模拟-等效声源混合法。万振华等[7]进行了方腔流致振荡及噪声的数值研究。这些研究主要集中在流动噪声理论及计算方法方面,而对噪声控制措施研究较少。
本文基于Fluent流体计算软件,采用大涡模拟方法计算了一定来流速度条件下表面开孔的非定常流场,分析了流场的非定常流频谱特性,采用边界元方法模拟了噪声源特征,进行了各种流动噪声控制措施的对比分析。
1 计算方法和程序验证 1.1 计算方法开孔流噪声计算采用CFD/CAA混合求解方法,首先对模型进行定常流场计算,将定常解作为非定常流动的初始条件,当非定常求解过程趋于稳定之后,开始进入声学计算模块。首先是存储足够多个时间步长上的物面压力脉动值,作为FW-H方程的声源输入项。
为了高效、准确捕捉非定常流动信息,流场计算采用大涡模拟方法。大涡模拟方法的基本思想为运用空间滤波的方法将流动变量划分为大尺度量和小尺度量两部分,滤波方程如下式:
|
$\left\{ {\begin{split}& {\displaystyle\frac{\partial }{{\partial {x_i}}}\left( {{{\bar u}_i}} \right) = 0}\text{,} \\& {\displaystyle\frac{\partial }{{\partial t}}\left( {{{\bar u}_i}} \right) + \frac{\partial }{{\partial {x_j}}}\left( {{{\bar u}_i}{{\bar u}_j}} \right) = - \frac{1}{\rho }\frac{{\partial p}}{{\partial {x_i}}} + \nu \frac{{{\partial ^2}{{\bar u}_i}}}{{\partial {x_i}\partial {x_j}}} - \frac{{\partial {\tau _{ij}}}}{{\partial {x_i}}}}\text{。} \end{split}} \right.$
|
(1) |
式中亚格子应力项
|
${\tau _{ij}} = {\bar u_i}{\bar u_j} - {\bar u_i}{\bar u_j}\text{。} $
|
(2) |
这里的上划线代表经空间滤波的变量;ui为速度;p为压力。由于
|
${\tau _{ij}} = - 2{\nu _t}{\bar S_{ij}} = - 2C_s^2{\Delta ^2}\left| {\bar S} \right|{\bar S_{ij}}\text{,} $
|
(3) |
|
$\left| {\bar S} \right| = \sqrt {2{{\bar S}_{ij}}{{\bar S}_{ij}}}\text{。} $
|
(4) |
式中:
|
${\bar S_{ij}} = \frac{1}{2}\left( {\frac{{\partial {{\bar u}_i}}}{{\partial {x_j}}} + \frac{{\partial {{\bar u}_j}}}{{\partial {x_i}}}} \right)\text{。} $
|
(5) |
声学量的计算采用Lighthill理论。利用广义函数理论,在Lighthill方程基础上发展的FW-H方程
|
$\frac{1}{{a_0^2}}\frac{{{\partial ^2}p}}{{\partial {t^2}}} \!-\! {\nabla ^2}p = \frac{\partial }{{\partial t}}\left[ {{\rho _0}{u_n}\delta (f)} \right] \!+\! \frac{{{\partial ^2}}}{{\partial {x_i}\partial {x_j}}}{T_{ij}} - \frac{\partial }{{\partial {x_i}}}\left[ {{P_{ij}}{n_j}\delta (f)} \right]\text{,} $
|
(6) |
其中压应力张量为
|
${P_{ij}} = p{\delta _{ij}} - \mu \left[ {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}} - \frac{2}{3}\frac{{\partial {u_k}}}{{\partial {x_k}}}{\delta _{ij}}} \right]\text{。}$
|
(7) |
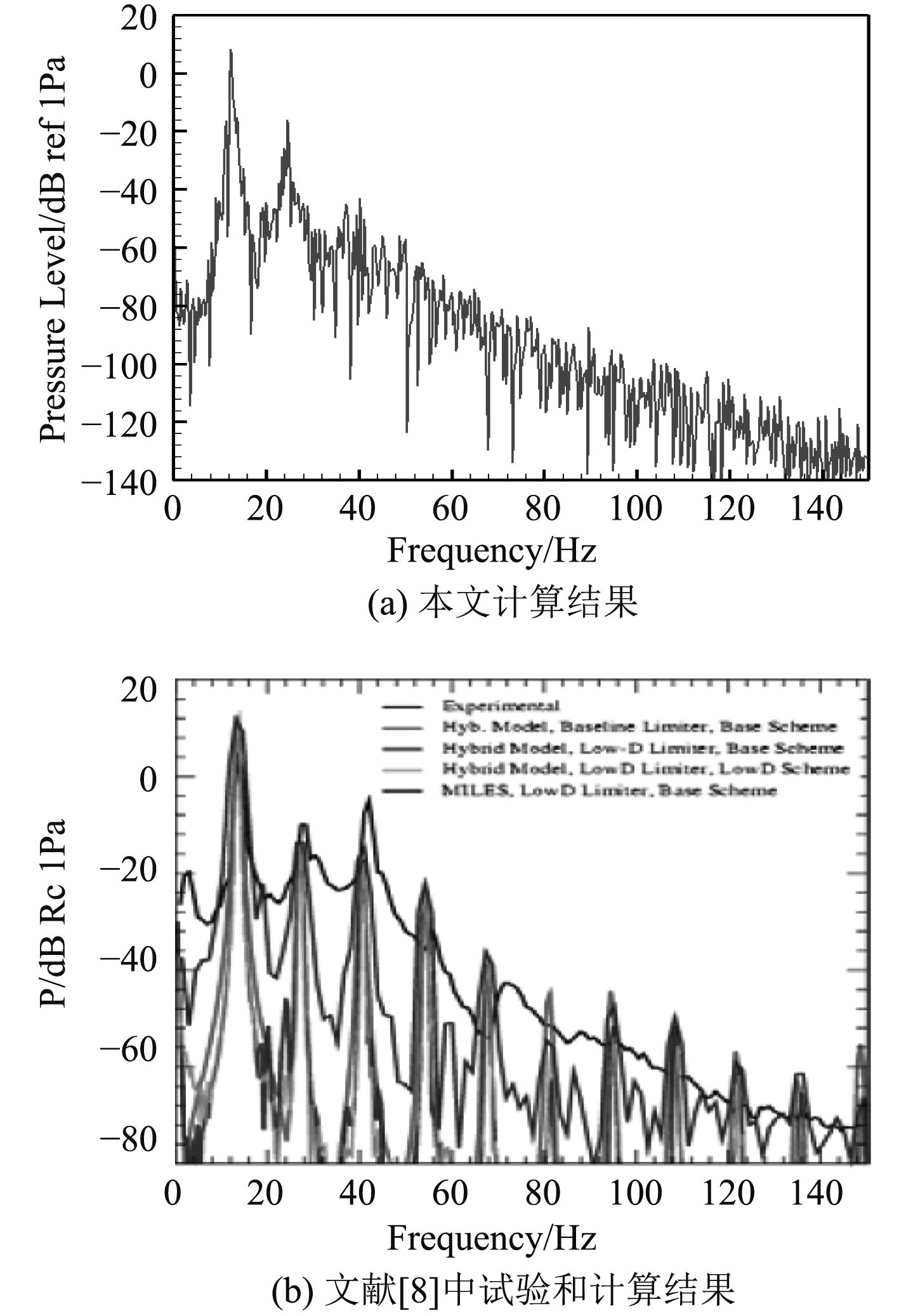
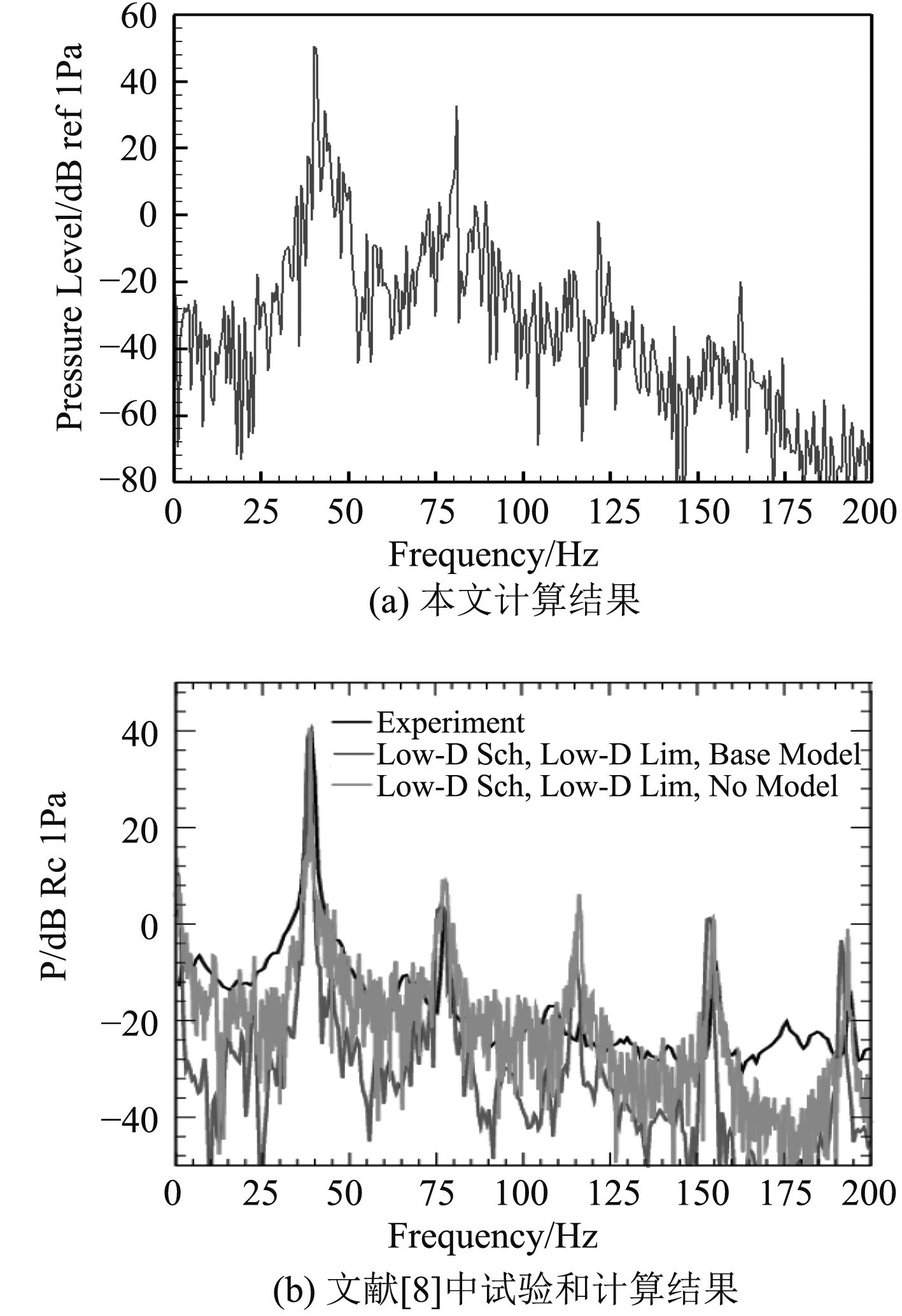
为了验证计算方法的有效性,计算了文献[8]中的三维空腔结构流动问题。为了捕捉到高频流动噪声,时间步长取10–5 s。计算网格数目约800万,全局采用结构化网格。计算了来流速度分别为U=9 m/s和30 m/s两种情况,得到压力频谱如图1和图2所示。U=9 m/s算例的前 3 阶模态频率分别为12.43 Hz,24.72 Hz,37.43 Hz;U=30 m/s算例的40.44 Hz,81.17 Hz,121.91 Hz。结果与文献[8]对比可见,计算得到的模态频率与文献中的结果吻合较好,说明了目前计算方法的可靠性。
|
图 1 U=9 m/s算例采样点的压力级频谱 Fig. 1 Pressure level spectrum of a sample point for case U=9 m/s |
|
图 2 U=30 m/s算例采样点的压力级频谱 Fig. 2 Pressure level spectrum of a sample point for case U=30 m/s |
本文的计算空腔基本模型为方腔圆开孔,空腔长宽高均为1 500 mm,开孔位于顶部中心,开孔的直径为500 mm。时间步长取
本节计算了 2 种不同结构加强形式的开孔流噪声及激励特性,这 2 种结构加强形式分别为沿流向方向结构加强以及横向方向结构加强,如图3所示。

|
图 3 开孔2种结构加强形式 Fig. 3 Hole with two types of structure |
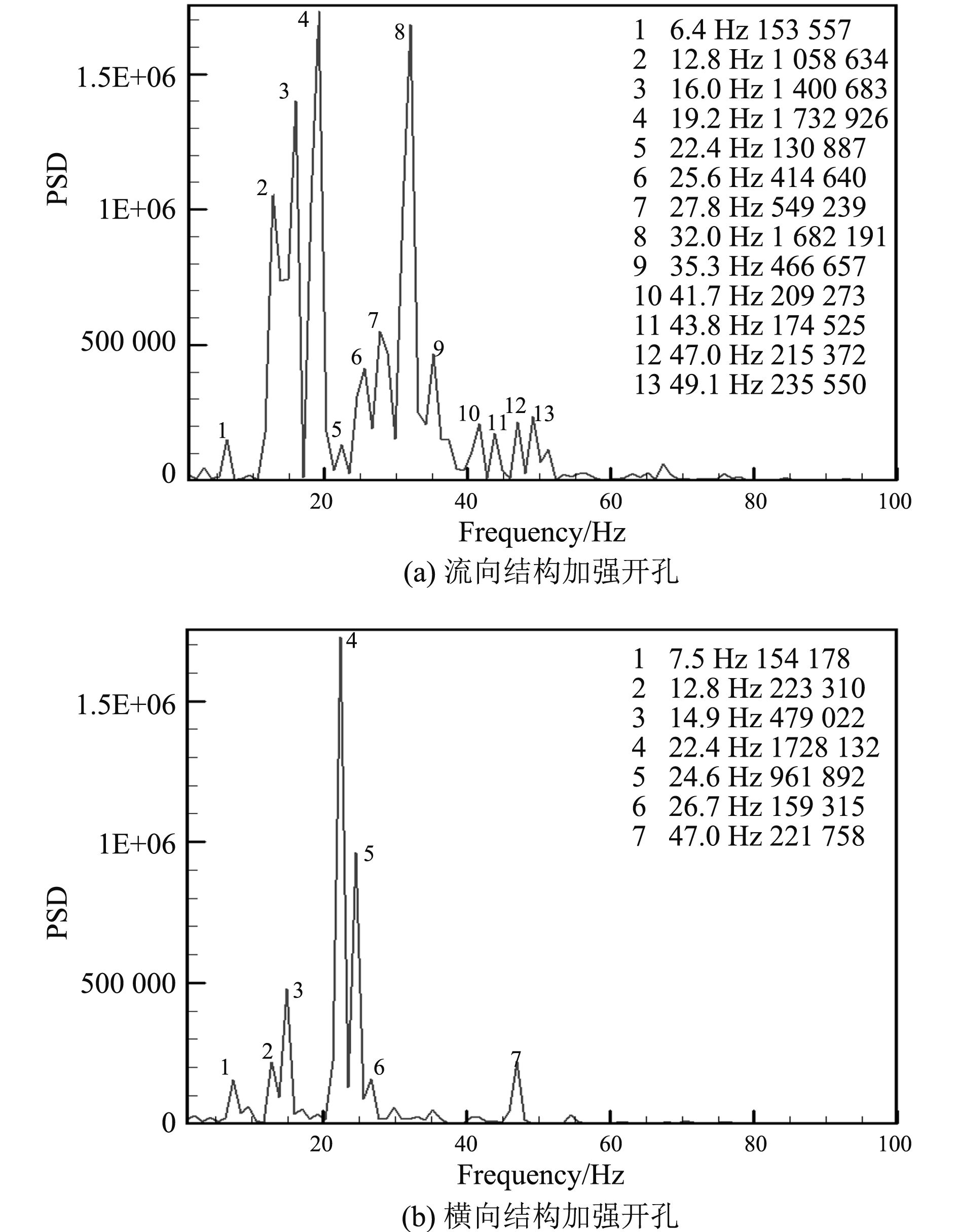
不同结构加强方式开孔的监测点脉动压力频谱如图4所示,监测点位于开孔中心,流体激励频谱主要线谱见表1。从图表中可以看出:沿流向方向结构加强开孔引起的流体激励频率成分更为复杂,且幅值较高,因此,从降低流体激励引起的结构振动噪声的角度考虑,建议开孔结构加强采用横向加强的结构形式。
|
图 4 两种结构加强方式开孔监测点脉动压力频谱 Fig. 4 Pressure spectrum of a sample point for two types of structure |
|
|
表 1 脉动压力主要线谱频率分布表(Hz) |
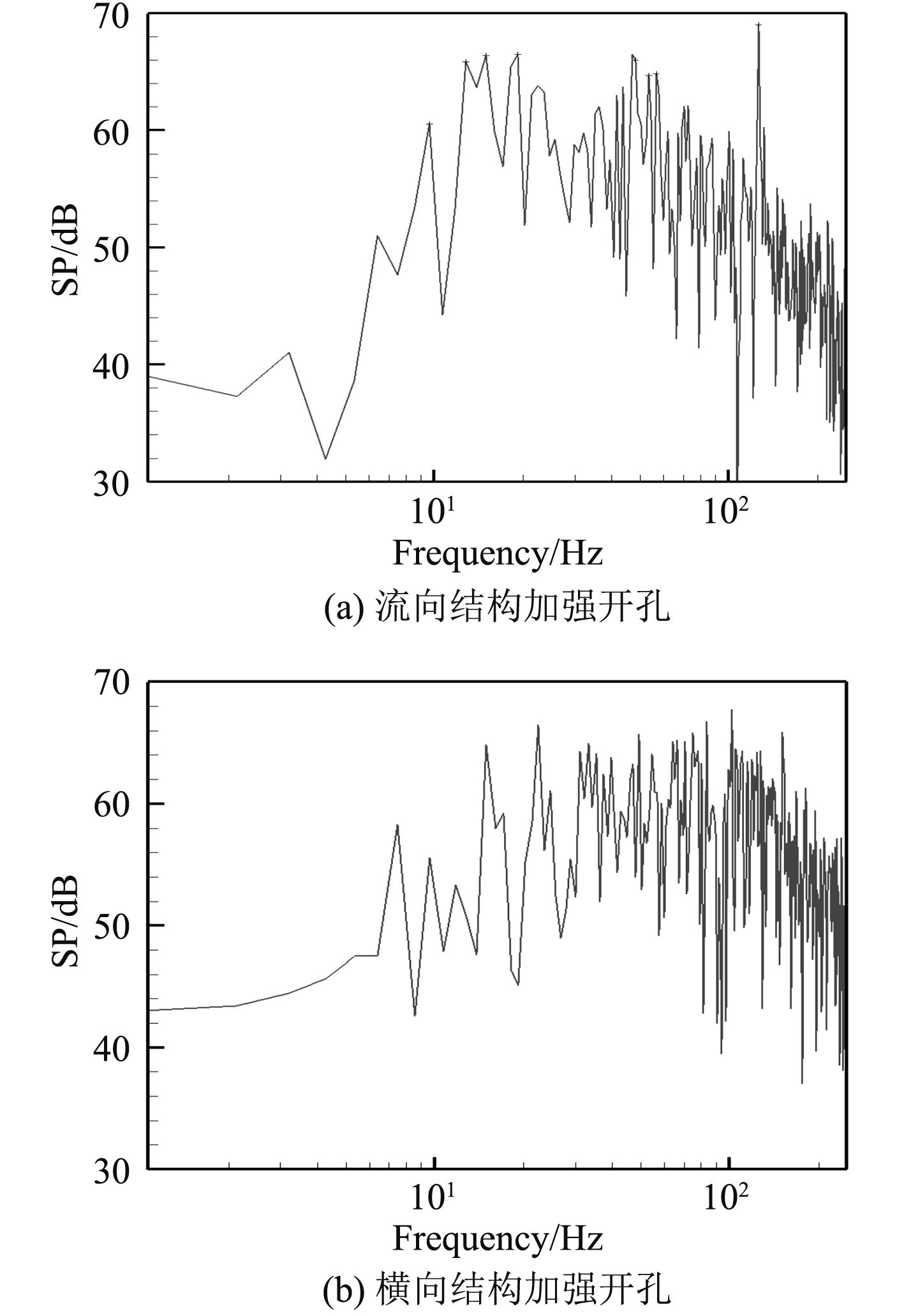
不同结构加强方式开孔的辐射噪声频谱如图5所示,图中监测点取开孔中心正上方100 m处,其主要线谱频率分布如表2所示。从频谱图中可以看出:2 种结构加强方式对辐射噪声总级影响不大;2 种结构加强方式下,一阶线谱频率发生了改变;2 种结构开孔辐射噪声存在部分相同成分的线谱频率,也有不同的频率成分。
|
图 5 两种结构加强方式开孔辐射噪声频谱 Fig. 5 Sound pressure level spectrum of a sample point for two types of structure |
|
|
表 2 辐射噪声主要线谱频率分布表(Hz) |
通过对比分析不同结构加强方式,相同大小开孔引起的流噪声以及流体激励特性,可以得出以下结论:开孔沿横向或流向方向结构加强对流体直发声辐射噪声总级影响不大;沿流向方向结构加强开孔引起的流体激励频率更加丰富,且幅值较高,建议开孔结构加强方式采用横向加强方式。
2.2 开孔流噪声控制措施及效果分析针对开孔引起的流体直发声以及流体激励中的强线谱,本节探索开孔流噪声的控制措施,通过数值计算分析该控制措施的降噪效果。
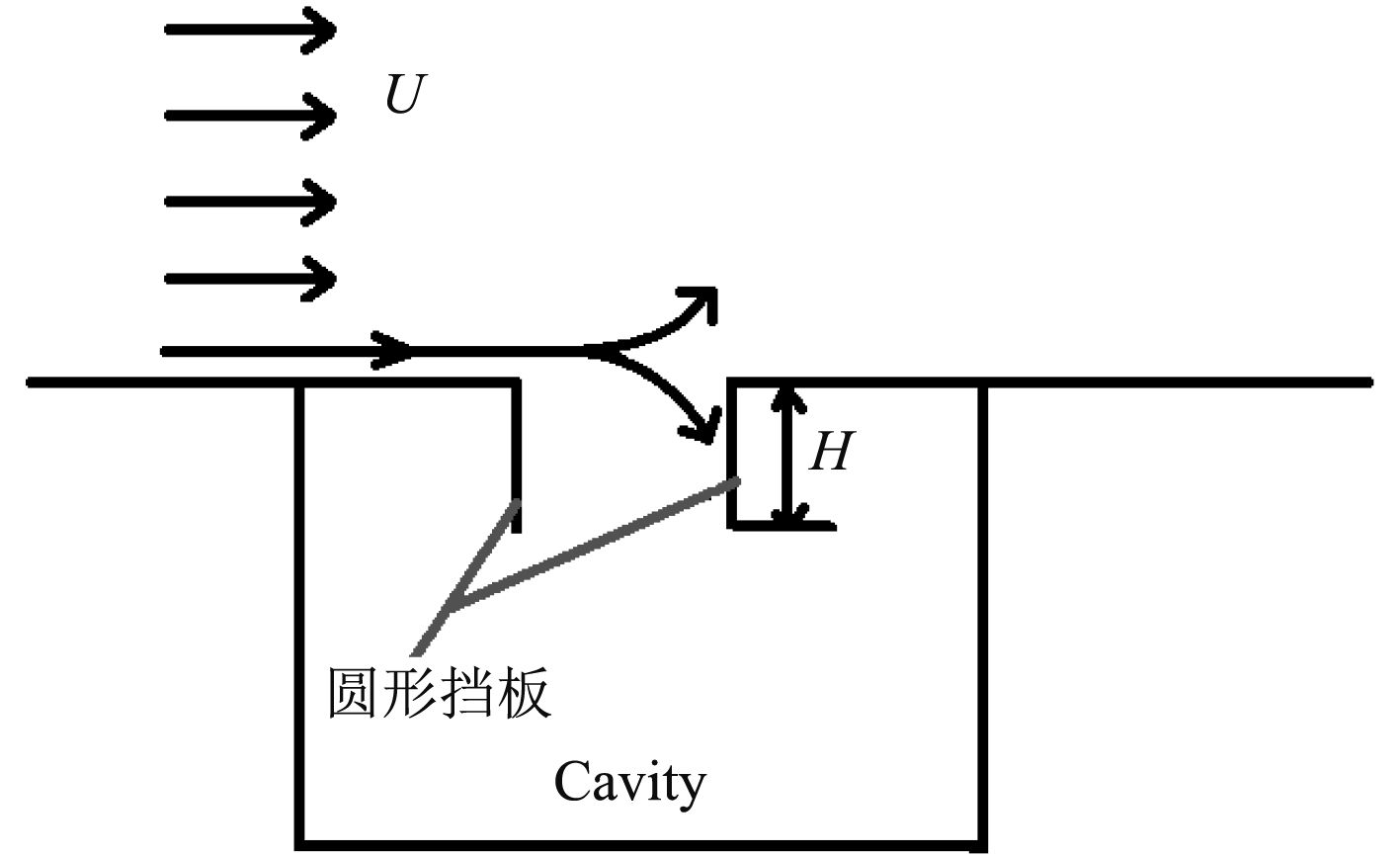
2.2.1 增装导流体本节计算的 2 种带导流板的开孔模型如图6所示。

|
图 6 两种带导流板的开孔模型 Fig. 6 Hole with two types of deflector |
不同高度导流体及无导流体情况下的开孔流致辐射噪声频谱如图7(a)所示,监测点位于开孔中心正上方100 m处。从图中可以看出:开孔前缘增加导流体后,其辐射噪声在各个频带内均较无导流体情况有所降低;导流体高度越高,开孔流致辐射噪声越低。图7(b)为增装不同高度导流体开孔引起的脉动压力频谱分布,其主要线谱频率见表3。从图表中可以看出,导流体高度增加后,主要流体激励频率向更低频率发展,且幅值明显增强。
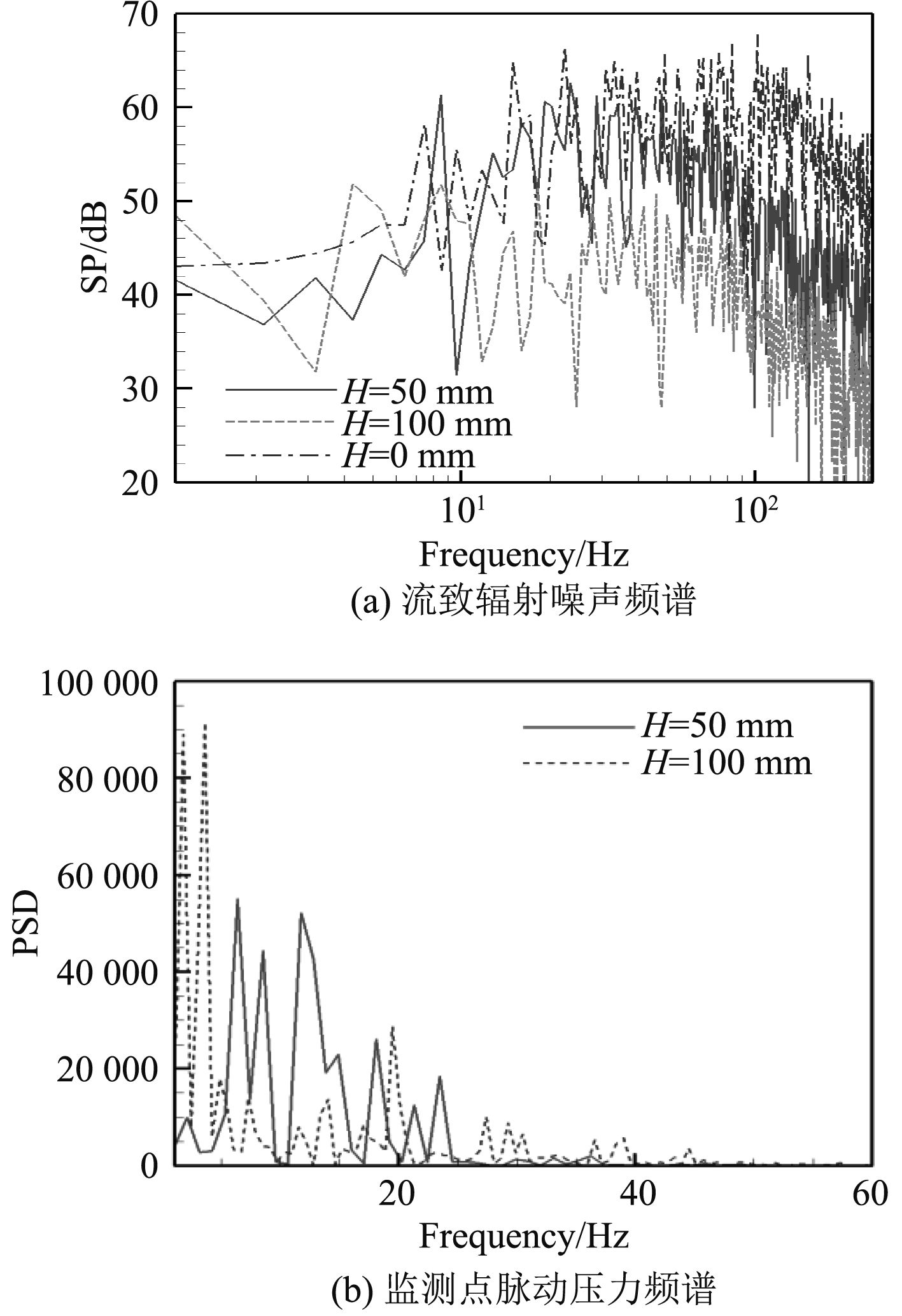
|
图 7 不同尺寸导流体的开孔噪声控制效果 Fig. 7 Comparisons of noise reduction for different deflectors |
|
|
表 3 脉动压力主要线谱频率分布表(Hz) |
接着分析开孔前缘增加导流体可以显著降低开孔流噪声的原理。如图8所示,从图中可以看到剪切层流体通过导流体之后,部分流体越过孔腔开孔,到达开孔后方,从而降低了由于剪切层流体撞击孔腔后缘引起的流体振荡反馈噪声。

|
图 8 导流体降噪示意图 Fig. 8 Sketch of noise reduction for deflectors |
本节计算的 3 种带导流板的开孔模型如图9所示。
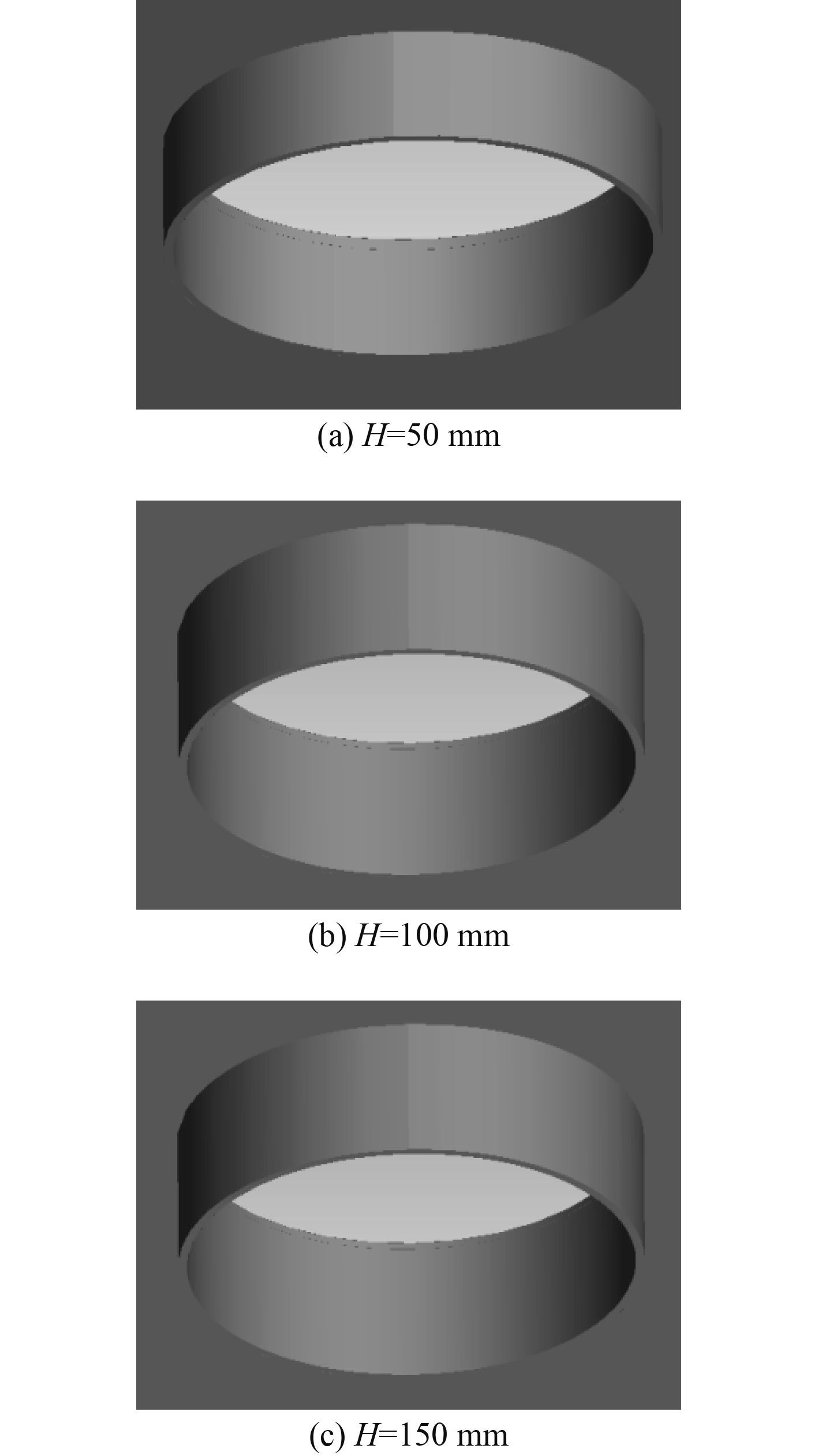
|
图 9 三种尺寸圆柱挡板示意图 Fig. 9 Sketch of three kinds of size for circular baffle |
不同高度圆形挡板引起的开孔流致辐射噪声频谱如图10(a)所示,监测点位于开孔中心正上方100 m处。从图中可以看出:开孔下方增设圆形挡板后,其辐射噪声在各个频带内均较无挡板情况均有所降低;圆形挡板高度越高,开孔流致辐射噪声越低。图10(b)为增装不同高度圆形挡板开孔引起的脉动压力频谱分布,其主要线谱频率见表4。从图表中可以看出:随着圆形挡板高度增加,脉动压力频谱幅值明显增大,但主要线谱频率变化不大。
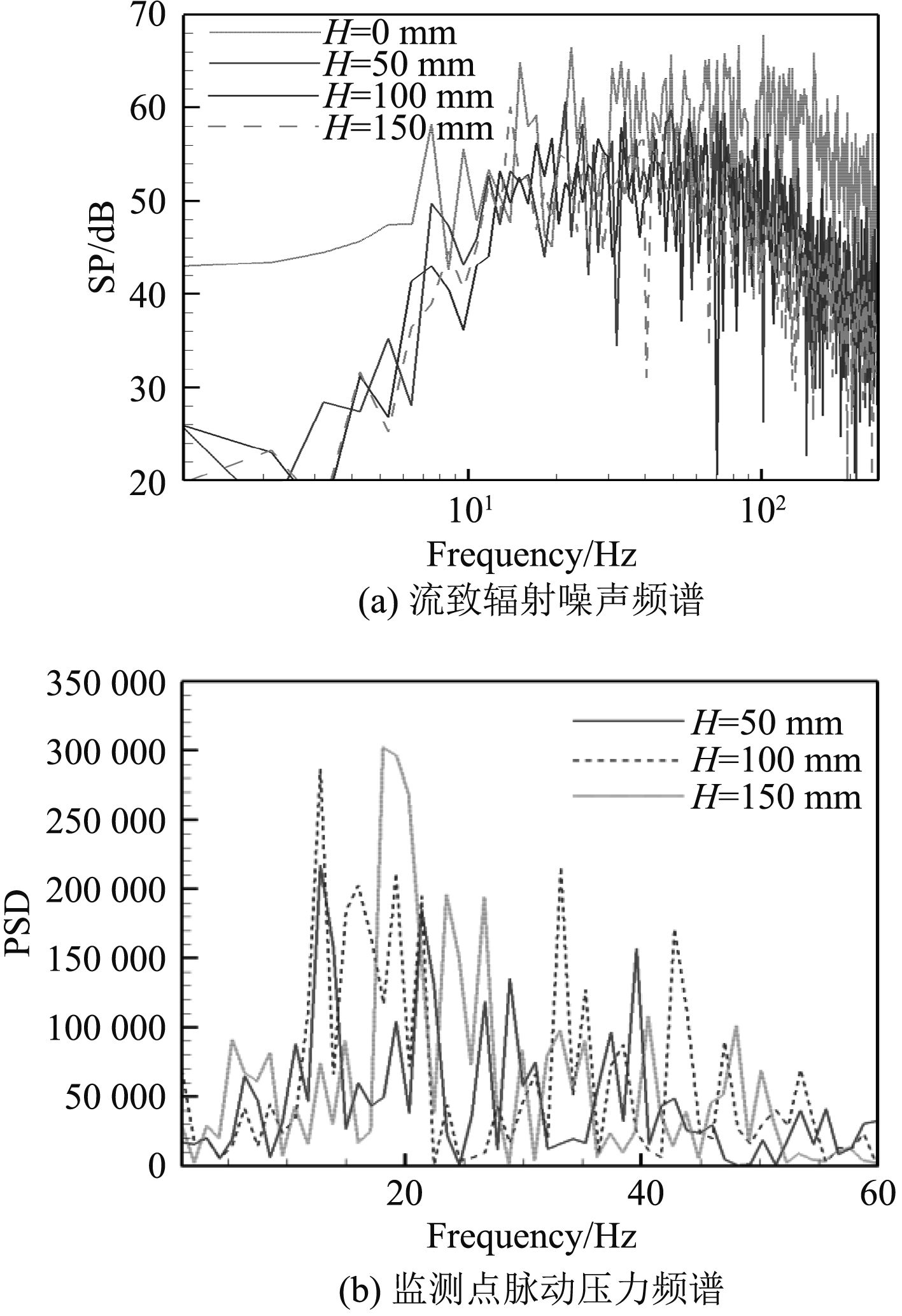
|
图 10 不同尺寸圆柱挡板的开孔噪声控制效果对比 Fig. 10 Comparisons of noise reduction for different circular baffles |
|
|
表 4 脉动压力主要线谱频率分布表 |
下面分析开孔下方设置圆形挡板可明显改善开孔流噪声的机理。如图11所示,从图中可以看到,来流经过开孔,撞击开孔后缘分成 2 股流体,一股向开孔后方运动,另一股向开孔内部流动。挡板的主要作用是“引流”,引导向开孔内部运动的流体流动更加光顺,减少腔内非稳定涡旋的产生,降低腔内流体直发生。其次,挡板减少了腔内的涡旋与剪切层来流的碰撞,抑制来流剪切层流体受扰动引起的直发声。
|
图 11 圆形挡板降噪示意图 Fig. 11 Sketch of noise reduction for circular baffles |
本文以舰船表面开孔为研究对象,通过对不同开孔形式的流体激励及流噪声特性进行数值仿真计算,得到以下结论:开孔沿横向或流向方向结构加强对流体直发声辐射噪声总级影响不大;沿流向方向结构加强开孔引起的流体激励频率更加丰富,且幅值较高,建议开孔结构加强方式采用横向加强方式;在开孔前缘增加导流体、开孔下方增设圆形挡板均能有效的降低流体直发声,且随着导流体的高度增加,圆形挡板越深,流体直发声的降噪效果越明显;增设导流体的降噪方式使得流体主要激励频率往更低频发展;增设圆形挡板对流体激励频率影响不大,但挡板高度越高,脉动压力幅值明显增加,采用此种降噪方式需综合考虑流激结构振动噪声的影响。
| [1] | POWELL A. Theory of vortex sound[J]. J. Acoust. Soc. Am, 1964, 36 : 177–195. DOI: 10.1121/1.1918931 |
| [2] | ROSSITER J. E. Wind tunnel experiments of the flow over rectangular cavities at subsonic and transonic speeds[R]. ARCR&M. TR3438, 1964. |
| [3] |
张楠, 沈泓萃, 姚惠之, 等. 带流水孔潜体流场数值模拟[J]. 船舶力学, 2004, 8 (1): 1–11.
ZHANG Nan, SHEN Hongcui, YAO Huizhi, et al. Numerical simulation of flow around a submerged body with flood hole[J]. Journal of Ship Mechanics, 2004, 8 (1): 1–11. |
| [4] |
赖焕新, 周邵萍, 罗开红. 空腔的非定常可压缩过流及相关气动声学问题[J]. 工程热物理学报, 2007, 28 (5): 755–758.
LAI Huanxin, ZHOU Shaoping, LUO Kaihong. Three-dimensional unsteady compressible flow over an open cavity and relevant aero-acoustics[J]. Journal of Engineering Thermophysics, 2007, 28 (5): 755–758. |
| [5] |
李晓东, 刘靖东, 高军辉. 空腔流激振荡发声的数值模拟研究[J]. 力学学报, 2006, 38 (5): 599–604.
LI Xiaodong, LIU Jingdong, GAO Junhui. Numerical simulation of flow-induced oscillation and sound generation in a cavity[J]. Chinese Journal of Theoretical and Applied Mechanics, 2006, 38 (5): 599–604. |
| [6] |
耿冬寒, 刘正先. 大涡模拟-Lighthill等效声源法的空腔水动噪声预测[J]. 哈尔滨工程大学学报, 2010, 31 (2): 182–187.
GENG Donghan, LIU Zhengxian. Predicting cavity hydrodynamic noise using a hybrid large eddy simulation-Lighthill’s equivalent acoustic source method[J]. Journal of Harbin Engineering University, 2010, 31 (2): 182–187. |
| [7] |
万振华, 周林, 孙德军. 方腔流致振荡及噪声的数值研究[J]. 空气动力学报, 2012, 30 (3): 291–298.
WAN Zhenhua, ZHOU Lin, SUN Dejun. Numerical study of flow-induced oscillation and noise of cavity[J]. Acta Aerodynamica Sinica, 2012, 30 (3): 291–298. |
| [8] | ARUNAJATESAN S, SINHA N. Modeling approach for reducing Helmholtz resonance in submarine structures[C]//AIAA Aeroacoustics Conference, 2005–2858. |
 2017, Vol. 39
2017, Vol. 39

