无人潜水器的应用越来越广泛。大多数潜水器外形复杂,在较高速度下潜水器的动力学模型是高度非线性、耦合的[1]。为了提高潜水器控制系统的性能及鲁棒性,基于模型设计非线性控制器,需要建立较精确的非线性模型。
潜水器在流体中运动,引起运动的水对其产生反作用力,即水动力。水动力的大小、方向及其分布,取决于潜水器本身的运动和几何外形;只有少数像球体、回转体等有解析解,一般都由模型试验或经验公式确定[2]。外形不规则、不对称的潜水器,其水动力特性非常复杂。一个典型ROV的非线性数学模型有200多个水动力系数[3]。根据流体力学分析,复杂外形潜水器所受的压差阻力更大,而且其外形曲率变化大,近壁面流体流动不能很好地贴合在其几何表面,边界层易发生分离,产生漩涡。因此,针对复杂形状的潜水器,水动力系数很难预测。
目前,潜水器的水动力参数主要通过经验公式法[4]、CFD法[5 – 8]、实验法[9 – 11]测得。经验公式法适用于细长体的潜水器,不能准确估算复杂外形潜水器的水动力。实验法的测量结果最为准确,但实验成本高。针对复杂外形的潜水器,文献[5, 8]都没有考虑耦合水动力的影响。本文以上海交通大学水下工程实验室DOE HD2+2 ROV为计算对象,建立其几何模型并划分网格,应用STAR-CCM+与WAMIT等CFD软件计算水动力,确定耦合的阻尼力/力矩参数和附加质量力/力矩参数,最终建立了较复杂的非线性数学模型。
工程应用中ROV的阻尼矩阵大多近似为对角矩阵[1],非对角元素很难通过实验和理论计算获得。为求解非对角阻尼矩阵,首先建立了复杂的ROV几何模型。其次,应用粘性流理论通过CFD软件计算阻尼水动力。为减少流体域网格的数量,并提高计算速度,采用多面体网格。这样流体域网格数量大大减少,在保证计算精度的前提下,实现了计算速度2~3倍的提高。同时,进一步验证网格的无关性[12-13],优化网格,确定较少的网格数量。为了检验动力学模型的精度,通过开环操控实验观测ROV的运动状态,并与仿真结果对比,结果显示较好的一致性。
1 阻尼矩阵计算 1.1 DOE HD2+2 ROV的几何建模DOE HD2+2 ROV重量为128 kg,长1.4 m,宽0.686 m,高0.673 m,最大作业深度为300 m。它有4个水平推进器,控制ROV的前进和回转运动,1个侧向推进器控制ROV的侧向运动,1个垂向推进器控制ROV的升沉运动,其本体结构从上往下主要为防撞框架、浮力块、推进器、配平铅块等。
多数ROV都是开架式的结构,通常有如下特点:2个对称面(左右、上下对称)、低的运动速度、缓慢解耦的运动。对于这种类型的ROV,六自由度运动方程可以简化。Fossen[1]给出了ROV简化的阻尼矩阵和附加质量矩阵,忽略了非对角元素。
然而针对DOE HD2+2 ROV,其外形复杂,上下、前后面都不对称,如图1所示,非对角阻尼元素不可以忽略。与文献[5 – 6]不同,主要考虑对潜水器阻力影响最大的主壳体,对ROV的几何部件作了一定简化,省略了螺旋桨等部件。为提高CFD计算结果的准确性,首先,建立较完整的复杂的几何模型。对阻力影响较大、裸露在水中的部件都包含在ROV几何模型中,包括照明灯、摄像机、导管及螺旋桨等。ROV的几何部件都是类似长方体等不规则形状的钝体,其迎流面法向方向与流体运动方向成较小夹角,余弦值较大,对流体的阻碍作用明显。例如,直径为D的圆柱体所受的阻力大约10倍相同厚度的流线体所受的阻力[14]。其次,建立了较为精确的1:1模型,在几何外形、尺寸上与实际ROV保持一致。以浮力块为例,浮力块表面用曲面近似,边界处通过圆弧倒角过渡,与实际ROV的浮力块几何特征保持一致。
潜水器完全浸没在水中运动,定义ROV浮心为载体坐标系原点,Z轴向下。通过实验测量ROV的重心,并估算其转动惯量,可得刚体参数如下:
xG=xB=0 m,yG=yB=0 m,zG≈0.054 m,Ix≈6.104 kg·m2,Iy≈13.315 kg·m2,Iz≈14.213 kg·m2,Ixy=Iyz≈0 kg·m2,Izx≈–0.858 kg·m2。

|
图 1 DOE HD2+2 ROV示意图 Fig. 1 Schematic diagram of DOE HD2+2 ROV |
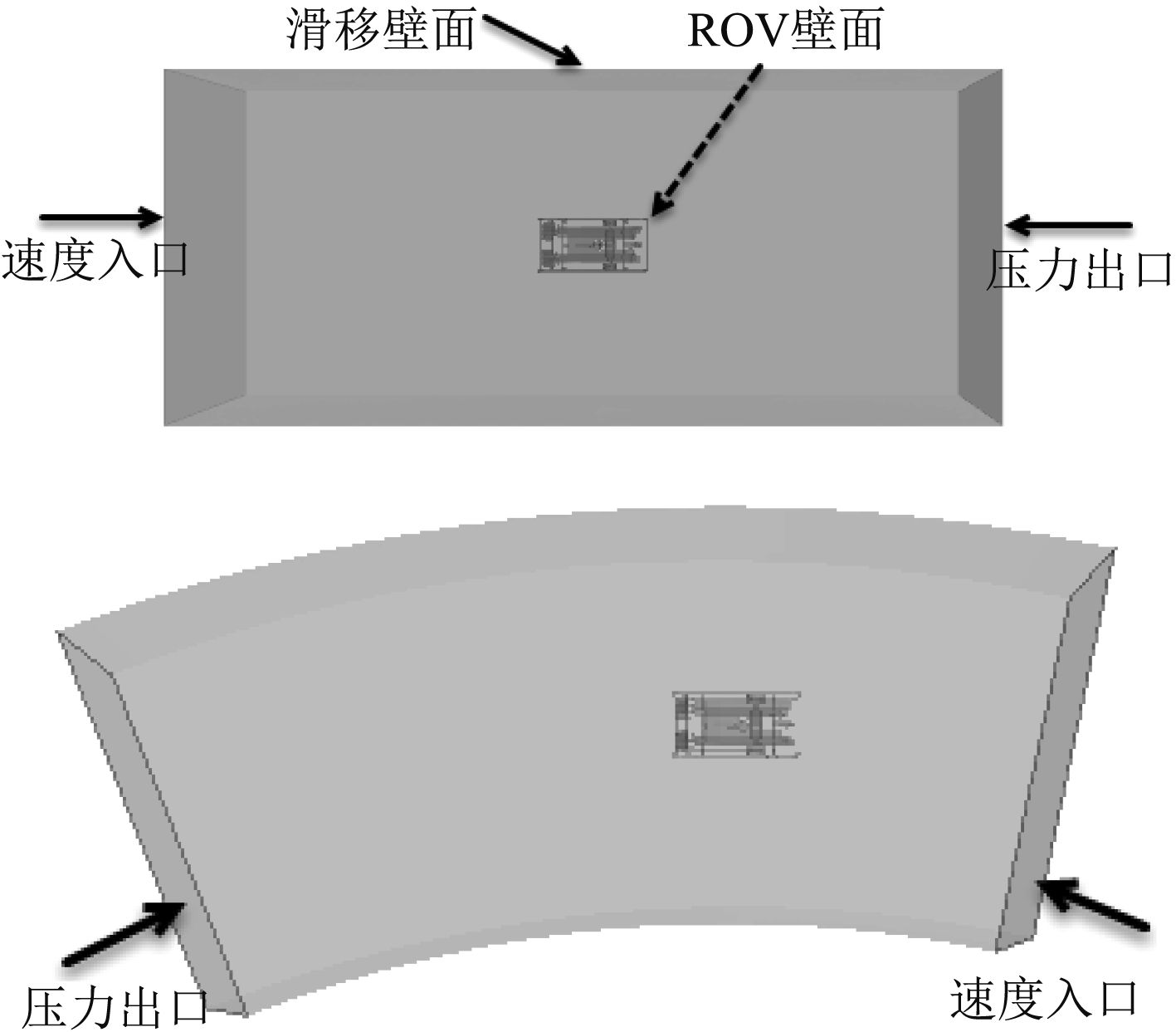
为了求解ROV在流体中作匀速运动所受的水动力,根据Galileo的运动相对性原理[15],先进行运动转换,把物体当作静止不动而让流体流过物体,使原来的非定常问题改变成定常问题。ROV在水中运动可分为:平移运动和旋转运动,分别建立了模拟ROV运动的流体域,如图2所示。由于ROV外形近似为长方体,选取其平移运动的计算域为长方体。旋转运动流体域为绕旋转中心的旋臂区域[16]。
以模拟ROV回转运动为例,令ROV纵荡速度u=ωr,ω为角速度,r为ROV原点到旋转中心的距离。回转运动中,保持ROV线速度1 m/s不变,横荡速度为0 m/s,通过改变旋臂半径的大小来改变角速度。因此,为了预测旋转水动力导数,需要建立多个旋转流体域。
1.3 网格划分求解任何流体流动问题,获得流动中所有细节的网格至关重要。为了准确获取ROV的复杂外形信息,例如螺旋桨、照明灯等,需要划分相对较细的网格,这势必会导致整个流体域网格数量的大大增加。为了生成高质量且较少数量的网格,针对复杂外形的ROV,采用多面体网格划分流体域,并设置相应的网格参数,使近壁面网格尺寸较小,远离壁面的流体域表面网格尺寸相对较大。这样既保证第 1 层网格厚度满足y+值的要求[3],又使网格自模型壁面向外由密到疏布置。流体域体网格分布与ROV壁面网格如图3所示。
针对复杂形状的几何结构,通常采用四面体网格划分,本文采用多面体网格。与四面体网格相比,生成多面体网格可以大大减少流体域的网格总数,如表1所示。这样节省了计算资源,计算速度提高了2倍以上。
|
图 2 模拟ROV平移和转动的计算域 Fig. 2 Computation domain of simulating ROV translational and rotational motion |

|
图 3 计算域切面与ROV壁面多面体网格示意图 Fig. 3 Polyhedral mesh of cut surface in the flow domain and near-wall surface |
网格划分好后,选取可实现K-Epsilon两层湍流模型。然后定义边界条件,分别定义速度入口和压力出口,用于设置不同大小的速度和湍流强度,其他边界取为滑移壁面。
|
|
表 1 多面体与四面体网格参数设置 Tab.1 Parameters setting for polyhedral and tetrahedral mesh |
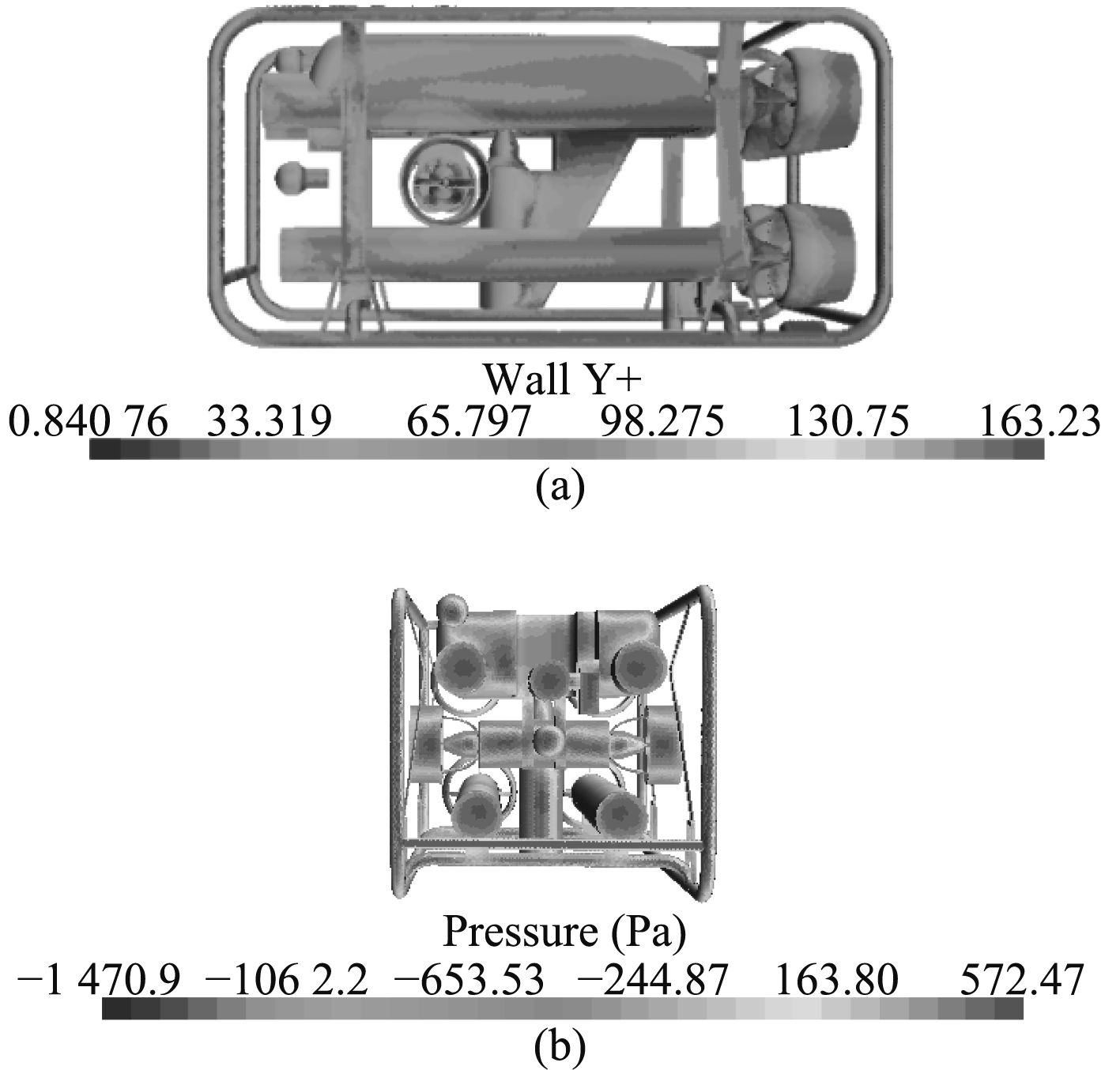
STAR-CCM+中ROV壁面的y+值基本在30~100之间,如图4(a)ROV壁面Y+图所示,第 1 层网格高度在湍流区域内。由图4(b)右压强云图可以看出DOE HD2+2 ROV的迎流面压强大,明显阻碍水流的运动。由图5速度云图可知旋转域内水流速度的大小与半径成正比,与文献[16]潜艇的速度云图不同,流经ROV的尾流速度在很长的流域内都不能恢复到进流段的流态,这是因为潜艇为流线型,对流体阻碍作用小,而ROV外形复杂,对壁面附近水流速度阻碍显著。
|
图 4 纵向来流1 m/s时ROV壁面的Y+值与压强云图 Fig. 4 Scalar contour of near wall domain when ROV surge motion at 1 m/s speed |

|
图 5 角速度为0.06 rad/s时旋转域平面的速度云图 Fig. 5 Velocity contour at ω=0.06 rad/s around the model |
为检验计算结果的准确性,进行了网格的独立性验证。表2为不同网格数量的参数设置。在保持计算结果一致性的前提下,以ROV纵荡和横荡运动为例,确定最少网格数量。
|
|
表 2 流体域网格参数和数量对比 Tab.2 Comparison of mesh settings |
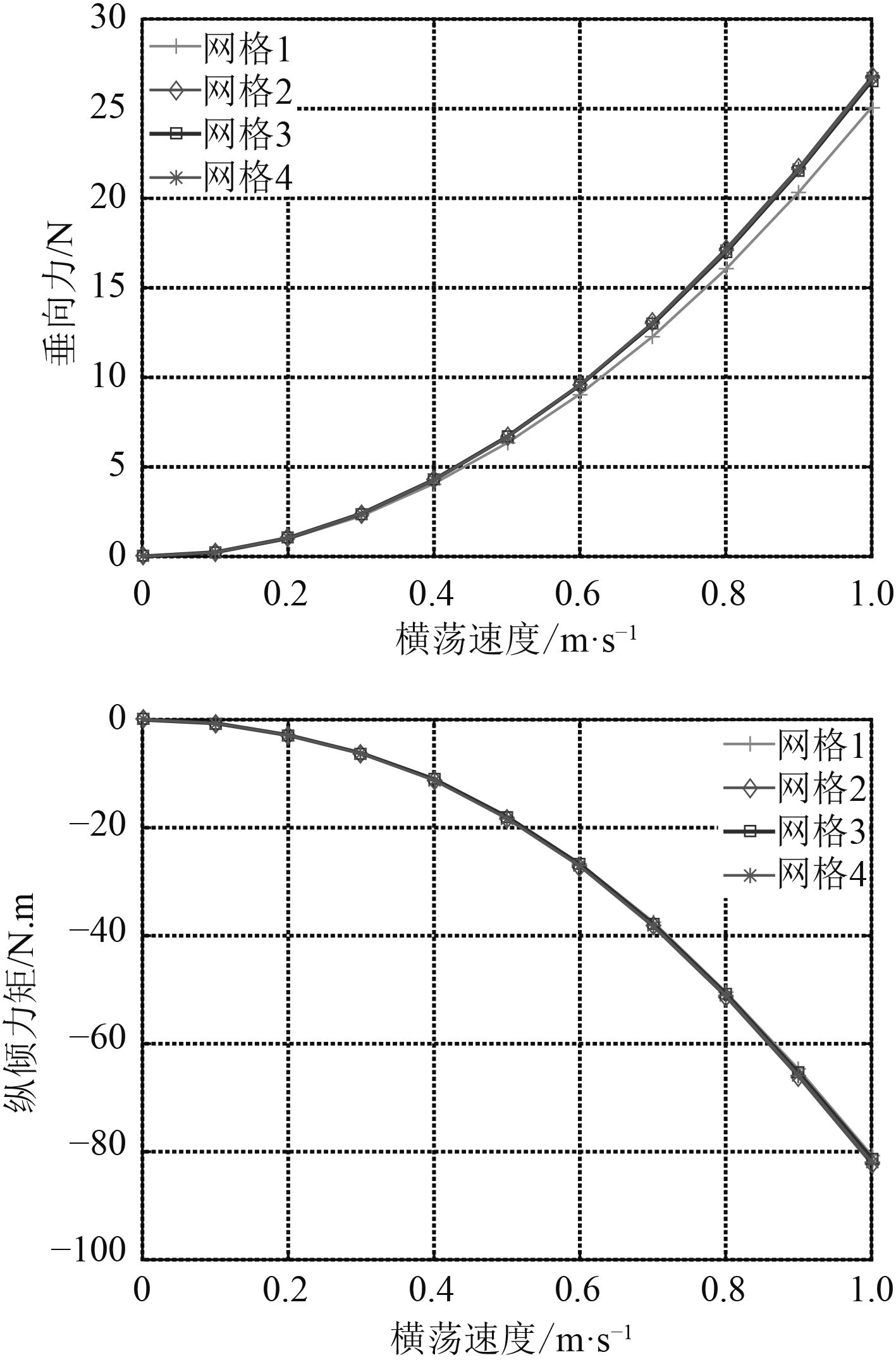
由图6和图7可知,第3和第4类网格下ROV纵向运动和侧向运动的计算结果几乎一致。最终选取较少网格数量的第3类网格参数。

|
图 6 不同网格数量下纵向来流时ROV所受的垂向力和纵倾力矩 Fig. 6 Heave force and pitch moment for surge motion for grid independence study |
|
图 7 不同网格数量下侧向来流时ROV所受的垂向力和回转力矩 Fig. 7 Heave force and yaw moment for sway motion for grid independence study |
通过STAR-CCM+软件模拟ROV的平移运动和旋转运动,计算得到了90多组水动力和力矩。基于最小二乘法将数据进行曲线拟合,得到线性和非线性的水动力系数。与潜艇[4]相似,由于ROV外形前后、上下不对称,其ROV运动方向改变,所引起的水动力/力矩也不同。
非线性阻尼矩阵D(V)如下:
|
${ D}\left( { V} \right) = - \left[ {\begin{array}{*{20}{l}}{{X_u} + {X_{u\left| u \right|}}\left| u \right|} & {{X_v} + {X_{vv}}v} & {{X_w} + {X_{ww}}w} & 0 & 0 & 0\\{{Y_u} + {Y_{uu}}u} & {{Y_v} + {Y_{v\left| v \right|}}\left| v \right|} & {{Y_w} + {Y_{ww}}w} & {{Y_P}} & 0 & {{Y_r}}\\{{Z_u} + {Z_{uu}}u} & {{Z_v} + {Z_{vv}}v} & {{Z_w} + {Z_{w\left| w \right|}}\left| w \right|} & 0 & {{Z_q}} & 0\\{{K_u} + {K_{uu}}u} & {{K_v} + {K_{v\left| v \right|}}\left| v \right|} & {{K_w} + {K_{ww}}w} & {{K_P}} & 0 & 0\\{{M_u} + {M_{u\left| u \right|}}\left| u \right|} & {{M_v} + {M_{vv}}v} & {{M_w} + {M_{w\left| w \right|}}\left| w \right|} & 0 & {{M_q}} & 0\\{{N_u} + {N_{u\left| u \right|}}\left| u \right|} & {{N_v} + {N_{v\left| v \right|}}v} & {{N_w} + {N_{ww}}w} & 0 & 0 & {{N_r}}\end{array}} \right]\text{。} $
|
(1) |
附加质量可通过动网格法、面元法进行数值模拟。然而,针对复杂外形的物体,动网格法很难有效。近壁面的网格都是非结构的,采用动网格方法模拟ROV的非定常运动,运动更新后网格很容易产生负体积,而且计算时间长。应用势流面元法,假设流体的运动为无旋的,已知边界条件,先求解6个自由度的速度势,再根据附加质量的定义求解各个模态的附加质量。
在惯性坐标系下,流体运动满足的边界条件如下:
|
$\left\{ {\begin{split}& {{\nabla ^2}\varphi \left( {x, y, z, t} \right) = 0,\; \left( {{\text{在整个流场}}} \right)}\text{,} \\& {\displaystyle\frac{{\partial \varphi }}{{\partial n}} = {V_n},\; \left( {{\text{在物面上}}} \right)}\text{,} \\& {\nabla \varphi = 0,\; \left( {{\text{无穷远处}}} \right)}\text{。} \end{split}} \right.$
|
(2) |
附加质量定义如下:
|
${\lambda _{ij}} = - \rho \iint_{{s_0}} {{\varphi _j}\frac{{\partial {\varphi _i}}}{{\partial n}}{\rm d}{S_0}}\text{,} $
|
(3) |
其中:φ为物体对流体的总的扰动速度势;φi为单一运动(平移或转动)的速度势;Vn为刚体在流体中运动的速度;ρ为流体的密度;S0为刚体表面积。
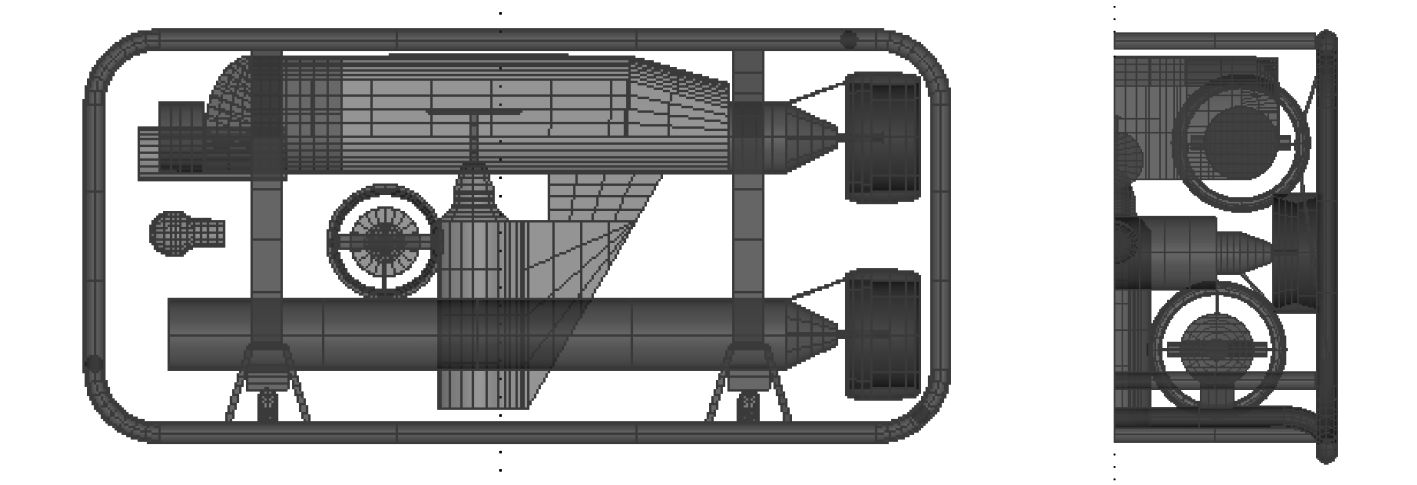
2.2 WAMIT计算使用MultiSurf软件将ROV的表面离散若干个网格单元,用网格去近似代替原来的物面,如图8所示。由于ROV近似左右对称,只建立了物面的一半面网格模型。另外,在平面处布置网格节点较少,曲面处布置较多网格。这样在保持计算精度的前提下,减小网格节点的总量,加快计算速度。
|
图 8 MultiSurf建立的ROV几何模型示意图 Fig. 8 Geomtry model of ROV in Multisurf |
将ROV几何模型文件导入势流软件WAMIT中,计算无因次的附加质量系数。为了验证WAMIT输入文件的准确性,以半径为1的圆球为例,其附加质量为2.140 5 kg,而圆球的理论附加质量值[17]
由于WAMIT所有的输出结果都是相对于其水面坐标系的,而所求的附加质量是相对于ROV载体坐标系的,这对ROV附加质量矩阵中具有质量矩和惯性矩的大小有影响。因此,需要将输出结果转化为相对于其载体坐标系的。应用坐标系变换,最终得到12个有量纲的附加质量系数。
最终得到的耦合的附加质量矩阵如下所示:
|
${{ M}_A} = \left[ {\begin{array}{*{20}{l}}{ - 33.481} & 0 & { - 1.510} & 0 & { - 2.009} & 0\\0 & { - 110.894} & 0 & {3.448} & 0 & {4.921}\\{ - 1.510} & 0 & { - 141.576} & 0 & { - 7.19} & 0\\0 & {3.448} & 0 & { - 5.843} & 0 & { - 0.792}\\{ - 2.009} & 0 & { - 7.190} & 0 & { - 11.746} & 0\\0 & {4.921} & 0 & { - 0.792} & 0 & { - 12.75}\end{array}} \right]\text{。} $
|
(4) |
基于CFD方法得到的水动力系数与刚体参数,本文利用Matlab Simulink建立ROV的动力学仿真模型。另外,在水下工程实验室完成ROV开环操控实验。

|
图 9 纵向推力下ROV高度随时间的运动变化 Fig. 9 Variations of altitude under longitudinal thrust |
|
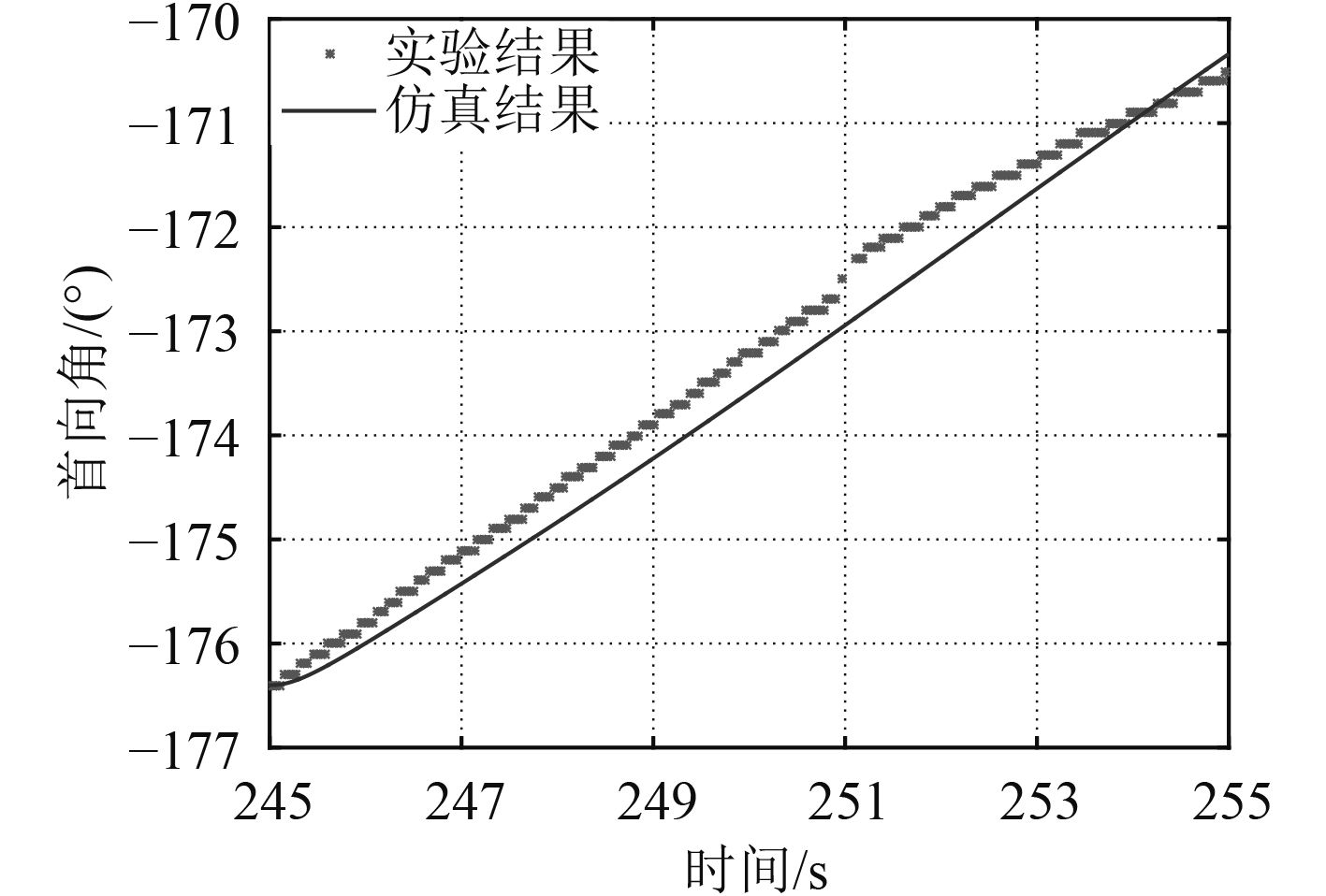
图 10 侧向推力下ROV首向角随时间的运动变化 Fig. 10 Variations of heading angle under lateral thrust |
|
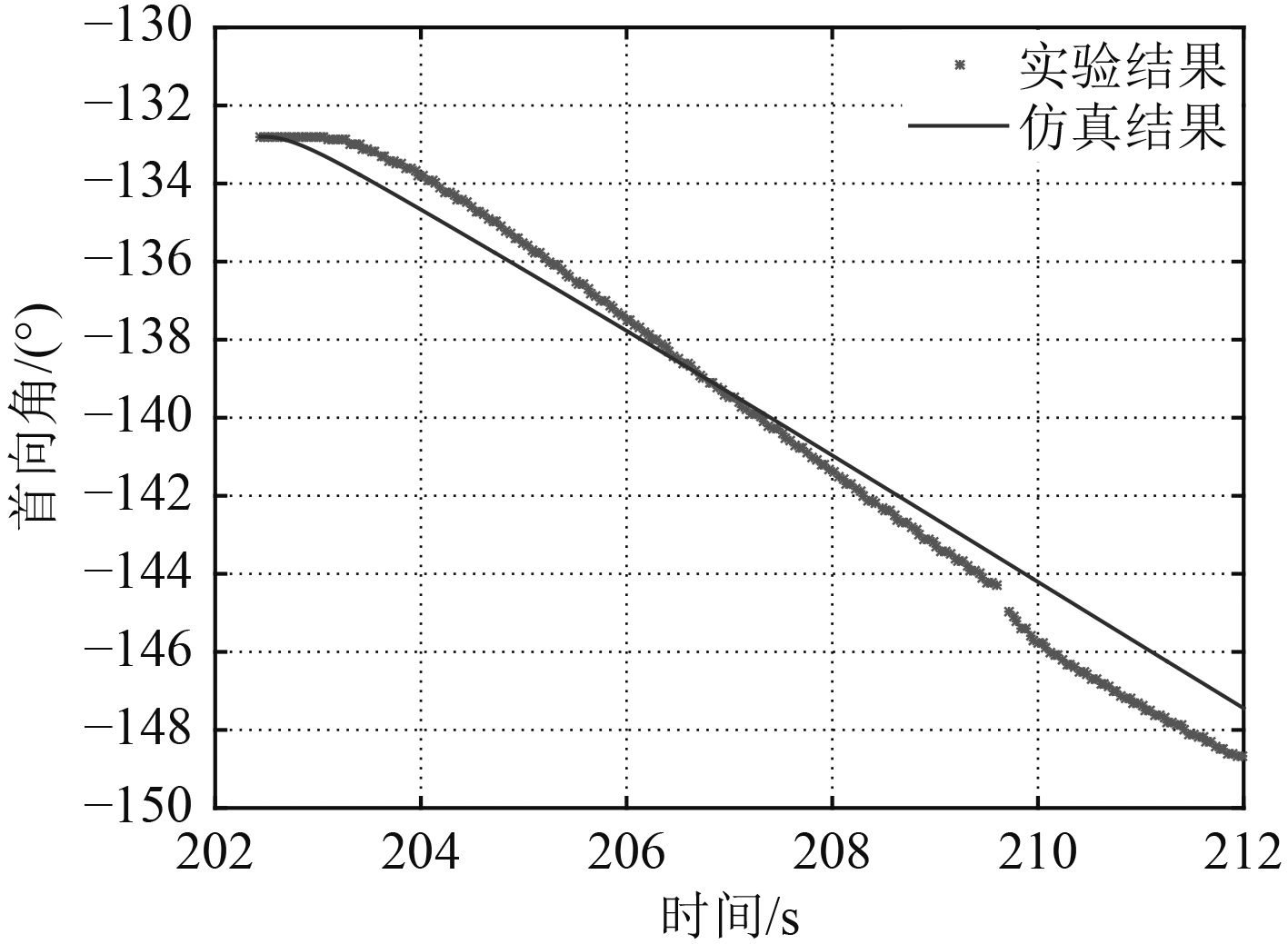
图 11 回转力矩下首向角随时间的运动变化 Fig. 11 Variations of heading angle under yaw moment |

|
图 12 垂向推力下ROV高度随时间的运动变化 Fig. 12 Variations of altitude under vertical thrust |
分别对比了ROV的纵荡、横荡、垂荡和回转 4 个自由度ROV姿态角的变化,由图9可得在纵向推力的作用下,ROV在前进运动时高度也发生变化。这主要是由于其几何外形上下不对称,由纵向速度u引起垂向水动力使ROV上升。由图10可知ROV在侧向推力下一直在偏转运动,这是其推力作用点与ROV的浮心不在同一垂线上,产生了回转力矩,使ROV偏转。在回转力矩作用下,对比了ROV的首向角变化,如图11所示,仿真结果与实验结果有一定的偏差,这主要由于旋转水动力系数计算偏差以及耦合运动产生的水动力项没有考虑。对比ROV在垂向推力下的高度变化,由图12可知仿真结果与实验结果非常接近。
ROV在高速运动下,其非线性模型是高度耦合的,涉及到更多非线性耦合项,难以预测。本文只是对比了ROV较低速下的运动响应,而且由于没有速度传感器和定位设备,只能通过ROV姿态变化验证DOE HD2+2 ROV动力学模型的有效性。
4 结 语本文以DOE HD2+2 ROV为计算对象,基于粘性流与势流理论采用CFD法计算其水动力,并建立其动力学模型,得到如下结论:
1)具有不规则、不对称外形的潜水器,正负方向运动所引起的水动力有差别,而且有耦合力产生。
2)通过开环操控实验与仿真对比,可证明建立的ROV动力学模型及采用CFD方法计算复杂外形的潜水器水动力有效。在保证计算结果精度的前提下,基于多面体网格的数值计算及面元法都大大提高了计算效率,该方法同样适用于其他潜水器的水动力计算。
本文是针对观测型的ROV水动力计算,若是针对作业型的ROV,考虑到机械手以及ROV耦合运动引起的相关水动力系数,水动力特性更加复杂。未来工作是,若条件允许下,将会通过平面运动机构验证部分水动力的计算结果,并进一步完善ROV动力学模型。
| [1] | FOSSEN T I. Guidance and control of ocean vehicles [M]. 1994. |
| [2] | 刘应中. 船舶原理. 下册 [M]. 上海: 上海交大出版社, 2005. |
| [3] | YOERGER D R, NEWMAN J, SLOTINE J J E. Supervisory control system for the JASON ROV[J]. IEEE Journal of Oceanic Engineering, 1986, 11 (3): 392–400. DOI: 10.1109/JOE.1986.1145191 |
| [4] | 施生达. 潜艇操纵性 [M]. 国防工业出版社, 1995. |
| [5] | YANG R, CLEMENT B, MANSOUR A, et al. Modeling of a Complex-Shaped Underwater Vehicle[J]. Journal of Intelligent & Robotic Systems, 2015, 80 (3): 491–506. |
| [6] | TYAGI A, SEN D. Calculation of transverse hydrodynamic coefficients using computational fluid dynamic approach[J]. Ocean Engineering, 2006, 33 (5-6): 798–809. DOI: 10.1016/j.oceaneng.2005.06.004 |
| [7] | TANG S, URA T, NAKATANI T, et al. Estimation of the hydrodynamic coefficients of the complex-shaped autonomous underwater vehicle TUNA-SAND[J]. Journal of Marine Science and Technology, 2009, 14 (3): 373–86. DOI: 10.1007/s00773-009-0055-4 |
| [8] | CHENG C, LAU M. Modeling and Testing of Hydrodynamic Damping Model for a Complex-shaped Remotely-operated Vehicle for Control[J]. Journal of Marine Science and Application, 2012, 11 (2): 150–63. DOI: 10.1007/s11804-012-1117-2 |
| [9] | ENG Y H, LAU W S, LOW E, et al. Estimation of the Hydrodynamics Coefficients of an ROV using Free Decay Pendulum Motion[J]. Engineering Letters, 2008, 16 (3): 329–42. |
| [10] | AVILA J P, ADAMOWSKI J C, MARUYAMA N, et al. Modeling and Identification of an Open-frame Underwater Vehicle: The Yaw Motion Dynamics[J]. Journal of Intelligent & Robotic Systems, 2012, 66 (1): 37–56. |
| [11] | AVILA J J, NISHIMOTO K, SAMPAIO C M, et al. Experimental Investigation of the Hydrodynamic Coefficients of a Remotely Operated Vehicle Using a Planar Motion Mechanism[J]. Journal of Offshore Mechanics & Arctic Engineering, 2012, 134 (2): 46–51. |
| [12] | KIM H, LEONG Z Q, RANMUTHUGALA D, et al. CFD modelling and validation of an AUV undergoing variable accelerations, F, 2014 [C]. |
| [13] | EBRAHIMI F, RASTGOO A. Evaluation of linear and nonlinear hydrodynamic coefficients of underwater vehicles using CFD[C]//proceedings of the ASME 2009 International Conference on Ocean, Offshore and Arctic Engineering, F, 2009 [C]. |
| [14] | MUNSON B R, YOUNG D F, OKIISHI T H. Fundamentals of fluid mechanics [M]. Wiley, 1990. |
| [15] | 刘岳元, 冯铁城, 刘应中. 水动力学基础 [M]. 上海交通大学出版社, 1990. |
| [16] | SHADLAGHANI A, MANSOORZADEH S. Calculation of linear damping coefficients by numerical simulation of steady state experiments [J]. 2016, 9(2): 653–60. |
| [17] | NEWMAN J N, LANDWEBER L. Marine Hydrodynamics[J]. Journal of Applied Mechanics, 1977, 45 (2): 457. |
 2017, Vol. 39
2017, Vol. 39
