目前国内外对水下爆炸冲击波载荷的研究主要有实验法、数值仿真法。由于实验研究中测量数据困难、危险大、实验费用高昂等原因,所以大部分研究采用的是数值仿真方法。水下爆炸过程非常不稳定,很难重复进行,很大程度上体现了爆炸载荷的随机性。虽然结构在爆炸载荷作用下的响应分析有许多学者做过相关的研究[1 – 4],并取得丰富成果,但对爆炸载荷的统计模型只有美国的USACE进行了43组爆炸试验,选择不同的爆距、装药量得到爆炸波压力时程曲线。而从国家安全性考虑,详细的载荷数据,尤其是装药量和爆距等参数都不对外公开[5]。
考虑到缺少关于爆炸载荷统计规律的信息,假设参数服从正态分布来实现对爆炸载荷的统计研究,目前水下爆炸载荷的计算公式仅限于Cole提出的经验公式[6]。本文采用蒙特卡罗方法,随机生成参数数组,通过有限元分析,得到冲击波的峰值压力,并检验其是否服从正态分布,利用最大熵法拟合其概率密度函数,得到不同爆距、不同时刻的冲击波峰值压力的概率密度函数,分析爆炸载荷参数对统计规律的影响。
1 最大熵法对于一个随机变量,熵定义为[7]
|
$S = - \int_R {f(X)\ln [f(X)]{\rm d}X}\text{,} $
|
(1) |
而对于离散随机变量,熵为
|
$S = - \sum\limits_{i = 1}^n {f({x_i})\ln [f({x_i})]} \text{,}$
|
(2) |
式中:f(X)为随机变量X的概率密度函数;f(xi)为离散点的概率密度函数。
最大熵法的基本方程为
|
${\rm Max}.\;\;S = - \int_R^{} {f(X)\ln \left[ {f(X)} \right]} {\rm d}X\text{,}$
|
(3) |
|
${\rm S.t.}\;\;\;\int_R^{} {f(X){\rm d}X = 1} \text{,}$
|
(4) |
|
$\int_R {{X^i}f(X){\rm d}X = {m_i}} \text{。}$
|
(5) |
式中,mi为X的第i阶原点矩。
即在满足式(3)和式(4)的约束条件下,通过调整概率密度函数f(X)使熵S取最大值。利用拉格朗日乘子法,构造拉格朗日函数
|
$\bar S = S + ({\lambda _0} + 1)[\int_R {f(X){\rm d}X} - 1] + \sum\limits_{i = 1}^N {{\lambda _i}} [\int_R {{X^i}f({X_i}){\rm d}X - {m_i}} ]\text{,}$
|
(6) |
由驻值条件
|
$\frac{{\partial \bar S}}{{\partial f(X)}} = 0\text{,}$
|
(7) |
可以得到
|
$\int_R^{} {\left[ { - \ln f\left( X \right) - 1 + {\lambda _0} + 1 + \sum\limits_{I = 1}^N {{\lambda _i}{X^i}} } \right]} {\rm d}X = 0\text{。}$
|
(8) |
由式(8)可知,要使等式成立,被积函数必定为0,所以有
|
$\ln f(X) = {\lambda _0} + \sum\limits_{i = 1}^N {{\lambda _i}} {X^i}\text{,}$
|
(9) |
由式(9)可以得到最大熵概率密度函数为
|
$f(X) = \exp ({\lambda _0} + \sum\limits_{i = 1}^N {{\lambda _i}} {X^i})\text{。}$
|
(10) |
下面确定拉格朗日乘子λ0和λi的值,将式(9)代入式(4)中,得到
|
$\int_R {\exp ({\lambda _0}} + \sum\limits_{i - 1}^N {{\lambda _i}{X^i}){\rm d}X = 1} $
|
(11) |
式(11)两边同乘以
|
${e^{ - {\lambda _0}}} = \int_R {\exp (} \sum\limits_{i = 1}^N {{\lambda _i}{X^i}){\rm d}X} \text{,}$
|
(12) |
|
${\lambda _0} = - \ln [\int_R {\exp (} \sum\limits_{i - 1}^N {{\lambda _i}{X^i}){\rm d}X} ]\text{。}$
|
(13) |
将式(12)对λi求导,可得
|
$\frac{{\partial {\lambda _0}}}{{\partial {\lambda _i}}} = - \int_R {{X^i}\exp ({\lambda _0} + \sum\limits_{i = 1}^N {{\lambda _i}{X^i}){\rm d}X} } = - {m_i}\text{,}$
|
(14) |
将式(13)对λi求导,可得
|
$\frac{{\partial {\lambda _0}}}{{\partial {\lambda _i}}} = - \frac{{\int_R {{X^i}\exp (\sum\limits_{i - 1}^N {{\lambda _i}{X^i}){\rm d}X} } }}{{\int_R {\exp (} \sum\limits_{i - 1}^N {{\lambda _i}{X^i}){\rm d}X} }}\text{,}$
|
(15) |
由式(14)和式(15)可得
|
${m_i} = \frac{{\int_R {{X^i}\exp (\sum\limits_{i - 1}^N {{\lambda _i}{X^i}){\rm d}X} } }}{{\int_R {\exp (} \sum\limits_{i - 1}^N {{\lambda _i}{X^i}){\rm d}X} }}\text{。}$
|
(16) |
根据式(16)可求得λ1,λ2,…,λi,再由式(14)可得到λ0,为了方便求解,将式(16)作如下变形:
|
${Q_i} = 1 - \frac{{\int_R {{X^i}\exp (\sum\limits_{i - 1}^N {{\lambda _i}{X^i}){\rm d}X} } }}{{{m_i}\int_R {\exp (} \sum\limits_{i - 1}^N {{\lambda _i}{X^i}){\rm d}X} }}\text{。}$
|
(17) |
然后利用最小二乘法原理,使余量的平方和为最小的条件来确定λi,即
|
${\rm{Min }}{Q^2} = \sum\limits_{i = 1}^N {Q_i^2}\text{。}$
|
(18) |
求解上式较好的方法是采用非线性优化方法。
采用Fortran语言编制最大熵法拟合概率密度函数的程序,分别用标准正态分布、对数正态分布、Weibull分布,极值Ⅰ型分布[8]来验证自编程序的正确性。
标准正态分布密度函数为
|
$f\left( x \right) = \frac{1}{{\sqrt {2\pi } }}\exp \left( { - \frac{{{x^2}}}{2}} \right)\text{。}$
|
(19) |
对数正态分布密度函数为
|
$f\left( x \right) = \frac{1}{{{\sigma _Y}\sqrt {2\pi } }}\frac{1}{x}\exp \left[ { - \frac{1}{2}{{\left( {\frac{{\ln x - {\mu _Y}}}{{{\sigma _Y}}}} \right)}^2}} \right]\text{。}$
|
(20) |
Weibull分布密度函数为
|
$f\left( x \right) = \frac{\beta }{k}{\left( {\frac{x}{k}} \right)^{\beta - 1}}\exp \left[ { - {{\left( {\frac{x}{k}} \right)}^\beta }} \right]\text{。}$
|
(21) |
极值Ⅰ型密度函数为
|
$f\left( x \right) = \exp \left[ { - \exp \left( { - \alpha \left( {p - u} \right)} \right) - \alpha \left( {p - u} \right)} \right]\alpha \text{。}$
|
(22) |
最大熵法与解析解的比较如图1所示,A实线曲线为采用最大熵法拟合得到的密度函数,B虚线曲线为概率密度的真实分布。从图1可看出,采用最大熵法拟合得到的密度函数与真实的密度函数分布比较,两者吻合较好,说明自编程序最大熵法能够很好地拟合密度函数。

|
图 1 概率密度函数比较图 Fig. 1 Comparison of probability density function |
水域的网格尺寸大小为50 mm,建模时避免三角形单元,采用Solid单元,水域添加无反射边界条件。有限元模型如图2所示。

|
图 2 有限元模型 Fig. 2 Finite element model |
选用TNT炸药,假设其密度ρ服从正态分布,水的密度服从正态分布。各随机变量的均值和变异系数如表1所示。
|
|
表 1 各随机变量的均值μ和变异系数V Tab.1 Mean and coefficient of variation of the random variables |
利用乘同余法产生均匀分布的随机数[9]:
|
${y_{i + 1}} = \alpha {y_i}\left( {od M} \right)\text{,}\left( {i = 1,2,3, \cdots } \right)\text{,}$
|
(23) |
|
${r_i} = \frac{{{y_i}}}{M}\text{。}$
|
(24) |
式中:α和M均为预先选定的常数;ri为[0,1]之间均匀分布的随机数。
采用随机数产生程序得到100个均匀分布随机数。
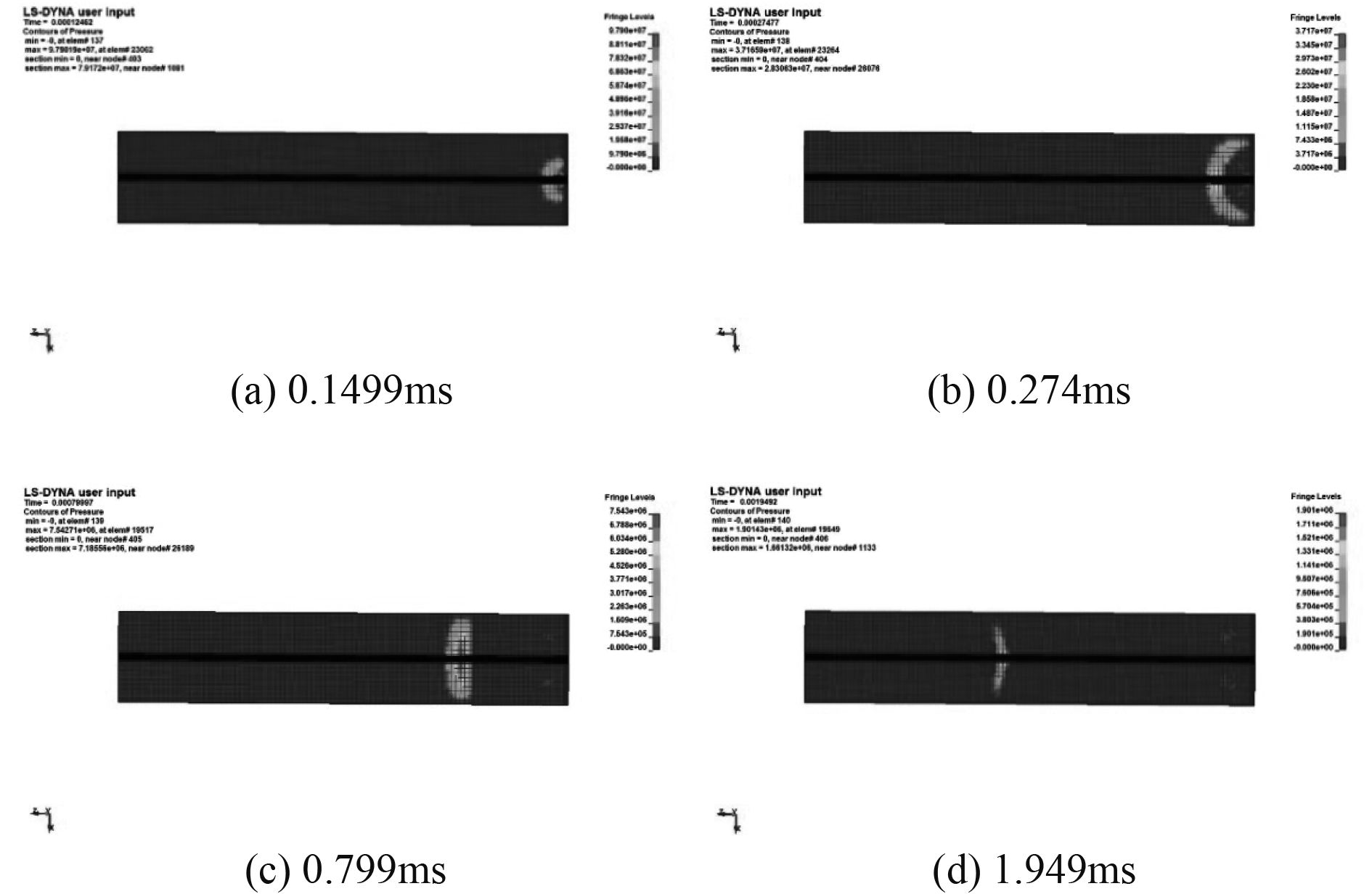
2.2.3 数值仿真计算结果冲击波在不同时刻的传播过程如图3所示,冲击波峰值压力呈指数衰减趋势。
|
图 3 冲击波传播过程 Fig. 3 Shock wave propagation |
|
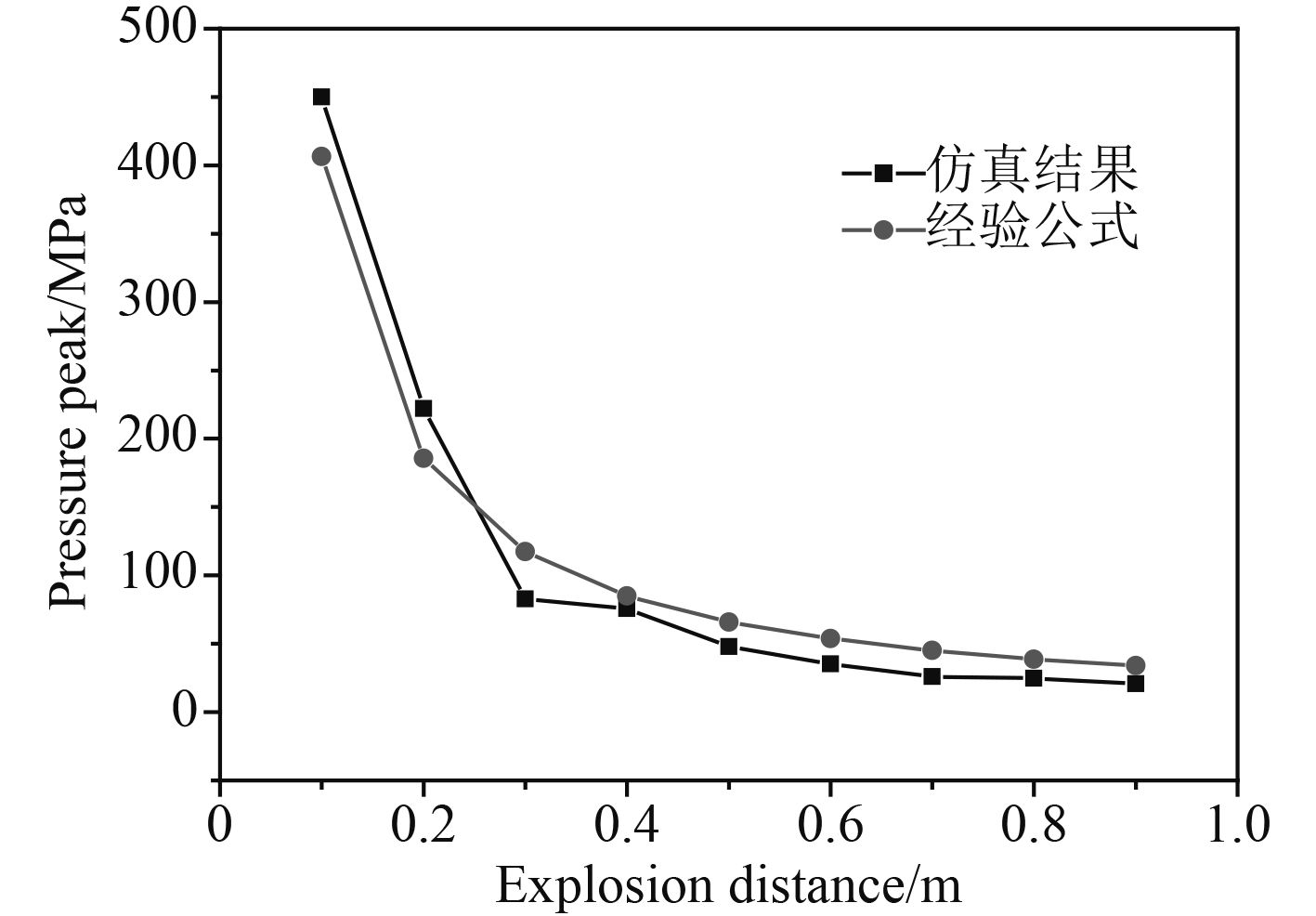
图 4 有限元仿真与经验公式[6] Fig. 4 Comparison of finite element simulation and empirical formula |
水中冲击波峰值压力的平均值与经验公式对比,如图4 所示。通过对峰值压力的统计分析,可看出:
1)随着爆距的增加,水下爆炸冲击波的峰值压力衰减较快,随着冲击波的传播,当爆距大于0.5 m时,冲击波的峰值压力的衰减速率相对减小;
2)水下爆炸冲击波的峰值压力与装药量呈线性相关,随着装药量的增加,峰值压力相应增大,同时传播介质(水)也影响着冲击波峰值压力大小,装药量相同的情况下随着水的密度增加冲击波峰值压力也相应增大,这表明了传播介质也影响了冲击波的压力峰值。
2.2.4 结果统计分析 2.2.4.1 W检验W检验,又称Shapiro-Wilk检验[9],是一种基于相关性的算法。通过计算可得到一个相关系数,如果数值越接近1,就表明数据和正态分布拟合得越好。
计算式为:
|
$W = \frac{{{{(\sum\limits_{i = 1}^n {{a_i}{x_i}} )}^2}}}{{\sum\limits_{i = 1}^n {{{({x_i}{\rm{ - }}\bar x)}^2}} }}\text{,}$
|
(25) |
其检验步骤如下:
①将数据按数值大小重新排列,使
②计算上式分母;
③计算α值;
④计算检验统计量W;
⑤若W值小于判断界限值Wα,按显著性水平α舍弃正态性假设;若W>Wα,接受正态性假设。
利用origin8.0程序直接进行W检验计算,若W>Wα,则服从正态分布。
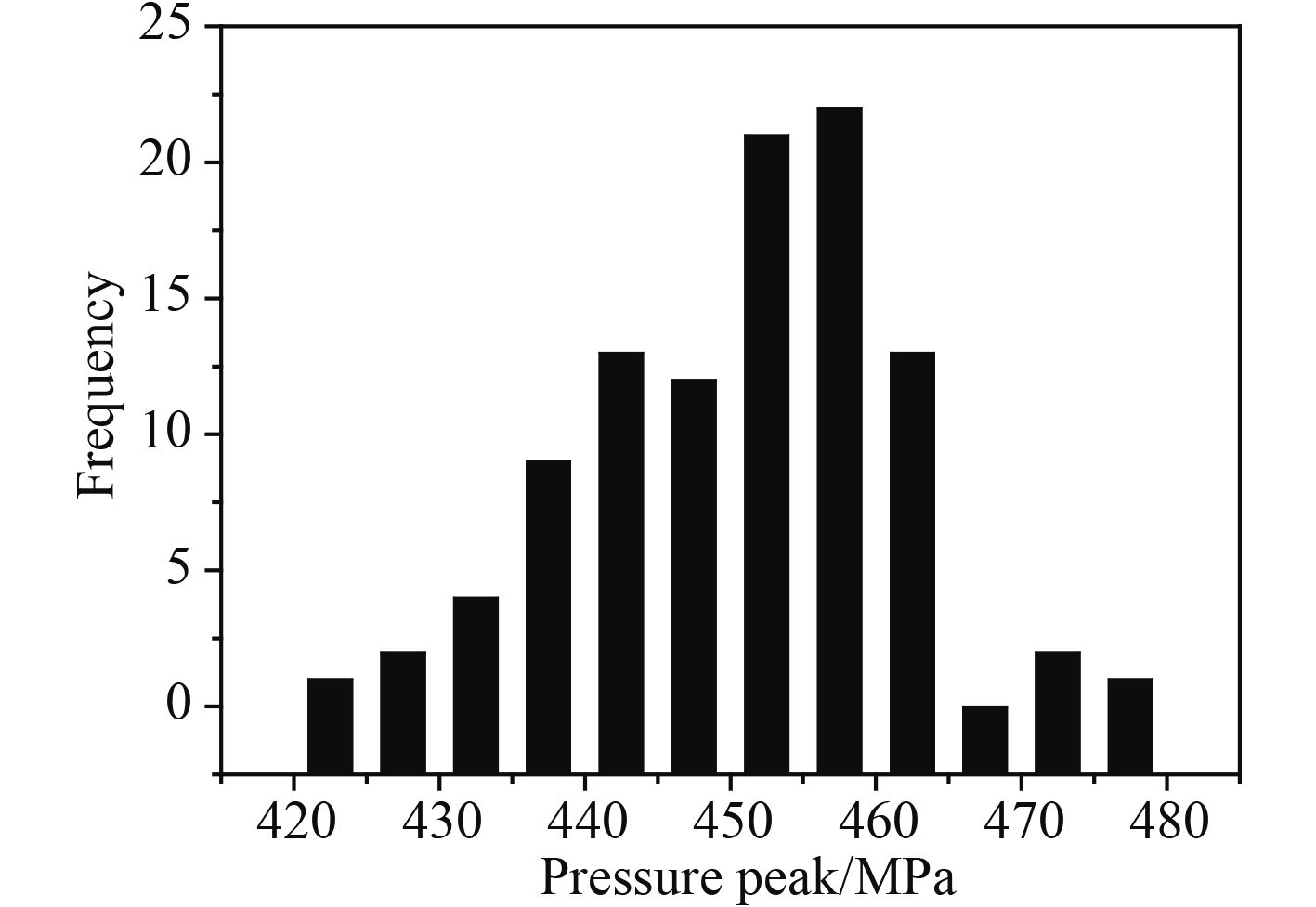
2.2.4.2 峰值压力概率密度统计对100组数据统计分析,选取爆距为0.1 m处的压力峰值进行频数统计,如图5所示。由于频数直方图的形状类似正态分布,假设0.1 m处冲击波峰值压力服从正态分布,则均值和标准差的估计值为:
|
$\mu = 450,\;\;\sigma = 10.15\text{,}$
|
拟合概率密度函数为:
|
$f = \frac{1}{{\sqrt {2\pi } \times 450}}{e^{ - \frac{{{{(x - 450)}^2}}}{{2 \times {{(10.15)}^2}}}}}\text{。}$
|
利用origin8.0程序直接进行W检验计算可知,W=0.982 0。对于n=50,显著性水平α=0.05时,W的Wα临界值=0.947。W>Wα,服从正态分布。概率密度曲线如图6所示。
|
图 5 频数直方图 Fig. 5 The statistic plot on columns of peak pressure |

|
图 6 冲击波峰值压力的概率密度曲线 Fig. 6 Probability density curve of peak pressure |
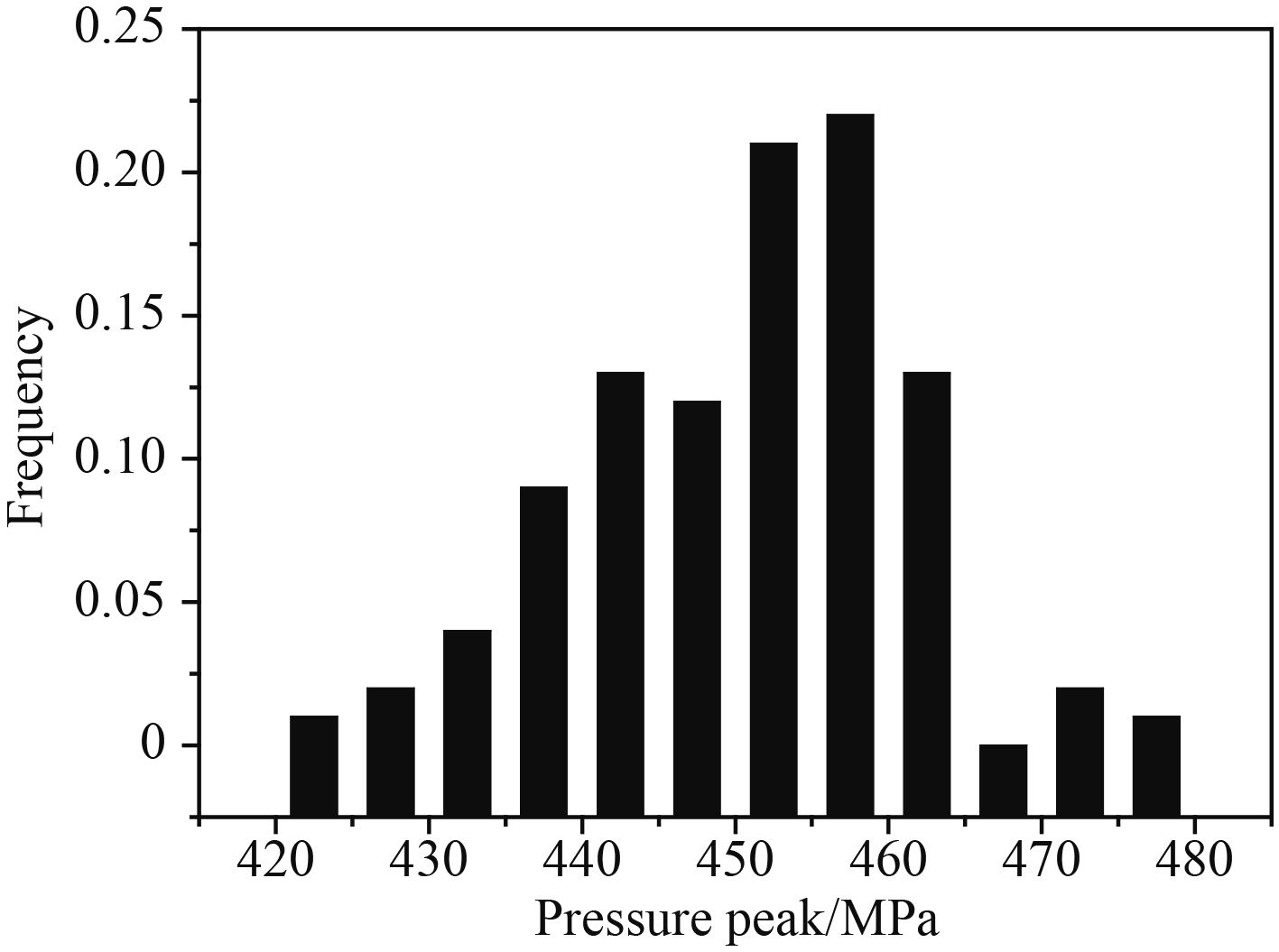
对0.002 48 ms冲击波压力峰值进行频数统计,如图7所示。由于频数直方图的形状类似正态分布,假设0.024 8 ms冲击波峰值压力服从正态分布,则均值和标准差的估计值为:
|
$\mu = 421,\;\;\sigma = 12.41$
|
拟合概率密度函数为:
|
$f = \frac{1}{{\sqrt {2\pi } \times 421}}{e^{ - \frac{{{{(x - 421)}^2}}}{{2 \times {{(12.41)}^2}}}}}\text{,}$
|
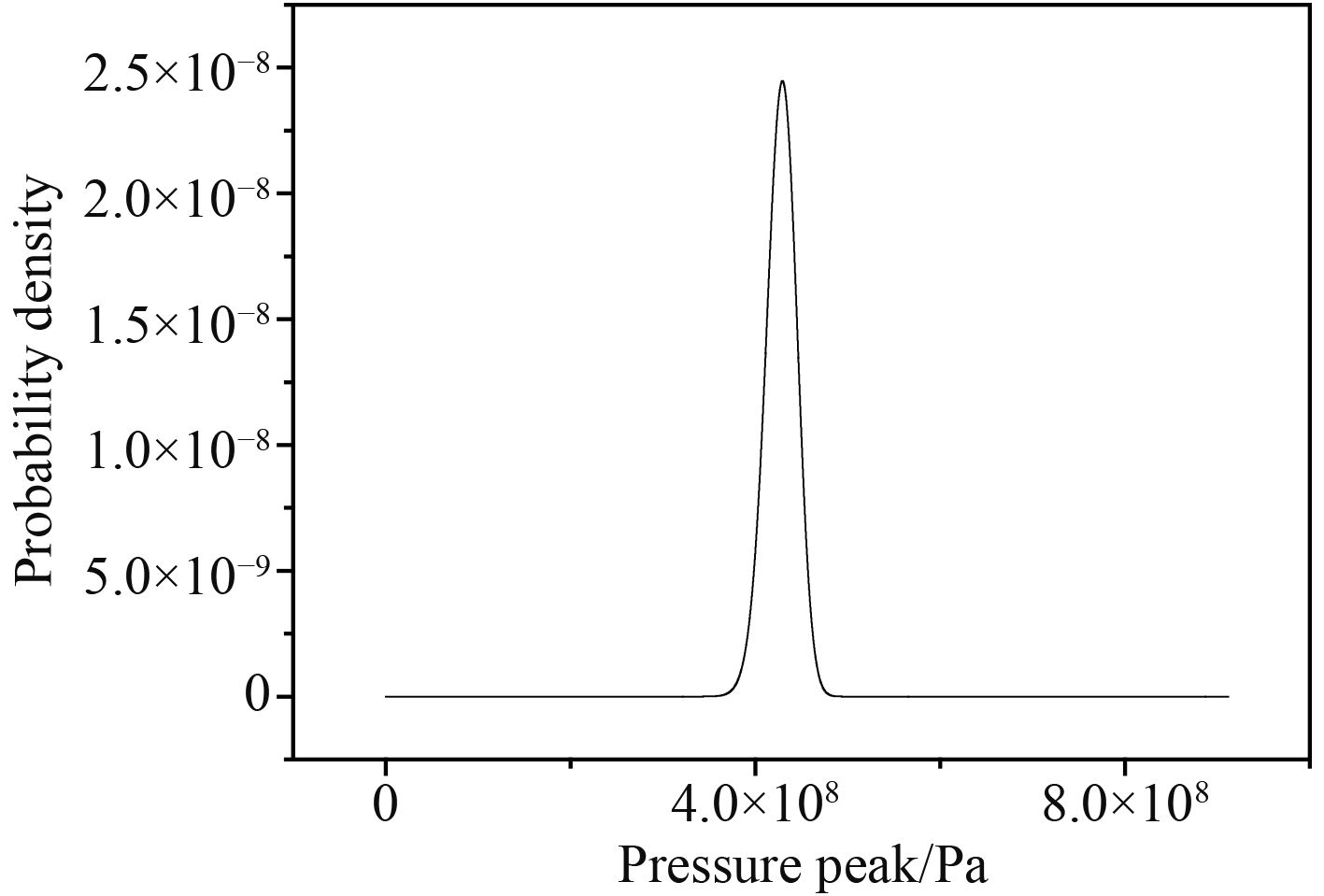
利用origin8.0程序直接进行W检验计算可知,W=0.972 5。对于n=50,显著性水平α=0.05时,W的Wα临界值=0.947。W>Wα,服从正态分布。冲击波峰值的概率密度曲线如图8所示。
|
图 7 0.002 48 ms冲击波峰值压力频数直方图 Fig. 7 Statistic plot on columns of peak pressure at 0.002 48 ms |
|
图 8 0.002 48 ms冲击波峰值压力的概率密度曲线 Fig. 8 Probability density curve of peak pressure at 0.002 48 ms |
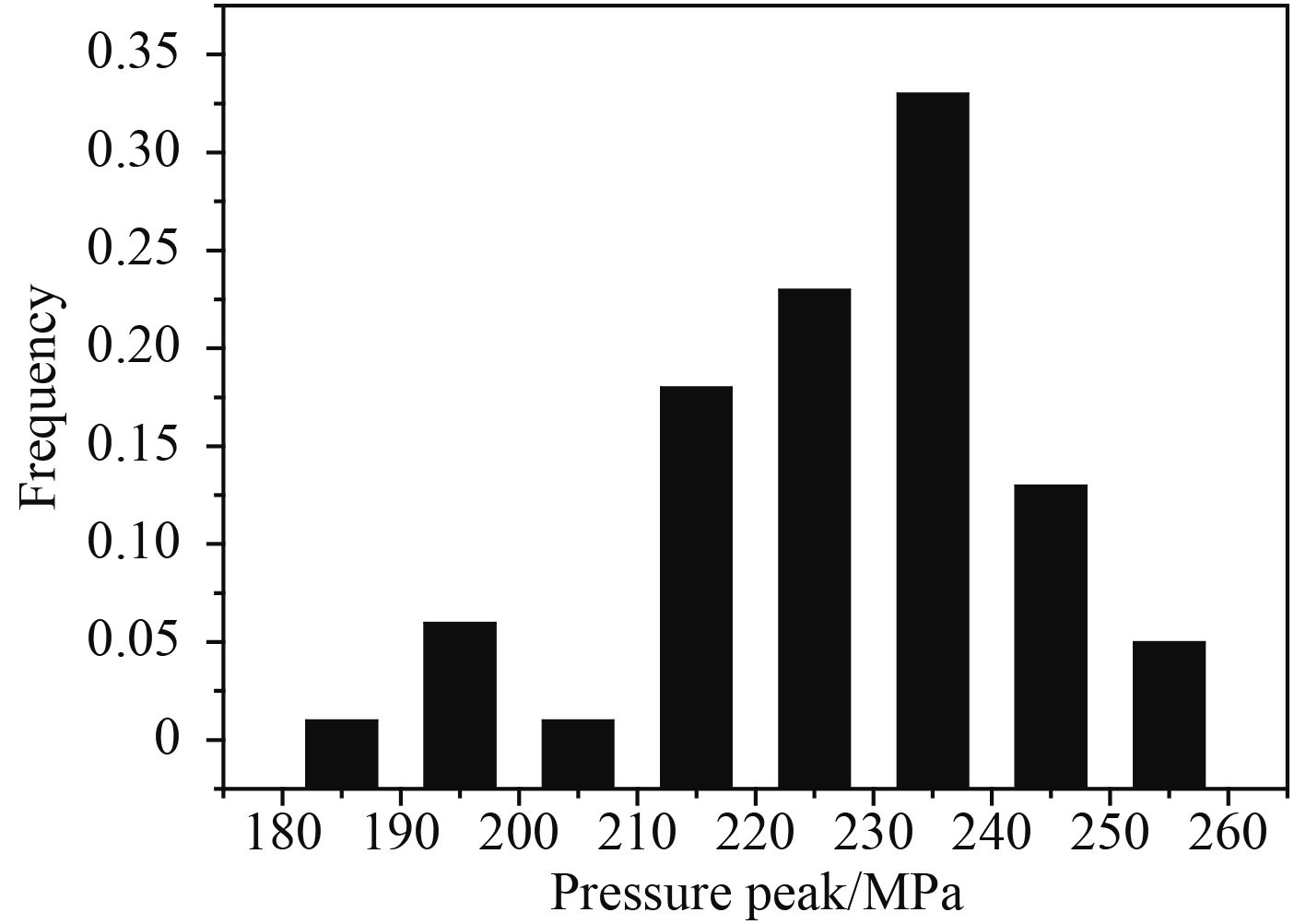
对0.007 47 ms冲击波压力峰值进行频数统计,如图9所示。利用origin8.0程序直接进行W检验计算可知,W=0.972 5。对于n=50,显著性水平α=0.05时,W的Wα临界值=0.947。W<Wα,不服从正态分布。利用最大熵法求解冲击波峰值的概率密度曲线如图10所示。
|
图 9 0.007 47 ms冲击波峰值压力频数直方图 Fig. 9 Statistic plot on columns of peak pressure at 0.007 47 ms |

|
图 10 0.007 47 ms冲击波峰值压力的概率密度曲线 Fig. 10 Probability density curve of peak pressure at 0.007 47 ms |
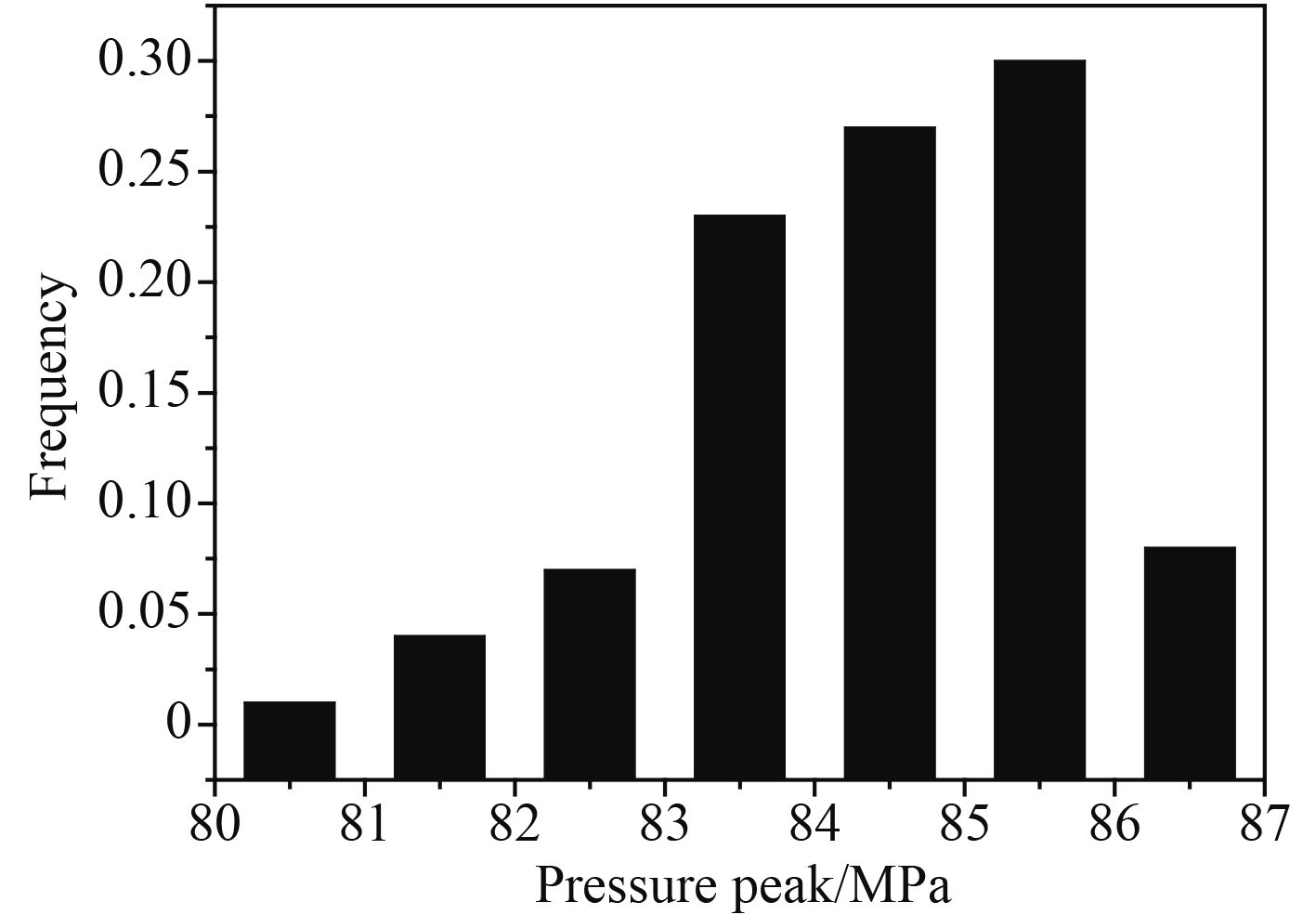
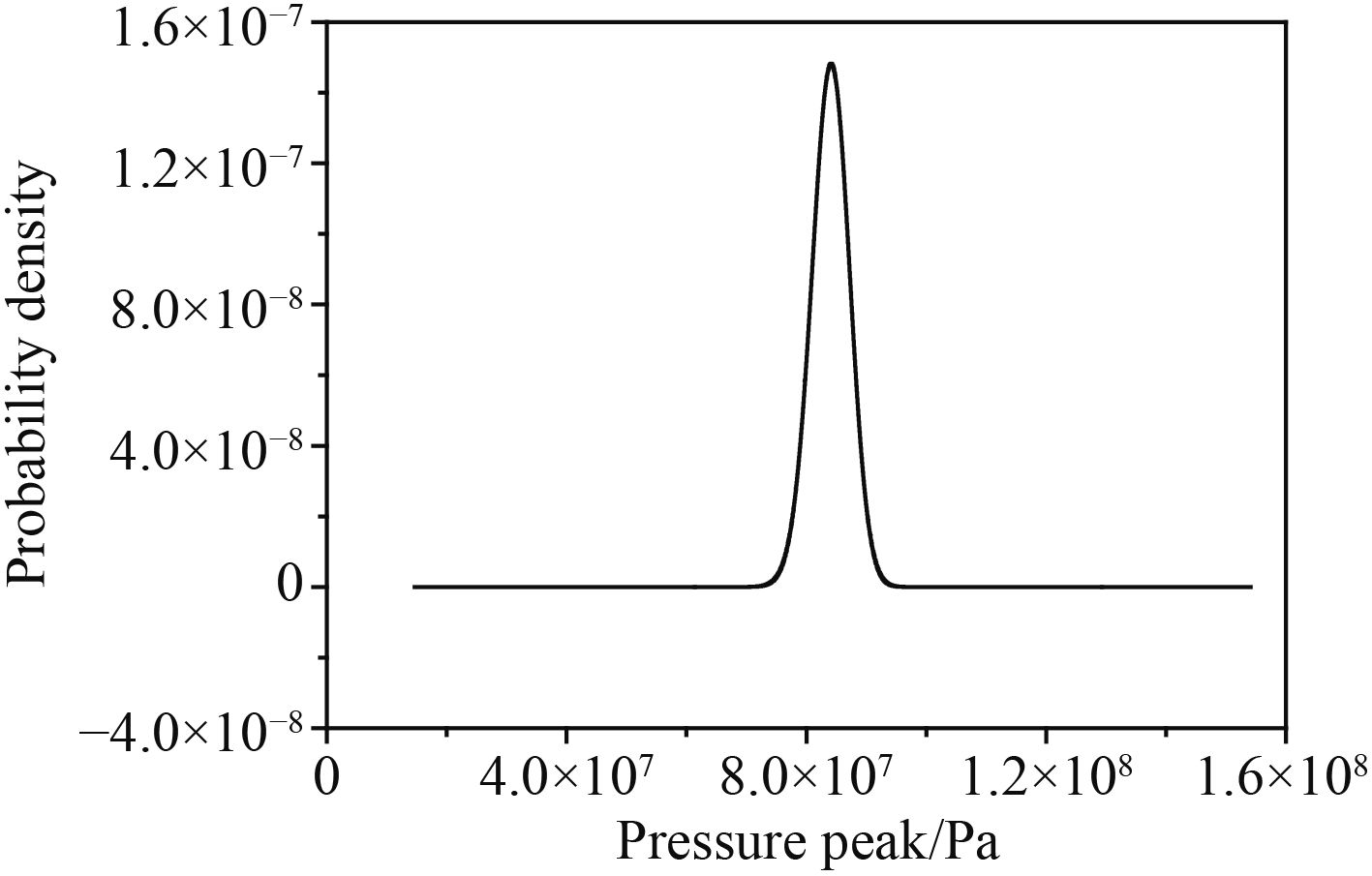
选取0.125 ms的压力峰值进行频数统计,如图11所示。利用origin8.0程序直接进行W检验计算可知,W=0.912 0。对于n=50,显著性水平α=0.05时,W的Wα临界值=0.947。W<Wα,不服从正态分布。利用最大熵法求解冲击波峰值的概率密度曲线如图12所示。
|
图 11 0.125 ms冲击波峰值压力频数直方图 Fig. 11 Statistic plot on columns of peak pressure at 0.125 ms |
|
图 12 0.125 ms冲击波峰值压力的概率密度曲线 Fig. 12 Probability density curve of peak pressure at 0.125 ms |
采用蒙特卡罗和有限元相结合的方法,对水下爆炸载荷的统计规律进行研究,得出如下结论:
1)水(传播介质)的密度影响了冲击波压力峰值,水(传播介质)的密度越大冲击波峰值压力也相应增大。
2)建立基于较少数量的样本数据得到水下爆炸载荷的随机信息的样本拟合法。给出了随机变量正态分布类型的检验方法以及利用最大熵法拟合非正态分布随机变量概率密度函数的方法。最大熵法可较好地拟合爆炸载荷的随机数理统计模型。
3)本文方法能够对较少数量的样本进行拟合的基础上,充分利用随机变量的具体信息,采用最大熵法拟合水下爆炸载荷的概率密度,方法简便,避免了成本较高的水下爆炸试验。
| [1] | WANG Z Y, LIANG X, FALLAH A S. A novel efficient method to evaluate the dynamic response of laminated plates subjected to underwater shock[J]. Journal of Sound and Vibration, 2013, 332 (21): 5618–5634. DOI: 10.1016/j.jsv.2013.05.028 |
| [2] |
姚熊亮, 郭君, 曹宇. 在水下爆炸冲击波作用下的新型冲击因子[J]. 中国造船, 2008, 49 (2): 52–60.
YAO Xiongliang, GUO Jun, CAO Yu. A New Impulsive Factors on the Underwater Shock Load[J]. Shipbuilding of China, 2008, 49 (2): 52–60. |
| [3] | ZONG Z, ZHAO Y J, LI H T. A numerical study of whole ship structural damage resulting from close-in underwater explosion shock[J]. Marine Structures, 2013, 31 : 24–43. DOI: 10.1016/j.marstruc.2013.01.004 |
| [4] | CHEN Y, CHEN F, DU Z P, et al. Protective effect of polymer coating on the circular steel plate response to near-field underwater explosions[J]. Marine Structures, 2015, 40 : 247–266. DOI: 10.1016/j.marstruc.2014.11.005 |
| [5] | EAMON C, BAYLOT J T, O'DANIEL J L. Modeling of concrete masonry walls subjected to explosive loads[J]. Journal of Engineering Mechanics, 2004, 130 (9): 1098–1106. DOI: 10.1061/(ASCE)0733-9399(2004)130:9(1098) |
| [6] | 库尔. 水下爆炸[M]. 北京: 国防工业出版社. 1960. |
| [7] | 陈虬, 刘先斌. 随机有限元法及其工程应用[M]. 成都: 西南交通大学出版社, 1993. |
| [8] | 何水清, 王善. 结构可靠性分析与设计(第一版)[M]. 北京: 国防工业出版社, 1993. |
| [9] | 肖刚, 李天柁. 系统可靠性分析中的蒙特卡罗方法(第二版)[M]. 北京: 科学出版社, 2003. |
 2017, Vol. 39
2017, Vol. 39
