虚拟现实(Virtual Reality,VR)技术是一种可以创建和体验虚拟世界的计算机仿真系统,它利用计算机生成一种模拟环境,是一种多源信息融合的交互式的三维动态视景和实体行为的系统仿真,并使用户沉浸到该环境中。近年来VR软件硬件技术得到了长足的发展,消费级的VR可穿戴设备也已经问世。如Oculus Rift DK2、索尼Project Morpheus、三星Gear VR等都是目前较好的虚拟现实装置。2016年2月教育部正式批准了100个国家级虚拟仿真实验教学中心的建设。作者认为此举意义非凡,不但是从国家层面对VR技术发展趋势的肯定,同时必将大大推进VR技术在教育及其他相关领域的大发展。
与此同时,2016年03月05日德意志银行发布了VR发展报告称2020年VR市场规模将达70亿美元,认为虚拟现实如2007年的智能手机,一切都在有条不紊地进行着。报告还指出,随着大众的需求远超预期,虚拟现实显得越发真实,尽管这项技术会进一步占据市场,但挑战依然存在,而包括Facebook、谷歌在内的科技巨头都明确表示将继续探索。德意志银行最后再次强调,进一步市场化的关键并不是硬件,而是内容。其中最重要的是,创建沉浸式的内容需要合适的故事情节,而这正是目前的一大软肋。
该报告从一方面肯定了VR大发展的时代即将到来,强调了VR的核心在于内容,而不是硬件设备,同时也不否认VR技术在进入人们的日常生活还有很长的一段路要走。这其中,VR技术中物理真实感的严重不足就是制约VR发展的关键因素之一。在创建高质量VR内容的时候,除了高沉浸感之外,人们还需要考虑场景中的物理真实感。目前国内外众多的学者就物理真实感及相关课题展开了广泛而深入的研究。如William Mell[1]建立了基于N-S方程和燃烧控制方程的草场火传播的数学模型,该模型考虑了风、火源宽度等因素对火场扩散的影响,并通过实验对进行了验证模型。柳有权[2]采用GPU加速策略,对带有复杂边界的流体进行实时三维模拟,该算法对于实时流体模拟具有重要的意义。王长波[3]针对自由表面流体的模拟,提出一种基于Lattice Boltzmann(LBM)的高效建模和绘制的方法。其基于浅水方程的LBM模型进行流体建模及表面高度场计算,并提出一种基于Marching Cubes和自由表面算法结合的方法来抽取流体的表面,随后采用考虑移动障碍物的外力叠加机制和自适应加密算法来进行流体交互及表面的网格重构。最后采用硬件加速技术实现了不同自由表面流体的绘制,如溪流、水池浅水流、洪水水淹等真实感效果。王顺利[4]针对以往舰首浪三维可视化中仅从实际观察出发建立动态模型,不能反映舰首浪物理运动规律的问题,提出一种基于物理模型的舰首浪三维可视化方法。该方法将舰首浪物理模型应用到三维可视化中,采用边界元方法计算得到舰首浪外形数据,利用粒子系统技术建立了三维动态模型。JIANG[5]采用质点方法对流体和固体的模拟。采用MPM(Material Point Method)方法 建立固体的变形模型,并针对热传导,固体融化和凝固过程进行模拟,取得了较好的可视化效果。
从已有的研究中可看出,虚拟现实技术的物理真实感一直都是一项具有挑战性的课题。
通过分析不难发现,影响物理真实感的因素主要包括:物理模型近似程度,数值计算方法的精度,数值计算的效率,硬件的性能等,渲染引擎的效率等。为了获得更加真实的物理真实感,作者从数值计算方法的精度和通用性方面进行了研究。针对PDE模型方程的时间导数项、梯度项、散度项及旋度项等,分别采用相应的数值离散算子。这样,在解算不同PDE 时,可以采用统一的离散算子接口,从而实现PDE解算方法的快速构建,并且其中的离散方法可以根据用户的需要进行扩充和完善。这样可以实现离散算子和求解器的重复利用,可以不必反复测试,大大节省人力物力成本。
本文首先对有限体积方法及其在PDE中的应用进行介绍,然后从典型的偏微分模型方程出发,采用开源计算流体力学库OpenFoam[6],建立针对不同类型PDE的求解器,并进行计算结果的验证。然后采用PISO算法,将该FVM离散方法应用于计算流体力学NS方程组,浅水方程组的计算中,设计相应的求解器,并对计算结果进行验证。
1 有限体积方法(FVM)和PDE的数值计算中的应用 1.1 PDE方程的分类偏微分方程的求解方法取决于偏微分方程的类型。因此,不同类型的PDE对应着不同的数值解法,求解时所需要的初值条件和边值条件是不尽相同的。
以一个2阶PDE为例:
| $\begin{split}{a_{11}}\frac{{{\partial ^2}\varPhi }}{{\partial {x^2}}} + & 2{a_{12}}\frac{{{\partial ^2}\varPhi }}{{\partial x\partial y}} + {a_{22}}\frac{{{\partial ^2}\varPhi }}{{\partial {y^2}}} + \\& {a_1}\frac{{\partial \varPhi }}{{\partial x}} + {b_1}\frac{{\partial \varPhi }}{{\partial y}} + c\varPhi + f = 0\text{,}\end{split}$ | (1) |
式中:
引入记号
| $\varDelta = - \left| {\begin{array}{*{20}{c}}{{a_{11}}}&{{a_{12}}}\\{{a_{21}}}&{{a_{22}}}\end{array}} \right| = a_{12}^2 - {a_{11}}{a_{12}}\text{,}$ | (2) |
1)若在点
2)若在点
3)若在点
很多物理问题通常都给出以下3种形式的边界条件的一种:
1)Dirichlet边界条件也称为第一类边界条件问题。在这种边界条件下,已知边界条件上变量的值是常数。这就允许进行简单代替来给边界定值。比如当给定边界的为恒定入流条件,这时就可以设置入流边界的速度为常数U,即
2)Neumann边界条件也称为第二类边界条件问题。这种边界条件下,边界给定的导数值是已知的,这时就给出了一个附加的方程,可以用这个方程得到边界上的值。如当给定的条件为出口压力恒定条件,这是压力的导数为0,即
3)Bobin边界条件也称为第三类边界问题也称为混合边界值问题。在边界
| $(\alpha \frac{{\partial u}}{{\partial n}} + \beta u){\left. \begin{array}{l}\\\end{array} \right|_\varGamma } = g\text{。}$ | (3) |
在进行数值计算时,必须根据特定问题进行边界条件或初始条件的指定,然后才能开始数值计算。否则可能无法得到准确的结果。
1.3 有限体积法目前数值离散方法主要有:有限差分方法,有限元方法和有限体积法。每种方法都会把一个简单的PDE方程转换成相应的数值近似方程。其中有限差分是基于泰勒级数来建立方程的数据库,把变量的导数变为空间和时间上不同点之间的差分方法。
在有限元方法中,PDE所使用的计算域被分割成有限个子域元。假定在每个元上因变量按一种规律变化,而且这种分片拼接的图像来描述和建立变量在整个域上的变化情况。
有限体积方法是当前最流行的在各种CFD软件中使用的数值离散方法。这种方法在某些方面与有限差分相似,但也体现出了从有限元法中吸取的一些特性。
1.4 有限体积法在PDE求解中的应用FVM法使用的规则网格提高了计算效率。近年来为了计算复杂的几何形状,发展了使用不规则网格的FVM。有限体积法结合了FDM和FEM方法的优点,因此在PDE求解中有着广泛的应用。如:Takeshi TSUKAMOTO[7]采用FVM离散方法,基于非规则网格进行VOF(volume fraction of fluid)模拟,提出了一套适合自由液面模拟的算法。F. Hermeline等[8]采用有限体积法对二维麦克斯韦方程进行离散求解,并就算法的稳定性、复杂度与其他离散方法进行了比较。Zhang Ming Liang[9]提出了一种基于非结构四叉树网格模型的有限体积法算法,该算法具有健壮的、准确的并且高效的特性,并成功用该算法对溃坝问题进行模拟。BORIS ANDREIANOV[10]提出了一种收敛的反应-扩散模型的FVM算法。并对该FVM算法解存在性和收敛性进行了理论分析,并对解的存在性进行了证明。Hrvoje Jasak[6]通过Volume Of Fluid(VOF)方法获得自由液面进行计算,进而采用有限体积法对船体阻力进行了计算
2 典型PDE的数值计算及验证选取具有代表性的抛物线型PDE进行解算和验证,其余类型方程求解器的设计方法类似。
算例验证与分析:
对于热扩散方程
| $\frac{{\partial T}}{{\partial t}} = \alpha (\frac{{{\partial ^2}T}}{{\partial {x^2}}} + \frac{{{\partial ^2}T}}{{\partial {y^2}}})\text{,}$ | (4) |
式中热扩散系数
定义域:
边界条件:当
初始条件:t=0时,
| ${\rm ddt}(T) = \alpha *{\rm laplacian}(T)\text{。}$ | (5) |
式中:ddt为对时间的一次导数项;laplacian 为拉普拉斯算子。时间步长取
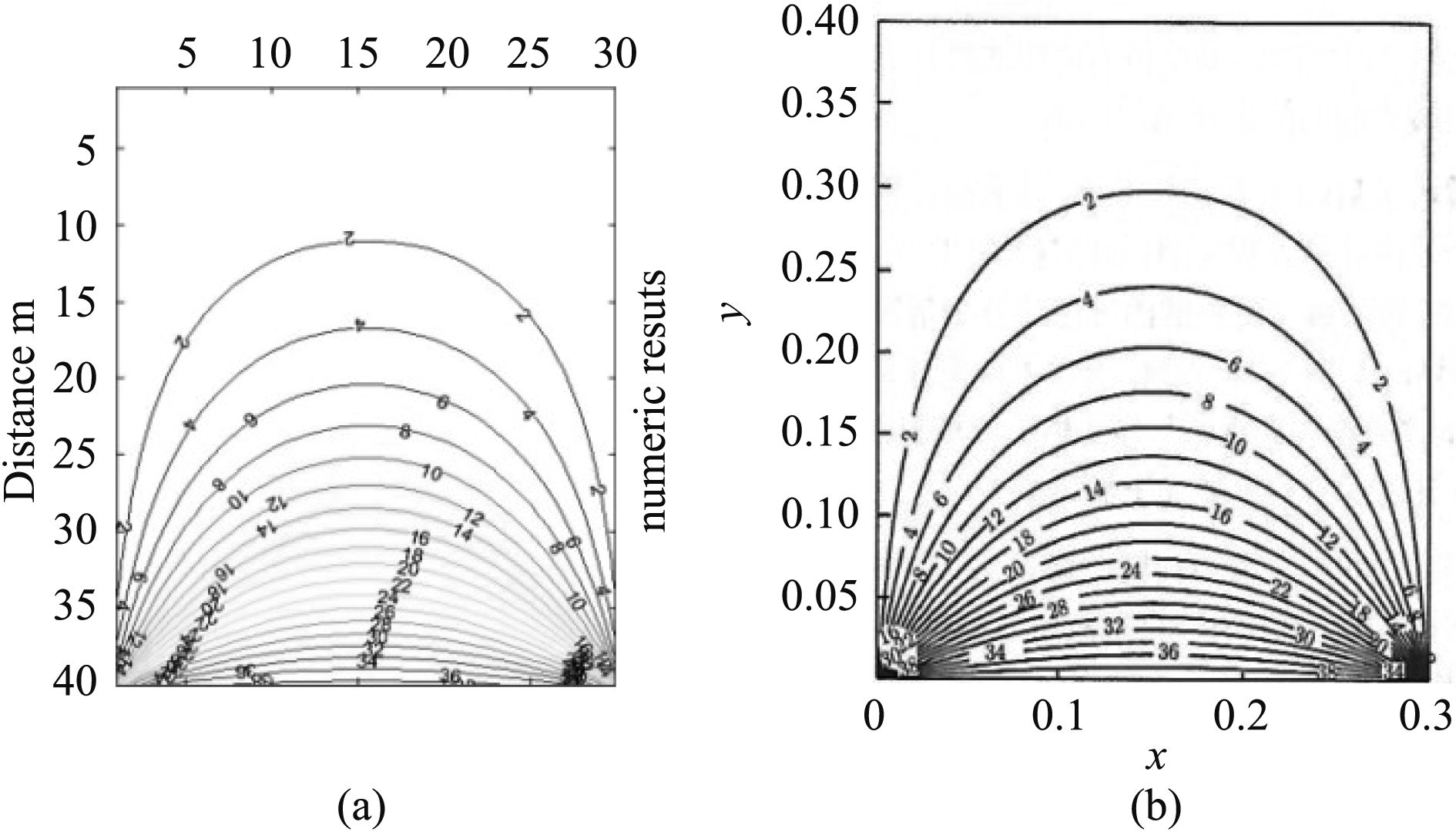
|
图 1 数值计算结果与解析解对比 Fig. 1 Comparison between numerical results and analytical solutions |
为了对不可压缩流体求解器进行验证,文章选用流体力学的典型问题方腔驱动问题和溃坝问题进行验证。通过采用PISO算法实现流体力学运动控制方程的求解。
3.1 PISO算法介绍PISO表示有分裂算子的压力隐式算法,由Issa于1986年提出,它最初作为对非定常可压缩流提出的一种非迭代的压力-速度计算方法,已经成功应用于求解定常状态的迭代问题。PISO包含1个预测过程和2个校正过程,可以把它看作是Simple的扩展,即对Simple算法再多一个修正过程以达到改善他的目的。PISO算法对压力修正方程进行2次求解,为了计算压力修正方程的源项,需增加存储量。
3.2 NS方程数值计算验证方腔驱动流的数值模拟在实际工程中有着广泛的应用,很多重要的理论和工程研究都是用此模型来分析的,尤其在气象、航运、机械、采矿等领域应用更为广泛。图2所示,腔体的长度和宽度都为单位长度,网格划分为100×100,上边界为固定速度边界,其余3面都为固壁边界。
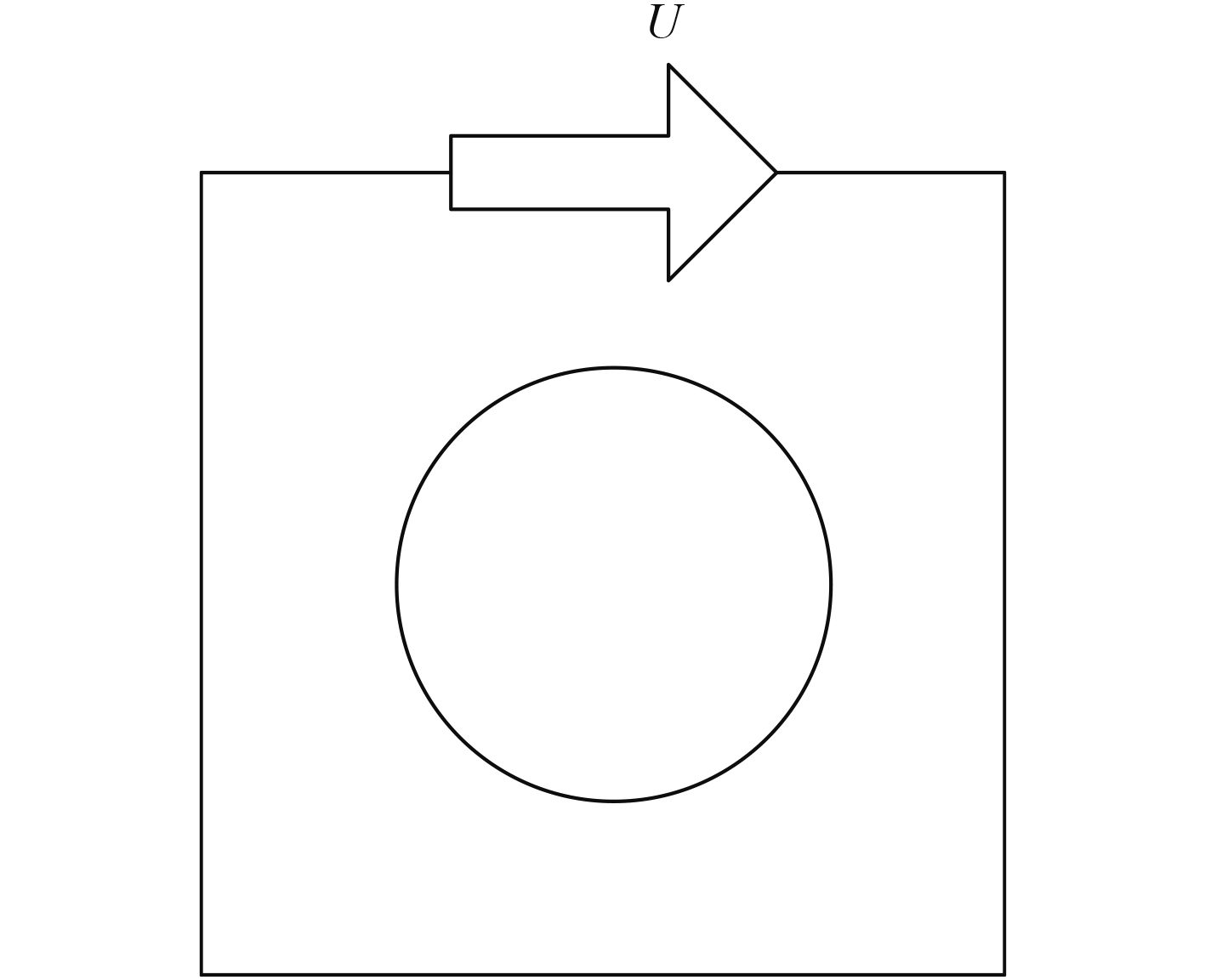
|
图 2 方腔驱动模型设置 Fig. 2 Cavity drive model setup |
对于不可压缩流体有控制方程:
| $\left. \begin{aligned}\frac{{\partial \rho }}{{\partial t}} + \nabla \cdot (\rho V) = 0\\\frac{{\partial \rho u}}{{\partial t}} \!+\! \nabla \cdot (\rho uV)\! =\! \! -\! \frac{{\partial p}}{{\partial x}} + \frac{{\partial {\tau _{xx}}}}{{\partial x}} \!+\! \frac{{\partial {\tau _{yx}}}}{{\partial y}} \!+\! \frac{{\partial {\tau _{zx}}}}{{\partial z}} \!+\! \rho {f_x}\\\frac{{\partial \rho v}}{{\partial t}} \!+\! \nabla \cdot (\rho vV)\! =\! \! -\! \frac{{\partial p}}{{\partial y}} \!+\! \frac{{\partial {\tau _{xy}}}}{{\partial x}} \!+\! \frac{{\partial {\tau _{yy}}}}{{\partial y}} \!+\! \frac{{\partial {\tau _{xy}}}}{{\partial z}} \!+\! \rho {f_y}\\\frac{{\partial \rho w}}{{\partial t}} \!+\! \nabla \cdot (\rho wV)\! =\! \! -\! \frac{{\partial p}}{{\partial z}} \!+\! \frac{{\partial {\tau _{xz}}}}{{\partial x}} \!+\! \frac{{\partial {\tau _{yz}}}}{{\partial y}} \!+\! \frac{{\partial {\tau _{zx}}}}{{\partial z}} \!+\! \rho {f_z}\end{aligned} \right\}\text{。}$ | (6) |
式中:t为时间;f为外力;p为流体压强;
针对该控制方程设计了专门的求解器,其中非稳态项采用隐式Crank-Nicolson格式,梯度项、散度项采用高斯离散格式。
求解器形式如下式所示:
| ${\rm ddt}(U) + div(phi,U) - {\rm laplacian}(nu,U) = - grad(p)\text{。}$ | (7) |
式中:div为散度,grad为梯度。分别模拟量雷诺数为400,800,1 000时的流动。如图3所示为雷诺数为1 000时中轴线上速度分布,可以看出,该计算结果与K Poochinapan[11]的计算结果高度吻合。
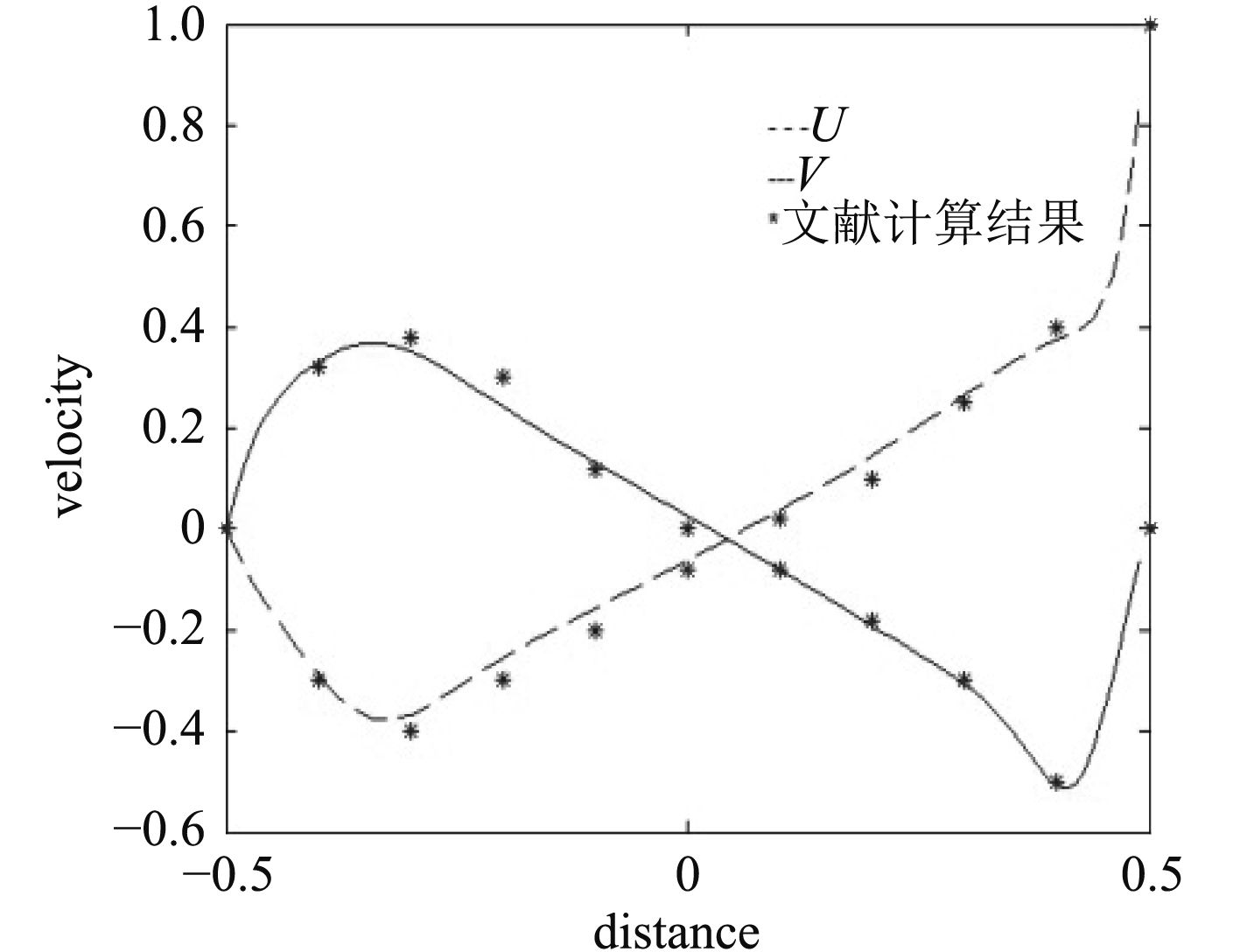
|
图 3 雷诺数为1 000计算结果对比 Fig. 3 Comparison of calculation results at reynolds numberr 1 000 |
浅水方程是水力学中的典型问题,有浅水波运动控制方程:
| $\left. \begin{aligned}\frac{{\partial u}}{{\partial t}} + u\frac{{\partial u}}{{\partial x}} + v\frac{{\partial u}}{{\partial y}} + w\frac{{\partial u}}{{\partial z}} - fv = - \frac{1}{\rho }\frac{{\partial p}}{{\partial x}} + \frac{1}{\rho }\frac{{\partial {\tau _x}}}{{\partial z}}\\\frac{{\partial v}}{{\partial t}} + u\frac{{\partial v}}{{\partial x}} + v\frac{{\partial v}}{{\partial y}} + w\frac{{\partial v}}{{\partial z}} + fu = - \frac{1}{\rho }\frac{{\partial p}}{{\partial y}} + \frac{1}{\rho }\frac{{\partial {\tau _y}}}{{\partial z}}\\0 = - \frac{1}{\rho }\frac{{\partial p}}{{\partial z}} - g\end{aligned} \right\}\text{。}$ | (8) |
式中:t为时间;
相应的求解器如下式:
| ${\rm ddt}(hU) + div(phi,hU) = - grad(h + {h_0}) + src(f)\text{。}$ | (9) |
式中:hU为速度;div为散度;grad为梯度;h0为水深;h为水位;src为源项。
边界条件:初始条件和边界条件是求解水体水流和水质方程所必须的条件。一般对于恒定流的计算,初始时刻的变量值可以定义为0,通常称为冷启动,它不会影响最终的计算结果。对于非恒定流的计算,也可以给定冷启动条件,经过一段时间的计算和调节,冷启动带来的影响可以被消除,计算也能满足精度要求[9]。
1)理想溃坝模拟
一般来说,溃坝洪水波的研究可分为数学模型、物理模型和两者结合等3种类型[9]。由于数值技术的优越性,操作简单,仅需给定地形条件、边界条件就能复演水波运动的过程,所以受到越来越多的关注。同时也由于强降水、地震等自然灾害,战争等因素导致水位的急剧升高,如果水流越过河堤和坝体,会导致堤身破坏形成溃口,引起下游河道的冲刷。溃坝所导致的后果极其严重,如1959年法国的Malpasset拱坝溃决,1975年河南板桥水库土石溃决等,都造成了巨大的生命和财产损失,因此有必要对溃坝问题进行深入细致的研究。
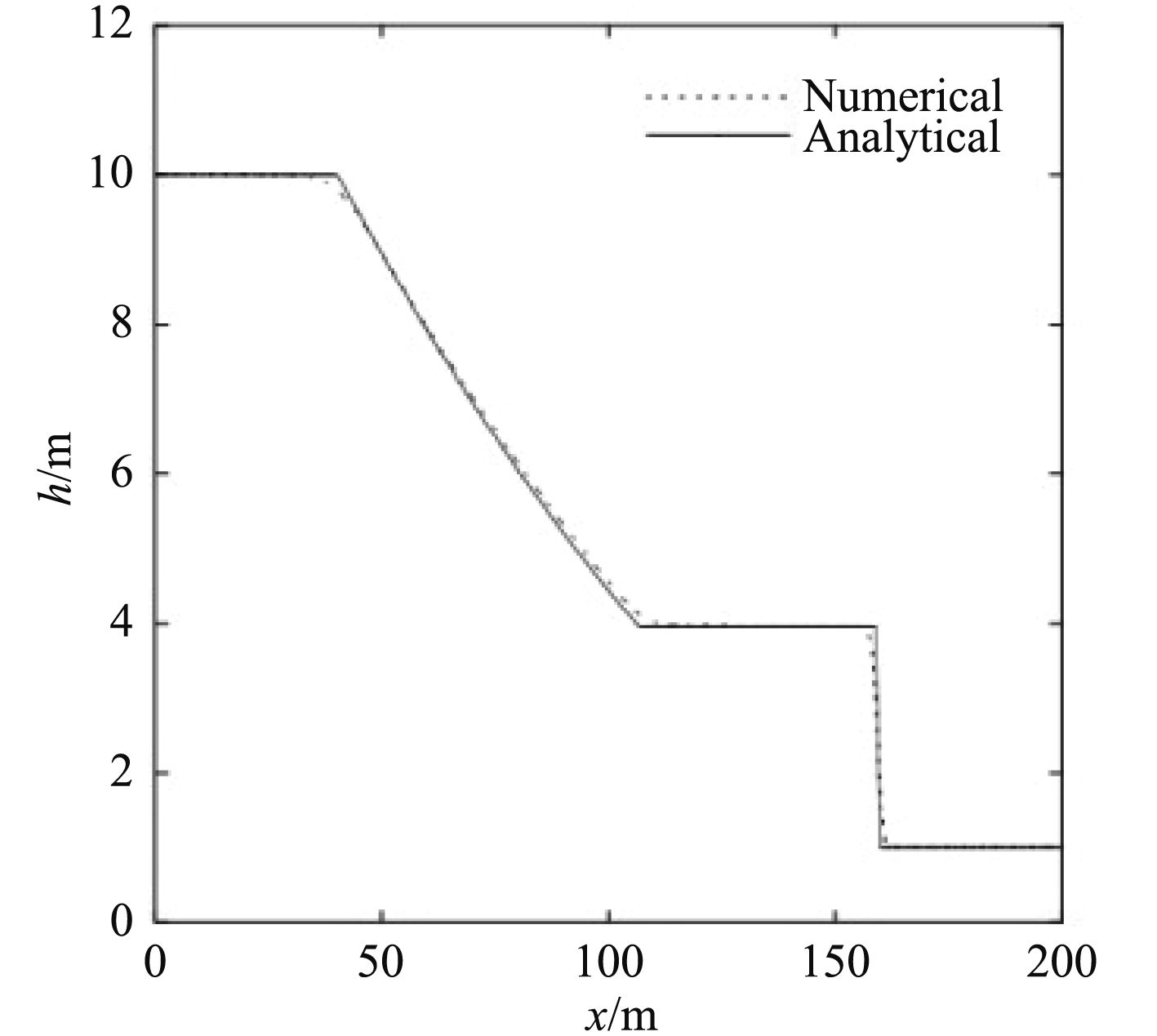
理想溃坝问题是典型的非线性流的例子,经常用来检验数值格式对强间断的捕捉能力,并且具有解析解,便于数值结果的对比。
算例中L=20 m,时间步长0.01 s,计算网格为200个,空间步长0.1 m,取
采用FVM方法在计算域中离散控制方程,在扩散项与源项中采用中心差分,在对流项的离散中还用混合格式。采用交错网格,
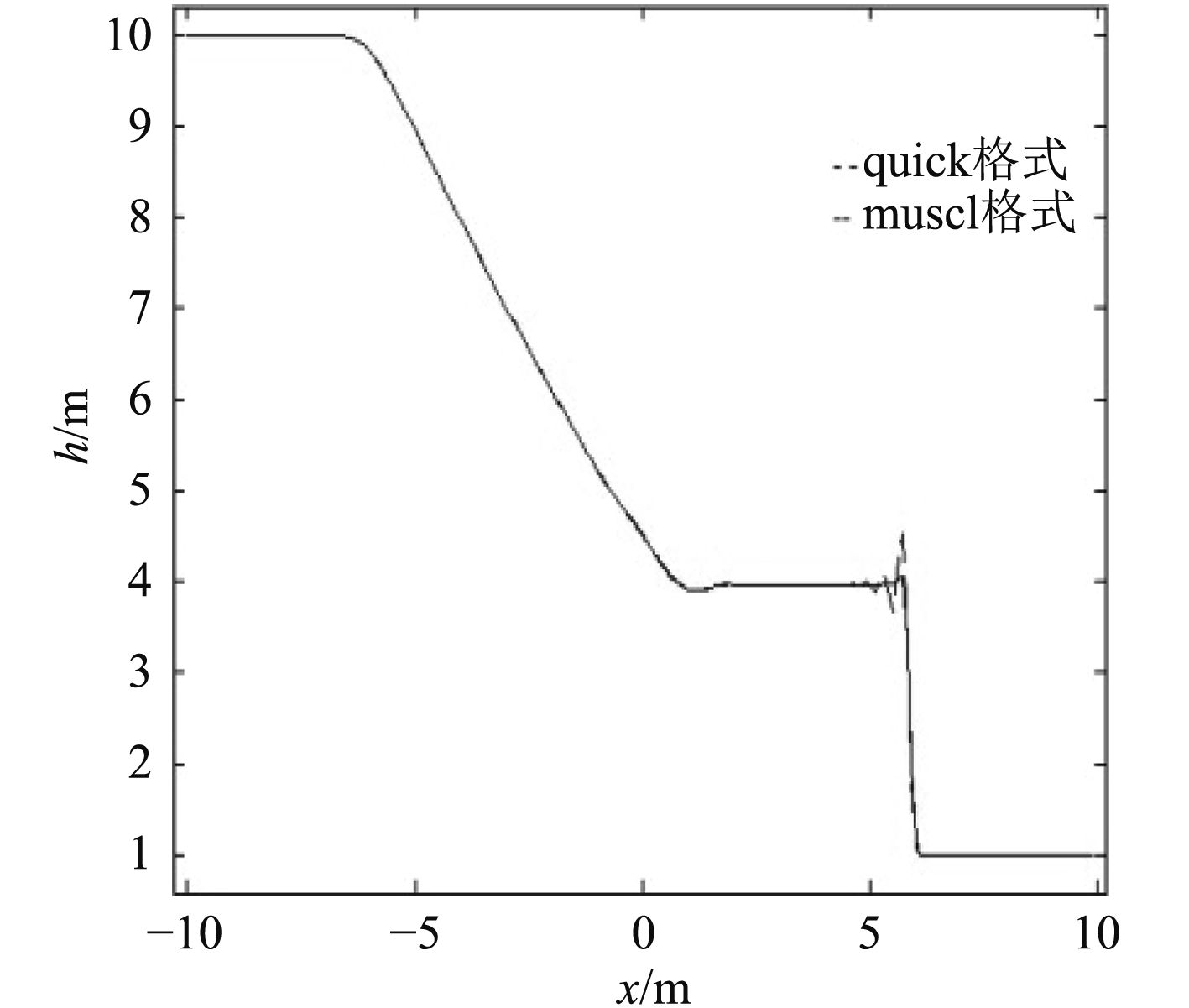
|
图 5 不同数值模式结果 Fig. 5 Results from different numerical scheme |
2)二维部分溃坝数值模拟
目前对天然河流大多采用平面二维数学模型进行模拟,并成功地解决了许多工程问题。平面二维数序模型沿垂向均匀分布考虑,忽略了垂向流速及加速度,水压力按静压分布。
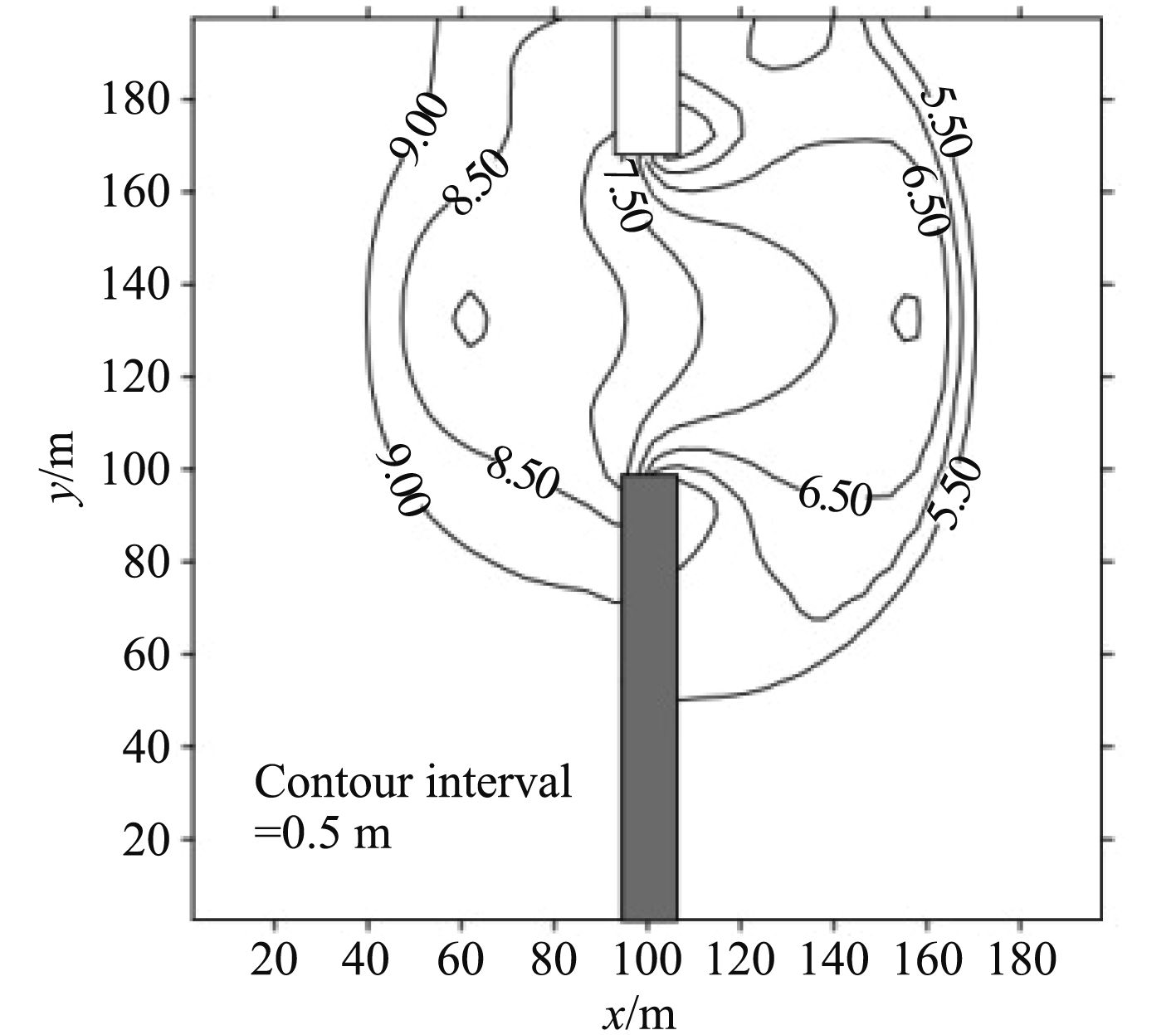
自Fennema和Chaudhry提出二维矩形部分溃坝模型验证数值算法处理激波捕捉的能力以来,许多学者研究了此模型,用来验证各种算法。数值模型的设置如图6所示,计算区域为200×200 m的矩形区域,中间有一挡水坝将区域一分为二,坝宽10 m,初始时刻,上下游水面静止,上游水深为10 m,下游水深为5 m。某一时刻,挡水坝突然开有75 m宽的非对称缺口,坝体瞬间部分溃决,数值计算中,空间步长为5 m,时间步长0.2 s。图7所示为7.2 s时的水面轮廓线。该结果与其他学者(图8)都得到了相近的数值解从中可以看出,该结果具有较高的准确性。
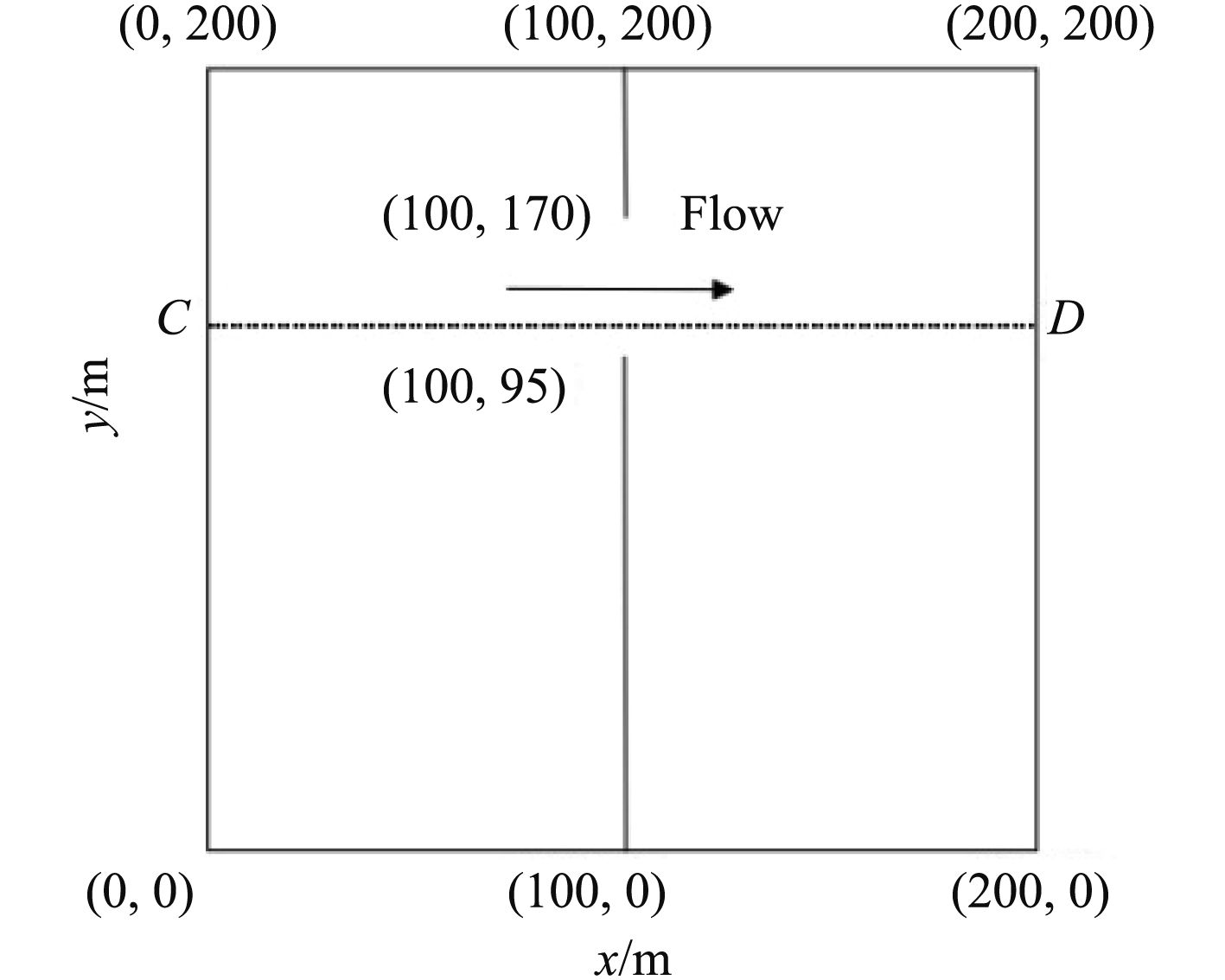
|
图 6 部分溃坝模型设置 Fig. 6 Partial dam-break model setup |
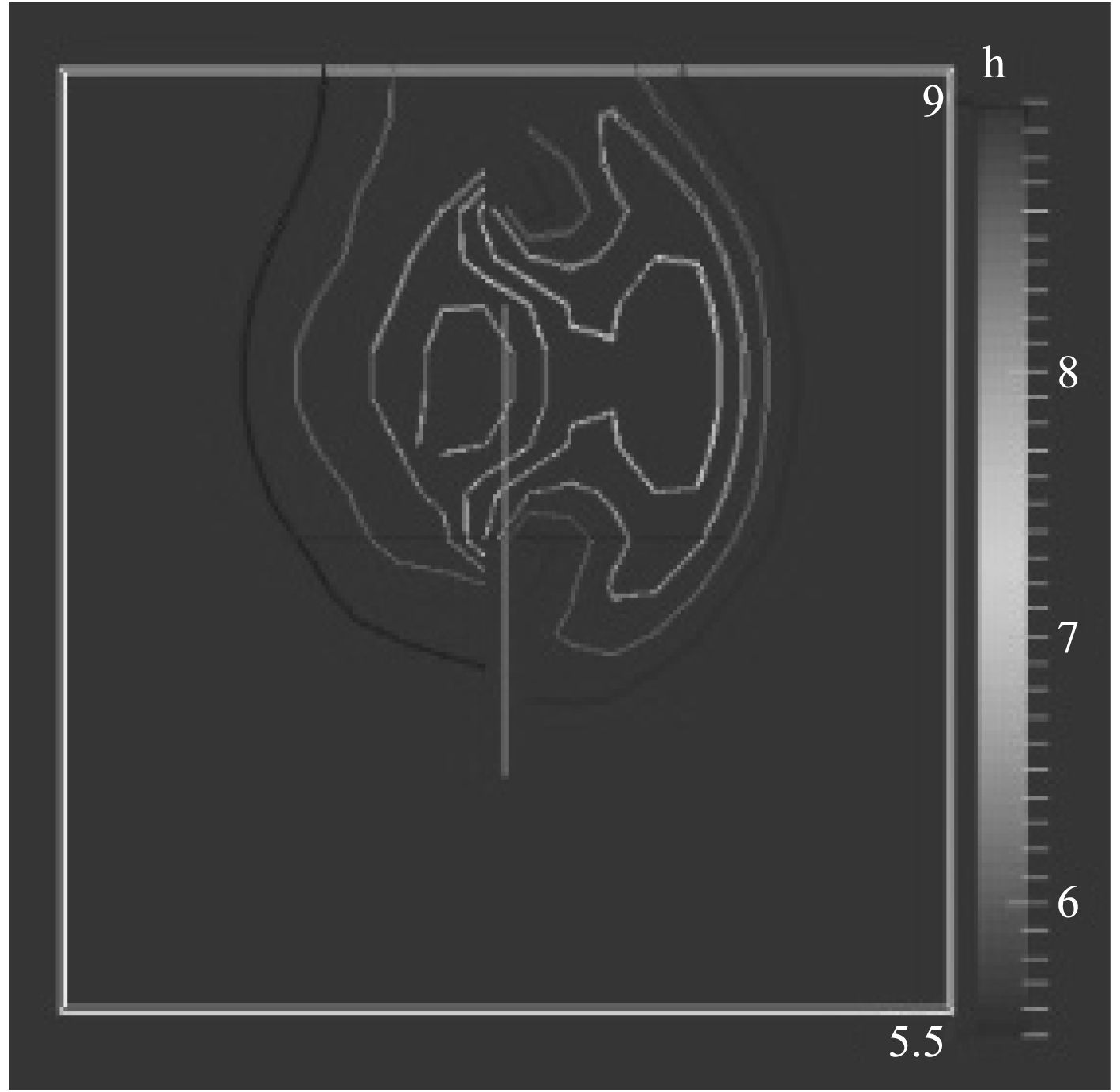
|
图 7 溃坝数值计算结果 Fig. 7 Numerical results of dam-break |
4 结 语
文章从提升虚拟现实真实感的角度出发,介绍了针对复杂PDE数学模型的通用离散数值计算框架,该框架能够被重复利用,并且能够根据用户的需求进行定制。而要提升虚拟场景中的物理真实感,不可避免的要从提升数值解算效率的角度进行研究。文章通过对典型PDE方程的数值计算,模拟了典型的物理模型问题,如抛物线型的热扩散PDE方程,并通过与已有文献的模拟结果和实验结果进行了验证。其次,针对计算流体力学的典型问题,方腔驱动和一维理想溃坝,二维部分理想溃坝问题进行的模拟,并对计算结果进行了验证,结果显示该方法具有较高的可信度。
同时在后续的研究中希望能够将数值计算的结果引入到虚拟现实系统中,将该成果应用于虚拟现实领域系统中,充分发挥出计算机在基于物理数值计算方面的价值。既满足虚拟现实系统的实时性的要求,又具有较高的准确性,更加逼真的再现复杂的物理场景。
| [1] | MELL W, JENKINS M A, GOULD J. A Physics-Based approach to modeling grassland fires[J]. International Journal of Wildland Fire, 2007, 16 (1): 1–22. DOI: 10.1071/WF06002 |
| [2] |
柳有权, 刘学慧, 吴恩华. 基于 GPU 带有复杂边界的三维实时流体模拟[J]. Journal of Software, 2006, 17(3): 568–576.
LIU You-quan, LIU Xue-hui, WU En-hua. Real-time 3D fluid simulation on GPU with complex obstacles[J]. Journal of Software, 2006. 3(17): p. 568–576. |
| [3] |
王长波, 张卓鹏, 张强. 基于LBM的自由表面流体真实感绘制[J]. 计算机辅助设计与图形学学报, 2011, 23(1): 104–110.
WANG Chang-bo, ZHANG Zhuo-peng, ZHANG Qiang. Realistic rendering of free surface fluid based on lattice boltzmann method[J]. Journal of Computer-Aided Design & Computer Graphics, 2011. 1(23): p. 104–110. |
| [4] |
王顺利, 康凤举. 基于物理模型的舰艏浪三维可视化[J]. 计算机工程与应用, 2014, 2014(3): 18–21.
WANG Shun-li, KANG Feng-ju. 3D visualization of bow wave based on physical model[J]. Computer Engineering and Applications, 2014. 3(2014): p. 18–21. |
| [5] | JIANG Chen fan-fu. The material point method for the Physics-Based simulation of solids and fluid[D]. Los Angeles: UNIVERSITY OF CALIFORNIA Los Angeles, 2015: 1–88. |
| [6] | HRVOJE J, VUKO V, DOMINIK C. Rapid free surface simulation for Steady-State hull resistance with FVM using openfoam[C]//30th Symposium on Naval Hydrodynamics. Hobart, Tasmania, Australia, 2014: 1–7. |
| [7] | TSUKAMOTO T, ANZAI K, NIYAMA E. A tracing technique for free surface of fluid flow by FVM method using an irregular grid[J]. Nihon Kikai Gakkai Ronbunshu B Hen/transaction, 1997, 63 (6): 77–82. |
| [8] | HERMELINE F, LAYOUNI S, OMNES P. A finite volume method for the approximation of Maxwell’s equations in two space[J]. Journal of Computational Physics, 2008, 227 (1): 9365–9388. |
| [9] | ZHANG M-l, WM W. A two dimensional hydrodynamic and sediment transport model for dam break based on finite volume method with quadtree grid[J]. Applied Ocean Research, 2011, 33 (4): 297–308. DOI: 10.1016/j.apor.2011.07.004 |
| [10] | BORIS A, MOSTAFA B, RICARDO R. ANALYSIS OF A FINITE VOLUME METHOD FOR A CROSS-DIFFUSION MODEL IN POPULATION DYNAMICS[J]. Mathematical Models & Methods in Applied Sciences, 2011, 21 (2): 307–344. |
| [11] | POOCHINAPAN K. Numerical implementations for 2D Lid-Driven cavity flow in stream function formulation[J]. ISRN Applied Mathematics, 2012, 2012 (4): 1–17. |
 2017, Vol. 39
2017, Vol. 39