分裂阵半波束处理作为经典阵列处理技术,一般用于声呐系统的测向[1]。它是利用共向分裂波束对的相位差来实现精确测向,其定向精度接近于克拉美罗下界,因此在实际声呐系统中得到了广泛应用。Stergios Stergiopoulos等[2]利用分裂阵互谱法提高拖曳线列阵的方位估计性能,并能获得较全阵常规处理更好测向精度,特别是在端射方向。分裂阵半波束不仅可以用于声呐测向,还可以用于声呐的宽带检测。David A. Miles等[3]根据信号和噪声在空间、频域差异特性,采用概率密度函数和累积分布函数对被动宽带分裂阵互相关处理的检测性能进行统计分析。马启明等[4]利用拖线阵的分裂子阵波束输出的相位差降低拖船干扰,提高弱目标信号检测能力。Fumitaka Maeda等[5]根据水下慢速目标与噪声、混响和静止目标的相位差变化特性,将分裂阵半波束处理应用于港口警戒声呐中,实现对低速目标自动检测跟踪。此外,分裂阵半波束处理还可以应用于声呐的窄带检测。文献[6]根据分裂阵半波束相位差设计相位滤波器,对多波束LOFAR谱图中每个波束谱图进行滤波,提高窄带检测中目标方位分辨力,实现水下目标快速自动检测。
上述文献都是分裂阵半波束在线阵中应用。文献[7]将分裂阵半波束应用于主动声呐圆阵处理中,消除主瓣之外的混响和杂波,有效抑制混响,降低了虚警。但是分裂阵半波束处理在圆阵被动宽带检测中报道不多。
圆阵作为一种典型的基阵形式,广泛使用于声呐系统中。由于圆阵的阵元均匀分布在一个圆周上,因此圆阵与线阵相比具有很大优越性。圆阵不仅能够同时提供方位角和俯仰信息,而且能够提供全方位无模糊信息。正因为圆阵这些优点,水面舰艇或潜艇的舰壳声呐中广泛使用圆形基阵声呐。
本文研究分裂阵半波束处理在圆阵中应用,首先分析了圆阵的半波束相位差,将分裂阵半波束应用于圆阵的宽带信号检测中,给出了一种应用圆阵的分裂阵宽带相关检测方法,可以有效地改善目标方位分辨率,提高被动声呐的宽带检测性能。最后给出仿真和试验数据处理结果。
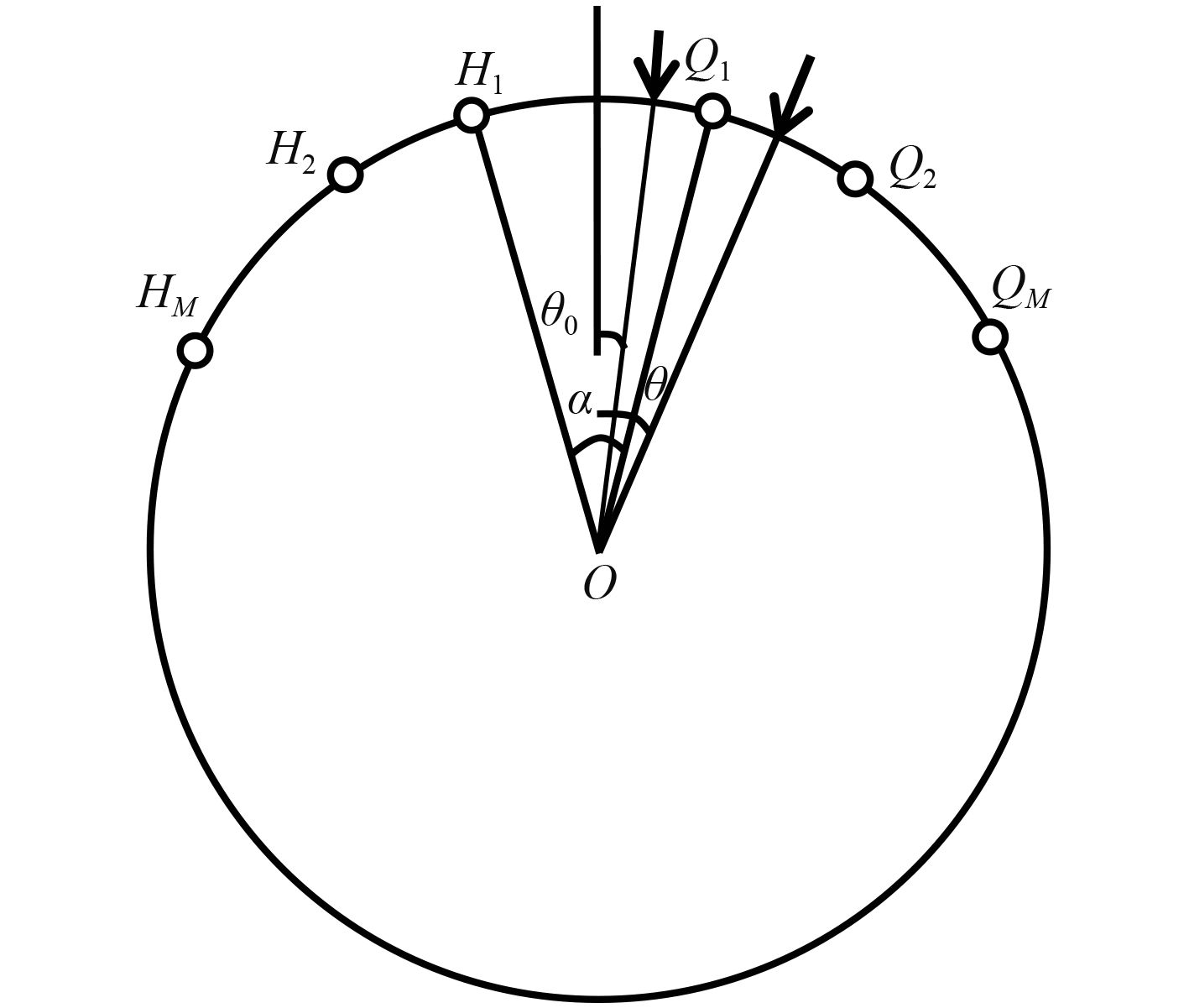
1 圆阵半波束相位差图1给出一个半径为r的圆阵半波束示意图。假设基元数为N,均匀分布在圆周上,则相邻2个基元的夹角为a=2π/N,取其中2M个基元形成一对半波束。
|
图 1 圆阵半波束示意图 Fig. 1 Schematic diagram of half beam of circular array |
假设信号入射方向与波束轴线的夹角为θ,到达圆心O的信号为cos2πft。
| ${\tau _i}(\theta ) = \frac{{r\cos (\theta + (i - 0.5)a)}}{c},$ | (1) |
式中:c为声速;
| ${x_i}(t) = \cos [2\pi f(t + {\tau _i}(\theta ))],$ | (2) |
若在θ0方向预成波束,则左波束输出为:
| $\begin{split}{B_l}(\theta ) = & \sum\limits_{i = 1}^M {\cos [\,\,2\pi f(t + {\tau _i}(\theta ) - {\tau _i}({\theta _0}))]} =\\& \left(\sum\limits_{i = 1}^M {{u_i}} \right)\cos (2\pi ft) - \left(\sum\limits_{i = 1}^M {{v_i}} \right)\sin (2\pi ft)=\\& A\cos (2\pi ft + {\phi _l}),\end{split}$ | (3) |
式中:
| $\sum\limits_{i = 1}^M {{u_i}} = \sum\limits_{i = 1}^M {\cos [2\pi f({\tau _i}(\theta ) - {\tau _i}({\theta _0})} )],$ | (4) |
| $\sum\limits_{i = 1}^M {{v_i}} = \sum\limits_{i = 1}^M {\sin [2\pi f({\tau _i}(\theta ) - {\tau _i}({\theta _0})} )]\text{。}$ | (5) |
则式(3)中幅度和相位分别为:
| $A = {[{(\sum\limits_{i = 1}^M {{u_i}} )^2} + {(\sum\limits_{i = 1}^M {{v_i}} )^2}]^{1/2}},$ | (6) |
| ${\phi _l} = \arctan (\sum\limits_{i = 1}^M {{v_i}} /\sum\limits_{i = 1}^M {{u_i}} ),$ | (7) |
同理,可以得到右波束输出为:
| ${B_r}(\theta )\; = B\cos (2\pi ft + {\phi _r}),$ | (8) |
式中B为右波束的幅度,其相位为:
| ${\phi _r} = 2\pi f{\tau _i}'(\theta ) = \arctan (\sum\limits_{i = 1'}^{M'} {{v_i}} /\sum\limits_{i = 1'}^{M'} {{u_i}} ),$ | (9) |
式中
| $\tau {'_i}(\theta ) = \frac{{r\cos (\theta - (i - 0.5)a)}}{c},$ | (10) |
则左右波束的相位差为:
| $\begin{aligned}\Delta \phi = & {\phi _r} - {\phi _l} = 2\pi f\Delta \tau =\\ & \arctan (\sum\limits_{i = 1'}^{M'} {{v_i}} /\sum\limits_{i = 1'}^{M'} {{u_i}} ) - \arctan (\sum\limits_{i = 1}^M {{v_i}} /\sum\limits_{i = 1}^M {{u_i}} )\text{。}\end{aligned}$ | (11) |
根据式(11)可知,圆阵半波束相位差较线阵复杂,并不是简单线性关系,因此直接通过该式计算半波束相位差比较麻烦。当
| $\Delta \phi = {\phi _r} - {\phi _l} = \frac{{4rc(\theta - {\theta _0})}}{{kf}}{\sin ^2}(k\pi )\text{。}$ | (12) |
式中k=M/N。
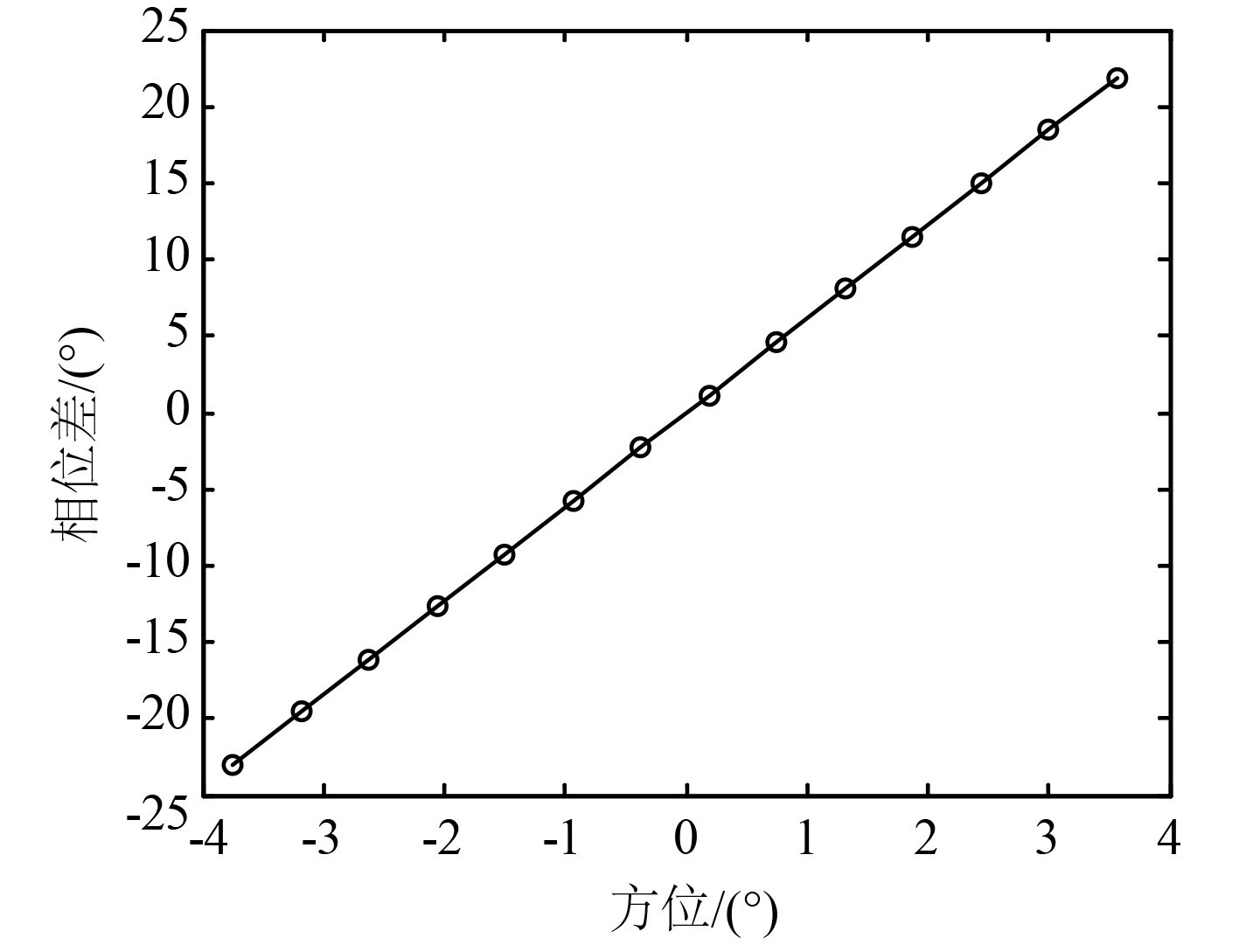
根据式(12)可知,圆阵半波束相位差信息除了与圆阵半径、基元数和信号频率有关外,还主要取决于信号实际入射方向与预成主波束方向间的角度差。当预成主波束方位与信号入射方向接近时,半波束相位差为接近于0°的小量。图2给出圆阵半波束相位差与预成波束方位覆盖范围内的方位关系曲线。
|
图 2 圆阵半波束相位差随方位变化曲线 Fig. 2 The phase difference of half beam against azimuth in circular array |
被动声呐宽带检测通常是采用宽带能量检测或宽带相关检测方法来实现目标探测功能。宽带能量检测是在一个宽的频带上对波束能量进行积分,它是非相关噪声场中单一目标的最优检测器,但是在复杂环境下,这种检测方法的性能迅速降低。宽带相关检测与宽带能量检测相比其处理增益减小1.5 dB,这是宽带相关检测提高多目标方位分辨力所付出的代价[8]。
宽带相关检测是分裂阵半波束处理在被动声呐宽带信号检测应用,它是把接收阵列划分为具有一定空间距离的不同子阵,对各子阵分别进行波束形成处理,利用不同子阵波束输出估计目标信号到达不同子阵的相位差信息[10]。
由于圆阵的指向性与线阵的指向性不同,因此圆阵中参与处理的基元跟预成的方位有关。通常圆阵根据预成主波束方位选取1/3圆周上的基元进行波束形成处理。圆阵宽带相关检测首先根据预成波束将接收阵等分为2个子阵,对双子阵分别进行波束形成得到左右波束输出频谱;然后将左右波束频谱进行互谱,并对互谱进行平滑相干变换;最后对平滑相干处理后互谱做逆FFT运算得到一组时延值,选取预成波束角度附近的相关值作为波束输出。图3给出圆阵的宽带相关检测处理流程图。

|
图 3 宽带相关检测流程图 Fig. 3 Flow chart of broadband correlation detection |
假设均匀圆阵由96个水听器组成,半径为2 m。设定2个目标信号,其入射方位分别为156°和160°,中心频率为5 000 Hz,带宽均为3 000 Hz,背景噪声为海洋环境噪声,信噪比均为–15 dB。以圆心为参考点,根据每个预成方位将参与处理的基元分成左右两子阵,然后分别进行宽带能量积分和相关处理。
|
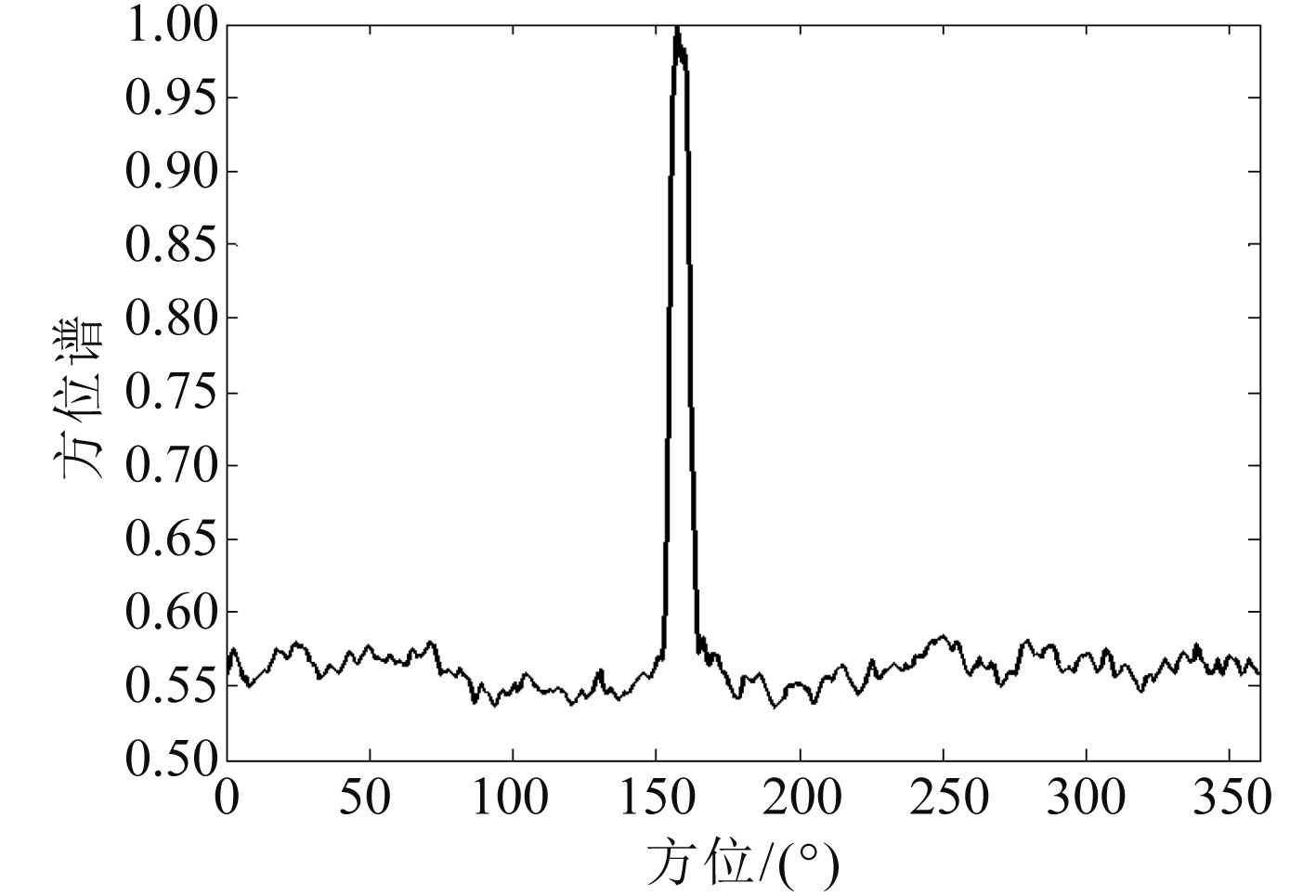
图 4 宽带能量检测 Fig. 4 Broadband energy detection |
|
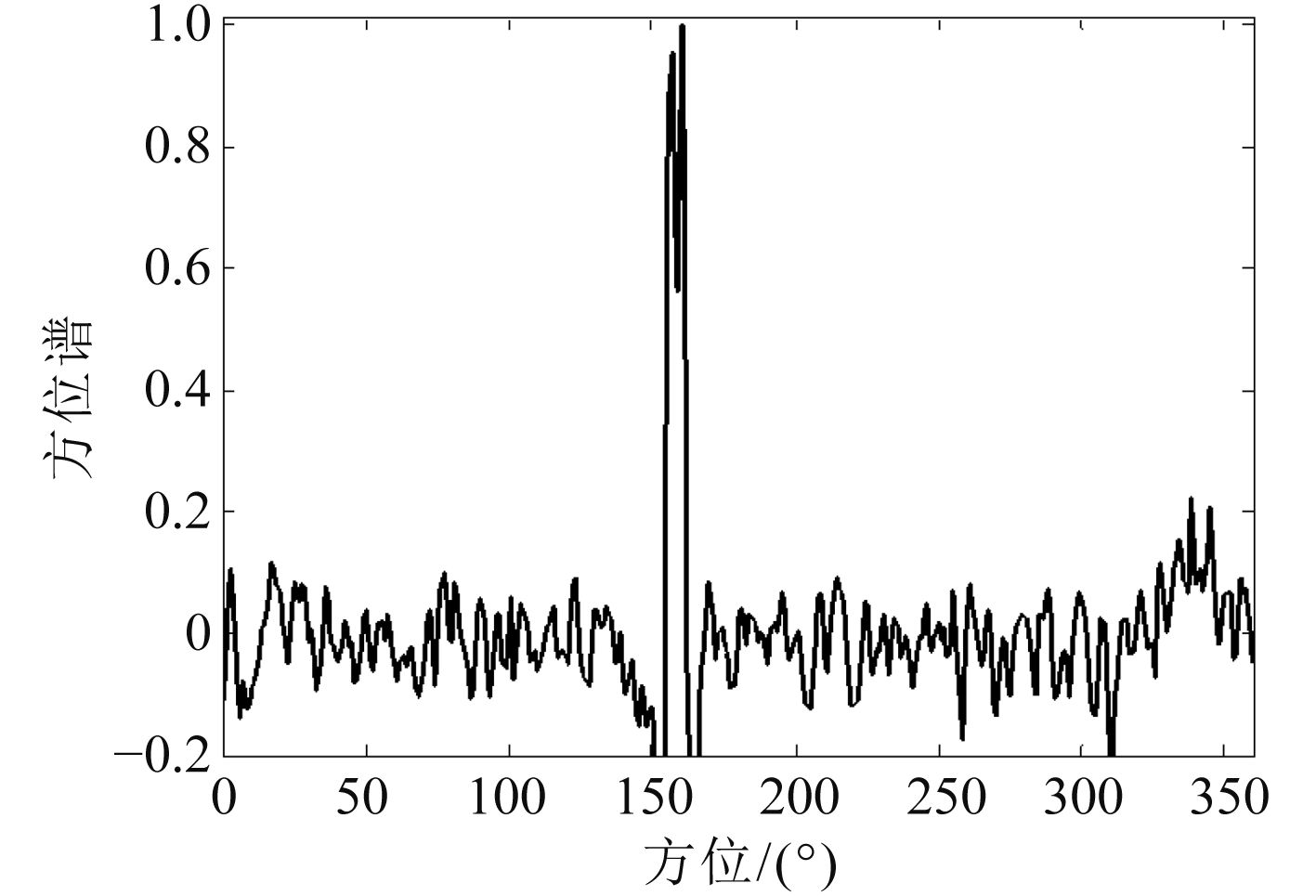
图 5 宽带相关检测 Fig. 5 Broadband correlation detection |
图4和图5给出了宽带能量检测和宽带相关检测的仿真结果。从图中可看出2个邻近信号处在同一波束宽度内,宽带能量检测不能分辨出从156°和160°入射的2个相邻信号。由于两子阵目标信号具有一定相关性和一定相位差,尽管其相位差起伏但可加以统计估计,而两子阵的环境噪声被认为不相关,其相位差统计均值小,对估计两子阵目标信号相位差影响不大,因此宽带相关检测利用子阵半波束相位差来提高目标方位分辨力,使得2个邻近信号得以区分,提高目标信号的检测能力。
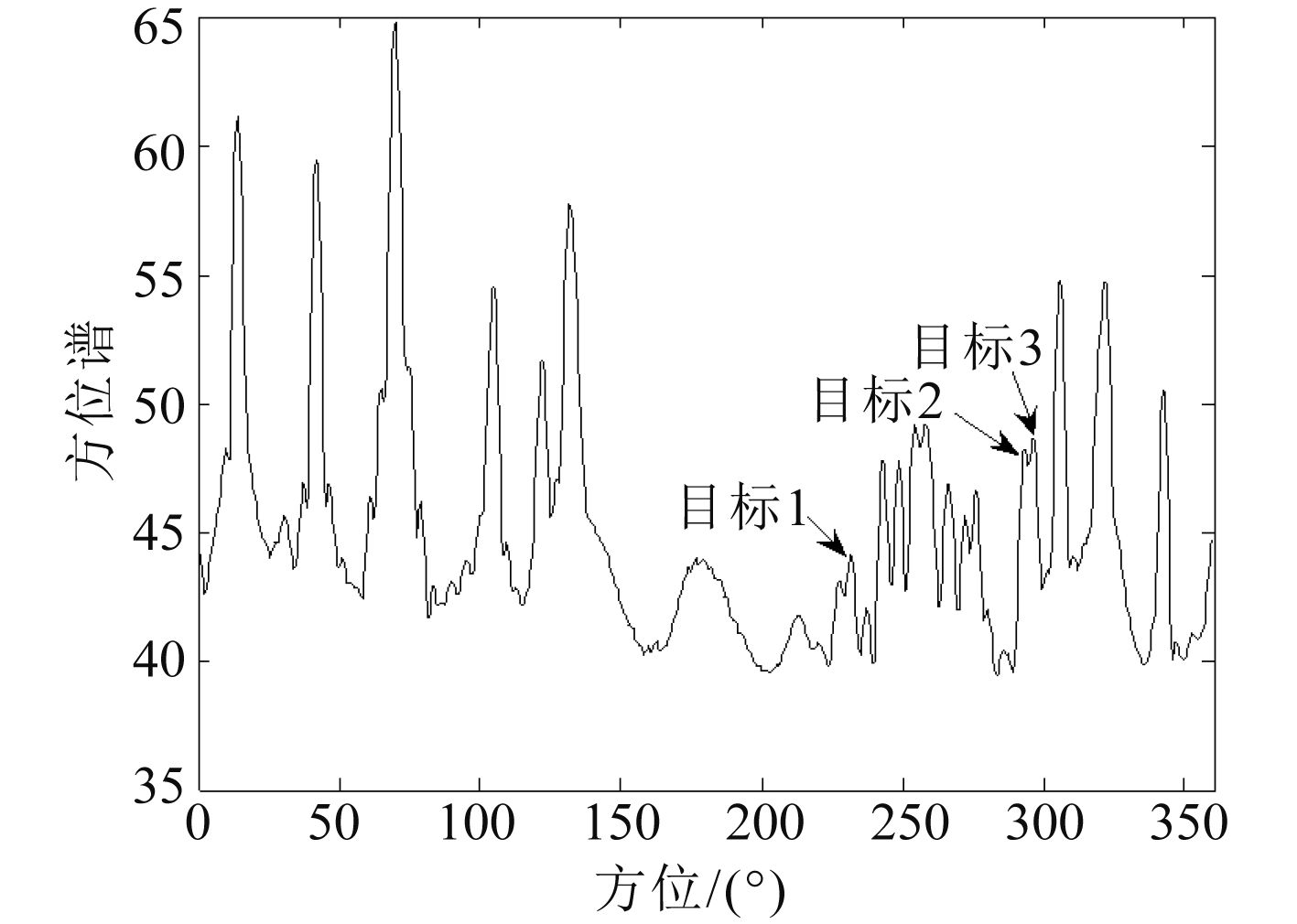
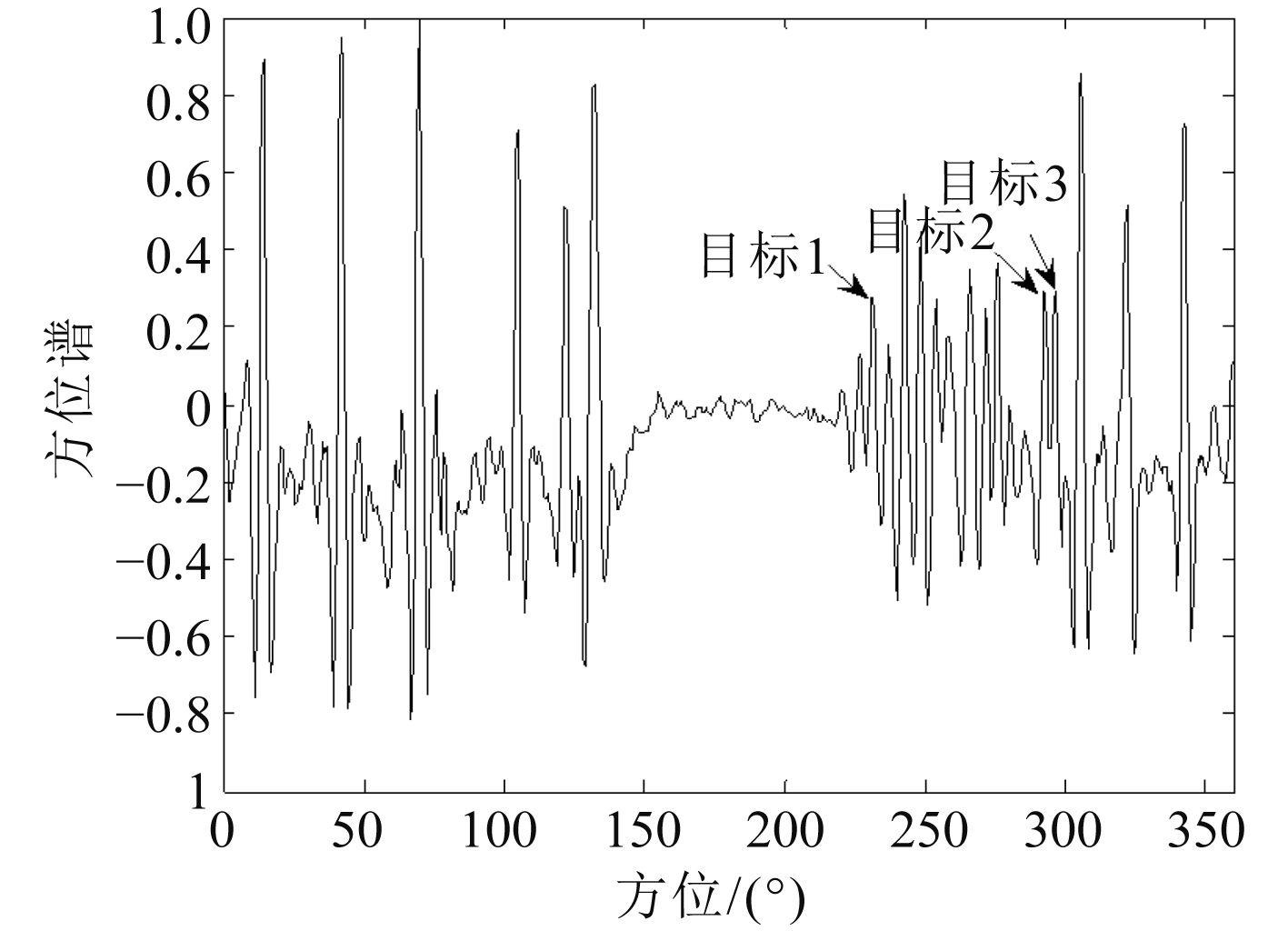
3.2 试验数据处理试验数据通过均匀圆阵获取,并对接收的数据进行宽带处理。图6和图7给出了宽带能量检测和宽带相关检测处理结果,其中目标1和目标2为合作目标,目标3为水面船只。从图6中可以观察到弱目标1(方位为230°)几乎淹没于背景噪声中,而图7中很清楚地发现该目标的峰值,提高了弱目标检测能力。对于目标2(方位为293°)和目标3(方位为297°),两者的方位相差4°。在图6中2个相邻目标轨迹几乎重叠,很难有效区分。而在图7中能清楚分辨出2个邻近目标峰值,提高了目标方位分辨率。因此在相同处理频带范围内,宽带相关检测与宽带能量检测相比能获得较高的方位分辨率,并能有效改善多目标交叉或邻近时目标检测能力。
|
图 6 宽带能量检测 Fig. 6 Broadband energy detection |
|
图 7 宽带相关检测 Fig. 7 Broadband correlation detection |
本文分析圆阵的半波束相位差,将分裂阵半波束应用于圆阵的宽带信号检测中,给出了一种应用圆阵分裂阵宽带相关检测方法。仿真和试验数据的处理结果表明,宽带相关检测可以改善目标方位分辨率,提高被动声呐的宽带检测性能。本文所提出应用圆阵中宽带检测方法性能稳定、计算量小,适合在被动声呐信号处理中进行工程应用。
| [1] | 李启虎. 声呐信号处理引论(2版)[M]. 北京: 海洋出版社, 2000. |
| [2] | Stergios Stergiopoulos, Anthony T Ashley. An experimental evaluation of split-beam processing as a broadband bearing estimator for line array sonar systems[J]. J.Acoust.Soc.Am, 1997, 102 (6): 3556–3563. DOI: 10.1121/1.420146 |
| [3] | David Miles, David Kirk, Timothy Clarke. A statistical analysis of the detection performance of a broadband splitbeam passive sonar[J]. IEEE Journal of Oceanic Engineering, 2006, 31 (4): 986–996. DOI: 10.1109/JOE.2006.880393 |
| [4] | MA Qiming, ZHOU Lisheng, DU Shuanping. Research of the weak signal detection algorithm for tow sonar based on the phase difference of the sub-array beam output[C]// UDT 2009 Europe. |
| [5] | Fumitaka Maeda, Kazuoki Kuramoto. Development of underwater low-speed moving target detection using spatiotemporal variance of phase difference for port surveillance sonar[J]. J.Acoust.Soc.Jpn, 2010, 37 (1): 34–45. DOI: 10.3135/jmasj.37.34 |
| [6] |
周胜增, 蒋小勇, 杜选民. 水下目标自动检测中的相位滤波技术研究[C]//2012年水下复杂战场环境目标识别与对抗及仿真技术学术论文集. 2012: 43–46.
ZHOU Sheng-zeng, JIANG Xiao-yong, DU Xuan-min. Research on the phase-filtering technique in underwater target automatic detection[C]//2012 Underwater Complex Batterfield Environment Target Recognition, Countermeasure and Simulation Research Papers, 2012: 43–46. |
| [7] |
朱伟, 沈文苗. 基于相位单元化处理的混响抑制方法[J]. 声学与电子工程, 2010 (4): 21–24.
ZHU Wei, SHEN Wenmiao. A reverberation suppression method to based on phase cell process[J]. Acoustics and Electronics Engineering, 2010 (4): 21–24. |
| [8] | WAITE A D, 王德石(译). 实用声呐工程(第三版)[M]. 北京: 电子工业出版社, 2004. |
| [9] | ZARNICH B E. A fresh look at broadband passive sonar processing[J]. Adaptive Sensor Array Processing Workshop, 1999 : 99–104. |
| [10] | Alan George, Keonwool Kim. Parallel algorithms for split-aperture conventional beamforming[J]. Journal of Computational Acoustics, 1999, 7 (4): 225–244. DOI: 10.1142/S0218396X99000151 |
 2017, Vol. 39
2017, Vol. 39
