0 引　言

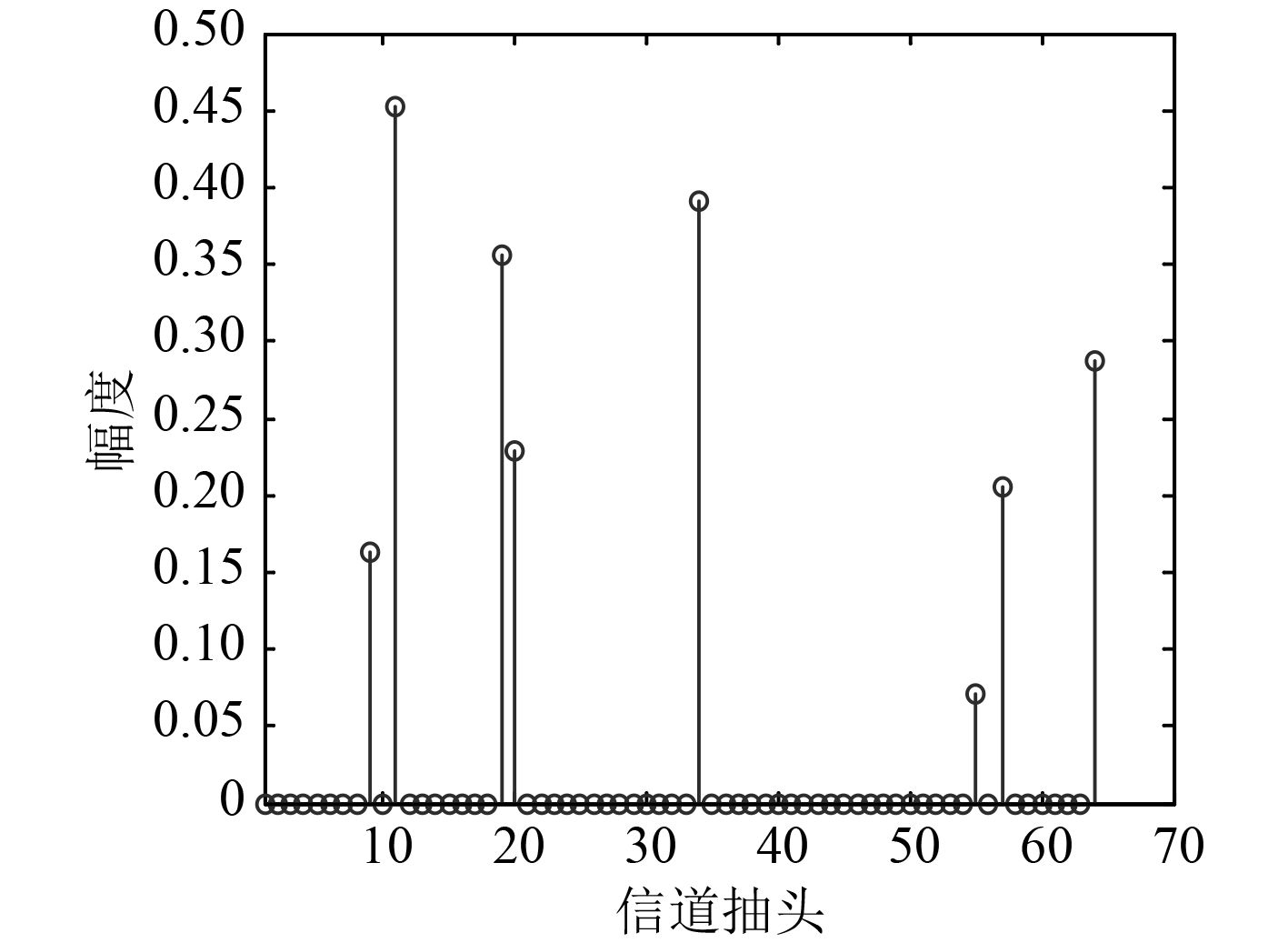
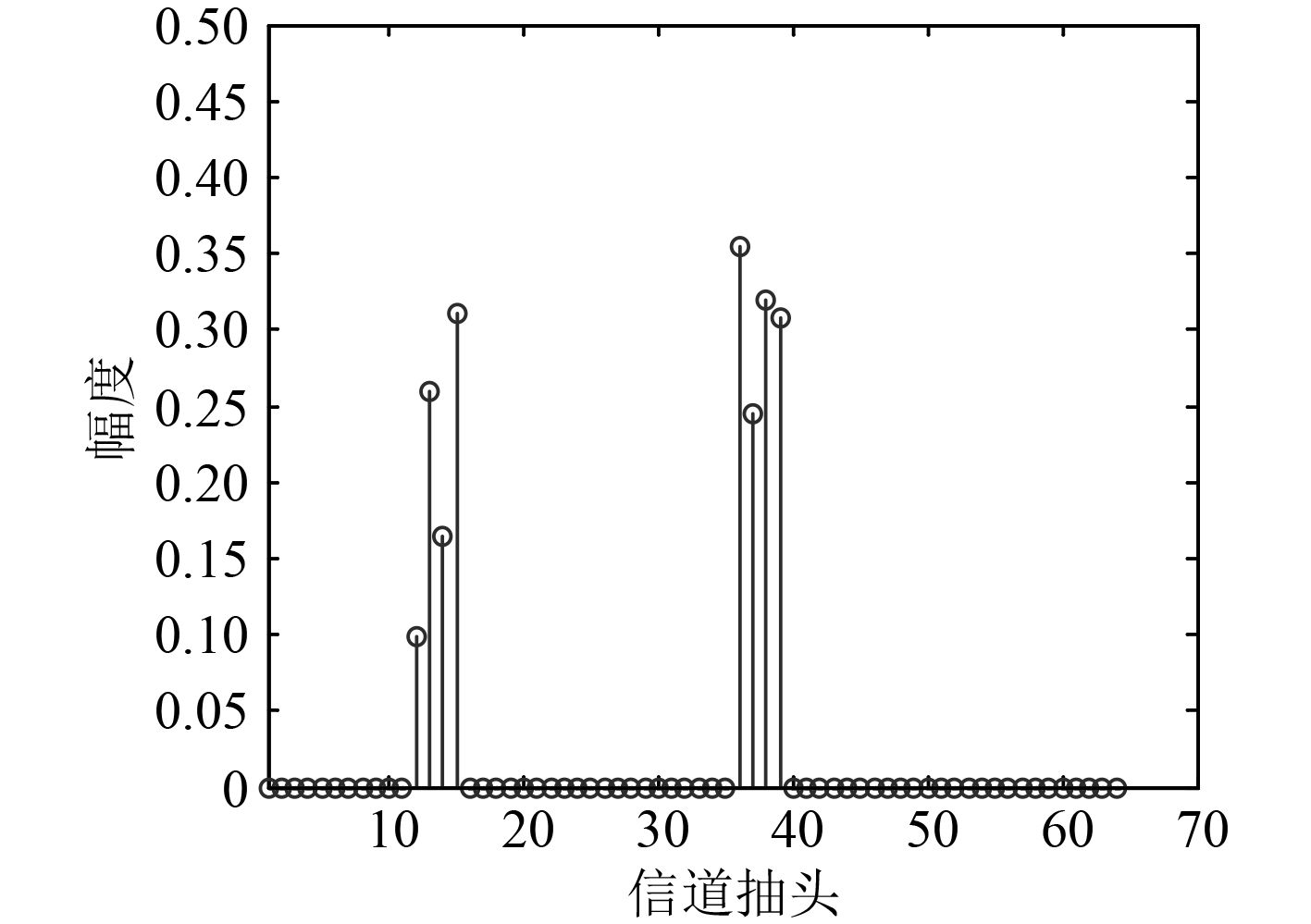
频率选择衰减信道是由发送信号的反射、衍射和散射导致的，因为建筑，船只的移动等^{[1 – 2]}。在高速移动水声通信应用中，这些衰落现象对通信系统的设计至关重要。因此，对于接收端来说，获取准确的信道状态信息成为这种通信系统的一个基本问题。物理信道测量验证水声信道呈现稀疏分布特性，稀疏信道模型如图1所示。近年来，进一步研究稀疏信号发现水声信道呈现块状结构稀疏特性，即非零抽头不是随机分布而是以块的形式呈现的，块结构稀疏信道模型如图2所示。

压缩感知理论可以从少量测量中有效重构出稀疏信号，水声信道的稀疏特性是使用压缩感知理论的前提^[3]。针对块结构稀疏特性，group Lasso^[4]、块正交匹配追踪（BOMP）^{[5 – 6]}和块压缩采样追踪^[7]等算法利用了信号内在的块结构先验信息。BOMP算法每次迭代只刷选出1个最大相关的块，本文针对这点，提出使用改进的BOMP算法进行信道估计，改进BOMP算法一次可以选出t个非零的块，在保证精度不变的前提下，将信道重构时间降低t倍。

1 压缩感知和块稀疏信号 1.1 压缩感知理论

CS理论通过测量矩阵将高维信号映射到低维空间，通过求解优化问题，高概率的重构出稀疏信号^[8]。CS基本原理：设x是一维实值离散信号，长度为N，稀疏度为K（x中最多有K个非零值），且K<<N。对信号x进行线性测量，得到测量值y，y是通过计算x和一组采样向量 $\{ {\phi _i}\} _{i = 1}^M$ 的内积得到：

$y = {\varPhi} x,$

(1)

式中：Φ为M×N的测量矩阵，通过将每个采样向量作为其列而生成，且M<N。由于M<N，从y恢复x是病态的，因此式（1）是欠定线性方程，Φ必须满足约束等距性质（RIP）^{[9 – 11]}：

$(1 - \varepsilon )\left\| x \right\|_2^2 \leqslant \left\| {{\varPhi} x} \right\|_2^2 \leqslant (1 + \varepsilon )\left\| x \right\|_2^3\text{。}$

(2)

其中ε为满足任意n稀疏向量x的最小正数。在这种情况下，矩阵保存信号Euclidean长度，并且Φ矩阵的n列子集是近似正交的。Bernoulli和Gaussian随机矩阵满足这个性质。

1.2 块稀疏信号

块稀疏信号是一种特殊结构的信号，可将其分为一个个串联的子块。考虑在给定N×d（且N<d）测量矩阵Φ下表示向量 $y \in {R^N}$ ，因此将x视为块的连接，如下所示：

$\begin{array}{l}x = {[{x_1},...{x_m},{x_{m + 1}},...{x_{2m}},...{x_{N - m + 1}},...{x_N}]^{\rm{T}}},\\x[1] = {[x1,...,{x_m}]^{\rm{T}}},\\x[2] = {[{x_{m + 1}},...,{x_{2m}}]^{\rm{T}}},\\\;\; \vdots \\x[n] = {[{x_{N - m + 1}},...,{x_N}]^{\rm{T}}},\end{array}$

(3)

式中：N=nm； $x[l](l = 1,2,...,n)$ l为第l块。

定义：

${\left\| x \right\|_{2,0}} = \sum\limits_{l = 1}^k {I({{\left\| {x[l]} \right\|}_{2,0}} > 0)},$

(4)

其中I（·）为指示函数，即

$I({\left\| {x[l]} \right\|_2} > 0) = \left\{ \begin{array}{l}1, \;\;\;\;\;\;{\left\| {x[l]} \right\|_2} > 0,\\0, \;\;\;\;\;\;{\left\| {x[l]} \right\|_2} = 0\text{。}\end{array} \right.$

(5)

若 ${\left\| x \right\|_{2,0}} \leqslant K$ ，则x称为K稀疏信号。当m=1时，块稀疏信号就退化为标准意义上的稀疏信号^[12]。与式（3）类似，将测量矩阵Φ表示为n×m列块Φ[l]的连接：

$\begin{array}{l}{\varPhi} = [{\phi _1},...{\phi _m},{\phi _{m + 1}},...{\phi _{2m}},...{\phi _{N - m + 1}},...{\phi _N}],\\\varPhi [1] = [{\phi _1},...{\phi _m}],\\\varPhi [2] = [{\phi _{m + 1}},...{\phi _{2m}}],\\\;\;\; \vdots \\\varPhi [n] = [{\phi _{N - m + 1}},...{\phi _N}]\text{。}\end{array}$

(6)

2 OFDM系统模型

水声信道通常是频率选择性衰落信道，信道冲击响应的数学表达式如式（7）所示：

$h(t,\tau ) = \sum\limits_{n = 0}^{N - 1} {{h_n}(t)\delta (\tau - {\tau _n}(t))}, $

(7)

式中：N为信道的多径数目； ${h_n}(t)$ 和 ${\tau _n}(t)$ 为第n路径在t时刻的复增益和时延。假设信道相干时间远大于OFDM符号周期，则可认为信道冲击响应是时不变的，再以OFDM系统的采样周期对信道冲击响应进行采样，得到离散时间信道模型：

$h(n) = \sum\limits_{l = 0}^L {{h_l}\delta (n - l)}, $

(8)

式中L为离散时间信道模型的总抽头个数，即信道长度。水声信道存在着块稀疏结构，即h中非零抽头以块的形式出现而不是随机分布的。假设h是由C个块级联而成，并且每个块有d个抽头，因此h可以写为：

$h = {[\underbrace {{h_1},...{h_d}}_{{h^T}[1]},\underbrace {{h_{d + 1}},...{h_{2d}}}_{{h^T}[2]},...,\underbrace {{h_{L - d + 1}},...{h_L}}_{{h^T}[c]}]^{\rm{T}}}\text{。}$

(9)

其中L=Cd。

假设OFDM系统采用N点DFT，有P个导频子载波，X（i）为OFDM符号内的数据，包含用户数据处理映射后的信号和导频信号，则接收端接收的N×1样值向量表示为：

$y = {X}H + n = X{W}h + n,$

(10)

式中： ${X} = diag(X(1),X(2),...,X(N))$ 为N×N对角矩阵；H为N×1向量的信道频率响应采样值；n为N×1向量的复加性高斯白噪声；W为N×N DFT矩阵的前L列。

${W} = \frac{1}{{\sqrt N }}\left[ \begin{array}{l}\;\;\;\;{w^{00}}\;\;\;\; \cdots \;\;\;\;{w^{(L - 1)0}}\;\\\;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \;\\{w^{0(N - 1)}}\;\;\; \cdots \;\;\;{w^{(L - 1(N - 1)}}\end{array} \right]\text{。}$

(11)

式中 ${w^{nl}} = {e^{ - \displaystyle\frac{{j2\pi nl}}{N}}}$ 。

设S为P×N的选择矩阵，利用S在N个子载波中选出P个导频所在的位置，从N×N单位矩阵中选择与导频位置对应的P行生成S矩阵。则接收的导频信号为：

${y_P} = {{X}_P}{{W}_P}h + {{n}_p}\text{。}$

(12)

式中： ${y_P} = Sy$ 为P×1向量； ${{X}_P} = {SXS}'$ 为P×P矩阵； ${{W}_P} = SW$ 为P×L矩阵； ${{n}_P} = Sn$ 为P×1向量。在接收端，y_P，X_P，W_P均为已知信号，通过相关的算法恢复h向量，再通过H=Wh可得到信道频域响应。

3 改进BOMP算法的信道估计实现

输入：观测向量y，观测矩阵Φ，信号稀疏度K；

输出：h的逼近信号 $\hat h$ 。

1）首先，进行初始化：设置迭代次数l=0，残差r₀=y，索引集 ${\varOmega _0} = \varphi $ ；

2）迭代步骤，第l次迭代（ $l = 1,2,......$ ）；

①选择出t个与迭代余量最匹配的块的索引： ${i_l} = \mathop {\max (}\limits_i {\left\| {{{\varPhi} ^*}[i]{r_{l - 1}}} \right\|_2},t)$ ；

②增大索引集 ${\varOmega _l} = {\varOmega _{l - 1}} \cup \{ {i_l}\}; $

③利用LS算法得到近似的估计 ${\hat h_l}$ ，在索引集之内的 ${\hat h_{l|{\varOmega _l}}} = \arg \;\mathop {\min }\limits_{{h_l} \in C} \left\| {y - {{\varPhi} _p}h} \right\| = {\varPhi} _p^ + y$ ，在索引集Ω_l之外的都是零，其中Φ⁺为Φ的伪逆矩阵；

④计算观测向量的新近似 ${y_l} = {\varPhi} {\hat h_l} = {{\varPhi} _p}{\hat h_{l|{\varOmega _l}}}$ ，更新残差 ${r_l} = y - {y_l}$ ；

⑤判断是否满足迭代停止条件，满足则停止，r=r_l，输出 $\hat h$ 。

4 仿真和结果分析

本文在Matlab平台上进行仿真，对比了LS、基于压缩感知的OMP、BOMP以及改进BOMP算法的估计性能。水声OFDM系统的参数设置为：子载波个数N=256，信道长度L=64，信道的每个分块中有4个抽头（信道分为16块），非零抽头的个数为8（即非零块的个数为2），改进的BOMP算法1次挑选2个非零块；采用16QAM方式进行数据调制，导频随机插入，选择矩阵记录导频插入的位置。

使用归一化均方误差（MSE）比较几种算法的信道估计的性能，归一化均方误差为：

$MSE = \frac{{E\left[ {\sum\limits_k {{{\left| {H(k) - \hat H(k)} \right|}^2}} } \right]}}{{E\left[ {\sum\limits_k {{{\left| {H(k)} \right|}^2}} } \right]}}\text{。}$

(16)

图3给出了当导频数量P=32时，LS、OMP、BOMP和改进BOMP四种算法估计性能随信噪比的变化曲线。

从图3（a）可看出，由于导频数量P<L采用LS算法进行信道估计得到的MSE比较大，算法基本失效。后面3种基于CS理论的算法，由于充分考虑了信号的稀疏性，插入少量导频可以获得很好的估计性能，同时算法的MSE大幅下降。从图可看出：基于块结构稀疏模型的BOMP及改进算法优于基于稀疏模型的OMP算法的估计性能；对比BOMP及其改进的算法可以看出：改进的BOMP算法基本保证了和BOMP算法相同的重构精度。图3（b）给出了对应的误码率（symbol error rate，BER）曲线，与图3（a）对比可发现两图曲线的走势吻合。其中LS算法的误码率维持在0.5左右，无法满足正常的通信需求。随着信噪比的增加，基于CS理论的OMP、BOMP和改进BOMP算法性能的优越性更加明显。

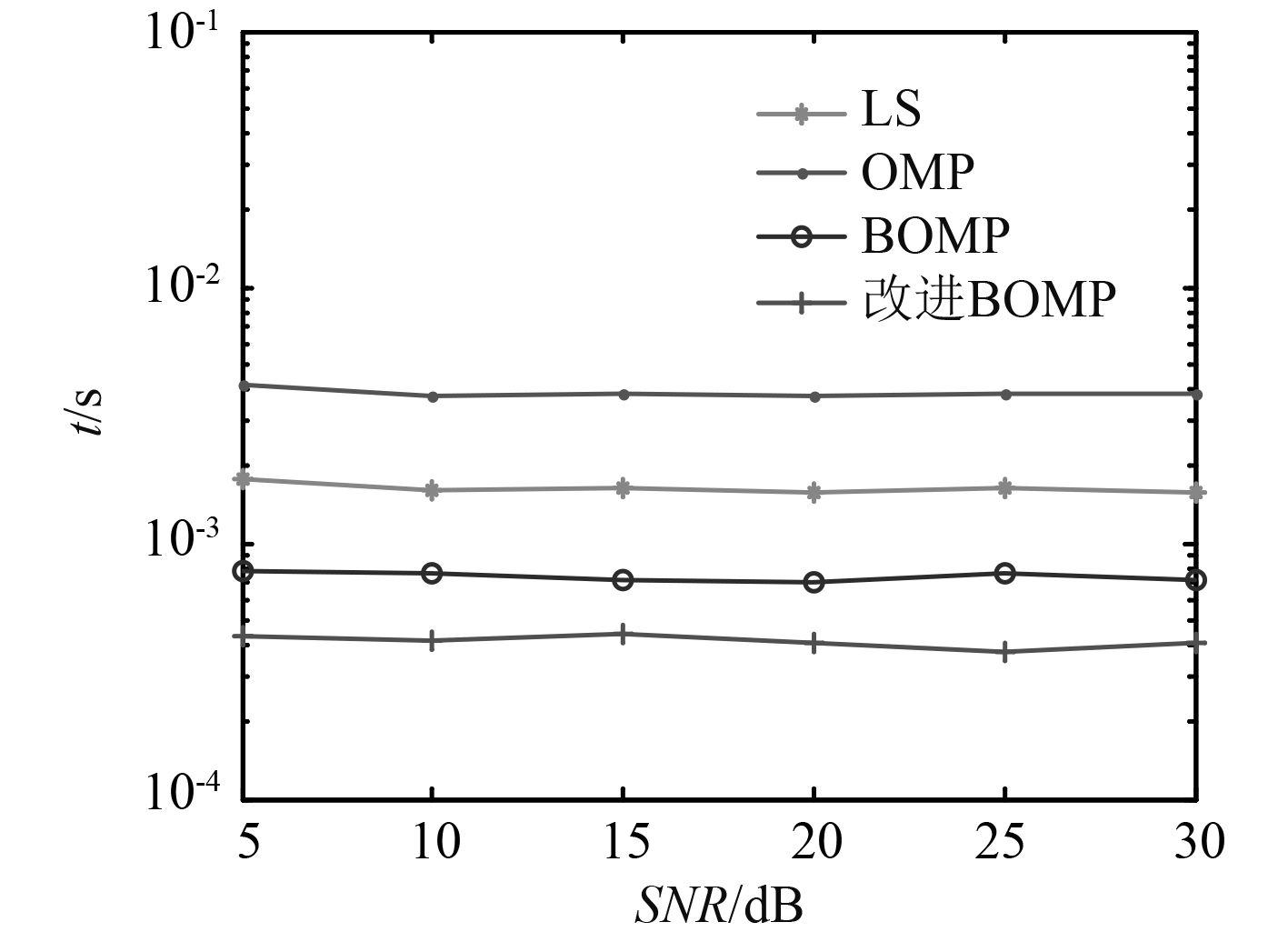
图4为LS，OMP，BOMP和改进BOMP四种算法在估计所需时间比较。

从表1可看出，BOMP算法的计算时间对比OMP算法的提高了约4倍，由于BOMP算法在OMP算法的基础上考虑了信号的块稀疏结构，OMP算法1次只能找到1个非零抽头，BOMP算法1次可以筛选出1个非零块的抽头（在本文仿真中即可1次取出4个抽头）。在本次仿真中，BOMP算法每次筛选出1个最大相关块，改进的BOMP算法每次迭代筛选出2个非零块，因此改进BOMP算法比BOMP算法运行时间约降低了2倍，仿真结果与理论相符合。

5 结　语

水声信道固有的稀疏性，是使用CS理论进行信道估计的前提条件。本文在稀疏性的基础上，进一步研究信号内在的块结构稀疏特性，在水声OFDM系统中，针对水声信道的块结构稀疏特性，提出使用改进的BOMP算法进行信道估计。仿真结果表明：由于改进BOMP算法1次可筛选出t个非零块，因此算法重构时间降低了t倍，同时改进的BOMP算法在保证了重构的精度。