在舰船水下噪声测量中,以大孔径多元线阵为平台,辅以高分辨的声源定位算法是实现噪声源准确定位、识别的有效手段。然而,对于布设于实验海区的多元线阵噪声测试系统,由于其尺度较大,会因为复杂的海况和环境(海风,海流)的影响而不可避免的发生形变。阵列的形变将会直接导致基于理想阵形状态下的算法性能急剧下降[1]。如今,水下噪声源定位识别常用的方法是基于特征分解理论的子空间类高分辨声源定位算法,典型的如最大似然方法(ML)、信号参数旋转不变(ESPIRT)算法和多重信号分类(MUSIC)算法等[2 – 4]。但在实际应用中,上述算法对于阵列流形的准确性要求比较苛刻。即使阵元位置存在较小的偏差,这类算法的性能都可能会急剧下降甚至失效[3],所以采取有效的措施对阵形进行校正成为研究的关键和热点。
目前存在许多阵形估计校正算法,然而由于它们各自的缺陷,能被用在实际系统中的却很少见。基于传感器直接测量方法可以对阵形进行实时校正,但这种算法的阵形估计精度受到传感器本身数量和精度的限制,且它使系统更加复杂,降低了系统的稳健性。尤其对于大尺度线阵,只适合做辅助手段[5]。基于水声同步测距定位的阵型校正方法,主要依靠水声测距和短基线定位原理算出任意阵元的空间位置坐标,进而实现阵形校正。该方法在实际应用中表现较好,但测距精度会对算法本身的精度产生较大的影响[6]。自校正方法不需要知道精确的信源方位,可以在线完成对辅助信源实际方位的估计,使算法无需受到信源方位精确度的制约,但由于阵列误差参数(通道幅相误差、阵元位置误差等)以及方位参数之间的耦合以及某些病态的阵列结构,算法无法保证参数估计的唯一辨识。此外,由于参数联合估计具有高维、多模非线性优化的特点,导致进行参数估计时算法的计算量急剧增加,从而难以保证算法的全局收敛性[7]。有源校正方法就是利用精确已知的校正源信源数目、信源方位等先验信息对阵列模型误差进行校正[8]。此方法可以通过选取符合实验要求的校正源,例如选择功率比较大的校正源来削弱噪声的影响或选择校正源的方位信息以便更好进行阵列误差校正。由于有源校正方法已知信号源方位信息,并且可以对信号源的方位,发射信号强度等属性进行调整,所以其具有运算量较小、校正精度较高的优点[7]。
针对水下多元线阵阵形校正需求,本文提出一种基于粒子群算法的远场阵形有源校正方法,该方法选用两个辅助源分时工作方式,利用无条件最大似然(Unconditional Maximum Likelihood,UML)方位估计方法构建目标函数,并通过粒子群算法对阵元位置进行寻优。仿真结果表明,该算法具有较好的稳健性和较高的估计精度。
1 信号模型

|
图 1 远场阵列示意图 Fig. 1 The array-source geometry of the far-filed case |
如图1所示,假定有N个阵元组成的均匀直线阵,阵元间距为d,M个远场窄带不相干信号从方向θm入射到该阵列上,
在此基础上,可推导出远场阵列的阵列流形向量A中的第nm个元素为:
| ${\rm{A}}\left( {{{\rm{\theta }}_m},{{\rm{\delta }}_n}} \right) = {\rm{exp}}\left\{ {{\rm{j}}\frac{{2{\rm{\pi }}}}{{\rm{\lambda }}}\left[ {\left( {{x_n} + {\rm{\Delta }}{x_n}} \right)\sin {{\rm{\theta }}_m} + \left( {{y_n} + {\rm{\Delta }}{y_n}} \right)\cos {{\rm{\theta }}_m}} \right]} \right\}$ | (1) |
则第k次快拍的输出向量为:
| ${X}\left( k \right) = {AS}\left( {\rm{k}} \right) + {N}\left( {\rm{k}} \right)\text{,}$ | (2) |
式中S(k)和N(k)分别为N×1的接收数据向量和噪声向量、噪声为零均值及方差为σ2的高斯加性白噪声。阵列的协方差矩阵为:
| ${{R}_{{\rm{xx}}}} = E\left[ {{X}\left( k \right){{X}^H}\left( {\rm{k}} \right)} \right] = {AS}{{A}^H} + {{\rm{\sigma }}^2}{I},$ | (3) |
其中S为信号协方差矩阵。对Rxx进行特征分解,得到信号特征向量ES和噪声特征向量EN两部分。两者张开的空间分别为信号子空间和噪声子空间且满足:
| ${{E}_{\rm{S}}}{E}_S^H + {{E}_N}{E}_N^H = {I},$ | (4) |
基于UML方位估计方法构造目标函数[9]为:
| $\widehat {\rm{\alpha }} = {\rm{arg}}\underbrace {{\rm{max}}}_{\rm{\alpha }}\left\{ { - {\rm{lndet}}\left[ {{{P}_A}\hat{ R}{{P}_A} + \frac{{{\rm{tr}}\left[ {{P}_A^ \bot \hat{ R}} \right]{P}_A^ \bot }}{{{\rm{N}} - {\rm{M}}}}} \right]} \right\},$ | (5) |
式中:
| $\hat{ R} = \frac{1}{K}\mathop \sum \limits_1^K {X}\left( k \right){{X}^H}\left( k \right)\text{。}$ | (6) |
由目标函数所得到的谱函数的峰值对应的方向即为信号源入射方向,为了防止阵元位置误差的影响,在空间谱搜索过程中,必须先对阵列流形A进行修正。
2 基于粒子群算法的阵形校正方法 2.1 粒子群优化算法粒子群算法[10 – 13](Particle Swarm Optimization,PSO)起源于对鸟类捕食的研究,是一种新兴的随机寻优仿真群智能算法。鸟类捕食时,最简单有效的确定食物位置的方法就是搜索当前距离食物最近的鸟的附近区域。粒子群算法的理论基础就来源于这种生物种群特征并用于决定的适应度值。用粒子来模拟鸟群,粒子的速度决定了粒子移动的距离和方向,且速度随自身及其他粒子的移动经验进行动态调整,从而实现个体在可解空间中的寻优。
粒子群算法首先在可解空间中设置一定数目的粒子,并根据实际需求进行初始化。这些粒子的特征主要由位置,速度和适应度三项指标来决定,代表极值优化问题的潜在最优解。适应度值来源于所设计的适应度函数,可以用来表现粒子的优劣。粒子在可解空间中运动,通过跟踪群体极值gbest以及个体极值pbest不断更新个体位置。在每次迭代过程中,粒子的速度和位置的更新,都以个体极值和群体极值的变化为依据[12]。
在一个D维空间中,由n个粒子组成的种群X=
| $V_{id}^{k + 1} = \omega V_{id}^k + {c_1}{r_1}\left( {P_{id}^k - X_{id}^k} \right) + {c_2}{r_2}\left( {P_{gd}^k - X_{id}^k} \right)\text{,}$ | (7) |
| $X_{id}^{k + 1} = X_{id}^k + V_{id}^{k + 1}\text{。}$ | (8) |
式中:ω为算法的惯性权重;
由信号模型可知,对于远场模型,选择2个分时工作的辅助声源,分别放置在θ1,θ2处,分别采集阵列输出信号,由K次快拍数据估计得到协方差矩阵
| ${F_n} = - det\left[ {{{P}_{An}}\widehat {{{R}_1}}{{P}_{An}} + \frac{{tr\left[ {{P}_{An}^ \bot \widehat {{{R}_2}}} \right]{P}_{An}^ \bot }}{{N - M}}} \right]\;n = 1,2\text{,}$ | (9) |
并有
| $F = {\rm arg\;min}\left( {{F_1} + {F_2}} \right)\text{。}$ | (10) |
式(10)即为所需的目标函数。
根据实际情况设置粒子群算法相关参数,包括迭代次数N、粒子个数n、加速度因子c1,c2、粒子最大速度为Vmax以及粒子位置取值范围
设置参数要同时考虑算法的精度和收敛速度,将每个阵元的位置误差设置为寻优过程中的需求的未知数。设置好参数后,设置粒子初始位置,进行迭代寻优,当达到迭代次数后或满足迭代终止条件时,结束迭代,得到寻优结果,即估计得出的阵元位置误差值。利用阵形校正结果构建阵列流形向量,并代入式(5)得到校正后的DOA估计值。
综上所述,本文提出的校正算法的具体实施步骤如下:
1)基于UML方位估计原理,利用式(9)和式(10)构建目标函数;
2)根据信号模型,设置粒子群算法的相关参数,使其兼顾校正精度和收敛速度;
3)利用粒子群算法对阵元位置进行寻优;
4)将寻优结果代入阵列流形中,利用校正过的阵列进行DOA估计,验证校正方法是否有效。
3 性能仿真结果分析 3.1 设计实例下面以均匀线阵为例,开展仿真实验。选取均匀线阵的阵元数为8,阵元间距为0.5λ,接收数据快拍数为1 000,信噪比为10 dB。令2个分时辅助源分别位于10°和50°方位,将第一个阵元所在位置设为坐标原点,阵元所在平面为XY平面,设定阵元位置误差
根据实际应用情况设计PSO算法的优化参数,同时兼顾迭代速度和迭代精度,设置迭代次数N=3 000,粒子个数n=30,粒子变化范围为[–0.2λ,0.2λ],粒子速度最大值为粒子变化范围的10%,c1=c2=2,设置开始,结束时的权值分别为0.9和0.4。
寻优后,得其估计结果如表1所示。
利用UML算法对校正好的阵列进行DOA估计,得到阵形校正前后的DOA估计功率谱,如图2所示。
|
|
表 1 位置误差估计结果 Tab.1 Estimate result of position errors |
|
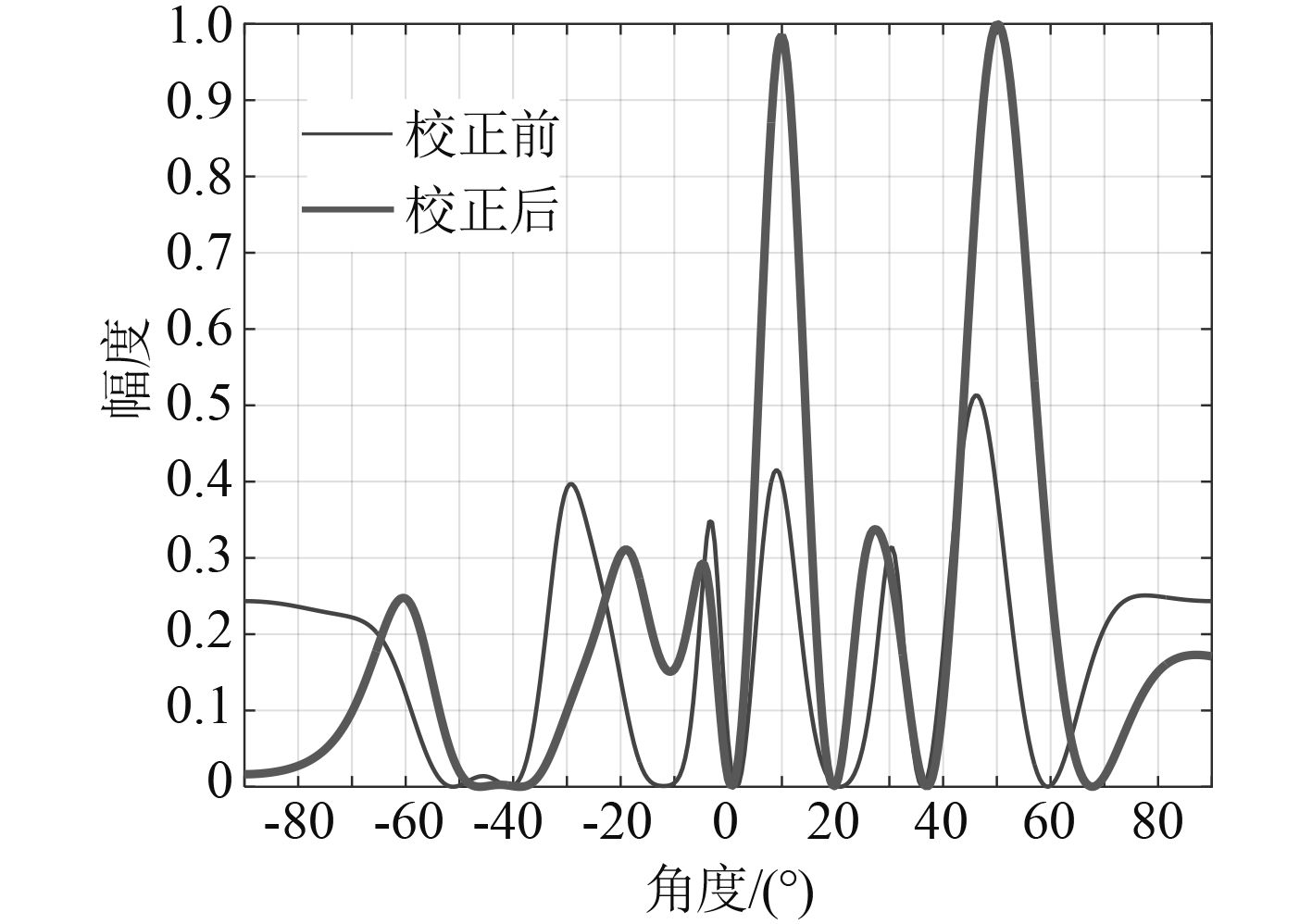
图 2 校正前后UML谱 Fig. 2 The DOA spectrum before and after calibration with UML |
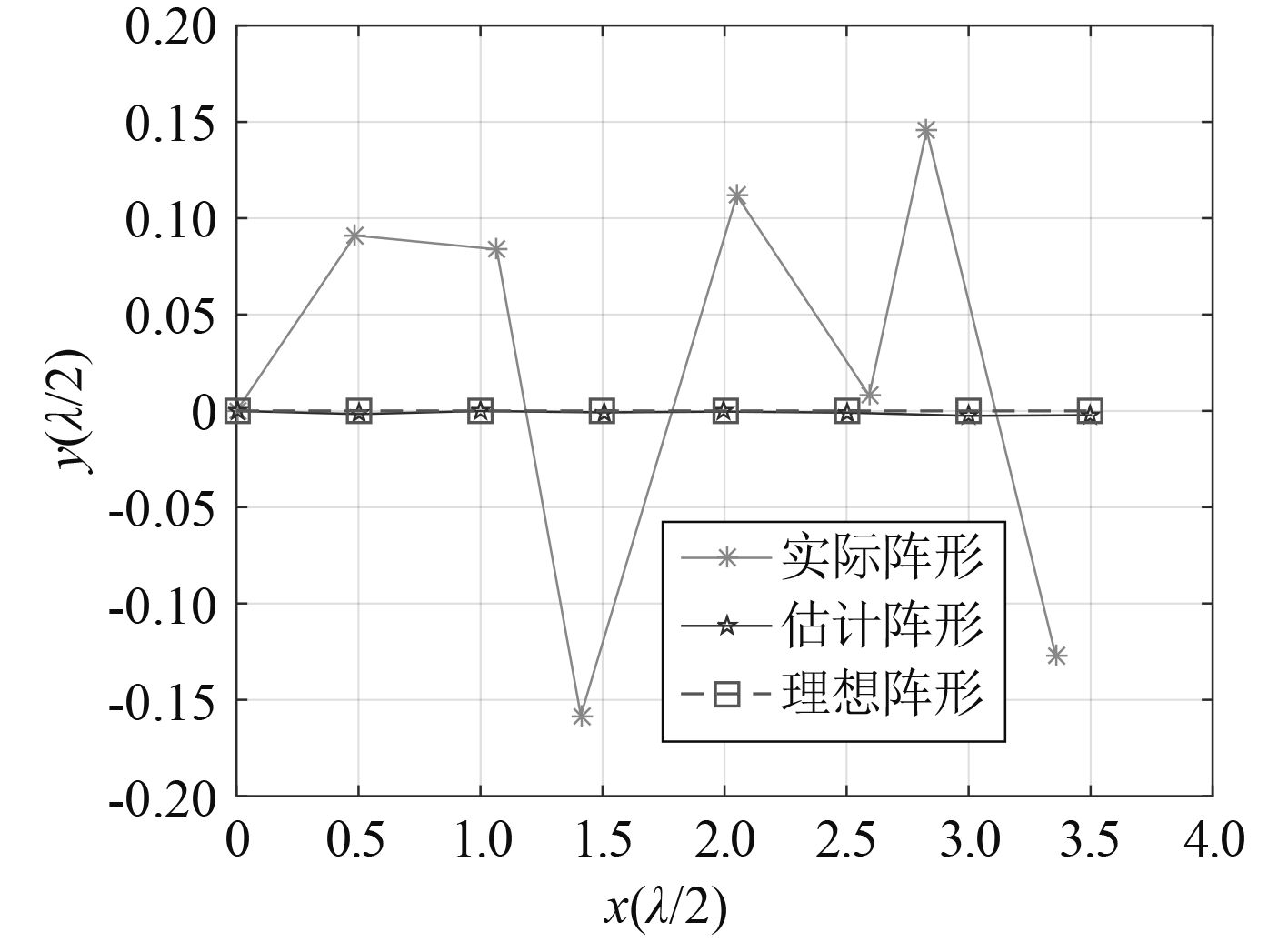
从图2可看出,经校正后,阵列所得到的DOA的精确度明显提高,这表明此校正方法有效。另外,由估计误差可以看出,X,Y方向上的绝对误差均小于0.003λ,由此可以判断,本文提出的阵形校正方法可以较准确估计出阵列阵元的位置。图3给出了典型的阵形校准结果。从图中可以看出,经本文算法校正后的阵形和理想阵形非常接近。
|
图 3 阵形校正前后阵元位置关系 Fig. 3 The array shape before and after calibration |
结合实际应用,下面重点信噪比、辅助源角度误差以及阵元位置误差等性能参数分别开展蒙特卡罗仿真实验,讨论不同条件对本文阵形校准精度的影响。
仿真过程中,设置阵元数为8,阵元间距d=0.5λ,快拍数k=1 000,信噪比snr=10 dB,两辅助源分别位于θ1=10°和θ2=50°方位,设置阵元位置误差
保证其他条件不变,分别在不同信噪比条件下进行阵形校正处理,并利用阵形校正结果进行目标方位估计,获取DOA估计均方误差,仿真实验结果如图4所示。
|
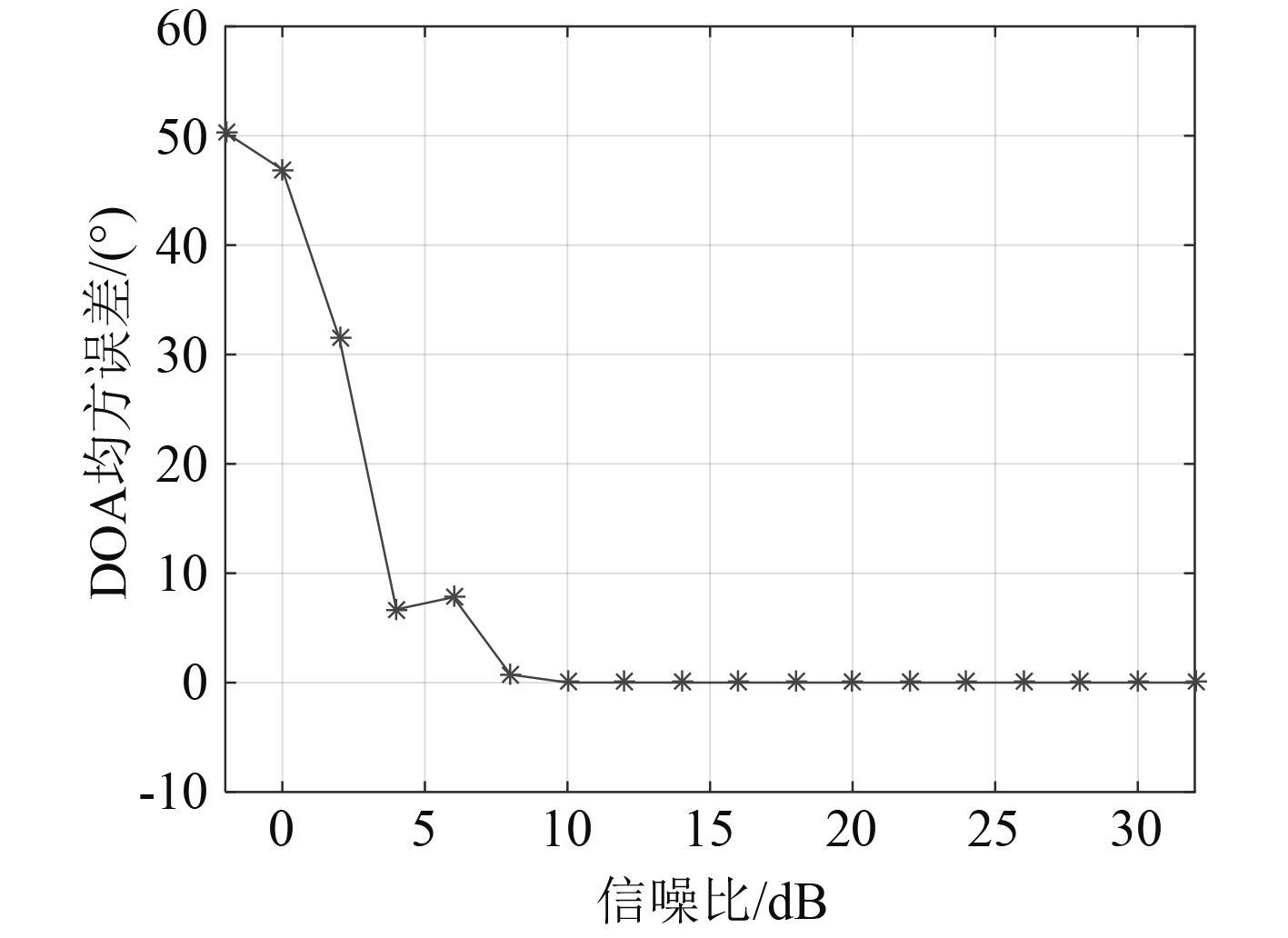
图 4 不同信噪比条件下DOA估计的均方误差 Fig. 4 Mean square error mse of DOA with different snr |
从图4可看出,对于基于粒子群算法的阵形校正过程,信噪比对校正精度有一定影响。当信噪比大于8 dB时,精度较高,所以在实际应用中,应控制辅助源信号强度,保证其信噪比大于8 dB。
3.2.2 辅助源角度差对校正精度的影响保证其他条件保持不变,令第一个辅助源位于10,改变第二个辅助源的位置,在两辅助源的角度差分别为10°,20°,30°,40°和50°的条件下进行校正,得到校正后的DOA估计均方误差,仿真结果如图5所示。
|
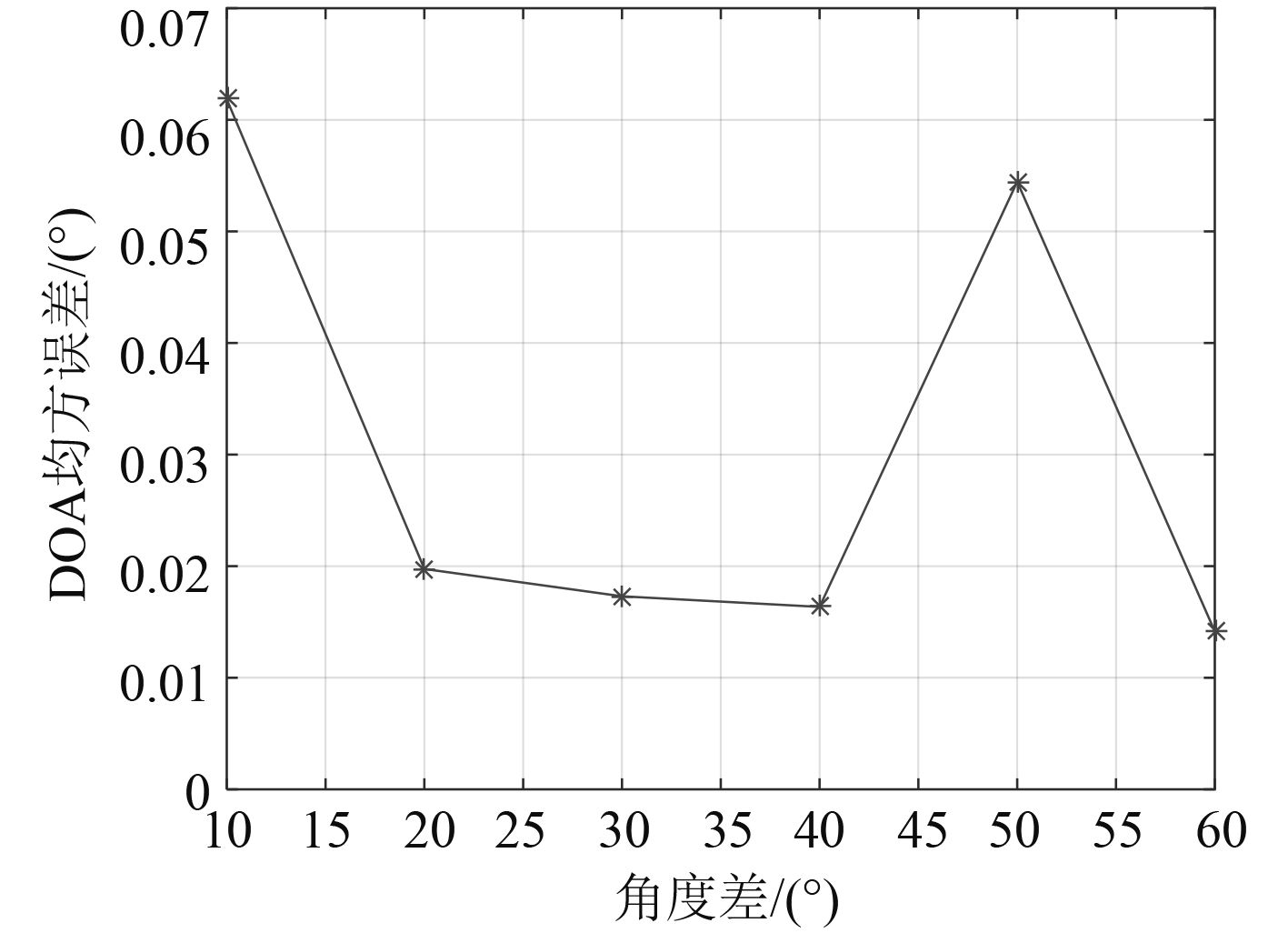
图 5 不同辅助源角度差条件下DOA估计的均方误差 Fig. 5 Mean square error(MSE)of DOA with different angles |
由图5可知,当其他条件不变,仅改变两辅助源角度差时,当两者角度差在10°~50°之间变化的情况下,DOA估计的均方误差均在0.07°以下,因此可见,两辅助源的角度差对粒子群阵形校正方法的精度影响较小,但相对而言,角度差位于20°~40°之间时校正精度更高。
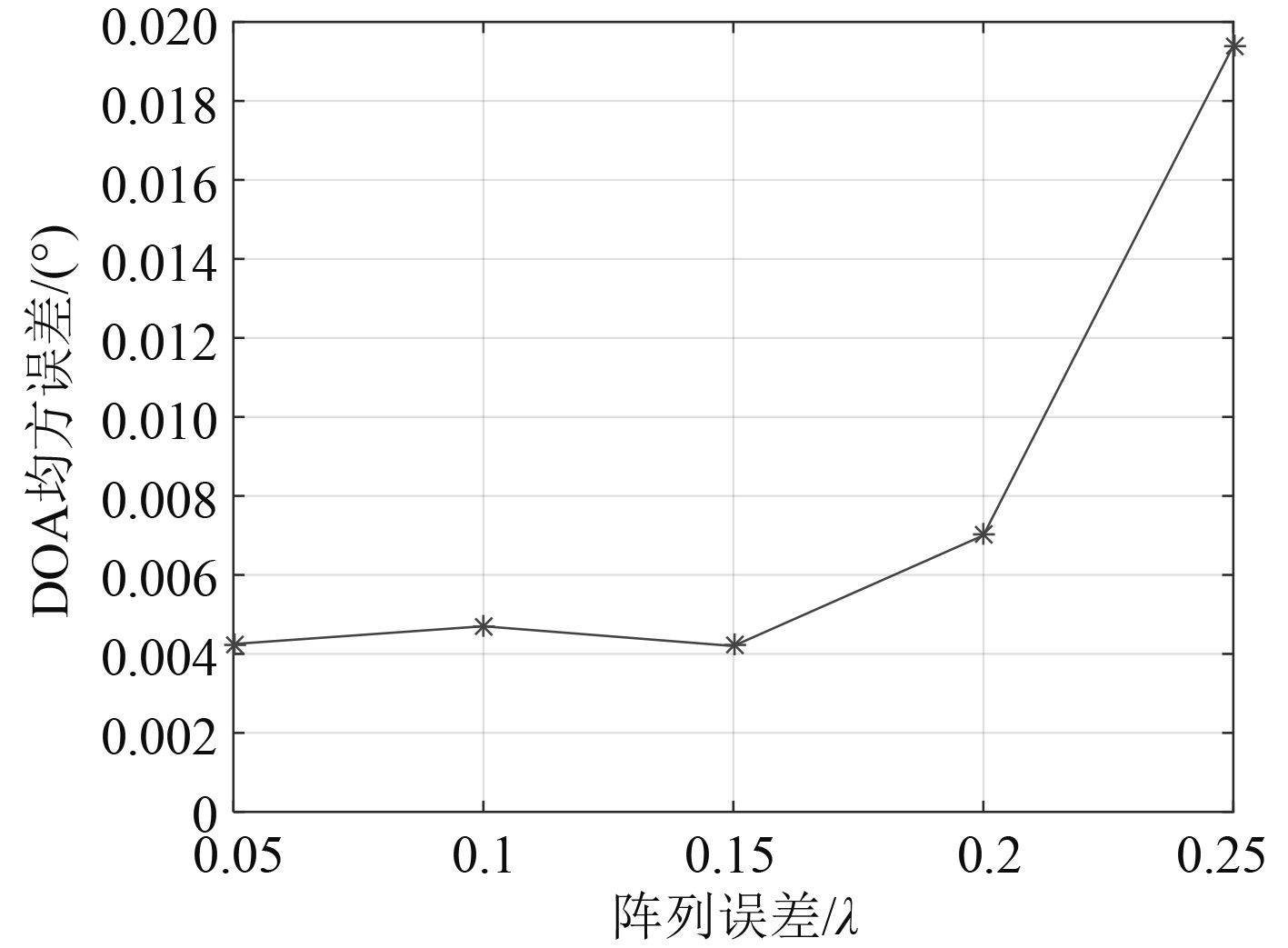
3.2.3 阵元位置对校正精度的影响保证其他参数不变,分别设置阵元位置误差分别为0.05λ,0.1λ,0.15λ,0.2λ和0.25λ(即为阵元间距的10%,20%,30%,40%,50%),得到校正后的DOA估计均方误差如图6所示。
从图6可看出,当阵列误差幅度在0.05λ到0.25λ之间时,DOA估计的均方误差均小于0.02°。由此可见,当误差在阵元间距50%以下时,阵元位置误差大小对算法精度的影响不大,但相对来说,当误差较小的时候,校正精度更好。
|
图 6 不同阵元位置误差条件下DOA估计的均方误差 Fig. 6 Mean square error (MSE) of DOA with different error range |
阵形校正是当前水下阵列信号处理中必须要解决的问题,本文提出了一种基于粒子群算法的水下多元线阵远场阵形校正方法,通过设置 2 个或多个分时工作的辅助源,利用UML方位估计原理构造目标函数,采用粒子群算法对阵元位置进行寻求。针对不同信噪比,辅助源角度差,幅度误差等性能参数开展了蒙特卡罗仿真实验。结果表明,该算法具有良好的校正精度和稳健性。通过适当增加辅助源的数量,可进一步提高阵形校正精度。另外,通过修改阵列模型,本算法也可应用于其他阵型的近、远场有源校正,具有广泛的应用前景。
| [1] | SCHMIDT R O. Multiple Emitter Location and Signal Parameter Estimation[J]. IEEE Trans. Antennas and Propagation, 1986, 34 : 276–280. DOI: 10.1109/TAP.1986.1143830 |
| [2] | SWINDLEHURST A L, KAILAITH T. A Performance Analysis of Subspace Based Methods in the Presence of Model Errors, Part I: The MUSIC Algorithm[J]. IEEE Trans. On TASSP, 1992, 40 (2): 1578–1774. |
| [3] | STOICA P. Nehorai. A MUSIC, Maximumlikelihood, and Cramer-Rao bound [C]//In Proc. ICASSP, 1998: 2296–2299. |
| [4] | FRIEDLANDER B, WEISS A J. Driection Finding in the Presence of Mutual Coupling[J]. IEEE Trans. on Antennas and Propagation, 1991, 39 (3): 273–284. DOI: 10.1109/8.76322 |
| [5] |
梁国龙, 刘凯, 嵇建飞, 等. 一种用于水平柔性长线水听器阵阵形估计的新算法[J]. 南京理工大学学报, 2011, 35 (3): 321–327.
LIANG Guo-long, LIU Kai, JI Jian-fei. Novel Algorithm for Array Shape Estimation of Horizontal Flexible Long-line Hydrophone Array[J]. Journal of Nanjing University of Science and Technology, 2011, 35 (3): 321–327. |
| [6] |
汪俊, 吴立新, Jim Lynch. 一种基于时延估计的双辅助声源阵形校准方法[J]. 声学学报, 2007, 32(2): 165–170.
WANG Jun, WU Li-xin, Jim Lynch. A method of array shape calibration based on tim delay estimation using two auxiliary sources [J]. Acta Acustica. 2007, 32(2): 165–170. |
| [7] | HUNG E. Matrix-construction Calibration Method for Antenna Arrays[J]. IEEE Trans. on Aerospace and Electronic Systems, 2000, 36 (3): 819–828. DOI: 10.1109/7.869501 |
| [8] | CHUNG P J, Wan S. Array self-calibration using sage algorithm[J]. IEEE Trans. Sensor Array and Multichannel Signal Processing Workshop, 2008, 7 : 165–169. |
| [9] | HARRY L, Van Trees, Optimum array processing part Ⅳof detection, mstimation, and modulation theory[M]. 汤俊, 等译 北京: 清华大学出版社, 2008. |
| [10] | KENNEDY J, EBERHART R C. Particle swarm optimization [C]//Proc of IEEE International Conference on Neural Networks, 1995: 1942–1948. |
| [11] |
吕阵肃. 自适应变异的粒子群优化算法[J]. 电子学报, 2004, 32 (3): 416–420.
LV-Zhen-su Zhi-rong. Particle Swarm Optimization with Adaptive Mutation[J]. Chinese journal of electronics, 2004, 32 (3): 416–420. |
| [12] | ALFI A. PSO with adaptive mutation and inertia weight and its application in parameter estimation of dynamic systems[J]. ActaAutomatica Sinica, 2001, 37 (5): 541–549. |
| [13] | MENDES R, KENNEDY J, NEVES J. The fully informed particle swarm: simpler, maybe better[J]. IEEE Trans. Evolutionary Computation, 2004, 8 (3): 204–210. DOI: 10.1109/TEVC.2004.826074 |
 2017, Vol. 39
2017, Vol. 39
