2. 洛阳舒诚机械有限公司,河南 洛阳 471000
2. Luoyang Shucheng Mechanical Equipment Co.,Ltd., Luoyang 471000, China
电磁轨道炮是以电能为发射能源,利用运动电荷或载流导体在磁场中受到电磁力来加速弹丸[1],其突破传统化学能发射弹丸的速度限制,具有初速高、射程远和快速打击等优越的战技性能,是自“冷”兵器过渡到“热”兵器之后的又一次武器革命,近年来得到了大力发展。本文从轨道炮发射过程中简化动力学模型入手,通过适当的模型简化,对临界速度进行理论计算和仿真分析,探讨其主要影响因子,为轨道炮结构设计提供支撑。
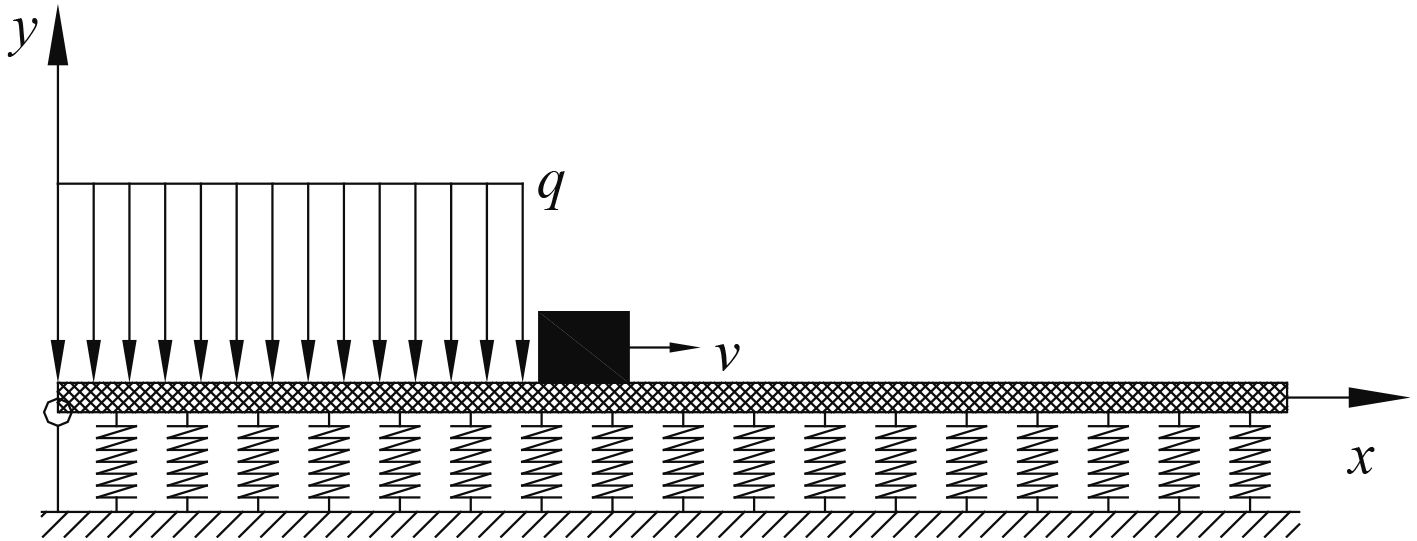
1 轨道炮临界速度分析 1.1 轨道炮简化模型当轨道中通有电流后,两轨道电流运动方向相反,轨道间存在相互作用的斥力;电枢在轨道表面运动过程中,导轨将承受移动载荷(电磁扩张力)的作用。弹性动力学理论表明,圆柱壳在移动内压作用下,当移动内压的速度趋于轴对称弯曲波波群速度(临界速度)时,壳体的结构响应理论上趋于无穷大,实际上是受同等水平静内压的结构响应的数倍。
在此,将轨道炮导轨简化为一固定在弹性支撑上的无限长Bernoulli-Euler梁,将导轨后面的支撑材料和封装简化为一系列离散弹簧[2 – 5],并固定在地面上,如图1所示。
|
图 1 轨道炮简化模型示意图 Fig. 1 Simplified model diagram for the railgun |
| $m\frac{{{\partial ^2}\omega }}{{\partial {t^2}}} + E{I_x}\frac{{{\partial ^4}\omega }}{{\partial {x^4}}} + {K_f}\omega = q[1 - H(x - Vt)]\text{,}$ | (1) |
式中:ω为轨道变形量,其与时间以及轴向坐标相关;m为轨道单位长度质量;B,h,ρ为轨道宽度;高度及密度;E为轨道材料的弹性模量;Ix为轨道截面惯性矩;Kf为轨道外侧支撑弹性系数;
| $q[1 - H(x - Vt)] = \left\{ \begin{array}{l}0,\quad(x > Vt),\\q,\quad(x \leqslant Vt),\end{array} \right.$ | (2) |
用数值方法求解方程(1),可求得临界速度:
| ${V_{cr}} = \sqrt[4]{{4\frac{{E{I_x} \cdot {K_f}}}{{{m^2}}}}} = \sqrt[4]{{\frac{1}{3}\frac{h}{B}\frac{{E{K_f}}}{{{\rho ^2}}}}},$ | (3) |
根据零初始条件求解,可得轨道的动态响应表达式为:
| $w(x,t) = \frac{2}{L}\sum\limits_{n = 1}^\infty {W(n,t)\sin \left( {\frac{{n\pi x}}{L}} \right)} \text{。}$ | (4) |
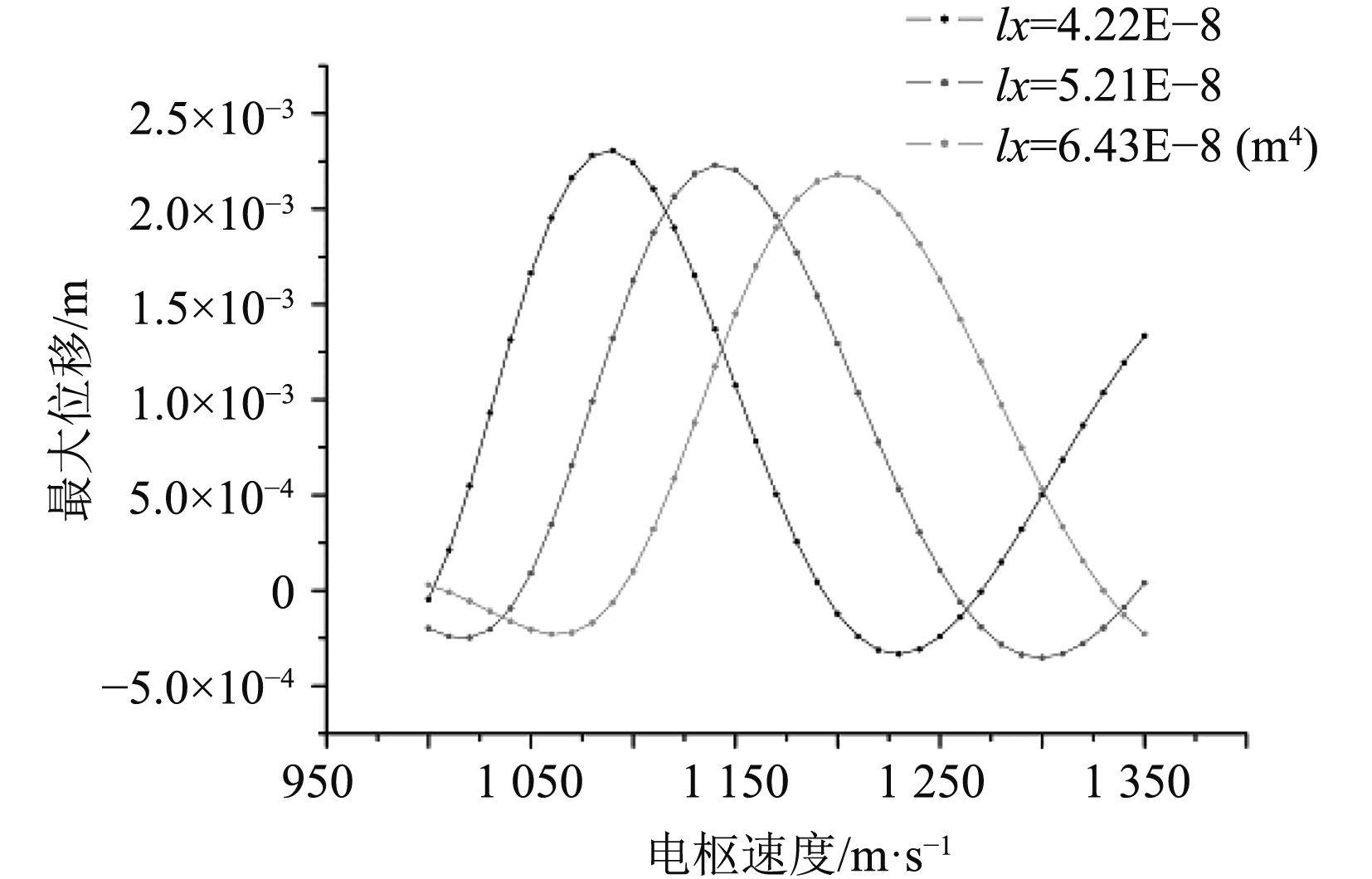
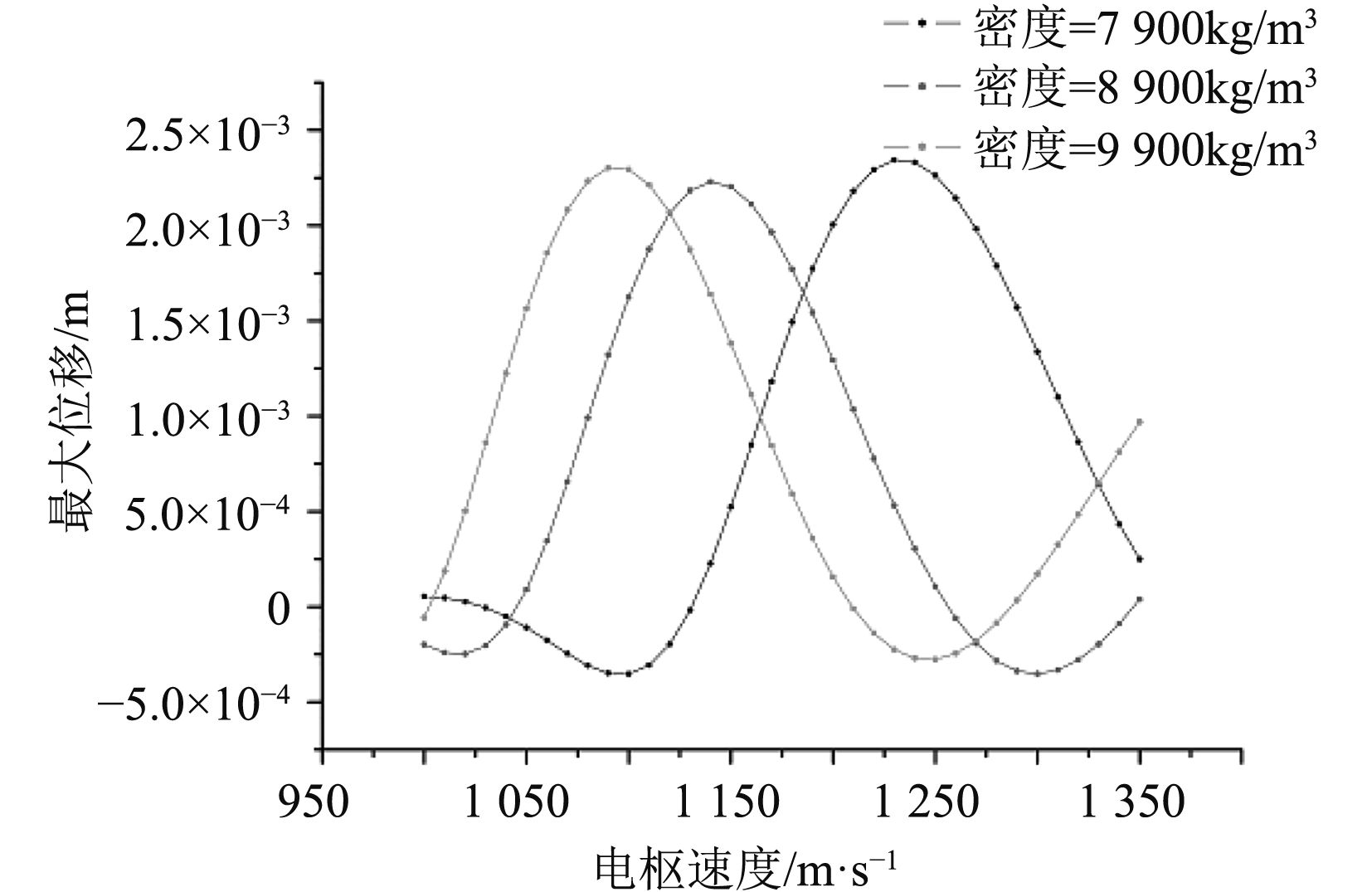
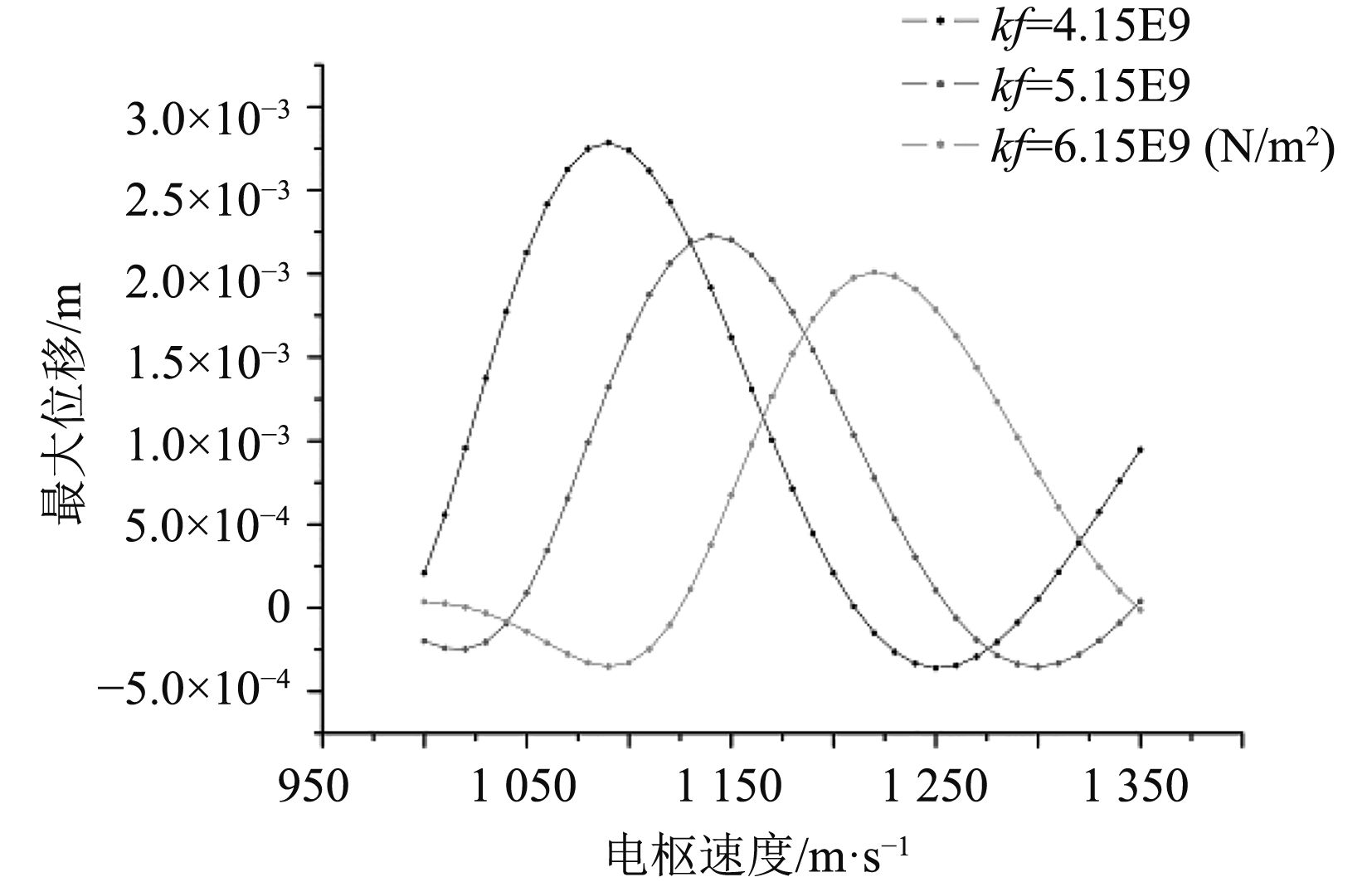
由式(3)可知,影响轨道炮临界速度的因素很多;分别改变弹性模量E,截面惯性矩Ix,轨道密度ρ及支撑弹性系数Kf,对不同参数时对应导轨中点的变形量进行分析,计算结果如图2~图5所示。

|
图 2 弹性模量E不同时轨道中点变形图 Fig. 2 Maximum displacement of the mid pointof the rail versus E with different velocity |
|
图 3 截面惯性矩Ix不同时轨道中点变形图 Fig. 3 Maximum displacement of the mid point of the rail versus Ix with different velocity |
|
图 4 轨道密度ρ不同时轨道中点变形图 Fig. 4 Maximum displacement of the mid point of the rail versus ρ with different velocity |
|
图 5 支撑弹性系数Kf不同时轨道中点变形图 Fig. 5 Maximum displacement of the mid point of the rail versus Kf with different velocity |
电枢达到临界速度时,导轨的变形最大,因此图5~图8中各个曲线的最高点所对应的速度即为轨道炮的临界速度,计算结果表明:
1)由图2和图3可知,随着轨道的弹性模量E、截面惯性矩Ix增加,其临界速度亦增加,但轨道最大变形量变化小于5%;
2)由图4可知,随着轨道的密度ρ增加其临界速度降低,但轨道的最大变形量变化不大于10%;
3)由图5可知,随着支撑弹性系数Kf增加,轨道炮临界速度增加,导轨的最大变形量减小40%。
因此,轨道支撑弹性系数Kf作为最敏感的主要变量因素,其数值的增加可以最快提高临界速度,从而降低轨道最大变形量,该结论对于轨道炮结构设计具有重要参考意义。
2 某轨道炮动力学仿真 2.1 有限元模型建立该轨道炮的主要参数如表1所示。
|
|
表 1 某轨道炮结构主要参数 Tab.1 Major parameters of the structure of a certain rail gun |
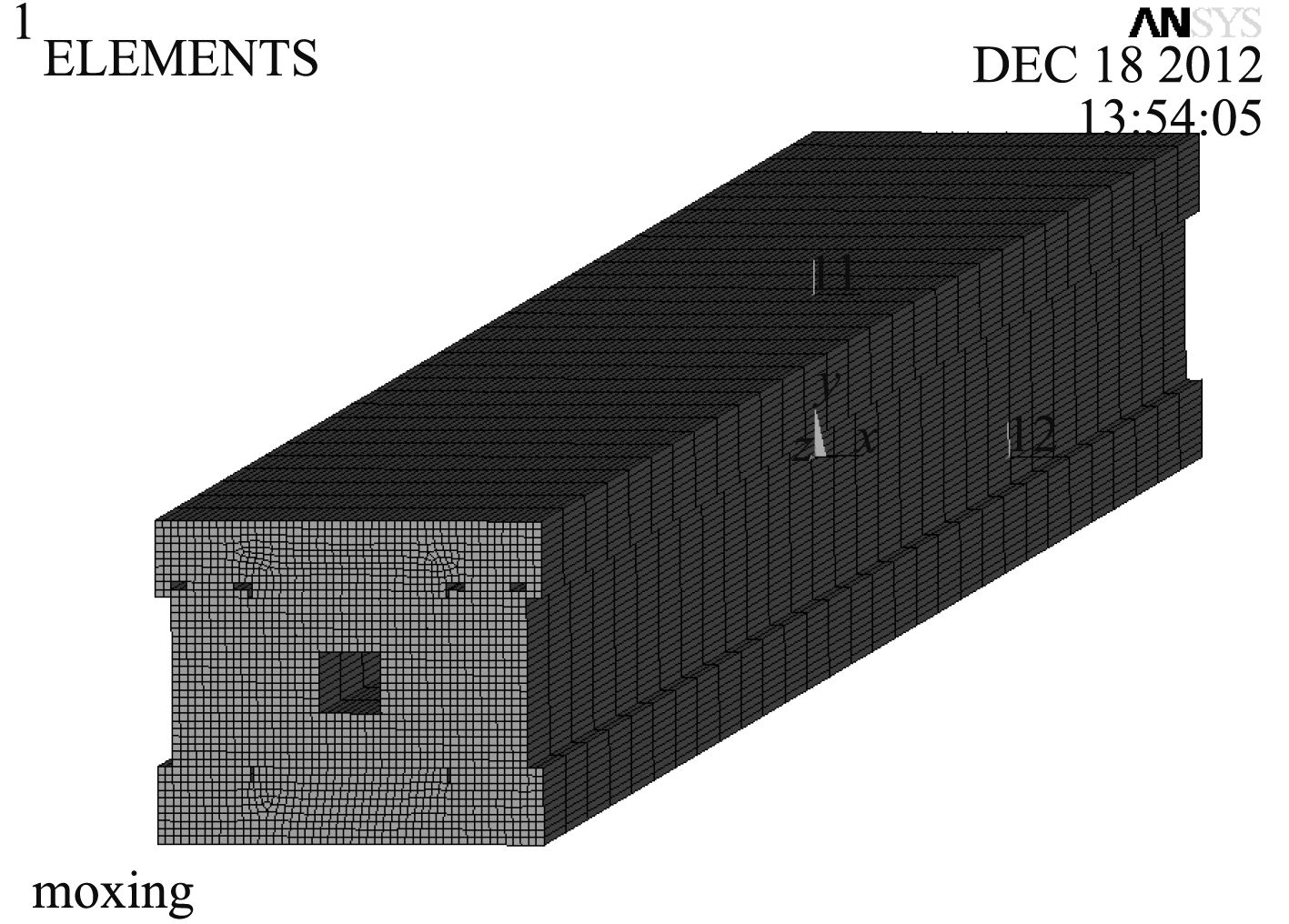
根据上述参数,利用APDL编程语言建立轨道炮实体模型,采用solid185实体单元进行网格划分,网格划分完成后,人工进行局部调整,结果见图6和图7。

|
图 6 某轨道炮实体模型 Fig. 6 Solid model of certain rail gun |
|
图 7 某轨道炮有限元模型 Fig. 7 Finite element model of certain rail gun |
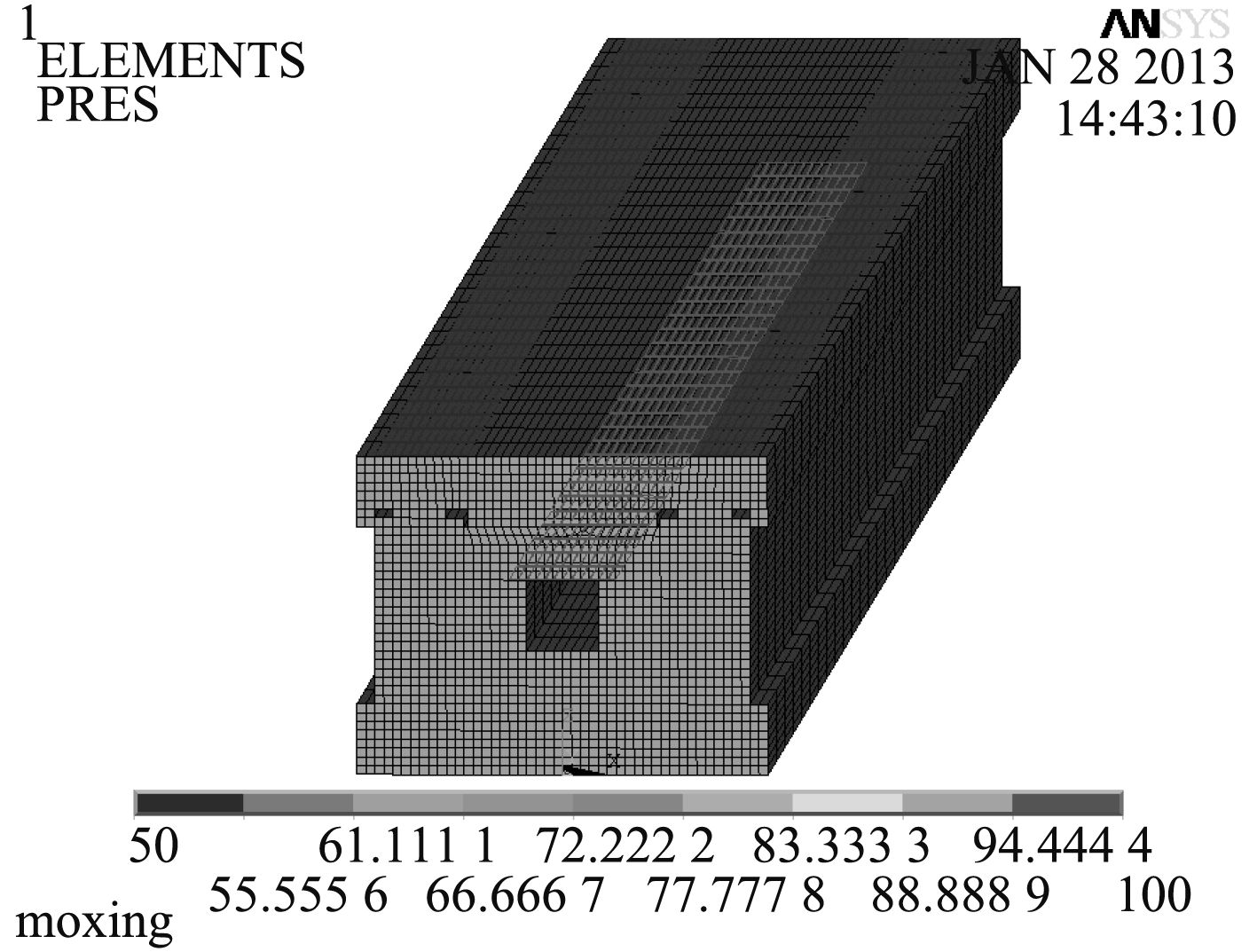
该轨道炮绝缘支撑弹性系数Kf求解如下:在一定预应力条件下,对轨道模型表面施加100 MPa均布荷载,如图8所示。计算各节点位移,提取轨道表面节点位移值,并求取平均值,利用胡克定律公式
|
图 8 在轨道上施加均布荷载 Fig. 8 Application of even load on the rail |
轨道表面各节点的平均位移为:
| $\Delta x = 0.2099{\rm E} - 3\;{\rm m},$ |
作用在轨道上的均布力的总和为:
| $\Delta F = P*A = 100{\rm E}6 \times 3 \times 0.06 = 1.8{\rm E}7{\rm N}\text{,}$ |
因此弹性系数为:
| ${K_f} = \Delta F/\Delta x = 8.57{\rm E}10{\rm N}/{\rm m}\text{,}$ |
由式(3)可得该轨道炮理论临界速度为:
| ${V_{cr}} = \sqrt[4]{{\frac{1}{3}\frac{h}{B}\frac{{E{K_f}}}{{{\rho ^2}}}}} = 2265\;{\rm m}/{\rm s}\text{。}$ |
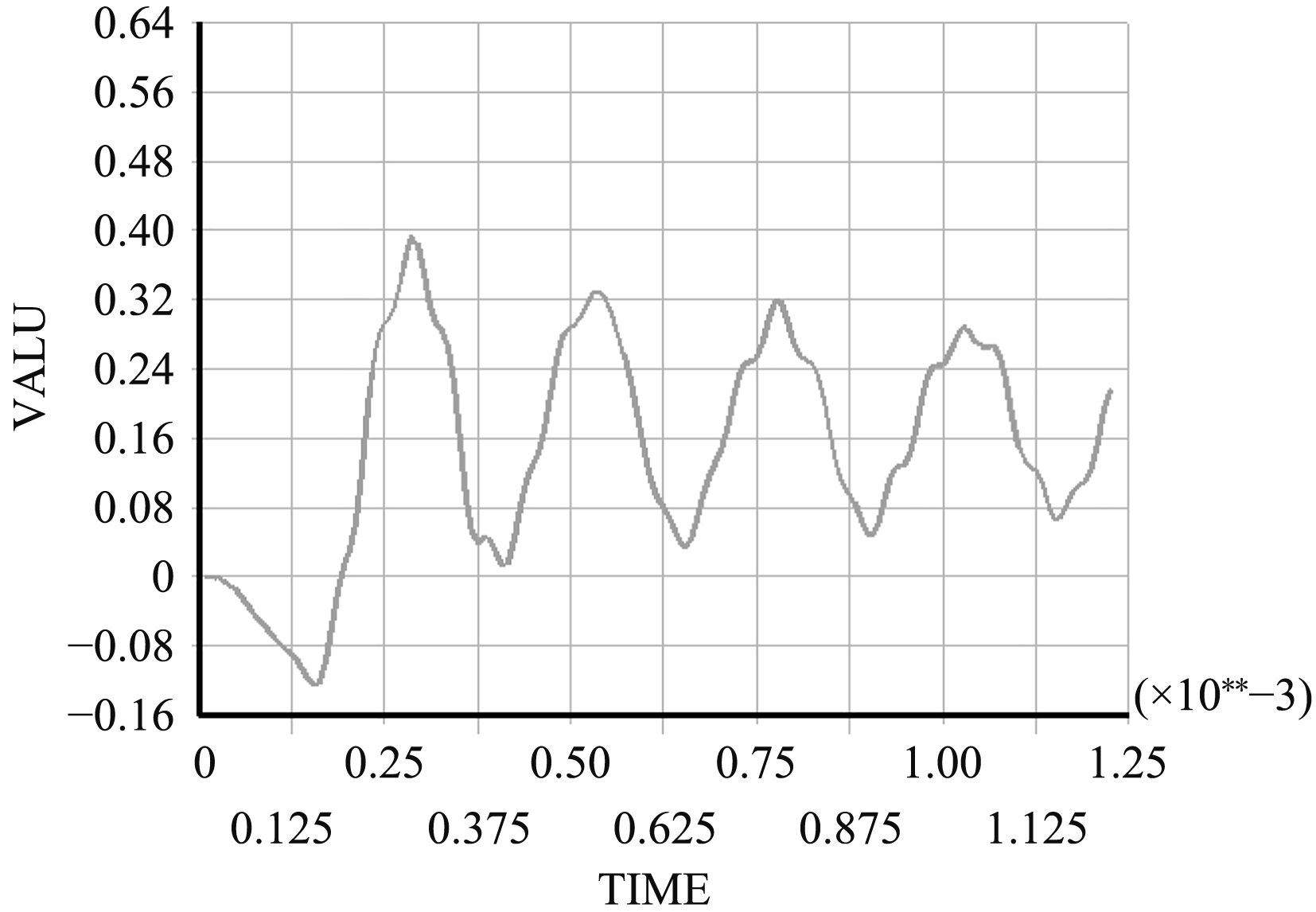
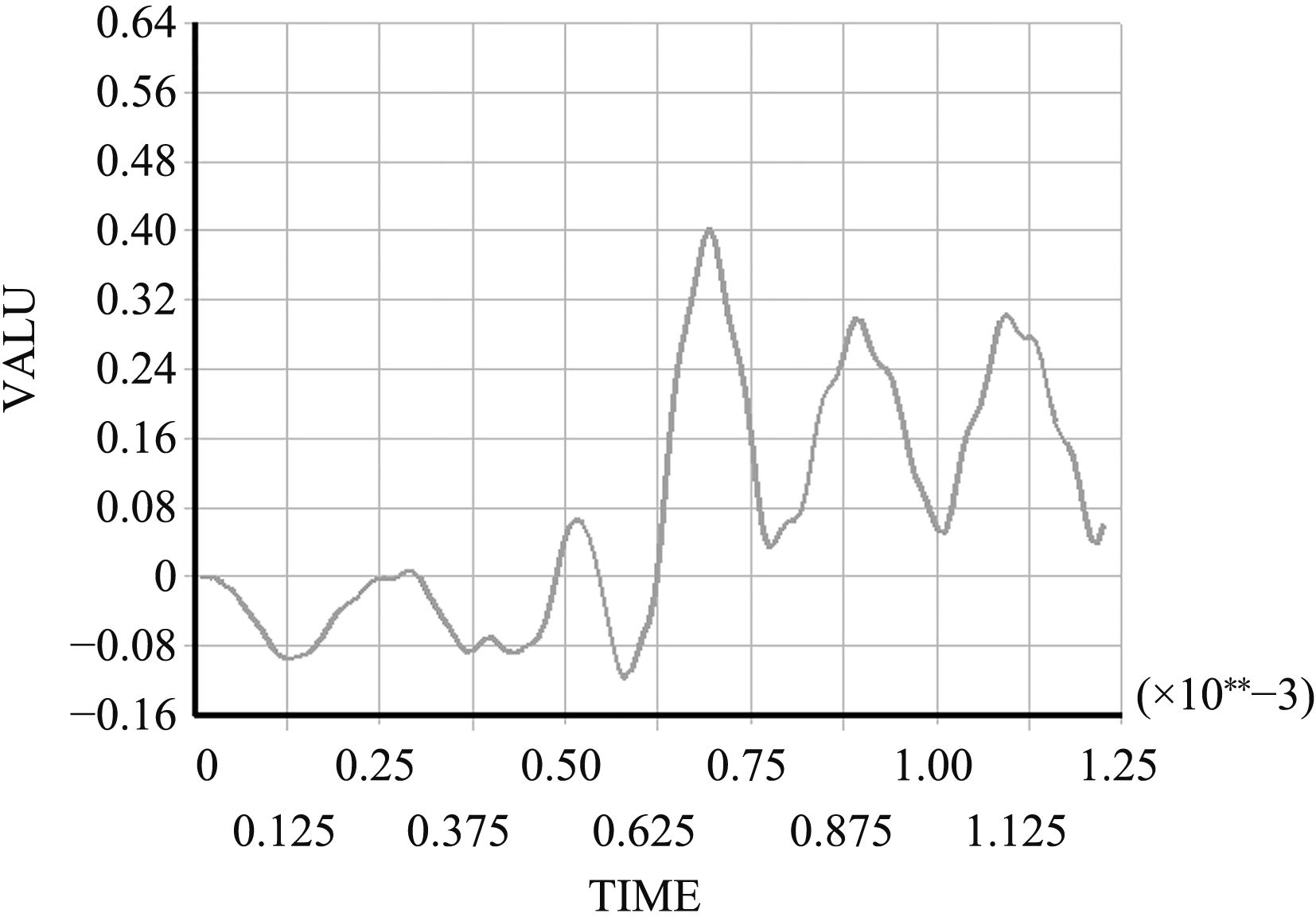
为了计算电枢运动过程中轨道各节点动态响应,对轨道炮导轨表面施加不同移动速度载荷,计算轨道各节点的位移。设置边界条件时,将轨道底面全约束,同时在连接螺栓处施加一定预应力;利用Ansys的宏命令APDL,编解命令流,实现载荷沿着轨道节点向前移动,同时保证载荷经过之处压力一直存在,从而计算出电枢在导轨表面运动时导轨所产生的变形量。在观察结果时,选取轨道的中线上的典型节点(炮尾节点,中间节点,炮口节点)作为研究对象。载荷移动速度为2 500 m/s条件下轨道典型节点位移随时间的变化曲线如图9~图11所示,
|
图 9 载荷移动速度为2 500 m/s时炮尾节点位移随时间的变化曲线 Fig. 9 When the load moving speed is 2 500 m/s, the deformation curve for the displacement of the joints of the gun tail with time |
|
图 10 载荷移动速度为2 500 m/s时中间节点位移随时间的变化曲线 Fig. 10 When the load moving speed is 2 500 m/s, the deformation curve for the displacement of the joints of the middle with time |

|
图 11 载荷移动速度为2 500 m/s时炮口节点位移随时间的变化曲线 Fig. 11 When the load moving speed is 2 500 m/s, the deformation curve for the displacement of the joints of the gun mouth with time |
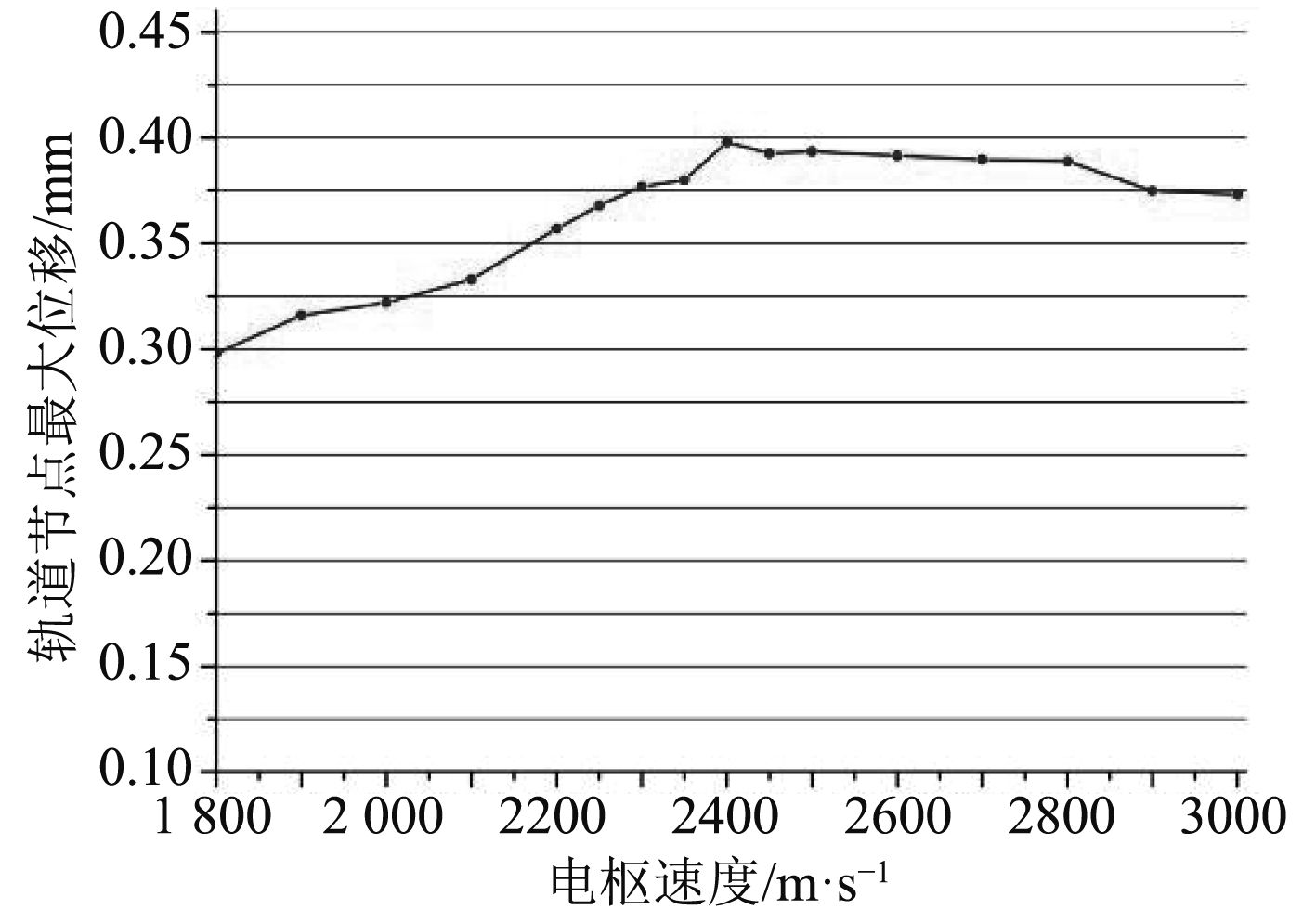
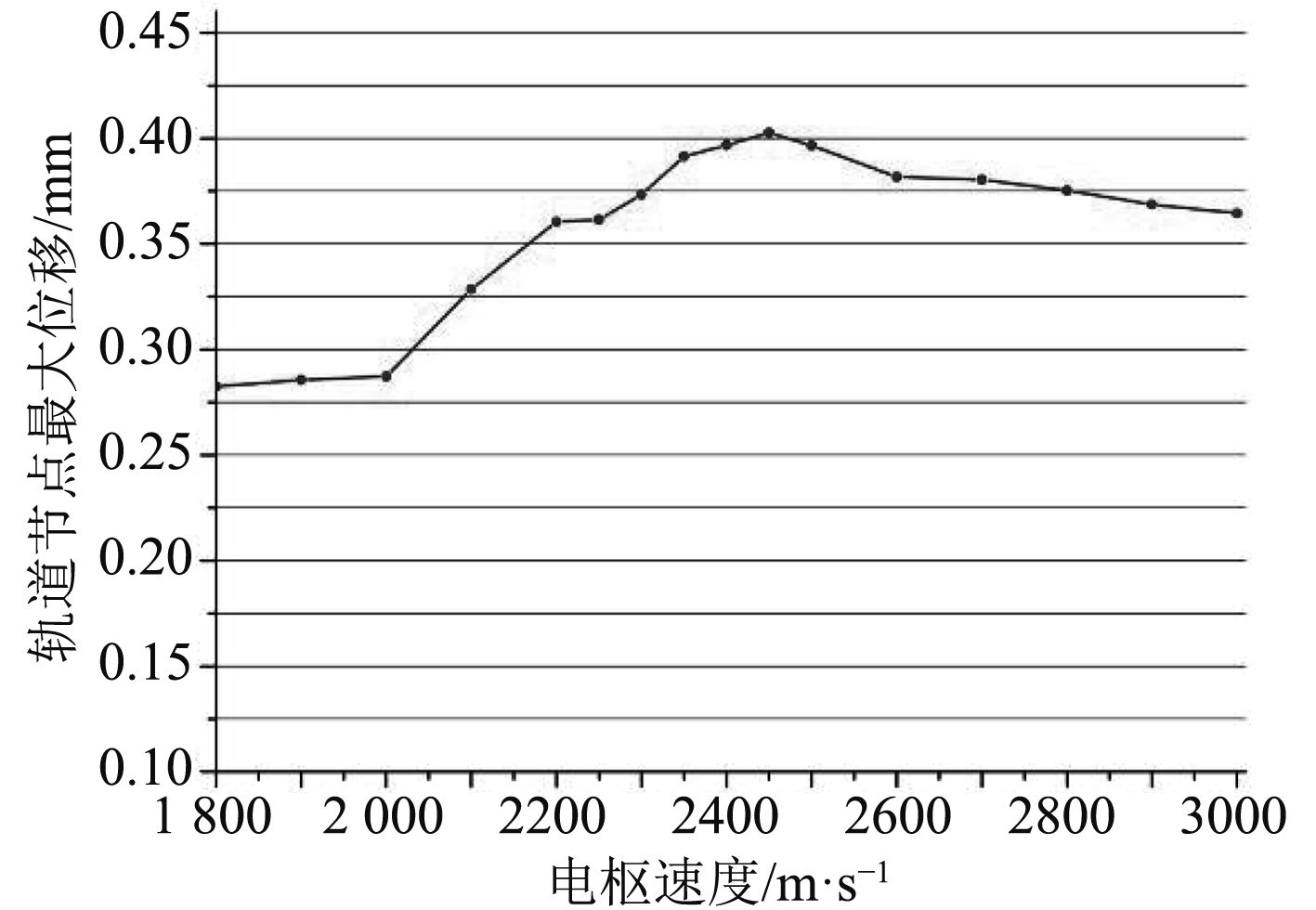
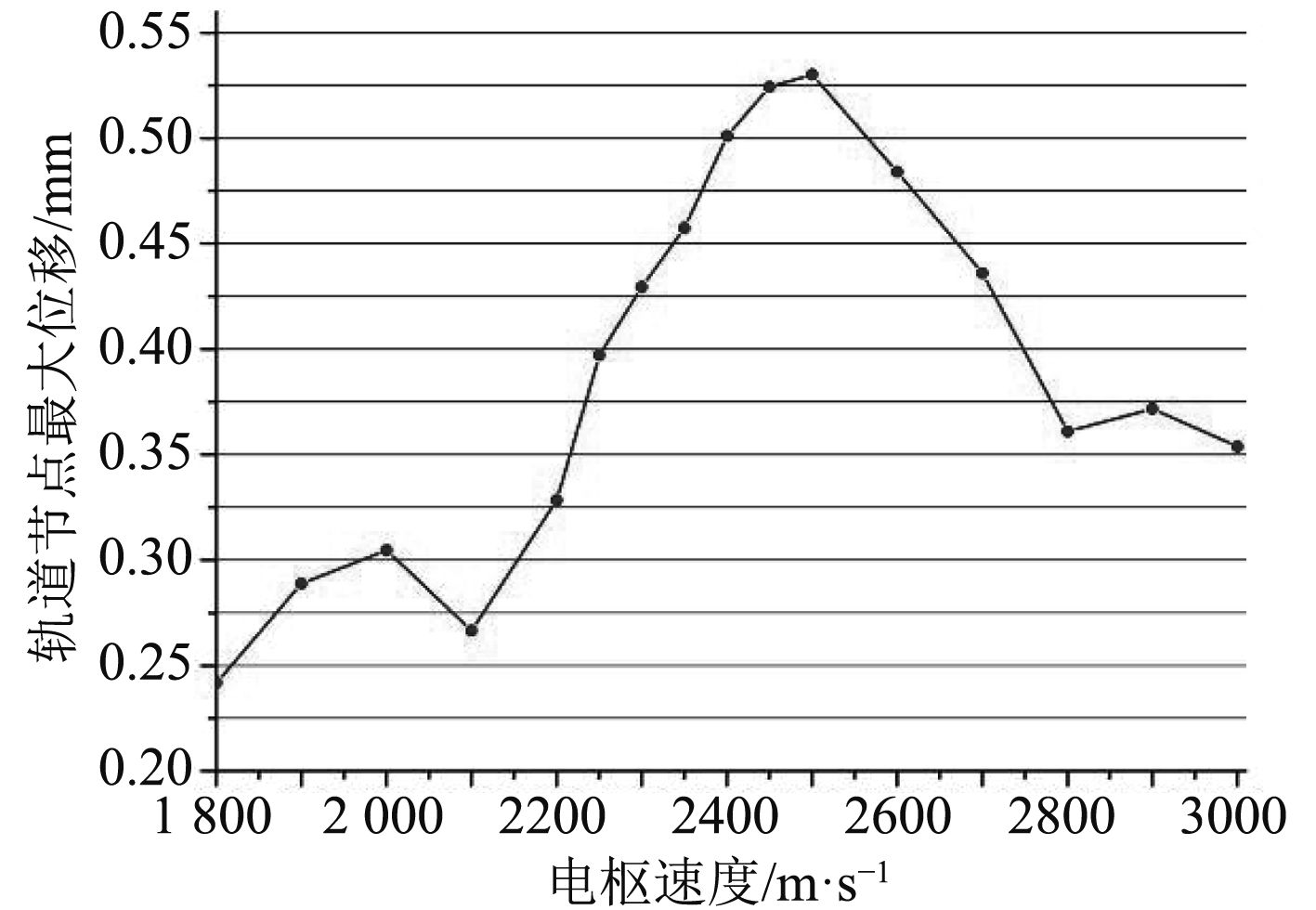
计算不同移动速度载荷时沿轨道中心线布置的炮尾节点、中间节点、炮口节点最大位移如图12~图14所示,其横坐标为移动载荷速度,纵坐标为节点最大位移值。
|
图 12 炮尾节点位移响应随速度变化值 Fig. 12 Deformation value of the displacement response of joints in the gun tail with the speed |
|
图 13 中间节点位移响应随速度变化值 Fig. 13 Deformation value of the displacement response of joints in the middle with the speed |
|
图 14 炮口节点位移响应随速度变化值 Fig. 14 Deformation value of the displacement response of joints in the gun mouth with the speed |
轨道表面各典型节点出计算出的临界速度如表2所示。
|
|
表 2 各典型节点对应临界速度 Tab.2 Corresponding critical speed of the respective typical joints |
由表2可知,该型轨道炮的临界速度约为2 400 m/s~2 500 m/s,与理论临界速度2 265 m/s相差5.96%,结果基本可信,由此可证明该仿真计算方法正确性。
前述分析表明,当移动载荷速度与轨道炮临界速度相等时,轨道表面节点的动位移最大,此时电枢与轨道间接触状态最差,容易发生烧蚀现象,因此为了避免轨道烧蚀,电枢最大发射速度应不大于2 265 m/s。
3 结 语1)轨道炮结构设计过程中一方面要充分考虑临界速度对轨道变形的影响,设计时要尽可能的通过优化轨道炮系统中的各个参数,以提高轨道炮的临界速度,至少要使轨道炮的临界速度大于所预定的炮口初速,从而减少对导轨的烧蚀影响。
2)支撑材料的弹性系数作为影响轨道炮临界速度主要因子,设计时要在其他条件允许的情况下应尽可能地提高该参数数值,从而以最快的方式提高轨道炮的临界速度,得到合理的结构形式。
3)本文的研究成果可为轨道炮结构特性研究奠定基础,为身管优化设计提供参考依据。
| [1] | ZHANG Jian-ge. Research on naval electromagnetic gun in USA[J]. Ship Science and technology, 2009, 31 (3): 154–159. |
| [2] | HARRY D. Fair electromagnetic launch science and technology in the united states enters a new era[J]. IEEE Trans on Magn, 2005, 41 (1): 158–164. DOI: 10.1109/TMAG.2004.838744 |
| [3] | HARRY Fair. Electromagnetic launch[J]. International Journal of Impact Engineering, 2003, 29 (1): 247–262. |
| [4] | JEROME T T. Dynamic response of lectromagnetic railgun due to projectile movement[J]. IEEE Transaction on Magnetics, Vol. 39, No. 1, 472–475, 2003. |
| [5] | TZENG J T. Structural mechanics for electromagnetic railguns[J]. IEEE Transactions on Magnetic, 2005, 41 (1): 246–250. DOI: 10.1109/TMAG.2004.839828 |
| [6] | LIU Zheng-guo, TIAN Fu-qing. Structure dynamic characteristic analysis of electromagnetic rail launcher[J]. Journal of Ship Mechanics, 2010, 14 (10): 1158–1164. |
| [7] | Gaobo. Critical speed analysis for railgun based on ANSYS[J]. Electrical Engineering, 2010 : 13–15. |
| [8] | LEI Xiao-yan. Study on critical velocity and vibration boom of track[J]. Chinese Journal of Geotechnical Engineering, 2006, 28 (3): 419–422. |
 2017, Vol. 39
2017, Vol. 39
